Blast Vibration Control in A Hydropower Station for the Safety of Adjacent Structure
Abstract
:1. Introduction
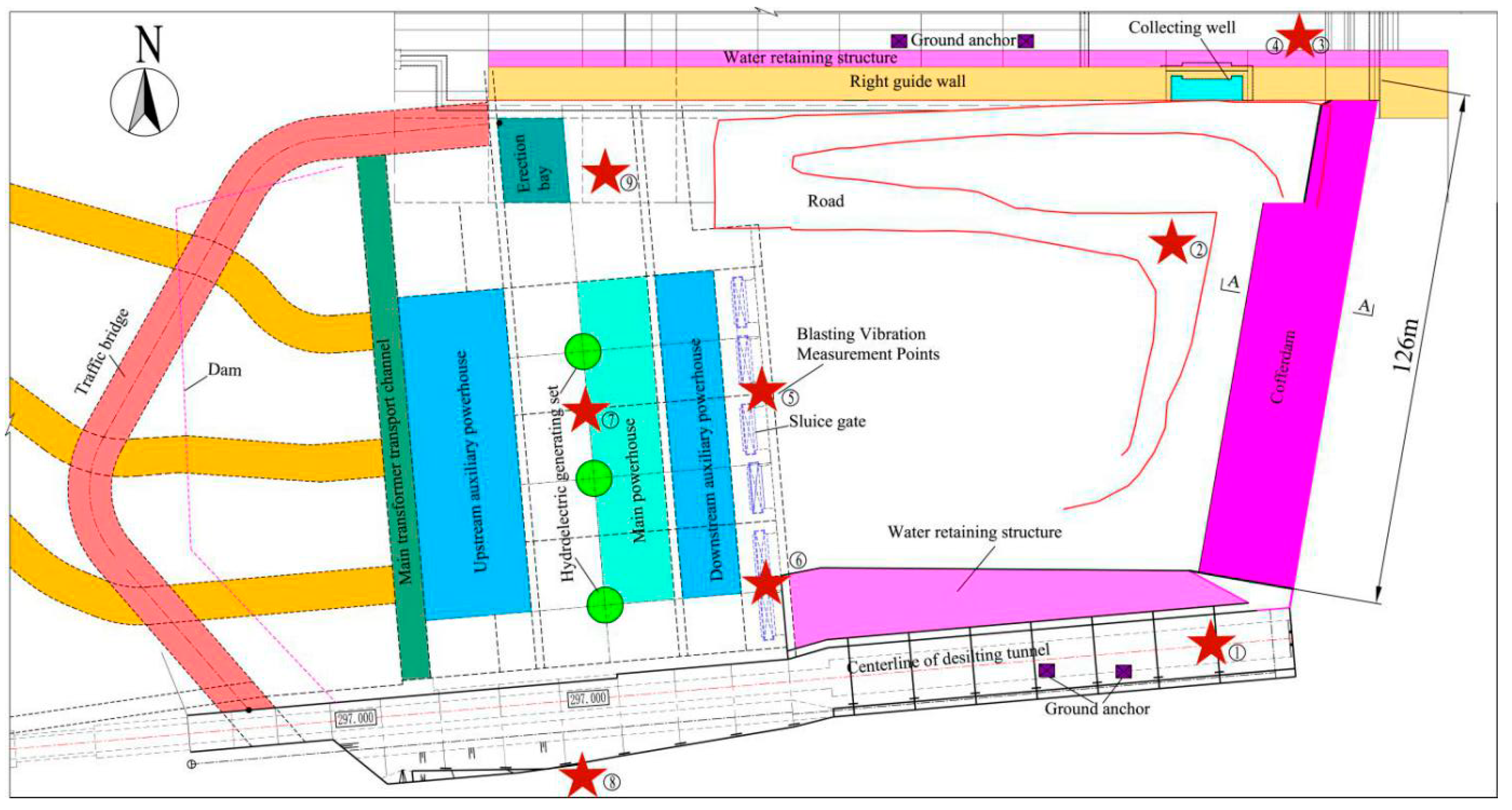
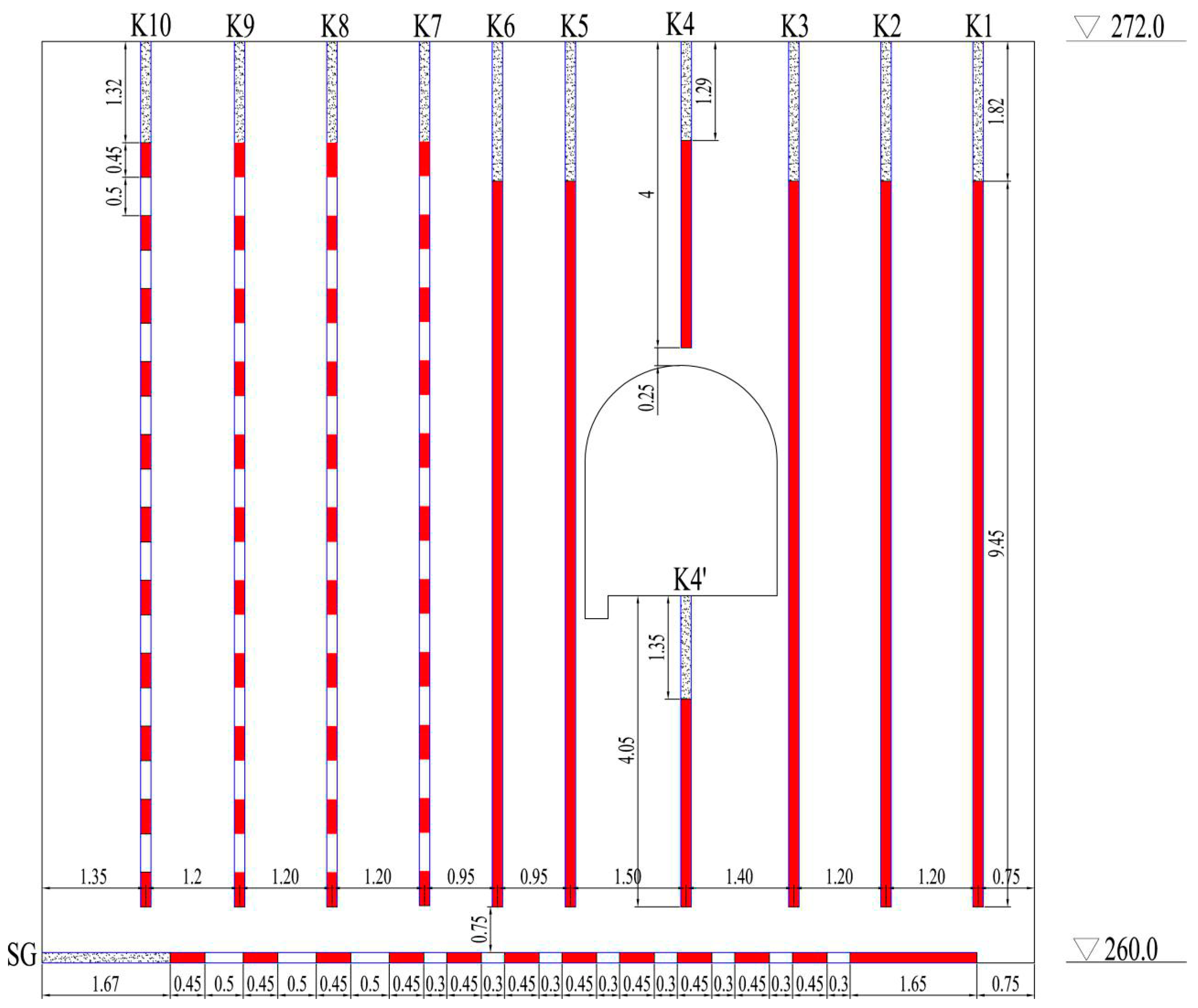
2. Engineering Background
3. Blast Design and Monitoring of Vibration
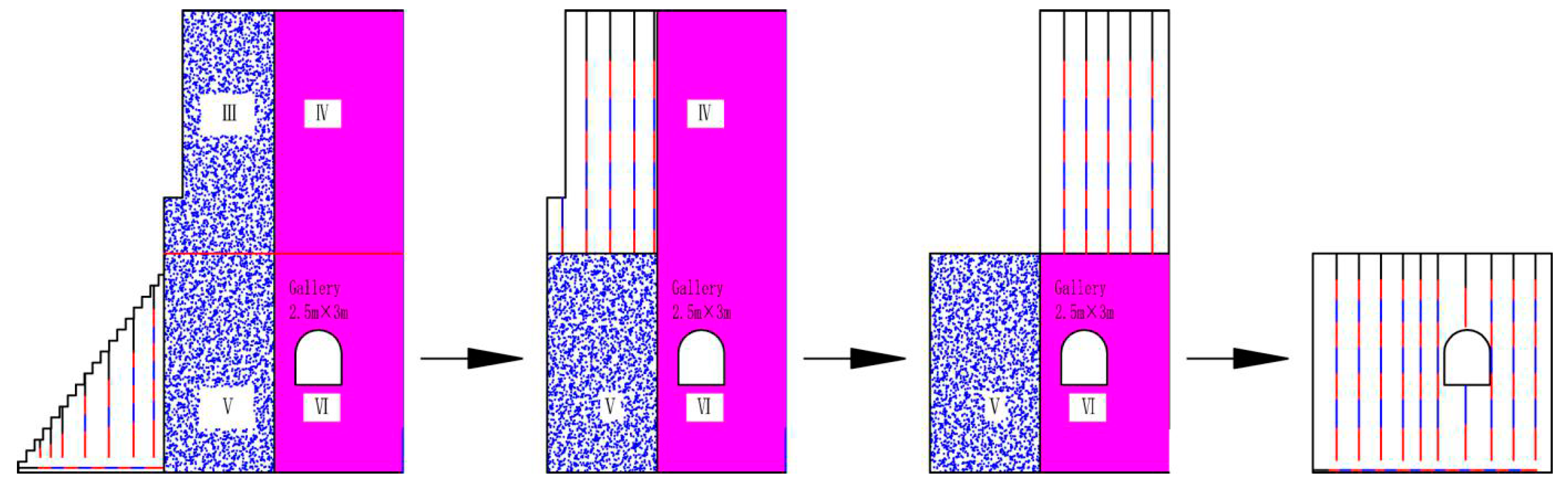
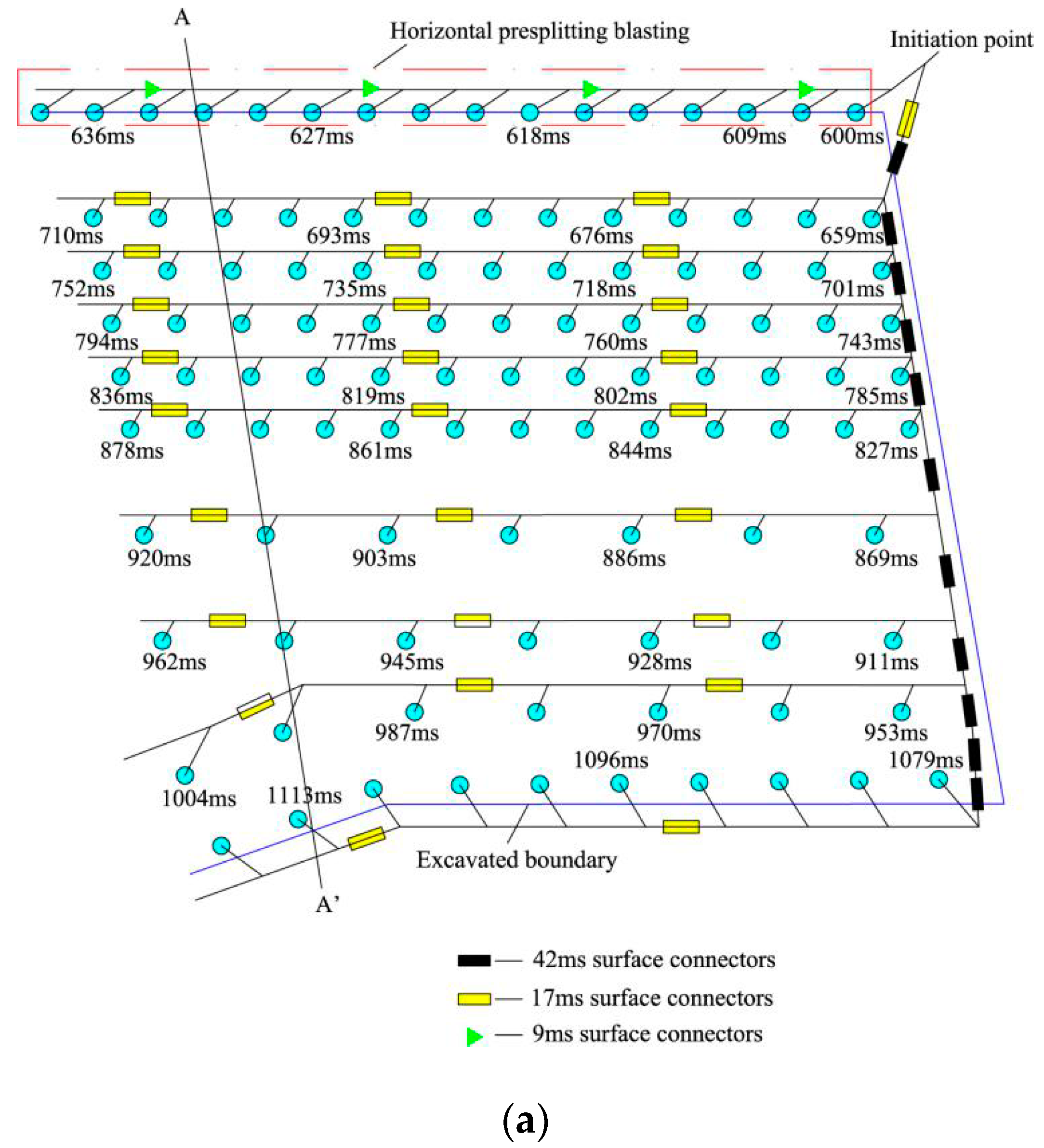
3.1. Blast Design
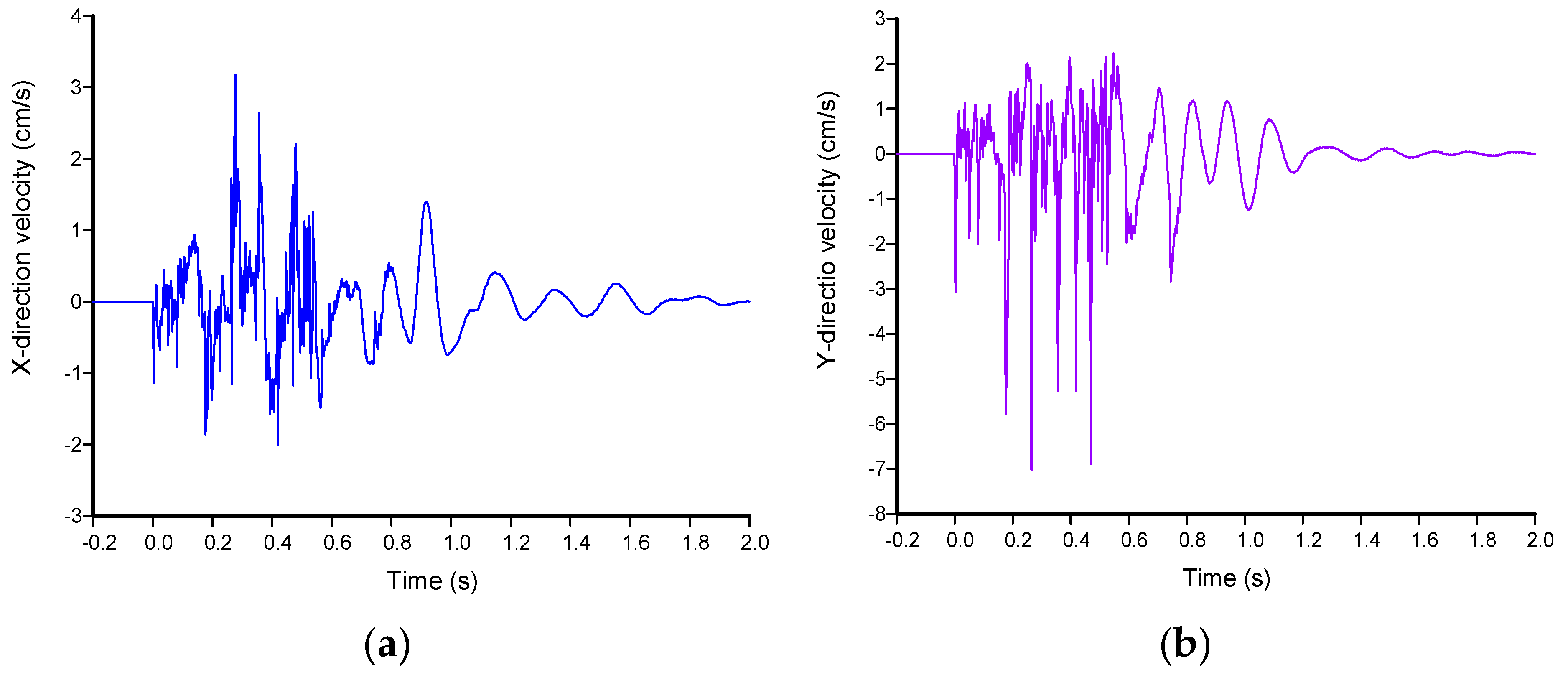
3.2. Monitoring of Vibration
- (1)
- Maximum sampling rate: 200 ksps/channel.
- (2)
- Analog input channel: 1–4 channels/each device, multiple sets can be expanded in parallel.
- (3)
- Acquisition mode: multi-channel parallel acquisition.
- (4)
- Input signal bandwidth: 0–20 KHz.
- (5)
- Dc accuracy error: ≤±0.5%.
- (6)
- Amplitude range: 0.001–35.5 cm/s.
4. Discussions
5. Conclusions
- (1)
- The transverse cofferdam of Xiangjiaba hydropower station was divided into six regions based on its structural features, which consisted of masonry, PC, and RCC. The maximum explosives charge weight per delay in the masonry structure, PC, and RCC above water were 26.4 kg, 28 kg, and 28.5 kg. The PPV reached 8.741 cm/s, 4.479 cm/s, and 3.878 cm/s, respectively.
- (2)
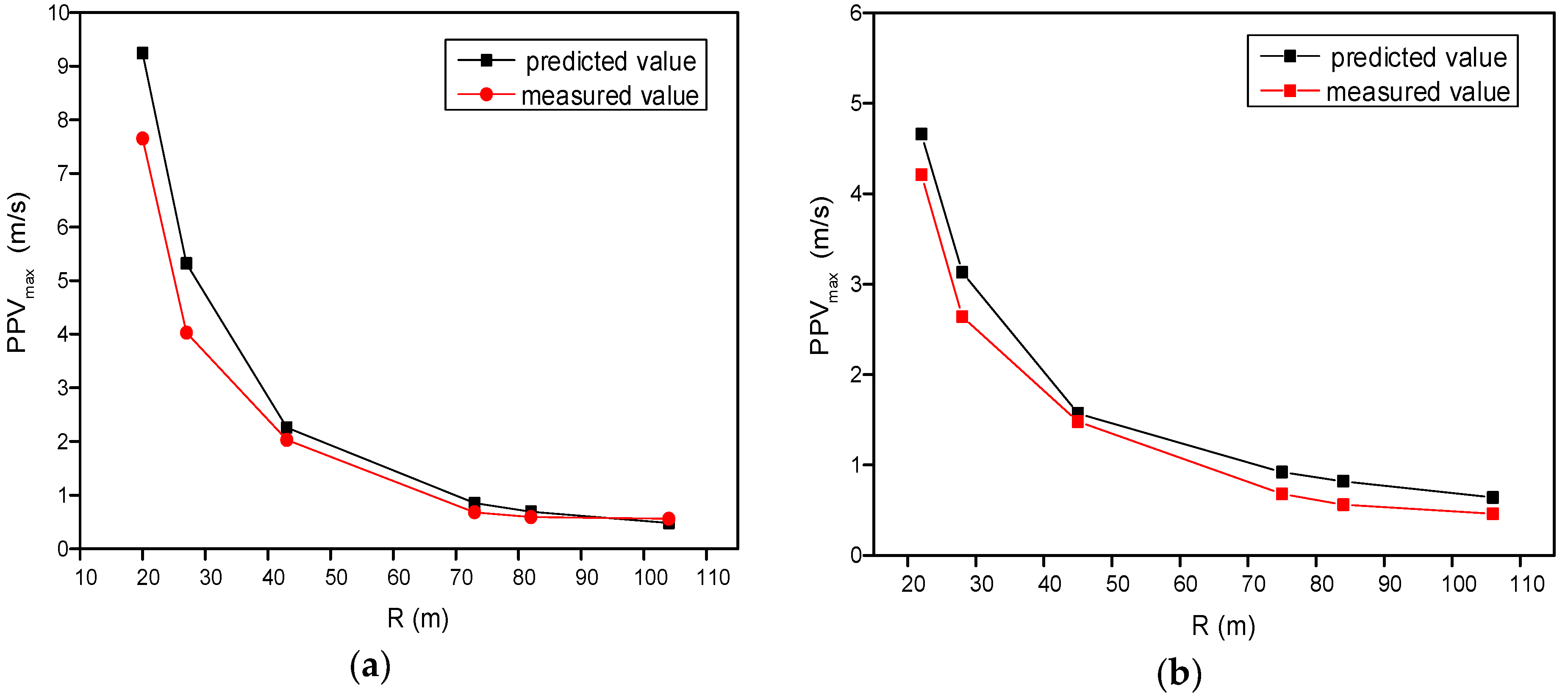
- The attenuation law of PPV land blasting was revealed in different structures through the blast-induced vibration data, and then the prediction formulas of explosives charge weight per delay in PC and RCC structures were put forward combining Newton’s third law.
- (3)
- Considering permissible blast-induced vibration values of adjacent structures in Xiangjiaba hydropower station, the maximum permissible explosives charge weight per delay in PC and RCC underwater structures were calculated by the prediction formulas, which were 67 kg and 27 kg, respectively.
- (4)
- The actual explosives per delay in PC and RCC underwater structures were 54 kg and 23.4 kg, respectively, where the PPV was 7.65 cm/s and 4.21 cm/s. Both of them were less than the maximum allowable values. Simultaneously, the prediction formulas were proven to meet the blast requirements by the analysis of MAPE. Consequently, the PPV underwater blasting could be predicted by analyzing the PPV of land blasting in same structure, which provided the basis for the design of underwater blasting parameters. A reliable method for cofferdam demolition in hydropower stations was proposed, which provided a reference for similar projects.
Author Contributions
Funding
Conflicts of Interest
References
- Xia, X.; Li, H.B.; Liu, Y.Q.; Yu, C. A case study on the cavity effect of a water tunnel on the ground vibrations induced by excavating blasts. Tunn. Undergr. Space Technol. 2018, 71, 292–297. [Google Scholar] [CrossRef]
- Avellan, K.; Belopotocanova, E.; Puurunen, M. Measuring, monitoring and prediction of vibration effects in rock masses in near-structure blasting. Procedia Eng. 2017, 191, 504–511. [Google Scholar] [CrossRef]
- Jiang, N.; Gao, T.; Zhou, C.; Luo, X. Effect of excavation blasting vibration on adjacent buried gas pipeline in a metro tunnel. Tunn. Undergr. Space Technol. 2018, 81, 590–601. [Google Scholar] [CrossRef]
- Lu, W.; Leng, Z.; Hu, H.; Chen, M.; Wang, G. Experimental and numerical investigation of the effect of blast-generated free surfaces on blasting vibration. Eur. J. Environ. Civ. Eng. 2016, 22, 1374–1398. [Google Scholar] [CrossRef]
- Qiu, X.; Shi, X.; Gou, Y.; Zhou, J.; Chen, H.; Huo, X. Short-delay blasting with single free surface: Results of experimental tests. Tunn. Undergr. Space Technol. 2018, 74, 119–130. [Google Scholar] [CrossRef]
- Tripathy, G.; Shirke, R.; Kudale, M. Safety of engineered structures against blast vibrations: A case study. J. Rock Mech. Geotech. Eng. 2016, 8, 248–255. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, H.; Mishra, A. Modified scaled distance regression analysis approach for prediction of blast-induced ground vibration in multi-hole blasting. J. Rock Mech. Geotech. Eng. 2019, 11, 202–207. [Google Scholar] [CrossRef]
- Blair, D. Blast vibration dependence on charge length, velocity of detonation and layered media. Int. J. Rock Mech. Min. Sci. 2014, 65, 29–39. [Google Scholar] [CrossRef]
- Blair, D. The free surface influence on blast vibration. Int. J. Rock Mech. Min. Sci. 2015, 77, 182–191. [Google Scholar] [CrossRef]
- Xia, Y.; Jiang, N.; Zhou, C.; Luo, X. Safety assessment of upper water pipeline under the blasting vibration induced by Subway tunnel excavation. Eng. Fail Anal. 2019, 104, 626–642. [Google Scholar] [CrossRef]
- Uysal, O.; Erarslan, K.; Cebi, M.A.; Akcakoca, H. Effect of barrier holes on blast induced vibration. Int. J. Rock Mech. Min. Sci. 2008, 45, 712–719. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, H.; Xia, X.; Liu, B.; Zuo, H.; Jiang, J. Blast-induced rock damage control in Fangchenggang nuclear power station, China. J. Rock Mech. Geotech. Eng. 2018, 10, 914–923. [Google Scholar] [CrossRef]
- Roy, M.P.; Singh, P.K.; Sarim, M.; Shkhawat, L.S. Blast design and vibration control at an underground metal mine for the safety of surface structures. Int. J. Rock Mech. Min. Sci. 2016, 83, 107–115. [Google Scholar] [CrossRef]
- Kim, J.-G.; Song, J.-J. Abrasive water jet cutting methods for reducing blast-induced ground vibration in tunnel excavation. Int. J. Rock Mech. Min. Sci. 2015, 75, 147–158. [Google Scholar] [CrossRef]
- Ongen, T.; Karakuş, D.; Konak, G.; Onur, A.H. Assessment of blast-induced vibration using various estimation models. J. Afr. Earth Sci. 2018, 145, 267–273. [Google Scholar] [CrossRef]
- Navarro Torres, V.F.; Leandro, G.C.S.; Paulo, F.T.L.; Hernani, M.L. Assessing and controlling of bench blasting-induced vibrations to minimize impacts to a neighboring community. J. Clean. Prod. 2018, 187, 514–524. [Google Scholar] [CrossRef]
- Yang, G.L. Discussion on blasting removal technology of concrete guide wall in Xiangjiaba Hydrppower station. Yangtze River 2015, 46, 37–39. (In Chinese) [Google Scholar]
- GB6722-2014 Safety Regulations for Blasting; Standards Press of China: Beijing, China, 2014. (In Chinese)
- Zhao, G. Study on Technology of the Cofferdam Demolition Blasting in Deep Water Conditions. Ph.D. Thesis, University of Science and Technology of China, Hefei, China, 2008. (In Chinese). [Google Scholar]
- Shao, W.; Wang, C.B. Study on vibration characteristics and attention law of underwater blasting. Eng. Blasting 2018, 24, 15–22. (In Chinese) [Google Scholar]




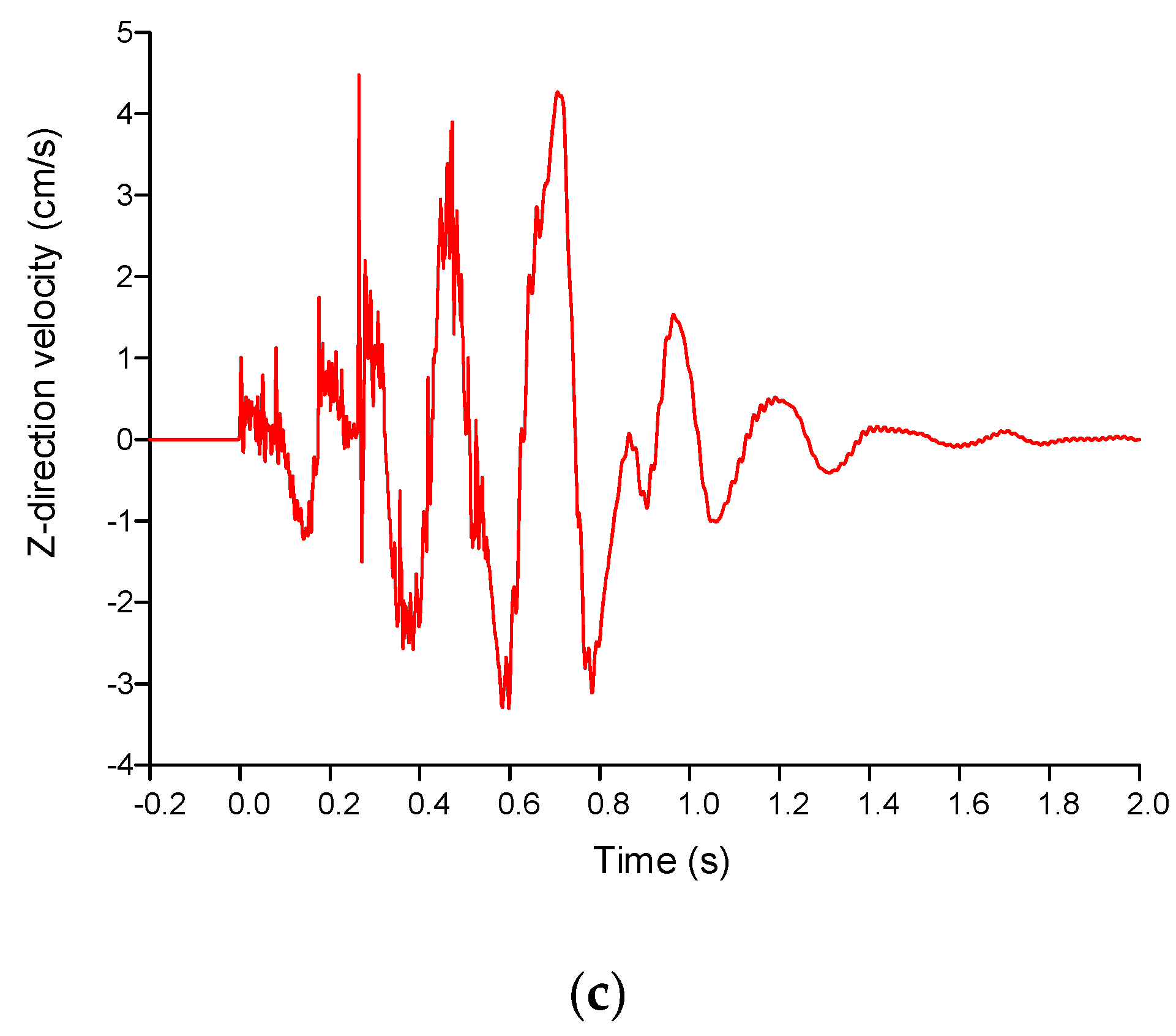
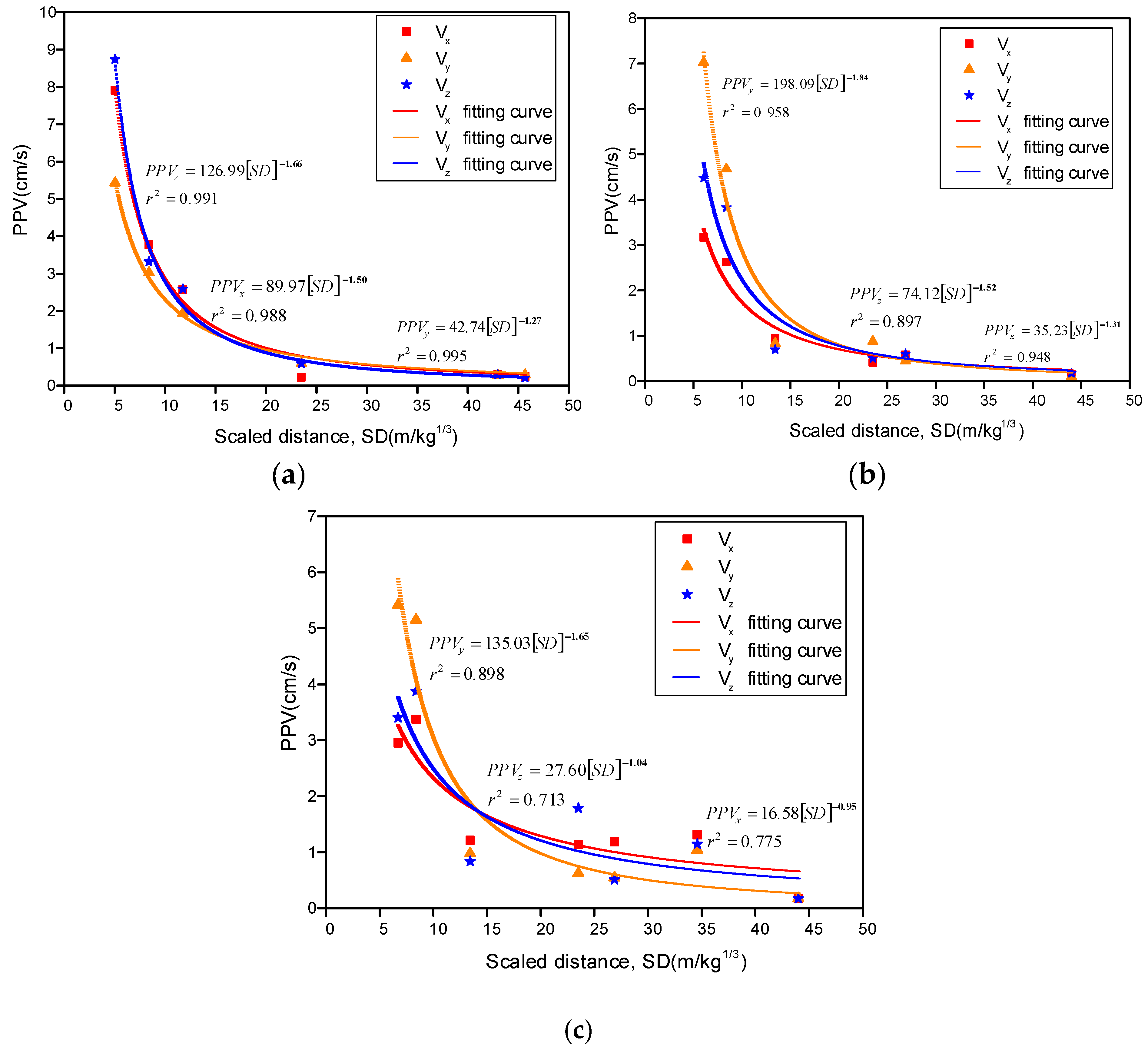

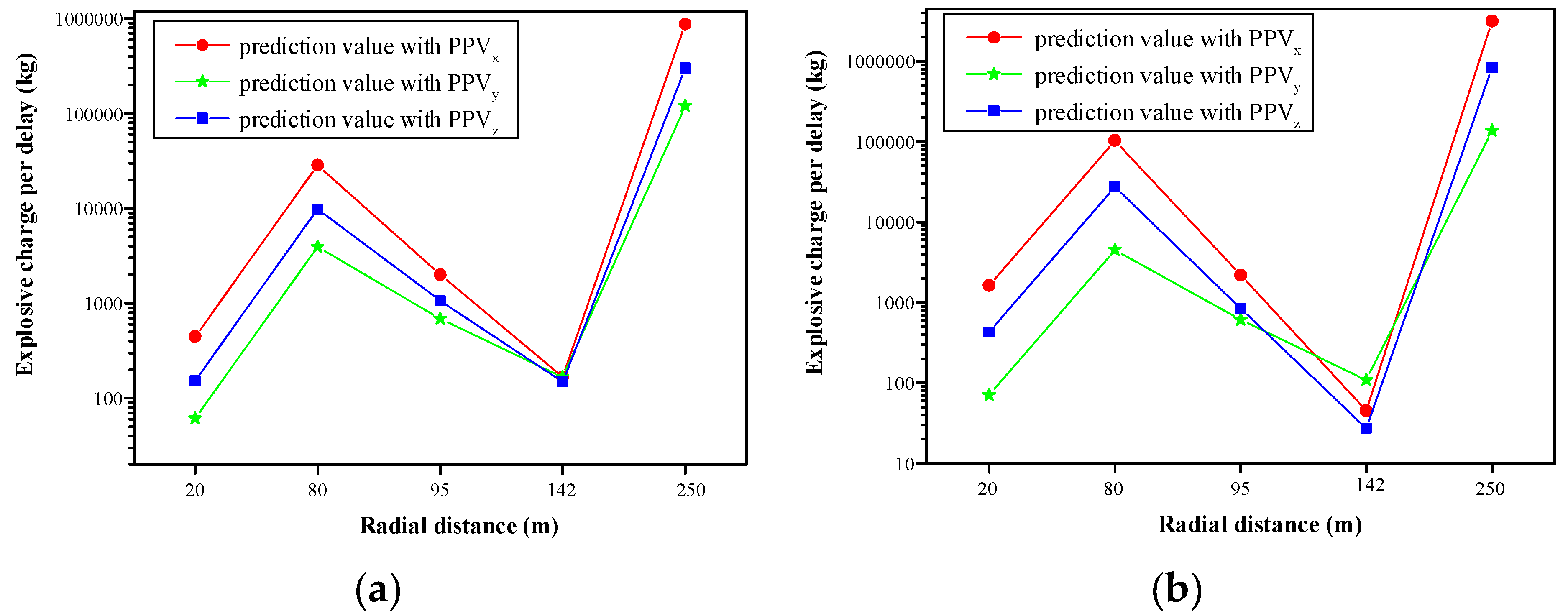
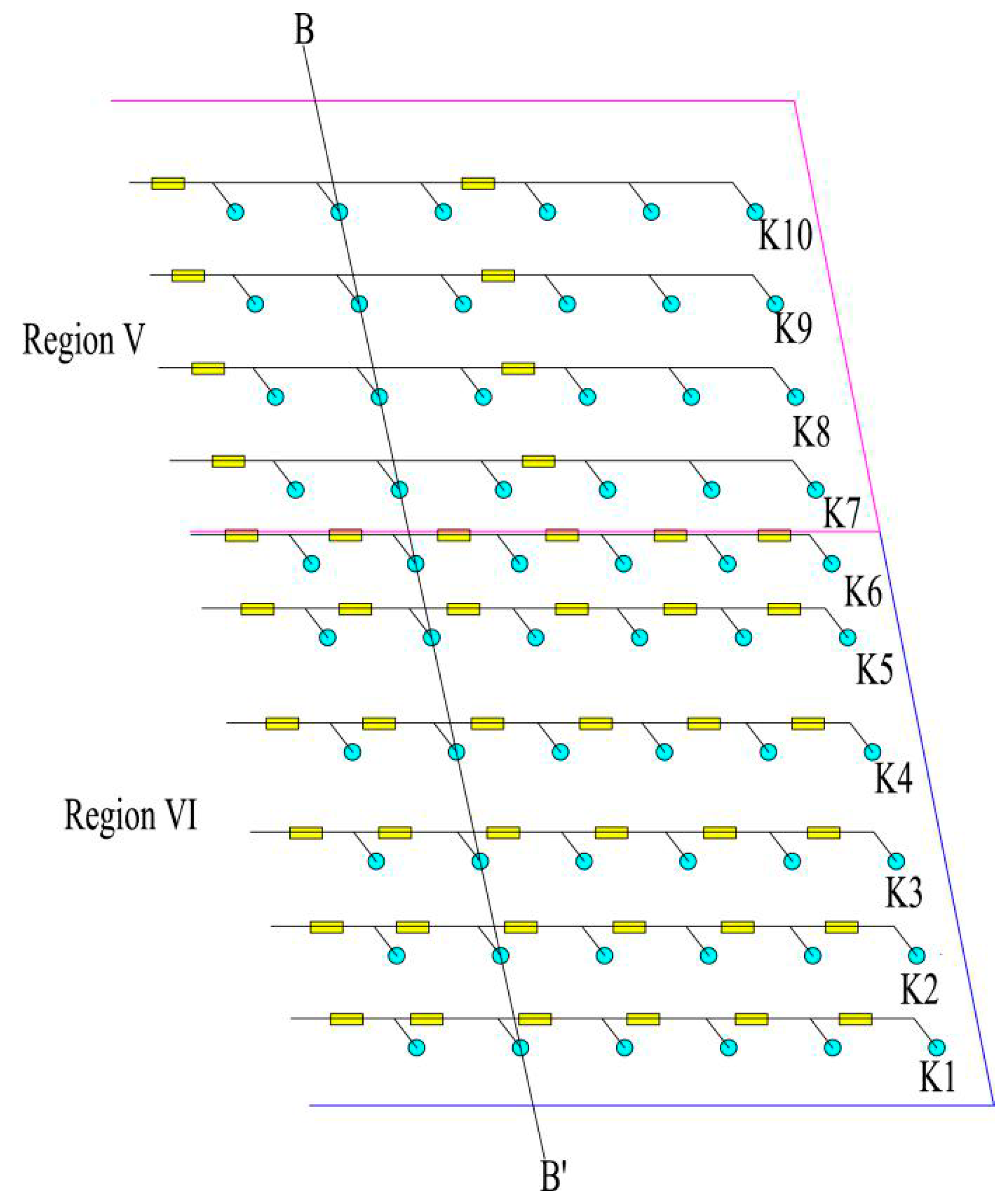
| Region | Shot No. | Charge Weight Per Delay (kg) | Total Charge Weight (kg) | Radial Distance (m) | Longitudinal Velocity (cm/s) | Transversal Velocity (cm/s) | Vertical Velocity (cm/s) |
|---|---|---|---|---|---|---|---|
| I | 1 | 26.4 | 2337.6 | 15 | 7.909 | 5.431 | 8.741 |
| 2 | 26.4 | 2337.6 | 70 | 0.224 | 0.591 | 0.588 | |
| 3 | 26.4 | 2337.6 | 25 | 3.772 | 3.025 | 3.318 | |
| 5 | 26.4 | 2337.6 | 35 | 2.567 | 1.943 | 2.588 | |
| 7 | 26.4 | 2337.6 | 128 | 0.296 | 0.278 | 0.289 | |
| 8 | 26.4 | 2337.6 | 136 | 0.238 | 0.289 | 0.209 | |
| III | 1 | 28 | 2578.9 | 18 | 3.168 | 7.027 | 4.479 |
| 2 | 28 | 2578.9 | 70 | 0.411 | 0.88 | 0.506 | |
| 3 | 28 | 2578.9 | 25 | 2.625 | 4.678 | 3.828 | |
| 4 | 28 | 2578.9 | 80 | 0.581 | 0.45 | 0.601 | |
| 5 | 28 | 2578.9 | 40 | 0.947 | 0.831 | 0.695 | |
| 8 | 28 | 2578.9 | 131 | 0.153 | 0.096 | 0.178 | |
| IV | 1 | 28.5 | 4724.8 | 20 | 2.955 | 5.415 | 3.408 |
| 2 | 28.5 | 4724.8 | 70 | 1.139 | 0.623 | 1.786 | |
| 3 | 28.5 | 4724.8 | 25 | 3.378 | 5.149 | 3.878 | |
| 4 | 28.5 | 4724.8 | 80 | 1.188 | 0.544 | 0.509 | |
| 5 | 28.5 | 4724.8 | 40 | 1.213 | 0.976 | 0.837 | |
| 6 | 28.5 | 4724.8 | 103 | 1.311 | 1.041 | 1.147 | |
| 8 | 28.5 | 4724.8 | 131 | 0.175 | 0.176 | 0.172 |
| Regions | h (m) | [σ] (MPa) | α | ρ1 (kg/m3) | CP1 (m/s) | ρ2 (kg/m3) | CP2 (kg/m3) | Q2/Q1 |
|---|---|---|---|---|---|---|---|---|
| V | 6 | 1.05 | 3 | 2400 | 2700 | 1000 | 1500 | 1.69 |
| VI | 6 | 1.65 | 2 | 2560 | 3000 | 1000 | 1500 | 1.91 |
| Location | PPVlimit (cm/s) | Radial Distance (m) | Explosive Charge Weight Per Delay (kg) | |
|---|---|---|---|---|
| Region V | Region VI | |||
| Concrete structure | <10 | 250 | 120,052 | 137,560 |
| Grouting of dam foundation, stilling basin and factory building | <2.5 | 95 | 687 | 606 |
| Rock mass-infrastructure surface | <10 | 20 | 61 | 70 |
| Stilling basin foundation | <10 | 80 | 3933 | 4507 |
| Precision control instrument (underground power house) | <0.5 | 142 | 148 | 27 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Liu, C.; Wang, P.; Zhu, J.; Zhou, X. Blast Vibration Control in A Hydropower Station for the Safety of Adjacent Structure. Appl. Sci. 2020, 10, 6195. https://doi.org/10.3390/app10186195
Ma Y, Liu C, Wang P, Zhu J, Zhou X. Blast Vibration Control in A Hydropower Station for the Safety of Adjacent Structure. Applied Sciences. 2020; 10(18):6195. https://doi.org/10.3390/app10186195
Chicago/Turabian StyleMa, Yuanjun, Changwu Liu, Ping Wang, Jun Zhu, and Xianliang Zhou. 2020. "Blast Vibration Control in A Hydropower Station for the Safety of Adjacent Structure" Applied Sciences 10, no. 18: 6195. https://doi.org/10.3390/app10186195





