Qualitative Prediction Model for Dynamic Behavior of Ballasted Tracks
Abstract
:1. Introduction
2. Qualitative Analysis
2.1. Qualitative Analysis for Track Engineering
2.2. Application of Qualitative Analysis to Track Dynamics
3. Field Measurements
4. Results and Discussion
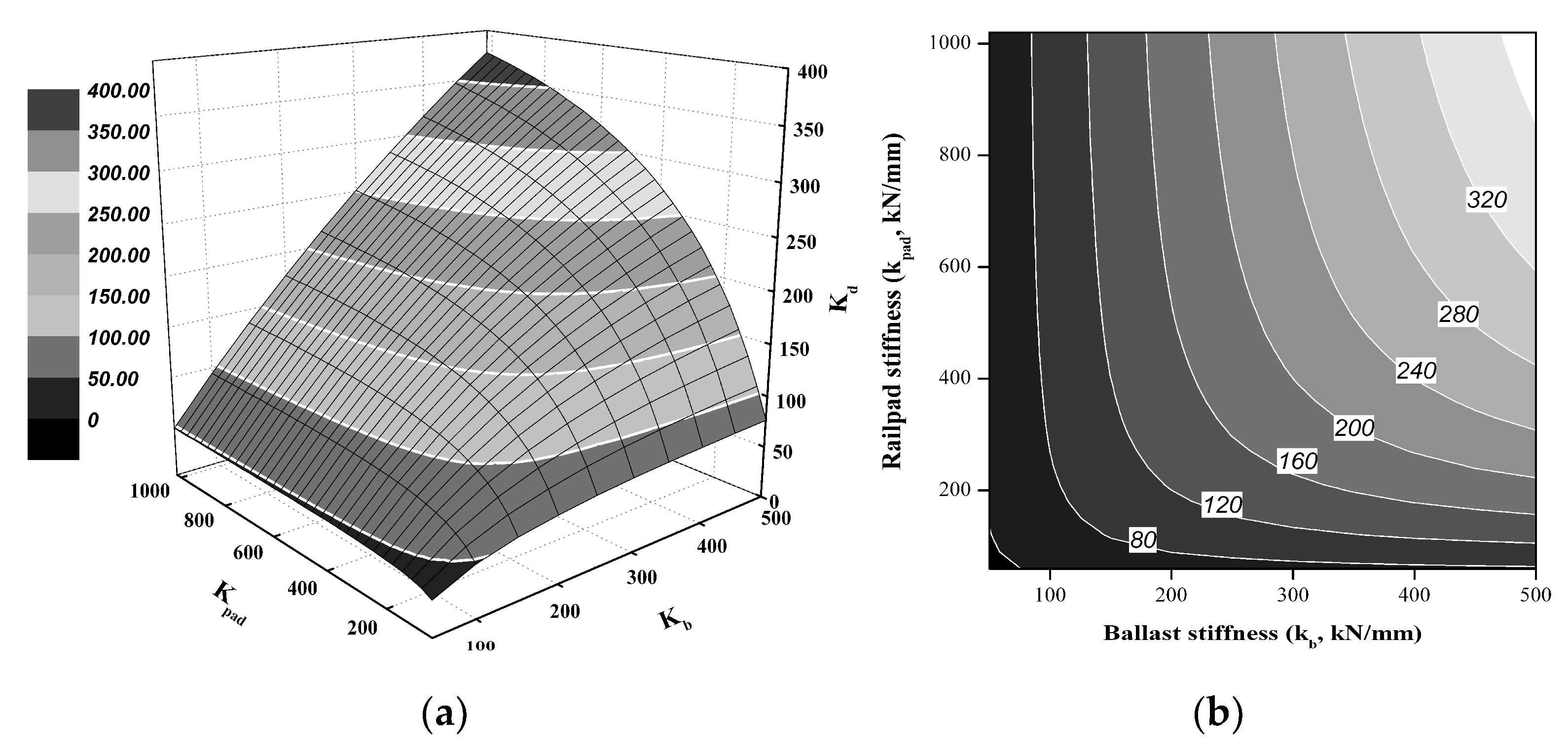
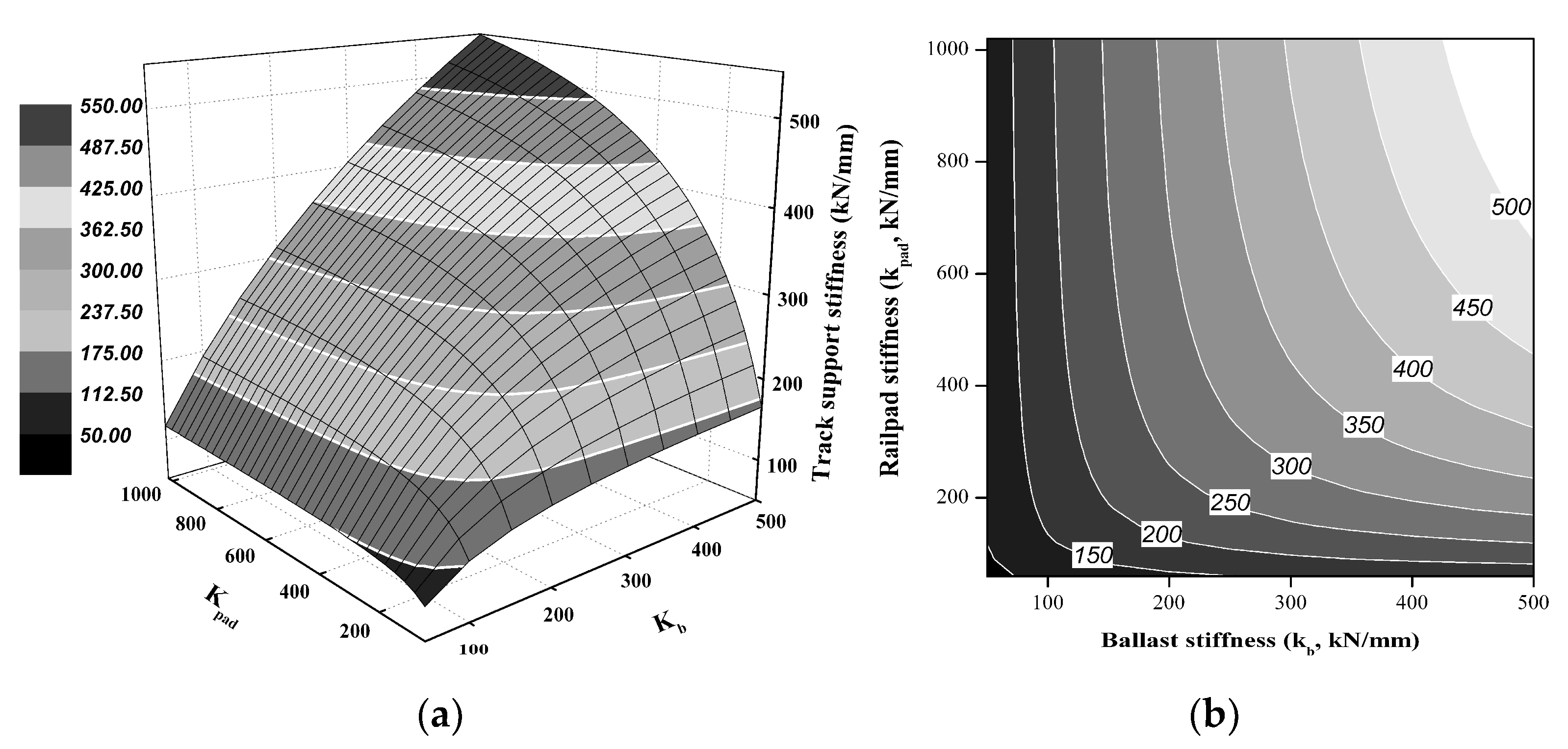
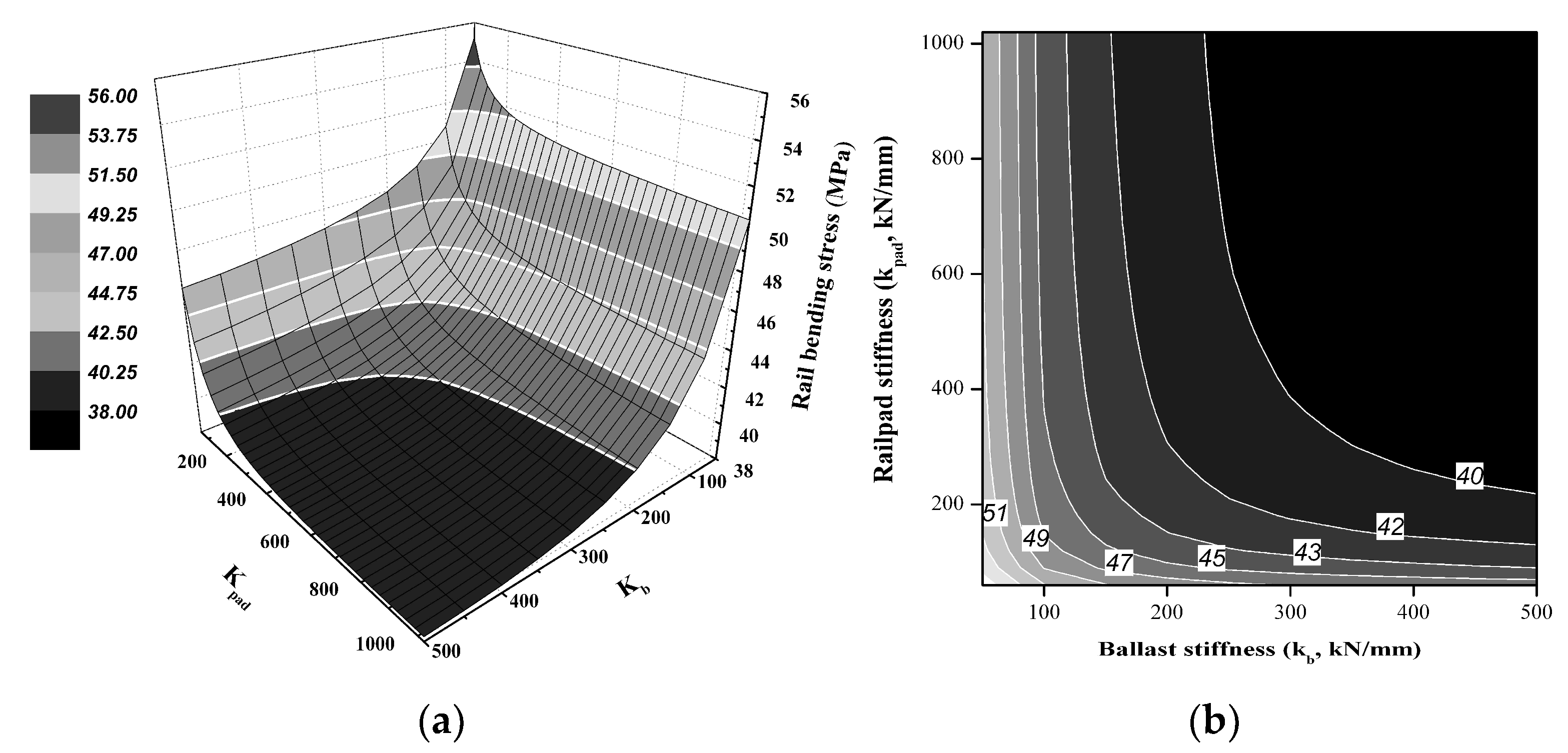
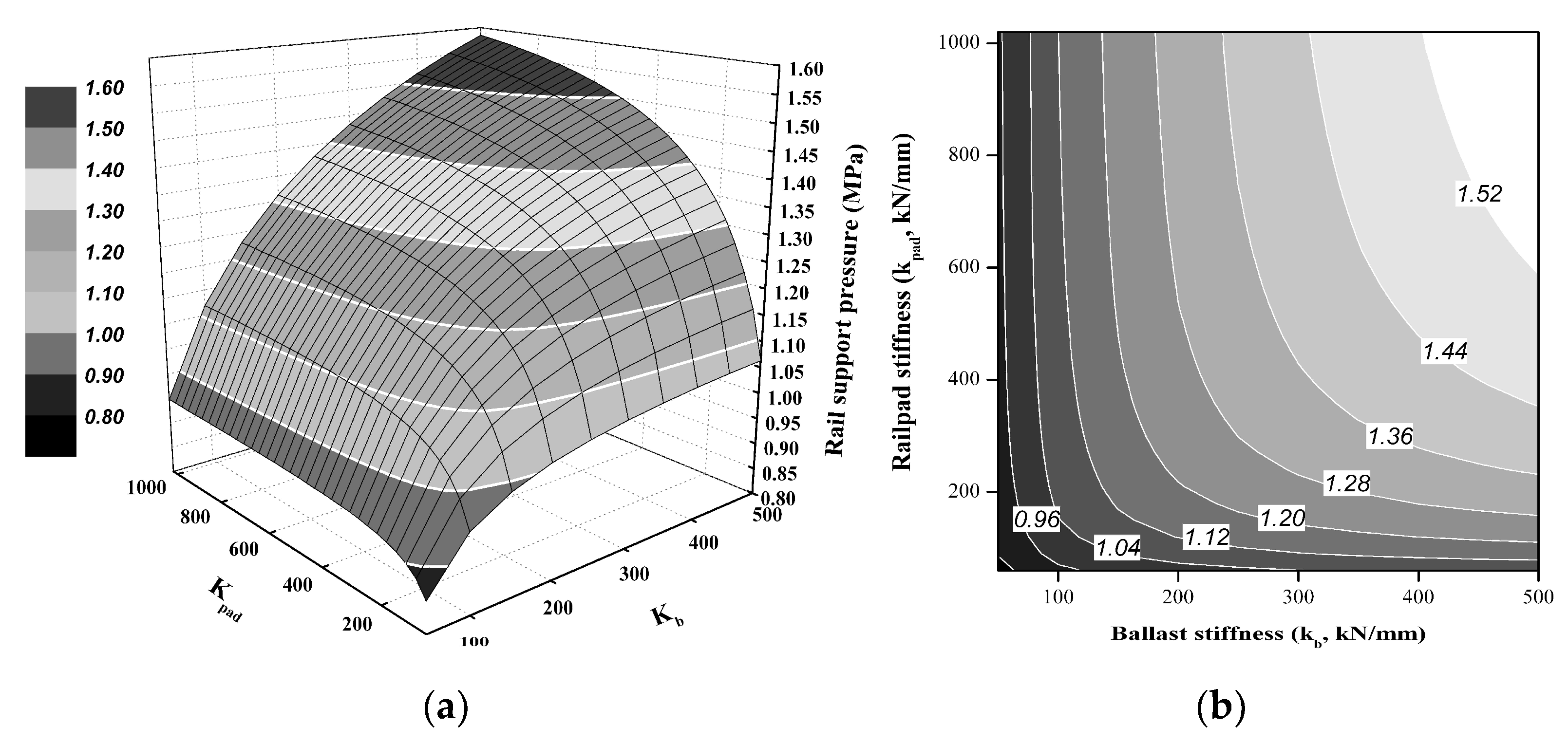
4.1. Assessment of the Track Parameters Using the Proposed Qualitative Analysis
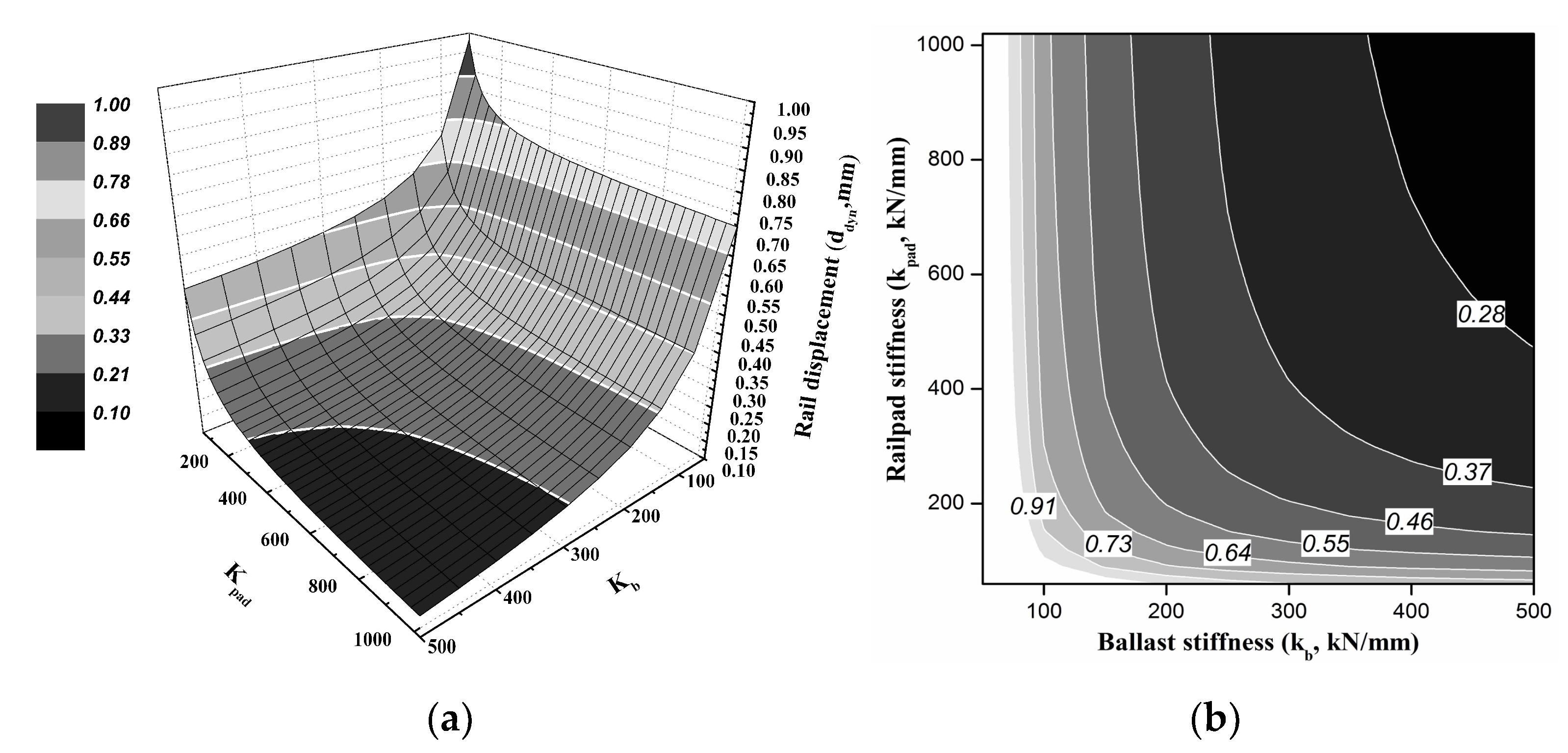
4.2. Assessment of the Dynamic Track Responses Using Qualitative Analysis
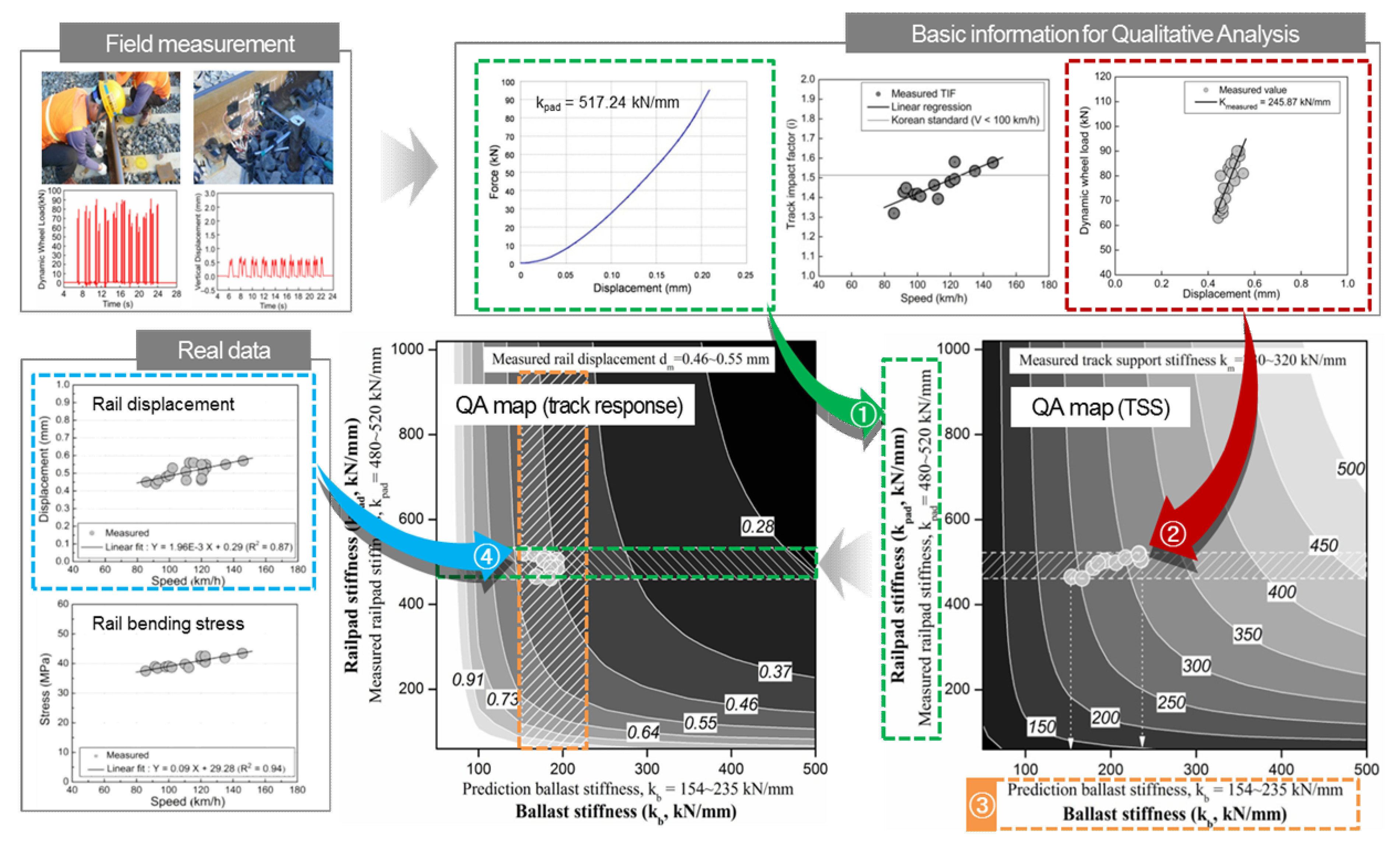
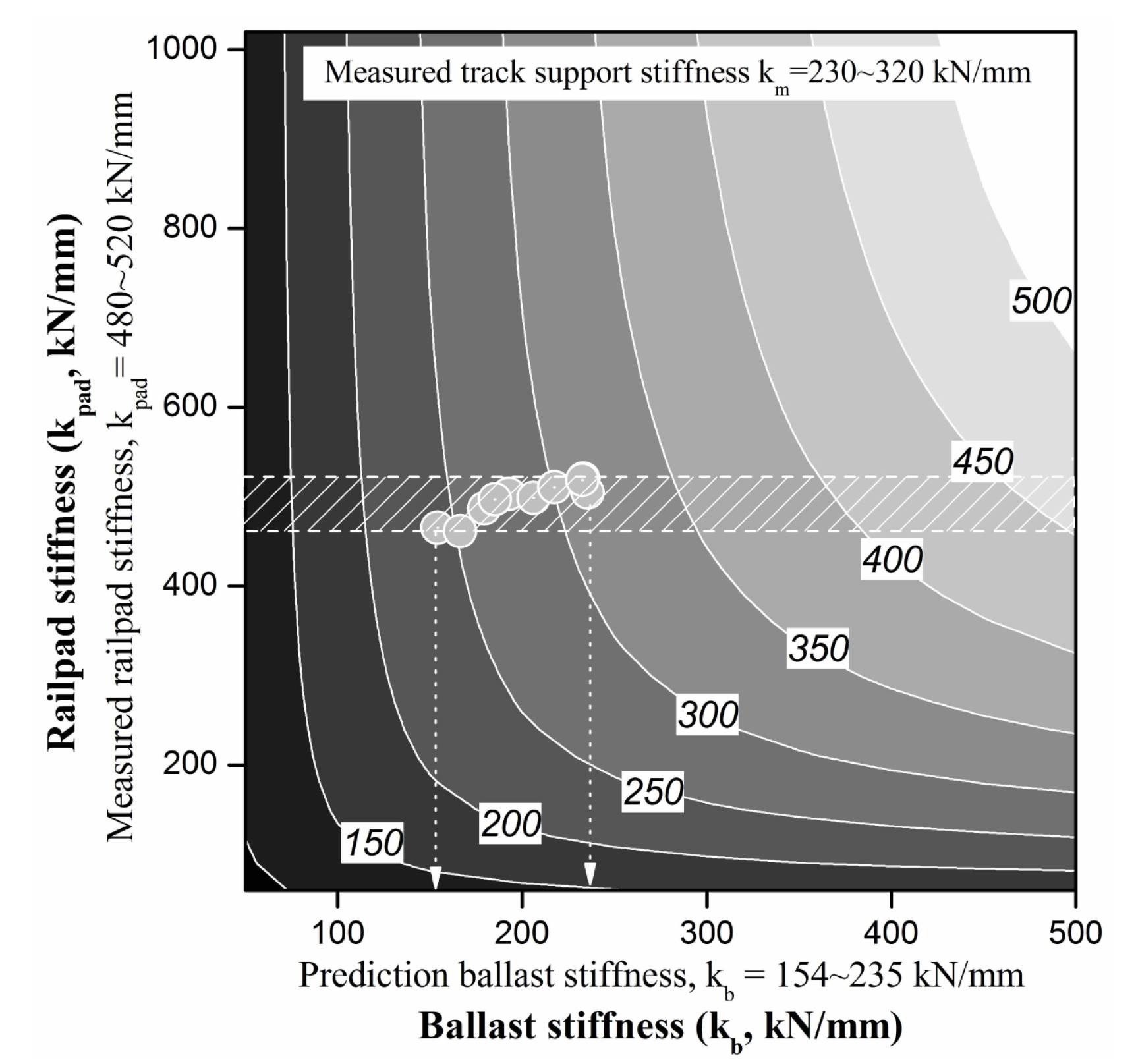
4.3. Validation of Proposed QPM
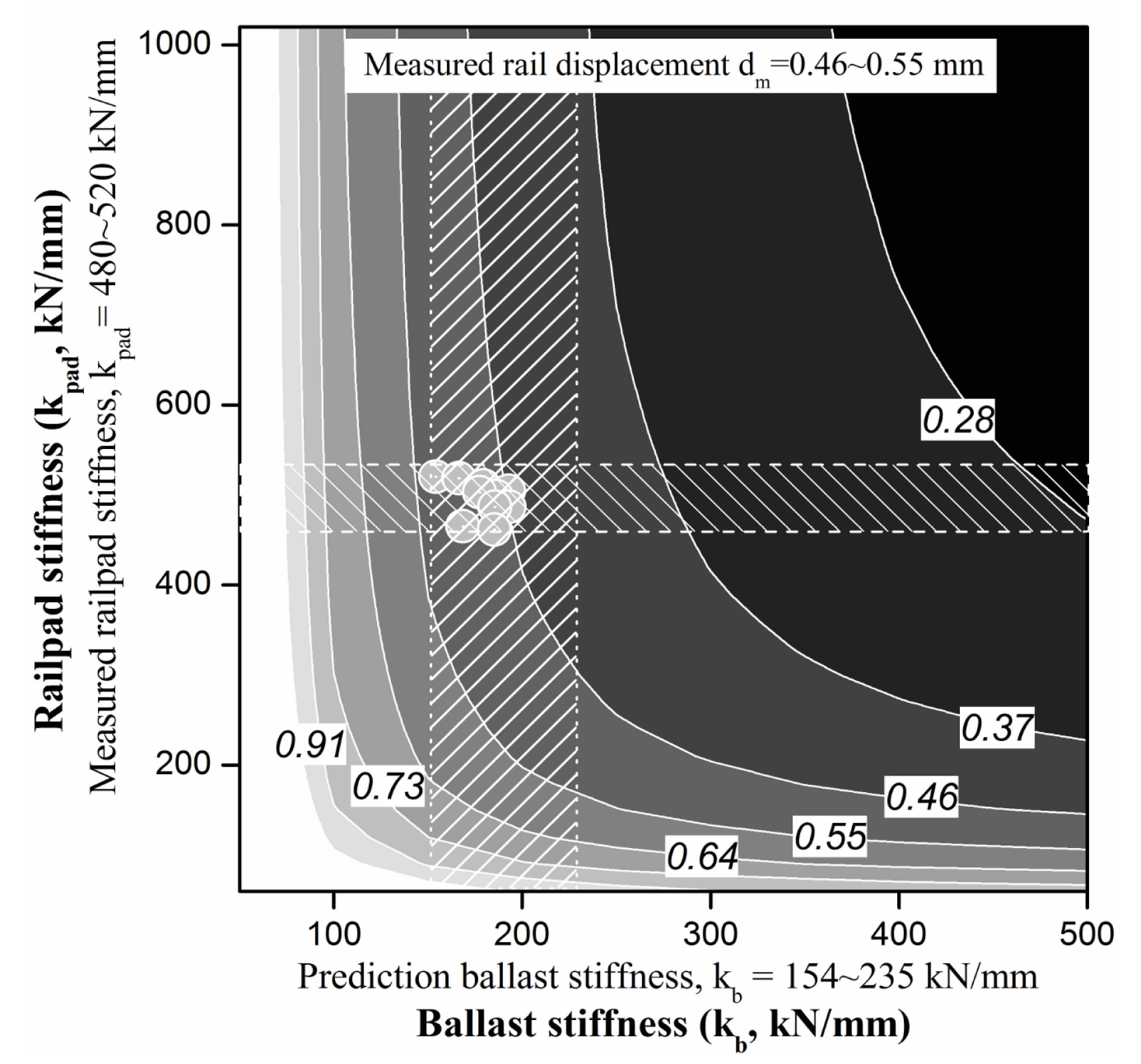
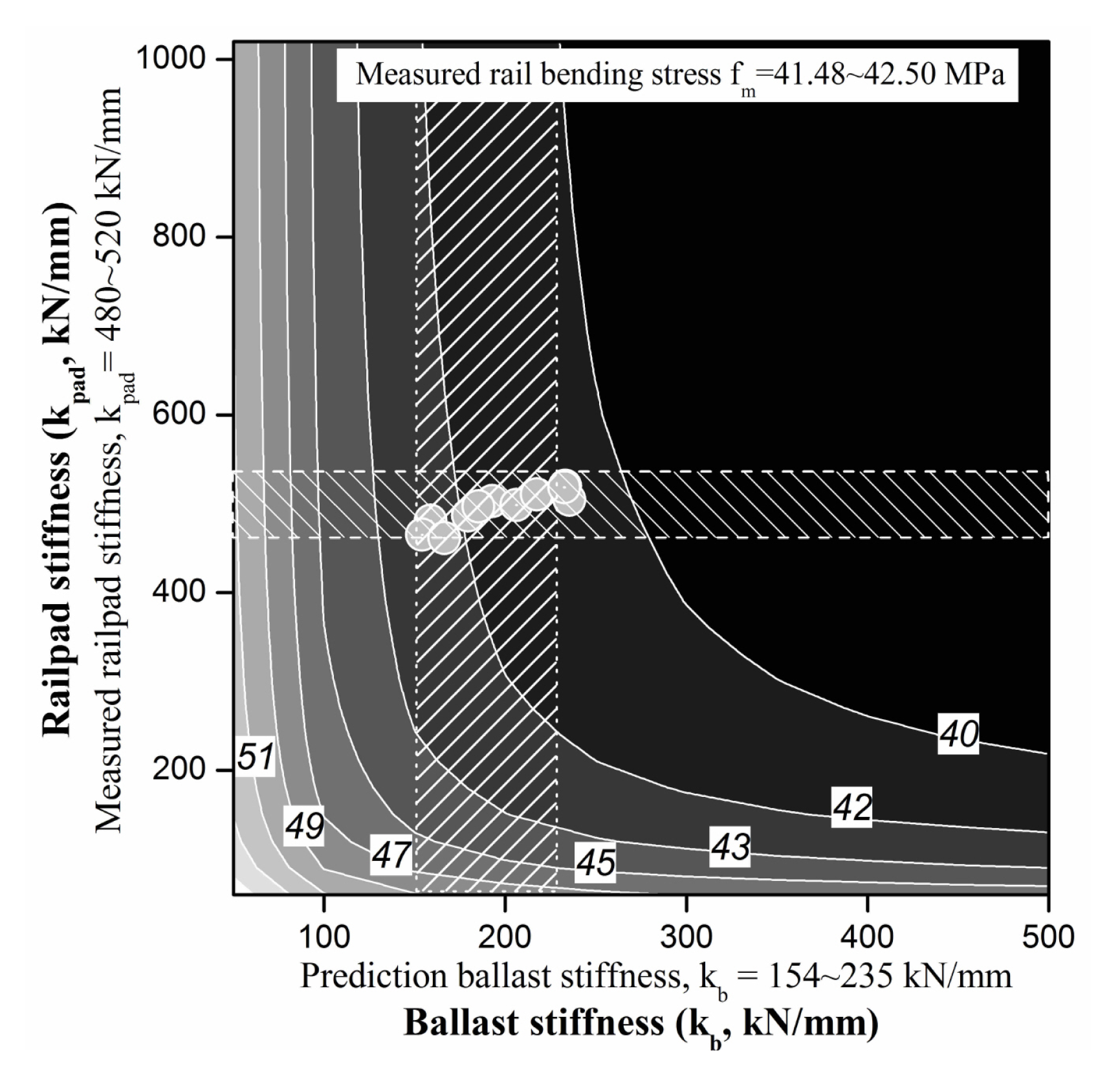
- Step 1: Draw the measured data block (the rail pad stiffness, Figure 13 (①) in horizontal direction on the qualitative analysis map (track support stiffness (TSS) map).
- Step 3: Draw the blocks in both the vertical and horizontal directions on the qualitative analysis map (track response map). Then, check that the intersection region of a duplicated zone between the vertical and horizontal direction; this represents the predicted response of the in-service ballasted track.
- Step 4: Verify the range of the predicted results (value in white box) using the real response data obtained from the target track (circles in Figure 13 (④)) from the intersection region of the proposed qualitative analysis map.
5. Conclusions
- (1)
- The ballasted track response should be a function of the variations in vertical spring stiffness of the rail pad or ballast. The QPM consists of a 2DOF dynamic track model and modified track properties, which define the rail pad and ballast stiffness ranges, based on designed and measured values. The proposed QPM is capable of simulating the complex interaction between the properties of track components and dynamic track responses.
- (2)
- The parameters and dynamic response of the ballasted track determined through field measurements and qualitative analysis showed that the TSS more strongly affects every parameter and is therefore more affected by ballast stiffness than by rail pad stiffness. A ballast stiffness of 200–300 kN/mm can reduce track deterioration (deflection and deformation) and dynamic response. Furthermore, an appropriate TSS is required to prevent exceeding the dynamic response of the in-service ballasted track, i.e., when the track forces, dynamic contribution, or vibration behavior is over the design specifications. The qualitative analysis results showed good agreement (within 2–5%) with the field measurement results.
- (3)
- The proposed QPM presents results as a discrete space of various track responses and parameters, rather than as of single values. The dynamic behavior of in-service ballasted tracks can thus be predicted qualitatively as a function of the rail pad and ballast stiffness using a simple field test and the proposed QPM.
- (4)
- Using the proposed QPM, a dynamic response map can be predicted and used to deal with uncertainties and design variables. The results of the qualitative analysis showed good agreement with field measurements and FE analysis results. The proposed QPM can predict the dynamic response of ballasted tracks using field-measured data, such as rail pad stiffness, rail bending stress, or rail displacement.
- (5)
- The dynamic track response obtained using qualitative analysis can be used to predict the constraint parameters determined by field measurements and should facilitate practical track maintenance operations. The proposed model thus allows for the use of measured track responses to predict the responses and parameters of the ballasted track using a solution space. Overall, the study successfully proposed a model to predict track field conditions and suitability for maintaining a ballasted track.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Choi, J.Y. Qualitative Analysis for Dynamic Behavior of Railway Ballasted Track. Ph.D. Thesis, Technical University of Berlin, Berlin, Germany, 2014. [Google Scholar]
- Dahlberg, T. Railway Track Dynamics—A Survey; Linköping University: Linköping, Sweden, 2003; (unpublished). [Google Scholar]
- Esveld, C. Modern Railway Track, 2nd ed.; MRT-Productions: Zaltbommel, The Netherlands, 2001. [Google Scholar]
- Lichtberger, B. Track Compendium, 2nd ed.; Eurail Press: Hamburg, Germany, 2010. [Google Scholar]
- Cai, Z. Modelling of Rail Track Dynamics and Wheel/Rail Interaction. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 1992. [Google Scholar]
- Choi, J.Y. Influence of track support stiffness of ballasted track on dynamic wheel-rail forces. J. Transp. Eng. ASCE 2013, 139, 709–718. [Google Scholar] [CrossRef]
- Hunt, G.A. Review of the Effect of Track Stiffness on Track Performance; Research Project T372, AEATR-II-2004–2018; Rail Safety and Standards Board: London, UK, 2005. [Google Scholar]
- Zhou, Y. Engineering Qualitative Analysis and Its Application on Fatigue Design Steel Structures. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2005. [Google Scholar]
- Li, M.X.D.; Berggren, E.G. A study of the effect of global track stiffness and its variations on track performance: Simulation and measurement. Proc. Inst. Mech. Eng. Part F 2010, 224, 375–382. [Google Scholar] [CrossRef]
- Li, M.X.D.; Berggren, E.G.; Berg, M. Assessment of vertical track geometry quality based on simulations of dynamic track-vehicle interaction. Proc. Inst. Mech. Eng. Part F 2009, 223, 131–139. [Google Scholar] [CrossRef]
- Li, M.X.D.; Ekevid, T.; Wiberg, N.E. An integrated vehicle–track-ground model for investigating the wheel/rail dynamic forces due to high axle loads. In Proceedings of the 6th International Conference on Contact Mechanics and Wear of Rail/Wheel Systems (CM2003), Gothenburg, Sweden, 10–13 June 2003; pp. 295–300. [Google Scholar]
- Zhou, Y.; Stiemer, S.F. Qualitative and Semi-Quantitative Analysis of Welding Distortion. In Proceedings of the Structural Specialty Conference of CSCE, Halifax, Nova Scotia, 10–13 June 1998. [Google Scholar]
- Fröhling, R.D. Deterioration of Railway Track due to Dynamic Vehicle Loading and Spatially Varying Stiffness. Ph.D. Thesis, University of Pretoria, Pretoria, South Africa, 2009. [Google Scholar]
- Graduate School of Railway, Seoul National University of Science and Technology. A Study on the Maintenance and Estimate of Fatigue Life for Used Rail; Seoul National University of Science and Technology: Seoul Metro, Korea, 2009. [Google Scholar]
- Kaewunruen, S.; Remennikov, A. Dynamic Properties of Railway Track and Its Components: A State-of-the-Art Review; University of Wollongong: New South Wales, Australia, 2008. [Google Scholar]
- Kaewunruen, S.; Remennikov, A. A State-of-the-Art Review Report on Vibration Testing of Ballasted Track Components; July-Dec Research Report; CRC Railway Engineering and Technologies: Rockhampton, Queensland, Australia, 2004. [Google Scholar]
- Kaewunruen, S.; Remennikov, A. Application of Experimental Modal Testing for Estimating Dynamic Properties of Structural Components. In Proceedings of the Australian Structural Engineering Conference 2005 (ASEC 2005), Newcastle, Australia, 1–14 September 2005. [Google Scholar]
- Kaewunruen, S.; Remennikov, A. In-Field Dynamic Testing and Measurements of Railway Tracks in Central Queensland; March-June Research Report; CRC Railway Engineering and Technologies: Rockhampton, Queensland, Australia, 2005. [Google Scholar]
- Kaewunruen, S.; Remennikov, A. Integrated field measurements and track simulations for condition assessment of railway tracks. In Proceedings of the 1st International Conference on Structural Condition Assessment, Monitoring, and Improvement, Perth, Australia, 12–14 December 2005; pp. 391–398. [Google Scholar]
- Kaewunruen, S.; Remennikov, A. Non-destructive evaluation for dynamic integrity of railway track structure. In Proceedings of the International Conference on Structural Integrity and Failure—SIF2006, Sydney, Australia, 27–29 September 2006; pp. 294–299. [Google Scholar]
- Kaewunruen, S.; Remennikov, A.M. Non-Destructive Testing (NDT): A Tool for Dynamic Health Monitoring of Railway Track Structures; Materials Australia: North Melbourne, Australia, 2006; Volume 39, pp. 14–16. [Google Scholar]
- Kaewunruen, S.; Remennikov, A. Field trials for dynamic characteristics of railway track and its components using impact excitation technique. NDT E Int. 2007, 40, 510–519. [Google Scholar] [CrossRef]
- Wu, T.X.; Thompson, D.J. The effects of local preload on the foundation stiffness and vertical vibration of railway track. J. Sound Vib. 1999, 219, 881–904. [Google Scholar] [CrossRef]
- Ngamkhanong, C.; Kaewunruen, S.; Afonso Costa, B.J. State-of-the-art review of railway track resilience monitoring. Infrastructures 2018, 3, 3. [Google Scholar] [CrossRef] [Green Version]
- Ngamkhanon, C.; Goto, K.; Kaewunruen, S. Dynamic responses of railway ballasted track considering rail pad deterioration. In Proceedings of the Modern Practice in Stress and Vibration Analysis (MPSVA) 2018, Cambridge, UK, 2–4 July 2018. [Google Scholar]
- Lim, N.H.; Kim, K.J.; Bae, H.U.; Kim, S.J. DEM analysis of track ballast for track ballast-wheel interaction simulation. Appl. Sci. 2020, 10, 2717. [Google Scholar] [CrossRef] [Green Version]
- Tsunashima, H. Condition monitoring of railway tracks from car-body vibration using a macine learning technique. Appl. Sci. 2019, 9, 2734. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Silvast, M.; Markine, V.; Wiljanen, B. Analysis of the dynamic wheel loads in railway transition zones considering the moisture condition of the ballast and subballast. Appl. Sci. 2017, 7, 1208. [Google Scholar] [CrossRef] [Green Version]
- Zbiciak, A.; Kra’skiewicz, C.; Sabouni-Zawadzka, A.; Pełczyński, J.; Dudziak, S. A novel approach to the analysis of under sleeper pads (USP) applied in the ballasted track structures. Materials 2020, 13, 2438. [Google Scholar] [CrossRef]
- Sayeed, M.A.; Shahin, M.A. Design of ballasted railway track foundations using numerical modelling. Part I: Development. Can. Geotech. J. 2018, 55, 353–368. [Google Scholar] [CrossRef] [Green Version]
- Esmaeili, M.; Amiri, S.; Jadidi, K. An investigation into the use of asphalt layers to control stress and stain levels in railway track foundations. Proc. Inst. Mech. Eng. Park F J. Rail Rapid Transit 2014, 228, 182–193. [Google Scholar] [CrossRef]
- Weston, P.; Roberts, C.; Yeo, G.; Stewart, E. Perspectives on railway track geometry condition monitoring from in-service railway vehicles. Int. J. Veh. Mech. Mobil. 2015, 53, 1063–1091. [Google Scholar] [CrossRef]
- Marsella, M.; Scaioni, M. Sensors for deformation monitoring of large civil infrastructures. Sensors 2018, 18, 3941. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Montanari, U. Networks of constraints: Fundamental properties and applications to picture process. Inf. Sci. 1974, 7, 95–132. [Google Scholar] [CrossRef]
- Tsang, E. Foundation of Constraint Satisfaction; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Gedig, M.H. A framework for qualitative and semi-quantitative analysis in engineering design and evaluation. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 1995. [Google Scholar]
- Mackworth, A. Consistency in networks of relations. Artif. Intell. 1977, 8, 99–118. [Google Scholar] [CrossRef]
- Moore, R.E. Interval Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 1966. [Google Scholar]
- Grassie, S.L.; Cox, S.J. The dynamic response of railway track with flexible sleepers to high frequency vertical excitation. Proc. Inst. Mech. Eng. Part D 1984, 198, 117–124. [Google Scholar] [CrossRef]
- Sadeghi, J. Investigation of Characteristics and Modeling of Railway Track System. Ph.D. Thesis, The University of Wollongong, Northfields Ave Wollongong, Australia, 1997. [Google Scholar]
- Oakdale Engineering. DataFit User’s Manual; Oakdale Engineering: Oakdale, PA, USA, 2005. [Google Scholar]
- Knothe, K.; Grassie, S. Modelling of railway track and vehicle/track interaction at high frequencies. Veh. Syst. Dyn. 1993, 22, 209–262. [Google Scholar] [CrossRef]
- Knothe, K.; Wu, Y. Receptance behaviour of railway track and subgrade. Arch. Appl. Mech. 1998, 68, 457–470. [Google Scholar] [CrossRef]
- Costa, P.A.; Calçada, R.; Cardoso, A.S.; Bodare, A. Influence of soil non-linearity on the dynamic response of high-speed railway tracks. Soil Dyn. Earthq. Eng. 2010, 30, 221–235. [Google Scholar] [CrossRef]
- Choi, J.Y.; Lee, D.W.; Park, Y.G. A study on the evaluation of track support stiffness on the various track type in urban transit. J. Korean Soc. Railw. 2011, 14, 262–270. [Google Scholar]
- Choi, J.Y.; Park, Y.G.; Lee, S.M. The evaluation of track impact factor on the various track type in urban transit. J. Korean Soc. Railw. 2011, 14, 248–255. [Google Scholar] [CrossRef]
- Man, A.P. Determination of dynamic track properties by means of excitation hammer testing. In Railway Engineering International 1996, 4th ed.; De Rooi Publications: Veenendaal, The Netherlands, 1996; pp. 8–9. [Google Scholar]
- Question D71, Stresses in the Track, Ballast and Formation as a Result of Rolling Loads, Stresses in Rails, Part 2: Calibration and Measuring Procedures; Report No. 1; International Union of Railways Office for Research and Experiments: Utrecht, The Netherlands, 1965.
- Korea Rail Network Authority. Railroad Track Design Standard, Part: Subgrade; Korea Rail Network Authority: Daejeon, Korea, 2011. (In Korean) [Google Scholar]
- Korea Rail Network Authority. Railroad Track Design Standard, Part: Track; Korea Rail Network Authority: Daejeon, Korea, 2011. (In Korean) [Google Scholar]
- Korea Railroad Research Institute. Evaluation for Stability of Track-Subgrade by Improving Speedup in the Gyeongchun Line; Korea Rail Network Authority (KR): Daejeon, Korea, 2009. (In Korean) [Google Scholar]
- Remennikov, A.M.; Kaewunruen, S. A review on loading conditions for railway track structures due to wheel and rail vertical interactions. Struct. Eng. Health Monit. 2008, 15, 207–234. [Google Scholar] [CrossRef]
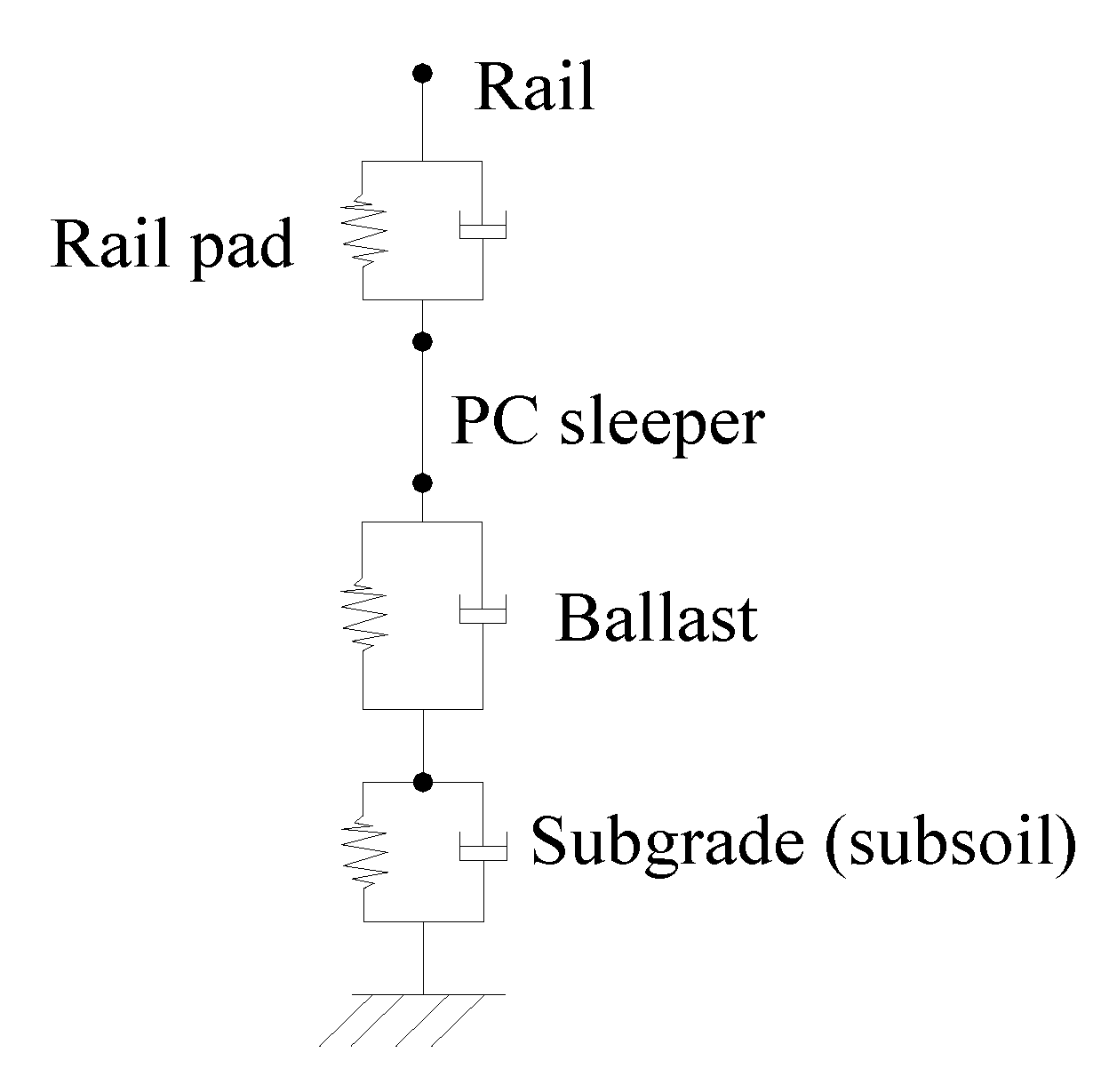






| Properties | Rail (60 kg/m) | Prestressed Concrete Sleeper | |
|---|---|---|---|
| Section Properties | Cross-sectional area (cm2) | 77.5 | 516.75 |
| Moment of inertia (cm4) | 3090 | 16,375 | |
| Section modulus (cm3) | 396 | – | |
| Supported area of half-sleeper (cm2) | – | 3021 | |
| Material Properties | Elastic modulus (kN/cm2) | 21,000 | 4000 |
| Weight density (kN/cm3) | 7.85 × 10−5 | 2.5 × 10−5 | |
| Poisson’s ratio (υ) | 0.30 | 0.18 | |
| Description | Properties |
|---|---|
| Track curvature (R) | ∞ (Straight) |
| Cant | 0 mm |
| Substructure | Earthwork |
| Subgrade modulus a | 0.15 N/mm³ |
| Rail | 60 kg N, Continuous welded rail |
| Sleeper | 250 kg, Prestressed concrete sleeper |
| Sleeper spacing | 600 mm |
| Sleeper mass a | 250 kg |
| Fastening type | Pandrol e-clip |
| Rail pad a | Thermoplastic Polyurethane (TPU) pad |
| Rail pad stiffness a | 400 kN/mm |
| Rail pad damping coefficient b | 12.934 kNs/m |
| Ballast stiffness a | 200 kN/mm |
| Ballast damping coefficient b | 223.130 kNs/m |
| Ballast thickness (depth) | 300 mm |
| Ballast mat | – |
| Train type | EMU (electric multiple unit) |
| Wheelset mass (Mw) | 1025 kg |
| Static wheel load Q | 80 kN |
| Operational speed | Average 130 km/h |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J.-Y.; Kim, S.-H. Qualitative Prediction Model for Dynamic Behavior of Ballasted Tracks. Appl. Sci. 2020, 10, 6258. https://doi.org/10.3390/app10186258
Choi J-Y, Kim S-H. Qualitative Prediction Model for Dynamic Behavior of Ballasted Tracks. Applied Sciences. 2020; 10(18):6258. https://doi.org/10.3390/app10186258
Chicago/Turabian StyleChoi, Jung-Youl, and Sun-Hee Kim. 2020. "Qualitative Prediction Model for Dynamic Behavior of Ballasted Tracks" Applied Sciences 10, no. 18: 6258. https://doi.org/10.3390/app10186258
APA StyleChoi, J.-Y., & Kim, S.-H. (2020). Qualitative Prediction Model for Dynamic Behavior of Ballasted Tracks. Applied Sciences, 10(18), 6258. https://doi.org/10.3390/app10186258




