Comparison of a Response Surface Method and Artificial Neural Network in Predicting the Aerodynamic Performance of a Wind Turbine Airfoil and Its Optimization

Abstract

To find the optimal design for an engineering object, thousands of (or even more) simulations should be implemented to obtain the outcome data for the variously designed objects. However, repeating simulations this many times is impossible because a typical simulation is a computationally expensive task. Instead of conducting all the required simulations, a more efficient way is predicting the outcome from the approximation model, called the surrogate model. The response surface method (RSM) with polynomials and artificial neural network (ANN) are the most prominent methods in constructing a surrogate model in the engineering fields. In this study, the prediction accuracy of the surrogate models computed by using an RSM and ANN is compared with several datasets showing different complexities. This comparison is investigated by constructing the surrogate models in predicting aerodynamic performance of a wind turbine airfoil. In the current paper, it is verified that the prediction accuracy of the ANN-computed surrogate model is higher than the RSM-computed one when the datasets have a high level of complexity, but the opposite phenomenon is observed if the datasets have a low level of complexity. When the surrogate models with different accuracies are used to enhance the performance of a wind turbine airfoil, the surrogate model with a high level of accuracy produces the optimal design, showing a high performance improvement. The current study is expected to give guidance on how to properly choose between an RSM and ANN to construct a highly accurate surrogate model that can help in finding a design with a high performance improvement during the optimization process.

1. Introduction

One important step in shape optimization is constructing a surrogate model, allowing us to predict output values as a function of input design variables. The response surface method (RSM) is a conventional way to explore the relationship between input and output variables, where the output variables are approximated by a form of polynomial function with the input design variables [1,2]. The degree of the polynomial can be set by users, but a second-order polynomial works well, as shown in Zheng and Das [3]. Using an artificial neural network (ANN) is another way to construct a surrogate model [4,5,6]. Neuron networks here consist of input, hidden, and output layers, and each layer has its own neurons with their own bias. Neurons in one layer are connected to the neurons in the next layer, and the strength of associations between two-connected neurons is measured by weights. Using the datasets obtained from the design of experiment, neuron networks are trained to find the best values of weights and biases that minimize the discrepancy between “real” output values and “trained” output values (output values computed from an ANN). Several factors influence the accuracy of an ANN’s prediction such as the number of hidden layers, the number of neurons in each hidden layer, and the number of training datasets, but an ANN usually provides a high accurate approximation, even when the relation between the input and output variables is complicated [7].

In the present study, the prediction accuracies of the surrogate models constructed using a RSM and ANN are compared in predicting the aerodynamic performance of a wind turbine airfoil. This is performed for two reasons. First, wind is a good source for converting economical and ecofriendly energy, so it has great significance as a form of renewable energy. In fact, according to U.S. Energy Information Administration, over 20% of renewable energy in the U.S. was provided by wind energy in 2018 [8]. The recent development of various types of wind turbines such as wind turbines with dimples [9,10] and Darrieus vertical wind turbines [11,12] broadens the usage of wind energy by overcoming previous simple horizontal wind turbines’ drawbacks such as noise and spatial limitation, leading to the expectation that more and more energy will be produced by wind in the future [13,14,15]. Second, a wind turbine airfoil shape and its operating conditions significantly affect the magnitude of the aerodynamic force acting on the wind turbine, and therefore, optimizing them is important. Several researchers have studied the development of high-performance wind turbine airfoil shapes to improve the overall efficiency in the conversion of wind energy. For example, Kamoun et al. [16] developed a new method called the singularities method to analyze and improve the performance of a wind turbine’s airfoil profile. Mohammadi et al. [17] modified the DU91-W2-250 wind turbine airfoil by creating various small flaps such as Gurney flaps and trailing edge wedges, and investigated those flaps’ effects on the lift and drag coefficient of the airfoil. Similar efforts to improve wind turbine airfoil by modifying the shapes of the wind turbine at the trailing edge have been performed in Standish and Van Dam [18], Aramendia et al. [19], Aramendia et al. [20], and Zhu et al. [21]. The effect of a dimple on the wind turbine airfoil on its efficiency is studied in Zhu et al. [22], Shukla and Kaviti [10], and Ismail and Vijayaraghavan [23]. The studies presented in Pires et al. [24] and Ju and Zhang [25] investigated the influence of wind turbine’s operating conditions such as Reynolds number and angle of attack on its aerodynamic performance, and the optimal designs of wind turbine airfoils are found at different operating conditions in Ram et al. [26] and Ju and Zhang [25]. The purpose of the current paper is to compare the prediction accuracy of the surrogate models computed by using the RSM and ANN in predicting the aerodynamic performance of a wind turbine airfoil and to figure out how the accuracy of a surrogate model affects the performance improvement ratio of a wind turbine airfoil if the wind turbine airfoil is optimized with the surrogate models that have a different prediction accuracy.

The remainder of the present paper is structured as follows: The background knowledge needed to understand this study is presented in Section 2. The settings for the prediction accuracy comparison between the surrogate models computed from the RSM and ANN are described in Section 3. The results of the prediction accuracy tests and optimization are explained in Section 4 and Section 5, respectively. Finally, the paper is concluded in Section 6.

2. Numerical Approach

2.1. Geometry Generation

To redesign a wind turbine airfoil, the shape of the baseline airfoil needs to be chosen, and the way to parameterize it should be defined first. The baseline wind turbine airfoil in the current paper is the DU21-A17 developed by Delft University of Technology. To parameterize the baseline airfoil, the Bezier curves-based geometry parameterization method [27,28] is used to make use of its good properties such as the convex hull property [29] and variation diminishing property [30].

In this paremetrization, the parametric curve $f\left(t\right)$ represented by the Bezier curves-based geometry parameterization can be expressed by

$$f\left(t\right)=\sum _{i=0}^n{b}_i{B}_i^n\left(t\right),$$

(1)

where $b_i$ is the i-th control point of the curve and $B_i^n\left(t\right)$ is the Bernstein polynomials of degree n, defined as

$$B_i^n\left(t\right)=\frac{n!}{i!(n-i)!}{t}^i{(1-t)}^{n-i}.$$

(2)

The parametric curve is influenced by the degree of the Bernstein polynomials (value of n), which are determined by the number of control points and the positions of the control points (values of $b_i$). The baseline airfoil is redesigned with two Bezier curves, one for the upper camber of the airfoil and the other for the lower camber. Each curve is defined by six controls points, making the variable n for this study be $n=5$. The control points used in the current paper are presented in Figure 1 with the baseline wind turbine airfoil. The six points from ${\mathbf{p}}_0$ to ${\mathbf{p}}_5$ are the control points of the Bezier curve and are used to modify the upper camber of the baseline airfoil. The six points from ${\mathbf{p}}_5$ to ${\mathbf{p}}_9$ and ${\mathbf{p}}_0$ are the control points of the Bezier curve for the lower camber. The eight control points excluding the ones on the leading and trailing edges (${\mathbf{p}}_0$ and ${\mathbf{p}}_5$) are allowed to move only vertically to create a new airfoil profile. The blue line in the figure shows the profile of the baseline wind turbine airfoil. Note that the control points on the leading and trailing edges of the airfoil are shared by the two Bezier curves for the upper and lower cambers so that 10 independent control points are presented in Figure 1.

2.2. Xfoil

XFOIL is a code that can compute the aerodynamic properties of an airfoil such as lift, drag, and moment coefficients based on a high order panel method and integral boundary layer method [31]. Once the two-dimensional shape of an airfoil, Reynolds number, and angle of attack for the simulation have been determined, XFOIL analyzes the flow and computes the pressure on the airfoil surface that can be numerically converted to the lift, drag, and moment coefficients of the airfoil. The reason that XFOIL is utilized to compute these values instead of more advanced computational fluid dynamic (CFD) based on Reynolds-averaged Navier-Stokes equations is because XFOIL enables us to obtain the values very efficiently in terms of computation time. Although XFOIL works well for a low Reynolds number and incompressible flow [32], it can compute the aerodynamic properties of a wind turbine airfoil with a reasonable accuracy under the simulation conditions that are the focus of the current study. From the author’s preliminary study with the mesh, which has 181,250 elements, a two-dimensional aerodynamic analysis for a baseline airfoil at Re $={10}^6$ and AOA = $5^{°}$ (which are the design and simulation conditions converging faster than other cases) takes approximately 5 min with an 8-core, 32 GB desktop using OpenFOAM, while XFOIL only needs approximately 12 s under these conditions. Because the total amount of calculations required in the current study is huge, XFOIL is selected as the simulation method.

Figure 2 shows a comparison of experiment data obtained from Barrett and Ning [33], XFOIL and CFD data with respect to drag and lift coefficients as a function of the angle of attack (varying from −${15}^{°}$ to ${15}^{°}$) at Re $={10}^6$. For most angles of attack, this data comparison shows good agreement between the lift and drag coefficients computed from the XFOIL simulation and the ones obtained from a wind turbine airfoil experiment.

2.3. Response Surface Method

The response surface method uses polynomials (usually the first or second order) to estimate the output value as a function of the input variables. For example, if $x_i$ and y are defined as the i-th input variable and output variable, respectively, the variable y explored by the first-order polynomial can be written as

$$y={\beta }_0+\sum _{i=1}^N{\beta }_i{x}_i,$$

(3)

where N is the total number of input variables and ${\beta }_0$, ${\beta }_1$, $\cdots ,{\beta }_N$ are the regression variables. This mathematical representation is a simple approximation that finds a linear association between the input and output variables. The more advanced representation using second-order polynomials, which is widely used in optimization, can be used in the form of [34,35]

$$y={\beta }_0+\sum _{i=1}^N{\beta }_i{x}_i+\sum _{i=1}^N{\beta }_{ii}{x}_i^2+\sum _{j=1}^N\sum _{\begin{array}{c}i=1\\ i<j\end{array}}^N{\beta }_{ij}{x}_i{x}_j.$$

(4)

Once the design of experiment is performed, the regression variables are computed using a least squares method.

2.4. Artificial Neural Network

With the recent developments in the machine learning area, the techniques related to machine learning has been applied in many fields such as image processing, data regression and classification, and optimization [36,37,38,39]. Among the many techniques in machine learning, an ANN is popularly used in constructing a surrogate model because an ANN can predict output values with good accuracy, as shown in Schweidtmann et al. [40]. To make use of this advantage, an ANN is used for surrogate model construction in the current paper, and its accuracy is investigated.

A loss function J, which is used to train the ANN in a reconstructing surrogate model by minimizing it, can be defined as

$$J=\frac{1}{N}\sum _{i=1}^N{({\varphi }_i-{\widehat{\varphi }}_i)}^2+{\lambda \left|\right|\mathbf{w}\left|\right|}_2^2,$$

(5)

where $\left|\right|·{\left|\right|}_2$ indicates $L_2$ norm, $\lambda$ is the regularization parameter, and $\mathbf{w}$ is a set of weights of the ANN in vector form. The ${\varphi }_i$ and ${\widehat{\varphi }}_i$ are the values of the output variables at the i-th test design obtained from simulation (in this study using XFOIL) and the ANN, respectively.

In Equation (5), the first term on the right hand side computes the discrepancy between the values computed from simulation and ANN in mean square form. The second term on the right hand side measures the complexity of the ANN to prevent the ANN from overfitting the output values of the given datasets, which is called $L_2$ regularization. The ANN in the present paper is implemented using the open-source software TensorFlow [41]. The constructed ANN has two hidden layers, and 64 neurons are used at each hidden layer. The rectified linear unit (ReLu) function is used as the ANN’s activation function. The Xavier initialization initializes the weights in the ANN, and the Proximal Adagrad algorithm is used for an optimizer [42]. The learning rate and regularization parameter are set to 0.01 and ${10}^{-4}$, respectively. The ANN training process is repeated until the maximum number of iterations (${10}^5$) is reached. Although the values of the ANN parameters defined in the current study are not thoroughly optimized, when the change of prediction accuracy of the ANN-computed surrogate models is investigated by varying the number of neurons and magnitude of the learning rate, the settings used in this study show good accuracy in most cases. Some test cases are provided in

Table 1. The influence of the number of neurons and learning rate on artificial neural network (ANN)-computed surrogate models’ prediction accuracy. The O-DLB-4-3 case is used for the prediction accuracy test.

Number of Neurons	Learning Rate	E
16	${10}^{-2}$	$0.286$
64	${10}^{-1}$	$0.232$
64	${10}^{-2}$	$0.225$
64	${10}^{-3}$	$0.266$
256	${10}^{-2}$	$0.227$

.

2.5. Optimization

Once a surrogate model is constructed, the optimal values of the input design parameters should be explored to find an optimal design. For the optimization algorithm, a genetic algorithm that searches through the optimal solutions heuristically without derivative information is used [43]. The advantage of using a genetic algorithm compared with using other gradient-based optimization methods such as the steepest descent method and conjugate gradient method is its capability to find a globally (rather than locally) optimal solution. This allows for the improvement ratio to be achieved from the optimal solution using the genetic algorithm better than the one from gradient-based optimization methods [44]. The population size and mutation rate of the genetic algorithm used in the current paper are set to 50 and 0.01, respectively. The genetic algorithm is terminated if the average change in the fitness value is less than ${10}^{-6}$ or if the number of iterations exceeds 1000.

3. Settings for Prediction Accuracy Tests

Creating datasets is an essential task in constructing a surrogate model, but one issue is how to create these datasets. There are many factors that should be considered here. For example, defining the types and a number of input variables significantly affects the accuracy of a surrogate model because these factors determine the complexity of the datasets. Determining the number of datasets used in constructing a surrogate model is also an important factor that influences the accuracy, which is also related to the design of experiment method. A way to set these factors will be explained in the following section.

3.1. Types of Input Variables

The input variables to compare the prediction accuracy of the RSM-computed and ANN-computed surrogate models can be classified into two different groups. The ones belonging to the first group are the control points of the Bezier curve that affect the shape of the baseline wind turbine airfoil. These input variables will be called the geometric variables in the rest of the paper. The other variables belonging to the second group do not have an influence on the shape of the baseline airfoil. Rather, they determine the operating conditions of a wind turbine airfoil. Although there are several parameters affecting the wind turbine airfoil’s operating conditions such as tip speed ratio and solidity, the Reynolds number and angle of attack are the ones being dealt with in this study. These variables will be referred to as the operational variables.

With these types of input variables, two types of prediction accuracy tests for the surrogate models are implemented. The difference between these two types of tests is the inclusion of operational variables in creating the datasets. In more detail, in the first type of prediction accuracy tests where all the input variables are geometric variables (no operational variables are included), the aerodynamic performance of a redesigned wind turbine airfoil from its baseline shape is estimated using the surrogate models at a fixed Reynolds number (Re $={10}^6$) and angle of attack (AOA = $5^{°}$), which implies no change of the wind turbine airfoil’s operating conditions. However, in the second type of prediction accuracy tests, two operational input variables, the Reynolds number and angle of attack, are set as variables besides geometric variables so that the performance of the redesigned wind turbine airfoil is predicted with the change in its operating conditions. The purpose of considering geometrical and operational parameters simultaneously in the second type of prediction accuracy tests is to make the output value more intricately related to the input variables and to check how this complex association affects the prediction accuracy of the RSM-computed and ANN-computed surrogate models. For clarification, the former prediction type of accuracy test will be referred to as “prediction accuracy test with geometric variables”, while the latter one will be called “prediction accuracy test with geometric and operational variables”. The reason for investigating these two types of prediction accuracy tests is to make datasets with different complexities and to test the prediction accuracy change of the RSM-computed and ANN-computed surrogate models depending on the complexity of the datasets.

3.2. Number of Input Variables

The complexity of datatsets is not only affected by the characteristics of the input variables, but it is also influenced by the number of input variables. To investigate a change of prediction accuracy as a function of the number of input variables, surrogate models with different degrees of freedom are constructed for the following tests: $n_1$-degree of freedom prediction accuracy test with geometric variables and $n_2$-degree of freedom prediction accuracy test with geometric and operational variables. Here, $n_1$ can be 2, 4, 6, and 8, and $n_2$ can be 4 and 6. 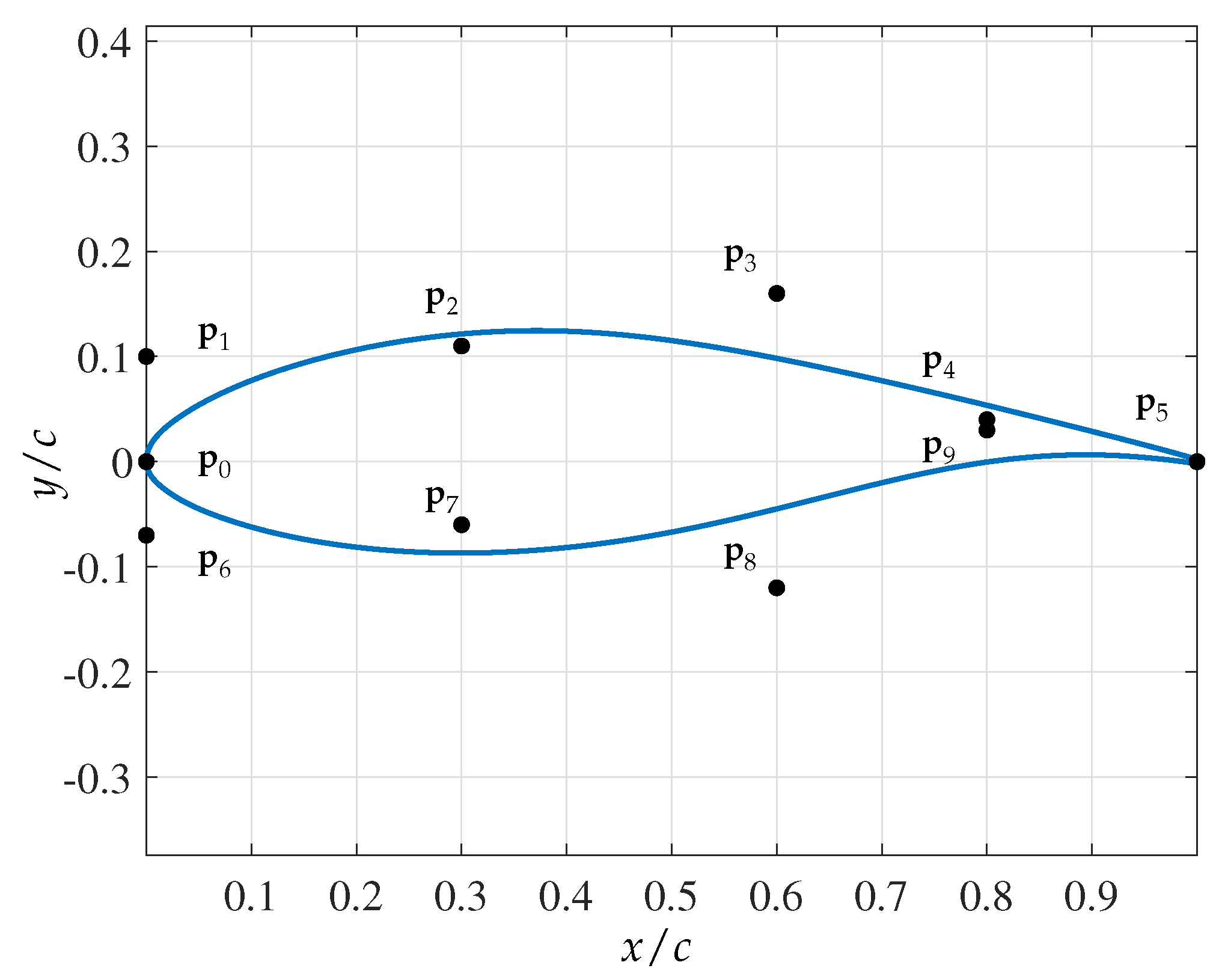Because the values of $n_1$ and $n_2$ are less than or equal to 8, which is the total number of the movable control points presented in Figure 1, only some of these control points should be set as input geometric variables in the prediction accuracy tests. Therefore, a rule to choose input geometric variables from the candidates is needed.

Table 2. Upper and lower limits of the eight movable control points that are the geometric input variables at the prediction accuracy tests and optimization problems.

Input Variables	Control Points	Ranges
Variable 1	${\mathbf{p}}_7$	$-0.03\le \Delta y\le 0.055$
Variable 2	${\mathbf{p}}_8$	$-0.035\le \Delta y\le 0.095$
Variable 3	${\mathbf{p}}_2$	$-0.015\le \Delta y\le 0.12$
Variable 4	${\mathbf{p}}_3$	$-0.08\le \Delta y\le 0.045$
Variable 5	${\mathbf{p}}_6$	$-0.015\le \Delta y\le 0.02$
Variable 6	${\mathbf{p}}_9$	$-0.005\le \Delta y\le 0.03$
Variable 7	${\mathbf{p}}_1$	$-0.03\le \Delta y\le 0.025$
Variable 8	${\mathbf{p}}_4$	$-0.01\le \Delta y\le 0.03$

shows the selection priority of the eight control points with their own upper and lower bounds. For example, the input variables at the 2- and 4-degrees of freedom prediction accuracy tests with geometric variables are the control points $\{{\mathbf{p}}_7$, ${\mathbf{p}}_8\}$ and $\{{\mathbf{p}}_7$, ${\mathbf{p}}_8$, ${\mathbf{p}}_2$, ${\mathbf{p}}_3\}$, respectively, meaning only these control points can move vertically within their own ranges during the tests. The selection priority of the control points here was defined under the expectation that the control points located in the middle of the airfoil profile (${\mathbf{p}}_2$, ${\mathbf{p}}_3,{\mathbf{p}}_7,{\mathbf{p}}_8$) has a greater impact on its aerodynamic property than the ones close to the leading and trailing edges (${\mathbf{p}}_1$, ${\mathbf{p}}_4,{\mathbf{p}}_6,{\mathbf{p}}_9$). Among the control points located in the same x position, the point located on the lower surface of the wind turbine airfoil is weighted more than the other. At a $n_2$-degree of freedom prediction accuracy test with geometric and operational input variables, the $(n_2-2)$ number of geometric input variables are selected because two variables are taken for the operational variables, Reynolds number and angle of attack. For example, four input parameters of the 4-degrees of freedom prediction accuracy test with geometric and operational variables are the control points $\{{\mathbf{p}}_7$, ${\mathbf{p}}_8\}$, Reynolds number, and angle of attack. The ranges of the Reynolds number and angle of attack here are defined as ${10}^5\le Re\le {10}^6$ and $0^{°}\le AOA\le {15}^{°}$, respectively. Here, because the range of Re is much larger than the other input variables, a logarithm of its value is given as the input in the prediction accuracy tests (Another way to deal this issue is normalizing the input parameters using the method, for example, with a batch normalization [45].). With the constructed surrogate model, the value of lift-to-drag ratio is predicted under the expectation that it is the simplest way to evaluate the aerodynamic performance of a wind turbine airfoil.

3.3. Design of Experiment

Constructing a surrogate model to discover the relationship between the input and output variables requires the value of the output variable at various sets of the input points. One crucial point here is how to efficiently represent the infinite space of input variables with a finite amount of data. There are many studies regarding the ways to create datasets inside input variables’ space in the design of experiment step such as the D-optimal and factorial methods [46,47]. Among them, the methods used in the current paper for the prediction accuracy comparison of surrogate models are the face-centered composite design (FCCD) method [48] and the discrete m-level-based method, which equally distributes m points at each input parameter [7]. The FCCD method is applied for its advantage of covering the whole space of input variables with a small number of data, while the discrete level-based method is chosen to test how prediction accuracy changes with respect to the number of datasets because a different number of datasets can be created in the discrete m-level-based method if the value of m is set differently, even for the same degree of freedom prediction accuracy test. (Note that the total number of datasets is equal to $2^n+2n+1$ at the n degree of freedom prediction accuracy test in the FCCD method, but it becomes $m^n$ when the discrete m-level-based method is used.) In the present paper, the different m values are used for the two types of prediction accuracy tests. In the prediction accuracy tests with geometric variables, the discrete 3-level-based method is used, while the discrete 3-, 4- and 5-level-based methods are used for the tests with geometric and operational variables. The higher discrete-level-based methods are tested in the latter types of tests because the aerodynamic performance (measured by lift-to-drag ratio here) of a wind turbine airfoil shows more complicated associations with the input variables than the one in the former case, requiring more data to build the surrogate models with reasonable accuracy.

3.4. Terminology Clarification

To clearly state the datasets used in the current paper, the following notations will be used. The letters “G” and “O”, which stand for “geometric” and “operational", are used to point out the datasets for the prediction accuracy tests with geometric design variables and with geometric and operational design variables, respectively. The abbreviations “FCCD” and “DLB” are used to state the type of design of experiment in producing the datasets. After these symbols, one or two numbers can follow (FCCD is followed by one number, while DLB is followed by two numbers), where the first number indicates the total degree of freedom and the second number shows the value of m of the m-level-based method. For example, the notation “G-FCCD-2” means the FCCD-created datasets for the 2-degrees of freedom prediction accuracy test with geometric variables. Similarly, the notation “O-DLB-4-5” indicates the datasets were created by the discrete 5-level based method for the 4-degrees of freedom prediction accuracy test with geometric and operational variables.

4. Results of Prediction Accuracy Tests

To evaluate the prediction accuracy of the surrogate models obtained from the RSM and ANN, 50 test samples randomly distributed inside the input variables’ space were created for each prediction accuracy test. These samples were not utilized for surrogate model construction and optimization but were used only for a quantitative prediction accuracy comparison. If M is defined as the number of test samples, which is 50 in the current study, the quantity to measure the prediction accuracy of the constructed surrogate model is defined using the normalized root-mean-square deviation:

$$E=\frac{\sqrt{\frac{1}{M}{\sum }_{i=1}^M{({\varphi }_i-{\widehat{\varphi }}_i)}^2}}{\overline{\varphi }},$$

(6)

where the variables ${\varphi }_i$ and $\widehat{{\varphi }_i}$ are the output values of the i-th test set computed from XFOIL and constructed surrogate model, respectively, and the $\overline{\varphi }$ is the mean value of ${\varphi }_i$, which can be computed from

$$\overline{\varphi }=\frac{1}{M}\sum _{i=1}^M{\varphi }_i.$$

(7)

Table 3. The values of the normalized root-mean-square deviation of the surrogate models constructed from an RSM and ANN using the various datasets whose parameters are the wind turbine airfoil’s geometric variables. Here, the RSM-computed and ANN-computed surrogate models are constructed with exactly the same sample data.

Types	E (RMS)	E (ANN)	$\mathit{\gamma }$
G-FCCD-2	$1.687\times {10}^{-3}$	$3.299\times {10}^{-3}$	0.511
G-FCCD-4	$5.779\times {10}^{-3}$	$1.184\times {10}^{-2}$	0.488
G-FCCD-6	$7.379\times {10}^{-3}$	$1.766\times {10}^{-2}$	0.418
G-FCCD-8	$4.648\times {10}^{-2}$	$2.505\times {10}^{-2}$	1.855
G-DLB-2-3	$1.749\times {10}^{-3}$	$2.582\times {10}^{-3}$	0.677
G-DLB-4-3	$4.949\times {10}^{-3}$	$1.027\times {10}^{-2}$	0.482
G-DLB-6-3	$5.768\times {10}^{-3}$	$9.717\times {10}^{-3}$	0.594
G-DLB-8-3	$3.201\times {10}^{-2}$	$1.472\times {10}^{-2}$	2.174

and

Table 4. The same as Table 3, but for the surrogate models using the datasets whose parameters are the wind turbine airfoil’s geometric and operational variables.

Types	E (RMS)	E (ANN)	$\mathit{\gamma }$
O-FCCD-4	$2.994\times {10}^{-1}$	$2.434\times {10}^{-1}$	1.230
O-FCCD-6	$3.922\times {10}^{-1}$	$1.428\times {10}^{-1}$	2.746
O-DLB-4-3	$3.193\times {10}^{-1}$	$2.250\times {10}^{-1}$	1.419
O-DLB-4-4	$2.577\times {10}^{-1}$	$1.454\times {10}^{-1}$	1.772
O-DLB-4-5	$2.415\times {10}^{-1}$	$4.873\times {10}^{-2}$	4.956
O-DLB-6-3	$2.778\times {10}^{-1}$	$1.036\times {10}^{-1}$	2.682
O-DLB-6-4	$2.240\times {10}^{-1}$	$6.568\times {10}^{-2}$	3.411
O-DLB-6-5	$2.071\times {10}^{-1}$	$5.492\times {10}^{-2}$	3.772

show the values of the normalized root-mean-square deviation E for the prediction accuracy tests with geometric variables and with geometric and operational variables, respectively. On the rightmost column of each table, the values of the variable $\gamma$, defined as

$$\gamma =\frac{E_{RSM}}{E_{ANN}},$$

(8)

are presented where $E_{RSM}$ and $E_{ANN}$ are the normalized root-mean-square deviation of the RSM-computed and ANN-computed surrogate models, respectively. If $\gamma$ is greater than unity, the ANN-computed surrogate model is more accurate in predicting the lift-to-drag ratio than the RSM-computed surrogate model; otherwise, the latter surrogate model is more accurate. When the values of E are compared with respect to the number of input variables in Table 3, all E values increase as the number of variables increases except for the ANN-computed surrogate model with G-DLB-6-3 whose value is slightly smaller than the ANN-computed surrogate model with G-DLB-4-3. The growth of the nonlinearity with an increase in the number of input variables is thought to cause this phenomenon, so the prediction accuracy of the surrogate models obtained from the RSM and ANN decreases for the tests with geometric input variables.

In addition, the fact that the values of E of the surrogate models with geometric input variables are smaller than the ones with geometric and operational input variables reveals that the lift-to-drag ratio prediction of wind turbine airfoils is more difficult to assess when the geometric variables and operating conditions are given as input parameters at the same time instead of when only geometric variables are presented.

From Table 4, it is shown that the prediction accuracy of the ANN-computed surrogate models is higher than the ones computed from the RSM for the prediction tests with geometric and operational variables. However, for the cases with geometric variables, the opposite phenomenon is observed, except for the tests with 8 degrees of freedom. Note here that the general complexity of the datasets for the prediction accuracy tests with geometric and operational variables is higher than the one with geometric variables. From this, it can be deduced that the prediction accuracy of the surrogate model computed from the ANN is better than the RSM-computed model if the datasets for the surrogate model construction have a high complexity; however, the RSM-computed surrogate model will have a higher accuracy, otherwise. Among the prediction accuracy tests with geometric variables, the datasets used to predict lift-to-drag ratio with eight input variables have the highest complexity. In this context, the fact that the ANN-computed surrogate models’ prediction accuracy for these tests is higher than the accuracy using the RSM-computed surrogate models is not a surprising phenomenon, and it can be explained by the complexity of the datasets. This corresponds to the claim presented in the current paper, which is the ANN-computed surrogate model works better than the RSM-computed surrogate model when the datasets have high complexity. This observation is supported by the findings in the previous studies of Youssefi et al. [49] and Mousavi et al. [50], which concluded that the ANN-computed surrogate model is better than the RSM-computed one for predicting the behavior of a nonlinear system.

The design of experiment’s type in creating the datasets does not appear to be a significant factor which it comes to causing accuracy differences between RSM-computed and ANN-computed surrogate models. Rather, the number of datasets tends to affect the prediction accuracy more. To quantitatively measure it, the variable ${\alpha }_n$

$${\alpha }_n=\frac{E_{n,3}}{E_{n,5}},$$

(9)

is defined for a n-degree of freedom prediction test where $E_{n,m}$ is the normalized root-mean-square deviation of the surrogate model constructed by using the datasets of the O-DLB-n-m. If this value is high, the prediction accuracy is highly improved because the value of m of the discrete m-level based method increases from 3 to 5, resulting in an increase of the number of datasets. Figure 3 shows the values of ${\alpha }_4$ and ${\alpha }_6$ of the surrogate models obtained from the RSM and ANN. Because these values for the RSM-computed surrogate models are greater than unity, the prediction accuracy of the corresponding surrogate models are improved when a large amount of datasets are offered. However, the ANN’s values of ${\alpha }_n$ are higher than the RSM’s values, showing that the ANN-computed surrogate models are more highly improved than the RSM’s when the number of datasets increases.

The prediction values for the lift-to-drag ratio using RSM-computed and ANN-computed surrogate models for the 50 test samples are plotted in Figure 4 with their exact (computed from XFOIL) values. The prediction values presented in the left column are computed from the RSM-computed surrogate models with G-DLB-4-3, G-DLB-8-3, and O-DLB-6-4 from the top to bottom rows, respectively. The prediction values presented in the right column are identical to the ones plotted in the left column, but these values are from the ANN-computed surrogate models. The dashed line in which the slope is unity and passes through the origin is also presented for each figure to show how accurately each surrogate model predicts the exact outcome values for the 50 test samples. With G-DLB-4-3, the prediction using the RSM-computed surrogate model shows slightly higher accuracy than the surrogate model computed from the ANN, but the ANN-computed models are better in the other two cases. This can be interpreted from the comparative analysis of E, whose values are smaller for the prediction accuracy tests of the ANN-computed surrogate models with G-DLB-8-3 and O-DLB-6-4 than the RSM-computed ones, allowing us to expect the phenomenon shown in Figure 4. A similar interpretation is possible for the prediction accuracy comparison of the surrogate models with G-DLB-4-3.

Note that the lift-to-drag ratios of the 50 test samples for O-DLB-6-4 were spread wider than the other cases because the performance of a wind turbine airfoil is affected by its operating conditions. For example, the lift-to-drag ratios of the three wind turbine airfoils presented in Figure 5 are 57.1, 98.7 and 114.5, respectively, with their own operating conditions. However, these values are respectively changed to 125.1, 121.8 and 119.3 at Re = ${10}^6$ and AOA = $5^{°}$, where the deviation of the three airfoils’ lift-to-drag ratios is much smaller than the case when each airfoil has its own operating conditions. When the distributions of pressure coefficients on these three wind turbine airfoils are compared between the two cases (when the airfoils are simulated with their own operating conditions and when the airfoils are simulated at the reference operating conditions), the effect of the operating conditions on the aerodynamic performance of the wind turbine airfoils is also observed (see Figure 6).

5. Results of Optimization

Using the surrogate models built in Section 4, a DU21-A17 wind turbine airfoil is optimized to enhance its aerodynamic performance. The main purpose of the optimization is to figure out how the optimization results (in terms of magnitude of lift-to-drag ratio) are affected by the level of prediction accuracy of the surrogate models. To do this, the quantity used to evaluate the airfoil’s performance should be defined first. The lift force acting on the airfoil needs to be increased while the drag force needs to be decreased to enhance the performance, which can be simply performed by maximizing the lift-to-drag ratio of the wind turbine airfoil.

To avoid obtaining a very thin and unrealistic wind turbine airfoil, two airfoil’s minimum thickness constraints are considered in the optimization process—first, the wind turbine airfoil at $x=0.34c$ (where the thickness of the baseline wind turbine airfoil is at its maximum) is set to be thicker than a certain thickness to avoid finding thin optimal wind turbine airfoils. Second, at $x=0.9c$, a minimum thickness of the optimal wind turbine airfoil is defined to reduce the risk of the trailing edge breaking, which can happen when the tip of the wind turbine airfoil is too thin. The criteria thickness values for both constraints are set based on the baseline wind turbine airfoil’s thickness at the corresponding positions. For example, when the thicknesses of the baseline and optimal wind turbine airfoils at $x=x_0$ are defined as $t_b\left(x_0\right)$ and $t_o\left(x_0\right)$, respectively, the airfoil thickness constraint at $x=x_0$ is defined as

$$t_o\left(x_0\right)\ge k{t}_b\left(x_0\right),$$

(10)

where k is the constant number determining the allowable thickness of the optimal wind turbine airfoil. In the current paper, the value of k is set as $k=0.95$, producing a reasonable shape for the optimal wind turbine airfoil.

The optimization process in the current study is as follows: First, N numbers of design sets are created based on the design of experiment described in Section 3.3. For each design set, the lift-to-drag ratio is computed using XFOIL. Using this calculation, the RSM-computed or ANN-computed surrogate model is constructed, allowing for the prediction of an output value at an arbitrary design set. With the constructed surrogate model, the genetic algorithm searches for the optimal input variables maximizing the lift-to-drag ratio, and then, the optimal wind turbine airfoil is created using the optimal input variables found by the genetic algorithm. Finally, the lift-to-drag ratio of the optimal wind turbine airfoil is computed using XFOIL, which is considered the performance of the optimal wind turbine airfoil.

To test the influence of the surrogate model’s prediction accuracy on the performance improvement of the wind turbine airfoil, optimization is performed several times with the RSM-computed and ANN-computed surrogate models constructed with G-DLB-8-3 and O-DLB-6-4. Here, the input variables of each datasets are treated as the design variables of the corresponding optimization problem so that the degrees of freedom of the optimization problems using the surrogate models with G-DLB-8-3 and O-DLB-6-4 are 8 and 6, respectively. These optimization problems will be respectively referred to as the optimization problems with G-DLB-8-3 and O-DLB-6-4. Note that both the optimization problems with G-DLB-8-3 and O-DLB-6-4 can be classified further into two independent problems based on the types of surrogate models used in the optimization process: RSM-computed and ANN-computed surrogate models. As a result, the total number of optimization problems solved in the current study is four.

The optimal wind turbine airfoil’s shapes obtained from the optimization problems with G-DLB-8-3 and O-DLB-6-4 are presented in Figure 7a,b, respectively. In each figure, the wind turbine airfoils plotted in blue and red are the optimal designs using the surrogate models computed from the RSM and ANN, respectively. Here, all eight design variables of the optimization problems with G-DLB-8-3 are geometric parameters. However, only four design variables are geometric parameters for the optimization problems with O-DLB-6-4, while the other two are the variables related to the airfoil’s operating conditions; therefore, the effect of these two design variables are not reflected in Figure 7b. The lift-to-drag ratios of the optimal designs are presented in

Table 5. The values of the lift-to-drag ratios of the optimal designs. Note that the lift-to-drag ratio of the baseline design at Re = ${10}^6$, AOA = $5^{°}$ is 118.16.

Optimization	Surrogate Model	Operational Conditions	Lift-to-Drag Ratio	E
G-DLB-8-3	RSM	Re = $1.00\times {10}^6$, AOA = ${5.00}^{°}$	139.85	$3.20\times {10}^{-2}$
	ANN	Re = $1.00\times {10}^6$, AOA = ${5.00}^{°}$	140.60	$1.47\times {10}^{-2}$
O-DLB-6-4	RSM	Re = $9.95\times {10}^5$, AOA = ${5.48}^{°}$	129.48	$2.24\times {10}^{-1}$
	ANN	Re = $9.97\times {10}^5$, AOA = ${7.57}^{°}$	140.09	$6.57\times {10}^{-2}$

with their operating conditions. The lift-to-drag ratio of the optimal design obtained from the optimization problem with O-DLB-6-4 using the RSM-computed surrogate model is relatively lower than the other optimal designs. Note here that the value of E for the RSM-computed surrogate model with O-DLB-6-4 is the highest compared with the other three surrogate models. Judging from the values of E, it is believed that inaccurate prediction of the RSM-computed surrogate model for the optimization problem with O-DLB-6-4 makes the input variables reach the “wrong destination” where the wind turbine airfoil’s performance is not maximized in reality because of the discrepancy between the surrogate model-computed and XFOIL-computed wind turbine airfoil’s performance, resulting in less performance improvement than the cases when the surrogate models predict the output value with a high level of accuracy. This is also supported by the fact that the lift-to-drag ratios of the optimal designs found with the high-accuracy surrogate models (ANN-computed surrogate models) are higher than the ones using the less-accurate surrogate models (RSM-computed surrogate models) for both optimization problems with G-DLB-8-3 and O-DLB-6-4.

The pressure coefficients (defined as $c_p$) of the optimal designs of the wind turbine airfoils shown in Figure 7a,b are presented in Figure 8a,b, respectively, with the baseline wind turbine airfoil’s pressure coefficient graph. The pressure difference between the upper and lower cambers grows wider for the optimal designs compared with the baseline design. This indicates high lift force is produced using the optimal designs, which is the reason for the performance enhancement of the optimal wind turbine airfoils compared with the baseline design.

6. Conclusions

The accuracy of the surrogate models computed by using the RSM and ANN are compared in predicting the lift-to-drag ratio of a wind turbine airfoil. The surrogate models were constructed with several datasets that can be categorized depending on the type of input variables, the number of input variables, and the method regarding the design of experiment to generate datasets. Then, the optimization to maximize the lift-to-drag ratio of a wind turbine airfoil was implemented with the RSM-computed and ANN-computed surrogate models with G-DLB-8-3 and O-DLB-6-4.

From the prediction accuracy tests of the surrogate models, the following conclusion are deduced: First, the ANN-computed surrogate model’s prediction accuracy is higher when the offered datasets have a high level of complexity, but when it is not, the accuracy of the RSM-computed surrogate models can be higher. Second, the accuracy of the RSM-computed and ANN-computed surrogate models is not highly affected by the two types of design of experiment (FCCD method and discrete m-level based method) when it comes to generating the datasets. Rather, they are more sensitive to the number of datasets. Finally, when a large number of datasets is provided, the prediction accuracy of the ANN-computed surrogate model improves more than the one computed from the RSM. From the optimization results, optimization with the high-accuracy surrogate model finds the better optimal design than the one with a low level of accuracy, which reveals the significance of constructing a surrogate model with a high level of accuracy.