Strain Field Evolution Characteristics of Free Surface during Crater Blasting in Sandstone under High Stress
Abstract
:1. Introduction
2. Test Apparatus, Specimens, and Procedure
2.1. Test Apparatus
2.2. Test Specimens
2.3. Test Procedure
3. Test Results and Analyses
3.1. Initial Strain Induced by the Static Stress
3.2. Calculation Method of Strain in DIC
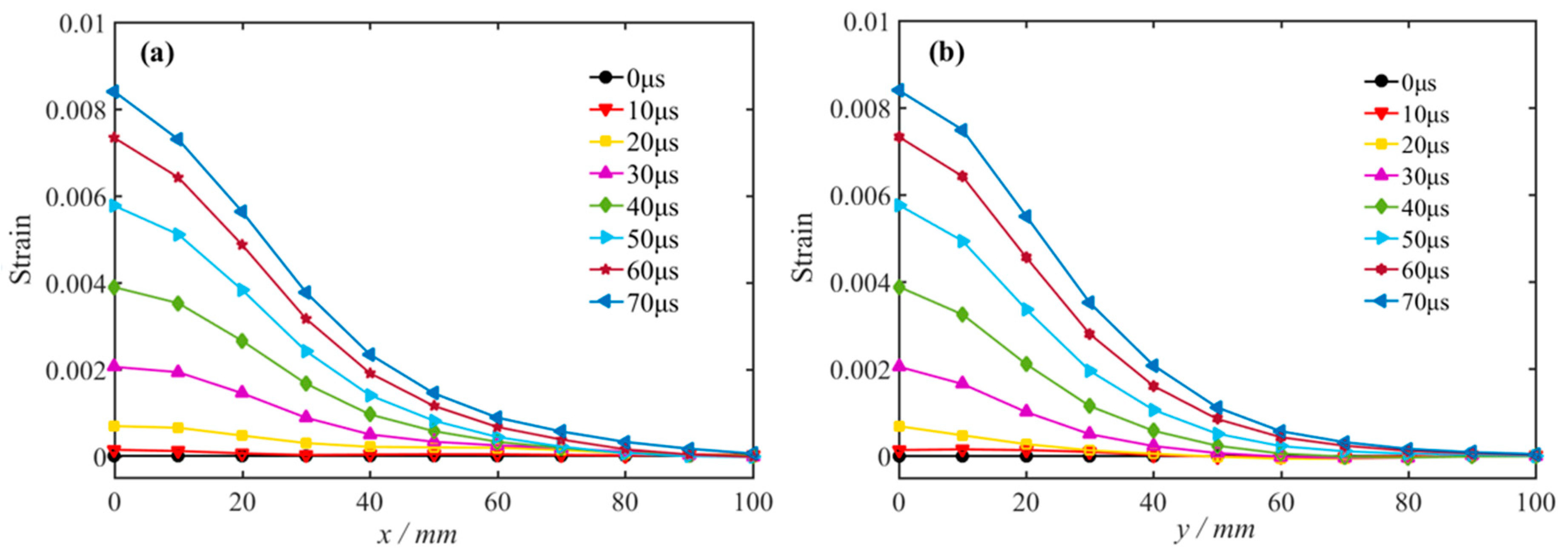
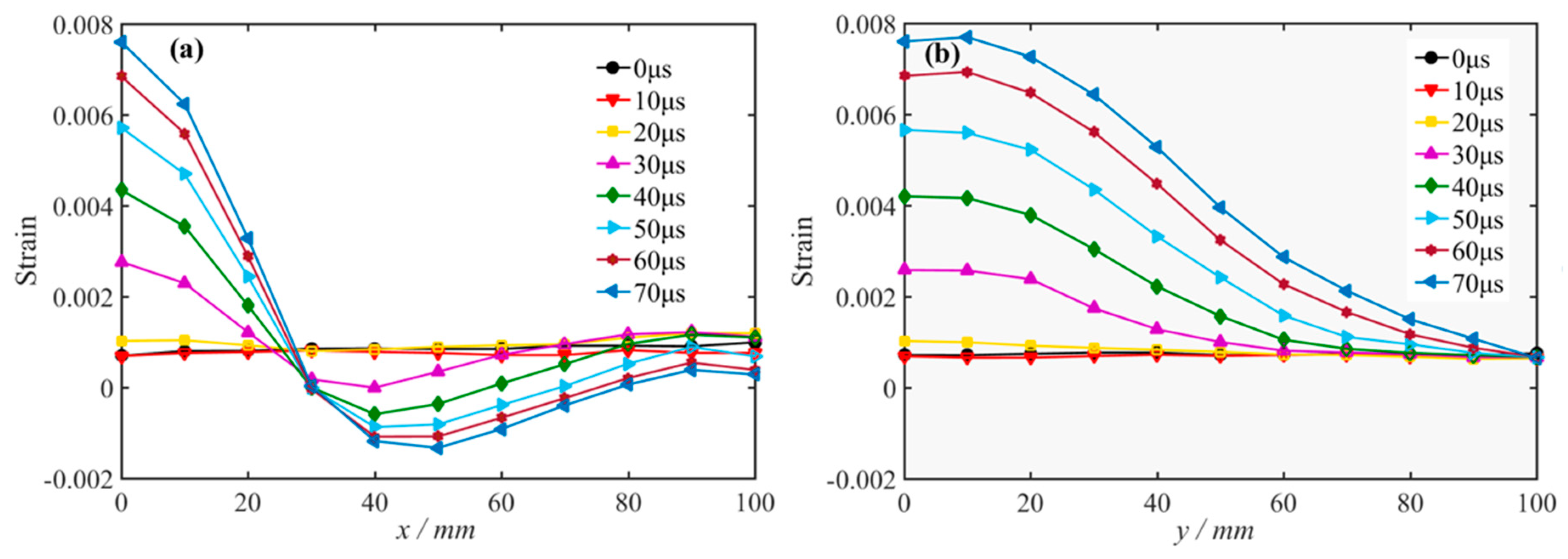
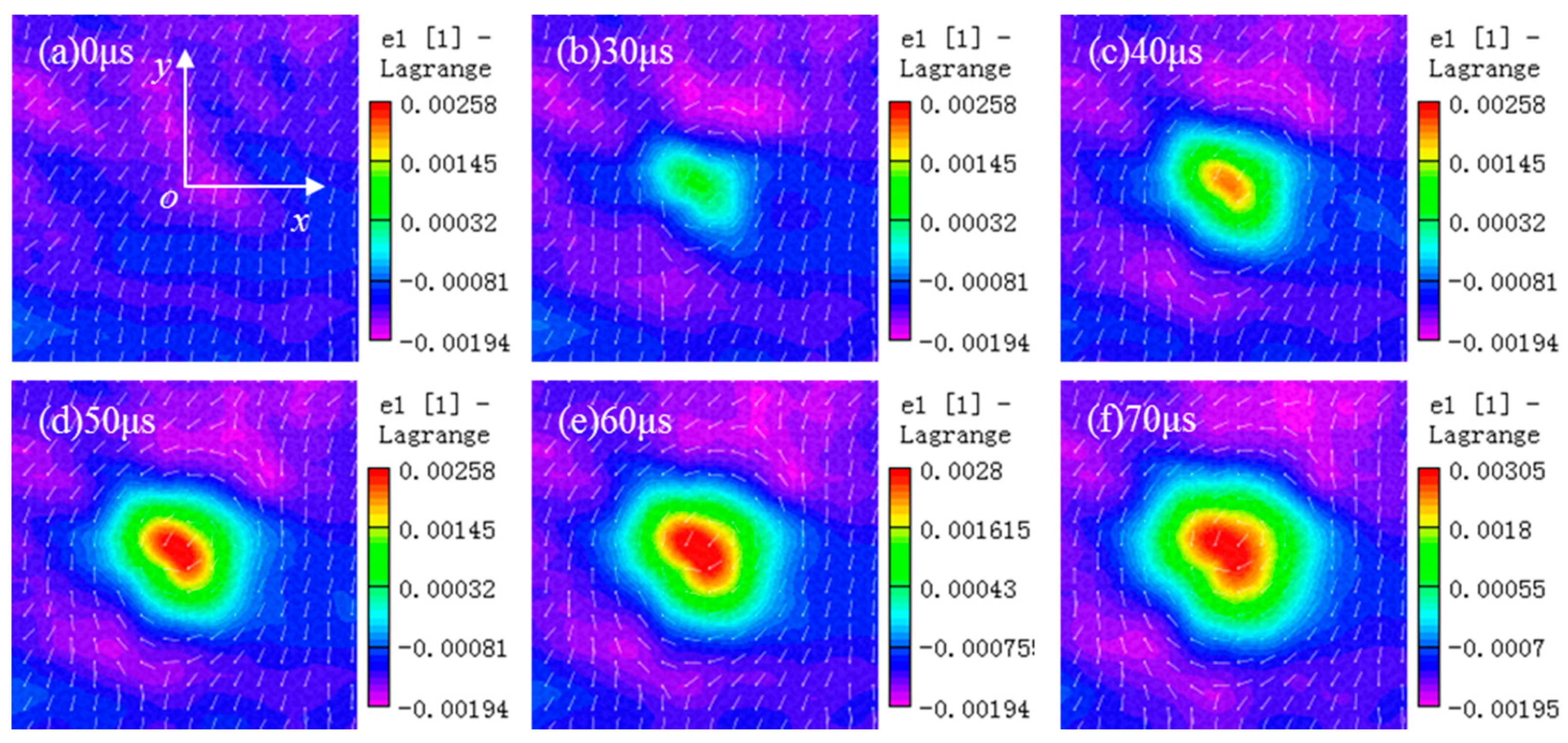
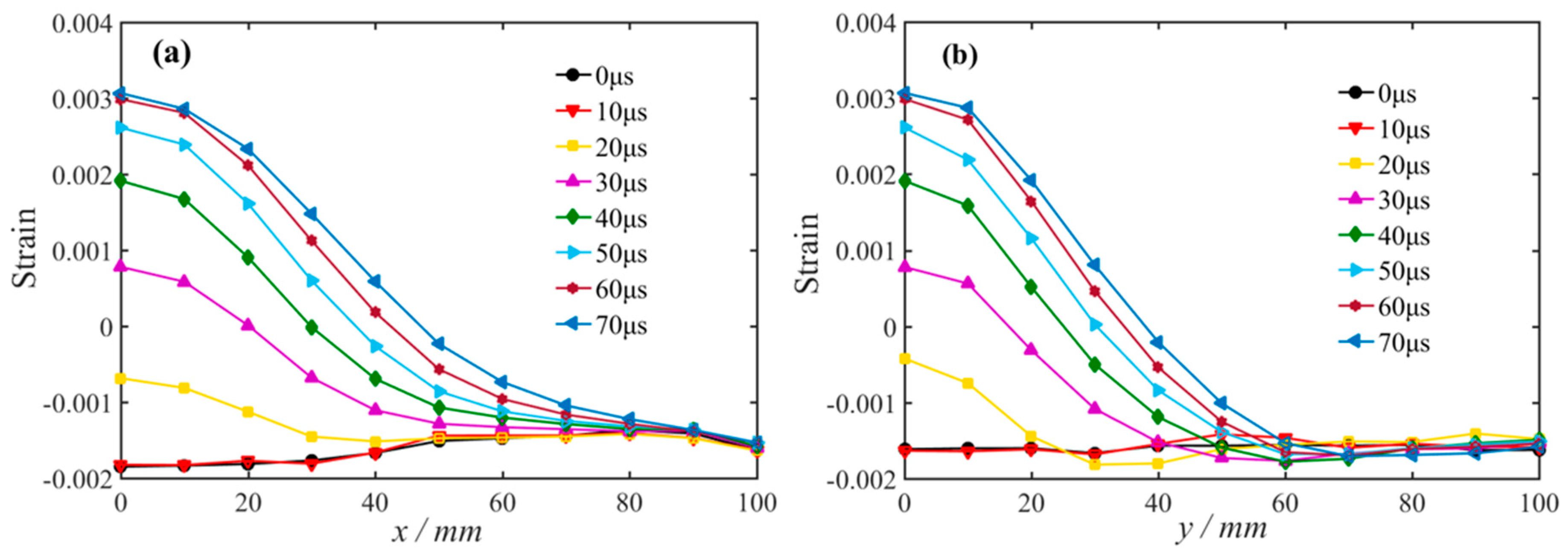
3.3. Strain Field Evolution Characteristics of the Free Surface
3.3.1. Without Static Load
3.3.2. Uniaxial Static Compressive Load
3.3.3. Biaxial Static Compressive Load
4. Discussion
4.1. Dynamic Tensile Fracture Strain and Its Determination Method
4.2. Effect of a High Stress on the Strain Field
5. Conclusions
- (1)
- Static stress controls the pattern of the maximum principal strain field during crater blasting. Without static load and under the equal biaxial compression, an axisymmetric circular tensile strain zone was formed on the free surface. The maximum principal strain was observed at the center of the circle and gradually decreased to the initial static strain with the increase in radius. Under the uniaxial static compression, an elliptical tensile strain field with the long axis parallel to the direction of static stress was formed. The long axis extended with the action time of blasting and the short axis was unchanged during the blasting. In the direction of vertical static stress, the maximum principal strain transitions from tensile strain to compressive strain, forming a concentration zone of compressive strain.
- (2)
- Static stress controls the direction of the maximum principal strain field during crater blasting, which in turn affects the formation of cracks. Without static load and under the equal biaxial compression, the direction of the maximum principal strain was perpendicular to the radius. Without static load, the maximum principal strain at the center of blasthole is greater than the dynamic fracture strain of rock, which led to the formation of randomly distributed radial tensile cracks on the free surface. Under the equal biaxial compressive static load and the stress-strength ratio was 0.42, the maximum principal strain at the center of blasthole did not reach the dynamic fracture strain of rock, which restrained the emergence of tensile cracks on the free surface. Under the uniaxial compressive static load, the maximum principal strain was perpendicular to the static loading direction. Under such tensile strain, initially, tensile cracks parallel to the loading direction emerged and propagated. Finally, only one macroscopic tensile crack parallel to the static loading direction was formed on the free surface and the other cracks were restrained.
- (3)
- Without static load and under the uniaxial compression, the dynamic tensile fracture strain of the sandstone was εtd = 0.00322. This indicated that, under the blasting-induced dynamic loading, the dynamic tensile fracture strain of the rock was independent of the initial static stress state. Therefore, considering the uniqueness of the tensile crack initiation and propagation on the free surface under the uniaxial compression, the proposed method can be used to measure the dynamic tensile fracture strains of various rocks at different loading rates.
Author Contributions
Funding
Conflicts of Interest
References
- Egger, P. Design and construction aspect of deep tunnels. Tunn. Undergr. Space Technol. 2000, 15, 403–408. [Google Scholar] [CrossRef]
- Ranjith, P.; Zhao, J.; Ju, M.; Silva, R.; Rathnaweera, T.; Bandara, A. Opportunities and challenges in deep mining: A brief review. Engineering 2017, 3, 546–551. [Google Scholar] [CrossRef]
- Kang, H.P.; Zhang, X.; Si, L.P.; Wu, Y.Z.; Gao, F.Q. In-situ stress measurements and stress distribution characteristics in underground coal mines in China. Eng. Geol. 2010, 116, 333–345. [Google Scholar] [CrossRef]
- Dong, L.J.; Zou, W.; Li, X.B.; Shu, W.W.; Wang, Z.W. Collaborative localization method using analytical and iterative solutions for microseismic/acoustic emission sources in the rockmass structure for underground mining. Eng. Fract. Mech. 2019, 210, 95–112. [Google Scholar] [CrossRef]
- Kong, P.; Jiang, L.H.; Jiang, J.Q.; Wu, Y.N.; Chen, L.J.; Ning, J.G. Numerical analysis of roadway rock-burst hazard under superposed dynamic and static Loads. Energies 2019, 12, 3761. [Google Scholar] [CrossRef] [Green Version]
- Li, X.B.; Gong, F.Q.; Tao, M.; Dong, L.J.; Du, K.; Ma, C.D.; Zhou, Z.L.; Yin, T.B. Failure mechanism and coupled static-dynamic loading theory in deep hard rock mining: A review. J. Rock Mech. Geotech. Eng. 2017, 9, 767–782. [Google Scholar] [CrossRef]
- Li, H.B.; Li, J.C.; Liu, B. Direct tension test for rock material under different strain rates at quasi-static loads. Rock Mech. Rock Eng. 2013, 46, 1247–1254. [Google Scholar] [CrossRef]
- Peng, J.Y.; Li, Y.H.; Zhang, F.P.; Qiu, Z.G. Failure process and mechanism of sandstone under combined equal biaxial static compression and impact loading. Strain 2018, 54, e12267. [Google Scholar] [CrossRef]
- Feng, P.; Dai, F.; Liu, Y.; Xu, N.W.; Fan, P.X. Effects of coupled static and dynamic strain rates on mechanical behaviors of rock-like specimens containing pre-existing fissures under uniaxial compression. Can. Geotech. J. 2018, 55, 630–652. [Google Scholar] [CrossRef] [Green Version]
- Xie, L.X.; Lu, W.B.; Zhang, Q.B. Analysis of damage mechanisms and optimization of cut blasting design under high in-situ stresses. Tunn. Undergr. Space Technol. 2017, 66, 19–33. [Google Scholar] [CrossRef]
- Li, Y.H.; Peng, J.Y.; Zhang, F.P.; Qiu, Z.G. Cracking behavior and mechanism of sandstone containing a pre-cut hole under combined static and dynamic loading. Eng. Geol. 2016, 213, 64–73. [Google Scholar] [CrossRef]
- Zhu, Z.M. Numerical prediction of crater blasting and bench blasting. Int. J. Rock Mech. Min. Sci. 2009, 46, 1088–1096. [Google Scholar] [CrossRef]
- Ma, G.W.; An, X.M. Numerical simulation of basting-induced rock fractures. Int. J. Rock Mech. Min. Sci. 2008, 45, 966–975. [Google Scholar] [CrossRef]
- Yi, C.P.; Johansson, D.; Greberg, J. Effects of in-situ stresses on the fracturing of rock by blasting. Comput. Geotech. 2018, 104, 321–330. [Google Scholar] [CrossRef]
- Yilmaz, O.; Unlu, T. Three dimensional numerical rock damage analysis under blasting load. Tunn. Undergr. Space Technol. 2013, 38, 266–278. [Google Scholar] [CrossRef]
- Yang, R.S.; Ding, C.X.; Li, Y.L.; Yang, L.Y.; Zhao, Y. Crack propagation behavior in slit charge blasting under high static stress conditions. Int. J. Rock Mech. Min. Sci. 2019, 119, 117–123. [Google Scholar] [CrossRef]
- Yang, L.Y.; Ding, C.X. Fracture mechanism due to blast-imposed loading under high static stress conditions. Int. J. Rock Mech. Min. Sci. 2018, 107, 150–158. [Google Scholar] [CrossRef]
- He, C.L.; Yang, J. Experimental and numerical investigations of dynamic failure process in rock under blast loading. Tunn. Undergr. Space Technol. 2019, 83, 552–564. [Google Scholar] [CrossRef]
- Zhang, F.P.; Peng, J.Y.; Qiu, Z.G.; Chen, Q.K.; Li, Y.H.; Liu, J.P. Rock-like brittle material fragmentation under coupled static stress and spherical charge explosion. Eng. Geol. 2017, 220, 266–273. [Google Scholar] [CrossRef]
- Zhang, F.P.; Yan, G.L.; Peng, J.Y.; Qiu, Z.G.; Dai, X.H. Experimental study on crack formation in sandstone during crater blasting under high geological stress. B Eng. Geol. Environ. 2020, 79, 1323–1332. [Google Scholar] [CrossRef]
- Peng, J.Y.; Zhang, F.P.; Yan, G.L.; Qiu, Z.G.; Dai, X.H. Experimental study on rock-like materials fragmentation by electric explosion method under high stress condition. Powder Technol. 2019, 356, 750–758. [Google Scholar] [CrossRef]
- Gao, G.; Yao, W.; Xia, K.W.; Li, Z. Investigation of the rate dependence of fracture propagation in rocks using digital image correlation (DIC) method. Eng. Fract. Mech. 2015, 138, 146–155. [Google Scholar] [CrossRef] [Green Version]
- Alam, S.Y.; Loukili, A.; Grondin, F.; Roziere, E. Use of the digital image correlation and acoustic emission technique to study the effect of structural size on cracking of reinforced concrete. Eng. Fract. Mech. 2015, 143, 17–31. [Google Scholar] [CrossRef]
- Xing, H.Z.; Zhang, Q.B.; Ruan, D.; Dehkhoda, S.; Lu, G.X.; Zhao, J. Full-field measurement and fracture characterisations of rocks under dynamic loads using high-speed three-dimensional digital image correlation. Int. J. Impact Eng. 2018, 113, 61–72. [Google Scholar] [CrossRef]
- Zhang, H.; Nath, F.; Parrikar, P.N.; Mokhtari, M. Analyzing the validity of brazilian testing using digital image correlation and numerical simulation techniques. Energies 2020, 13, 1441. [Google Scholar] [CrossRef] [Green Version]
- Blaber, J.; Adair, B.; Antoniou, A. Ncorr: Open-source 2D digital image correlation matlab software. Exp. Mech. 2015, 55, 1105–1122. [Google Scholar] [CrossRef]
- Fauchille, A.; Hedan, S.; Valle, V.; Prêt, D.; Cabrera, J.; Cosenza, P. Effect of microstructure on hydric strain in clay rock: A quantitative comparison. Appl. Clay Sci. 2019, 182, 105244. [Google Scholar] [CrossRef]
- Wesseloo, J.; Stacey, T. A reconsideration of the extension strain criterion for fracture and failure of rock. Rock Mech. Rock Eng. 2016, 49, 4667–4679. [Google Scholar] [CrossRef]
- Fujii, Y.; Kiyama, T.; Ishijima, Y.; Kodama, J. Examination of a rock failure criterion based on circumferential tensile strain. Pure Appl. Geophys. 1998, 152, 551–577. [Google Scholar] [CrossRef]

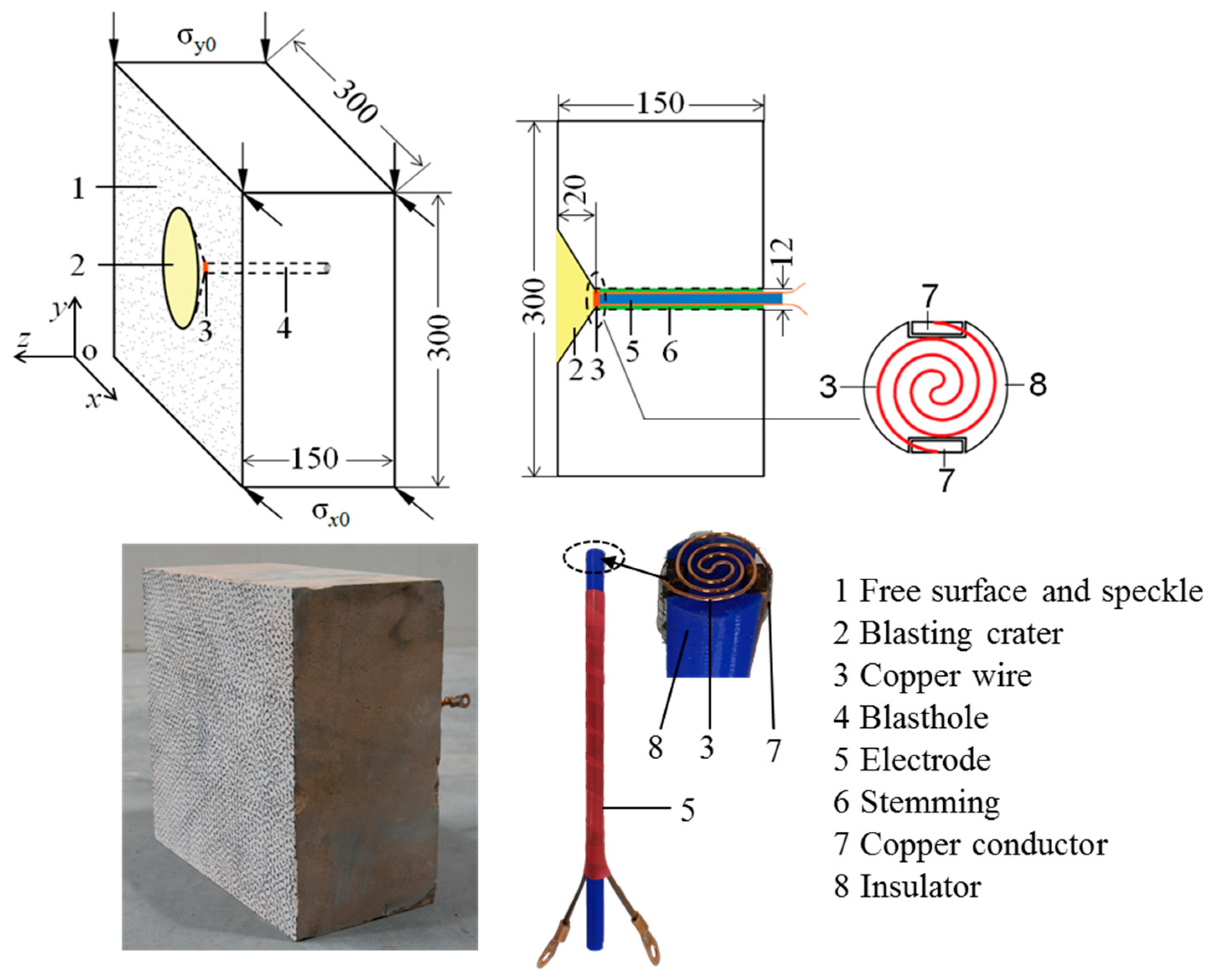






| Camera | Specialised Imaging, Kirana05M |
| Image resolution | 924 × 768 pixels2 |
| Strain measurement accuracy | 3D ≤ 50 με; 2D ≤ 10 με |
| Measurement range | 0.005%–2000% |
| Maximum image acquistion rate | 5 million Hz, with 180 frames per shot |
| Image acquistion rate in experiment | 1 million Hz |
| Lens | Nikon, AF 80–200 mm f/2.8D ED |
| Field-of-view | 320 × 385 mm2 |
| Image scale | 2.4 pixels/mm |
| Stand-off distance | 2.0 m |
| Patterning technique | Base of specimen surface with black ink stamped speckles |
| Pattern feature size (approximate) | 6 pixels |
| DIC software | CSI, Vic-2D 6.0.6 |
| Subset size | 17 pixels/7.08 mm |
| Step size | 7 pixels/2.92 mm |
| Subset shape function | Affine |
| Matching criterion | Zero-normalized squared differences |
| Interpolant | Optimized 8-tap |
| Strain window | 6219 data points |
| Virtual strain gauge size | 600 pixels/250 mm |
| Strain Formulation | Lagrange |
| Displacement noise-floor | 0.01 pixels/0.0042 mm |
| Strain noise-floor | 10 μm/m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Yan, G.; Yang, Q.; Gao, J.; Li, Y. Strain Field Evolution Characteristics of Free Surface during Crater Blasting in Sandstone under High Stress. Appl. Sci. 2020, 10, 6285. https://doi.org/10.3390/app10186285
Zhang F, Yan G, Yang Q, Gao J, Li Y. Strain Field Evolution Characteristics of Free Surface during Crater Blasting in Sandstone under High Stress. Applied Sciences. 2020; 10(18):6285. https://doi.org/10.3390/app10186285
Chicago/Turabian StyleZhang, Fengpeng, Guangliang Yan, Qibo Yang, Jikai Gao, and Yuanhui Li. 2020. "Strain Field Evolution Characteristics of Free Surface during Crater Blasting in Sandstone under High Stress" Applied Sciences 10, no. 18: 6285. https://doi.org/10.3390/app10186285




