UWB Indoor Localization Using Deep Learning LSTM Networks

Abstract

Localization using ultra-wide band (UWB) signals gives accurate position results for indoor localization. The penetrating characteristics of UWB pulses reduce the multipath effects and identify the user position with precise accuracy. In UWB-based localization, the localization accuracy depends on the distance estimation between anchor nodes (ANs) and the UWB tag based on the time of arrival (TOA) of UWB pulses. The TOA errors in the UWB system, reduce the distance estimation accuracy from ANs to the UWB tag and adds the localization error to the system. The position accuracy of a UWB system also depends on the line of sight (LOS) conditions between the UWB anchors and tag, and the computational complexity of localization algorithms used in the UWB system. To overcome these UWB system challenges for indoor localization, we propose a deep learning approach for UWB localization. The proposed deep learning model uses a long short-term memory (LSTM) network for predicting the user position. The proposed LSTM model receives the distance values from TOA-distance model of the UWB system and predicts the current user position. The performance of the proposed LSTM model-based UWB localization system is analyzed in terms of learning rate, optimizer, loss function, batch size, number of hidden nodes, timesteps, and we also compared the mean localization accuracy of the system with different deep learning models and conventional UWB localization approaches. The simulation results show that the proposed UWB localization approach achieved a 7 cm mean localization error as compared to conventional UWB localization approaches.

1. Introduction

Recent advancements in indoor localization technologies [1] give accurate position results when the GPS signals are unable to detect user position in an indoor scenario. The most popular building dependent localization technology is the ultra-wideband (UWB) localization system. In UWB localization, multiple anchors are placed in the experiment area and the user uses a UWB tag to communicate with anchors. The anchors and the tag communicate through UWB signals and the time of arrival (TOA) [2] of UWB signals are used to estimate the distance of the user from anchors. The position accuracy of a UWB system depends on the UWB signal shapes, TOA of UWB signals and user distance estimation from the anchors. For an accurate user position estimation in UWB systems, it is necessary to estimate the user distance with a minimum error. In UWB localization, the localization algorithms use the user distance information from the TOA-distance model. The trilateration algorithm is the most common localization algorithm used in UWB localization. However, the position accuracy of the trilateration algorithm depends on the user distance from the anchors [3]. The multipath effects, channel conditions between anchors and tag, and the UWB signal shapes affect the distance estimation accuracy. This leads to a high position error in the UWB localization systems.

To reduce the user position errors in the UWB system, we propose a deep learning approach to UWB localization. The proposed model consists of a deep neural network which takes as input the distance information from the TOA-distance model and predicts the user positions. The proposed model uses a two layer long short-term memory (LSTM) network [4] which identifies the accurate user positions. As compared to neural network (NN), the LSTM has feedback loop which serves as a memory and gives better performance for time series analysis. The flexibility in controlling the input data from the LSTM model gives a better localization performance than other models. The constant error backpropagation within memory cells results in LSTM model can able to bridge very long-time lags for UWB localization. The unique features of LSTM model show that it is the best choice for our localization purpose.

Deep learning for UWB localization has been investigated through several approaches to improve localization performance. Many researchers proposed different deep learning approaches such as convolutional neural networks (CNN) for UWB transmitter-receiver distance estimation [5], non-line of sight (NLOS) channel classification using channel impulse response (CIR) information [6,7] and the neural network for UWB fingerprint-based localization [8]. However, to the best of our knowledge, there is no comparative analysis of hyperparameter tuning for LSTM based UWB localization. Therefore, it is necessary to investigate the best hyperparameters for LSTM based UWB localization and this paper analyses the performance of LSTM deep learning networks in terms of learning rate, optimizer, loss function, batch size, number of hidden nodes and timesteps. The best parameters for LSTM networks are identified through several simulation results and finally, we compare the proposed model prediction results with conventional UWB localization approaches such as linearized least square estimation (LLSE), fingerprint estimation (FPE), maximum likelihood estimation (MLE) and weighted centroid estimation (WCE) algorithms [9]. The performance of the LSTM model also analyzed by mean localization error with a different number of LSTM layers, training and testing time of UWB data in LSTM model and the mean localization error with a different number of anchors. Through extensive simulations, we demonstrated the superior performance of the proposed LSTM model. The following are the main contributions to this paper:

• We simulated a UWB system with three anchors and one tag, and generated Gaussian pulses as UWB signals. The Gaussian pulses transmitted through UWB channel conditions from anchors to tag and estimated the TOA of UWB pulses.
• We formulated a TOA-distance model and estimated the tag distance from anchors. The estimated tag distances from anchors are used for predicting the user position.
• We introduced the LSTM deep learning architecture for UWB localization. The performance of the LSTM architecture was analyzed and we estimated the best parameters for the LSTM model.

The rest of the paper is organized as follows—Section 2 summarizes the previous work on UWB localization, Section 3 discusses the proposed UWB indoor localization approach using deep learning LSTM networks. The analysis of simulation results is provided in Section 4. Finally, the conclusions are summarized in Section 5.

2. Related Work

Indoor localization using UWB measurement has been studied in the past and in recent times based on TOA [10], time difference of arrival (TDOA) [11], phase of arrival (PoA) [12], angle of arrival (AOA) [13], joint TOA and AOA [14] and UWB localization algorithms have also been studied [15,16]. In this section, we discuss different UWB localization systems that leverage the advantages of deep learning networks.

The idea of machine learning in the UWB indoor localization research area was proposed in Reference [17] and this proposed system combines grid-search-based kernel support vector machine and principle component analysis (PCA). The results from Reference [17] show that the proposed approach reduces the localization error and improves the computational efficiency when compared to k-nearest neighbor (kNN), back propagation neural network (BPNN) and support vector machine (SVM) based methods. An SVM-based localization approach which classify the UWB NLOS conditions for indoor localization is presented in Reference [18]. The SVM model in Reference [18] reached 92% average identification accuracy for NLOS conditions and improved the UWB position accuracy in multipath conditions. To improve the localization accuracy of the UWB system during NLOS conditions, A two stage SVM classification for UWB LOS/NLOS channel conditions is discussed in Reference [19]. The system from Reference [19] shows 93.7% efficiency for identifying the LOS/NLOS channel conditions. However, selecting the adequate kernel and the parameter optimization are the major challenges faced by the SVM based localization systems. A logistic regression-based localization approach is an alternative way to improve the UWB localization performance for the non-line-of-sight (NLOS) condition. The regression model presented in Reference [20] addressed the NLOS detection error mitigation of differential time of arrival (TDoA) topologies and suppresses the NLOS error up to 80%. In Reference [21], the authors also introduced another regression-based localization method for identifying the LOS conditions. The PCA, kNN, SVM and logistic regression approaches gives better performance for UWB localization, however, the multipath effects, signal interference, sensitive to channel inconsistency and computational complexity of the models add localization errors to the UWB system. To extract the correct ToA during multipath scenarios, a signal processing method that uses deep learning to estimate the absolute UWB tag position directly from the raw channel impulse response (CIR) data is proposed in Reference [22]. The localization system explained in Reference [22] uses convolutional neural network (CNN) and achieved 17.3 cm mean absolute localization error for NLOS conditions. However, the overfitting & underfitting, parameter tuning and processing time of data from CNN models give challenges to the UWB localization. Most recent works on deep learning for UWB localization are explained in References [23,24,25]. The discussed localization systems from References [23,24,25] effectively minimize the ranging errors and computational burden and achieve excellent localization performance with much lower network complexity for UWB indoor localization.

The UWB localization systems discussed in the related works addressed localization accuracy challenges and proposed a number of systems to improve indoor position accuracy. However, the UWB system still needs improvement in terms localization accuracy. Therefore, it is necessary to propose a new localization approach for UWB based indoor localization. To reduce the localization error, this paper proposes an LSTM based localization approach based on the simulation environment. The simulation results indicate that the proposed approach gives reasonable position accuracy for indoor localization and reduces the UWB localization errors.

3. The Conventional and Proposed UWB Localization Approaches

Conventional UWB localization approaches tend to use different localization algorithms in the system controller to estimate the current user positions. The positional accuracy of the conventional methods depends on the type of the localization algorithm and the configuration of the system controller. To improve the indoor position accuracy for UWB localization, we used deep learning instead of localization algorithms and this proposed UWB indoor localization system leverages the advantages of LSTM networks in predicting user positions. As compared to the conventional UWB system, the proposed system utilizes a deep learning architecture in the system controller to predict the user position. The deep learning model is trained on user distance from anchors and gives accurate position results. Figure 1 shows the conventional and proposed UWB localization systems.

The proposed model consists of anchor-tag communication using UWB pulses, the TOA-distance model and deep learning system for user position prediction. First, we place the anchor nodes (ANs) with known coordinates in the experiment area. The UWB tag sends UWB pulses to the ANs. All ANs receive UWB pulses and estimate the distances from each AN. Since the anchors receive UWB pulses at different intervals from the UWB tag, the signals arrive at each anchor at a different time. The signal arrival of time from UWB tag is multiplied by the constant speed of light in the air resulting in the ANs and UWB tag distances. To estimate the UWB tag position, the concept of trilateration is used. To use trilateration, it is necessary to use at least three anchors in the experiment area. In our simulation, we created an experiment area with three anchors and the anchors were placed in known coordinates to cover the entire experiment area. To generate UWB pulses, we used Gaussian pulses with the IEEE 802.15.4a UWB system standard. The generated UWB pulses transmitted from the UWB tag to all anchors. The UWB tag moved in the predefined paths and sends pulses to the ANs. The ANs use UWB TOA information and estimate the tag distances from ANs. The distance information matrix from TOA-distance model is used as the input to the deep learning system. The deep learning system uses two LSTM layers to predict the tag’s x and y positions. The LSTM layer takes three inputs, the three distance values from three anchors, and predicts the current UWB tag position. The proposed LSTM model predicts accurate tag position results with minimal localization errors. The experiment results show that the proposed deep learning approach solved the LOS problems associated with UWB localization systems and reduces the computational complexity of localization algorithms. As compared to conventional localization approaches, the proposed method can be easily used for complex trajectories and estimate the user position with minimum position errors.

3.1. UWB Model

The model presented in Reference [26] is used for the UWB simulation. Figure 2 shows the flow chart of the UWB localization system.

The UWB localization system consists of UWB signal generation, transmission of UWB signals through indoor channel, cross relation of received UWB signals with reference signal, TOA estimation of UWB signals, distance estimation from TOA and finally estimate the current user position using the trilateration approach. To generate the UWB pulses as input signal for UWB simulation, we use the Gaussian pulse and is defined as

$$y\left(t\right)=\frac{A}{\sqrt{2\pi {\sigma }^2}}{e}^{-\left(\frac{t^2}{2{\sigma }^2}\right)},$$

(1)

where A is the amplitude of the signal and $\sigma$ is the standard deviation related to the pulse shape factor. The simulation uses the pulse width of 0.5 $ns$ and Figure 3 shows the generated UWB pulse for transmission.

The UWB transmitted signal is expressed as [26]

$$s\left(t\right)=\sum _{i=0}^{N-1}p\left(t-i\times T_{\mathrm{int}}\right),$$

(2)

where $p\left(t\right)$ is the UWB pulse, $T_{\mathrm{int}}$ is the sum of guard time and pulse width, N is the number of pulses. Then the received signal is expressed as

$$r\left(t\right)=h\left(t\right)\times s\left(t\right)+n\left(t\right),$$

(3)

where $h\left(t\right)$ is the channel impulse response and $n\left(t\right)$ is the AWGN noise. When we consider the average time of received signal, the noise term is eliminated and is expressed as

$$r_{\mathrm{avr}}\left(t\right)=\sum _{i=0}^{N-1}\left\{p\left(t\right)\times h_i\left(t+i\times T_{\mathrm{int}}\right)\right\}.$$

(4)

After the average operation of received signal, we perform a correlation between the averaged signal and the template signal and is expressed as

$$S_{\mathrm{Crr}}\left(t\right)={\int }_0^{T_{\mathrm{int}}}{r}_{\mathrm{avr}}\left(\tau \right)\times p\left(t-\tau \right)d\tau .$$

(5)

The correlated output signal from one anchor node to UWB tag is shown in Figure 4.

The correlated output signal is used in the peak detector for estimating the TOA of signal. In the simulation process, we considered IEEE 802.15 4a UWB channel model [27], which characterizes industrial LOS environment. The UWB pulses propagate through a large number of paths and the channel impulse response is expressed as

$$h\left(t\right)=\sum _{l=0}^L\sum _{k=0}^k{\alpha }_{k,l}exp\left(j{\varphi }_{k,l}\right)\delta \left(t-T_l-{\tau }_{k,l}\right),$$

(6)

where ${\alpha }_{k,l}$ is the multipath gain coefficient, $T_l$ is the delay of the $l^{th}$ cluster and ${\tau }_{k,l}$ is the delay of the $k^{th}$ multipath component relative to the $l^{th}$ cluster arrival time $\left(T_l\right)$. The phases ${\varphi }_{k,l}$ are uniformly distributed in the range $[0,2\pi ]$ and the number of clusters L are assumed to be the Poisson distribution.

Table 1. UWB simulation parameter values.

UWB Simulation Parameter	Value
Speed of Light	$3\times {10}^8$ m/s
Pulse shape	Gaussian pulse
Number of anchors	3
Coordinates of anchors $(x,y)$	[5 18; 18 5; 18 18]
Tag’s initial coordinate $(x,y)$	[0 2]
Number of bits	100
Pulse repetition interval	200 ns
SNR range (in dB)	3 dB
Sample rate	20 GHz
Pulse width	0.5 ns

shows the parameter settings for the UWB simulation.

The overall UWB simulation stages are summarized in Figure 5. To generate the UWB simulation data, our simulation ran on MATLAB and defined an indoor experiment area in the MATLAB simulation environment. The anchors positions are defined and the UWB tag moved in the predefined trajectories. In the UWB transmitter, we generated Gaussian pulses for transmission and these signals are transmitted through the indoor UWB channel. On the receiver side, the UWB receiver receives the UWB signal with Gaussian noise through the UWB channel. To remove the Gaussian noise, the receiver took the average of the signal and passed the signal onto the correlation block. In the correlation block, correlation between the received signals and reference signal is performed and the correlation output is used in the peak detector block. The peak detector block estimates the TOA of the UWB signal based on the threshold setting and the overall UWB transmission-reception is illustrated in Figure 5 as a block diagram.

3.2. Trilateration Approach for UWB Localization

To train the proposed LSTM network with distance information from anchors and user position coordinates, we use trilateration. The trilateration algorithm estimates the true trajectory coordinates and many position coordinates from trajectory which covers the entire experiment area. The UWB tag distance from anchors and the user positions from trilateration approach are used in training the LSTM model. Figure 6 shows the trilateration approach for UWB localization.

The distance $d_i$ between the UWB tag $P(x_p,y_p)$ and the anchors $R_i(x_i,y_i)$ is expressed as

$$d_i^2={(x_i-x_p)}^2+{(y_i-y_p)}^2.$$

(7)

The expanded form of (7) is

$$d_i^2=x_i^2+x_p^2-2x_i{x}_p+y_i^2+y_p^2-2y_i{y}_p.$$

(8)

When we consider a reference point K, then (8) can be expressed as

$$d_k^2=x_k^2+x_p^2-2x_k{x}_p+y_k^2+y_p^2-2y_k{y}_p.$$

(9)

Subtracting (9) from (8), we get

$$d_i^2-d_k^2+x_k^2+y_k^2-x_i^2-y_i^2=2(x_k-x_i)x_p+2(y_k-y_i)y_p.$$

(10)

Considering $i=1$ and varying index $k=2,3$ we obtain

$$\left[\begin{array}{cc}2(x_2-x_1)& 2(y_2-y_1)\\ 2(x_3-x_1)& 2(y_3-y_1)\end{array}\right]\left[\begin{array}{c}{x}_p\\ y_p\end{array}\right]=\left[\begin{array}{c}{d}_1^2-d_2^2+x_2^2+y_2^2-x_1^2-y_1^2\\ d_1^2-d_3^2+x_3^2+y_3^2-x_1^2-y_1^2\end{array}\right].$$

(11)

The coordinates $P(x_p,y_p)$ of the UWB tag can be obtained by solving the above system of equations. We can obtain a linear equation with three unknowns, $Ax=b$. The A, x and b values of liner equation is expressed

$$A=\left[\begin{array}{cc}2\left(x_2-x_1\right)& 2\left(y_2-y_1\right)\\ 2\left(x_3-x_1\right)& 2\left(y_3-y_1\right)\end{array}\right]$$

(12)

$$x=\left[\begin{array}{c}{x}_p\\ y_p\end{array}\right]$$

(13)

$$b=\left[\begin{array}{c}{d}_1^2-d_2^2+x_2^2+y_2^2-x_1^2-y_1^2\\ d_1^2-d_3^2+x_3^2+y_3^2-x_1^2-y_1^2\end{array}\right].$$

(14)

The solution of the equations can be $(x_p,y_p)$ that minimizes the $\delta$ defined by the following

$$\delta ={(Ax-b)}^T(Ax-b)$$

(15)

$$x={\left[\begin{array}{cc}{x}_p& y_p\end{array}\right]}^T.$$

(16)

Applying MMSE (Minimum Mean Square Error) method, we can obtain x with the following expression

$$x={\left(A^{T}A\right)}^{-1}{A}^{T}b.$$

(17)

For more details on trilateration algorithm implementation, refer to our previous works in References [28,29].

3.3. LSTM Based UWB Localization

The UWB data is time dependent and LSTM model is the best deep learning model for UWB localization as compared to recurrent neural networks (RNN) [30], and extreme learning machine (ELM) [31] models. LSTM is the improved form of RNN and it is used to connect historical information to the current input. The long-term dependence problem of RNN makes them unsuitable for UWB-based localization systems and the unique long-time dependence characteristics of LSTM [32] gives accurate localization results when compared to other deep learning models. The LSTM result shows that it reduces the vanishing gradient problem [33] which exists when we use RNN networks for UWB localization. In this paper we followed the LSTM model presented in References [34,35] for deep LSTM implementation. The LSTM model consists of a layered structure with a state c (cell state) in each hidden layer. The output of the LSTM model is a regression output and not a classification one [36].

In a particular UWB indoor localization scenario, the number of anchors is N, the UWB localization could be estimated only with $N\in \left\{3,4,5,6,\dots \right\}$. Assume that the localization system uses only one UWB tag, the distance received from anchor i, $i\in \left\{1,2,3,\dots N\right\}$, can be written as $\left[D_{i-1},D_{i-2},\dots ,D_{i-M_i}\right]$, where $M_i$ is the distance from anchor i. The distance measurements from TOA- distance model converts into a fingerprint map and the fingerprint map in a certain location $(x,y)$ is expressed as

$$D_{x,y}=\left[\begin{array}{c}{D}_{1-1},D_{1-2},\dots ,D_{1-M_1},\\ D_{2-1},D_{2-2},\dots ,D_{2-M_2},\\ \dots ,\\ D_{N-1},D_{N-2},\dots ,D_{N-M_N}\end{array}\right].$$

(18)

Let t denote the time interval of the current fingerprint, UWB distance data and $D_{(xt,yt)},h_{(t-1)}$ and $c_{(t-1)}$ be the current network input values. The output of the LSTM network is expressed as [35]

$$h_t=\left[{\tilde{x}}_t,{\tilde{y}}_t\right],$$

(19)

where ${\tilde{x}}_t$ and ${\tilde{y}}_t$ are the coordinates of the predicted user position at a time t. The value of $c_t$ is defined by the forget gate (FG) and input gate (IG) functions in the LSTM. The FG function saves the information of $c_{(t-1)}$ to $c_t$ and IG saves the information $c_t$ to $h_t$. The calculation process in FG is expressed as

$$f_t=\sigma \left(w_f\times \left[h_{t-1},D_{xt,yt}\right]+b_f\right),$$

(20)

where $\sigma$ is the rectified linear unit (ReLU), $w_f$ is the weight matrix and $b_f$ is the offset item. The calculation process in IG function is expressed as

$$g_t=\sigma \left(w_g\times \left[h_{t-1},D_{xt,yt}\right]+b_g\right),$$

(21)

where $w_g$ is the weight matrix of IG and $b_g$ is the offset. The cell state in forward direction of LSTM is expressed as

$${\tilde{c}}_t=tanh\left(w_c\times \left[h_{t-1},D_{xt,yt}\right]+b_c\right),$$

(22)

$$c_t=f_t\times c_{t-1}+g_t\times {\tilde{c}}_t,$$

(23)

where ${\tilde{c}}_t$ and $c_t$ are input and output of the cell state at time t. The long term message in LSTM network is formed from an iterative process and the output function $\left(o_t\right)$ is expressed as

$$o_t=\sigma \left(w_o\times \left[h_{t-1},D_{xt,yt}\right]+b_o\right),$$

(24)

where $W_o$ and $b_o$ are weight matrix and offset which are estimated from training process. The last stage of LSTM forward process is to estimate $h_t$ from cell state and network and is defined as

$$h_t=o_t\times tanh\left(c_t\right).$$

(25)

Figure 7 shows the overall forward propagation of the LSTM network. The output of this network is the user x and y position results $\left[{\tilde{x}}_t,{\tilde{y}}_t\right]$.

The error function from Figure 7 is expressed in time dimension and layer structure and is given by

$$E_t=\sqrt{{\left(x_t-{\tilde{x}}_t\right)}^2+{\left(y_t-{\tilde{y}}_t\right)}^2}.$$

(26)

The input of LSTM network is the combination of $h_{(t-1)}$ and $D_{(xt,yt)},W_f,W_g,W_c$ and $W_o$. These values can be divided into $W_{f}x,W_{f}h,W_{g}x,W_{g}h,W_{c}h,W_{f}ox$ and $W_{o}h$. An example of backpropagation using $W_{o}h$ is expressed as

$$\frac{\partial E_t}{\partial W_{oh,t}}=\frac{\partial E_t}{\partial ne{t}_{o,t}}\times \frac{\partial ne{t}_{o,t}}{\partial W_{oh,t}}$$

(27)

$$\frac{\partial E_t}{\partial W_{oh,t}}={\delta }_{o,t}^T\times h_{t-1}^T$$

(28)

$$\frac{\partial E_t}{\partial W_{oh,t}}={\delta }_t^T\times tanh\left(c_t\right)\times o_t\times \left(1-o_t\right)\times h_{t-1}^T,$$

(29)

where ${\delta }_t^T$ is the error term in time dimension of layer o and is expressed as

$${\delta }_{o,t}^T=\prod _{t_o}^{t-1}({\delta }_{o,t}^T{W}_{oh}+{\delta }_{f,t}^T{W}_{fh}+{\delta }_{g,t}^T{W}_{gh}+{\delta }_{\tilde{c},t}^T{W}_{ch}).$$

(30)

The LSTM network builds the regression model based on the iteration and the initial weight settings. The ReLu function in the model reduces the vanishing gradient problems and converges faster than RNN models. The localization algorithm using LSTM network is summarized in Algorithm 1.

Algorithm 1 LSTM Based Localization.

Input: $D_{(xt,yt)}$ in each time slot, M output: Regression model based on LSTM Collect the distance values from the trajectory when the user moves and repeat this step until the amount of data in this trajectory is enough. Generate the distance database in each time slot Initialize the structure of LSTM Train LSTM and compute the LSTM parameters Collect distance data for testing, then verify the trained LSTM model in step 4 Change the LSTM parameters and estimate the best parameters for accurate localization using steps 5 and 6.

From Algorithm 1, it can be seen that the proposed approach uses the distance values from anchors to tag for localization. When the UWB system reaches the enough number of distance data from the simulation trajectory, the system initializes the two-layer LSTM model. The total amount of data collected from the trajectory is divided into train data and test data. The LSTM model uses the train data for training the model with initial hyperparameter settings. Next, the system changes the hyperparameter values by several simulations and reach the best LSTM hyperparameter values for localization. After the hyperparameter estimation, the system collects another set of data for testing. Using the test data, the system verifies the LSTM model and predicts the user positions.

Localization using the LSTM model is efficient when the user moves a certain trajectory in the experiment area. Figure 8 shows the LSTM structure used for the localization.

The model structure of LSTM from Figure 8 shows that the proposed model uses two LSTM layers after the input layer. The two LSTM layers improve the performance of our model and gives reasonable position results than conventional neural network models. To compensate the overfitting problem, we add a dropout layer after each LSTM layer and these dropout layers enhance the localization accuracy of our proposed model. For the last layer of the proposed network, we use a time distributed dense layer which enables an interaction between the values within its own timesteps.

4. Simulation Results and Analysis

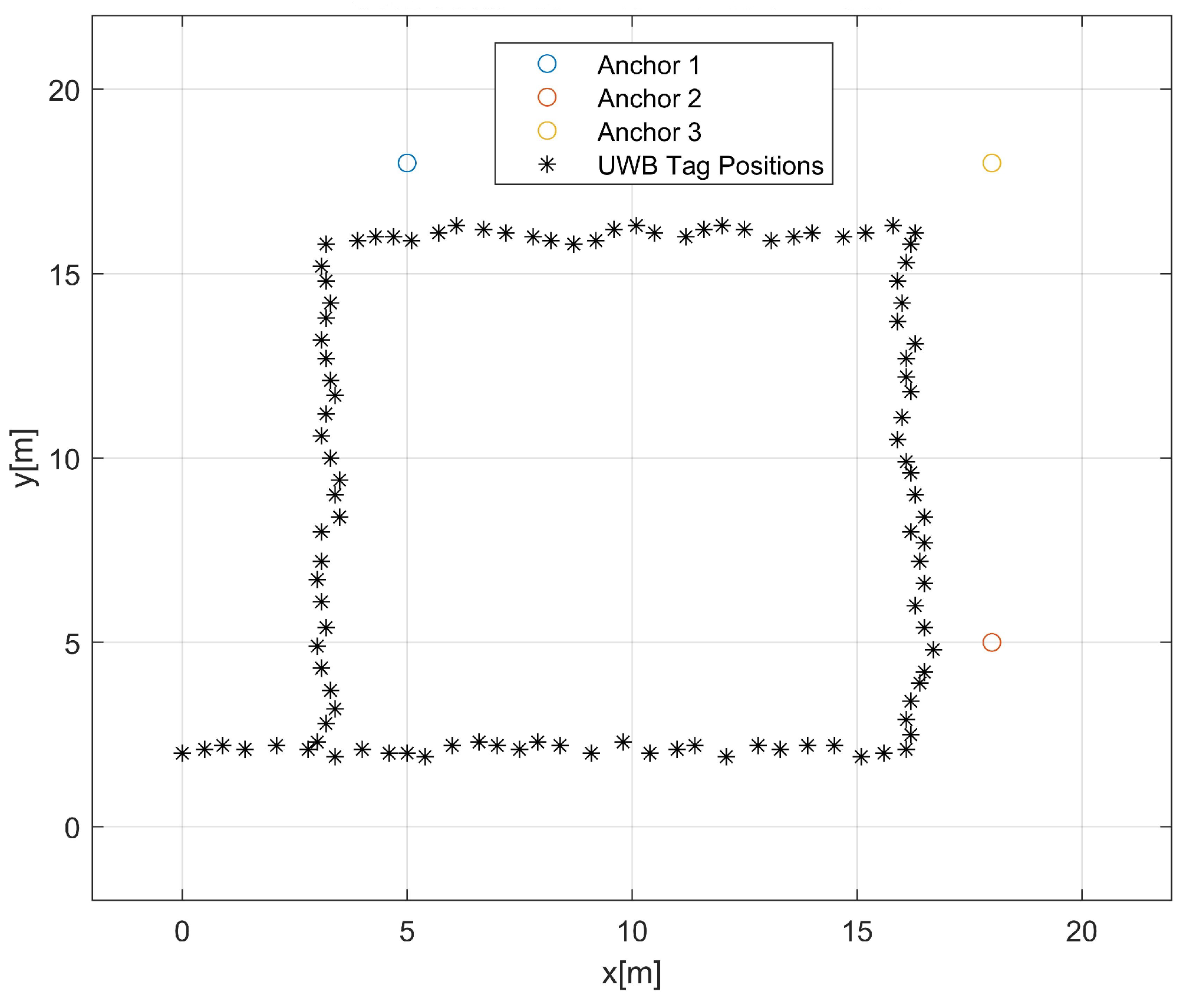
To evaluate the performance and position accuracy of our proposed LSTM model, we used the MATLAB R2019b (MathWorks, 1 Apple Hill Dr, Natick, MA 01760, United States, 2019) simulation environment with all built in tools. We simulated an experiment area with UWB anchors and a tag. Figure 9 indicates the UWB anchors and tag positions from a MATLAB simulation. In Figure 9, the starting position of the UWB tag is defined as (0, 2) and moved the UWB tag at a constant speed. We placed three anchors in the simulation environment based on the UWB tag motion. The positions of the anchors depend on the UWB tag motion and which covers the simulation environment. The UWB tag communicates with three anchors and estimates the tag distance from all anchors. The small circles in the Figure 9 show the anchor positions and the black star marks indicate the UWB tag motion. We moved the UWB tag in a random position based on a rectangular motion.

The TOA-distance model from the simulation estimates the distances for all tag positions in the experiment area and used the distances as training data. The data sample consists of 2582 samples with three distance and user x and y position values. Seventy-five percent of data samples were used for training the model and 25% samples used in testing. The LSTM model uses three input neurons for the three distance values from anchors and two output neurons to predict the user x and y positions. The performance of proposed LSTM model was analyzed in terms of learning rate, optimizer, loss function, batch size, number of hidden nodes and timesteps. Figure 10 shows the localization accuracy of training data with varies learning rates.

From Figure 10, it can be seen that the accuracy of the system increases with a lower learning rate. For large learning rates, the model tends to be unstable during training and with very low rates, the system fails to train the model. To compensate for these issues, we simulated different learning rates and obtained the optimum learning rate for training the model through a process called hyperparameter tuning. In our simulation, we selected 0.0001 value as learning rate for training the model. The selected learning rate controls how much the model responds to the output error when the model weights are updated.

Next, we analyzed the significance of different optimizers for the LSTM model. The optimizers play a very crucial role to increase the accuracy of the model. When we consider deep neural networks for localization, the neural networks have the tendency to either vanish or explode as the energy is propagated through the function. When the function is more complex, the network performs worse due to the cumulative nature. To avoid the vanishing and exploding gradient issue, we use a suitable optimizer and it is necessary to identify the best optimizer for localization. In our simulation we analysed the performance of the stochastic gradient descent (SGD), Root Mean Square Propagation (RMSProp), adaptive gradient algorithm (Adagrad), adaptive moment estimation (Adam), nesterov-accelerated adaptive moment estimation (Nadam), Adadelta and Adamax. Figure 11 shows the performance of these different optimizers for the LSTM model.

From Figure 11, the Nadam optimizer gives best localization accuracy and a lower loss value when compared to other optimizers. The SGD and Adadelta shows the worst performance. The optimizers Adam, Adamax, Adagrad and RMSProp are very similar algorithms and RMSProp was found to slightly outperform the other optimizers.

Next, we consider the effect of different loss functions for the LSTM model. The loss function used in the deep leaning model reduces the error in the prediction. For the regression loss function, networks use mean squared error loss (MSE), mean squared logarithmic error loss (MSLE) and mean absolute error loss (MAE). To find the best loss function, we analysed the effect of different loss functions and Figure 12 shows their performance.

From Figure 12, the MSLE loss function shows a slightly better performance than MSE but much better performance than MAE loss function. However, the MSLE loss function has high possibilities to overfit and is commonly used to predict large values. The results from MSE are slightly similar to MSLE and it has a lower probability to overfit. The performance and convergence behavior of our model suggests that MSE loss function is a good match for training the LSTM network for our regression problem. The results from the MAE loss function shows that it is not a good fit for our LSTM model.

Another important hyperparameter that affects the performance of the LSTM model is the batch size and it plays a major role in training the model faster. The batch size controls the amount of data samples that will be propagated through the LSTM networks. If we use a larger batch size to train the model, it increases the computational speed of the training data. However, a large batch size leads to poor generalization and the learning process converges slowly. Figure 13 shows the localization accuracy and network loss of training data in terms of the batch size.

From Figure 13, it can be seen that the lower batch size values give a learning process that converges quickly. The lower batch size value also uses less memory for training. Since the network is trained by fewer samples, the overall training procedure requires less memory. However, the lower value of batch size is not guaranteed to converge to the global optima. In our simulation, we used the batch size as 5 without any computational constraints.

The performance of LSTM model also depends on the number of hidden nodes. The number of hidden nodes depend on the complexity of the dataset, number of input features, number of data points and the data generating process. To find the optimum number of hidden nodes without overfitting, the following expression is used.

$$N_h=\frac{N_s}{\left(\alpha \times \left(N_i+N_o\right)\right)},$$

(31)

where $N_i$ is the number of input neurons, $N_o$ is the output neurons, $N_s$ is the number of samples in training data and $\alpha$ is the arbitrary scaling factor usually 2–10. Figure 14 shows the localization accuracy and network loss of training data in terms of number of hidden nodes.

In Figure 14, the localization accuracy during the training in terms of epochs with varying hidden nodes from 16 to 512 with batch size of 5 is shown. If we use few hidden nodes, the result shows a high training error and high generalization error due to underfitting. On the other hand, for the high number of hidden nodes, the result shows low training error and high generalization error due to over fitting. Through our several simulation results, we obtained the number of hidden node as 256.

The localization accuracy of training data for different timesteps also affects the performance of LSTM model. It is necessary to analyse the performance of different timesteps for better localization accuracy. The overall performance of the model increases with increase in timesteps. The timestep is equivalent to the amount of timestep runs the LSTM model. Figure 15 shows the localization accuracy and network loss of training data in terms of timestep.

From Figure 15, it is clear that the higher timestep gives better accuracy and lower network loss. When we increase the timestep value from very low to high, the network converges quickly without any overfitting problems. From all the simulation results and analysis, we obtained the best LSTM hyperparameters for position prediction.

Table 2. LSTM parameter values.

LSTM Parameter	Value
Ratio of training data to overall data	0.75
Number of epochs	100
Batch size	5
Timesteps	30
Hidden nodes	256
Optimizer	Nadam
Loss	Mean squared error (MSE)
Dropout Rate	0.2

shows the optimized LSTM parameters based on the training data.

The Table 2 configuration of LSTM parameters are used in the proposed approach for predicting the current user position. To validate the performance of the proposed LSTM based localization, we estimated the mean localization error from average localization error $\left(E\right)$ results. The estimation of E is expressed as

$$E=\sum _{i=1}^L{\left({\left(x_i^{true}-x_i^{est}\right)}^2+{\left(y_i^{true}-y_i^{est}\right)}^2\right)}^{0.5},$$

(32)

where $(x_i^{true},y_i^{true})$ is the actual UWB tag position and $(x_i^{est},y_i^{est})$ denotes the estimated UWB tag position calculated by proposed localization approach. The L value indicates the total number of data samples used for the localization.

The performance of the proposed LSTM approach evaluated with a number of LSTM layers, training and testing time of the model and mean localization error with different number of UWB anchors. Figure 16 shows the mean localization errors with different number of LSTM layers.

From Figure 16, the proposed two-layer LSTM approach shows better performance than standard LSTM (one LSTM layer) and a higher number of LSTM layers. The results show that if we increase the number of LSTM layers, the UWB system shows worst performances. This is due to the overfitting of the networks with more layers. The proper selection of the number of LSTM layers is an influencing factor of the localization performances and our system used the two-layer LSTM network for better performances.

The training and testing time of the proposed model is an important parameter for real time indoor localization. The training and testing time of all models are summarized in

Table 3. Training and testing time of all models.

Time	BP	ELM	LSTM	RNN
Training time (sec)	740	520	1080	900
Testing time (sec)	0.287	0.215	0.795	0.321

.

From Table 3, the training time of the proposed approach is still much higher than the approaches of BP, ELM and RNN. However, when we consider the accuracy of the localization system, the proposed LSTM approach gives acceptable localization accuracy with reasonable computational time. The testing time of the proposed approach with all testing samples is acceptable for real time indoor localization.

To investigate the impact of the number of anchors for UWB localization for all the approaches, we perform an additional simulation with the data from different number of anchors in the simulation environment. Figure 17 shows the simulation results with the number of anchors from 3 to 5 for all approaches.

From Figure 17, the mean localization error decreases with increase the number of anchors. The mean localization error results indicate that the proposed approach achieves the best localization performance in all situations. The results from RNN are better than ELM and BP models. However, the ELM model gives faster learning speed, better generalization performance and with least human intervention when compared to BP model. The results from BP model are not suitable for UWB indoor localization when we use multiple anchors. In the case of conventional localization approaches, the FPE algorithm shows less localization error than other conventional approaches. However, localization using fingerprint maps is not a common approach in UWB localization systems due to the anchors and tag distance limitation. The UWB anchors and tag should maintain minimum distances for accurate localization. The most common conventional UWB localization approach is the LLSE and which gives accurate position results than the MLE and WCE approaches. The WCE approach has a high localization error and it is not suitable for our simulation scenario. From all the simulation results and analysis, the proposed LSTM approach outperforms conventional localization approaches and gives better localization accuracy for UWB localization.

5. Conclusions

In this paper, we presented a UWB indoor localization system using a deep learning approach. The proposed method uses two LSTM networks and predicts the user position using anchor-tag distance information. The performance of the proposed LSTM model is analyzed on the basis of the learning rate, optimizer, loss function, batch size, hidden nodes and timesteps. Through analyzing several simulation results, we estimated the best LSTM hyperparameters for user position prediction. We also analyzed the LSTM model performance in terms of mean localization error with different number of LSTM layers, training and testing time of UWB data in LSTM model and the mean localization error with different number of anchors. From the simulation results, the proposed method shows reasonable position results for UWB based indoor localization. The proposed approach solved the LOS problems associated UWB system and gives a better localization accuracy than conventional localization approaches. In the future work, we intend to implement a CNN-LSTM model for predicting the current user position.