Form-Finding of Spine Inspired Biotensegrity Model
Abstract
:Featured Application
Abstract
1. Introduction
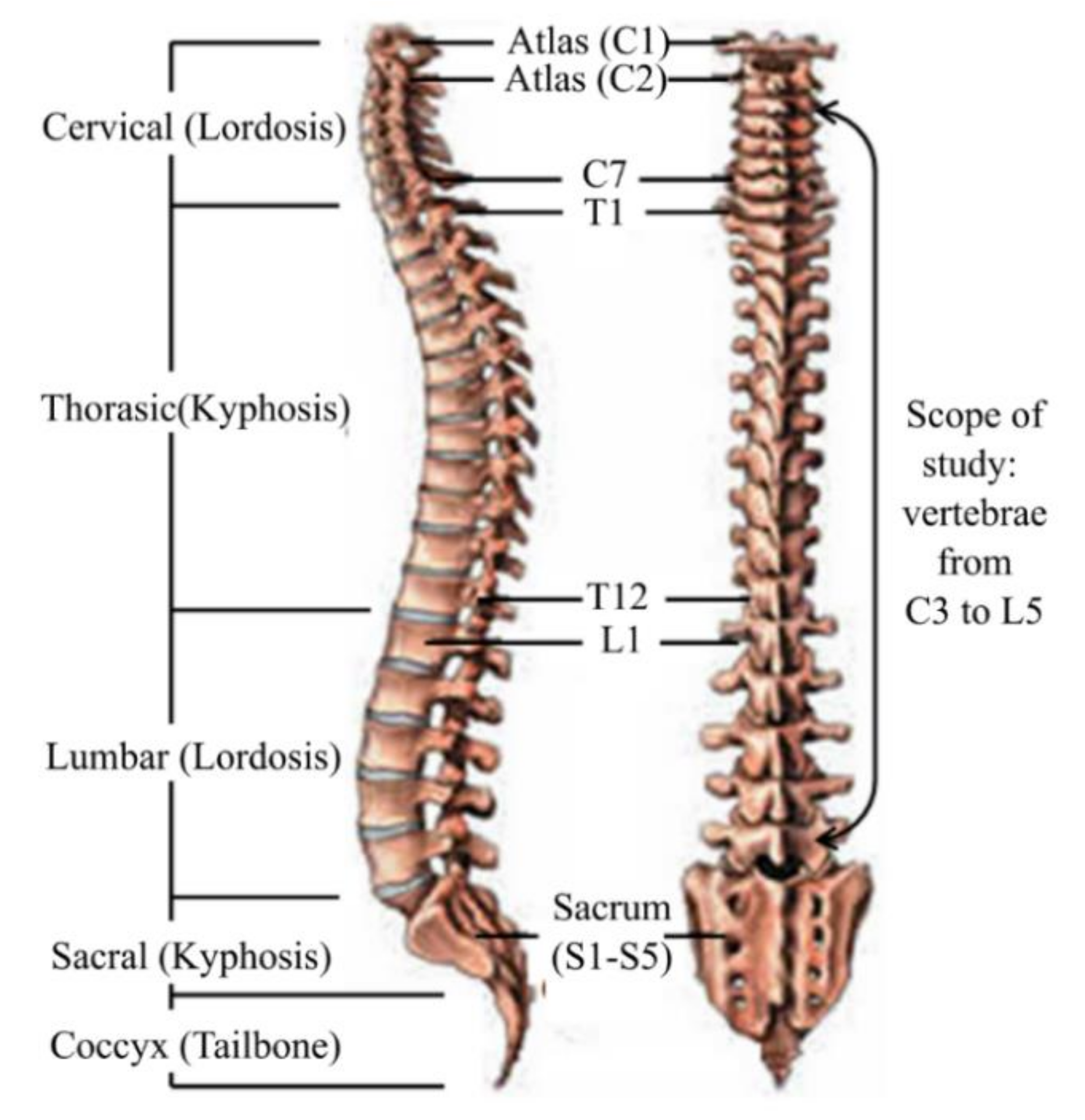
2. Geometrical Input of Spine
2.1. Vertebrae Anatomical Parameters
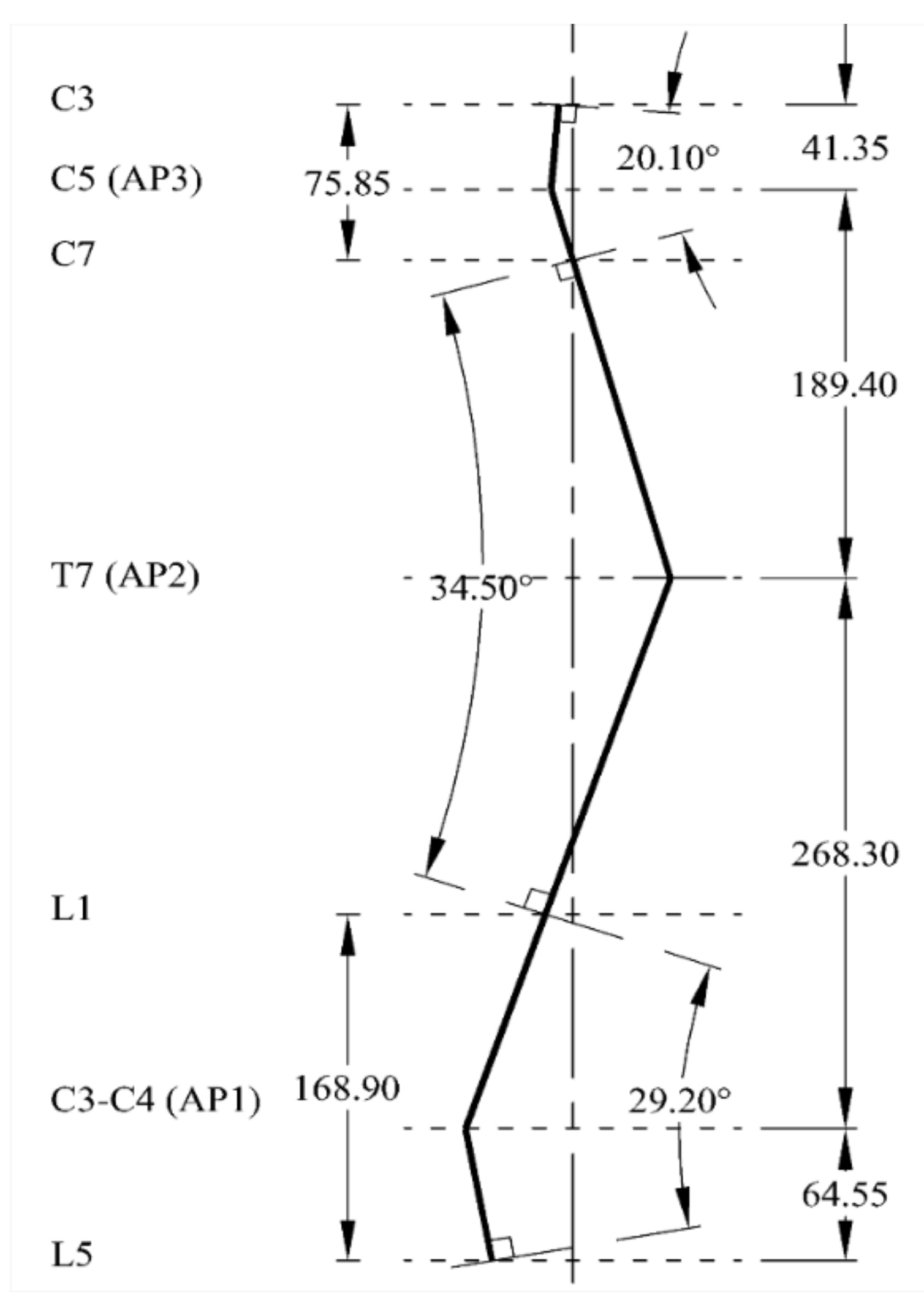
2.2. Natural Sagittal Curvature
3. Search Strategies for Spine Biotensegrity Models
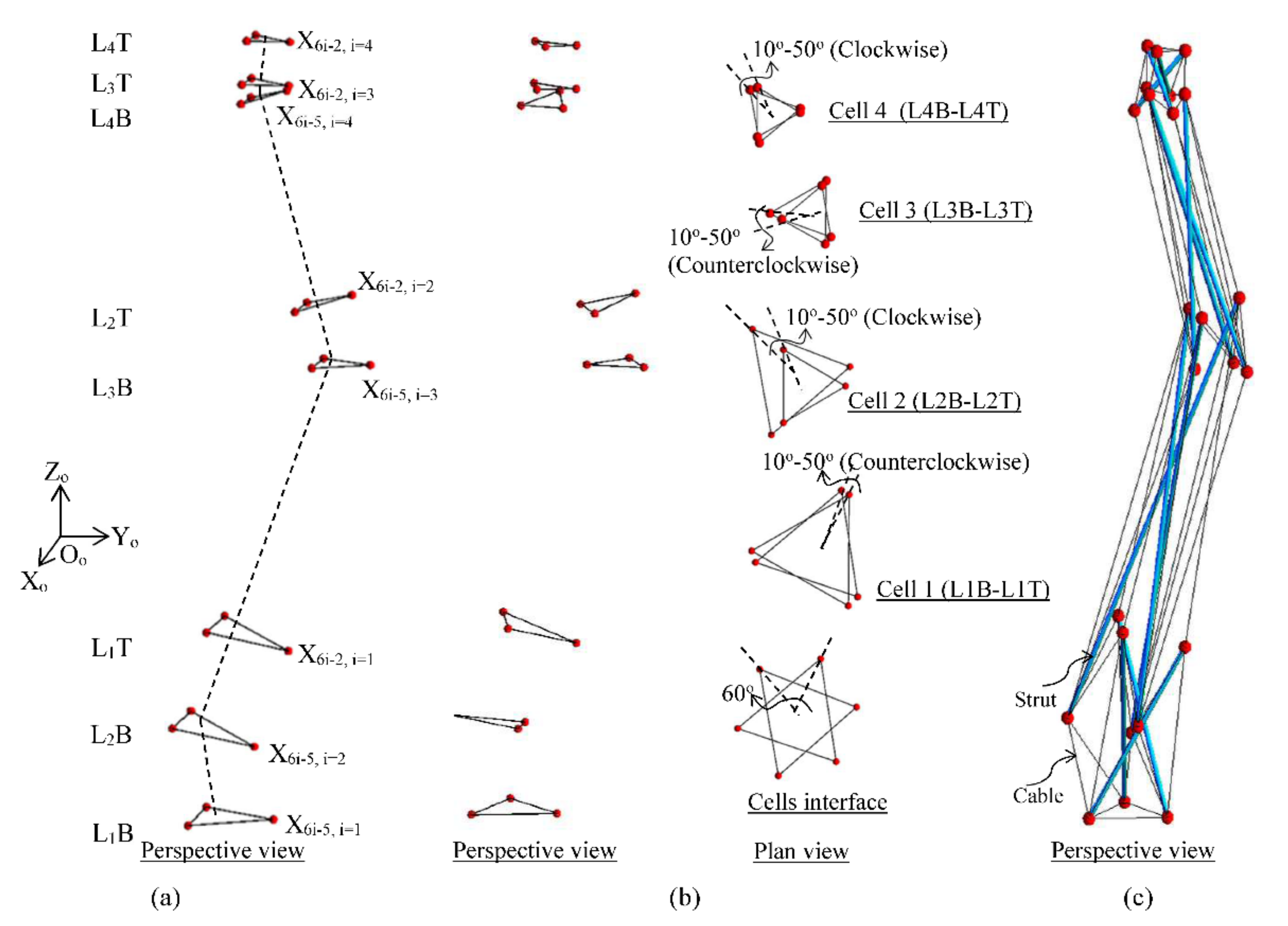
3.1. Geometry of the Spine Biotensegrity Model
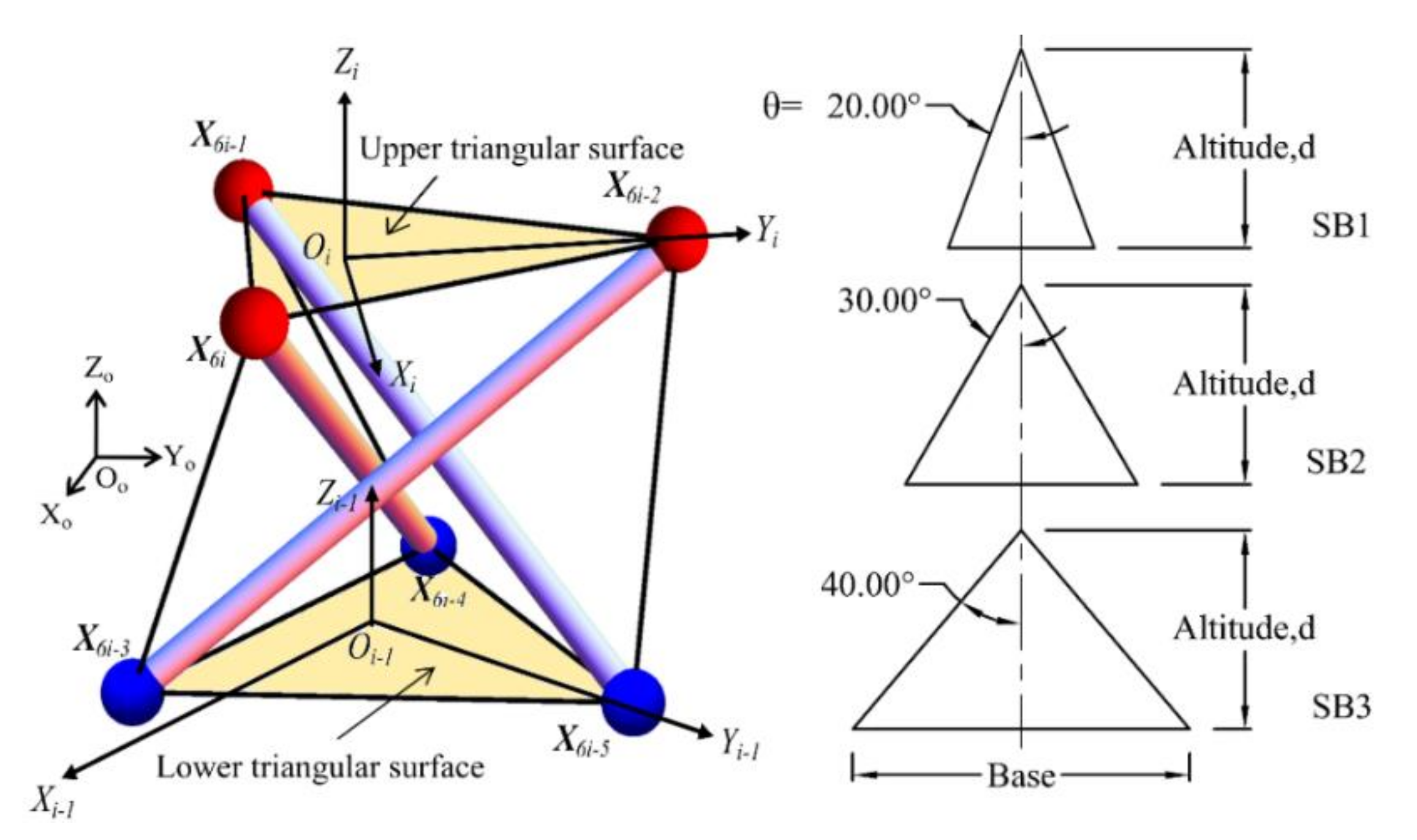
3.1.1. Definition of Basic Cell
3.1.2. Definition of Basic Cell
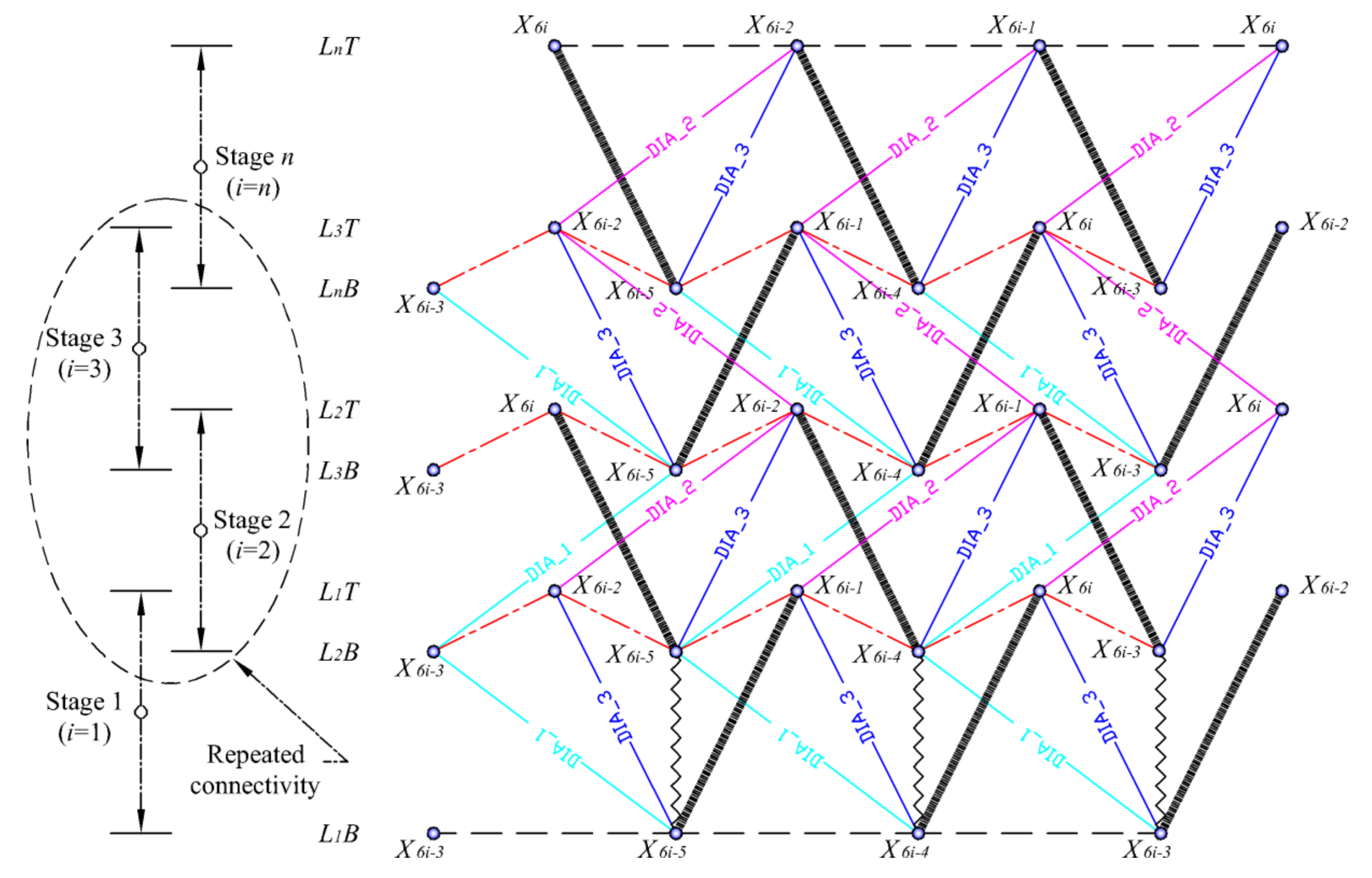
3.1.3. Assemblage of Spine Biotensegrity Models
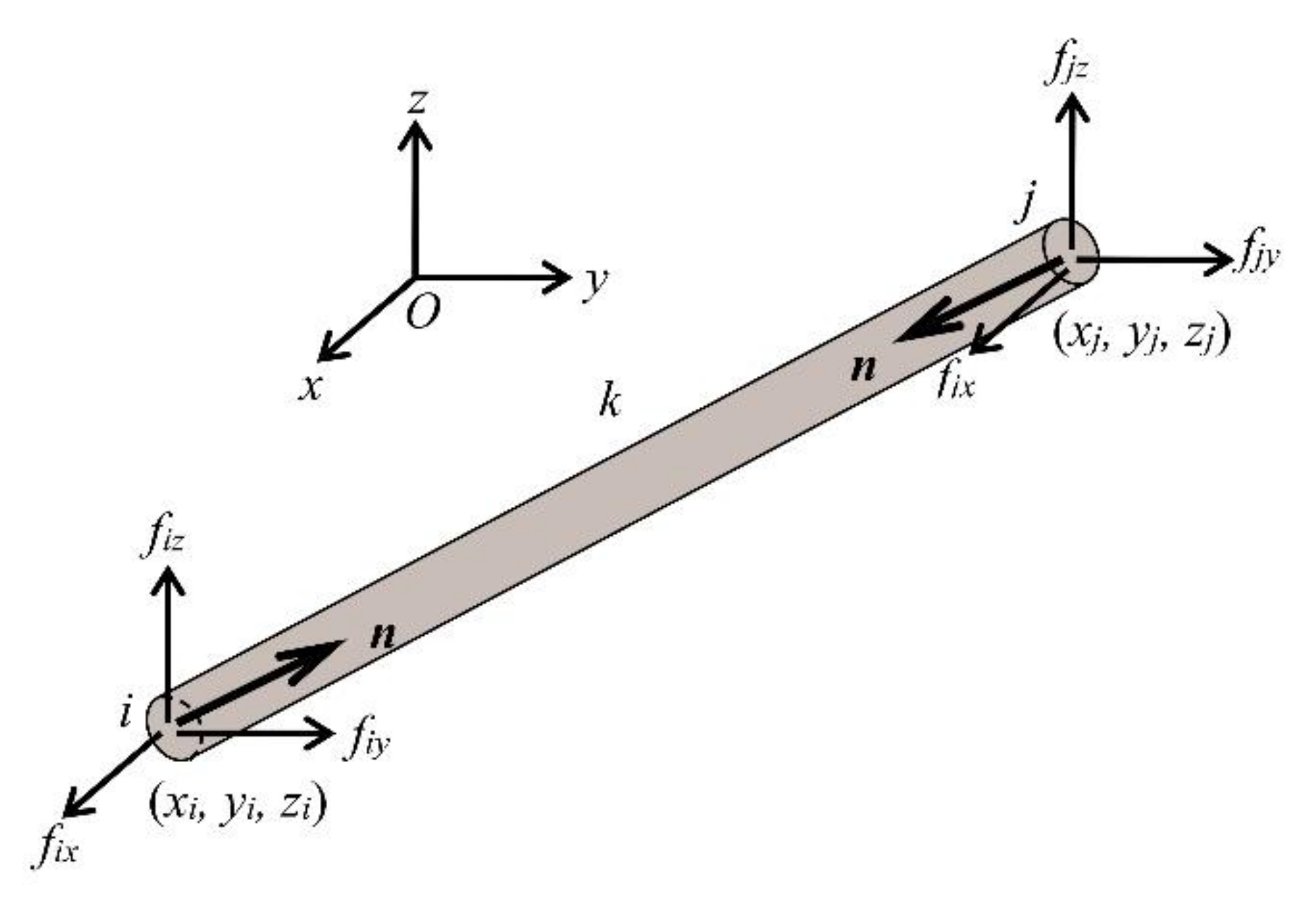
3.2. Equilibrium Equations of Spine Biotensegrity Model
3.2.1. Basic Assumptions
- Self-weight of struts and cables are neglected due to the reason that the stress resulted from self-weight is insignificantly small compared to the level of pre-stress [19].
- There is no external force acting on the models. It is necessary to ensure the self-equilibrium position as shown under the topology of biotensegrity model (Figure 7) is rational. Against any disturbance, the self-equilibrium and stability of the obtained topology should be retained. Analysis to study the capability of the established spine biotensegrity to undergo change in shape is not the scope of the study.
3.2.2. Equilibrium Equations: Formulation
3.2.3. Equilibrium Equations: Solutions
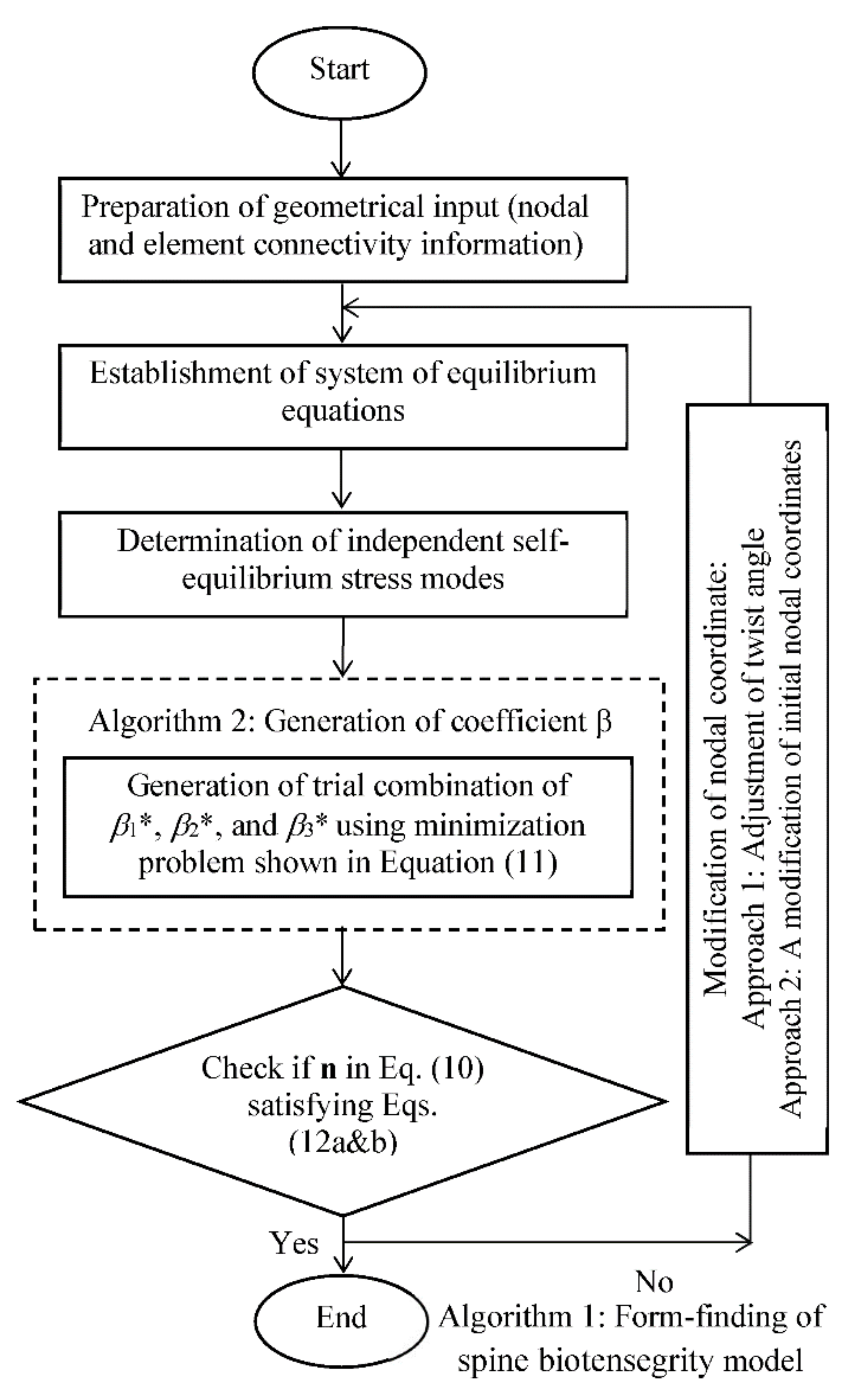
3.3. Algorithm for Form-Finding of Spine Biotensegrity Model
4. Search Results for Spine Biotensegrity Models
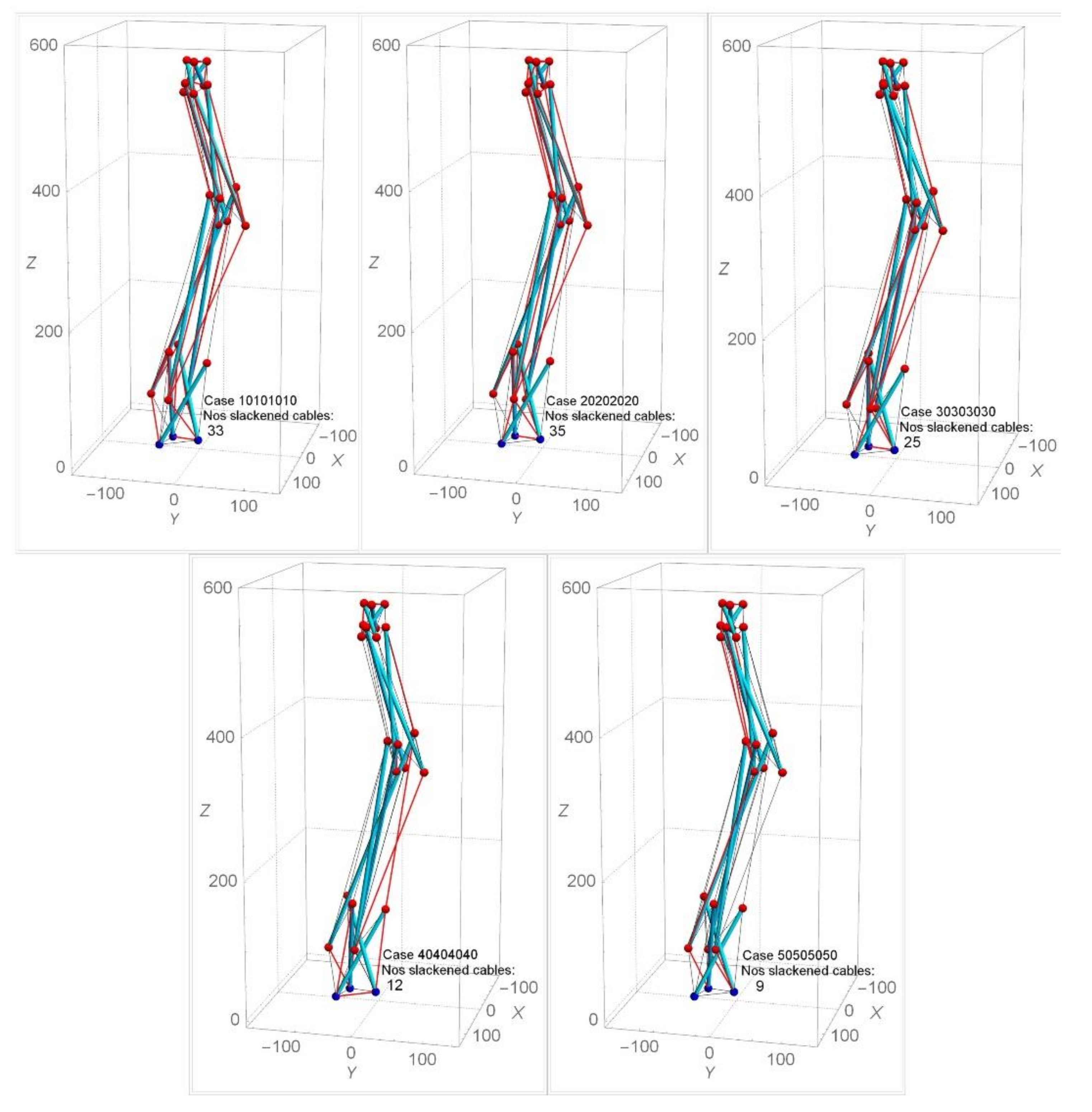
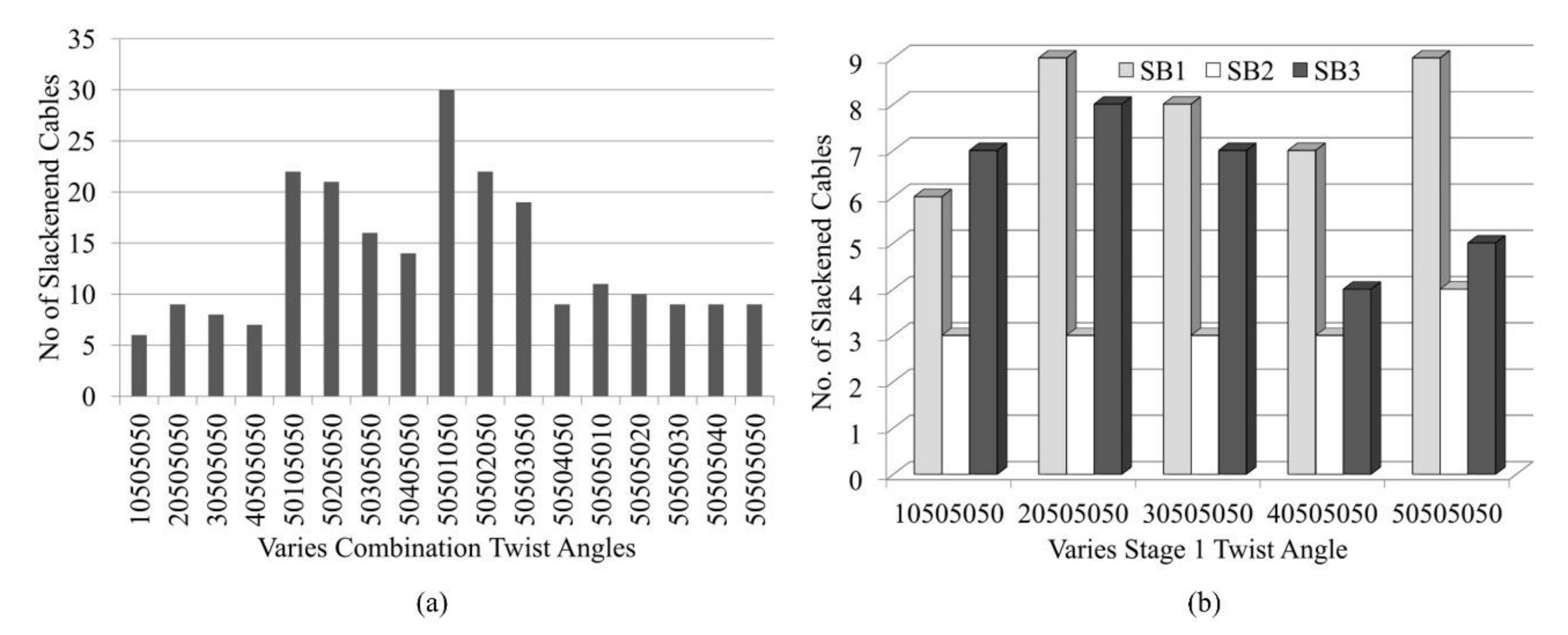
4.1. Analysis Results Using Approach One
4.2. Iterative Results Using Approach Two
4.3. Spine Biotensegrity Models
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Ac | Cross sectional area of cable |
| As | Cross sectional area of strut |
| B | Matrix of directional cosines |
| B+ | Moore-Penrose generalized inverse of matrix B |
| β* | Vector of arbitrary coefficients for linearly independent self-equilibrium stress modes |
| D | Triangle altitude |
| Es | Young modulus of strut |
| F | Vector of nodal forces |
| Φ | Eigenvector associated with the eigenvalue Λ |
| G | Matrix for existence of solution for Equation (2) (see Equation (7)) |
| Is | Moment inertia of section |
| Ls | Length of strut |
| LT | Length of cable or strut element |
| Λ | Eigenvalues of matrix G |
| λ | Vector of directional cosines |
| n | Vector of axial forces |
| nc | Axial forces of cable |
| ns | Axial forces of strut |
| θ | Half of the vertex angle |
| σc | Yield stress of cable |
| σs | Yield stress of strut |
| Vector of nodal coordinates |
Appendix A
| Nodes | SB1 | SB2 | SB3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| x | y | z | x | y | z | x | y | z | |
| 1 | 9.33 | −1.23 | 0 | 9.33 | -1.23 | 0 | 9.33 | −1.23 | 0 |
| 2 | −24.01 | −48.3 | 0 | −35.34 | −45.27 | 0 | −49.24 | -41.54 | 0 |
| 3 | 14.67 | −58.67 | 0 | 26 | −61.7 | 0 | 39.91 | −65.43 | 0 |
| 4 | −8.9 | 9.49 | 123.78 | −8.9 | 9.49 | 123.78 | −8.9 | 9.49 | 123.78 |
| 5 | −14.71 | −55.48 | 141.36 | −25.95 | −48.49 | 141.36 | −39.72 | −52.18 | 141.36 |
| 6 | 23.61 | −35.21 | 141.36 | 34.85 | −44.2 | 141.36 | 48.62 | −45.51 | 141.36 |
| 7 | −33.22 | -39 | 52.83 | −33.22 | −39 | 52.83 | −33.22 | −39 | 52.83 |
| 8 | 11.48 | −71.52 | 70.41 | 8.47 | −82.75 | 70.41 | 4.77 | −96.53 | 70.41 |
| 9 | 21.75 | −33.19 | 70.41 | 24.76 | −21.96 | 70.41 | 28.45 | 1.82 | 70.41 |
| 10 | −10.04 | 52.87 | 382.82 | −10.04 | 52.87 | 382.82 | −10.04 | 59.87 | 382.82 |
| 11 | −7.19 | 14.89 | 372.81 | −14.34 | 11.56 | 372.81 | −23.12 | 0.46 | 372.81 |
| 12 | 17.23 | 30.28 | 372.81 | 24.38 | 29.61 | 372.81 | 33.16 | 33.7 | 372.81 |
| 13 | 14.15 | 63.71 | 332.85 | 14.15 | 63.71 | 332.85 | 14.15 | 63.71 | 332.85 |
| 14 | −18.11 | 34.13 | 332.85 | −24.57 | 45.65 | 332.85 | −32.51 | 51.21 | 332.85 |
| 15 | 3.96 | 18.67 | 332.85 | 10.42 | 16.15 | 332.85 | 18.36 | 10.49 | 332.85 |
| 16 | −5.08 | 10.05 | 531.04 | −5.08 | 10.05 | 531.04 | −5.08 | 10.05 | 531.04 |
| 17 | −7.84 | −21.15 | 533.31 | −13.91 | −22.77 | 533.31 | −21.37 | −24.77 | 533.31 |
| 18 | 12.91 | −15.59 | 533.31 | 18.99 | −13.96 | 533.31 | 26.44 | −11.96 | 533.31 |
| 19 | −18.29 | 2.21 | 527.57 | −18.29 | −9.79 | 527.57 | −18.29 | −4.79 | 527.57 |
| 20 | 6.37 | −27.52 | 519.59 | 4.74 | −28.59 | 519.59 | 2.74 | −36.05 | 519.59 |
| 21 | 11.93 | −1.77 | 519.59 | 13.56 | 4.31 | 519.59 | 15.55 | 4.77 | 519.59 |
| 22 | −7.58 | 9.77 | 564.29 | −7.58 | 9.77 | 564.29 | −7.58 | 9.77 | 564.29 |
| 23 | −5.12 | −18.78 | 564.29 | −10.33 | −21.21 | 564.29 | −16.74 | −24.21 | 564.29 |
| 24 | 12.7 | −10.47 | 564.29 | 17.91 | −8.04 | 564.29 | 24.33 | −5.05 | 564.29 |
References
- Levin, S.M. Continuous tension, discontinuous compression: A model for biomechanical support of the body. Bull. Struct. Integr. 1982, 8, 1. [Google Scholar]
- Ingber, D.E.; Madri, J.A.; Jamieson, J.D. Role of basal lamina in neoplastic disorganization of tissue architecture. Proc. Natl. Acad. Sci. USA 1981, 78, 3901–3905. [Google Scholar] [CrossRef] [Green Version]
- Stamenović, D.; Fredberg, J.J.; Wang, N.; Butler, J.P.; E Ingber, D. A Microstructural Approach to Cytoskeletal Mechanics based on Tensegrity. J. Theor. Boil. 1996, 181, 125–136. [Google Scholar] [CrossRef]
- Wang, N.; Naruse, K.; Stamenović, D.; Fredberg, J.J.; Mijailovich, S.M.; Tolić-Nørrelykke, I.M.; Polte, T.; Mannix, R.; Ingber, D. Mechanical behavior in living cells consistent with the tensegrity model. Proc. Natl. Acad. Sci. USA 2001, 98, 7765–7770. [Google Scholar] [CrossRef] [Green Version]
- Swanson, R.L. Biotensegrity: A unifying theory of biological architecture with applications to osteopathic practice, education, and research&x#2014;A review and analysis. J. Am. Osteopat. Assoc. 2013, 113, 34–52. [Google Scholar] [CrossRef] [Green Version]
- Ingber, D.E.; Wang, N.; Stamenović, D. Tensegrity, cellular biophysics, and the mechanics of living systems. Rep. Prog. Phys. 2014, 77, 046603. [Google Scholar] [CrossRef] [Green Version]
- Oh, C.L.; Choong, K.K.; Low, C.Y. Biotensegrity Inspired Robot–Future Construction Alternative. Procedia Eng. 2012, 41, 1079–1084. [Google Scholar] [CrossRef] [Green Version]
- Lian, O.C.; Choong, K.K.; Nishimura, T.; Kim, J.Y.; Hassanshahi, O. Shape change analysis of tensegrity models. Lat. Am. J. Solids Struct. 2019, 16. [Google Scholar] [CrossRef] [Green Version]
- Panjabi, M.M. The Stabilizing System of the Spine. Part I. Function, Dysfunction, Adaptation, and Enhancement. J. Spinal Disord. 1992, 5, 383–389. [Google Scholar] [CrossRef]
- Levin, S.M. The tensegrity-truss as a model for spine mechanics: Biotensegrity. J. Mech. Med. Boil. 2002, 2, 375–388. [Google Scholar] [CrossRef]
- Flemons, Tom. Available online: https://tensegritywiki.com/w/index.php?title=Flemons,_Tom&oldid=1315 (accessed on 21 July 2020).
- Chen, T.-J.; Wu, C.-C.; Su, F.-C. Mechanical models of the cellular cytoskeletal network for the analysis of intracellular mechanical properties and force distributions: A review. Med. Eng. Phys. 2012, 34, 1375–1386. [Google Scholar] [CrossRef]
- Ingber, D.E. Cellular tensegrity: Defining new rules of biological design that govern the cytoskeleton. J. Cell Sci. 1993, 104, 613–627. [Google Scholar]
- Fraldi, M.; Palumbo, S.; Carotenuto, A.R.; Cutolo, A.; Deseri, L.; Pugno, N.M. Buckling soft tensegrities: Fickle elasticity and configurational switching in living cells. J. Mech. Phys. Solids 2019, 124, 299–324. [Google Scholar] [CrossRef] [Green Version]
- Tibert, A.G.; Pellegrino, S. Review of Form-Finding Methods for Tensegrity Structures. Int. J. Space Struct. 2011, 26, 241–255. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, X.; Cai, J.; Zhang, J.; Feng, J. Closed-Form Solutions for the Form-Finding of Regular Tensegrity Structures by Group Elements. Symmetry 2020, 12, 374. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Yan, J.; Feng, J.; Sareh, P. A hybrid symmetry–PSO approach to finding the self-equilibrium configurations of prestressable pin-jointed assemblies. Acta Mech. 2020, 231, 1485–1501. [Google Scholar] [CrossRef]
- Arcaro, V.; Adeli, H. Form-finding and analysis of hyperelastic tensegrity structures using unconstrained nonlinear programming. Eng. Struct. 2019, 191, 439–446. [Google Scholar] [CrossRef]
- Ohsaki, M.; Zhang, J. Nonlinear programming approach to form-finding and folding analysis of tensegrity structures using fictitious material properties. Int. J. Solids Struct. 2015, 69, 1–10. [Google Scholar] [CrossRef]
- Cai, J.; Feng, J. Form-finding of tensegrity structures using an optimization method. Eng. Struct. 2015, 104, 126–132. [Google Scholar] [CrossRef]
- Maddio, P.D.; Meschini, A.; Sinatra, R.; Cammarata, A. An optimized form-finding method of an asymmetric large deployable reflector. Eng. Struct. 2019, 181, 27–34. [Google Scholar] [CrossRef]
- Lee, S.; Gan, B.S.; Lee, J. A fully automatic group selection for form-finding process of truncated tetrahedral tensegrity structures via a double-loop genetic algorithm. Compos. Part B Eng. 2016, 106, 308–315. [Google Scholar] [CrossRef]
- Li, X.; Kong, W.; He, J. A task-space form-finding algorithm for tensegrity robots. IEEE Access 2020, 2020, 1. [Google Scholar] [CrossRef]
- Busscher, I.; Ploegmakers, J.J.W.; Verkerke, G.J.; Veldhuizen, A.G. Comparative anatomical dimensions of the complete human and porcine spine. Eur. Spine J. 2010, 19, 1104–1114. [Google Scholar] [CrossRef] [Green Version]
- Mejia, E.A.; Hennrikus, W.L.; Schwend, R.M.; Emans, J.B. A prospective evaluation of idiopathic left thoracic scoliosis with magnetic resonance imaging. J. Pediatr. Orthop. 1996, 16, 354–358. [Google Scholar] [CrossRef]
- Been, E.; Kalichman, L. Lumbar lordosis. Spine J. 2014, 14, 87–97. [Google Scholar] [CrossRef]
- Anatomy of the Spine. Available online: https://www.sonsa.org/spine-surgery/spine-anatomy/ (accessed on 21 July 2020).
- Roussouly, P.; Pinheiro-Franco, J.L. Sagittal parameters of the spine: Biomechanical approach. Eur. Spine J. 2011, 20, 578–585. [Google Scholar] [CrossRef] [Green Version]
- Masharawi, Y.; Salame, K.; Mirovsky, Y.; Peleg, S.; Dar, G.; Steinberg, N.; Hershkovitz, I. Vertebral body shape variation in the thoracic and lumbar spine: Characterization of its asymmetry and wedging. Clin. Anat. 2007, 21, 46–54. [Google Scholar] [CrossRef]
- Knox, J.B.; Lonner, B.S. Sagittal Balance. In Minimally Invasive Spinal Deformity Surgery; Springer: Berlin/Heidelberg, Germany, 2014; pp. 33–37. [Google Scholar]
- Vrtovec, T.; Pernuš, F.; Likar, B. A review of methods for quantitative evaluation of spinal curvature. Eur. Spine J. 2009, 18, 593–607. [Google Scholar] [CrossRef] [Green Version]
- Skelton, R.E.; de Oliveira, M.C. Tensegrity Systems; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Hangai, Y.; Kawaguchi, K. General Inverse and Its Application to Shape Finding Analysis; Baifukan: Tokyo, Japan, 1991. [Google Scholar]




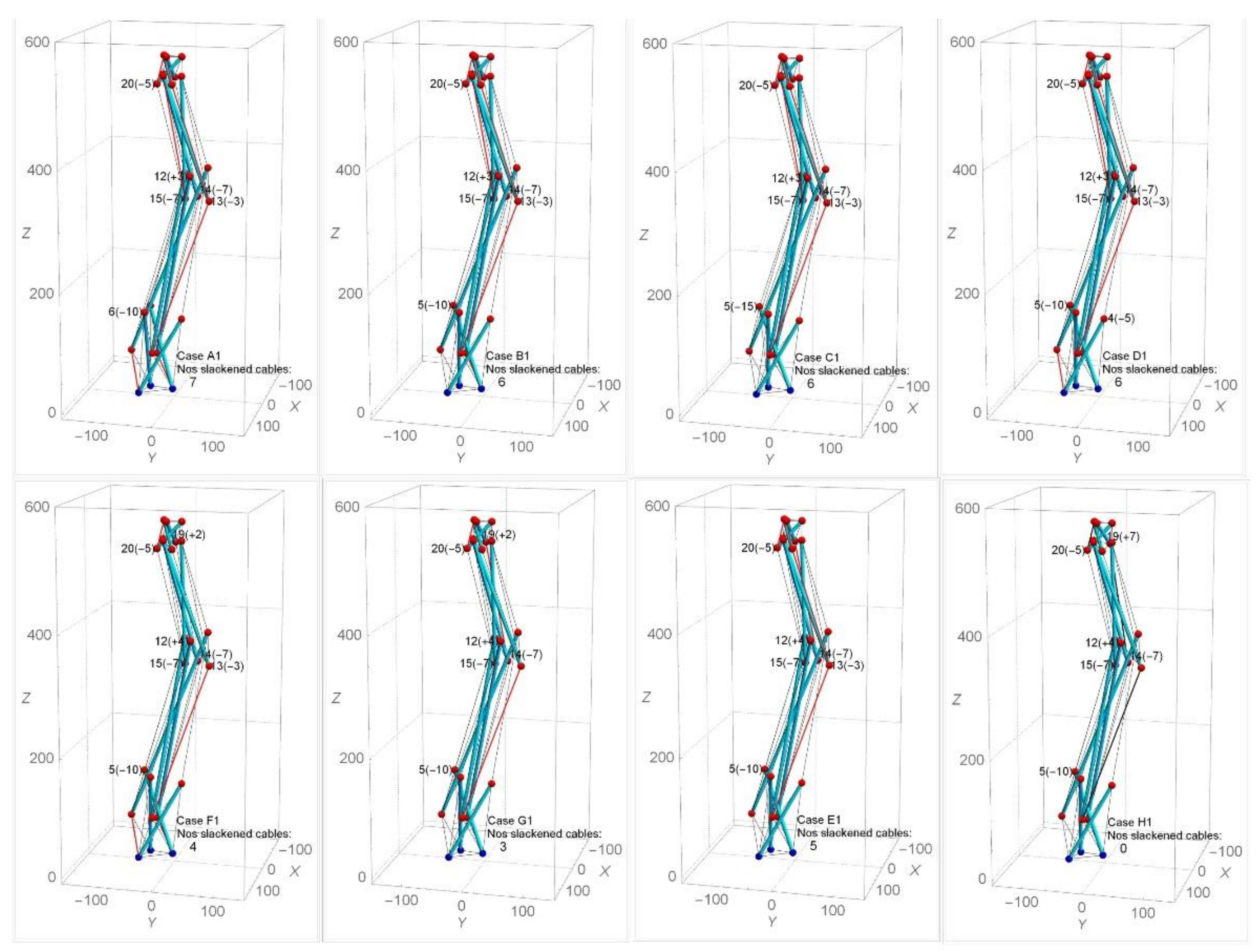
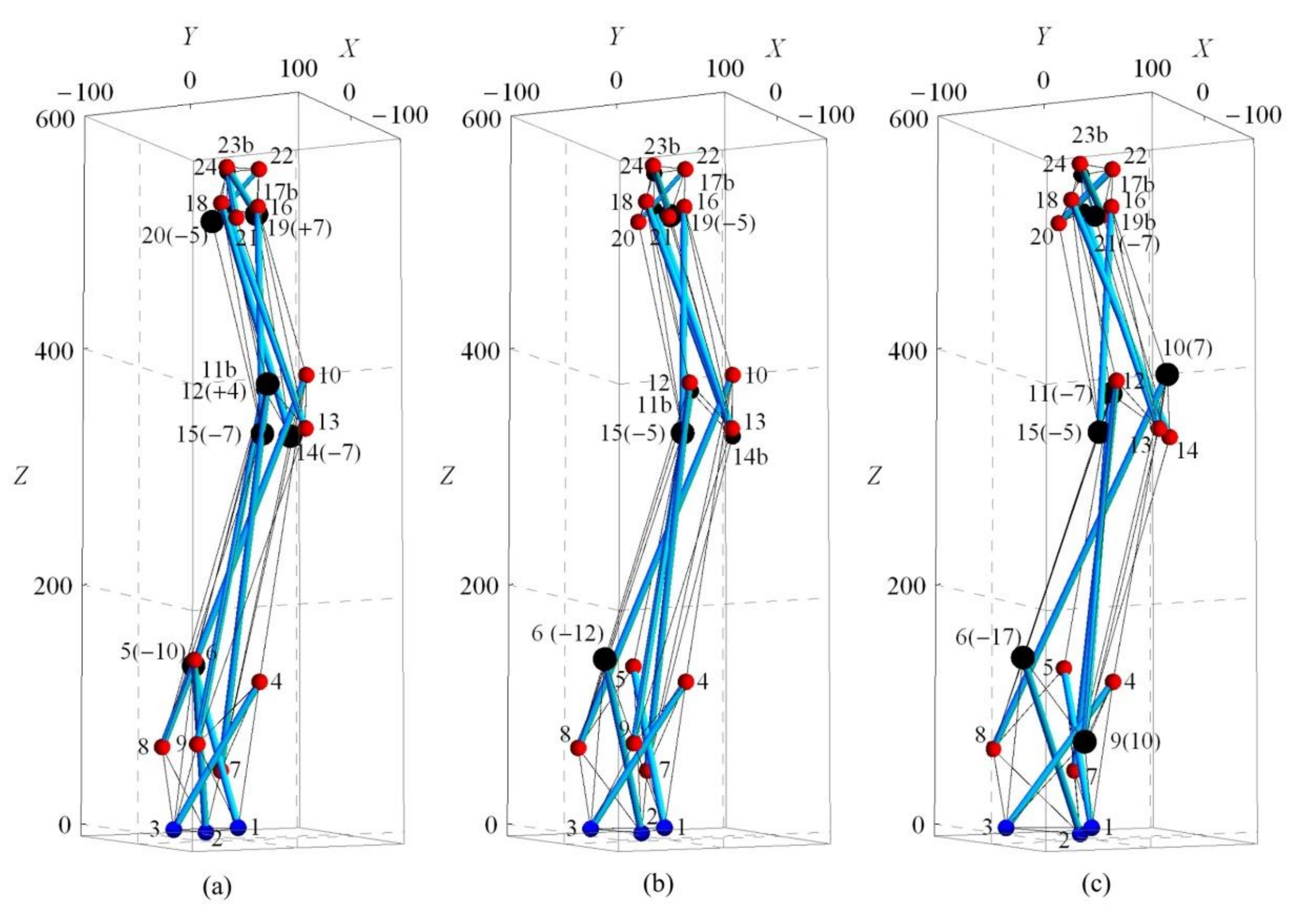
| Modification of Nodal Coordinates (mm) in Y-Direction for Cases A1-H1 | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case | Nodes | Case | Nodes | ||||||||||||||||||||||||
| 6 | 20 | 15 | 12 | 13 | 14 | 5 | 4 | 19 | 6 | 20 | 15 | 12 | 13 | 14 | 5 | 4 | 19 | ||||||||||
| A1 | −10 | −5 | −7 | 3 | −3 | −7 | 0 | 0 | 0 | E1 | 0 | −5 | −7 | 4 | −3 | −7 | −10 | 0 | 0 | ||||||||
| B1 | 0 | −5 | −7 | 3 | −3 | −7 | −10 | 0 | 0 | F1 | 0 | −5 | −7 | 4 | −3 | −7 | −10 | 0 | 2 | ||||||||
| C1 | 0 | −5 | −7 | 3 | −3 | −7 | −15 | 0 | 0 | G1 | 0 | −5 | −7 | 4 | 0 | −7 | −10 | 0 | 2 | ||||||||
| D1 | 0 | −5 | −7 | 3 | −3 | −7 | −10 | −5 | 0 | H1 | 0 | −5 | −7 | 4 | 0 | −7 | −10 | 0 | 7 | ||||||||
| Axial Force (N) for Case 30505050 and Cases A1-H1 | |||||||||||||||||||||||||||
| Cable | 30505050 | A1 | B1 | C1 | D1 | E1 | F1 | G1 | H1 | ||||||||||||||||||
| 40 | −7.73 | 1.65 | 3.94 | 10.00 | 10.00 | 5.00 | 10.00 | 5.00 | 6.07 | ||||||||||||||||||
| 42 | 10.00 | −2.74 | 0.11 | 1.58 | −2.24 | 1.93 | −7.74 | 1.85 | 0.79 | ||||||||||||||||||
| 50 | −8.82 | 18.54 | 13.10 | 17.25 | 18.81 | 13.31 | 13.63 | 10.88 | 3.82 | ||||||||||||||||||
| 51 | −1.11 | −2.27 | −2.77 | −4.06 | −3.73 | −5.45 | −4.13 | −4.44 | 0.03 | ||||||||||||||||||
| 57 | −28.56 | −2.52 | −1.69 | −1.44 | −2.10 | 8.42 | 12.57 | 14.38 | 22.26 | ||||||||||||||||||
| 58 | 12.93 | −8.27 | −8.49 | −12.13 | −11.63 | −5.71 | 0.45 | 6.28 | 30.40 | ||||||||||||||||||
| 59 | −6.35 | 0.43 | 0.68 | 0.93 | 0.85 | −0.59 | 0.16 | −1.07 | 4.27 | ||||||||||||||||||
| 65 | −5.27 | −13.28 | −9.38 | −12.76 | −13.66 | −14.13 | −11.70 | −12.91 | 0.03 | ||||||||||||||||||
| 66 | 10.00 | −5.29 | −5.64 | −8.06 | −7.67 | −3.06 | 1.97 | 5.88 | 24.13 | ||||||||||||||||||
| 67 | −2.89 | −1.41 | −0.81 | −0.10 | 0.05 | 0.13 | −0.60 | 0.03 | 0.03 | ||||||||||||||||||
| 68 | −7.86 | 10.00 | 6.65 | 10.91 | 11.04 | 2.91 | 10.00 | 3.09 | 6.57 | ||||||||||||||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai Lian, O.; Kok Keong, C.; Nishimura, T.; Jae-Yeol, K. Form-Finding of Spine Inspired Biotensegrity Model. Appl. Sci. 2020, 10, 6344. https://doi.org/10.3390/app10186344
Chai Lian O, Kok Keong C, Nishimura T, Jae-Yeol K. Form-Finding of Spine Inspired Biotensegrity Model. Applied Sciences. 2020; 10(18):6344. https://doi.org/10.3390/app10186344
Chicago/Turabian StyleChai Lian, Oh, Choong Kok Keong, Toku Nishimura, and Kim Jae-Yeol. 2020. "Form-Finding of Spine Inspired Biotensegrity Model" Applied Sciences 10, no. 18: 6344. https://doi.org/10.3390/app10186344
APA StyleChai Lian, O., Kok Keong, C., Nishimura, T., & Jae-Yeol, K. (2020). Form-Finding of Spine Inspired Biotensegrity Model. Applied Sciences, 10(18), 6344. https://doi.org/10.3390/app10186344






