A Diversity Combination Model Incorporating an Inward Bias for Interaural Time-Level Difference Cue Integration in Sound Lateralization
Abstract
1. Introduction
- (i)
- TO: Only ITD cue moves from to either or .
- (ii)
- LO: Only ILD cue moves from to either or .
- (iii)
- TL: Both ITD and ILD cues move from to either or .
2. Experimental Methodology
2.1. Participants
2.2. Stimulation
2.3. Experiments
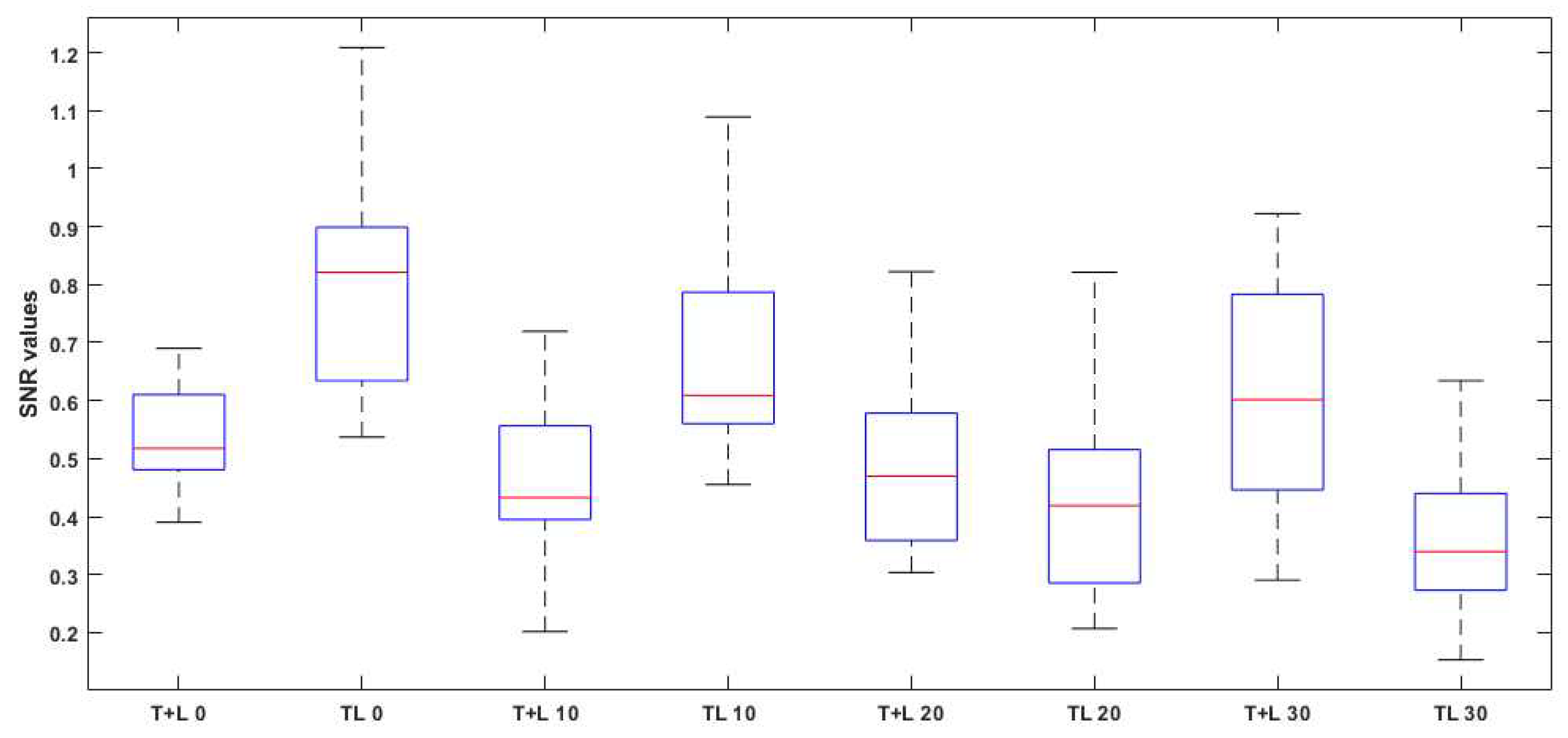
3. Experimental Results
3.1. Experimental Data
3.2. Statistical Results
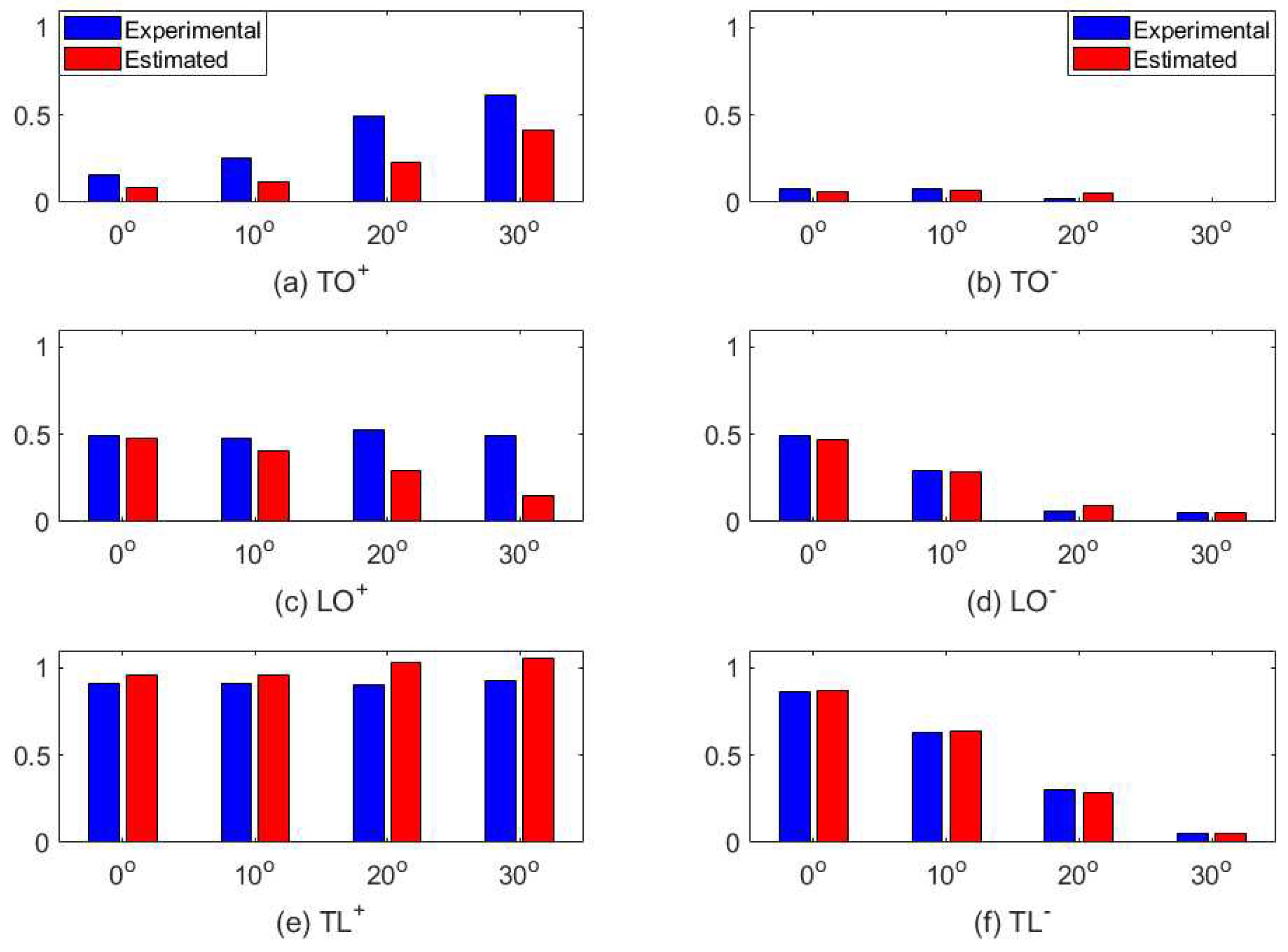
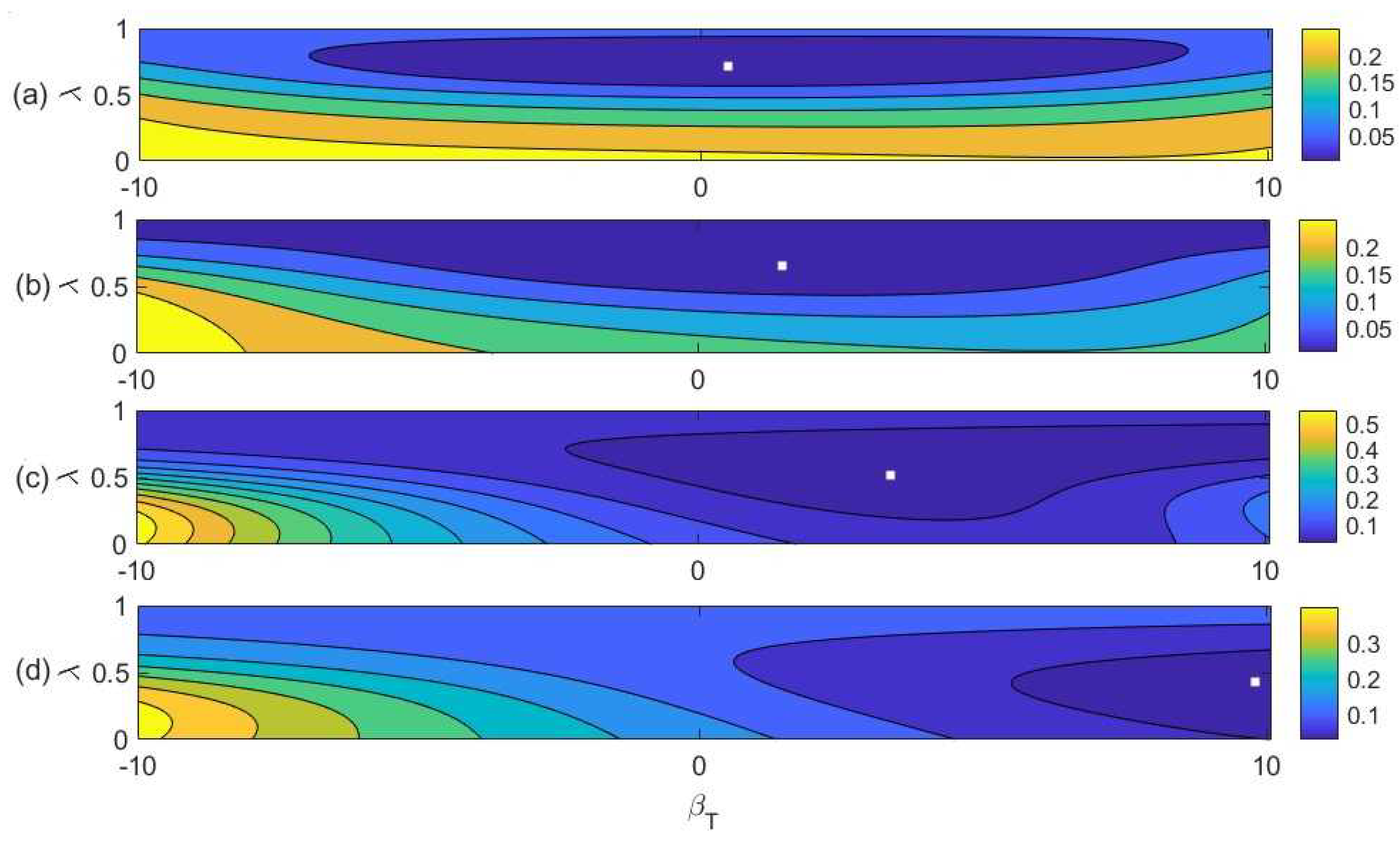
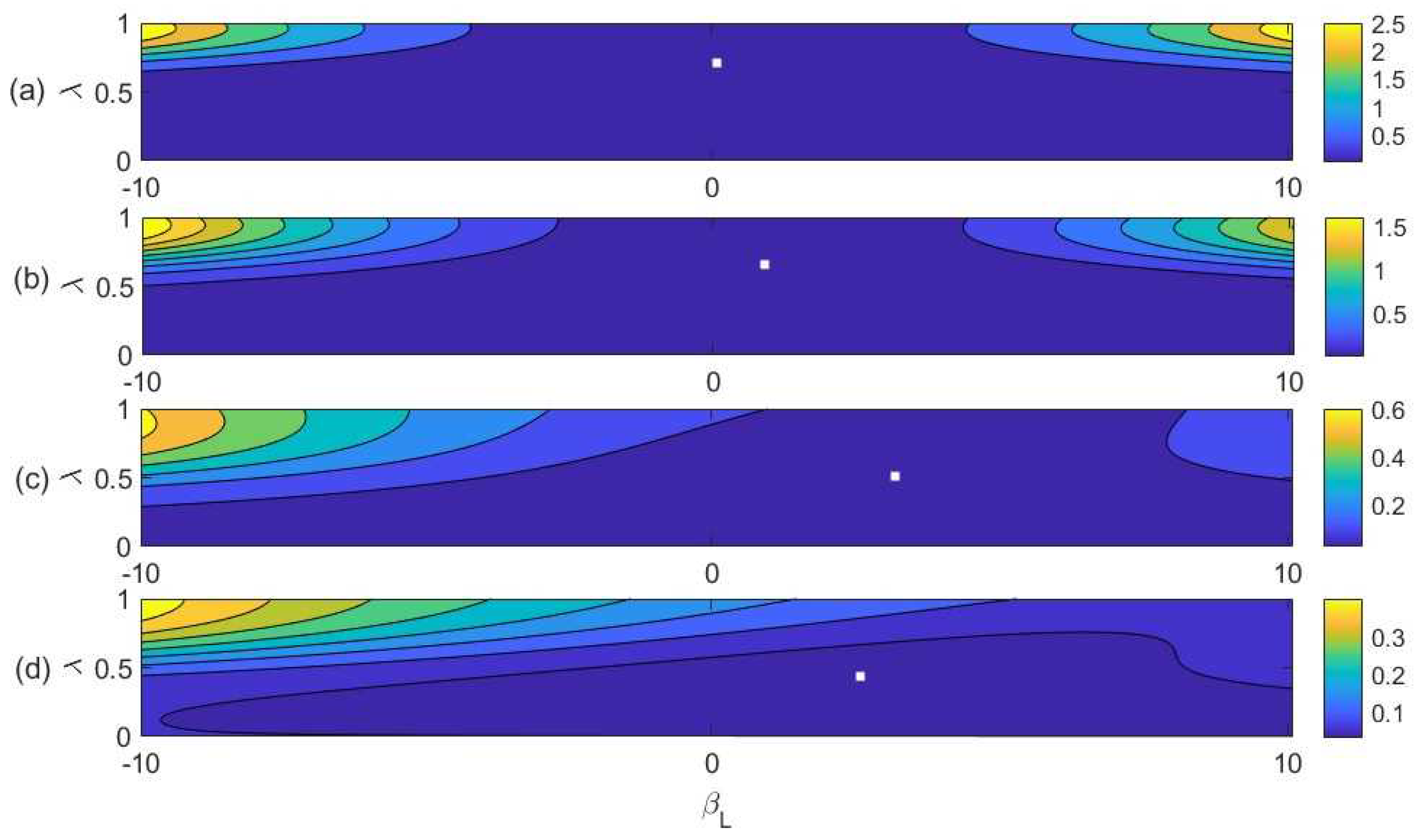
4. Modeling
4.1. Biased Diversity Combination
4.2. Fitting the Model to Experimental Data
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Middlebrooks, J.; Green, D. Sound localization by human listeners. Annu. Rev. Psychol. 1991, 42, 135–159. [Google Scholar] [CrossRef] [PubMed]
- Rubel, E. The Auditory System, Central Auditory Pathways; Saunders: Philadelphia, PA, USA, 1990. [Google Scholar]
- Sanes, D. An in vitro analysis of sound localization mechanism in the gerbil lateral superior olive. J. Neurosci. 1990, 10, 3494–3506. [Google Scholar] [CrossRef] [PubMed]
- Joseph, A.; Hyson, R. Coincidence detection by binaural neurons in the chick brainstem. J. Neurophysiol. 1993, 69, 1197–1211. [Google Scholar] [CrossRef]
- Jeffress, L.A. A place theory of sound localization. J. Comp. And Physiol. Psychol. 1948, 41, 35–39. [Google Scholar] [CrossRef] [PubMed]
- Abel, S.; Kunov, H. Lateralization based on interaural phase difference effects of frequency, amplitude, duration and shape of rise/delay. J. Acoust. Soc. Am. 1983, 73, 955–961. [Google Scholar] [CrossRef] [PubMed]
- Strutt, J. On our perception of sound direction. Philos. Mag. 1907, 13, 214–232. [Google Scholar]
- Macpherson, E.A.; Middlebrooks, J.C. Listener weighting of cues for lateral angle: The duplex theory of sound localization revisited. J. Acoust. Soc. Am. 2002, 111, 2219–2236. [Google Scholar] [CrossRef]
- Wightman, F.L.; Kistler, D.J. The dominant role of low-frequency interaural time differences in sound localization. J. Acoust. Soc. Am. 1992, 91, 1648–1661. [Google Scholar] [CrossRef]
- Cunningham, S. Adapting to remapped auditory localization cues: A decision-theory model. Percept. Psychophys. 2000, 62, 33–47. [Google Scholar] [CrossRef]
- Gaik, W. Combined evaluation of interaural time and intensity differences: Psychoacoustic results and computer modeling. J. Acoust. Soc. Am. 1993, 94, 98–110. [Google Scholar] [CrossRef]
- Lang, A.G.; Buchner, A. Relative influence of interaural time and intensity differences on lateralization is modulated by attention to one or the other cue: 500-hz sine tones. J. Acoust. Soc. Am. 2008, 124, 3120–3131. [Google Scholar] [CrossRef] [PubMed]
- Wightman, F.L.; Kistler, D.J. Monaural sound localization revisited. J. Acoust. Soc. Am. 1997, 101, 1050–1063. [Google Scholar] [CrossRef] [PubMed]
- Bernstein, L.R.; Trahiotis, C. Detection of interaural delay in high-frequency sinusoidally amplitude-modulated tones, two-tone complexes, and bands of noise. J. Acoust. Soc. Am. 1994, 95, 3561–3567. [Google Scholar] [CrossRef] [PubMed]
- Schroger, E. Interaural time and level differences: Integrated or separated processing? Hear. Res. 1996, 96, 191–198. [Google Scholar] [CrossRef]
- Salminen, N.H.; Altoe, A.; Takanen, M.; Santala, O.; Pulkki, V. Human cortical sensitivity to interaural time difference in high-frequency sounds. Hear. Res. 2015, 323, 99–106. [Google Scholar] [CrossRef]
- Blauert, J. Spatial Hearing: The Psychophysics of Human Sound Localization; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Hafter, E.R.; Carrier, S.C. Binaural Interaction in Low-Frequency Stimuli: The Inability to Trade Time and Intensity Completely. J. Acoust. Soc. Am. 1972, 51, 1852–1862. [Google Scholar] [CrossRef]
- Hafter, E.R.; Dye, R.H., Jr.; Wenzel, E.M.; Knecht, K. The combination ofinteraural time and intensity in the lateralization of high-frequency complex signals. J. Audio Eng. Soc. Audio Eng. Soc. 1990, 87, 1702–1708. [Google Scholar]
- Wood, K.C.; Bizley, J.K. Relative sound localisation abilities in human listeners. J. Acoust. Soc. Am. 2015, 138, 674–686. [Google Scholar] [CrossRef]
- Hartmann, W.; Rakerd, B. On the minimum audible angle—A decision theory approach. J. Acoust. Soc. Am. 1989, 85, 2031–2072. [Google Scholar] [CrossRef]
- Magezi, D.; Krumbholz, K. Evidence for opponent-channel coding of interaural time differences in human auditory cortex. J. Neurophysiol. 2010, 104, 1997–2007. [Google Scholar] [CrossRef]
- Ihlefeld, A.; Alamatsaz, N.; Shapely, R.M. Human Sound Localization Depends on Sound Intensity: Implications for Sensory Coding. bioRxiv 2018, 378505. [Google Scholar] [CrossRef]
- Bramley, T.; Oates, T. Rank ordering and paired comparisons—The way Cambridge Assessment is using them in operational and experimental work. Int. J. Educ. Dev. 2011, 23, 275–289. [Google Scholar]
- Buus, S.; Schorer, E.; Florentine, M.; Zwicker, E. Decision rules in detection of simple and complex tones. J. Acoust. Soc. Am. 1986, 80, 1646–1657. [Google Scholar] [CrossRef] [PubMed]
- Morimoto, M.; Aokata, H. Localization cues of sound sources in the upper hemisphere. J. Acoust. Soc. Jpn. 1997, 5, 165–173. [Google Scholar] [CrossRef]
- Rakerd, B.; Hartmann, W.M. Localization of sound in rooms. V. Binaural coherence and human sensitivity to interaural time differences in noise. J. Acoust. Am. 2010, 128, 3052–3063. [Google Scholar] [CrossRef] [PubMed]
- Harper, N.S.; McAlpine, D. Optimal neural population coding of an auditory spatial cue. Nature 2004, 430, 682–686. [Google Scholar] [CrossRef] [PubMed]
- Ungan, P.; Yagcioglu, S.; Goksoy, C. Differences between the N1 waves of the responses to interaural time and intensity disparities: Scalp topography and dipole sources. Clin. Neurophysiol. 2001, 112, 485–498. [Google Scholar] [CrossRef]
- Asahi, M.; Matsuoka, S. Effect of the sound anti resonance by pinna on median plane localization—Localization of sound signal passed dip filter. Tech. Rep. Hear. Acoust. Soc. Jpn. 1977, H-40-1. [Google Scholar]
- Morimoto, M.; Yoshimura, K.; Kazhiro, I.; Motokuni, I. The role of low frequency components in median plane localization. J. Acoust. Soc. Jpn. E 2003, 24, 76–82. [Google Scholar] [CrossRef][Green Version]
- Salminen, N.H. Human cortical sensitivity to interaural level differences in low- and high-frequency sounds. J. Acoust. Soc. Am. 2015, 137, 190–193. [Google Scholar] [CrossRef] [PubMed]
- Begault, E.M.; Wenzel, E.M.; Anderson, M.R. Direct comparison of the impact of head tracking, reverberation, and individualized head-related transfer functions on the spatial perception of a virtual speech source. J. Audio Eng. Soc. Audio Eng. Soc. 2001, 49, 904–916. [Google Scholar]
- Kayser, H.; Ewert, S.; Anemuller, J.; Rohdenbudrg, T.; Hohmann, V.; Kollmeier, B. Database of multichannel in-ear and behind-the-ear head-related and binaural room impulse response. Eurasip J. Adv. Signal Process. 2009, 2009, 298605. [Google Scholar] [CrossRef]
- Shankar, P.M. Fading and Shadowing Wireless System; Springer International Publishing: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Rosenbrock, H.H. An automatic method for finding the greatest or least value of a function. Comput. J. 1960, 3, 175–184. [Google Scholar] [CrossRef]
- MATLAB. Matlab Optimization Toolbox; The MathWorks: Natick, MA, USA, 2020. [Google Scholar]
- Hebrank, J.; Wright, D. Spectral cues used in the localization of sound sources on the median plane. J. Acoust. Soc. Am. 1974, 56, 1829–1834. [Google Scholar] [CrossRef] [PubMed]
- Morikawa, D. Effect of interaural difference for localization of spatially segregated sound. In Proceedings of the Tenth International Conference on Intelligent Information Hiding and Multimedia Signal Processing, Kitakyushu, Japan, 27–29 August 2014; pp. 602–605. [Google Scholar]
- Edmonds, B.; Krumbholz, K. Are interaural time and level differences represented by independent or integrated codes in the human auditory cortex? J. Acoust. Soc. Am. 2013, 15, 103–114. [Google Scholar] [CrossRef] [PubMed]
- Calvert, G.; Thesen, T. Multisensory integration: Methodological approaches and emerging principles in the human brain. J. Physiol. 2004, 98, 191–205. [Google Scholar] [CrossRef]
- Briley, P.M.; Kitterick, P.T.; Summerfield, A.Q. Evidence for opponent process analysis of sound source location in humans. J. Assoc. Res. Otolaryngol. 2013, 14, 83–101. [Google Scholar] [CrossRef]
- Salminen, N.H.; Tiitinen, H.; Yrttiaho, S.; May, P.J. The neural code for interaural time difference in human auditory cortex. J. Acoust. Soc. Am. 2010, 127, EL60–EL65. [Google Scholar] [CrossRef]
- Altmann, C.F.; Terada, S.; Kashino, M.; Goto, K.; Mima, T.; Fukuyama, H.; Furukawa, S. Independent or integrated processing of interaural time and level differences in human auditory cortex? Hear. Res. 2014, 312, 121–127. [Google Scholar] [CrossRef]
- Higgins, N.C.; McLaughlin, S.A.; Rinne, T.; Stecker, G.C. Evidence for cue independent spatial representation in the human auditory cortex during active listening. Proc. Natl. Acad. Sci. USA 2017, 114, E7602–E7611. [Google Scholar] [CrossRef]
- McLaughlin, S.A.; Higgins, N.C.; Stecker, G.C. Tuning to binaural cues in human auditory cortex. J. Assoc. Res. Otolaryngol. 2016, 17, 37–53. [Google Scholar] [CrossRef] [PubMed]
- Ozmeral, E.J.; Eddins, D.A.; Eddins, A.C. Electrophysiological responses to lateral shifts are not consistent with opponent-channel processing of interaural level differences. J. Neurophysiol. 2019, 122, 737–748. [Google Scholar] [CrossRef] [PubMed]
- Knudsen, E.I. Auditory and visual maps of space in the optic tectum of the owl. J. Neurosci. 1982, 2, 1177–1194. [Google Scholar] [CrossRef]
- Stern, R.; Shear, G. Lateralization and detection of low-frequency binaural stimuli: Effects of distribution of internal delay. J. Acoust. Am. 1996, 100, 2278–2288. [Google Scholar] [CrossRef]
- Salminen, N.; May, P.; Alku, P.; Tiitinen, H. A population rate code of auditory space in the human cortex. PLoS ONE 2009, 4, e7600. [Google Scholar] [CrossRef]
- Harper, N.S.; Scott, B.H.; Semple, M.N.; McAlpine, D. The neural code for auditory space depends on sound frequency and head size in an optimal manner. PLoS ONE 2014, 9, e108154. [Google Scholar] [CrossRef]
- Näätänen, R. Attention and Brain Function; Erlbaum: Hiildile, NJ, USA, 1992. [Google Scholar]
- Von Kriegstein, K.; Griffiths, T.D.; Thompson, S.K.; McAlpine, D. Responses to interaural time delay in human cortex. J. Neurophysiol. 2008, 100, 2712–2718. [Google Scholar] [CrossRef] [PubMed]
- Näätänen, R.; Alho, K. Mismatch negativity-a unique measure of sensory processing in audition. Int. J. Neurosci. 1995, 80, 317–337. [Google Scholar] [CrossRef]
- Schroger, E. Measurement and interpretation of the mismatch negativity. Behav. Res. Methods Instrum. Comput. 1998, 30, 131–145. [Google Scholar] [CrossRef]
- Polich, J. Updating P300: An Integrative Theory of P3a and P3b. Clin. Neurophysiol. 2007, 118, 2128–2148. [Google Scholar] [CrossRef]


| P∖R | −40 | −30 | −20 | −10 | 0 | +10 | +20 | +30 | +40 |
|---|---|---|---|---|---|---|---|---|---|
| −40 | − | * | − | − | − | − | − | − | − |
| −30 | * | − | * | − | − | − | − | − | − |
| −20 | − | * | − | * | − | − | − | − | − |
| −10 | − | − | * | − | * | − | − | − | − |
| 0 | − | − | − | * | − | * | − | − | − |
| +10 | − | − | − | − | * | − | * | − | − |
| +20 | − | − | − | − | − | * | − | * | − |
| +30 | − | − | − | − | − | − | * | − | * |
| +40 | − | − | − | − | − | − | − | * | − |
| 0.154 | 0.073 | 0.490 | 0.497 | 0.941 | 0.866 | |
| 0.249 | 0.074 | 0.474 | 0.293 | 0.915 | 0.634 | |
| 0.496 | 0.023 | 0.528 | 0.064 | 0.907 | 0.298 | |
| 0.618 | 0.0004 | 0.494 | 0.054 | 0.924 | 0.055 |
| 0.721 | 0.900 | 0.000 | 25.316 | 10.697 | |
| 0.660 | 1.418 | 0.825 | 22.777 | 12.364 | |
| 0.540 | 3.142 | 2.872 | 18.600 | 17.900 | |
| 0.489 | 9.868 | 2.508 | 23.365 | 22.453 |
| 0.084 | 0.058 | 0.476 | 0.473 | 0.961 | 0.869 | |
| 0.119 | 0.067 | 0.403 | 0.289 | 0.960 | 0.636 | |
| 0.227 | 0.054 | 0.295 | 0.089 | 1.032 | 0.283 | |
| 0.410 | 0.000 | 0.149 | 0.053 | 1.053 | 0.055 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mojtahedi, S.; Erzin, E.; Ungan, P. A Diversity Combination Model Incorporating an Inward Bias for Interaural Time-Level Difference Cue Integration in Sound Lateralization. Appl. Sci. 2020, 10, 6356. https://doi.org/10.3390/app10186356
Mojtahedi S, Erzin E, Ungan P. A Diversity Combination Model Incorporating an Inward Bias for Interaural Time-Level Difference Cue Integration in Sound Lateralization. Applied Sciences. 2020; 10(18):6356. https://doi.org/10.3390/app10186356
Chicago/Turabian StyleMojtahedi, Sina, Engin Erzin, and Pekcan Ungan. 2020. "A Diversity Combination Model Incorporating an Inward Bias for Interaural Time-Level Difference Cue Integration in Sound Lateralization" Applied Sciences 10, no. 18: 6356. https://doi.org/10.3390/app10186356
APA StyleMojtahedi, S., Erzin, E., & Ungan, P. (2020). A Diversity Combination Model Incorporating an Inward Bias for Interaural Time-Level Difference Cue Integration in Sound Lateralization. Applied Sciences, 10(18), 6356. https://doi.org/10.3390/app10186356






