Multi-Pass Stamping Forming a Concave Ring
Abstract
:1. Introduction
2. Die Design and Process Parameter Selection
3. Simulation Analysis of the Concave Ring Formed by Multi-Pass Bending
3.1. Establishment of Finite Element Model
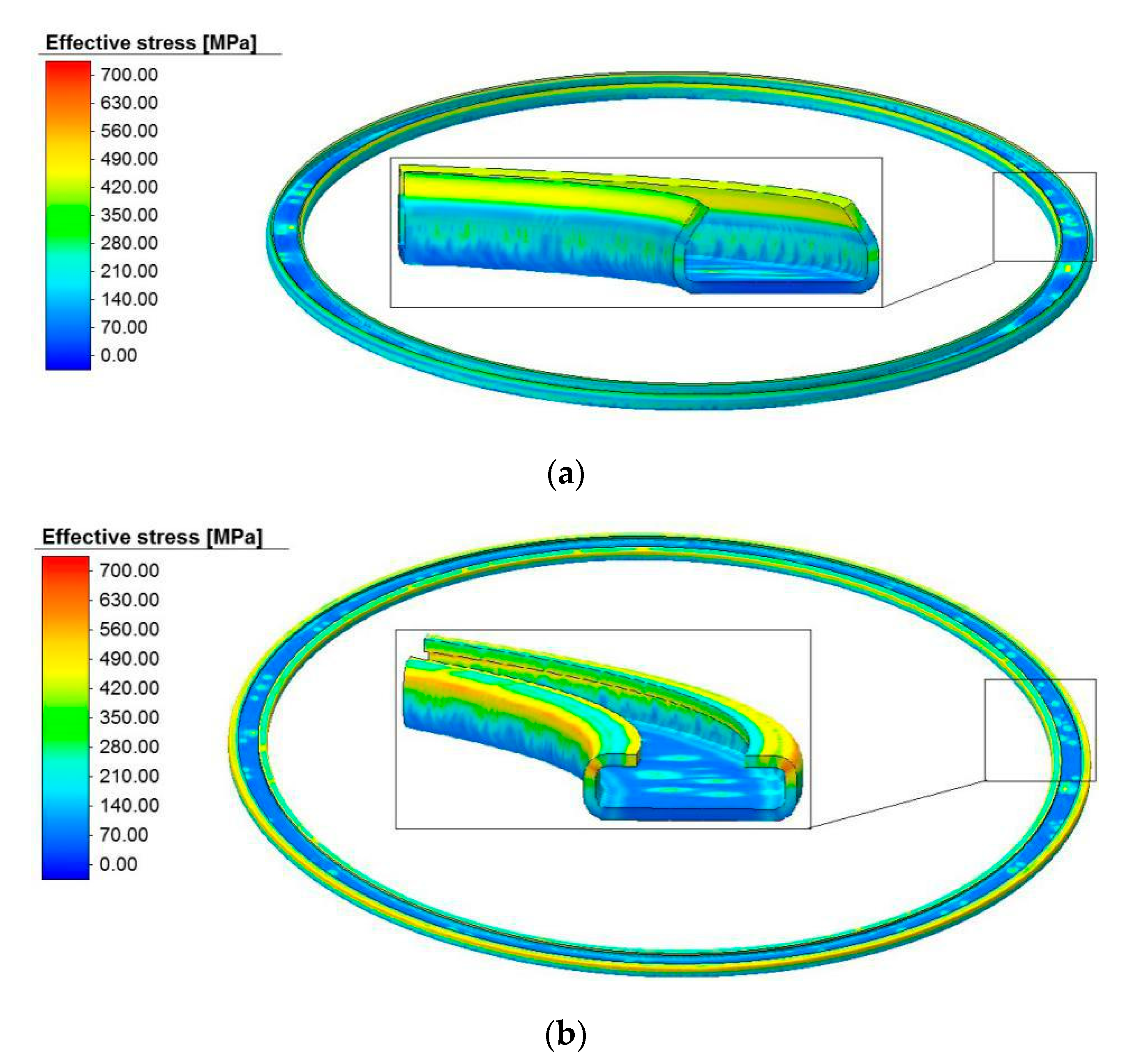
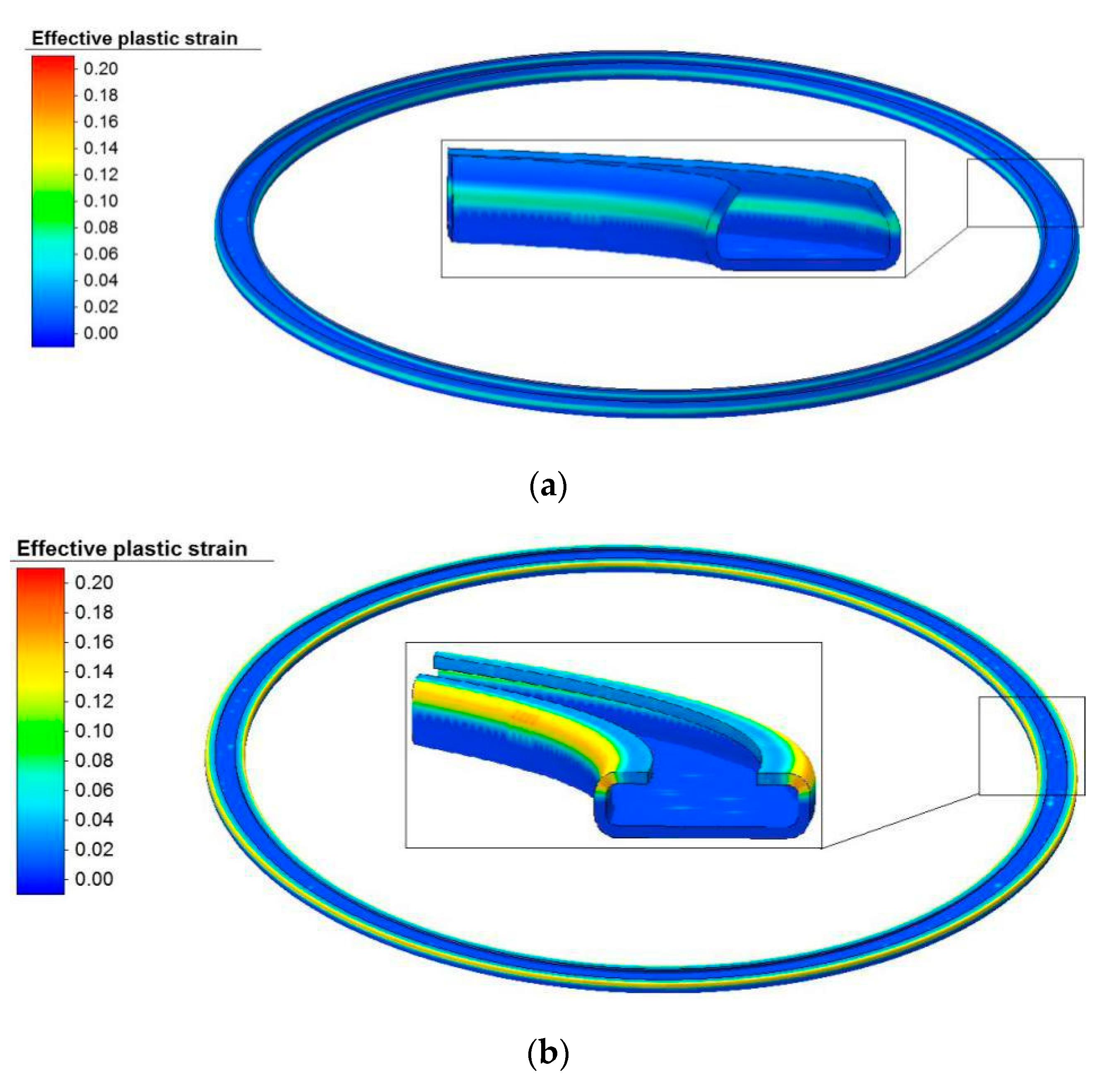
3.2. Stress–Strain Field
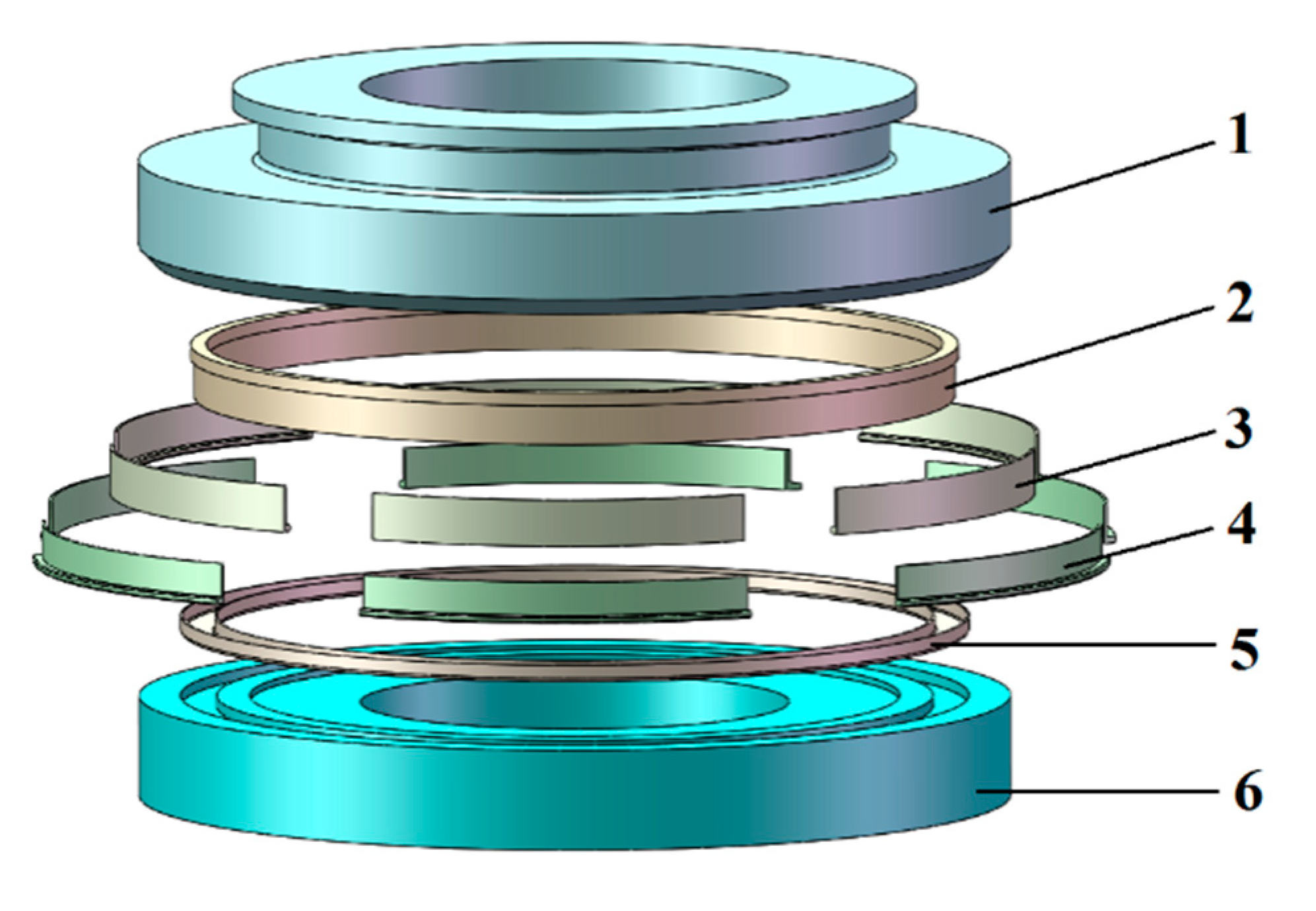
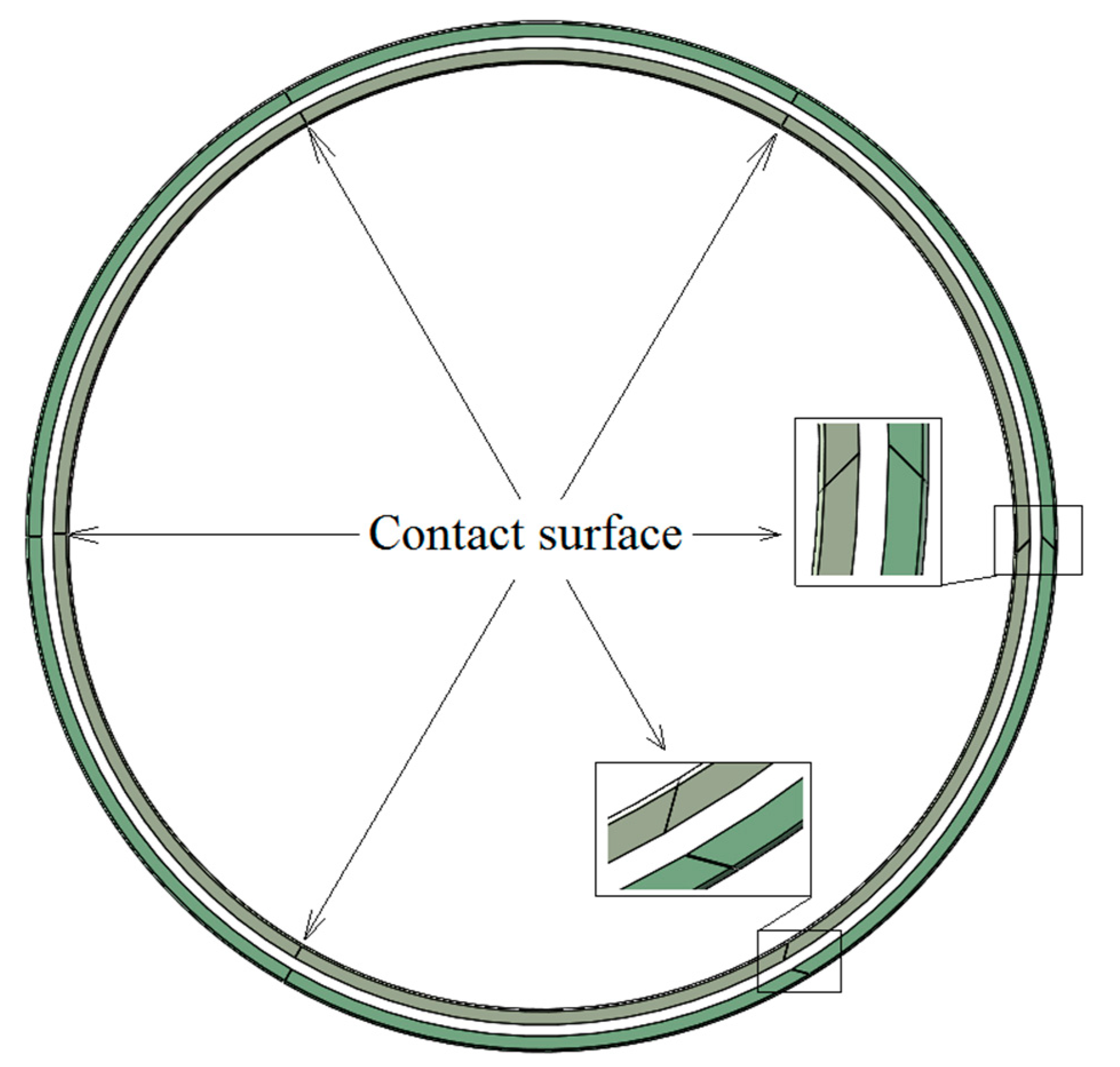
4. Multi-Pass Stamping Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, Z.G.; Ye, G.N.; Zhang, D.; Wang, Z.Y. Research on the Spinning Forming Process of Deflector of an Aeroengine. New Technol. New Process 2016, 2, 16–18. [Google Scholar]
- He, Z. Research on Ball Spinning Flanging Technology and Design of Special Equipment. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2017. [Google Scholar]
- Li, F.; Zhou, X.H.; Ruan, X.Y. Manufacturability Evaluation of Sheet Metal Parts. Forg. Stamp. Technol. 1999, 24, 24–26. (In Chinese) [Google Scholar]
- Chu, X.N.; Hans, H. Product manufacturability control for Concurrent engineering. Comput. Ind. 1994, 24, 29–38. [Google Scholar] [CrossRef]
- Tan, Z. An Empiric Model for Controlling Springback in V-die Bending of Sheet Metal. J. Mater. Process. Technol. 1992, 34, 402–405. [Google Scholar] [CrossRef]
- Wang, C.T.; Kinzel, G.; Altan, T. Mathematical modeling of plane-strain bending of sheet and plate. J. Mater. Process. Technol. 1993, 39, 279–304. [Google Scholar] [CrossRef]
- Tekiner, Z. An experimental study on the examination of springback of sheet metals with several thicknesses and properties in bending dies. J. Mater. Process. Technol. 2004, 145, 109–117. [Google Scholar] [CrossRef]
- Gomes, C.; Onipede, O.; Lovell, M. Investigation of springback in high strength anisotropic steels. J. Mater. Process. Technol. 2005, 159, 91–98. [Google Scholar] [CrossRef]
- Batoz, J.L. An inverse finite element procedure to estimate the large plastic strain in sheet metal forming. 3rd ICTP 1994, 3, 1403–1408. [Google Scholar]
- Ablat, M.A.; Qattawi, A. Numerical simulation of sheet metal forming: A review. Int. J. Adv. Manuf. Technol. 2017, 89, 1235. [Google Scholar] [CrossRef]
- Panthi, S.K.; Ramakrishnan, N.; Pathak, K.K.; Chouhan, J.S. An analysis of springback in sheet metal bending using finite element method (FEM). J. Mater. Process. Technol. 2007, 186, 120–124. [Google Scholar] [CrossRef]
- Li, Y. Rapid prototyping of sheet metal workpieces using bending-machining hybrid process. Int. J. Adv. Manuf. Technol. 2018, 99, 287–300. [Google Scholar] [CrossRef]
- Cho, J.R.; Moon, S.J.; Moon, Y.H.; Kang, S.S. Finite element investigation on spring-back characteristics in sheet metal U-bending process. J. Mater. Process. Technol. 2003, 141, 109–116. [Google Scholar] [CrossRef]
- Fu, Z.; Mo, J. Multiple-step incremental air-bending forming of high-strength sheet metal based on simulation analysis. Mater. Manuf. Process. 2010, 25, 808–816. [Google Scholar] [CrossRef]
- Malikov, V.; Ossenbrink, R.; Viehweger, B.; Michailov, V. Investigation of air bending of structured sheet metals by multistage FE simulation. Int. J. Adv. Manuf. Technol. 2012, 63, 449–455. [Google Scholar] [CrossRef]
- Parsa, M.H.; Al Ahkami, S.N. Bending of work hardening sheet metals subjected to tension. Int. J. Mater. Form. 2008, 1 (Suppl. 1), 173–176. [Google Scholar] [CrossRef]
- Wu, S.C.; Zheng, J.S. An experimental study of laser bending for sheet metals. J. Mater. Process. Technol. 2001, 110, 160–163. [Google Scholar]
- Ji, Z.; Wu, S. FEM simulation of the temperature field during the laser forming of sheet metal. J. Mater. Process. Technol. 1998, 74, 89–95. [Google Scholar] [CrossRef]
- Tian, G.H.; Lin, H.Q. Mould Design and Manufacturing, 2nd ed.; Peking University Press: Beijing, China, 2015; pp. 61–73. (In Chinese) [Google Scholar]
- Zhang, X.B.; Li, J.M.; Liu, W.C. Numerical Simulation of Deep Drawing of 0Cr18Ni9 Stainless Steel Sheet. Hot Work. Technol. 2013, 42, 132–134. (In Chinese) [Google Scholar]

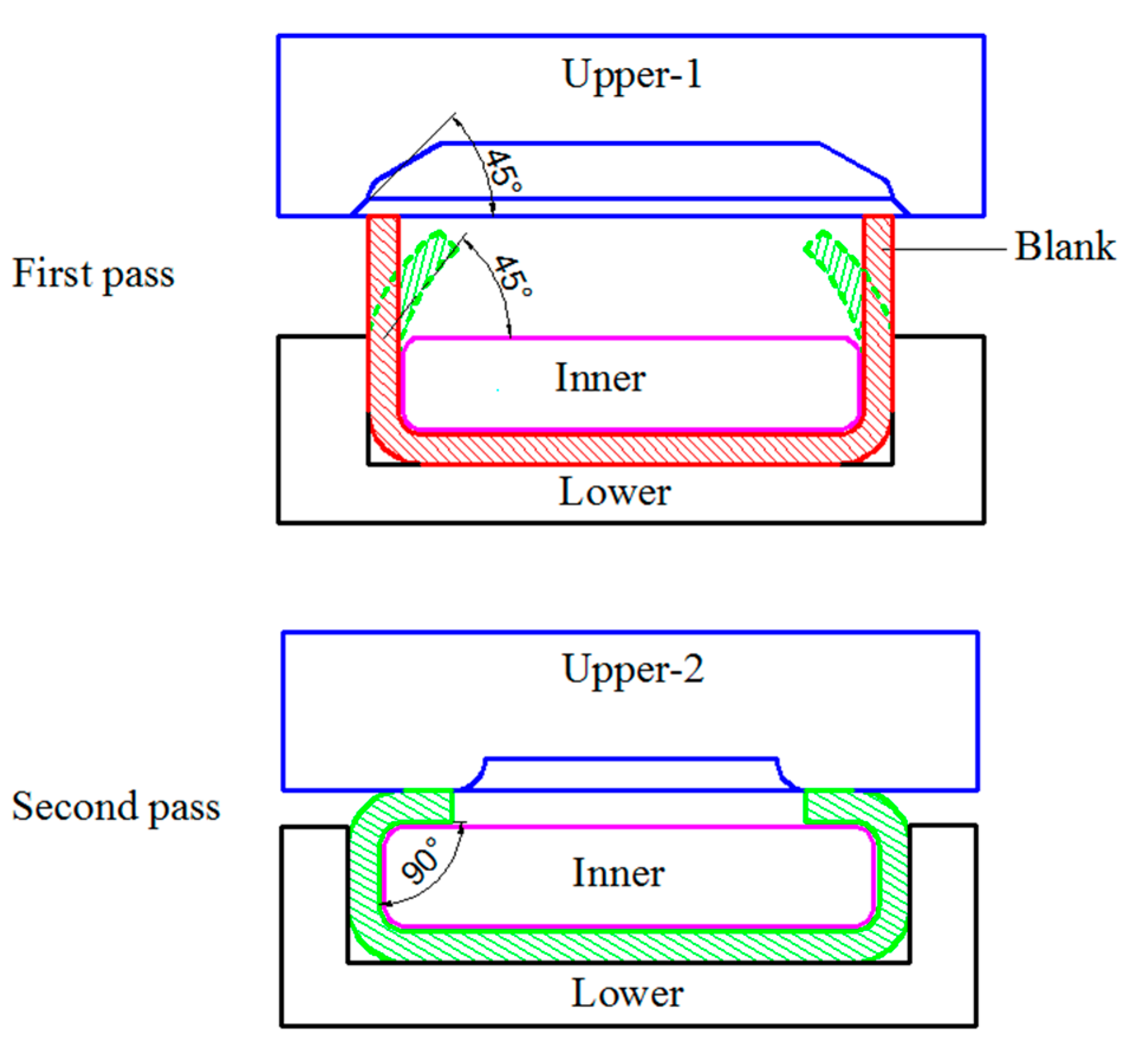
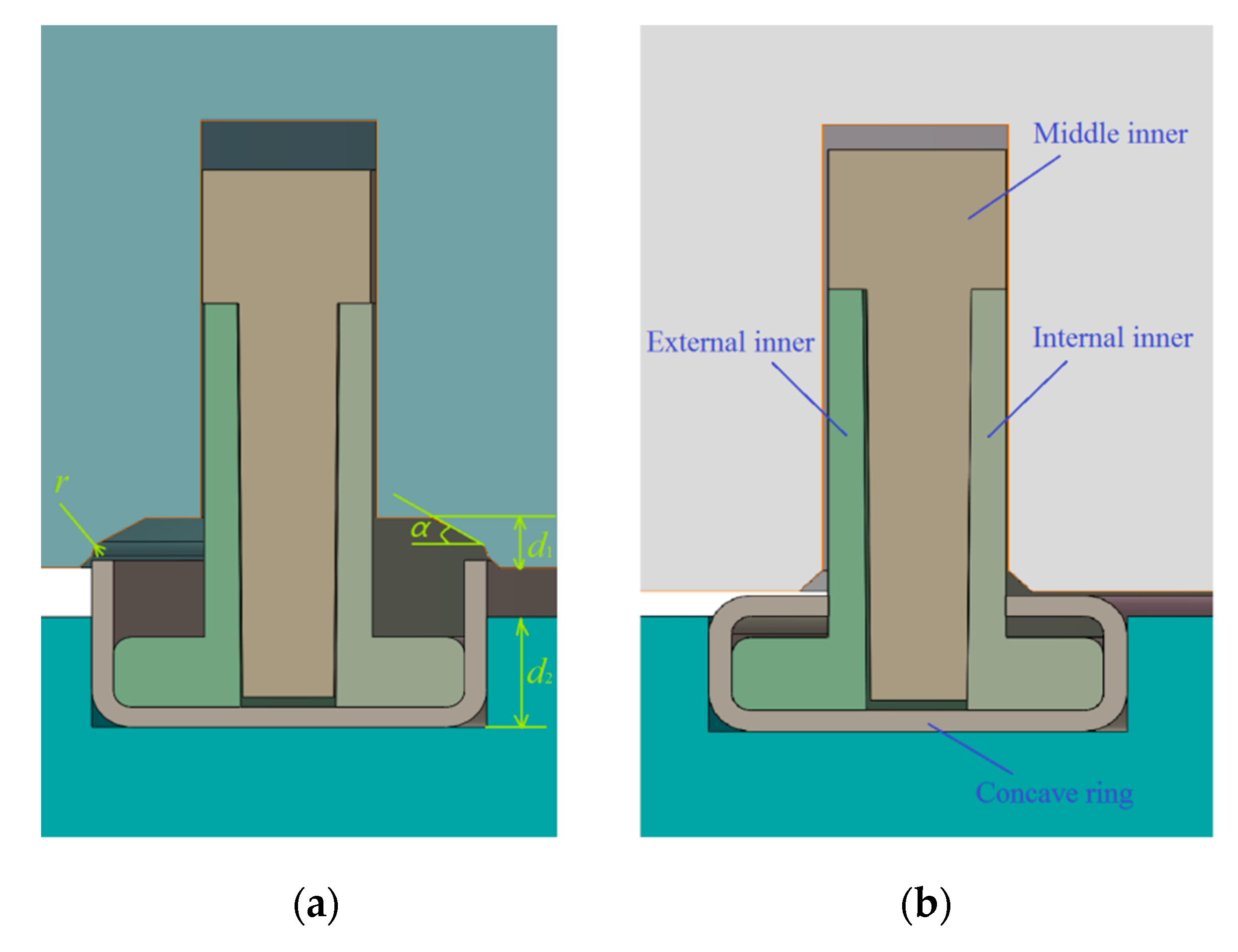
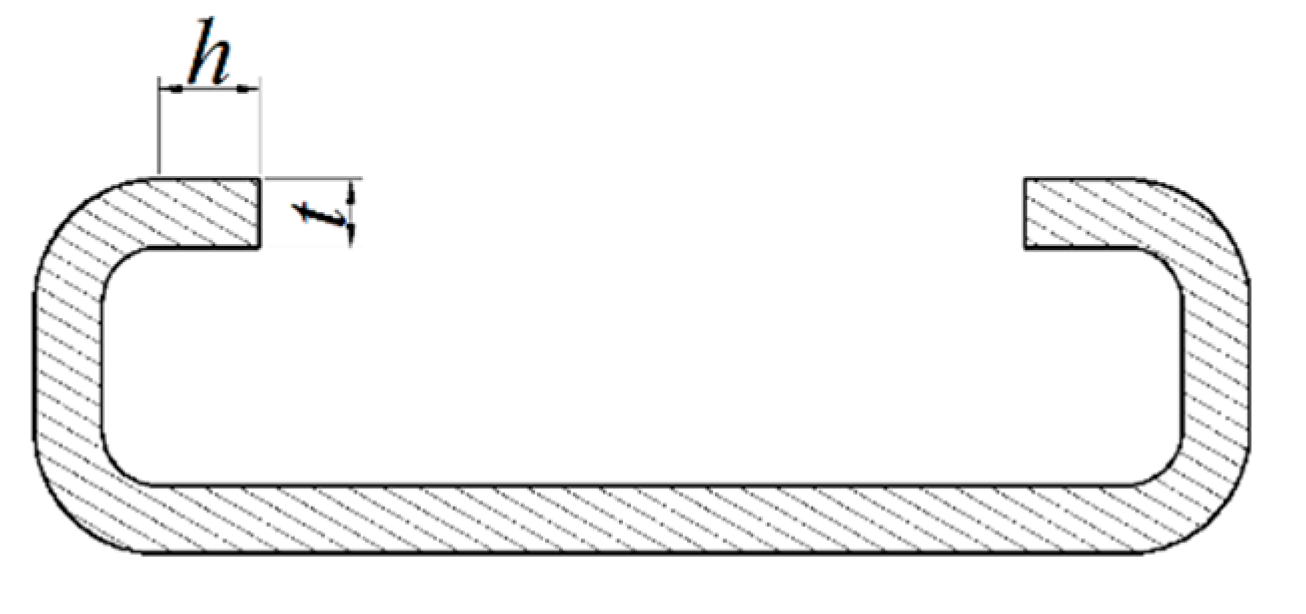








| Parameter | Value |
|---|---|
| Angle of inclined straight line of upper-1 groove α/° | 30 |
| Radius of arc of upper-1 groove r/mm | 0.5 |
| Depth of upper-1 groove d1/mm | 1.5 |
| Depth of lower groove d2/mm | 0.5 |
| Length of straight edge h/mm | 1.5 |
| Height of the Workpiece (mm) | Width of the Workpiece (mm) | |
|---|---|---|
| Design Value | 3.30 | 10.80 |
| Actual Value | 3.31 | 10.82 |
| Error | 0.3% | 0.2% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Shu, X.; Shi, J.; Li, Z. Multi-Pass Stamping Forming a Concave Ring. Appl. Sci. 2020, 10, 6434. https://doi.org/10.3390/app10186434
Zhang S, Shu X, Shi J, Li Z. Multi-Pass Stamping Forming a Concave Ring. Applied Sciences. 2020; 10(18):6434. https://doi.org/10.3390/app10186434
Chicago/Turabian StyleZhang, Song, Xuedao Shu, Jianan Shi, and Zixuan Li. 2020. "Multi-Pass Stamping Forming a Concave Ring" Applied Sciences 10, no. 18: 6434. https://doi.org/10.3390/app10186434
APA StyleZhang, S., Shu, X., Shi, J., & Li, Z. (2020). Multi-Pass Stamping Forming a Concave Ring. Applied Sciences, 10(18), 6434. https://doi.org/10.3390/app10186434







