Analysis of the Target Detection Performance of Air-to-Air Airborne Radar Using Long-Range Propagation Simulation in Abnormal Atmospheric Conditions

Abstract

In this paper, we propose the analysis of the target detection performance of air-to-air airborne radars using long-range propagation simulations with a novel quad-linear refractivity model under abnormal atmospheric conditions. The radar propagation characteristics and the target detection performance are simulated using the Advanced Refractive Effects Prediction System (AREPS) software, where the refractivity along the altitude, array antenna pattern, and digital terrain elevation data are considered as inputs to obtain the path loss of the wave propagation. The quad-linear model is used to approximate the actual refractivity data, which are compared to the data derived using the conventional trilinear refractivity model. On the basis of the propagation simulations, we propose a detection performance metric in terms of the atmosphere (DPMA) for intuitively examining the long-range propagation characteristics of airborne radars in air-to-air situations. To confirm the feasibility of using the DPMA map in various duct scenarios, we employ two actual refractive indices to observe the DPMA results in relation to the height of the airborne radar.

1. Introduction

Recent dramatic advances in radar systems have resulted in the extensive use of a variety of long-range airborne radars, including active electronically scanned array (AESA) radars, synthetic aperture radars (SARs), and airborne early warning (AEW) radars [1,2,3,4,5,6]. Such radars are generally required to exhibit extreme high-performance in order to accurately detect long-range targets in the case of even a low radar cross-section (RCS). However, regardless of the radar performance, the target detection probability can be decreased by various factors, for example, external noise, clutter, atmospheric gas attenuation, polarization mismatches, multipath interference, and the atmospheric refractive index [7]. In particular, the gradient of the atmospheric refractive indices along the altitude usually changed by the temperature, atmospheric pressure, and dew-point temperature, causes the refraction of the wave propagation, that is, sub-, super-, normal-, and duct refraction. These propagation characteristics make it difficult to estimate the long-range target position [8], and it is essential to model the atmospheric refractivity along the altitude to precisely predict the propagation direction, path loss, and propagation factor. Thus, many studies involving the modeling of atmospheric refractive indices at low altitudes of less than 1 km have been conducted by estimating the duct phenomena through the measured path loss values [9], the clutter power values [10], and statistical analyses based on stored atmospheric data [11]. In addition, various studies have also been carried out to estimate the wave propagation characteristics when considering the oversea atmospheric characteristics in ground-to-air and ground-to-ground scenarios. For example, substantial low-altitude atmospheric data concerning certain coastal areas in the United States, Europe, and China have been used to analyze the path loss for wave propagation characteristics. Although previous studies have shown a sufficient analysis of the radar propagation characteristics in a low-altitude situation, it still needs in-depth research regarding the propagation characteristics at high altitudes of over 5 km in air-to-air situations considering the atmospheric effects.

In this paper, we analyze the target detection performance of air-to-air airborne radars using long-range propagation simulations with a novel quad-linear refractivity model under abnormal atmospheric conditions. Both the radar propagation characteristics and the target detection performance are simulated using the Advanced Refractive Effects Prediction System (AREPS) software, as based on a propagation hybrid model [12,13]. In the AREPS simulation conditions, the refractivity along the altitude, the antenna radiation pattern, and the digital terrain elevation data (DTED) are considered to be inputs to obtain the path loss of the wave propagation. The quad-linear lines are employed to model the modified refractive indices for the abnormal atmospheres associated with various elevated ducts. In addition, the radiation pattern is calculated based on a 32 × 32 array antenna with a triangular array configuration used for modeling the airborne radar antenna. Then, the path loss results obtained using the quad-linear model are compared to the results obtained using the conventional trilinear refractivity model and to the actual refractivity data. Subsequently, the resulting path loss and the other radar parameters are used to calculate the radar target detection probability in order to estimate the target detection performance of the airborne radar. Using the calculated target detection probability, we propose a detection performance metric in terms of the atmosphere (DPMA) for intuitively examining the long-range propagation characteristics in air-to-air situations. To investigate the effects of abnormal atmospheric conditions on the radar performance, the DPMA map is examined by varying the height and thickness of the elevated duct. Further, to confirm the feasibility of the DPMA map in various duct scenarios, two actual refractive indices are employed to observe the DPMA results in accordance with the height of the airborne radar. The results demonstrate that the proposed method of analysis can intuitively determine the target detection performance of air-to-air airborne radars under abnormal atmospheric conditions.

2. Long-Range Propagation Analysis of Air-to-Air Airborne Radars

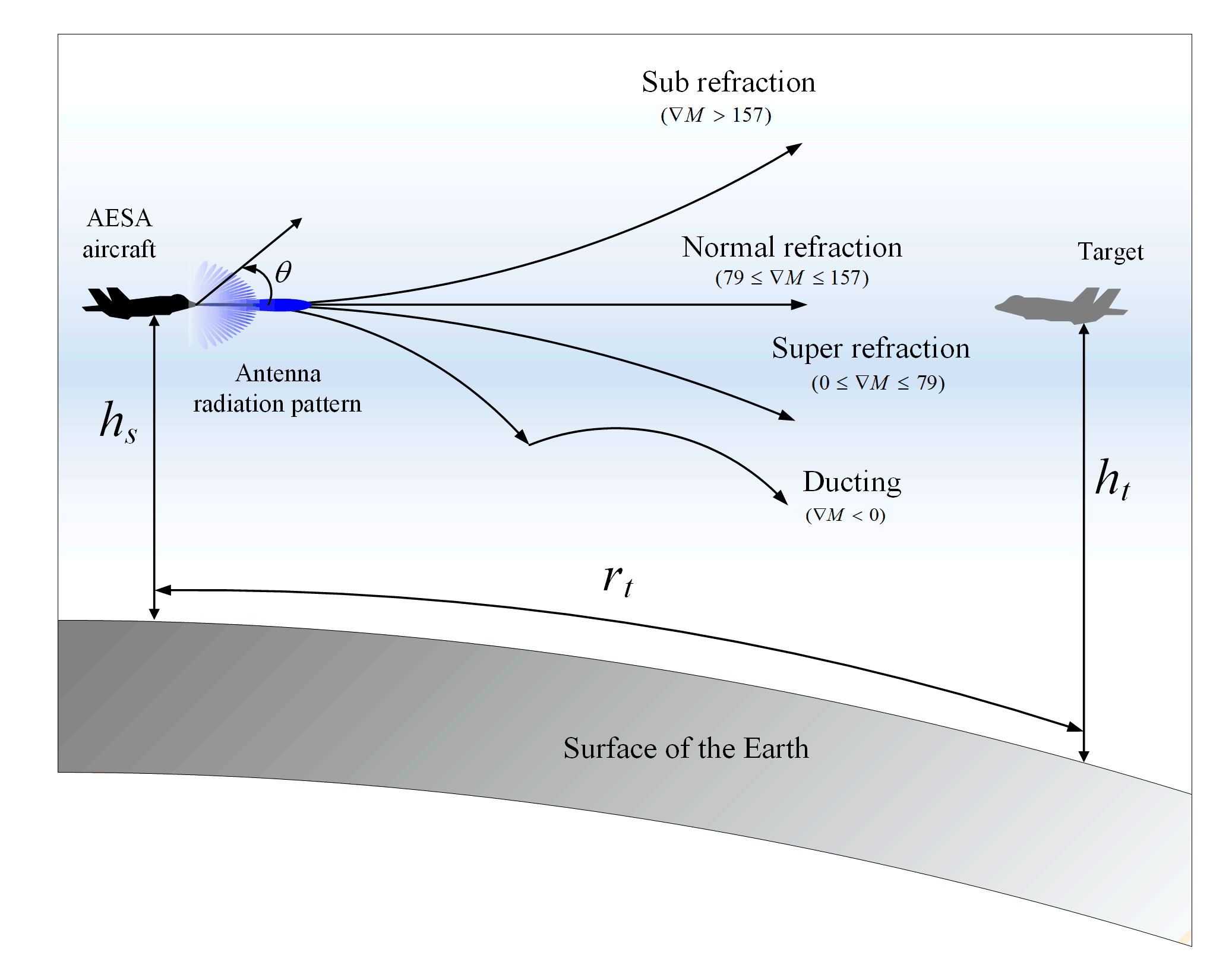
2.1. Abnormal Atmospheric Conditions and Propagation Characteristics

In general, the atmosphere is usually expressed by the refractive index n according to the height, and it can be changed into the modified refractive index M on a hypothetical flat Earth when considering the Earth’s curvature, as expressed in Equation (1) [14].

$$M=\left(n-1\right){10}^6+0.157h$$

(1)

In fact, with regard to radio wave propagation, the gradient of the modified refractive index M in terms of the height considerably affects the propagation direction.

As shown in Figure 1, there are four typical refractions associated with the wave propagations of an air-to-air airborne radar: sub (157 < ∇M), normal (79 < ∇M ≤ 157), super refraction (0 < ∇M ≤ 79), and duct (∇M < 0). In particular, the duct condition represents the most abnormal phenomenon, which causes the wave to become trapped in the atmosphere as if it propagates in a waveguide. Figure 2 illustrates the modified refractive indices of the elevated duct atmospheres according to the altitude at the Heuksando meteorological observatory on 4 September 2010, 5 June 2015, and 10 December 2015, which are all calculated using the air pressure, temperature, and dew point temperature. Such atmospheric data can be approximated by combinations of linear lines, and there is a conventional method (i.e., a trilinear model) for modeling the refractivity using three linear lines. However, at a high altitude of over 5 km, we find that many elevated duct cases require an additional linear line to accurately model the modified refractivity. Thus, we propose a quad-linear model of the modified refractive indices alongside the higher altitude with four linear lines in order to approximate the elevated duct condition, as shown in Figure 3. The first to third linear lines have heights of h₁, h₂, and h₃, as well as slopes of d₁, d₂, and d₃. The fourth line is modeled by a height of h_max and a slope of d₄. Herein, the height and thickness of the elevated duct are indicated by h₁ and Δh, respectively.

Figure 4 presents comparisons of the quad-linear and trilinear modeling of the actual refractivity data obtained at the Osan meteorological observatory on 1 February 2015. The detailed values of the quad-linear model parameters are h₁ = 4.98 km, h₂ = 5.16 km, h₃ = 5.5 km, h_max = 10 km, d₁ = 132.5, d₂ = −817.8, d₃ = 587, and d₄ = 142. The quad-linear modeling result exhibits a good level of agreement with the actual refractivity data when compared with the conventional trilinear model result, where the deviations of each model can be calculated by the equation as follows:

$$RMSD=\sqrt{{\displaystyle \sum _{i=1}^I\frac{\left|M_{act}\left[i\right]-M_{model}\left[i\right]\right|}{I}}},$$

(2)

where RMSD is the root-means-square deviation of the refractivity. M_act indicates the refractivity along the altitude, and M_model specifies the refractivity in terms of the tri- or quad-linear model along the altitude. The RMSD values are 7.2 M-unit for the quad-linear model and 60.2 M-unit for the trilinear model, respectively. To observe the propagation characteristics in an air-to-air situation, we include both these refractivity models and the actual data in the analysis involving the AREPS simulation software, while the radiation pattern of a conventional airborne array antenna is also applied as a simulation parameter. Figure 5a represents the 32 × 32 triangular array configuration of an airborne array antenna with array distances of 0.475 λ and 0.538 λ along the x- and y-axis. Each element pattern is assumed to be an ideal isotropic pattern, and then the total array pattern with 1204 array elements is calculated in the Az/El domain, as shown in Figure 5b. Figure 5c shows the directivity of the array antenna in the H-plane, which has a half-power beamwidth (HPBW) of 2.85° and a side lobe level (SLL) of −13.5 dB. Figure 6 illustrates comparisons of the AREPS simulation path loss results at h_s of 5 km when using the refractivity of the actual data, the quad-linear model, and the trilinear model. The path loss results using the actual data, and the quad-linear model exhibit similar trends in terms of the propagation characteristics in the abnormal atmospheric condition. On the other hand, the trilinear model shows significant deviations in relation to the path loss characteristics. Note that, it is possible that the path loss results can be more different according to the refractivity model, although the RMSD values are small. These AREPS simulation results were previously validated by the measurement in references [15,16] of a long-range propagation in a ground-to-ground situation. Furthermore, to verify these results, we compare the path loss of the AREPS simulation with that of the ITU-R P.528 model [17] and the MATLAB PETOOL software [18]. Figure 7 represents the comparison of the path loss results as a function of range in accordance with the atmospheric conditions without the terrain effects. In the normal atmosphere, all results have a similar tendency of path loss according to the range. In the abnormal atmosphere, the AREPS and PETOOL results also show a similar fluctuation, and both results follow the ITU-R model trend in the long-range propagation. Therefore, the resulting propagation characteristics demonstrate that the quad-linear model of refractivity can provide a highly accurate wave propagation estimation for air-to-air airborne radar simulation in abnormal atmospheric conditions.

2.2. Target Detection Performance in Abnormal Atmosphere

In general, many studies on target detection performance have been investigated considering RCS fluctuations with clutters [19], multipath effects [20], regional environments [21], and refractive profiles [22,23,24]. In this research, we calculate the probability of the target detection using thresholds derived from the free-space path loss levels to examine the target detection performance. To calculate the path loss threshold, the detectable range with regard to the detection probability is defined using the radar equation in free space, as written in Equation (3) [25].

$$R_{fs}\left(P_d\right)=\sqrt[4]{\frac{c_0^2{P}_t\sigma \tau G^2}{{\left(4\pi \right)}^{3}k{T}_0\left(D\left(P_d\right)\right)f^2{N}_f{L}_s}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left[m\right],$$

(3)

where c₀ is the speed of light in m/s, and P_t is the transmitting power in W. σ is the RCS in m², and τ is the pulse length of the radar in s. G is the array antenna gain for the airborne radar, and k is the Boltzmann’s constant. T₀ is the absolute temperature in K, and D is the detectability factor. P_d is the detection probability, and f is the operating frequency in Hz. N_f is the noise figure of the radar, and L_s is the miscellaneous system loss. In this equation, all the airborne radar parameters are set as constant, except for the detectability factor D, which is simply approximated by Blake [25]. This factor includes the probability of the target detection and of a false alarm. Thus, it can simply approximate the functional relationship between the target detection probability and the radar equation in free space. Therefore, the free-space propagation loss for the threshold can be defined as follows:

$$L_{Th}\left(P_d\right)=20\log \left(R_{fs}\left(P_d\right)\right)+20\log \left(f\right)+20\log \left(\frac{4\pi }{c_0}\right).$$

(4)

To determine the detection probability in the air-to-air situation for the airborne radar, we obtain the path loss values using the AREPS simulation software, and then we calculate the probability by including the airborne radar system parameters. The detailed parameter values are listed in

Table 1. Detailed airborne radar parameters and values.

Parameters	Values	Parameters	Values
Pt	106 W	T0	290 K
σ	15 m2	D	0.04–17.9
τ	2 × 10−6 s	Pd	0.01–0.99
Pfa	10−8	f	10 × 109 Hz
G	103	Nf	100.5
k	1.38 × 10−23	Ls	100.3

.

Figure 8a,b illustrates the detection probability results for the air-to-air scenario in terms of the normal and abnormal duct atmospheres when the source height h_s is 4.8 km. The dashed lines indicate the wave propagation direction at θ = 0.5θ_HPBW, 0°, and −0.5θ_HPBW, where θ_HPBW is an HPBW angle of the airborne radar antenna radiation pattern. As can be seen in Figure 8b, the target detection performance is seriously degraded within the HPBW region as a result of the abnormally elevated duct. To more intuitively analyze the target detection performance, we propose a DPMA, which is defined as the ratio of the detectable area of the normal atmosphere to that of the abnormal atmosphere, as follows:

$$DPMA=\frac{A_{d,atm}}{A_{d,nor}},$$

(5)

$$A_{d,atm}={\displaystyle {\int }_{-0.5{\theta }_{HPBW}}^{0.5{\theta }_{HPBW}}{F}_{atm}\left(\theta \right)d\theta },\hspace{0.17em}$$

(6)

$$A_{d,nor}={\displaystyle {\int }_{-0.5{\theta }_{HPBW}}^{0.5{\theta }_{HPBW}}{F}_{nor}\left(\theta \right)d\theta },\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}$$

(7)

where A_d,_atm and A_d,_nor indicate the detectable areas for the abnormal and normal atmospheres, respectively. When the DPMA value is close to 1, the target detection performance is similar to that associated with the normal atmosphere. F_atm and F_nor indicate the contour lines for the detectable areas under the abnormal and normal atmosphere conditions, respectively. To examine the effects of the abnormal atmosphere, the elevated duct height and thickness are varied to provide a DPMA map for the air-to-air radar propagation when the airborne radar is located at heights of 3 km and 5 km, as shown in Figure 9. Due to the elevated duct, low DPMA levels are obtained, particularly near the airborne radar (3 km and 5 km). According to the DPMA map, the minimum values are 0.65 at an h₁ of 3 km and 0.69 at an h₁ of 5 km, respectively. To verify the feasibility of using the DPMA map, two representative elevated duct conditions, namely Case 1 (Jeju; 5 October 2017) and Case 2 (Pohang; 5 October 2017), are analyzed in more detail. Figure 10a,c presents the refractivity of the duct conditions for the two cases using actual refractivity data with the tri-and quad-linear models. Red solid, blue dashed, green dotted, and black dash-dotted lines specify the actual refractivity, quad-linear model, tri-linear model, and the normal atmosphere, respectively. The duct height and thickness are 4.79 km and 495 m for Case 1 as well as 7.37 km and 715 m for Case 2. Figure 10b,d shows the DPMA results according to the airborne radar height for both cases. In the simulation results, the lowest DPMA values of 0.87 and 0.93 are obtained for Case 1 and Case 2, when the radar height h_s is close to the elevated duct height h₁. In addition, the DPMA of the quad-linear model well follows that of the actual data, while the DPMA upper h₁ of the tri-linear model has a great difference with that of the actual data.

3. Conclusions

In this paper, we analyzed the target detection performance of air-to-air airborne radars using long-range propagation simulations involving a novel quad-linear refractivity model under abnormal atmospheric effects. The radar propagation characteristics and the target detection performances were simulated using the AREPS software. In relation to the AREPS simulation conditions, the quad-linear refractivity model as well as the altitude, the antenna radiation pattern, and the DTED were considered as inputs to obtain the path loss of the wave propagation. The quad-linear modeling result well agreed with the actual refractivity data when compared with the conventional trilinear model, with the root-mean-square deviations of the refractivity being 7.2 M-unit for the quad-linear model and 60.2 M-unit for the trilinear model. The radiation pattern of the 32 × 32 triangular array antenna had an HPBW of 2.85° and an SLL of −13.5 dB, which were used as inputs for the simulation parameters. In terms of the AREPS simulations, the resulting path losses when using the quad-linear model and the actual data exhibited similar propagation characteristic trends. To examine the effects of the abnormal atmosphere, the DPMA maps at airborne radar heights of 3 km and 5 km were provided according to the duct height h₁ and thickness Δh, where the minimum DPMA values were 0.65 at an h₁ of 3 km and 0.69 at an h₁ of 5 km. To verify the feasibility of using the DPMA map, two representative elevated duct conditions (Case 1 and Case 2) were analyzed in more detail. According to the simulation results, the lowest DPMA values of 0.87 and 0.93 were obtained for Case 1 and Case 2, respectively, when the radar height h_s was close to the elevated duct height h₁. These results confirmed that the proposed analysis could intuitively determine the target detection performances of air-to-air airborne radars under abnormal atmospheric conditions.