Trends in the Characterization of the Proximal Humerus in Biomechanical Studies: A Review
Abstract
:1. Introduction
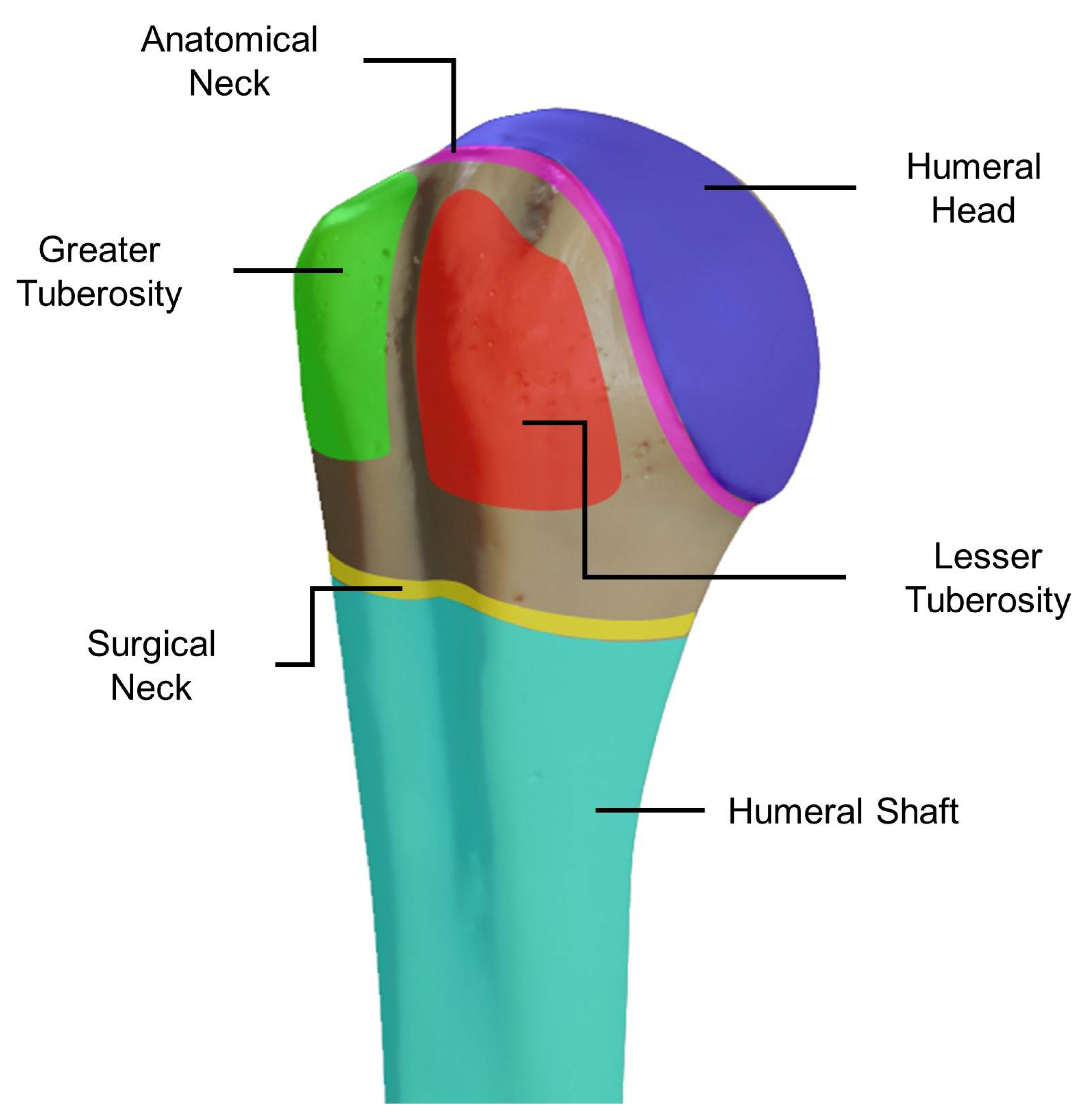
2. Proximal Humerus Anatomy and Bone Composition
2.1. Bone Shape
2.2. Muscles, Tendons, and Movements
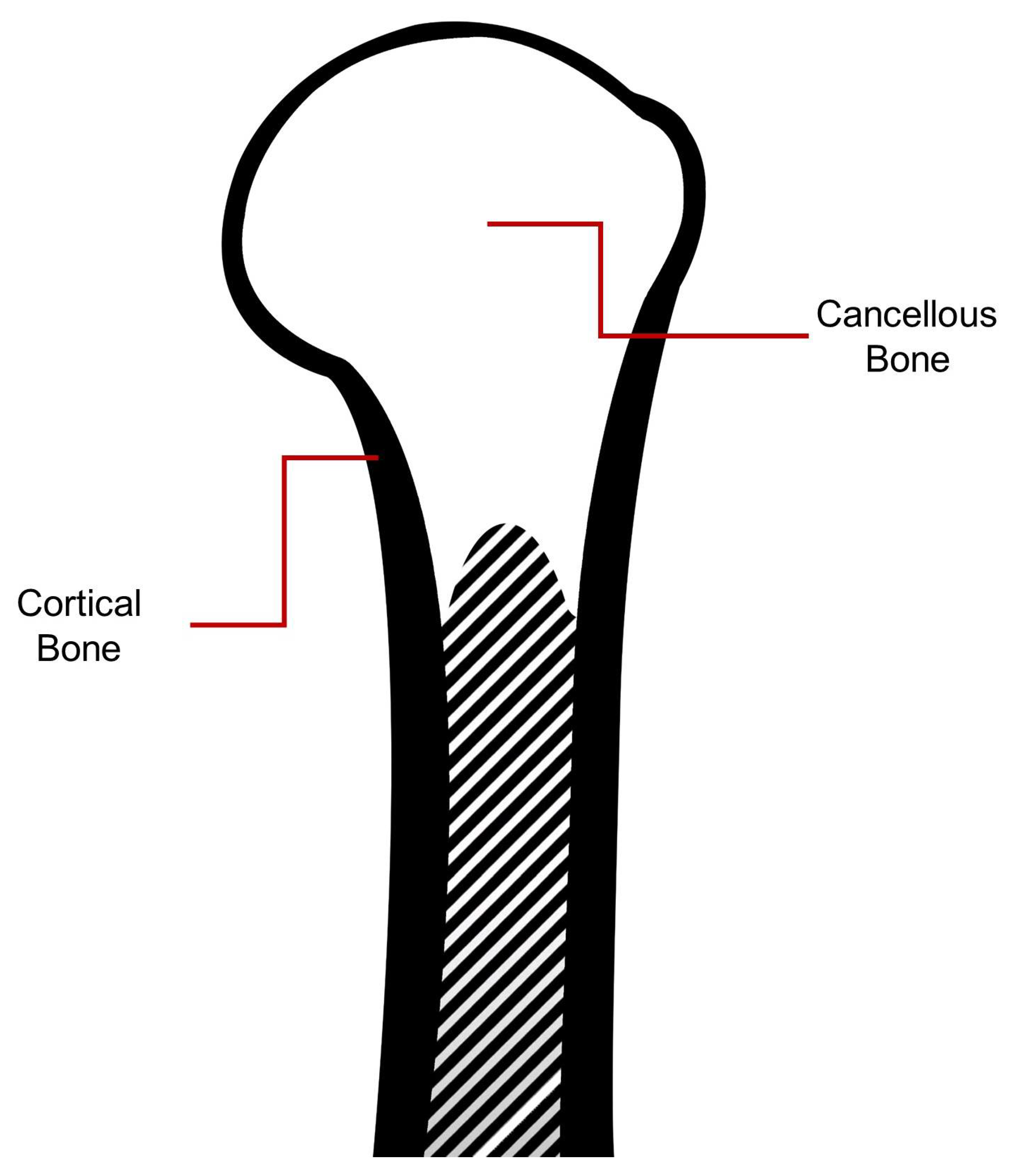
2.3. Bone Composition: Proximal Humerus
3. Biomechanical FEA Studies for Proximal Humerus Fractures
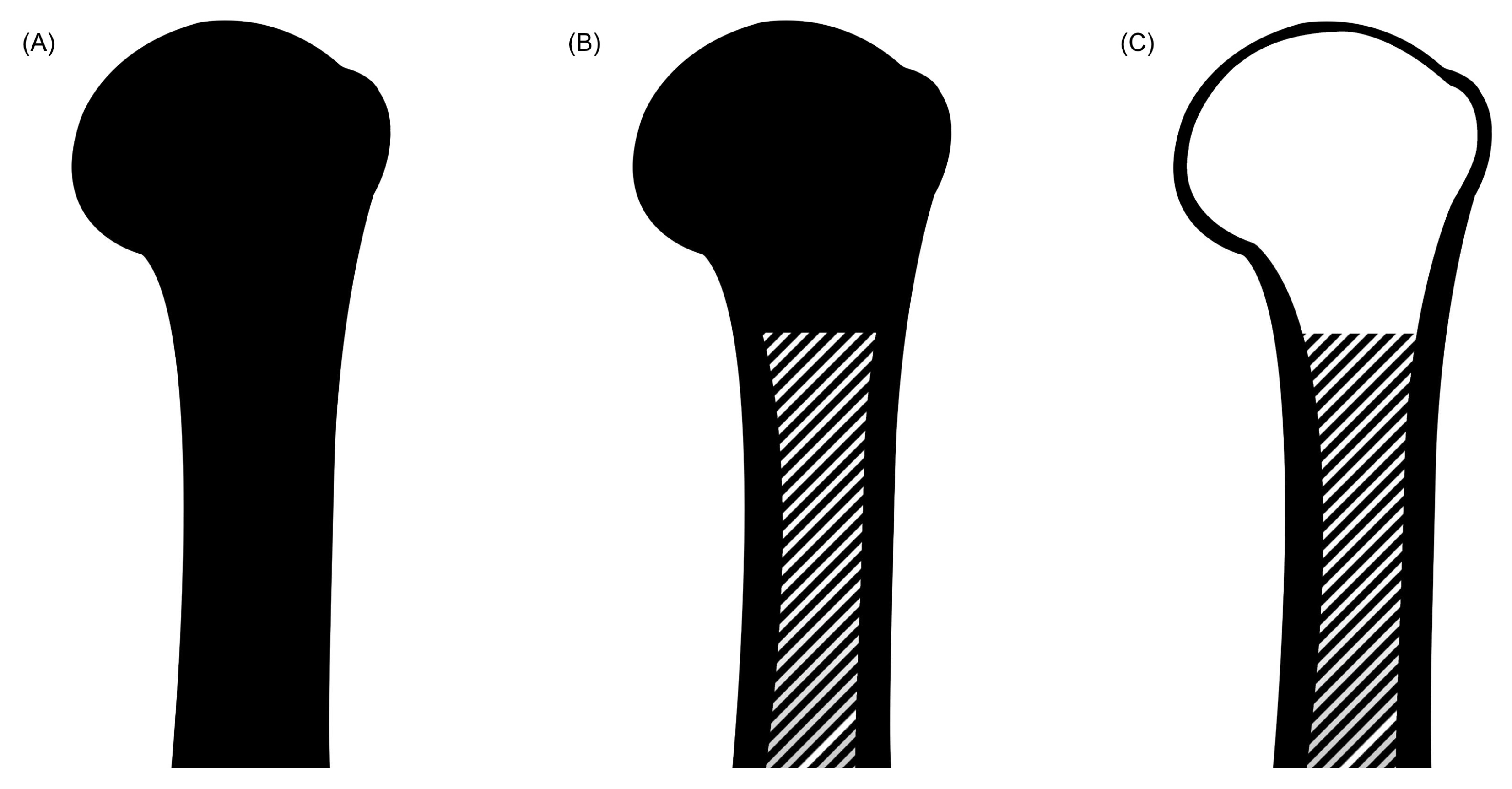
4. Simplification of the Geometry Characteristics of the Bone
5. From Reality to 3D Model: Mechanical Properties Assignment
5.1. Cortical Bone
5.2. Cancellous Bone
6. Proximal Humerus Meshing Properties
7. Discussion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Al Anouti, F.; Taha, Z.; Shamim, S.; Khalaf, K.; Al Kaabi, L.; Alsafar, H. An insight into the paradigms of osteoporosis: From genetics to biomechanics. Bone Rep. 2019, 11, 100216. [Google Scholar] [CrossRef] [PubMed]
- Court-Brown, C.M.; Duckworth, A.D.; Clement, N.D.; McQueen, M.M. Fractures in older adults. A view of the future? Injury 2018, 49, 2161–2166. [Google Scholar] [CrossRef] [PubMed]
- Dahan, G.; Trabelsi, N.; Safran, O.; Yosibash, Z. Finite element analyses for predicting anatomical neck fractures in the proximal humerus. Clin. Biomech. 2019, 68, 114–121. [Google Scholar] [CrossRef] [PubMed]
- Kamer, L.; Noser, H.; Popp, A.W.; Lenz, M.; Blauth, M. Computational anatomy of the proximal humerus: An ex vivo high-resolution peripheral quantitative computed tomography study. J. Orthop. Transl. 2016, 4, 46–56. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.-K.; Wei, H.-W.; Lin, K.-P.; Chen, W.-C.; Tsai, C.-L.; Lin, K.-J. Biomechanical effect of the configuration of screw hole style on locking plate fixation in proximal humerus fracture with a simulated gap: A finite element analysis. Injury 2016, 47, 1191–1195. [Google Scholar] [CrossRef]
- Baidwan, N.; Naranje, S. Epidemiology and recent trends of geriatric fractures presenting to the emergency department for United States population from year 2004–2014. Public Health 2017, 142, 64–69. [Google Scholar] [CrossRef]
- Hamidi, M.; Joseph, B. Changing Epidemiology of the American Population. Clin. Geriatr. Med. 2019, 35, 1–12. [Google Scholar] [CrossRef]
- United Nations. World Population Prospects 2019; Highlights: New York, NY, USA, 2019. Available online: https://bit.ly/2MXgwm4 (accessed on 16 August 2019).
- Khanuja, K.; Joki, J.; Bachmann, G.; Cuccurullo, S.; Joki, J. Gait and balance in the aging population: Fall prevention using innovation and technology. Maturitas 2018, 110, 51–56. [Google Scholar] [CrossRef]
- Reske-Nielsen, C.; Medzon, R. Geriatric Trauma. Emerg. Med. Clin. N. Am. 2016, 34, 483–500. [Google Scholar] [CrossRef]
- Ronthal, M. Gait Disorders and Falls in the Elderly. Med Clin. N. Am. 2019, 103, 203–213. [Google Scholar] [CrossRef]
- World Health Organization. World Report on Ageing and Health; World Health Organization: Geneva, Switzerland, 2015; pp. 3–223.
- Khoriati, A.; Antonios, T.; Bakti, N.; Mohanlal, P.; Singh, B. Outcomes following non operative management for proximal humerus fractures. J. Clin. Orthop. Trauma 2019, 10, 462–467. [Google Scholar] [CrossRef] [PubMed]
- Nowak, L.L.; Dehghan, N.; McKee, M.D.; Schemitsch, E.H. Plate fixation for management of humerus fractures. Injury 2018, 49, S33–S38. [Google Scholar] [CrossRef]
- Woodmass, J.M.; Welp, K.; Chang, M.J.; Borque, K.A.; Wagner, E.R.; Warner, J.J. Three- and four-part proximal humerus fractures in the elderly: Eminence versus evidence. Semin. Arthroplast. 2017, 28, 102–108. [Google Scholar] [CrossRef]
- Goharian, A.; Kadir, M.R. Humerus Trauma Plating Fixation. In Trauma Plating Systems; Elsevier BV: Amsterdam, The Netherlands, 2017; pp. 183–215. [Google Scholar]
- Padegimas, E.M.; Zmistowski, B.; Lawrence, C.; Palmquist, A.; Nicholson, T.A.; Namdari, S. Defining optimal calcar screw positioning in proximal humerus fracture fixation. J. Shoulder Elb. Surg. 2017, 26, 1931–1937. [Google Scholar] [CrossRef]
- Boyd, S.; Müller, R. Microimaging. In Principles of Bone Biology, 4th ed.; Bilezikian, J.P., Martin, T.J., Clemens, T.L., Rosen, C.J., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 1833–1856. [Google Scholar]
- Simkins, D.C.; Alford, J.B. The Role of Computational Tools in Biomechanics. In Biomechanics of the Female Pelvic Floor; Elsevier: Amsterdam, The Netherlands, 2016; pp. 351–366. [Google Scholar]
- Zhao, L.-M.; Tian, D.-M.; Wei, Y.; Zhang, J.-H.; Di, Z.-L.; He, Z.-Y.; Hu, Y.-C. Biomechanical Analysis of a Novel Intercalary Prosthesis for Humeral Diaphyseal Segmental Defect Reconstruction. Orthop. Surg. 2018, 10, 23–31. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, H.; Kim, S.-H.; Chang, S.-H. Finite element analysis using interfragmentary strain theory for the fracture healing process to which composite bone plates are applied. Compos. Struct. 2011, 93, 2953–2962. [Google Scholar] [CrossRef]
- Yosibash, Z.; Trabelsi, N.; Milgrom, C. Reliable simulations of the human proximal femur by high-order finite element analysis validated by experimental observations. J. Biomech. 2007, 40, 3688–3699. [Google Scholar] [CrossRef]
- Marcián, P.; Narra, N.; Borák, L.; Chamrad, J.; Wolff, J. Biomechanical performance of cranial implants with different thicknesses and material properties: A finite element study. Comput. Boil. Med. 2019, 109, 43–52. [Google Scholar] [CrossRef]
- Goshulak, P.; Samiezadeh, S.; Aziz, M.S.; Bougherara, H.; Zdero, R.; Schemitsch, E.H. The biomechanical effect of anteversion and modular neck offset on stress shielding for short-stem versus conventional long-stem hip implants. Med. Eng. Phys. 2016, 38, 232–240. [Google Scholar] [CrossRef]
- Chaudhry, V.; Kumar, K.N.; Panwar, K.S.; Shaikh, A.; Avikal, S. Static structural analysis of humerus bone to find out the load at which fracture occurs and predict suitable alternative materials for bone implants. Mater. Today: Proc. 2020, 26, 1701–1706. [Google Scholar] [CrossRef]
- Shaikh, A.; Negi, S.; Aswal, A.; Chaudhry, V.; Kishore, C.; Kumar, K.N. Modal analysis of Humerus bone using CAE tools. Mater. Today: Proc. 2020, 26, 2108–2112. [Google Scholar] [CrossRef]
- Razfar, N.; Reeves, J.M.; Langohr, D.G.; Willing, R.; Athwal, G.S.; Johnson, J.A. Comparison of proximal humeral bone stresses between stemless, short stem, and standard stem length: A finite element analysis. J. Shoulder Elb. Surg. 2016, 25, 1076–1083. [Google Scholar] [CrossRef] [PubMed]
- Jabran, A.; Peach, C.; Zou, Z.; Ren, L. Parametric Design Optimisation of Proximal Humerus Plates Based on Finite Element Method. Ann. Biomed. Eng. 2019, 47, 601–614. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fletcher, J.W.A.; Windolf, M.; Richards, G.; Gueorguiev, B.; Buschbaum, J.; Varga, P. Importance of locking plate positioning in proximal humeral fractures as predicted by computer simulations. J. Orthop. Res. 2019, 37, 957–964. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, J.W.; Windolf, M.; Richards, R.G.; Gueorguiev, B.; Varga, P. Screw configuration in proximal humerus plating has a significant impact on fixation failure risk predicted by finite element models. J. Shoulder Elb. Surg. 2019, 28, 1816–1823. [Google Scholar] [CrossRef] [PubMed]
- Mischler, D.; Windolf, M.; Gueorguiev, B.; Nijs, S.; Varga, P. Computational optimisation of screw orientations for improved locking plate fixation of proximal humerus fractures. J. Orthop. Transl. 2020. [Google Scholar] [CrossRef]
- Pahr, D.H.; Zysset, P.K. From high-resolution CT data to finite element models: Development of an integrated modular framework. Comput. Methods Biomech. Biomed. Eng. 2009, 12, 45–57. [Google Scholar] [CrossRef]
- Inzana, J.A.; Varga, P.; Windolf, M. Implicit modeling of screw threads for efficient finite element analysis of complex bone-implant systems. J. Biomech. 2016, 49, 1836–1844. [Google Scholar] [CrossRef]
- Boileau, P.; Walch, G. The three-dimensional geometry of the proximal humerus. Implications for surgical technique and prosthetic design. J. Bone Jt. Surg. Br. 1997, 79, 857–865. [Google Scholar] [CrossRef]
- Pearl, M.L.; Volk, A.G. Coronal plane geometry of the proximal humerus relevant to prosthetic arthroplasty. J. Shoulder Elb. Surg. 1996, 5, 320–326. [Google Scholar] [CrossRef]
- Gogna, R.; Bhabra, G.; Modi, C.S. Fractures of the proximal humerus: Overview and non-surgical management. Orthop. Trauma 2019, 33, 315–321. [Google Scholar] [CrossRef]
- Hinson, J.A. Anatomy and Classification of Proximal Humerus Fractures. In Proximal Humerus Fractures; Springer International Publishing: Cham, Switzerland, 2015; pp. 1–22. [Google Scholar]
- Iannotti, J.; Gabriel, J.; Schneck, S.; Evans, B.; Misra, S. The normal glenohumeral relationships. An anatomical study of one hundred and forty shoulders. JBJS 1992, 74, 491–500. [Google Scholar] [CrossRef]
- Neer, C.S. THE CLASSIC: Displaced Proximal Humeral Fractures. Clin. Orthop. Relat. Res. 2006, 442, 77–82. [Google Scholar] [CrossRef] [PubMed]
- Hertel, R.; Hempfing, A.; Stiehler, M.; Leunig, M. Predictors of humeral head ischemia after intracapsular fracture of the proximal humerus. J. Shoulder Elb. Surg. 2004, 13, 427–433. [Google Scholar] [CrossRef]
- Meinberg, E.G.; Agel, J.; Roberts, C.S.; Karam, M.D.; Kellam, J.F. Fracture and Dislocation Classification Compendium—2018. J. Orthop. Trauma 2018, 32, S1–S10. [Google Scholar] [CrossRef]
- Varga, P.; Inzana, J.A.; Gueorguiev, B.; Südkamp, N.P.; Windolf, M. Validated computational framework for efficient systematic evaluation of osteoporotic fracture fixation in the proximal humerus. Med. Eng. Phys. 2018, 57, 29–39. [Google Scholar] [CrossRef]
- Wattanaprakornkul, D.; Cathers, I.; Halaki, M.; Ginn, K.A. The rotator cuff muscles have a direction specific recruitment pattern during shoulder flexion and extension exercises. J. Sci. Med. Sport 2011, 14, 376–382. [Google Scholar] [CrossRef]
- Otis, J.C.; Jiang, C.-C.; Wickiewicz, T.L.; Peterson, M.G.E.; Warren, R.F.; Santner, T.J. Changes in the moment arms of the rotator cuff and deltoid muscles with abduction and rotation. J. Bone Jt. Surg. Am. 1994, 76, 667–676. [Google Scholar] [CrossRef]
- Kuechle, D.K.; Newman, S.R.; Itoi, E.; Niebur, G.L.; Morrey, B.F.; An, K.-N. The relevance of the moment arm of shoulder muscles with respect to axial rotation of the glenohumeral joint in four positions. Clin. Biomech. 2000, 15, 322–329. [Google Scholar] [CrossRef]
- Vicenti, G.; Antonella, A.; Filipponi, M.; Conserva, V.; Solarino, G.; Carrozzo, M.; Moretti, B. A comparative retrospective study of locking plate fixation versus a dedicated external fixator of 3- and 4-part proximal humerus fractures: Results after 5 years. Injury 2019, 50, S80–S88. [Google Scholar] [CrossRef]
- Handoll, H.H.; Keding, A.; Corbacho, B.; Brealey, S.D.; Hewitt, C.; Rangan, A. Five-year follow-up results of the PROFHER trial comparing operative and non-operative treatment of adults with a displaced fracture of the proximal humerus. Bone Jt. J. 2017, 99, 383–392. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Passaretti, D.; Candela, V.; Sessa, P.; Gumina, S. Epidemiology of proximal humeral fractures: A detailed survey of 711 patients in a metropolitan area. J. Shoulder Elb. Surg. 2017, 26, 2117–2124. [Google Scholar] [CrossRef] [PubMed]
- Mendoza-Muñoz, I.; González-Angeles, A.; Jacobo-Galicia, G.; Castañeda, A.; Valenzuela-Gutiérrez, J. Análisis de los elementos principales en el diseño de placas de bloqueo en una fractura de 2-partes del cuello quirúrgico del húmero utilizando MEF y análisis estadístico. Matéria (Rio de Janeiro) 2018, 23. [Google Scholar] [CrossRef] [Green Version]
- Roe, S. Biomechanics of Fracture Fixation. Veter. Clin. N. Am. Small Anim. Pract. 2019, 50, 1–15. [Google Scholar] [CrossRef]
- Röderer, G.; Brianza, S.; Schiuma, D.; Schwyn, R.; Scola, A.; Gueorguiev, B.; Gebhard, F.; Tami, A. Mechanical Assessment of Local Bone Quality to Predict Failure of Locked Plating in a Proximal Humerus Fracture Model. Orthopedics 2013, 36, e1134–e1140. [Google Scholar] [CrossRef] [Green Version]
- Unger, S.; Erhart, S.; Kralinger, F.; Blauth, M.; Schmoelz, W. The effect of in situ augmentation on implant anchorage in proximal humeral head fractures. Injury 2012, 43, 1759–1763. [Google Scholar] [CrossRef]
- Mendoza-Muñoz, I.; González-Angeles, A.; Siqueiros-Hernández, M.; Montoya-Reyes, M. Biomechanical Principles Used in Finite Element Analysis for Proximal Humeral Fractures with Locking Plates. Med. Sci. Technol. 2017, 58, 128–136. [Google Scholar] [CrossRef]
- Yosibash, Z.; Mayo, R.P.; Dahan, G.; Trabelsi, N.; Amir, G.; Milgrom, C. Predicting the stiffness and strength of human femurs with real metastatic tumors. Bone 2014, 69, 180–190. [Google Scholar] [CrossRef]
- Perren, S.M. Basic Aspects of Internal Fixation. In Manual of Internal Fixation; Springer: Berlin/Heidelberg, Germany, 1991; Volume 53, pp. 1–158. [Google Scholar]
- Dragomir-Daescu, D.; Buijs, J.O.D.; McEligot, S.; Dai, Y.; Entwistle, R.C.; Salas, C.; Melton, L.J.; Bennet, K.E.; Khosla, S.; Amin, S. Robust QCT/FEA Models of Proximal Femur Stiffness and Fracture Load During a Sideways Fall on the Hip. Ann. Biomed. Eng. 2011, 39, 742–755. [Google Scholar] [CrossRef] [Green Version]
- Ling, B.; Wei, K.; Wang, Z.; Yang, X.; Qu, Z.; Fang, D. Experimentally program large magnitude of Poisson’s ratio in additively manufactured mechanical metamaterials. Int. J. Mech. Sci. 2020, 173, 105466. [Google Scholar] [CrossRef]
- Schileo, E.; Dall’Ara, E.; Taddei, F.; Malandrino, A.; Schotkamp, T.; Baleani, M.; Viceconti, M. An accurate estimation of bone density improves the accuracy of subject-specific finite element models. J. Biomech. 2008, 41, 2483–2491. [Google Scholar] [CrossRef] [PubMed]
- Keyak, J.; Falkinstein, Y. Comparison of in situ and in vitro CT scan-based finite element model predictions of proximal femoral fracture load. Med. Eng. Phys. 2003, 25, 781–787. [Google Scholar] [CrossRef]
- Knowles, N.K.; Reeves, J.M.; Ferreira, L. Quantitative Computed Tomography (QCT) derived Bone Mineral Density (BMD) in finite element studies: A review of the literature. J. Exp. Orthop. 2016, 3, 36. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morgan, E.F.; Bayraktar, H.H.; Keaveny, T.M. Trabecular bone modulus–density relationships depend on anatomic site. J. Biomech. 2003, 36, 897–904. [Google Scholar] [CrossRef]
- Keller, T.S. Predicting the compressive mechanical behavior of bone. J. Biomech. 1994, 27, 1159–1168. [Google Scholar] [CrossRef]
- Schliemann, B.; Risse, N.; Frank, A.; Müller, M.; Michel, P.; Raschke, M.J.; Katthagen, J.C. Screws with larger core diameter and lower thread pitch increase the stability of locked plating in osteoporotic proximal humeral fractures. Clin. Biomech. 2019, 63, 21–26. [Google Scholar] [CrossRef]
- Wittek, A.; Miller, K. Computational biomechanics for medical image analysis. In Handbook of Medical Image Computing and Computer Assisted Intervention; Elsevier: Amsterdam, The Netherlands, 2020; pp. 953–977. [Google Scholar]
- Tilton, M.; Lewis, G.S.; Wee, H.B.; Armstrong, A.; Hast, M.W.; Manogharan, G. Additive manufacturing of fracture fixation implants: Design, material characterization, biomechanical modeling and experimentation. Addit. Manuf. 2020, 33, 101137. [Google Scholar] [CrossRef]
- Reeves, J.M.; Langohr, G.D.G.; Athwal, G.S.; Johnson, J.A. The effect of stemless humeral component fixation feature design on bone stress and strain response: A finite element analysis. J. Shoulder Elb. Surg. 2018, 27, 2232–2241. [Google Scholar] [CrossRef]
- Bergmann, G.; Graichen, F.; Bender, A.; Rohlmann, A.; Halder, A.; Beier, A.; Westerhoff, P. In vivo gleno-humeral joint loads during forward flexion and abduction. J. Biomech. 2011, 44, 1543–1552. [Google Scholar] [CrossRef]
- Gooch, J.W. Law of Mixtures. In Encyclopedic Dictionary of Polymers; Gooch, J.W., Ed.; Springer: New York, NY, USA, 2011; p. 421. [Google Scholar]

| Reference | Study’s Aim | Type of Fracture Studied | Mechanical Test |
|---|---|---|---|
| Mischler et al. [31] | Optimize the proximal humerus open reduction and internal fixation (ORIF) treatment locking plate by changing the orientation of the plate screws. | 3-part | Abduction and flexion |
| Dahan et al. [3] | Predict performance load and baseline location of an anatomical neck fracture using finite element analysis (FEA). | 2-part | Compression |
| Fletcher et al. [30] | Investigate and quantify the effect of ORIF locking plate screw configuration on failure risk prediction of the fracture fixation. | 3-part | Abduction and flexion |
| Fletcher et al. [29] | Investigate the effect of the position (proximal-distal) variations of the ORIF locking plate on failure risk prediction of the fracture fixation. | 3-part | Abduction and flexion |
| Jabran et al. [28] | Optimize the proximal humerus locking plate parametric design by determining the orientation of the inferomedial ORIF locking plate screws. | 2-part | Bending |
| Inzana et al. [33] | Develop and evaluate an FEA technique to approximate the behavior of a threaded screw using a cylinder in ORIF. | 3-part | Bending |
| Zhang et al. [5] | Investigate the effect of the screw hole style design on the locking plate stress distribution in ORIF. | 2-part | Compression |
| Reference | Bone Studied | Elastic Modulus, E (GPa) |
|---|---|---|
| Zhao et al. [20] | Humerus | 13.4 |
| Inzana et al. [33] | Humerus | 17 |
| Zhang et al. [5] | Humerus | 12 |
| Perren [55] | Humerus | 20 |
| Reference | Bone Studied | Elastic Modulus, E (GPa) |
|---|---|---|
| Zhao et al. [20] | Humerus (Young bone) | 2 |
| Inzana et al. [33] | Humerus (Old bone) | 0.2–1 |
| Zhang et al. [5] | Humerus (Old bone) | 0.1 |
| Reference | Bone Studied | vBMD |
|---|---|---|
| Mischler et al. [31] | Humerus (Old bone) | 46–135.1 (mean 91.1) |
| Fletcher et al. [30] | 68.9–129.6 (mean 107.4) | |
| Schliemann et al. [63] | 17.8–130 | |
| Varga et al. [42] | 68.9–178.2 (mean 121.7) | |
| Kamer et al. [4] | 26–152.4 (mean 82.3) | |
| Röderer et al. [51] | 109.8 |
| Reference | Mesh Type | Element Type | Number of Nodes per Element | Element Edge Length (mm) |
|---|---|---|---|---|
| Mischler et al. [31] | Tetrahedral | Linear | ~ | (mean) 0.85 |
| Tilton et al. [65] | Quadratic | ~ | 1–5 (mean 1.5) | |
| Dahan et al. [3] | Quadratic | ~ | ~ | |
| Jabran et al. [28] | Quadratic | 10 | 1–1.5 | |
| Reeves et al. [66] | Quadratic | ~ | 2 | |
| Varga et al. [42] | Quadratic | ~ | 0.2–2 | |
| Zhao et al. [20] | Quadratic | 8 | 3 | |
| Inzana et al. [33] | Quadratic | ~ | (mean) 0.97 | |
| Razfar et al. [27] | Quadratic | ~ | 2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castro-Franco, A.D.; Mendoza-Muñoz, I.; González-Ángeles, Á.; Cruz-Sotelo, S.E.; Castañeda, A.M.; Siqueiros-Hernández, M. Trends in the Characterization of the Proximal Humerus in Biomechanical Studies: A Review. Appl. Sci. 2020, 10, 6514. https://doi.org/10.3390/app10186514
Castro-Franco AD, Mendoza-Muñoz I, González-Ángeles Á, Cruz-Sotelo SE, Castañeda AM, Siqueiros-Hernández M. Trends in the Characterization of the Proximal Humerus in Biomechanical Studies: A Review. Applied Sciences. 2020; 10(18):6514. https://doi.org/10.3390/app10186514
Chicago/Turabian StyleCastro-Franco, Angel D., Ismael Mendoza-Muñoz, Álvaro González-Ángeles, Samantha E. Cruz-Sotelo, Ana Maria Castañeda, and Miriam Siqueiros-Hernández. 2020. "Trends in the Characterization of the Proximal Humerus in Biomechanical Studies: A Review" Applied Sciences 10, no. 18: 6514. https://doi.org/10.3390/app10186514
APA StyleCastro-Franco, A. D., Mendoza-Muñoz, I., González-Ángeles, Á., Cruz-Sotelo, S. E., Castañeda, A. M., & Siqueiros-Hernández, M. (2020). Trends in the Characterization of the Proximal Humerus in Biomechanical Studies: A Review. Applied Sciences, 10(18), 6514. https://doi.org/10.3390/app10186514








