Multi-Scale Probabilistic Analysis for the Mechanical Properties of Plain Weave Carbon/Epoxy Composites Using the Homogenization Technique
1
Commercial Vehicle Innovation Growth Center, Jeonbuk Institute of Automotive Convergence Technology, Kunsan 54158, Korea
2
Department of Mechanical Engineering, Kunsan National University, Kunsan 54150, Korea
*
Author to whom correspondence should be addressed.
Appl. Sci. 2020, 10(18), 6542; https://doi.org/10.3390/app10186542
Submission received: 6 August 2020
/
Revised: 16 September 2020
/
Accepted: 16 September 2020
/
Published: 18 September 2020
(This article belongs to the Special Issue Homogenization for Composite Materials)
Abstract
:Probabilistic analyses of carbon fabric composites were conducted using the Monte Carlo simulation based on a homogenization technique to evaluate the mechanical properties of composites and their stochastic nature. First, the homogenization analysis was performed for a micro-level structure, which fiber and matrix are combined. The effective properties obtained from this analysis were compared with the results from the rule of mixture theory to verify the homogenization analysis. And, tensile tests were conducted to clearly evaluate the result and the reliability was verified by comparing the results of the tensile tests and homogenization analysis. In addition, the Monte Carlo simulation was performed based on homogenization analyses to consider the uncertainties of the micro-level structure combined of fiber and matrix. Next, the results of this simulation were applied to the macro-level structure combined of the tow and matrix to perform the Monte Carlo simulation based on the homogenization technique. Finally, the sensitivity analysis was conducted to identify the effect of constituents of the carbon plain weave composite and the linear correlation of the micro- and macro-level structures combined of the fiber/matrix and tow/matrix, respectively. The findings of this study verified that the effective properties of the plain weave carbon/epoxy composite and their uncertainties depended on the properties of the carbon fiber and epoxy, which are the basic constituents of plain weave carbon/epoxy composites.
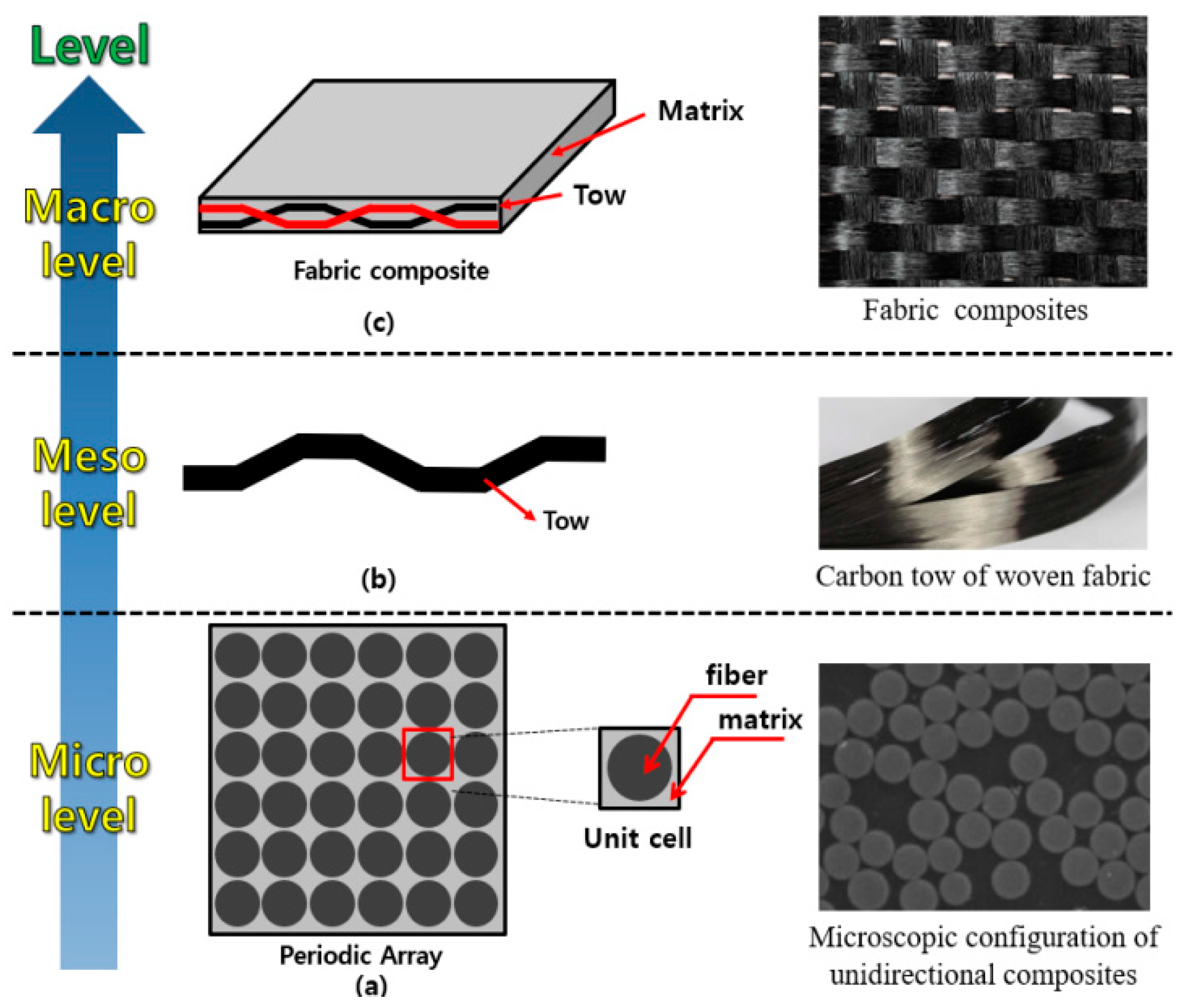
1. Introduction
Carbon fiber reinforced composites are extensively utilized in various industries including aerospace, defense, automotive, and sports, due to their high specific strength and specific stiffness and excellent fatigue resistance. These composites can be classified into unidirectional (UD) and woven composite materials. In particular, woven carbon/epoxy composites feature improved in-plane mechanical properties and impact resistance due to tow structure [1,2,3,4,5]. Consequently, woven carbon/epoxy composites are mainly used in industries instead of the UD composites.
The design of structures using carbon fabric composites requires highly reliable mechanical properties. The homogenization technique is a numerical procedure in which a heterogeneous elastic media is converted into an equivalent model, which is energetically equivalent to the authentic heterogeneous media. For fiber reinforced composites, the homogenization technique assumes the composite structures are composed of a periodic microstructure as shown in Figure 1, and reduces to a unit cell problem [6,7,8]. Hence, the homogenization method is used to estimate the various mechanical properties of composite materials, which takes into consideration their constituents and microstructure [9,10,11]. For example, Babu et al. [12] created four representative volume elements (RVEs) including square and hexagonal arrays that have different fiber orientations in UD composites. Furthermore, they predicted the effective properties by comparing the random sequential adsorption (RSA) algorithm developed in this study with the Halpin-Tsai and Mori-Tanaka homogenization techniques. Qi et al. [13] modeled the RVEs by considering the fiber orientation and ply angle of carbon fiber reinforced plastics (CFRPs), predicted the effective properties based on cross-scale simulations, and compared them with the tensile test results. Gao et al. [14] suggested the Integrated Computational Material Engineering framework implemented by the rule of mixture (ROM) to produce a unidirectional CFRP laminated structure, and compared the tensile tests and 3-point bending tests results with the simulation results. The abovementioned studies proposed various RVE models to predict the effective properties of the fiber level. However, these models have limitations because they do not consider the uncertainties of mechanical properties caused by the structural characteristics of the fiber-matrix composites and various inherent defects [15]. For this, Lee et al. [16] identified the linear correlation of the effective and material properties using the Monte Carlo simulation (MCS) to consider the uncertainties of the properties of fiber and matrix. Kamiński and Kazimierczak [17] analyzed the material properties according to deviations based on the square RVEs including single cylindrical fibers. However, the abovementioned studies only investigated the fiber levels of UD composites with considerably simpler internal structural shapes than those of the fabric composites.
Fabric composites are disadvantageous because it is difficult to evaluate the mechanical properties using the conventional homogenization techniques at the fiber level due to the complexity of the internal structure of the constituents. To overcome this, the structural characteristics of fabric composites should be considered by conducting multi-scale analyses to consider the tow level, which fiber and matrix are combined, and the higher level with the tow/matrix combination. Goda et al. [18] predicted the mechanical behavior of different plain weave structures using the discrete homogenization approach for the fabric composites. Chen et al. [19] developed a multi-level homogenization model to determine the effective properties of the woven glass/epoxy composite multilayer printed circuit board. However, the abovementioned studies did not consider the uncertainties of the properties in each constituent at the micro level of fiber/matrix combination (tow) and macro-level of tow/matrix combinations (laminae) in the fabric composite, respectively. Several studies have been conducted to evaluate the effective properties by considering the uncertainties of the mechanical properties of fabric composites. For example, Zhou et al. [20] used the MCS method to consider the uncertainties related to the elastic properties of plain weave composites and evaluated the effective properties of the composite. Hayat et al. [21] developed a multi-scale homogenization technique to predict the elastic behavior of fabric composites. The abovementioned studies analyzed the effective properties of the fabric composites by considering the variability at the macro-level. However, the variability of the mechanical properties of composites comes from the uncertainties of the fiber and matrix at the micro-level. The effective properties of composites should be, therefore, evaluated under the multi-scale condition from the micro-level to the macro-level. Furthermore, these studies have the limit in that the linear correlation of the properties at the micro- and macro-levels was not analyzed.
In this study, the multi-scale probabilistic analysis on the mechanical properties of plain-weave carbon/epoxy composites using the homogenization technique was performed. First, the effective properties of tow (meso, Figure 2b) were evaluated through homogenization analysis at the micro-level with fiber/matrix combination (Figure 2a). In addition, the homogenization analysis result was verified using the ROM theory and the reliability was verified by comparing the tensile test result and volume fraction measurement with the homogenization analysis results. Next, the probabilistic homogenization analysis was performed using the MCS to consider the uncertainties of the properties of the constituents. Finally, the effective properties of the fabric composites at the macro-level with tow/matrix combinations (Figure 2c) were obtained by using the mechanical properties results derived from the homogenization analyses at the micro-level. Furthermore, the linear correlation between the basic constituents (fiber and matrix) for effective properties, and the probabilistic analysis result were analyzed.
2. Verification of Homogenization Analysis for Unidirectional Composites
2.1. Material and Specimen
To verify the homogenization technique, we performed the tensile tests for carbon/epoxy composites from USN 175B (SK Chemicals, Seong-Nam City, Korea) consisting of TR50S 12K carbon fibers and resin. USN 175B from SK Chemical is a unidirectional lamina, the material properties are thickness of 0.171 mm, weight of 261 g/m2, tensile modulus of 240 GPa, fiber density of 1.77 g/cm3, and resin density of 1.2 g/cm3 (Provided by the manufacturer, SK Chemicals, Seong-Nam City, Korea) [25]. The specimens were manufactured using the Autoclave method for UD prepreg and their volume fraction (VF) was 60.08%. The manufacturing conditions were atmospheric pressure of 0.5 MPa, 3 min at 90 °C, 90 min at 125 °C, and vacuum was applied. The tensile tests were performed on seven specimens in accordance with ASTM D3039 [26]. Test conditions were carried out at a crosshead speed of 2 mm/min under atmospheric conditions at room temperature, and sandpaper was used for the grip of the specimen.
2.2. Homogenization Analysis Technique
The experiments for predicting the properties of the carbon composites described in the previous section has disadvantages in terms of the cost and time consumption [27]. Therefore, an analytical method is required for predicting the properties of composites. However, it is practically impossible to individually analyze each fiber array by modeling in random order. To address this, the homogenization technique was utilized, which predicts the effective properties by selecting an RVE model based on the assumption that the unit structures are repeatedly arranged in ideal structure. The RVE model can define a unit cell by a repetitive pattern of carbon fiber and matrix, which typically use square and hexagonal arrays [28,29].
In this study, the unit cells of the unidirectional carbon/epoxy composites under micro-scale were modeled as square arrays to predict the effective properties using the homogenization technique, as shown in Figure 3a. Here, the total volume of unit cell was assumed to be unity, and the unit cells were modeled for carbon fiber volume fractions of 10–70% to predict the mechanical properties of composites with the volume fraction using the ABAQUS [30]. Figure 3b depicts the FE model of the unit cell defined. Element of C3D8R with eight nodes per element and six degrees of freedom per node were used for this model. Here, the total number of elements and nodes was 10,836 and 12,166, respectively. The Mori-Tanaka theory [31,32] was utilized for the homogenization technique to calculate the mechanical behavior. This theory predicts the interaction between the each phase by assuming each inclusion is embedded; reversely, in an infinite matrix, is remotely loaded by the average media strain or stress, respectively. Here, we obtained the mechanical properties of carbon/epoxy composites using the Mori-Tanaka theory implemented in ABAQUS.
As shown in Figure 4, the repetitive boundary conditions were applied to derive the effective properties for each orientation: E11,tow, E22,tow, E33,tow, G12,tow, G13,tow, G23,tow, v12,tow, v13,tow, and v23,tow. Also, as shown in Table 1, the mechanical properties of the fiber and matrix provided by manufacturer were used.
2.3. Homogenization Analysis and Experimental Results
The effective properties of the homogenization analysis are outlined in Table 2 based on the change in volume fraction. To verify the homogenization technique used in this study, the effective properties were calculated using the ROM [33,34], then compared with the homogenization analysis results. Table 3 compares the results of the homogenization analysis and the simple ROM (SROM) for the E11 tow. From table, the homogenization analysis results are well conformed with the SROM results.
The aforementioned analysis results should be compared with the experimental results to enable a more detailed evaluation of the homogenization technique. To compare the homogenization analysis results with the experimental results, tensile tests were performed in accordance with the method described in Section 2.1 for unidirectional carbon/epoxy composites (TR50S/Epoxy); the results are shown in Figure 5. Table 4 summarizes the homogenization analysis and experimental results. The error rates of E11,tow and v12,tow were 1.13 and 9.09%, respectively. Thus, the homogenization analysis result correlated well with the tensile test results. From these results, the homogenization analysis technique in this study was verified for the carbon/epoxy composites.
3. Probabilistic Homogenization Analysis at the Micro-Level for Plain-Weave Composites
3.1. Random Variables for the Probabilistic Homogenization Technique at the Micro-Level
The homogenization technique described in Section 2 could evaluate the effective properties at the micro-level in which fibers and matrix are physically combined to form tow. However, probabilistic analysis, rather than deterministic analysis, should be employed because the composites have uncertainties in material properties due to several inherent features [35]. To address this, the probabilistic homogenization analysis based on the MCS was performed using the commercial software ABAQUS and ISIGHT [36]. Table 5 lists the selected random variables. Each random variable was assumed to have a normal distribution consisting of 1000 samples. For the coefficient of variation (COV) of 0.05 was applied. Table 6 shows a portion of the set of random variables calculated using this method.
3.2. Effective Properties at the Micro-Level
The probabilistic homogenization analysis was performed by considering the variability of the fiber/matrix due to the inherent features for the 60% volume fraction; the distribution of the effective properties is shown in Figure 6. From figure, the effective properties calculated at the micro-level by probabilistic homogenization analysis follow the normal distribution, which are similar to those of the random variables selected in Section 3.1. This indicates that the variability of the effective properties at the micro-level with fiber and matrix combinations depends on the variability of the fiber and matrix, which are the basic constituents.
4. Probabilistic Homogenization Analysis at the Macro-Level for Plain Weave Composites
4.1. Homogenization Analysis Technique at the Macro-Level
Fabric composites have reinforced structures with the weave form of tow and are geometrically more complex than the UD composites. Furthermore, non-homogeneity of the structure and the uncertainties in properties are caused by the unique characteristics of manufacturing and weaving deviations.
The tow, which is an intermediate material of fabric composites, is a combination of UD fiber and matrix. Thus, the properties of tow are also influenced by the properties of the fiber and matrix and their variability, as mentioned in Section 3. Therefore, to effectively evaluate the effective properties at the macro-level of fabric composites, the probabilistic homogenization analysis should be performed by considering the properties and their variability at the micro-level. Therefore, the representative unit cell (RUC) of the fabric composites was selected and the fabric composite was designed according to the literature [37,38,39]. The design geometry is shown in Figure 7a and Table 7. The tow thickness was designed by changing the size according to the volume fractions of 40, 50, 60, and 70%. Figure 7b exhibits the finite element (FE) model for RUC for the fabric composite. C3D10 with five nodes per element and six degrees of freedom per node was used for the FE model. The total numbers of elements and nodes were 267,578 and 375,805, respectively. The Mori-Tanaka theory was used for the homogenization technique. The repetitive boundary condition was applied for the boundary condition which is same condition for the micro-level with fiber/matrix combination. Furthermore, a set of 1000 data derived from the micro-level were applied to the properties of tow and epoxy to perform the homogenization technique based on MCS. Table 8 outlines these values.
4.2. Effective Properties at the Macro-Level
Figure 8 shows the homogenization analysis results based on MCS for the volume fractions of 40, 50, 60, and 70%. All the effective properties including E11,eq,macro, E33,eq,macro, and G12,eq,macro followed the normal distribution. This trend was maintained, even when the volume fraction changed. However, the average and standard deviations of the stiffness increased with the volume fraction, whereas the opposite was true for the Poisson’s ratio. The reason is that as the volume fraction of the tow increases, the stiffness also increases; thus resulting in differences in the standard deviation. However, Poisson’s ratio is influenced more strongly by the matrix, thus exhibiting a different trend than observed for the stiffness. Particularly in the case of v23,eq,macro, the increase in stiffness in the direction of E33,eq,macro is insignificant; thus, it shows a significant decreasing tendency when the volume fraction increases. To quantify the inherent uncertainties in the properties of composites, the COV was derived from each effective property and compared. Table 9 outlines the results. The COV of the stiffness changed minimally against the volume fraction. However, the COV of v12,eq,macro showing a ratio of in-plane strain stiffness increased with the volume fraction. In contrast, v23,tow, which indicates the ratio of out-of-plane strain shows the opposite trend. Therefore, the effects of the design variables on the stiffness and Poisson’s ratio of the fabric composite appear differently between the two, and they also have the same out-of-plane strain.
4.3. Sensitivity Analysis
The linear correlations were evaluated to accurately determine the effects of the mechanical properties of the fiber and matrix, i.e., the constituents of fabric composites, on the effective properties at the macro-level. First, the linear correlation of the mechanical properties between the constituents and the effective properties of the micro-level was analyzed using the simple correlation analysis method of statistical method and the results are shown in Figure 9a. Figure 9a shows that E11,tow has the highest and second highest correlation with Ef and Em, respectively. There are also correlations with Gm, Gf, and vm, but none with vf. In a positive correlation, when the mechanical properties increase, the other effective properties also increase, whereas in a negative correlation, the opposite is true. Furthermore, when there is no correlation, even if the mechanical properties change, the other effective properties remain unchanged. Hence, the results suggest that E11,tow is under the dominant influence of the elastic modulus of the fiber, whereas E22,tow and E33,tow are under the dominant influence of the elastic modulus and Poisson’s ratio of the matrix. Furthermore, G12,tow, G13,tow, and G23,tow are under the dominant influence of the shear modulus of elasticity of the matrix, whereas v12,tow and v13,tow are under the influences of the Poisson’s ratios of the fiber and the matrix. Lastly, v23,tow is under the dominant influence of the Poisson’s ratio of the matrix. Through this analysis, the linear correlation between the mechanical properties of the constituents (carbon fiber and epoxy) and the effective properties of the micro level could be identified.
Figure 9b shows the linear correlation between the effective properties of the micro- and macro-levels. For example, E11,eq, macro exhibits the highest correlations with E11,tow, E22,tow, and E33,tow and the second highest correlation with Em. Furthermore, correlations with other properties excluding these can be also identified. The reason for this is the geometrical shape of the fabric composites of tow with fiber and matrix combination, which was woven in three dimensions.
Since the properties of the macro-level are ultimately determined by the mechanical properties of the constituents, the linear correlation analysis for the effective properties of the macro-level and the mechanical properties of the constituents is also necessary. The results are shown in Figure 9c. For example, E11,eq,macro and E22,eq,macro have the highest correlation with Ef and the second highest correlation with, Em. Furthermore, the existence of correlations with other properties excluding them could be also identified. By contrast, the shear modulus of elasticity at the macro-level is significantly impacted by the shear modulus of elasticity of epoxy. Finally, the Poisson’s ratio of the macro-level is greatly influenced by the Poisson’s ratios of epoxy. From the above results, the fabric composites are significantly impacted by the mechanical properties of constituents, and are also influenced by the matrix mechanical properties due to the complex geometric shapes.
5. Conclusions
In this study, the effective properties of the fabric composites and their uncertainties were probabilistically evaluated using the homogenization analysis based on the Monte Carlo Simulation. In addition, the linear correlation between the mechanical properties of constituents and the effective properties of fabric composites were analyzed.
- To verify the effective properties of the homogenization technique applied in this study, the analysis results of the effective properties at the micro-level with the combination of the carbon fiber and epoxy were compared with the ROM theory. In addition, the UD composites with the same geometry of the micro-level was fabricated and compared with the tensile test results to experimentally verify the homogenization technique.
- The MCS based on the homogenization analysis technique was performed at the micro-level to evaluate the uncertainties in the mechanical properties of the composites. The results showed that the effective properties of the micro-level followed the normal distribution same as those of the carbon fiber and epoxy.
- The MCS was performed based on the homogenization technique for the fabric composite (macro-level) combined with the tow and matrix was performed based on the effective properties of the micro-level. The effective properties of the macro-level had the same distribution characteristics as those of the tow and matrix.
- The sensitivity analysis between the properties of constituents (carbon fiber and epoxy) and the effective properties of the macro-level exhibits that the fabric composite is ultimately dependent on the mechanical properties of the carbon fiber and epoxy.
Author Contributions
Data curation, J.-W.J. and K.-W.K.; software, B.-W.J. and C.-W.C.; writing—review and editing, K.-W.K. All authors have read and agree to the published version of the manuscript.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (NRF-2018R1C1B6002221) and by the Korea Institute of Energy Technology Evaluation and Planning (KETEP, 20194010201800).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, D.W.; Song, J.I. Research on simple joint method using fiber-metal laminate design for improved mechanical properties of CFRP assembly structure. Compos. Part B Eng. 2019, 164, 358–367. [Google Scholar] [CrossRef]
- Muflikhun, M.A.; Yokozeki, T.; Aoki, T. The strain performance of thin CFRP-SPCC hybrid laminates for automobile structures. Compos. Struct. 2019, 220, 11–18. [Google Scholar] [CrossRef]
- Tang, E.; Li, W.; Han, Y. Research on the interacting duration and microscopic characteristics created by high-velocity impact on CFRP/Al HC SP structure. J. Mater. Res. Technol. 2019, 9, 1640–1651. [Google Scholar] [CrossRef]
- Golewski, P.; Sadowski, T. Description of thermal protection against heat transfer of carbon fiber reinforced plastics (CFRP) coated by stiffened ceramic mat (TBC). Compos. Struct. 2019, 229, 111489. [Google Scholar] [CrossRef]
- Behera, A.; Dupare, P.; Thawre, M.M.; Ballal, A. Effects of hygrothermal aging and fiber orientations on constant amplitude fatigue properties of CFRP Multidirectional composite laminates. Int. J. Fatigue 2020, 136, 105590. [Google Scholar] [CrossRef]
- Tian, W.; Qi, L.; Liang, J.; Chao, X.; Zhou, J. Evaluation for elastic properties of metal matrix composites with randomly distributed fibers: Two-step mean-field homogenization procedure versus FE homogenization method. J. Alloys Compd. 2016, 658, 241–247. [Google Scholar] [CrossRef]
- Adumitroaie, A.; Barbero, E.J. Beyond plain weave fabrics–I. Geometrical model. Compos. Struct. 2011, 93, 1424–1432. [Google Scholar] [CrossRef]
- Gilioli, A.; Manes, A.; Giglio, M. Evaluation of the effects of the numerical modelling choices on the simulation of a tensile test on CFRP composite. Procedia Struct. Integr. 2018, 8, 33–42. [Google Scholar] [CrossRef]
- Hale, P.; Ng, E.G. Non-linear material characterization of CFRP with FEM utilizing cohesive surface considerations validated with effective tensile test fixturing. Mater. Today Commun. 2020, 23, 100872. [Google Scholar] [CrossRef]
- Li, H.X. Limit analysis of composite materials with anisotropic microstructures: A homogenization approach. Mech. Mater. 2011, 43, 574–585. [Google Scholar] [CrossRef]
- Muflikhun, M.A.; Chua, A.Y. Load-displacement experimental data from axial tensile loading of CFRP-SPCC hybrid laminates. Data Brief 2020, 29, 105306. [Google Scholar] [CrossRef] [PubMed]
- Babu, K.P.; Mohite, P.M.; Upadhyay, C.S. Development of an RVE and its stiffness predictions based on mathematical homogenization theory for short fibre composites. Int. J. Solids Struct. 2018, 130, 80–104. [Google Scholar] [CrossRef]
- Qi, Z.; Liu, Y.; Chen, W. An approach to predict the mechanical properties of CFRP based on cross-scale simulation. Compos. Struct. 2019, 210, 339–347. [Google Scholar] [CrossRef]
- Gao, J.; Shakoor, M.; Domel, G.; Merzkirch, M.; Zhou, G.; Zeng, D.; Su, X.; Liu, W.K. Predictive multiscale modeling for Unidirectional Carbon Fiber Reinforced Polymers. Compos. Sci. Technol. 2020, 186, 107922. [Google Scholar] [CrossRef]
- Mustafa, G.; Suleman, A.; Crawford, C. Probabilistic micromechanical analysis of composite material stiffness properties for a wind turbine blade. Compos. Struct. 2015, 131, 905–916. [Google Scholar] [CrossRef]
- Lee, S.P.; Jin, J.W.; Kang, K.W. Probabilistic analysis for mechanical properties of glass/epoxy composites using homogenization method and Monte Carlo simulation. Renew. Energy 2014, 65, 219–226. [Google Scholar] [CrossRef]
- Kamiński, M.; Kazimierczak, M. 2D versus 3D probabilistic homogenization of the metallic fiber-reinforced composites by the perturbation-based stochastic Finite Element Method. Compos. Struct. 2014, 108, 1009–1018. [Google Scholar] [CrossRef]
- Goda, I.; Assidi, M.; Ganghoffer, J.F. Equivalent mechanical properties of textile monolayers from discrete asymptotic homogenization. J. Mech. Phys. Solids 2013, 61, 2537–2565. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, F.; Meguid, S.A. Multi-level modeling of woven glass/epoxy composite for multilayer printed circuit board applications. Int. J. Solids Struct. 2014, 51, 3679–3688. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.Y.; Gosling, P.D.; Pearce, C.J.; Ullah, Z.; Kaczmarczyk, L. Perturbation-based stochastic multi-scale computational homogenization method for woven textile composites. Int. J. Solids Struct. 2016, 80, 368–380. [Google Scholar] [CrossRef] [Green Version]
- Hayat, K.; Lei, X.; Ali, H.T. Prediction of elastic behavior of woven fabric reinforced plastics composites using two-step homogenization. In Proceedings of the 2018 15th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 9–13 January 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 36–42. [Google Scholar]
- COMPOSITES PLAZA. Available online: https://compositesplaza.com/ (accessed on 6 July 2020).
- FIBRE GLAST. Available online: https://www.fibreglast.com/ (accessed on 6 July 2020).
- Ostapiuk, M.; Surowska, B.; Bienias, J. Interface analysis of fiber metal laminates. Compos. Interfaces 2014, 21, 309–318. [Google Scholar] [CrossRef]
- Choi, H.; Huang, H.; Kim, D.U.; Joe, C.R. Fracture behavior of carbon/epoxy laminated composite reinforced by iron powder. Korean J. Chem. Eng. 2008, 25, 1208–1211. [Google Scholar] [CrossRef]
- ASTM D3039/D3039M-17. Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials; ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar]
- Hu, A.; Li, X.; Ajdari, A.; Jiang, B.; Burkhart, C.; Chen, W.; Catherine Brinson, L. Computational analysis of particle reinforced viscoelastic polymer nanocomposites–statistical study of representative volume element. J. Mech. Phys. Solids 2018, 114, 55–74. [Google Scholar] [CrossRef]
- Bayat, M.; Aghdam, M.M. A micromechanics-based analysis of effects of square and hexagonal fiber arrays in fibrous composites using DQEM. Eur. J. Mech. A Solids 2012, 32, 32–40. [Google Scholar] [CrossRef]
- Macedo, R.Q.; Ferreira, R.T.L.; Guedes, J.M.; Donadon, M.V. Intraply failure criterion for unidirectional fiber reinforced composites by means of asymptotic homogenization. Compos. Struct. 2017, 159, 335–349. [Google Scholar] [CrossRef]
- Abaqus Documentation. Available online: https://abaqus-docs.mit.edu/2017/English/SIMACAEEXCRefMap/simaexc-c-docproc.htm (accessed on 17 September 2020).
- Tan, H.; Huang, Y.; Liu, C.; Geubelle, P.H. The Mori–Tanaka method for composite materials with nonlinear interface debonding. Int. J. Plast. 2005, 21, 1890–1918. [Google Scholar] [CrossRef]
- Klusemann, B.; Svendsen, B. Homogenization methods for multi-phase elastic composites. Tech. Mech. Sci. J. Fundam. Appl. Eng. Mech. 2010, 30, 374–386. [Google Scholar]
- Hyer, M.W.; Waas, A.M. Micromechanics of Linear Elastic Continuous Fiber Composites; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Halpin, J.C. Effects of Environmental Factors on Composite Materials; Air Force Materials Lab Wright-Patterson AFB OH: Greene, OH, USA, 1969. [Google Scholar]
- Kang, K.W.; Lim, D.M.; Kim, J.K. Probabilistic analysis for the fatigue life of carbon/epoxy laminates. Compos. Struct. 2008, 85, 258–264. [Google Scholar] [CrossRef]
- Isight. Available online: https://www.3ds.com/fileadmin/PRODUCTS-SERVICES/SIMULIA/RESOURCES/DS_SIMULIA_IsightV40_GettingStartedGuide.pdf (accessed on 17 September 2020).
- Carvelli, V.; Poggi, C. A homogenization procedure for the numerical analysis of woven fabric composites. Compos. Part A Appl. Sci. Manuf. 2001, 32, 1425–1432. [Google Scholar] [CrossRef]
- Jiang, Y.; Tabiei, A.; Simitses, G.J. A novel micromechanics-based approach to the derivation of constitutive equations for local/global analysis of a plain-weave fabric composite. Compos. Sci. Technol. 2000, 60, 1825–1833. [Google Scholar] [CrossRef]
- Obert, E.; Daghia, F.; Ladeveze, P.; Ballere, L. Micro and meso modeling of woven composites: Transverse cracking kinetics and homogenization. Compos. Struct. 2014, 117, 212–221. [Google Scholar] [CrossRef]
Figure 1.
The assume structure composites of periodic; square array [16].
Figure 1.
The assume structure composites of periodic; square array [16].
Figure 2.
Schematic diagram of a multiscale model: (a) Micro level; (b) Meso level; (c) Macro level [22,23,24].
Figure 3.
Square unit cells for carbon/epoxy composites: (a) Geometrical model of micro-level unit cell of fabric composites; (b) Finite element model of unit cell for unidirectional composites.
Figure 3.
Square unit cells for carbon/epoxy composites: (a) Geometrical model of micro-level unit cell of fabric composites; (b) Finite element model of unit cell for unidirectional composites.
Figure 4.
Schematic representation of the displacement boundary conditions required to estimate the equivalence elastic properties.
Figure 4.
Schematic representation of the displacement boundary conditions required to estimate the equivalence elastic properties.
Figure 5.
Stress-strain curve.
Figure 6.
Result of MCS for the micro-level: (a) Equivalent longitudinal modulus (E11,tow); (b) Equivalent transverse modulus (E22,tow); (c) Equivalent shear modulus (G12,tow); (d) Equivalent shear modulus (G23,tow); (e) Equivalent Poisson’s ratio (v12,tow); (f) Equivalent Poisson’s ratio (v23,tow).
Figure 6.
Result of MCS for the micro-level: (a) Equivalent longitudinal modulus (E11,tow); (b) Equivalent transverse modulus (E22,tow); (c) Equivalent shear modulus (G12,tow); (d) Equivalent shear modulus (G23,tow); (e) Equivalent Poisson’s ratio (v12,tow); (f) Equivalent Poisson’s ratio (v23,tow).
Figure 7.
Repeat unit cells model for the fabric composites: (a) Repeat unit cell model size for fabric composites; (b) Finite element model of macro-level repeat unit cells for fabric composites.
Figure 7.
Repeat unit cells model for the fabric composites: (a) Repeat unit cell model size for fabric composites; (b) Finite element model of macro-level repeat unit cells for fabric composites.
Figure 8.
Result of MCS for the macro-level: (a) Equivalent longitudinal modulus (E11,eq,macro); (b) Equivalent transverse modulus (E33,eq,macro); (c) Equivalent shear modulus (G12,eq,macro); (d) Equivalent shear modulus (G23,eq,macro); (e) Equivalent Poisson’s ratio (v12,eq,macro); (f) Equivalent Poisson’s ratio (v23,eq,macro).
Figure 8.
Result of MCS for the macro-level: (a) Equivalent longitudinal modulus (E11,eq,macro); (b) Equivalent transverse modulus (E33,eq,macro); (c) Equivalent shear modulus (G12,eq,macro); (d) Equivalent shear modulus (G23,eq,macro); (e) Equivalent Poisson’s ratio (v12,eq,macro); (f) Equivalent Poisson’s ratio (v23,eq,macro).
Figure 9.
Linear correlation results; (a) Comparison of the micro-level and mechanical properties of the fiber and matrix; (b) Comparison of the macro- and micro-levels; (c) Comparison of the macro-level and mechanical properties of the fiber and matrix.
Figure 9.
Linear correlation results; (a) Comparison of the micro-level and mechanical properties of the fiber and matrix; (b) Comparison of the macro- and micro-levels; (c) Comparison of the macro-level and mechanical properties of the fiber and matrix.
Table 1.
Material properties of the fiber and matrix (TR50S/Epoxy).
| Fiber (Carbon) | Matrix (Epoxy) | |
|---|---|---|
| Young’s modulus (GPa) | 240.00 | 2.45 |
| Shear modulus (GPa) | 93.39 | 0.91 |
| Poisson’s ratio | 0.285 | 0.350 |
Table 2.
Homogenization analysis results of the micro-level.
| VF 10% | VF 20% | VF 30% | VF 40% | VF 50% | VF 60% | VF 70% | |
|---|---|---|---|---|---|---|---|
| E11,tow (GPa) | 27.20 | 49.80 | 72.40 | 97.20 | 120.90 | 144.75 | 168.47 |
| E22,tow (GPa) | 5.84 | 6.74 | 7.80 | 6.62 | 9.06 | 13.19 | 22.42 |
| E33,tow (GPa) | 5.84 | 6.74 | 7.80 | 6.62 | 9.06 | 13.19 | 22.42 |
| G12,tow (GPa) | 1.95 | 2.24 | 2.57 | 2.09 | 2.71 | 3.75 | 6.14 |
| G13,tow (GPa) | 1.95 | 2.24 | 2.57 | 2.09 | 2.71 | 3.75 | 6.14 |
| G23,tow (GPa) | 1.90 | 2.12 | 2.35 | 1.63 | 1.96 | 2.51 | 3.79 |
| ν12,tow | 0.342 | 0.324 | 0.307 | 0.320 | 0.313 | 0.306 | 0.298 |
| ν13,tow | 0.342 | 0.324 | 0.307 | 0.320 | 0.313 | 0.306 | 0.298 |
| ν23,tow | 0.504 | 0.496 | 0.472 | 0.392 | 0.326 | 0.252 | 0.170 |
Table 3.
Normalized E11,tow comparison for the rule of mixture and the homogenization analysis result.
Table 3.
Normalized E11,tow comparison for the rule of mixture and the homogenization analysis result.
| VF (%) | SROM (GPa) | Result of Homogenization Analysis (GPa) | Error (%) |
|---|---|---|---|
| 10 | 26.21 | 27.20 | 3.78 |
| 20 | 49.96 | 49.80 | 0.32 |
| 30 | 73.71 | 72.40 | 1.78 |
| 40 | 97.47 | 97.20 | 0.28 |
| 50 | 121.23 | 120.90 | 0.27 |
| 60 | 144.98 | 144.75 | 0.16 |
| 70 | 168.74 | 168.47 | 0.16 |
Table 4.
Comparison of the homogenization analysis and tensile test results for unidirectional composites.
Table 4.
Comparison of the homogenization analysis and tensile test results for unidirectional composites.
| Result of Homogenization Analysis | Result of Tensile Test | Error (%) | |
|---|---|---|---|
| E11,tow (GPa) | 144.75 | 146.40 | 1.13 |
| v12,tow | 0.30 | 0.32 | 6.25 |
Table 5.
Design variable of the micro-level.
| Design Variable | Type | Mode | Distribution | Mean | COV |
|---|---|---|---|---|---|
| Ef | real | continuous | normal | 240 GPa | 0.05 |
| Em | real | continuous | normal | 2.45 GPa | 0.05 |
| Gf | real | continuous | normal | 93.40 GPa | 0.05 |
| Gm | real | continuous | normal | 0.91 GPa | 0.05 |
| vf | real | continuous | normal | 0.285 | 0.05 |
| vm | real | continuous | normal | 0.350 | 0.05 |
Table 6.
Input data extraction for Monte Carlo Simulation of micro level.
| No. | Ef | Em | Gf | Gm | vf | vm |
|---|---|---|---|---|---|---|
| 1 | 216.79 | 2.56 | 98.53 | 0.95 | 0.292 | 0.366 |
| 2 | 247.96 | 2.51 | 105.71 | 866.32 | 0.287 | 0.334 |
| ⁞ | ⁞ | ⁞ | ⁞ | ⁞ | ⁞ | ⁞ |
| 999 | 249.48 | 2.56 | 91.49 | 0.92 | 0.284 | 0.359 |
| 1000 | 244.37 | 2.44 | 93.29 | 0.83 | 0.310 | 0.353 |
Table 7.
Representative unit cell model size.
| Size (mm) | |
|---|---|
| H (Overall height) | 0.225 |
| W (Overall width) | 0.9 |
| L (Overall length) | 0.9 |
| TL (Tow length) | 0.99 |
| TW (Tow width) | 0.376 |
| TT (Tow thickness) | 0.093 (VF 60%) |
Table 8.
Input data extraction for the MCS of macro-level (VF 60% output data of micro-level).
| No. | E11,tow | E22,tow | E33,tow | G12,tow | G13,tow | G23,tow | v12,tow | v13,tow | v23,tow | Em | Gm | vm |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 130.90 | 14.30 | 14.30 | 3.94 | 3.94 | 2.64 | 0.317 | 0.317 | 0.275 | 2.56 | 0.95 | 0.366 |
| 2 | 149.55 | 12.91 | 12.91 | 3.61 | 3.61 | 2.41 | 0.301 | 0.301 | 0.234 | 2.51 | 866.32 | 0.334 |
| ⁞ | ⁞ | ⁞ | ⁞ | ⁞ | ⁞ | ⁞ | ⁞ | ⁞ | ⁞ | ⁞ | ⁞ | ⁞ |
| 999 | 150.47 | 14.13 | 14.13 | 3.80 | 3.80 | 2.56 | 0.310 | 0.310 | 0.260 | 2.56 | 0.92 | 0.359 |
| 1000 | 147.37 | 13.24 | 13.24 | 3.44 | 3.44 | 2.32 | 0.324 | 0.324 | 0.258 | 2.44 | 0.83 | 0.353 |
Table 9.
MCS result of the macro-level.
| VF 40% | VF 50% | VF 60% | VF 70% | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Average | Std. Dev | COV | Average | Std. Dev | COV | Average | Std. Dev | COV | Average | Std. Dev | COV | |
| E11,eq,macro | 21.23 | 0.698 | 0.033 | 24.88 | 0.828 | 0.033 | 26.70 | 0.877 | 0.033 | 29.67 | 0.969 | 0.033 |
| E33,eq,macro | 5.183 | 0.368 | 0.071 | 6.00 | 0.432 | 0.072 | 7.04 | 0.501 | 0.071 | 8.64 | 0.601 | 0.070 |
| G12,eq,macro | 1.90 | 0.091 | 0.048 | 2.14 | 0.101 | 0.047 | 2.35 | 0.111 | 0.047 | 2.56 | 0.121 | 0.047 |
| G23,eq,macro | 1.29 | 0.062 | 0.048 | 1.48 | 0.071 | 0.048 | 1.72 | 0.081 | 0.047 | 2.09 | 0.097 | 0.046 |
| v12,eq,macro | 0.096 | 0.006 | 0.063 | 0.087 | 0.006 | 0.069 | 0.082 | 0.006 | 0.073 | 0.075 | 0.006 | 0.080 |
| v23,eq,macro | 0.407 | 0.027 | 0.066 | 0.386 | 0.025 | 0.065 | 0.364 | 0.023 | 0.063 | 0.342 | 0.021 | 0.061 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
MDPI and ACS Style
Jin, J.-W.; Jeon, B.-W.; Choi, C.-W.; Kang, K.-W. Multi-Scale Probabilistic Analysis for the Mechanical Properties of Plain Weave Carbon/Epoxy Composites Using the Homogenization Technique. Appl. Sci. 2020, 10, 6542. https://doi.org/10.3390/app10186542
AMA Style
Jin J-W, Jeon B-W, Choi C-W, Kang K-W. Multi-Scale Probabilistic Analysis for the Mechanical Properties of Plain Weave Carbon/Epoxy Composites Using the Homogenization Technique. Applied Sciences. 2020; 10(18):6542. https://doi.org/10.3390/app10186542
Chicago/Turabian StyleJin, Ji-Won, Byung-Wook Jeon, Chan-Woong Choi, and Ki-Weon Kang. 2020. "Multi-Scale Probabilistic Analysis for the Mechanical Properties of Plain Weave Carbon/Epoxy Composites Using the Homogenization Technique" Applied Sciences 10, no. 18: 6542. https://doi.org/10.3390/app10186542
APA StyleJin, J. -W., Jeon, B. -W., Choi, C. -W., & Kang, K. -W. (2020). Multi-Scale Probabilistic Analysis for the Mechanical Properties of Plain Weave Carbon/Epoxy Composites Using the Homogenization Technique. Applied Sciences, 10(18), 6542. https://doi.org/10.3390/app10186542
Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.
