Clarification of Features of the Wheel Movement with a Perspective Constructive Scheme on a Rail
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of a Wheel Movement with a Traditional Wheel Design
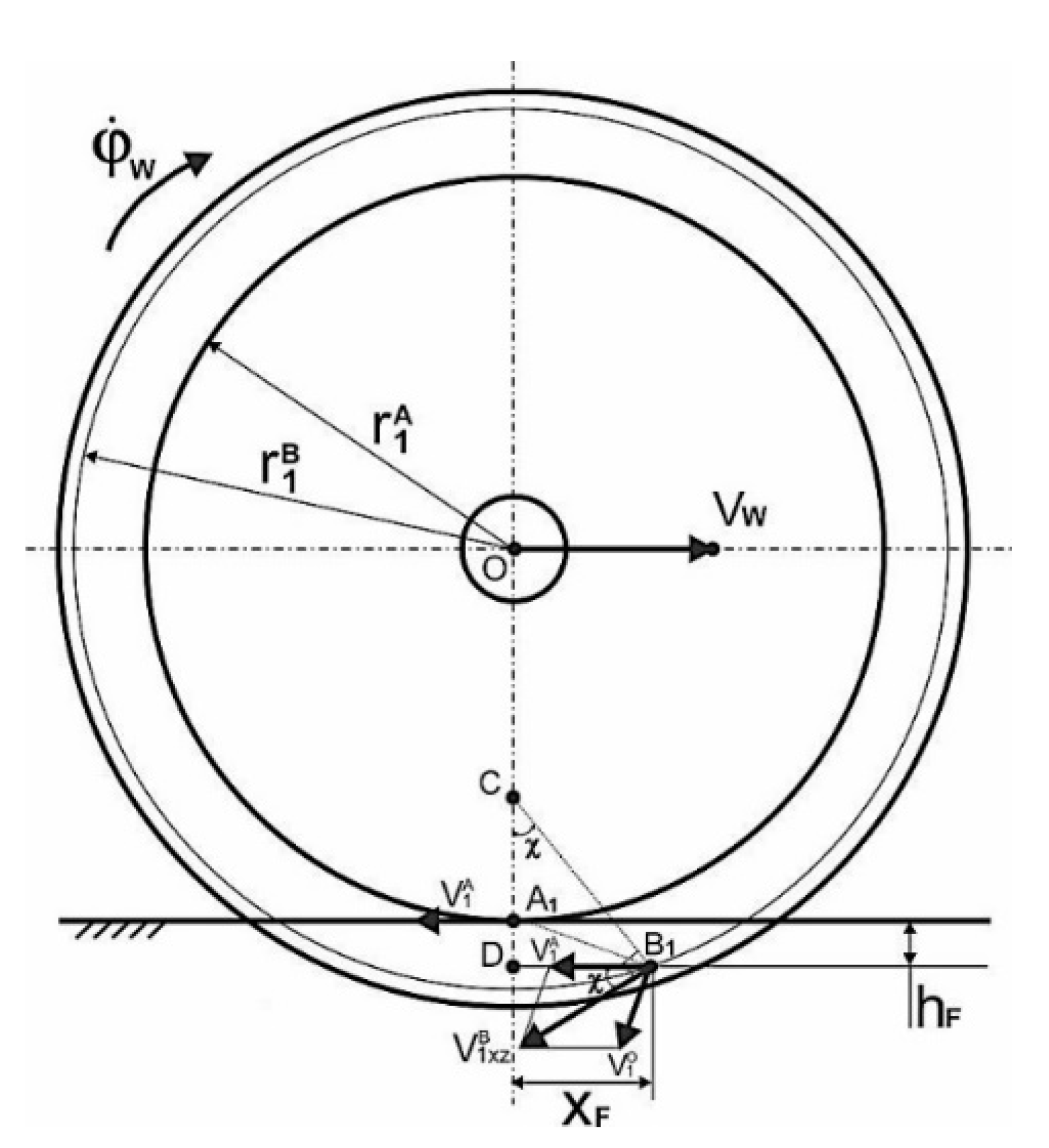
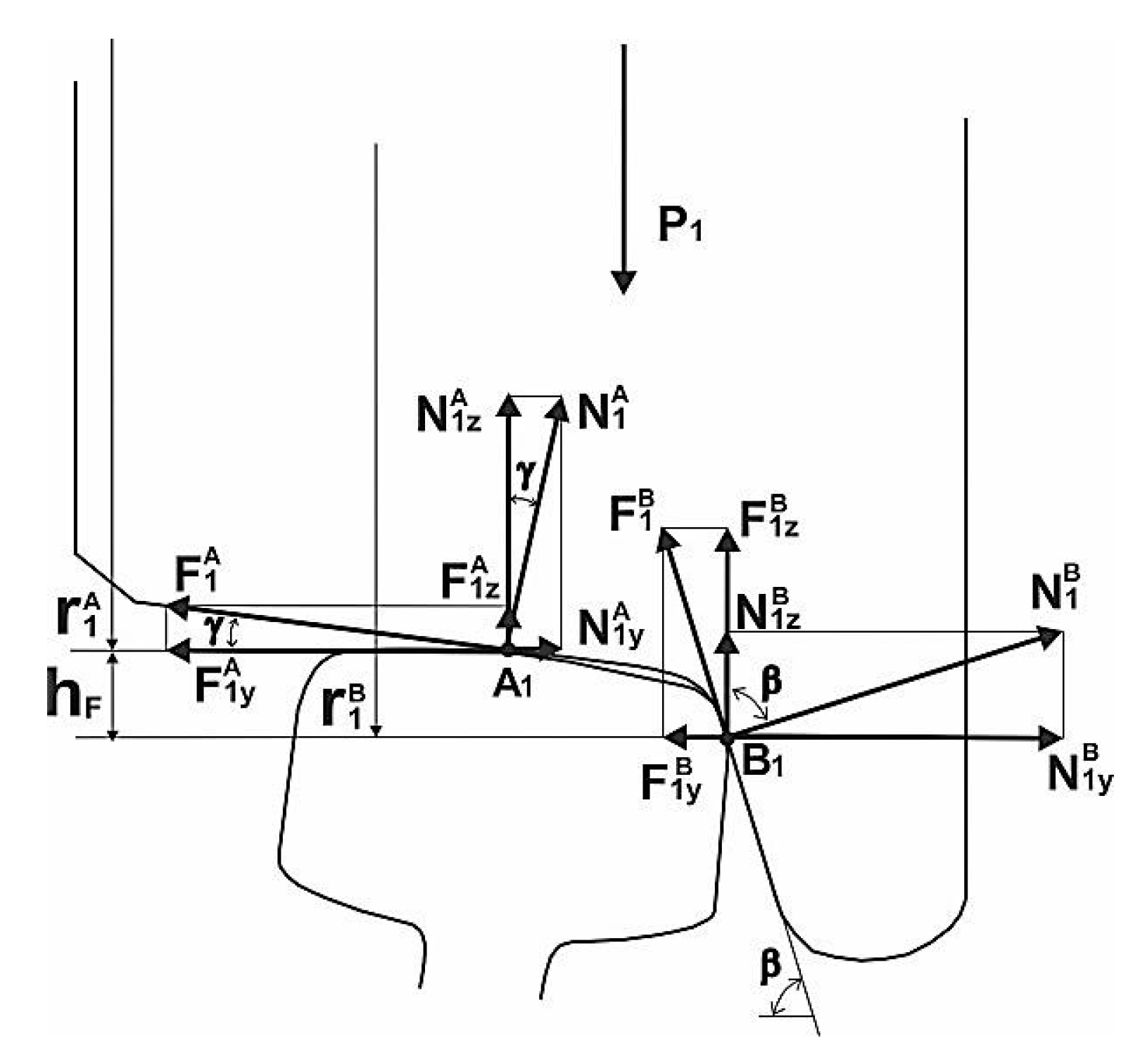
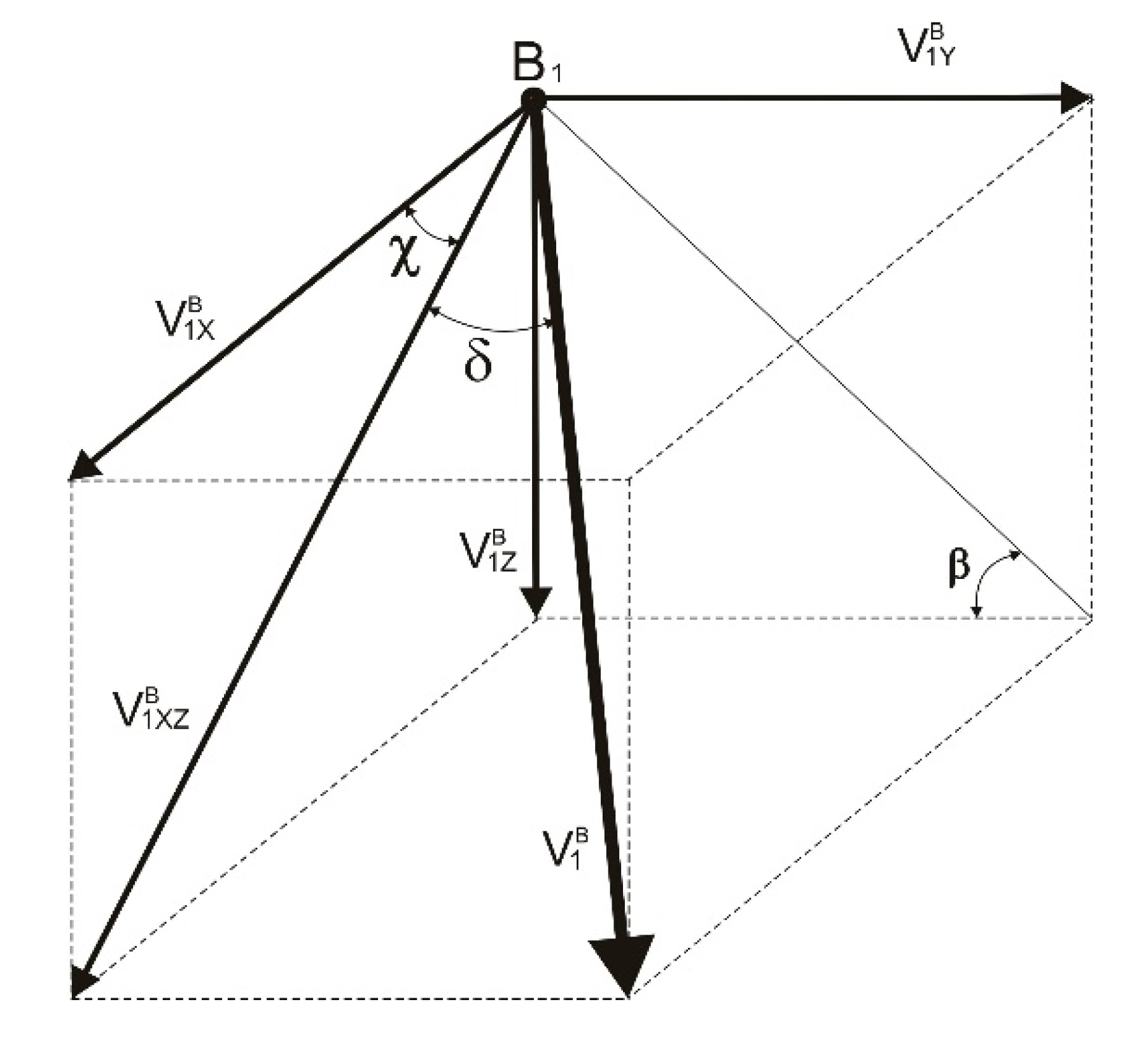
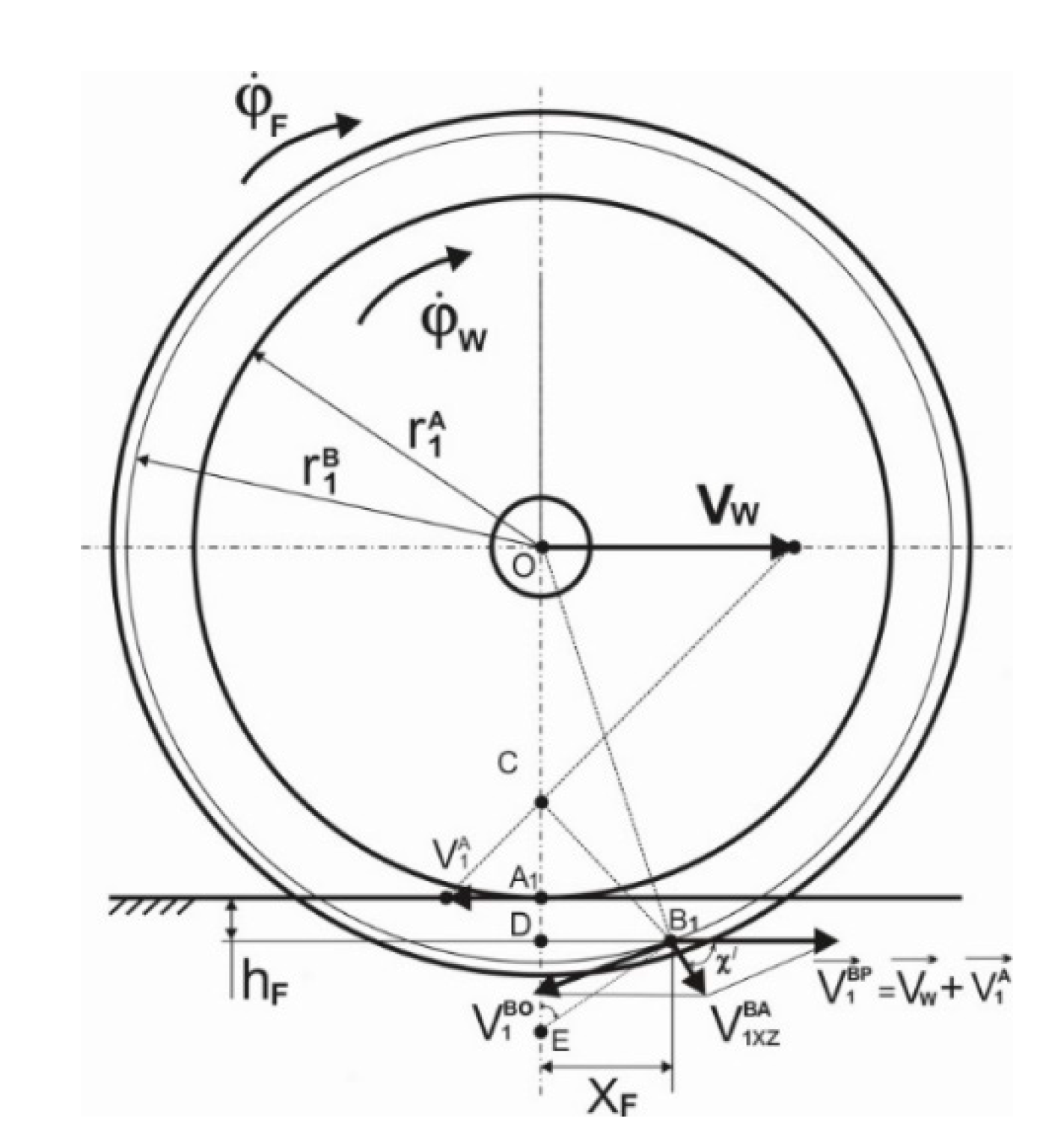
2.2. Description of the Wheel Movement with a Perspective Wheel Design
- From one side:
- From the opposite side:where
3. Results and Discussion of the Research
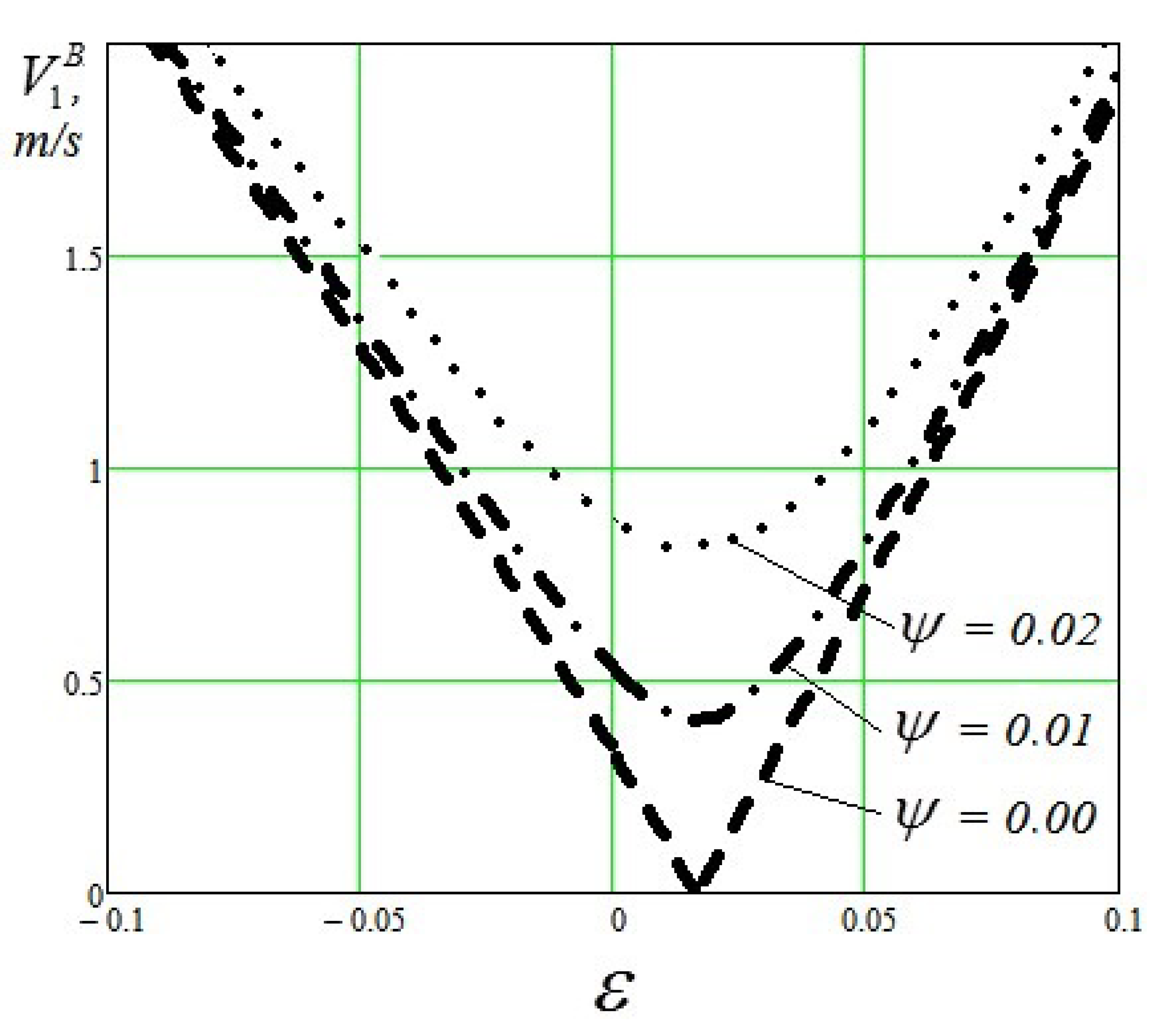
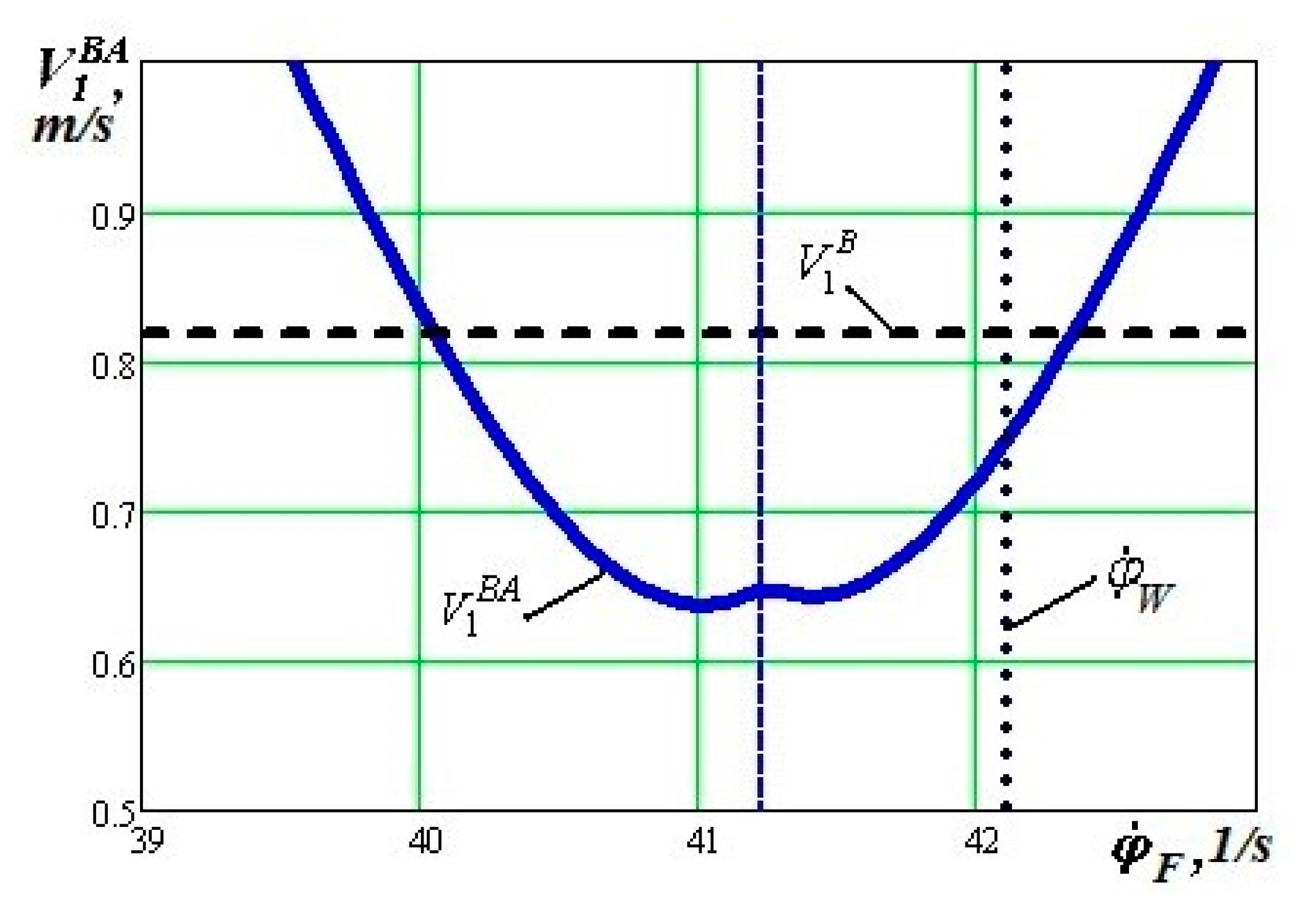
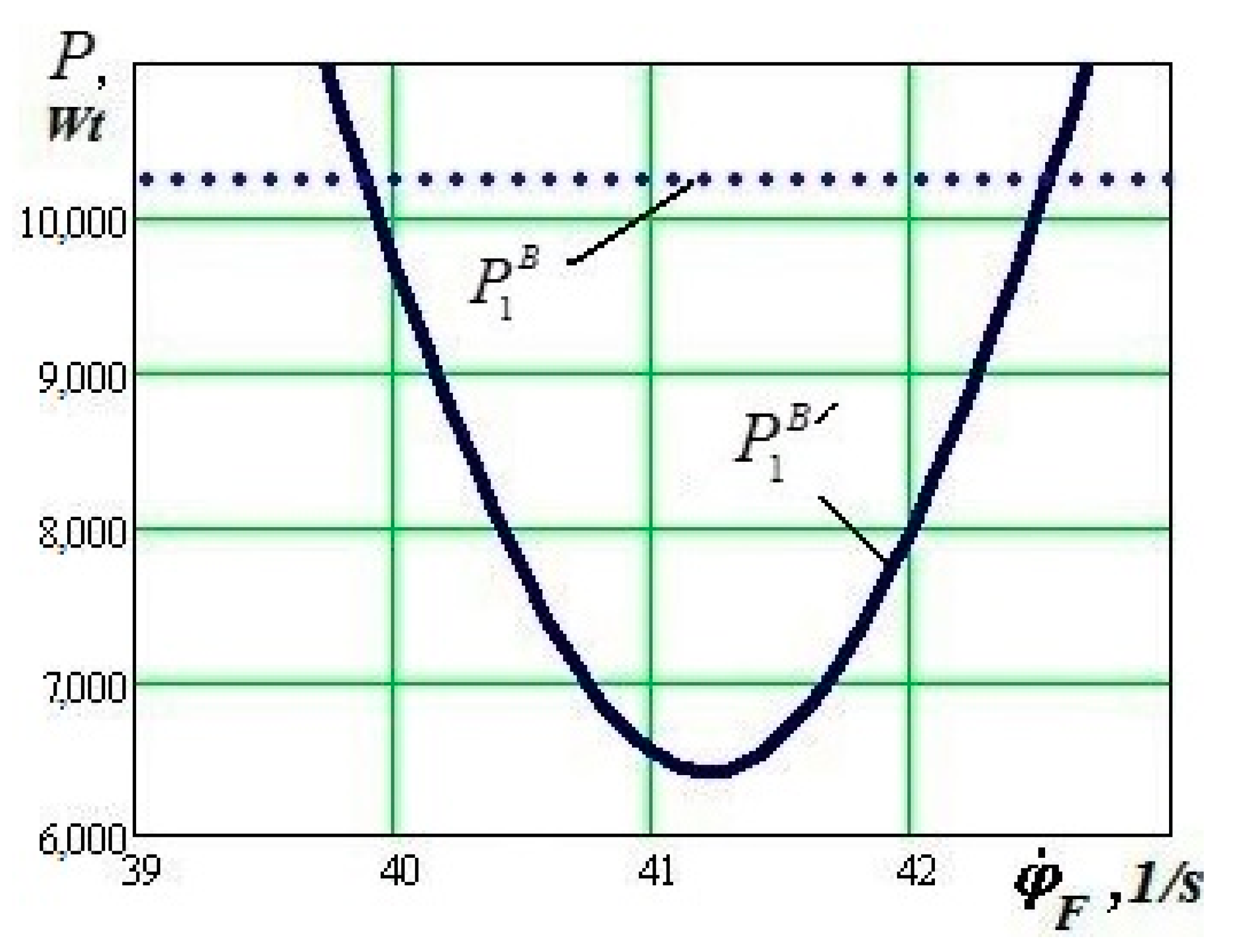
- The level of slippage in the main contact of the perspective wheel design insignificantly influences the value of slippage speed in its flange contact. For the traditional wheel design, this effect is more significant
- The results of the calculations confirm the possibility of a significant reduction of the slip rate in the flange contact for the perspective wheel design compared with the traditional wheel design. This gives reason to expect a reduction of the corresponding friction forces power in these contacts and a reduction of the resistance to move the rail vehicles if they were equipped with wheels with the perspective wheel design, especially when they move in curved sections of a railway track
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tkachenko, V.P.; Sapronova, S.J.; Fomin, O.V.; Kul’bovs’kij, I.I.; Zub, E.P. Movement Resistance and Control-Lability of Rail Vehicles; Monograph: Kiev, Ukraine, 2017; p. 188. (In Ukrainian) [Google Scholar]
- Tkachenko, V.P. Kinematic Resistance to the Movement of Rail Vehicles; VUGU: Lugansk, Ukraine, 1996; p. 200. (In Russian) [Google Scholar]
- Mikhailov, E.; Semenov, S.; Panchenko, E. The possibility of reducing kinematic slip with two-point contacting with rail wheel railway vehicle. TEKA Komisji Motoryzacji i Energetyki Rolnictwa 2013, 13, 139–145. [Google Scholar]
- Mikhailov, E.; Semenov, S.; Tkachenko, V.; Sapronova, S. Reduction of Kinematic Resistance to Movement of the Railway Vehicles. MATEC Web Conf. 2018, 235. [Google Scholar] [CrossRef]
- Mikhailov, E.; Semenov, S.; Dižo, J.; Kravchenko, K. Research of possibilities of reducing the driving re-sistance of a railway vehicle by means of the wheel construction improvement. Transp. Res. Procedia 2019, 40, 831–838. [Google Scholar] [CrossRef]
- Simson, S.A.; Pearce, M.E. Wheel wear losses from bogie rotation resistance, effects of cant and speed. In Proceedings of the Joint Rail Conference on Restoring and Upgrading Rail Infrastructure, Rolling Stock and Systems, Atlanta, GA, USA, 4–6 April 2006. [Google Scholar]
- Efficiency of Rail Lubrication. Railways of the World. Available online: http://www.railsystem.net/rail-wheel-lubrication/ (accessed on 26 September 2020).
- Masliev, V.G. Locomotive Dynamics with Devices That Reduce Railway Wheel Wear; NTU: Kharkiv, Ukraine, 2008; p. 288. (In Russian) [Google Scholar]
- Liang, B.; Iwnicki, S.D. An Experimental Study of Independently Rotating Wheels for Railway Vehicles. In Proceedings of the International Conference on Mechatronics and Automation, Harbin, China, 5–8 August 2007. [Google Scholar]
- Pombo, J.A.; Ambrósio, M.S. New wheel-rail contact model for railway dynamics. Veh. Syst. Dyn. 2007, 45, 165–189. [Google Scholar] [CrossRef]
- Ma, Y.; Markine, V.; Mashal, A.A.; Ren, M. Modelling verification and influence of operational patterns on tribological behaviour of wheel-rail interaction. Tribol. Int. 2017, 114, 264–281. [Google Scholar] [CrossRef]
- Masek, J.; Kendra, M.; Milinkovic, S.; Veskovic, S.; Barta, D. Proposal and Application of Methodology of Revitalisation of Regional Railway Track in Slovakia and Serbia. Part 1: Theoretical Approach and Proposal of Methodology for Revitalisation of Regional Railways. Transp. Probl. 2015, 10, 85–95. [Google Scholar] [CrossRef]
- Seo, S.I.; Mun, H.S. Development of technologies for mountain trams driven through sharp curves. J. Mech. Sci. Technol. 2019, 33, 2019–2027. [Google Scholar] [CrossRef]
- Ilgakojyte-Bazariene, J.; Lebeckas, J.; Kersys, R. Quality of Public Transport Service in Kaunas. In Proceedings of the Transport Means 2016 Conference, Juodkrante, Lithuania, 5–7 October 2016. [Google Scholar]
- Leitner, B.; Mocova, L.; Hromada, M. A new Approach to Identification of Critical Elements in Railway Infrastructure. Procedia Eng. 2017, 187, 143–149. [Google Scholar] [CrossRef]
- Dvorak, Z.; Leitner, B.; Novak, L. Software Support for Railway Traffic Simulation under Restricted Conditions of the Rail Section. Procedia Eng. 2016, 134, 245–255. [Google Scholar] [CrossRef]
- Stastniak, P.; Smetanka, P. Study of a Railway Wheel Running Surface Wear by Using of Simulation Tools. In Proceedings of the 24th International Conference on Current Problems in Rail Vehicles, Zilina, Slovakia, 17–19 September 2019. [Google Scholar]
- Melnik, R.; Sowinski, B. Analysis of Dynamics of a Metro Vehicle Model with Differential Wheelsets. Transp. Probl. 2017, 12, 113–124. [Google Scholar] [CrossRef]
- Kostrzewski, M.; Melnik, R. Numerical dynamics study of a rail vehicle with differential gears. Procedia Eng. 2017, 192, 439–444. [Google Scholar] [CrossRef]
- Lu, Z.G.; Yang, Z.; Huang, Q.; Wang, X.C. Robust active guidance control using the mu-synthesis method for a tramcar with independently rotating wheelsets. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 233, 33–48. [Google Scholar] [CrossRef]
- Datoussaid, S.; Verlinden, O.; Wenderloot, L.; Conti, C. Computer-aided analysis of urban railway vehicles. Veh. Syst. Dyn. 1998, 30, 213–227. [Google Scholar] [CrossRef]
- Ji, Y.J.; Ren, L.H.; Zhou, J.S. Boundary Conditions of Active Steering Control of Independent Rotating Wheelset Based on Hub Motor and Wheel Rotating Speed Difference Feedback. Veh. Syst. Dyn. 2018, 56, 1883–1898. [Google Scholar] [CrossRef]
- Hauser, V.; Kravchenko, K.; Nozhenko, O.; Fomin, A. Tram Car Bogie Concept and Consideration of his Impact to the Track. In Proceedings of the 24th International Conference on Current Problems in Rail Vehicles, Zilina, Slovakia, 17–19 September 2019. [Google Scholar]
- Nozhenko, O.; Hauser, V.; Kravchenko, K.; Loulova, M. Proposal of Wheel with Additional Tread for Vehicle to Strongly Curved Track Interaction Improvement. In Proceedings of the 23rd Conference: Current Problems in Rail Vehicles 2017, Ceska Trebova, Czech Republic, 20–22 September 2017. [Google Scholar]
- Shiler, A. Analysis and Simulation of New Wheel Pair Construction. Procedia Eng. 2015, 100, 1714–1723. [Google Scholar] [CrossRef]
- Mikhailov, E.; Semenov, S.; Sapronova, S.; Tkachenko, V. On the Issue of Wheel Flange Sliding along the Rail. In Lecture Notes in Intelligent Transportation and Infrastructure; Springer: Berlin/Heidelberg, Germany, 2020; pp. 377–385. [Google Scholar]
- Gerlici, J.; Lack, T. Wheelset/Rail Geometric Characteristics and Contact Forces Assessment with Regard to Wheelset Rolling. MATEC Web Conf. 2019, 254. [Google Scholar] [CrossRef]
- Lack, T.; Gerlici, J.; Stastniak, P. Wheelset/Rail Geometric Characteristics and Contact Forces Assessment with Regard to Angle of Attack. MATEC Web Conf. 2019, 254. [Google Scholar] [CrossRef]
- Gerlici, J.; Tkachenko, V.; Sapronova, S.T.; Lack, T. Steerability Research of Railway Vehicles. In Proceedings of the 24th International Conference on Current Problems in Rail Vehicles, Zilina, Slovakia, 17–19 September 2019. [Google Scholar]
- Sapietova, A.; Gajdos, L.; Dekys, V.; Sapieta, M. Analysis of the Influence of Input Function Contact Parameters of the Impact Force Process in the MSC. ADAMS. Adv. Mechatron. Solut. 2016, 393, 243–253. [Google Scholar]
- Skocilasova, B.; Skocilas, J.; Klimenda, F.; Soukup, J.; Handrik, M. Vertical Oscillation Investigation of Spatially Elastically Supported Rigid Plate—Vehicle Model. MATEC Web Conf. 2019, 254. [Google Scholar] [CrossRef]
- Skvireckas, R.; Kersys, A.; Kersys, R.; Lukosevicius, V. Research of lateral vibrations of a passenger wagon running along the curved path. J. Vibroeng. 2012, 14, 706–714. [Google Scholar]
- Steisunas, S.; Bureika, G. Study of Freight Wagon Running Dynamic Stability Taking into Account the Track Stiffness Variation. Transp. Probl. 2014, 9, 131–143. [Google Scholar]
- Saga, M.; Jakubovickova, L. Simulation of Vertical Vehicle Non-Stationary Random Vibrations Con-sidering Various Speeds. Sci. J. Sil. Univ. Technol. 2014, 84, 113–118. [Google Scholar]
- Baeza, L.; Thompson, D.J.; Squicciarini, G.; Denia, F.D. Method for Obtaining the Wheel-Rail Contact Location and its Application to the Normal Problem Calculation through “CONTACT”. Veh. Syst. Dyn. 2018, 56, 1734–1746. [Google Scholar] [CrossRef]
- Bizic, M.B.; Petrovic, D.Z.; Tomic, M.C.; Djinovic, Z.V. Development of method for experimental determination of wheel-rail contact forces and contact point position by using instrumented wheelset. Meas. Sci. Technol. 2017, 28, 75902. [Google Scholar] [CrossRef]
- Stastniak, P.; Moravcik, M.; Baran, P.; Smetanka, L. Computer aided structural analysis of newly developed railway bogie frame. MATEC Web Conf. 2018, 157. [Google Scholar] [CrossRef]
- Suchanek, A. Measuring and Calculation of Residual Stresses in a Railway Wheel. In Proceedings of the XXIV 24th International Conference on Current Problems in Rail Vehicles, Zilina, Slovakia, 17–19 September 2019. [Google Scholar]
- Klebanov, I.M.; Kuraeva, Y.V. Finite Element Analysis of Railway Wheel-Rail Contact Interaction. Vestn. Samar. Gos. Tekhnicheskogo Univ. Seriya Fiz. Mat. Nauk. 2008, 1, 59–62. [Google Scholar]
- Milosevic, M.S.; Stamenkovic, D.S.; Milojevic, A.P.; Tomic, M.M. Modeling Thermal Effects in Braking Systems of Railway Vehicles. Therm. Sci. 2012, 16, 515–526. [Google Scholar] [CrossRef]
- Dindar, S.; Kaewunruen, S. Assessment of turnout-related derailments by various causes. In Proceedings of the International Congress and Exhibition Sustainable Civil Infrastructures: Innovative Infrastructure Geotechnology GeoMEast 2017, Sharm Elsheikh, Egypt, 15–17 July 2017. [Google Scholar]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mikhailov, E.; Semenov, S.; Kliuiev, S.; Dižo, J.; Blatnický, M.; Gerlici, J.; Harušinec, J.; Kovtanets, M. Clarification of Features of the Wheel Movement with a Perspective Constructive Scheme on a Rail. Appl. Sci. 2020, 10, 6758. https://doi.org/10.3390/app10196758
Mikhailov E, Semenov S, Kliuiev S, Dižo J, Blatnický M, Gerlici J, Harušinec J, Kovtanets M. Clarification of Features of the Wheel Movement with a Perspective Constructive Scheme on a Rail. Applied Sciences. 2020; 10(19):6758. https://doi.org/10.3390/app10196758
Chicago/Turabian StyleMikhailov, Evgeny, Stanislav Semenov, Sergii Kliuiev, Ján Dižo, Miroslav Blatnický, Juraj Gerlici, Jozef Harušinec, and Maxim Kovtanets. 2020. "Clarification of Features of the Wheel Movement with a Perspective Constructive Scheme on a Rail" Applied Sciences 10, no. 19: 6758. https://doi.org/10.3390/app10196758
APA StyleMikhailov, E., Semenov, S., Kliuiev, S., Dižo, J., Blatnický, M., Gerlici, J., Harušinec, J., & Kovtanets, M. (2020). Clarification of Features of the Wheel Movement with a Perspective Constructive Scheme on a Rail. Applied Sciences, 10(19), 6758. https://doi.org/10.3390/app10196758






