ERF-IMCS: An Efficient and Robust Framework with Image-Based Monte Carlo Scheme for Indoor Topological Navigation
Abstract
:1. Introduction
- An efficient and robust framework with image-based Monte Carlo scheme for indoor topological navigation, namely ERF-IMCS, is presented which combines the image retrieval and Monte Carlo localization to provide the robot with the capability to avoid perceptual aliasing.
- To the best of our knowledge, ERF-IMCS is the first work to employ hash encoding technology to perform efficient CNN feature indexing and visual localization in topological navigation.
- We proposed a effective visual localization method, simultaneously employing the global and local CNN features of images to construct discriminative representation for environment, which makes the navigation system more robust to the interference of occlusion, translation and illumination. Experiments on a real robot platform show that ERF-IMCS exhibits great performance in terms of robustness and efficiency.
2. Related Work
2.1. Image Retrieval
2.2. Topological Mapping and Localization
3. Main Design of ERF-IMCS
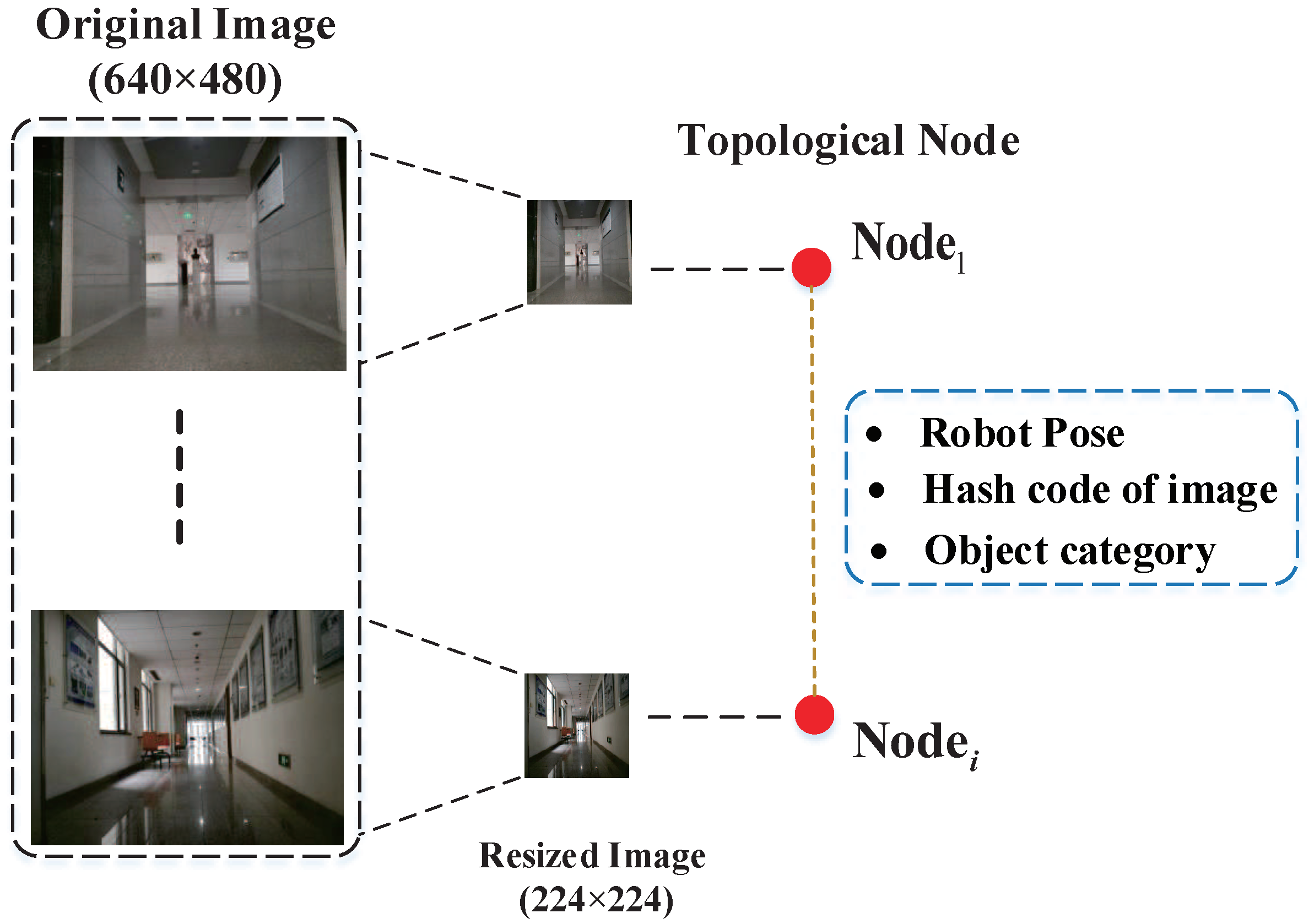
3.1. Vision-Based Topological Mapping
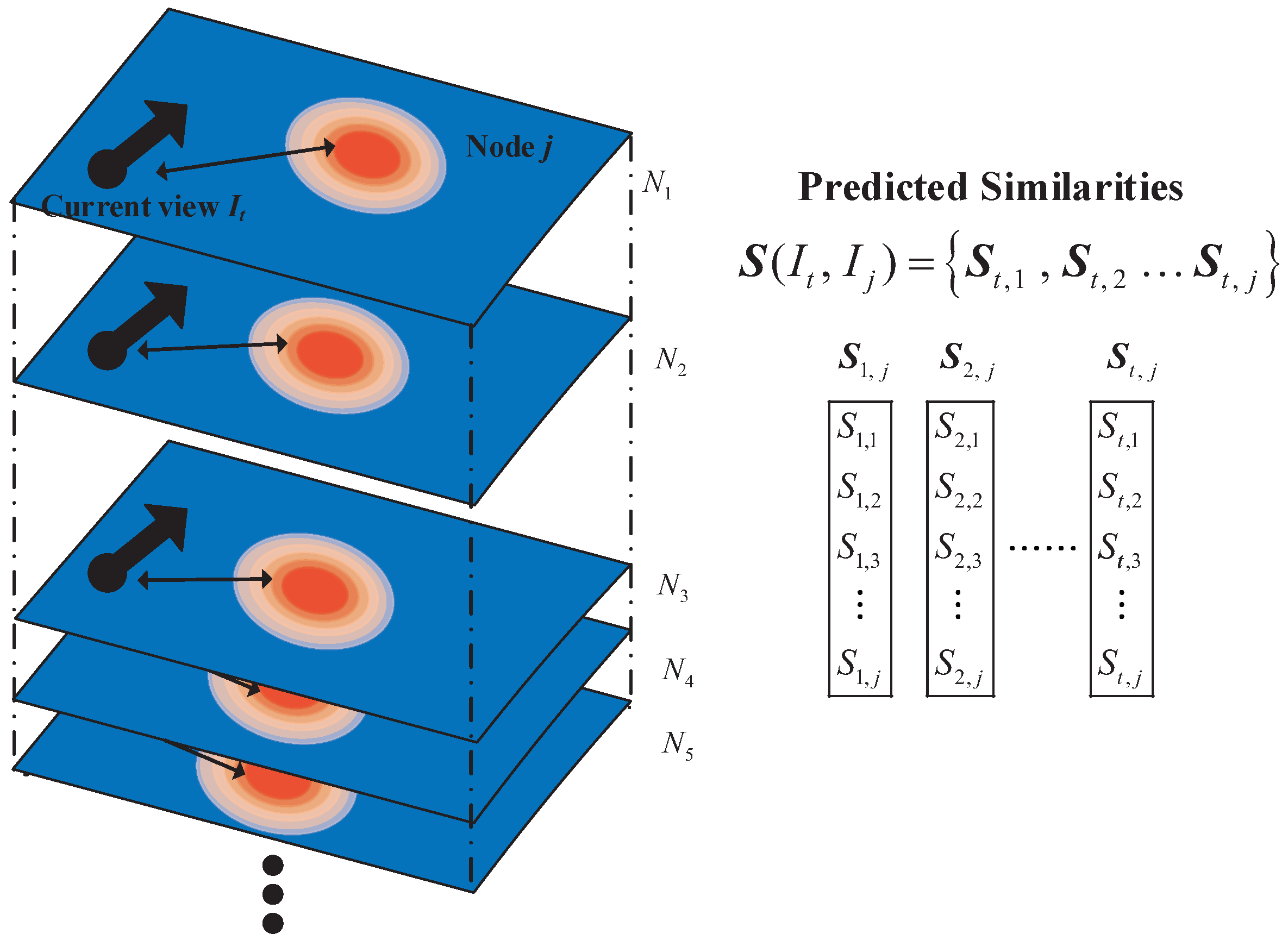
3.2. Image Retrieval
3.3. Image-Based Monte Carlo Localization
| Algorithm 1 Image-based Monte Carlo localization |
| Input: observation information , control information ; |
Output: the state of robot ;
|
4. Experiments
4.1. Image Retrieval Experiment
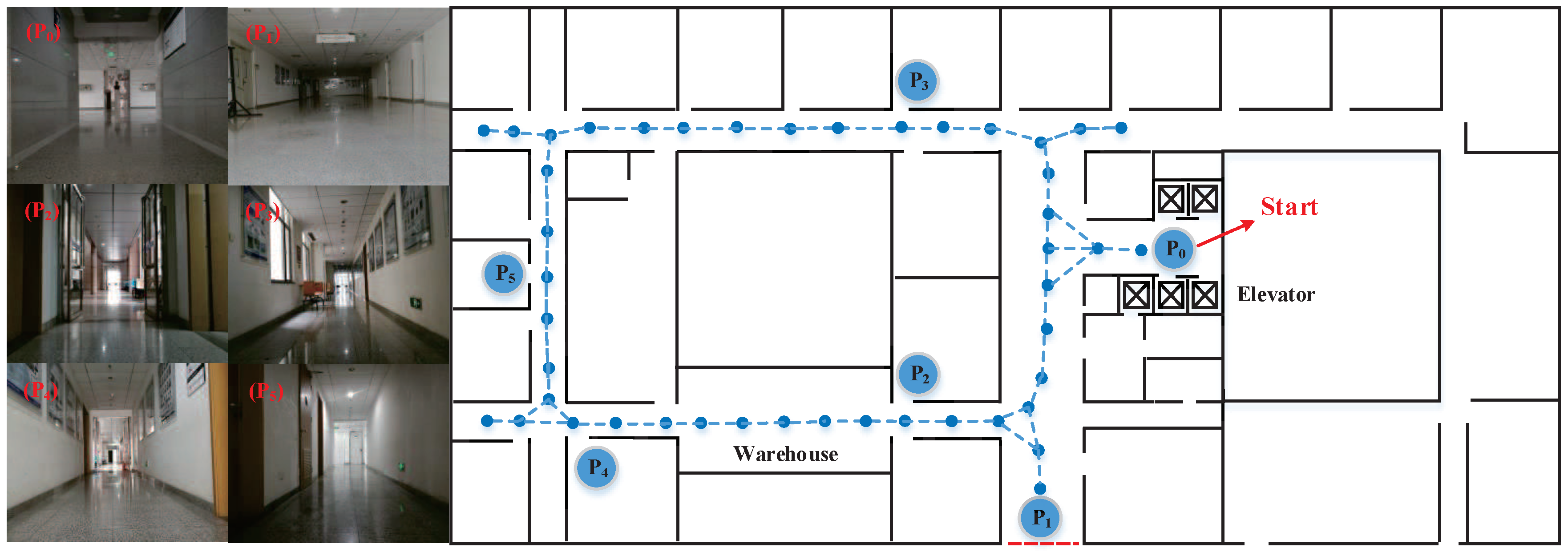
4.2. Image-Based Monte Carlo Localization
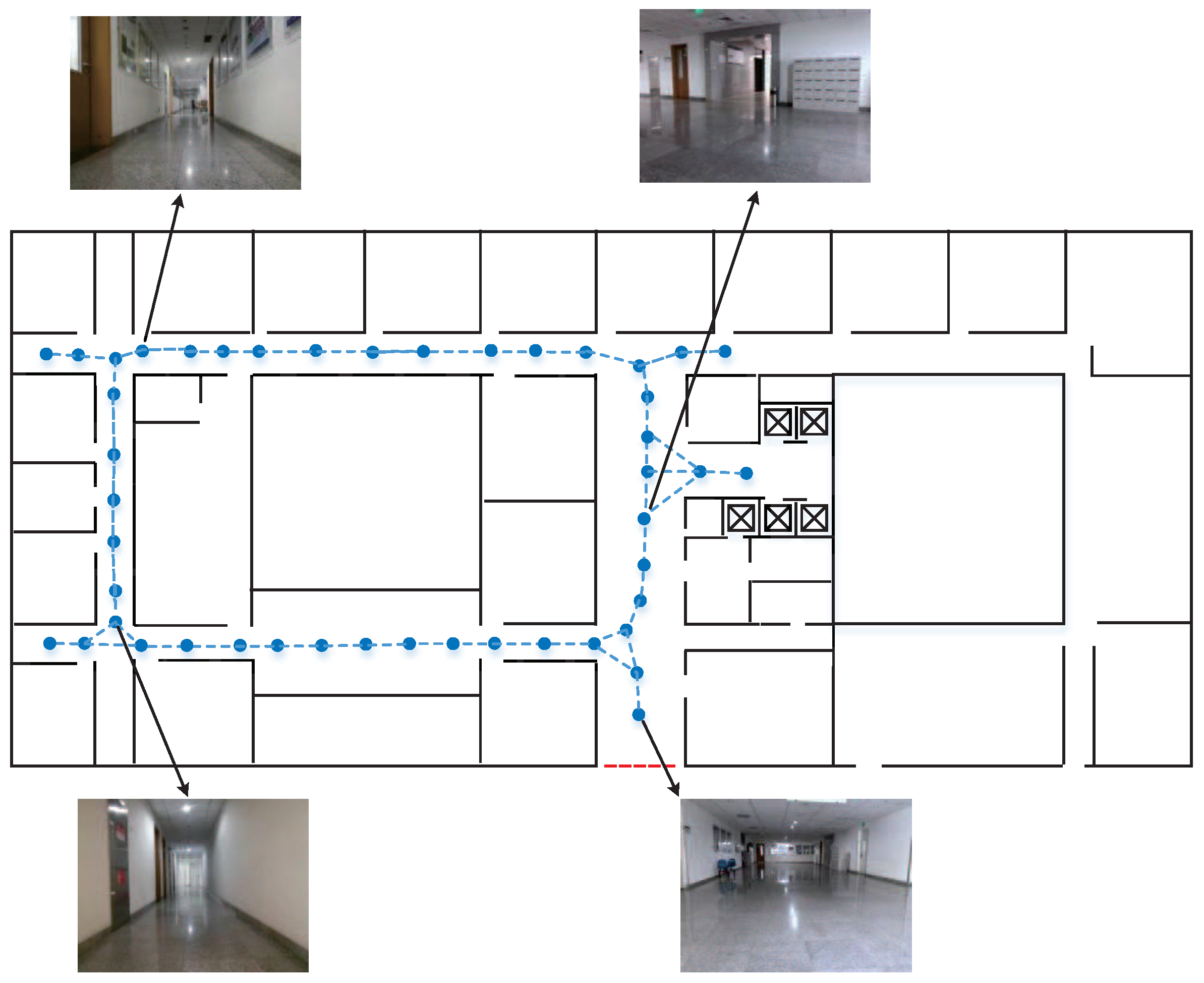
4.3. Vision-Based Topological Navigation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Park, S.; Roh, K.S. Coarse-to-Fine Localization for a Mobile Robot Based on Place Learning With a 2-D Range Scan. IEEE Trans. Robot. 2016, 32, 528–544. [Google Scholar] [CrossRef]
- Chen, X.; Sun, H.; Zhang, H. A New Method of Simultaneous Localization and Mapping for Mobile Robots Using Acoustic Landmarks. Appl. Sci. 2019, 9, 1352. [Google Scholar] [CrossRef] [Green Version]
- Bista, S.R.; Giordano, P.R.; Chaumette, F. Combining line segments and points for appearance-based indoor navigation by image based visual servoing. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 2960–2967. [Google Scholar]
- Ferro, M.; Paolillo, A.; Cherubini, A.; Vendittelli, M. Vision-Based Navigation of Omnidirectional Mobile Robots. IEEE Robot. Autom. Lett. 2019, 4, 2691–2698. [Google Scholar] [CrossRef] [Green Version]
- Luo, R.C.; Shih, W. Topological Map Generation for Intrinsic Visual Navigation of an Intelligent Service Robot. In Proceedings of the 2019 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 11–13 January 2019; pp. 1–6. [Google Scholar]
- Valiente, D.; Gil, A.; Paya, L.; Sebastian, J.M.; Reinoso, O. Robust Visual Localization with Dynamic Uncertainty Management in Omnidirectional SLAM. Appl. Sci. 2017, 7, 1294. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Zha, H.; Cipolla, R. Coarse-to-fine vision-based localization by indexing scale-Invariant features. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2006, 36, 413–422. [Google Scholar] [CrossRef]
- Maldonadoramirez, A.; Torresmendez, L. A Collaborative Human-Robot Framework for Visual Topological Mapping of Coral Reefs. Appl. Sci. 2019, 9, 261. [Google Scholar] [CrossRef] [Green Version]
- Maohai, L.; Han, W.; Lining, S.; Zesu, C. Robust omnidirectional mobile robot topological navigation system using omnidirectional vision. Eng. Appl. Artif. Intell. 2013, 26, 1942–1952. [Google Scholar] [CrossRef]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. BRIEF: Binary Robust Independent Elementary Features. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6314, pp. 778–792. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, J. Robust Topological Navigation via Convolutional Neural Network Feature and Sharpness Measure. IEEE Access 2017, 5, 20707–20715. [Google Scholar] [CrossRef]
- Sattler, T.; Leibe, B.; Kobbelt, L. Efficient & Effective Prioritized Matching for Large-Scale Image-Based Localization. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1744–1756. [Google Scholar]
- Kalantidis, Y.; Tolias, G.; Avrithis, Y.; Phinikettos, M.; Spyrou, E.; Mylonas, P.; Kollias, S. VIRaL: Visual Image Retrieval and Localization. Multimed. Tools Appl. 2011, 51, 555–592. [Google Scholar] [CrossRef] [Green Version]
- Mansourian, L.; Abdullah, M.T.; Abdullah, L.N.; Azman, A.; Mustaffa, M.R. An effective fusion model for image retrieval. Multimed. Tools Appl. 2018, 77, 16131–16154. [Google Scholar] [CrossRef]
- Arandjelović, R.; Gronat, P.; Torii, A.; Pajdla, T.; Sivic, J. NetVLAD: CNN Architecture for Weakly Supervised Place Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 1437–1451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Preethy Byju, A.; Demir, B.; Bruzzone, L. A Progressive Content-Based Image Retrieval in JPEG 2000 Compressed Remote Sensing Archives. IEEE Trans. Geosci. Remote. Sens. 2020, 58, 5739–5751. [Google Scholar] [CrossRef]
- Smeulders, A.W.M.; Worring, M.; Santini, S.; Gupta, A.; Jain, R. Content-based image retrieval at the end of the early years. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1349–1380. [Google Scholar] [CrossRef]
- Jing, F.; Li, M.; Zhang, H.-J.; Zhang, B. A unified framework for image retrieval using keyword and visual features. IEEE Trans. Image Process. 2005, 14, 979–989. [Google Scholar] [CrossRef]
- Zhou, X.S.; Huang, T.S. Relevance Feedback in Image Retrieval: A Comprehensive Review. Multimed. Syst. 2003, 8, 536–544. [Google Scholar] [CrossRef]
- Jégou, H.; Douze, M.; Schmid, C.; Pérez, P. Aggregating local descriptors into a compact image representation. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 3304–3311. [Google Scholar]
- Perronnin, F.; Dance, C. Fisher Kernels on Visual Vocabularies for Image Categorization. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Jose, A.; Lopez, R.D.; Heisterklaus, I.; Wien, M. Pyramid Pooling of Convolutional Feature Maps for Image Retrieval. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 480–484. [Google Scholar]
- Liu, P.; Guo, J.; Wu, C.; Cai, D. Fusion of Deep Learning and Compressed Domain Features for Content-Based Image Retrieval. IEEE Trans. Image Process. 2017, 26, 5706–5717. [Google Scholar] [CrossRef]
- Babenko, A.; Slesarev, A.; Chigorin, A.; Lempitsky, V. Neural codes for image retrieval. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2014; pp. 584–599. [Google Scholar]
- Sharif Razavian, A.; Azizpour, H.; Sullivan, J.; Carlsson, S. CNN Features Off-the-Shelf: An Astounding Baseline for Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Gordo, A.; Almazán, J.; Revaud, J.; Larlus, D. Deep image retrieval: Learning global representations for image search. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016; pp. 241–257. [Google Scholar]
- Salvador, A.; Giró-i Nieto, X.; Marqués, F.; Satoh, S. Faster r-cnn features for instance search. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 9–16. [Google Scholar]
- Shalev, O.; Degani, A. Canopy-Based Monte Carlo Localization in Orchards Using Top-View Imagery. IEEE Robot. Autom. Lett. 2020, 5, 2403–2410. [Google Scholar] [CrossRef]
- Marinho, L.B.; Almeida, J.S.; Souza, J.W.M.; Albuquerque, V.H.C.; Reboucas Filho, P.P. A novel mobile robot localization approach based on topological maps using classification with reject option in omnidirectional images. Expert Syst. Appl. 2017, 72, 1–17. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, H.; Liu, Y. Topological Indoor Localization and Navigation for Autonomous Mobile Robot. IEEE Trans. Autom. Eng. 2015, 12, 729–738. [Google Scholar] [CrossRef]
- Blochliger, F.; Fehr, M.; Dymczyk, M.; Schneider, T.; Siegwart, R. Topomap: Topological mapping and navigation based on visual slam maps. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 1–9. [Google Scholar]
- Liu, M.; Siegwart, R. Topological Mapping and Scene Recognition With Lightweight Color Descriptors for an Omnidirectional Camera. IEEE Trans. Robot. 2017, 30, 310–324. [Google Scholar] [CrossRef]
- Goedemé, T.; Nuttin, M.; Tuytelaars, T.; Gool, L.V. Omnidirectional Vision Based Topological Navigation. Int. J. Comput. Vis. 2007, 74, 219–236. [Google Scholar] [CrossRef] [Green Version]
- Hao, J.; Dong, J.; Wang, W.; Tan, T. What Is the Best Practice for CNNs Applied to Visual Instance Retrieval? arXiv 2016, arXiv:1611.01640. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In European Conference on Computer Vision (ECCV); Springer: Berlin/Heidelberg, Germany, 2014; pp. 818–833. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yue-Hei Ng, J.; Yang, F.; Davis, L.S. Exploiting local features from deep networks for image retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–12 June 2015; pp. 53–61. [Google Scholar]
- Gong, Y.; Lazebnik, S.; Gordo, A.; Perronnin, F. Iterative Quantization: A Procrustean Approach to Learning Binary Codes for Large-Scale Image Retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2916–2929. [Google Scholar] [CrossRef] [Green Version]
- Philbin, J.; Chum, O.; Isard, M.; Sivic, J.; Zisserman, A. Object retrieval with large vocabularies and fast spatial matching. In Proceedings of the IEEE Computer Society Conference on Computer Vision & Pattern Recognition, Minneapolis, MI, USA, 18–23 June 2007. [Google Scholar]
- Philbin, J.; Chum, O.; Isard, M.; Sivic, J.; Zisserman, A. Lost in quantization: Improving particular object retrieval in large scale image databases. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Jégou, H.; Zisserman, A. Triangulation embedding and democratic aggregation for image search. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014; pp. 3310–3317. [Google Scholar]
- Babenko, A.; Lempitsky, V. Aggregating Local Deep Features for Image Retrieval. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1269–1277. [Google Scholar]
- Tolias, G.; Sicre, R.; Jégou, H. Particular Object Retrieval With Integral Max-Pooling of CNN Activations. In Proceedings of the International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016; pp. 1–12. [Google Scholar]
- Thrun, S.; Fox, D.; Burgard, W.; Dellaert, F. Robust Monte Carlo localization for mobile robots. Artif. Intell. 2001, 128, 99–141. [Google Scholar] [CrossRef] [Green Version]








© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Zhou, H.; Chou, W. ERF-IMCS: An Efficient and Robust Framework with Image-Based Monte Carlo Scheme for Indoor Topological Navigation. Appl. Sci. 2020, 10, 6829. https://doi.org/10.3390/app10196829
Xu S, Zhou H, Chou W. ERF-IMCS: An Efficient and Robust Framework with Image-Based Monte Carlo Scheme for Indoor Topological Navigation. Applied Sciences. 2020; 10(19):6829. https://doi.org/10.3390/app10196829
Chicago/Turabian StyleXu, Song, Huaidong Zhou, and Wusheng Chou. 2020. "ERF-IMCS: An Efficient and Robust Framework with Image-Based Monte Carlo Scheme for Indoor Topological Navigation" Applied Sciences 10, no. 19: 6829. https://doi.org/10.3390/app10196829
APA StyleXu, S., Zhou, H., & Chou, W. (2020). ERF-IMCS: An Efficient and Robust Framework with Image-Based Monte Carlo Scheme for Indoor Topological Navigation. Applied Sciences, 10(19), 6829. https://doi.org/10.3390/app10196829





