SETNDS: A SET-Based Non-Dominated Sorting Algorithm for Multi-Objective Optimization Problems

Abstract

Non-dominated sorting, used to find pareto solutions or assign solutions to different fronts, is a key but time-consuming process in multi-objective evolutionary algorithms (MOEAs). The best-case and worst-case time complexity of non-dominated sorting algorithms currently known are O(MNlogN) and O(MN²); M and N represent the number of objectives and the population size, respectively. In this paper, a more efficient SET-based non-dominated sorting algorithm, shorted to SETNDS, is proposed. The proposed algorithm can greatly reduce the number of comparisons on the promise of ensuring a shorter running time. In SETNDS, the rank of a solution to be sorted is determined by only comparing with the one with the highest rank degree in its dominant set. This algorithm is compared with six generally existing non-dominated sorting algorithms—fast non-dominated sorting, the arena’s principle sort, the deductive sort, the corner sort, the efficient non-dominated sort and the best order sort on several kinds of datasets. The compared results show that the proposed algorithm is feasible and effective and its computational efficiency outperforms other existing algorithms.

1. Introduction

In many practical living and production activities, we often need to make decisions through weighing the pros and cons of multiple objectives, but they always conflict with each other. Manufacturers need to select the optimal production program to make a tradeoff between the cost of production, time and quality and so on, which can be formalized as a multi-objective optimization problem (MOP) [1]. Evolutionary algorithms are more suitable to solve the MOPs than traditional optimization algorithms, as a set of optimal solutions can be found running at once [2]. Various kinds of multi-objective evolutionary algorithms (MOEAs) have been proposed over the past few decades to deal with MOPs; e.g., MOEA/D [3], SPEA 2 [4], NSGA II [2] and its improved version NSGA III [5], etc.

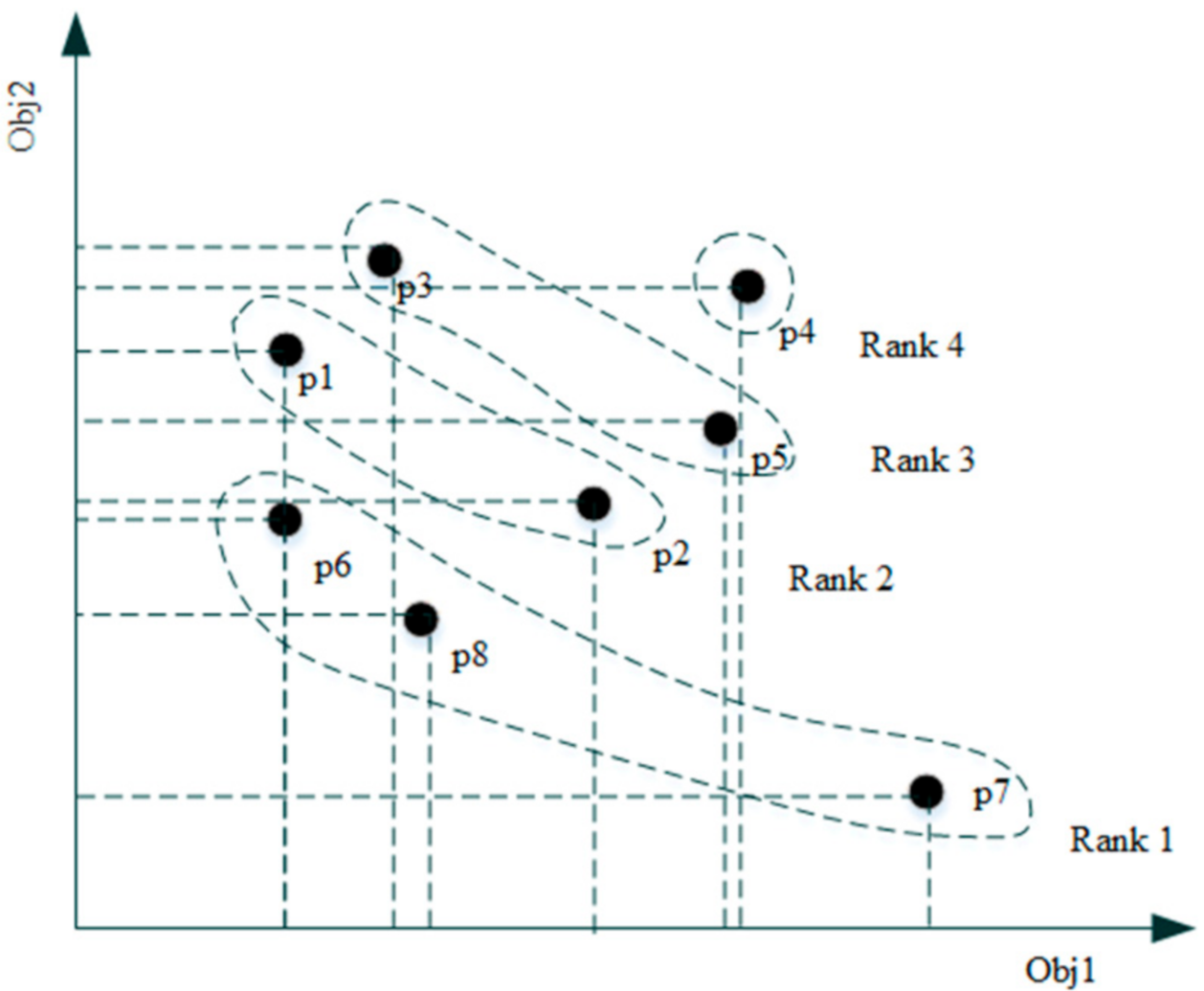
As described in [2], non-dominated sorting, used to find pareto solutions or assign solutions to different fronts, is a key but time-consuming process in multi-objective evolutionary algorithms (MOEAs). It is very meaningful to improve the computational efficiency of non-dominated sorting to improve the whole efficiency of MOEAs. Studying existing non-dominated sorting algorithms, we come to the conclusion that there are two strains of thought to find the front each solution belongs to. A fast non-dominated sorting algorithm (FNDS) [2] is a representative of the first method. In this method, solutions which are not dominated by others are recognized as non-dominated solutions or a pareto set and they will be assigned to the first rank and deleted from the population. These solutions correspond to p6, p7 and p8 in Figure 1 (an example of a bi-objective minimization problem with eight solutions). Then p1 and p2 are found as rank 2 through the same process. The process will be repeated until the population is empty. Another typical representative of the second method to assign solutions to the related rank is given in [6,7]. In this method, every solution needs to compare with solutions whose ranks have been assigned. Suppose p2 has the maximum rank in the dominant set {p2, p6, p8} who dominates p5, and the rank of p2 is 2, so the rank of p5 is 2+1, i.e., 3. Above all, there are four fronts in Figure 1, set {p6, p8, p7} of rank 1, {p1, p2} of rank 2, {p3, p5} of rank 3 and {p4} of rank 4. In this paper, based on the analysis and study of the previous algorithms, a novel non-dominated sorting algorithm, combining the advantage of characteristics of the set, is proposed.

The research contents of this paper are given below. Some general and recently studied nondominated sorting algorithms to find a pareto set or rank the solutions are introduced in Section 2. Section 3 presents the fundamental concepts and definitions as they will come up through the whole paper. Section 4 describes the proposed non-dominated algorithm and a detailed example explains how the proposed algorithm implemented is also given in this section. An algorithm complexity analysis is given in Section 4. Simulations and experimental results are discussed in Section 5. Finally, Section 6 makes a summary on the process of the work, and plans the next steps for following work.

2. Related Work

In this section, we will discuss and analyze the methods for non-dominated sorting that have been researched and utilized in MOPs. Through reviewing lots of broad research on non-dominated sorting [2,6,7,8,9,10,11,12,13,14,15,16,17,18,19], the common methods for sorting multi-objective solutions can be classified into two classes: one front after another (OFAA) and one solution after another (OSAA). The basic idea of OFAA is to compare each solution with others to obtain non-dominated solutions, then assign them to the current rank and remove them temporarily. This process is repeated until the population is empty. Some of the general methods are basic non-dominated sorting algorithm (BNDS) [2], improved version fast non-dominated sorting algorithm (FNDS) [2], quick non-dominated sorting algorithm (QNDS) [8], the arena’s principle (AP) [9], deductive sort (DS) [12] and climbing sort (CLS) [12], corner sort (CS) [11] and so on.

BNDS [20] compares a solution to others to judge whether it is dominated or not, if there is no solution dominating it, it will be added to the current rank. The time complexity of this method is O(MN³) because of lots of redundancy comparisons. FNDS [2] is proposed in reference to basic insertion sorting algorithms, which reduces the time complexity to O(MN²), but its space complexity increases to O(N²). In order to reduce the negative impact of multiple conflicting objectives on the running efficiency of the evolutionary algorithms, parallelization is introduced to the non-dominated sorting process, e.g., paper [21] develops three parallel NDS versions based on FNDS, a multicore, a Graphic Processing Unit (GPU) and a hybrid, respectively. QNDS [8] adopts the realization idea of quick sort, and can reduce the best-case time complexity to O(MN√N). It is better than FNDS, but the worst-case time complexity remains O(MN²).

The AP [9] is shown to be a more effective algorithm than other OSAA algorithms in empirical evaluations. The idea of AP is to select a solution as the “arena host” randomly (always choose the first solution of the population) and for the remaining solutions to challenge the arena one by one. If the challenger wins then the challenger is better and it will be the new “arena host”—the old arena will be eliminated. The challenger who is worse than the arena host will be removed. The new arena host will compare with the rest of the solutions until the last one. Best-case time complexity can be enhanced to O(MN√N), yet it is still O(MN²) in the worst case.

CS [11] first proposes to sort the population with one or multiple objectives as the solution with the best objective values are non-dominated. The under-compared solution is always dominating or unrelated to the remaining solutions. The dominated solutions are removed and unrelated solutions are reserved as the AP method. Its time complexity is the same as the FNDS and space complexity is O(N).

Two non-dominated sorting methods to solve the multi-objective solutions, DS and CLS, are proposed in [12]. The former is shown to be better than CLS. DS records the comparison result for avoiding unnecessary comparisons. DS also gives O(MN√N) and O(MN²) for the best case and worst case, respectively.

A new data structure, which is composed of a K-d tree and M-list called M-front, is proposed in [22] and used to decrease the computational cost of non-dominated sorting. In M-front, utilizing the over-non-domination phenomenon as an advantage with the increase in the number of objectives. To hold the invariance property of the M-front, an interval query is used to reduce the scope of query and speed up the selection of the non-dominated individual. The best-case time complexity is O(MN) or O(MNlnN) when the K-d tree is used, and the worst-case time complexity is O(MN²).

Different from OFAA, the realization process of OSAA is to assign solutions to fronts one by one, and every individual needs to be compared with ones that have already been sorted [6,7,19]. Efficient non-dominated sorting strategy-sequential strategy (ENS-SS) and its improved version Efficient non-dominated sorting strategy-binary strategy (ENS-BS) [7], Best Order Sort (BOS) [6] and its improved version (BBOS) [19], are representative algorithms. The key preparing process in these methods is to sort the population with one or multiple objectives in an ascending order, and the lexicographic order is used in case any solutions have the same values. ENS [7] can reduce the time complexity in the best case to O(MN√N) but it remains O(MN²) in the worst case. BOS [6] performs better than the abovementioned methods with more objectives, and its time complexity in the best case and the worst case are O(MNlogN) and O(MN² + MNlogN). The search strategy to find the front of solutions also influences the efficiency of the algorithm which is shown in the proposed method and its improved versions. Based on the BOS algorithm, combined with the development of high performance computing systems, paper [23] proposes two efficient parallel BOS algorithms, which are based on high performance processing units, one based on multicore processors (MCs), called MC-BOS and the other one based on GPUs, called GPU-BOS. MC-BOS runs on multicore processors, while GPU-BOS utilizes the GPU architecture to implement parallelism. Different from the proposed MC-BOS and GPU-BOS, two other different parallel BOS versions considering the PRAM CREW model are proposed in [24] from a theoretical point of view. The best-case and worst-case time complexity is O(log³N) and O(logM + N²), and the relevant space complexity is O(MN²). Inspired from the production-grade sorting algorithm, a hybrid approach which combines the divide-and-conquer strategy and BOS is proposed to improve performance, and a heuristic mechanism is designed to determine when to use the BOS algorithm to solve the subproblem [25].

Based on the divide-and-conquer mechanism [26], some researchers proposed recursive non-dominated sorting approaches, which is another means of achieving OSAA [10,26,27,28]. Kung’s algorithm [27] is used to find the maxima of a set of vectors. Jensen [28] extends Kung’s algorithm—the time complexity with bi-objectives is O(MNlogN), while O(Nlog (M − 1) N) is more than or equal to three objectives. When the population has a large number of objectives, the proposed algorithm will work inefficiently. To decrease redundancy comparisons, a dominance tree is presented in [10] which is used to record the dominant relations between solutions, and this dominance tree is combined with the divide-and-conquer algorithm to acquire the fronts of solutions. Similar to [24], a parallel NDS based on a divide-and-conquer mechanism considering the PRAM-CREW model is proposed in [29]. This paper also explores parallelism from the angle of theory. The best time complexity is proved to be O(logM + N) and the space complexity is also O(MN²).

A tree-based non-dominated sorting algorithm, termed T-ENS, an extension of the ENS algorithm, is proposed in paper [16]. Similar to the most basic algorithm FNDS, the algorithm finds the non-dominated solutions that belongs to the first front, and then deletes them and then the second front, until the population is empty. A tree structure which is formed of unrelated solutions can help to reduce the number of comparisons as the non-domination relationships between solutions have been saved in the tree. The best- and worst-case time complexities of T-ENS are O(MNlnN/lnM) and O(MN²).

To quicken the domination check process and reduce unnecessary comparisons, paper [17] gives another way to improve and extend the ENS-BS algorithm, named Efficient Non-Dominated Sort with Non-dominated Tree (ENS-NDT). Different from the T-ENS in [16], END-NDT uses a variant of the bucket k-d tree to build a tree-like structure to easy the domination checks in each front. The best-case time complexity of ENS-NDT is O(MNlogN) when M > logN or O(Nlog²N) and the worst-case time complexity is O(MN²).

Different from the abovementioned algorithms, paper [18] first proposes a new non-dominated sorting algorithm—Merge Non-Dominated Sorting Algorithm (MNDS)—to calculate the dominance set of each solution, instead of obtaining the dominance relationship though a comparison with others. The authors of [18] also adapt the advantageous merge sort algorithm to find duplicate solutions. Additionally, a new data structure bitset is used to speed up the intersection operation between dominance sets. The best- and worst-case complexity is O(NlogN) and O(MN²).

As we can see from the aforementioned introduction, reducing the number of comparisons is the ordinary means to improve the efficiency of sorting algorithms. These studies show that the fewer comparisons one algorithm has, the better the algorithm performs. Taking full advantage of the hidden positional information and the idea of set theory, we propose a novel non-dominated sorting algorithm. The proposed algorithm can greatly reduce the comparing times by determining the dominant region of the solution to be sorted first.

3. Basic Concepts and Definitions

To facilitate the understanding of this work, the mathematical model of multi-objective optimization problems and the relevant concepts and definitions which are used in this paper are introduced in this section.

3.1. Mathmatical Model

It is important to note that throughout the whole paper we focus on minimal optimization problems and vice versa. Therefore, a minimal multi-objective optimization problem can be stated as follows:

$$\begin{array}{c}\min F\left(x\right) = {\left(f_1\left(x\right), f_2\left(x\right),\dots ,f_M\left(x\right)\right)}^T\\ s.t. xϵD\end{array}$$

where D denotes the decision space, x represents an individual of D, $R^M$ is called the objective space, and $F\left(x\right)ϵR^M$, namely F(x) is an individual of $R^M$. Since the non-dominated sorting process focuses mainly on the objective space, we use s instead of F(x) for convenience.

3.2. Concepts

3.2.1. Parameters

N number of solutions

M number of objectives

s solution

A_j(s) objective value of solution s on objective j

r rank level

3.2.2. Variables

We define $D\left(p,s\right)$ as the result of dominate comparison between solution p and solution s, the formula is as follows:

$$D\left(p,s\right)=\left\{\begin{array}{cc}\hfill 1,& p dominates s\hfill \\ \hfill 0,& p is unralated to s\hfill \\ \hfill -1,& p is dominated by s\hfill \end{array}\right.$$

3.2.3. SETS

P set of solutions

A set of sorted objectives of solutions

AP_j(s) set of preferential solutions of s in the jth objective

${\Omega }_1(s)$ set of solutions which dominate solution s

PS objective position information set

F set of solutions’ fronts

3.3. Definitions

Dominant Relationships between different solutions: Suppose solution p and s are any two members of solution set P, if $\forall j\in \left\{1,2,\mathrm{...},M\right\}, A_j(p)\le A_j(s)\mathrm{and}\exists i\in \{1,2,\mathrm{...},M\}, A_i(p)<A_i(s)$ is satisfied, we will say that p dominates s, which can be expressed as $p\succ s$, else $s\succ p$ instead. If p and s are not dominated by each other, we will say that p is unrelated to s, which can be expressed as $p{\succ }_{d}s$ and vice versa.

Partition of objective space: The objective values of any point in the objective space can divide the space into several parts, based on the relationships between solutions with the under-sorted solution s, these parts can be named the dominant region, unrelated region and dominated region. As shown in Figure 2, the objective values of point s can divide the bi-objective space into four parts; the relationships between point s and these parts are given as follows:

${\Omega }_1(s):$ located in the lower left part of s, also called the dominant region—any point located here dominates s, which can be expressed as $\forall p\in {\Omega }_1(s), p\succ s$.

${\Omega }_2(s)\cup {\Omega }_4(s)$: located in the upper left and lower right of s, also called the unrelated region—any point located at this part is unrelated to s, which can be expressed as $\forall p\in {\Omega }_2(s)\cup {\Omega }_4(s), p{\succ }_{d}s$.

${\Omega }_3(s)$: located in the upper right of s, also called the dominated region, any point located here is dominated by s, which can be expressed as $\forall p\in {\Omega }_3(s), s\succ p$.

Determination of the solution’s rank: As shown in Figure 3, it is enough to only consider the dominant region ${\Omega }_1(s)$ of s to determine the rank of s. Suppose the highest rank level in ${\Omega }_1(s)$ is r and the corresponding point is p, i.e., F(p) = r. Then the rank of s will be r + D (p, s).

4. Proposed Non-Dominated Sorting Algorithm

This section mainly introduces the draft non-dominated algorithm: SET-based non-dominated sorting algorithm (SETNDS). Figure 4 shows the realized idea, making full use of the hidden positional information of solutions and utilizing the idea of set theory to find the dominant region. From the sorted set A for M objectives, a preferential set AP_j(s) will be acquired, which belongs to solutions that are not worse than solution s for objective j. By intersecting the M sets, we will get the dominant region of s; that is ${\Omega }_1(s) = A{P}_1(s)\cap A{P}_2(s)\cap \mathrm{...}\cap A{P}_M(s)$. The smallest preferential set AP_m(s) will be considered first since it represents the first time solution s appears in set A.

4.1. Algorithm Description

Algorithm 1 describes the whole implementation process of the proposed algorithm. The algorithm mainly contains three steps: population initialization, determination of the dominant set and dominant comparison.

Algorithm1: Set-based Non-Dominated Sort Algorithm--SETNDS

Input population P

Output the rank fronts F for solutions in P

1 Begin

2 [N, M] ← size(P);        %obtain size N and objective M

3 for j = 1 to M

4  A(j)← sort(P, j);    % sort P in an ascending order of objective j;

5 end

6 [SA, pos_s] ← unique(A(1, N*M)); % get sequence of solutions and locations

7 MA ← repmat(1:M, 1, N*M)(pos_s); % get objective index of the solutions

8 PS ← makeRelation(P, SA, A);   % associate solution with locations

9 for i = 1 to N

10  s ← SA(i)

11  m ← MA(i)

12  Ω(s) ← ObtainDominantSet(s, m, A, PS);  % obtain dominant set

13    if isempty(Ω(s)) % if empty

14    F(s) ← 1

15    else

16     [p, F(p)] ← max{F{Ω(s)}}; % obtain the highest rank in Ω(s)

17     r ← DominateComparision(p, s);  % dominate relation

18     F(s)←r + F(p);       % obtain the rank of s

19   end

20 end

The population initialization process is realized in Algorithm 1, lines 2–8. At first, the size and number of objectives of the population P, represented as N and M, respectively, are obtained (Algorithm 1 line 2). Then, the solutions are sorted by each objective value s_j in the jth objective and the sorted sequence is stored in set A_j. If any objective values are the same, then the values of the next objective are considered. This idea comes from the lexicographic order [6] (Algorithm 1 lines 3–5). Certain sequence list SA, which is used to obtain the rank for each solution, is determined from the objective set A. The relative objective sequence list MA is generated according to SA and A. The positional information which associates the solution to A is stored to the location set PS (Algorithm 1 line 8).

The method to find the dominant set (Algorithm 1 line 12) is realized in Algorithm 2. The algorithm starts to find the position pos_m of s from PS. Then, based on pos_m, a judgement is made on whether to continue searching the preferential sets in other objectives. This is because if pos_m equals 1, there will be no other solution better than s in objective m and the dominant set of s will be empty; it is unnecessary to search other objectives once the dominant set is empty. Otherwise, other preferential sets will be intersected to obtain the common solutions composed by the dominant set (Algorithm 2 line 8–12). The dominant set that dominates s will be back to Algorithm 1 at line 12 and assigned to ${\Omega }_1(s)$. If ${\Omega }_1(s)$ is empty, it means there are no solutions better than s and that the rank of s is 1 (Algorithm 1 line 14). If ${\Omega }_1(s)$ is not empty, any solution in ${\Omega }_1(s)$ dominates s and the solution with the highest front rank—supposing solution p has the highest rank r—determines the rank of s. If there are no identical solutions in population P, the rank of s is r + 1. We will make a dominate comparison in Algorithm 3 for avoiding the identical solutions assigned to different ranks.

Algorithm2: Obtain Dominant Set

Input solution s, objective index m, objective set A, position information PS

Output dominant setΩ(s)

1 Begin

2 Ω(s) ← empty;

3 pos_m ← PS(s, m);        % position s first appears

4 if pos_m equals 1

5  Ω(s) ← empty;

6 else

7  Ω(s) ← A(m, 1:pos_m − 1);     % the smallest preferential set

8  for j = 1 to M and j is not equal to m

9   pos_j(s) ← PS(s, j);      % get position in objective j

10   AP(s, j) ← A(j, 1: pos_j − 1);      % get preferential set

11   Ω(s) ←intersect(Ω(s), AP(s, j)); % update dominant set

12  end

13 end

14 return Ω(s)

15 end

The comparing process is realized in Algorithm 3 lines 3–8. This algorithm is used to check whether solution p dominates s or they are equal. If any objective value of p is better than s, the returned value is 1 which means p dominates s and the final rank of s is r + 1; otherwise, if the returned value is 0 it means that s is identical to p and the rank of s is r (Algorithm 1 line 18).

Algorithm 3: Dominate Comparision

Input solution p, s

Output value equals 1 if p dominates s, equals 0 if p is identical to s

1 Begin

2 value ← 0;

3 for j=1 to M

4   if A(j, p) < A(j, s)

5    value←1 % p dominates s

6    break;

7   end

8 end

9 return value

10  end

4.2. Example Illustration of the Proposed Algorithm

The number of dominating comparisons is one of the important evaluation indicators to assess the efficiency of non-dominated sorting algorithms. Most current algorithms improve performance by reducing unnecessary comparisons [7]. A population with a bi-objective example is given in Figure 5. Several well-known non-dominated sorting algorithms, FNDS, DS, AP, ENS-SS, BOS and CS, were used to get the number of comparisons—the corresponding results are presented in

Table 1. Number of comparisons for algorithms.

Algorithm	Com.
FNDS	39
DS	27
AP	30
ENS-SS	23
BOS	18
CS	27

.

The implementation process of the given example in Figure 5—adopting the proposed algorithm SETNDS—is shown in

Table 2. The implementation process for the example shown in Figure 4.

Index	$\mathbf{Dominant}\mathbf{Region}{\mathit{\Omega }}_1$	Comparison	Rank
p6		-	F1
p8		-	F1
p1			F2
p7			F2
p2			F2
p10			F2
p4			F3
p5			F3
p3			F4
p9			F4

. From the algorithm description, we know that we should find the dominant region for the solution ranked as shown in the second column. The rank is determined by comparing the one with the highest rank in the dominant region. There is only the need to compare eight times, which is much smaller than the existing non-dominated algorithms.

4.3. Algorithm Complexity Analysis

The algorithm complexity of SETNDSs are analyzed in this section. N and M represent the size and number of objectives as defined above. As is analyzed in [6], the time complexity of sorting with lexicographic order is O(MNlogN). The worst time complexity is O(MN²) since each solution needs to find M preferential sets to combine into a dominant region. From the previous description, each solution only needs to compare with at most one solution from its dominant region to determine the rank of it, so at most N−1 times of comparing will be employed, and the relevant time complexity is O(M(N−1)). In total, the best time complexity will be O(MNlogN) and the worst will be O(MN²). From the perspective of storage space, it will need two M * N storage spaces for the sorted objective set A and location information set PS, respectively, so the space complexity is O(MN).

Table 3. Time and space complexity of non-dominated sorting algorithms.

Algorithm	Time Complexity		Space Complexity
	Best Case	Worst Case
BNDS [20]	O(MN3)	O(MN3)	O(N)
FNDS [2]	O(MN2)	O(MN2)	O(N2)
AP [9]	O(MN$\sqrt{N}$)	O(MN2)	O(N)
DS [12]	O(MN$\sqrt{N}$)	O(MN2)	O(N)
ENS-SS [7]	O(MN$\sqrt{N}$)	O(MN2)	O(N)
BOS [6]	O(MNlogN)	O(MNlogN+MN2)	O(MN)
CS [11]	O(MN$\sqrt{N}$)	O(MN2)	O(N)
SETNDS	O(MNlogN)	O(MN2)	O(MN)

gives the time and space complexity of the SETNDS algorithm we proposed together with other seven general non-dominated sorting algorithms. The time complexity in the worst case remains stuck at O(MN²), though the efficiency of the improved sorting algorithms is improved. Only BOS reduces the best-case time complexity to O(MNlogN), while other improved algorithms are reduced to O(MN$\surd N$). The SETNDS algorithm reduces the best-case time complexity to O(MNlogN) and worst-case time complexity to O(MN²).

A series of experiments will be discussed in the next section to demonstrate the efficiency of the proposed algorithm.

5. Experimental Simulation and Result

A series of experiments on SETNDS algorithms and the other six algorithms mentioned above are discussed in this section. The domination comparing times and running time are used as the performance indicators without loss of generality [6,7,11,19]. All the mentioned algorithms are conducted by using MATLAB on a PC with Inter(R) Core i7-8550U CPU, 1.80GHz, 8GB RAM. The population with a randomly generated dataset and predefined fronts are used for the following simulation (described in [11]).

5.1. Experiments on Populations with Random Data

To show the impact of population size N on the performance indicators, we set N to change from 500 to 10,000 with increments of 500, and the number of objectives was specified as 2, 5 and 10. Figure 6 gives the simulation results. On the whole, the comparing times and running time of all algorithms increased with the population size at different rates. Whichever way one views this figure, it is clear that the algorithm we proposed is far superior to other algorithms with shorter comparing times and a shorter running time. The conclusions that ENS-SS outperforms other algorithms for bi-objective optimization problems and BOS performs best for multi-objective problems if our algorithm is not taken into consideration can also be drawn from the figure.

With an increase in objective numbers, the process of change of the comparing times and running time for size N equals 100, 500 and 1000 (shown in Figure 7), respectively. FNDS performs worst compared with other algorithms. ENS-SS performs little better than AP and they are both better than DS, and BOS is the second-best algorithm among the rest of the algorithms. SETNDS behaves best, as its comparing times change very little for the same population size N and the growth rate of the running time with an increasing number of objectives is much smaller than other algorithms.

To further verify the efficiency of the proposed algorithm, size N varies from 50 to 10,000 with an increment of 50. The simulation experimental results of the proposed algorithm, SETNDS with 2, 5 and 10 objectives, are given in Figure 8. This figure not only records the change of the comparing times and running time, but also the number of fronts each population processed on. As we can see from this figure, the comparing times increase linearly with the change of size N, and the maximum upper limit is N; the running time increases logarithmically with the change of population size N.

5.2. Experiments on Population with Fixed Fronts

To verify the changing process of computational efficiency of the sorting algorithms with increasing fronts, this paper adopts a fixed front generation algorithm which is proposed in paper [11]. The number of fronts changes from 1 to 50 with an increment value of 1, and the population size N was chosen to be 1000, which is neither too small nor too large. The number of objectives M still choose 2, 5, 10 and 15. The experimental results in Figure 9 reveal that FNDS takes the highest number of comparisons and running time, while SETNDS takes the lowest ones. DS performs better than CS as it spends less time than corner sort. ENS and AP exhibit a similar performance as their comparing times and running time are about the same under multi-objective circumstances. ENS is the second-best for the bi-objective optimization problems, while BOS is second for the multi-objectives. This result is consistent with the previous experiments mentioned above.

5.3. Experiments on NSGA II with Test on Problems DTLZ1 and DTLZ2

In order to investigate the performance of the proposed sorting algorithm utilized in MOEAs, the test problems DTLZ1 and DTLZ2 are used as benchmarks [30]. The adopted evolutionary algorithm is NSGA II as described in [2], and the parameters are: the population size is N = 200, the iterations are 200, the selection operator is binary tournament, and the simulation binary crossover (SBX) (with distribution index mu = 20) and polynomial mutation operator (with nonnegative real number, num = 20) are used in NSGA II, as in paper [2]. The dimension of variables is set as 20. The crossover rate and mutation rate are 0.8 and 1/n, respectively. The number of objectives M to be tested are 2, 5, 10 and 15. The number of comparisons and running time are also considered to be the performance indicators. Each algorithm runs independently ten times to get the average value of the performance indicators.

Table 4. Number of comparisons and running time (in seconds) for DTLZ1 and DTLZ2.

Algorithm		DTZL1
		2	5	10	15
FNDS	Com.	1.25 × 107	1.44 × 107	1.5 × 107	1.49 × 107
	Time	139.23	173.11	176.71	189.61
AP	Com.	7.07 × 106	7.78 × 106	8.07 × 106	7.89 × 106
	Time	44.07	49.96	50.90	53.16
CS	Com.	1.17 × 107	1.29 × 107	1.32 × 107	1.30 × 107
	Time	74.64	85.83	89.00	97.16
DS	Com.	1.20 × 107	1.41 × 107	1.47 × 107	1.46 × 107
	Time	52.10	65.70	68.95	72.80
ENS-SS	Com.	9.82 × 106	1.28 × 107	1.39 × 107	1.37 × 107
	Time	58.63	80.52	83.49	89.87
BOS	Com.	6.39 × 106	5.06 × 106	3.74 × 106	2.97 × 106
	Time	34.64	34.11	31.91	33.80
SETNDS	Com.	2.37 × 104	1.53 × 104	1.28 × 104	1.32 × 104
	Time	9.16	11.07	14.28	16.54
Algorithm		DTZL2
		2	5	10	15
FNDS	Com.	1.46 × 107	1.49 × 107	1.55 × 107	1.57 × 107
	Time	167.92	191.26	187.76	197.01
AP	Com.	9.08 × 106	9.22 × 106	1.06 × 107	1.15 × 107
	Time	53.16	59.66	67.05	80.92
CS	Com.	1.32 × 107	1.31 × 107	1.39 × 107	1.41 × 107
	Time	87.15	95.19	94.72	101.09
DS	Com.	1.45 × 107	1.49 × 107	1.52 × 107	1.56 × 107
	Time	64.24	69.10	77.03	84.11
ENS-SS	Com.	1.32 × 107	1.39 × 107	1.50 × 107	1.53 × 107
	Time	79.85	87.74	98.69	103.47
BOS	Com.	7.25 × 106	5.37 × 106	4.13 × 106	3.32 × 106
	Time	41.93	42.17	36.42	39.94
SETNDS	Com.	1.50 × 104	1.22 × 104	0.99 × 104	0.91 × 104
	Time	9.40	11.76	14.59	16.92

gives the mean values of comparing times and running time of the NSGA II algorithm with FNDS, AP, CS, DS, ENS-SS, BOS and SETNDS on DTLZ1 and DTLZ2, respectively. SETNDS works better than the others with a minimum number of comparisons as shown in Table 4. At the same time, we can also get the information that the running time of the NSGA II algorithm with SETNDS is the smallest, and algorithm with FNDS performs the worst. The sorting algorithm we improved can hugely shorten the running time in the same cases.

6. Conclusions

A novel efficient non-dominated sorting algorithm—SETNDS for MOEA—is proposed in this paper. Unlike other non-dominated sorting algorithms, this paper adopts the positional information of solutions and combines them with set theory to find the dominant set that dominates the solution that needs to be sorted first. In SETNDS, the rank of solutions can be determined by, at most, one comparison, therefore the number of comparisons of the algorithm is far less than the existing algorithms. The experimental results indicate that SETNDS is superior to its competitors—namely the fast non-dominated sort, the arena’s principle sort, the deductive sort, the corner sort, the efficient non-dominated sort and the best order sort, especially with vast populations. The shortcoming of the proposed algorithm is that it will take more time on pre-ordering with the growth of the objectives. There are two directions of our future work: one is to parallelize the algorithm in order to increase its speed. The other one is to combine the proposed algorithm and MOEAs (e.g., NSGA II) to solve practical problems.