An Experimental Approach on Beating in Vibration Due to Rotational Unbalance

Abstract

This paper proposes a study in theoretical and experimental terms focused on the vibration beating phenomenon produced in particular circumstances: the addition of vibrations generated by two rotating unbalanced shafts placed inside a lathe headstock, with a flat friction belt transmission between the shafts. The study was done on a simple computer-assisted experimental setup for absolute vibration velocity signal acquisition, signal processing and simulation. The input signal is generated by a horizontal geophone as the sensor, placed on a headstock. By numerical integration (using an original antiderivative calculus and signal correction method) a vibration velocity signal was converted into a vibration displacement signal. In this way, an absolute velocity vibration sensor was transformed into an absolute displacement vibration sensor. An important accomplishment in the evolution of the resultant vibration frequency (or combination frequency as well) of the beating vibration displacement signal was revealed by numerical simulation, which was fully confirmed by experiments. In opposition to some previously reported research results, it was discovered that the combination frequency is slightly variable (tens of millihertz variation over the full frequency range) and it has a periodic pattern. This pattern has negative or positive peaks (depending on the relationship of amplitudes and frequencies of vibrations involved in the beating) placed systematically in the nodes of the beating phenomena. Some other achievements on issues involved in the beating phenomenon description were also accomplished. A study on a simulated signal proves the high theoretical accuracy of the method used for combination frequency measurement, with less than 3 microhertz full frequency range error. Furthermore, a study on the experimental determination of the dynamic amplification factor of the combination vibration (5.824) due to the resonant behaviour of the headstock and lathe on its foundation was performed, based on computer-aided analysis (curve fitting) of the free damped response. These achievements ensure a better approach on vibration beating phenomenon and dynamic balancing conditions and requirements.

1. Introduction

Rotating unbalance is a topic frequently mentioned in the analysis of the dynamics of rotary bodies (rotordynamics [1]). The rotating unbalance occurs due to an asymmetry of mass distribution (in some different regions of the rotary body, the center of mass is not placed on the axis of rotation). Centrifugal forces occur in these unbalanced regions of the rotary body. The resultant of these centrifugal forces is transmitted through the bearings to the structure where the rotary body is placed. In each bearing the resultant of centrifugal forces has two components at orthogonal directions. Each component acts as a harmonic excitation force against the structure, thus generating vibrations.

For some specific appliances these vibrations are desirable (e. g. in vibration shakers used also as mechanical vibration exciters [2,3], vibration alert systems in mobile phones, electronic vibrating bracelets [4], and haptic feedback devices with vibrations [5]). Generally, the vibrations due to the rotating body unbalances have highly undesirable effects (e.g., bad surface quality in the grinding process [6,7], premature bearing destruction [8,9]), and human body discomfort [10]). In order to measure [11] and to eliminate the unbalance of rotary bodies [12,13,14] (using additional balancing masses and additional inertia [15]), several special requirements must be met and specialized equipment must be used [16,17]. Actually, one of the best ways to balance rotary unbalanced bodies is through the use of self-balancing systems [18,19].

Sometimes two rotary unbalanced bodies having almost the same angular speed (or rotational frequency) which rotate in the same structure (e.g., in centerless grinding machines, [20]) produce a vibration beating phenomenon [10,21,22].

Each rotary unbalanced body generates a vibration. The addition of two vibrations, having slightly different frequencies, produces the aforementioned beating phenomenon. This is a resultant vibration with periodical variation of amplitude, with nodes (where the amplitude has a minimum value, the addition of the two vibrations produces destructive interference, 180 degrees out of phase between the constituents of the resultant vibration) and anti-nodes (a maximum amplitude, where the addition of the two vibrations produces constructive interference, with zero degrees shift of phase between constituents) [23]. Obviously the beating phenomenon in mechanics is not solely related to the vibrations produced by rotary unbalanced bodies, it also occurs when two vibration modes with almost the same modal frequency are excited [24,25], and it occurs as well when a system vibrates simultaneously due to forced sinusoidal excitation close to a resonant frequency and due to a free response [26,27,28,29].

Some specific appliances use the vibration beating phenomenon to monitor the condition of mechanical systems, e.g., monitoring the adhesion integrity of single lap joints [30], monitoring the structural integrity of helicopter rotor blades [31], and for seismic vibration testing [32]. A vibration beating mechanism in piezoelectric energy harvesting systems is proposed in [33].

In machine tools, in addition to a critical source of vibrations (self-excited vibrations in turning [34], milling [35] or grinding [36] processes), the vibrations produced by rotary unbalance (generated by tools [37], shafts [38] or work pieces [36]) and particularly the beating phenomenon [6] created by rotary unbalanced bodies, are important items. This paper proposes some approaches, in theoretical and experimental terms, to address the vibration beating phenomenon produced inside a Romanian lathe headstock SNA 360, by two inner unbalanced rotary shafts, rotating with very close angular speeds. The main achievements of this paper are producing results in the areas of: vibration beating monitoring, conversion of a velocity vibration signal into a displacement signal (by antiderivative calculus), and the evolution of beating vibration signal frequency (pattern, simulation, measurement and accuracy measurement), as well as producing a study of the influence of headstock and lathe foundation dynamics on vibration amplitudes.

2. A Theoretical Approach

Assume that the rotary unbalance of each shaft (each of which rotates at angular speeds of ω₁ and ω₂, respectively) is reducible at the asymmetry of mass distribution with unbalance masses m₁ and m₂, respectively, placed in a single plane at distances r₁ and r₂, respectively, to the rotation axis. The horizontal projection of the centrifugal forces of each rotary unbalance ($F_1 = m_1{\omega }_1^2{r}_1$ and $F_2 = m_2{\omega }_2^2{r}_2$) generates vibration displacements y₁ = kD_af1F₁cos(θ₁) and y₂ = kD_af2F₂cos(θ₂), where k is the stiffness of the headstock and the lathe foundation, D_af1 and D_af2 are the dynamic amplification factors and θ₁ = ω₁t+φ₁ and θ₂ = ω₂t+φ₂ are the instantaneous values of the angle of the centrifugal forces with respect to the horizontal direction (φ₁ and φ₂ being the instantaneous values of these angles at t = 0). With these considerations, a complete description of y₁ and y₂ of the vibrations is given below:

$$y_1 = k{D}_{af1}{m}_1{\omega }_1^2{r}_{1}cos\left({\omega }_{1}t+{\phi }_1\right) = A_{1}cos\left({\omega }_{1}t+{\phi }_1\right)$$

(1)

$$y_2 = k{D}_{af2}{m}_2{\omega }_2^2{r}_{2}cos\left({\omega }_{2}t+{\phi }_2\right) = A_{2}cos\left({\omega }_{2}t+{\phi }_2\right)$$

(2)

Here $A_1 = k{D}_{af1}{m}_1{\omega }_1^2{r}_1$ and $A_2 = k{D}_{af2}{m}_2{\omega }_2^2{r}_2$ are the vibration amplitudes of the two shafts, respectively. The headstock and the lathe vibrate as a single body on its foundation (as a mass–spring–damper system) with a vibratory motion which is the result of the addition y₁ + y₂ of these two vibrations, a periodical non-harmonic motion that presents itself as a beating phenomenon [23], with nodes and anti-nodes (as the simulation from Figure 1 proves). According to Figure 1, if the period of vibration y₁ is T₁ = 2π/ω₁ and T₂ = 2π/ω₂ is the period of vibration y₂, then the period T_b of the beating phenomenon (the beat period being the time between two anti-nodes or between two nodes, as well) and the periods T₁, T₂ (with T₂ < T₁) should fulfill this obvious condition:

$$T_b = n{T}_1 = \left(n+1\right)T_2$$

(3)

with n being a natural number, defined from Equation (3) as:

$$n = T_2/\left(T_1-T_2\right)$$

(4)

In Figure 1 n = 7. If in Equations (3) and (4) the periods are replaced by frequencies (T_b = 1/f_b, T₁ = 1/f₁, T₂ = 1/f₂), then the resulting frequency f_b of the beating phenomenon (beat frequency or the number of nodes per second, as well) is:

$$f_b = f_2-f_1$$

(5)

In Figure 1 f₂ = 8 Hz and f₁ = 7 Hz; these generate f_b = 1 Hz with T_b = 1s (A₁ = 10, A₂ = 8, φ₁ = 0, φ₂ = -π/2).

According to [39], the resultant waveform of the vibration addition y₁ + y₂ has the frequency f_c = 1/T_c (as a combination frequency or modulation frequency, with the period T_c highlighted on Figure 1) defined as:

$$f_c = \left(f_1+f_2\right)/2$$

(6)

This paper will prove by simulations and experiments that this definition is not accurate, especially when A₁ ≠ A₂.

These theoretical considerations and some other supplementary issues and procedures will be confirmed by experimental approach in this paper.

3. Experimental Setup

Figure 2a presents a lateral view of both shafts (1 and 2, placed in the headstock) involved in the beating phenomenon due to rotary unbalance.

A friction belt transmission with a flat drive belt 3, a pulley 4 (on shaft 1) and a pulley 5 (on shaft 2) synchronously rotates both shafts (the theoretical value of transmission speed ratio is 1:1). Here 6 depicts an additional mass (10.8 g, a permanent magnet) placed in different angular positions on pulley 5 and used to change the internal unbalancing of the shaft 2.

The shaft 1 is also the lathe main spindle (with the jaw chuck labelled with 7 on Figure 2b placed on the opposite side of Figure 2a). Figure 2b shows an absolute velocity vibration sensor 8 (an electrodynamic seismic geophone Geo Space GS 11D, now HGS Products HG4 as described in [40]), placed on the headstock. The geophone corner frequency (8 Hz) is smaller than the minimum frequency of the headstock vibration (17 Hz). No significant resonant amplification at the corner frequency can be identified (the open circuit damping being 34% of critical damping). The geophone sensitivity is 31.89 V/m/s.

The signal delivered by the vibration sensor (a voltage proportional to the vibration velocity of the headstock) is numerically acquired by a personal computer via a computer-assisted numerical oscilloscope PicoScope 4424 from Pico Technology, Saint Neots, UK (USB powered, four channels, 12 bits resolution, 80 MS/s maximum sampling, 32 MS memory) [41]. Due to the high sensitivity of the geophone and oscilloscope features (e.g., a numerically controlled internal amplifier) the supplementary amplification of the signal delivered by vibration sensor is not necessary.

The computer-aided processing of this signal was done in Matlab. Firstly, the signal delivered by sensor must be mathematically divided by the sensitivity of the sensor in order to obtain the vibration velocity evolution. Secondly, the velocity of vibration must be numerically integrated (by antiderivative calculus) in order to obtain the vibration displacement evolution. The description and analysis of the evolution of some of the other vibration features (e.g., the combination frequency f_c, the beat vibration amplitude and the free vibrations of the lathe on foundation) were also performed.

In order to measure the average value of the instantaneous angular speed (IAS) ω₁ of the main spindle (shaft 1) rigorously, the technique described in our previous work [42] was used (with a two phase multi-pole AC generator placed in the jaw chuck, as an IAS sensor). The same technique (which refers only to signal processing, briefly described later on) was used for an accurate measurement of the combination frequency f_c.

4. Experimental Results and Discussion

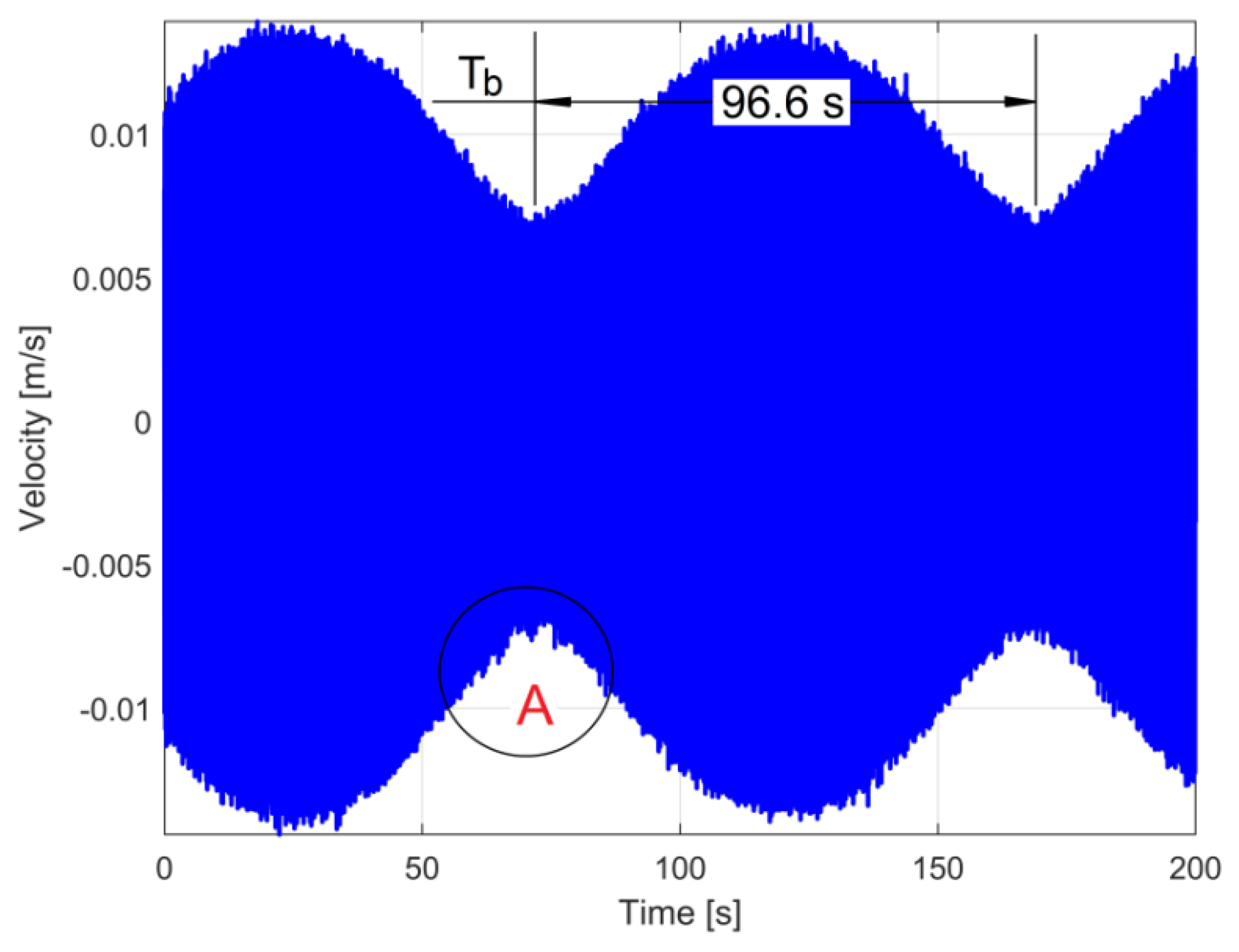
4.1. A Beating Phenomenon Described in Vibration Velocity

Figure 3 presents the evolution of the headstock vibration velocity during a time interval of 200 s, described with 1 MS (or 1,000,000 samples as well) so a sampling interval of Δt = 200 μs, when the main spindle (shaft 1) rotates (and shaft 2, as well) in the steady-state regime, with constant IAS, with an average value of ω₁ = 109.2369 rad/s (for f₁ = 17.3856 Hz average rotation frequency, or 1043.1 revolutions per minute on average).

It is obvious that Figure 3 depicts a vibration beating phenomenon with nodes and anti-nodes, with a very high value of the period T_b (96.6 s) and consequently with a very small value of beat frequency f_b = 1/T_b = 1/96.6 Hz. The beating phenomenon proves that the IASs ω₁ and ω₂ and also rotation frequencies f₁ and f₂ as well, are slightly different because the diameters of pulleys 4 and 5 involved in belt transmission are not strictly the same. With T₁ = 1/f₁ and the relationship between T₁ and T_b from Equation (3) there are n ≈ T_b·f₁ ≈ 1679 periods T₁ between nodes (and between anti-nodes as well). This is an approximated value of n because the frequency f₁ is not rigorously constant (as is proved, later in this paper). According to Equation (3), at each n complete rotations of shaft 1, the shaft 2 makes n + 1 or n − 1 rotations (one rotation difference), which means that the experimentally revealed value of the belt transmission speed ratio is ω₂/ω₁ = T₁/T₂ = n/(n ± 1) ≈ 1679/(1679 ± 1). This is also the ratio between pulleys diameters: the diameter of pulley 4 divided by the diameter of pulley 5 (assuming that there is no slipping between the belt and the pulleys).

The additional mass 6 (Figure 2a) was placed in a certain angular position on pulley 5, in order to obtain a maximum value of the amplitude A₂, and a maximum difference between amplitudes in anti-nodes and nodes as well. It is obvious that the main spindle (shaft 1) is also unbalanced; otherwise the beating phenomenon does not occur.

Figure 4 presents a zoomed-in detail in the area labelled A in Figure 3. Here the dominant component (≈6 mm/s amplitude) is the sum of two vibrations created by rotary unbalances; the other low amplitude (and high frequency) components are related by vibrations generated by some other headstock rotary components.

With the values for f₁ and f_b revealed before, the frequency f₂ is a result of Equation (5), with two possible values (f₂ = f₁ − f_b = 17.3752 Hz or f₂ = f₁ + f_b = 17.3959 Hz). Because in Equation (5) the notations f₁ and f₂ are arbitrary, this equation should be reconsidered as $f_b = \left|f_2-f_1\right|$.

As a consequence, the angular speed ω₂ = 2πf₂ has two possible values (ω₂ = 109.1716 rad/s or ω₂ = 109.3016 rad/s), as does the speed ratio (ω₂/ω₁) of the driving belt (with ω₁ = 109.2369 rad/s). To find the right value of f₂ (and ω₂ as well) the technique described in [42] should be used (with an IAS sensor placed on shaft 2).

The evolution from Figure 3 is an addition of vibrations velocities (v = dy₁/dt + dy₂/dt) generated by both of the unbalanced shafts (1 and 2). It is expected that the beating phenomenon keeps the main characteristics (e.g., T_b, T_c values or f_b, f_c values, as well) if it is described using the addition of vibration displacements (s = y₁ + y₂), except for the amplitudes in nodes and anti-nodes which significantly decreases.

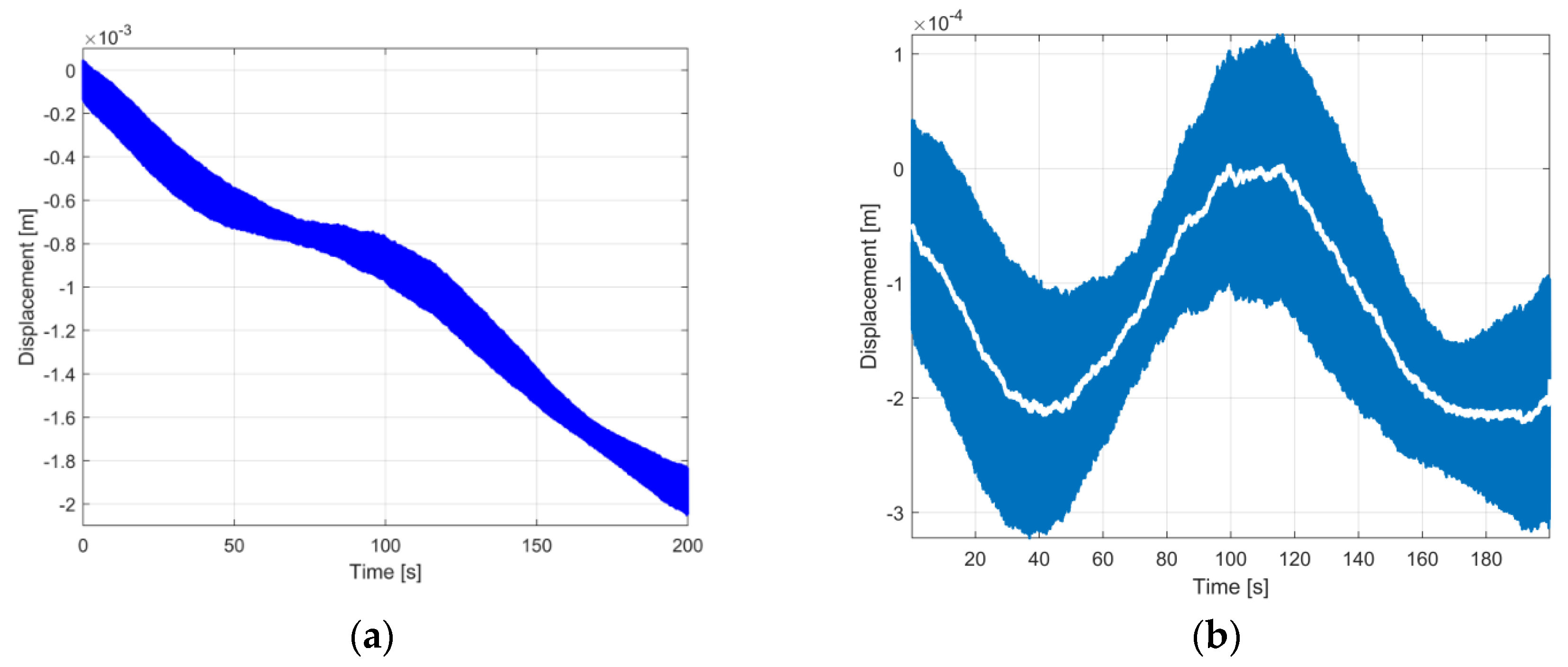
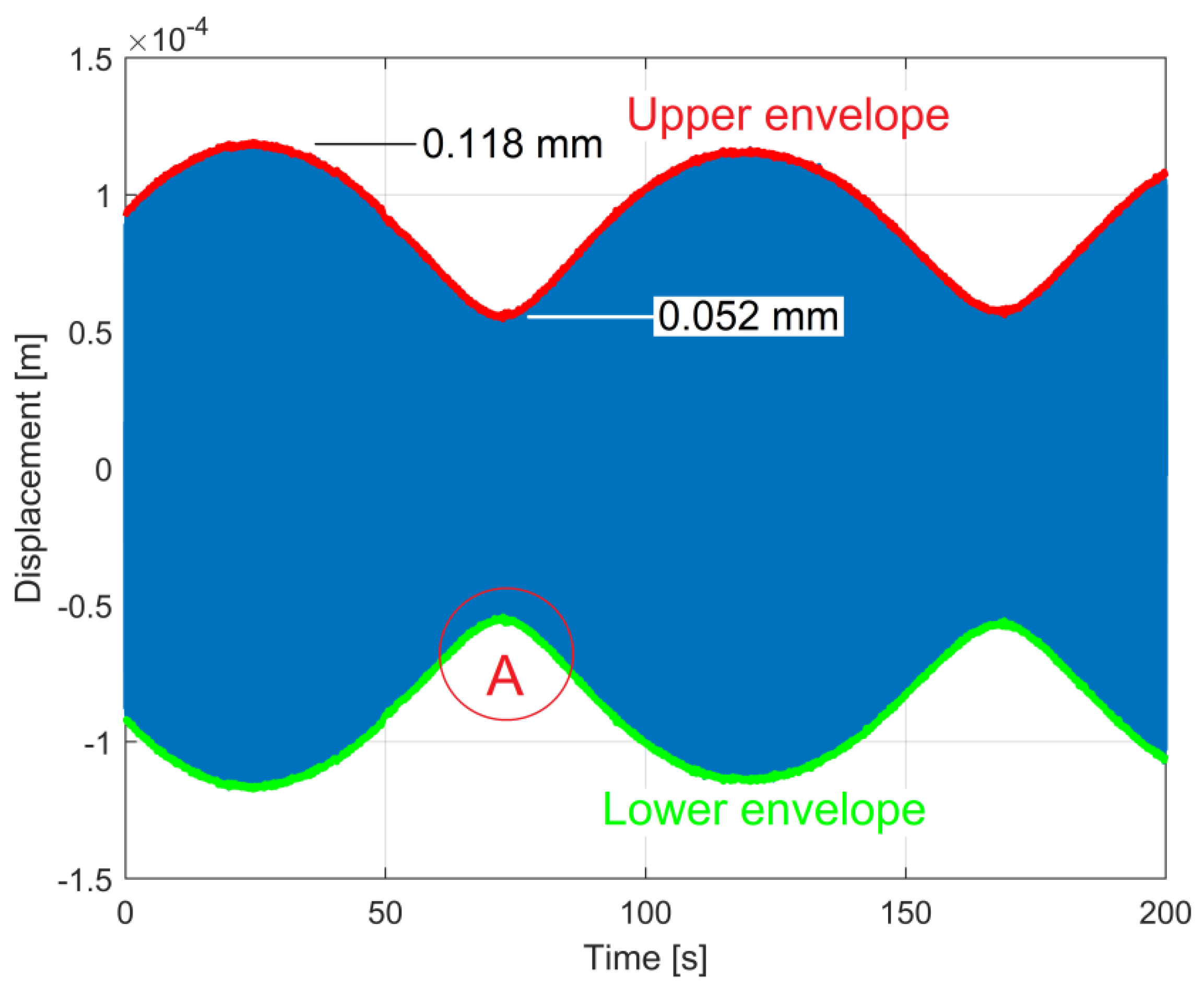
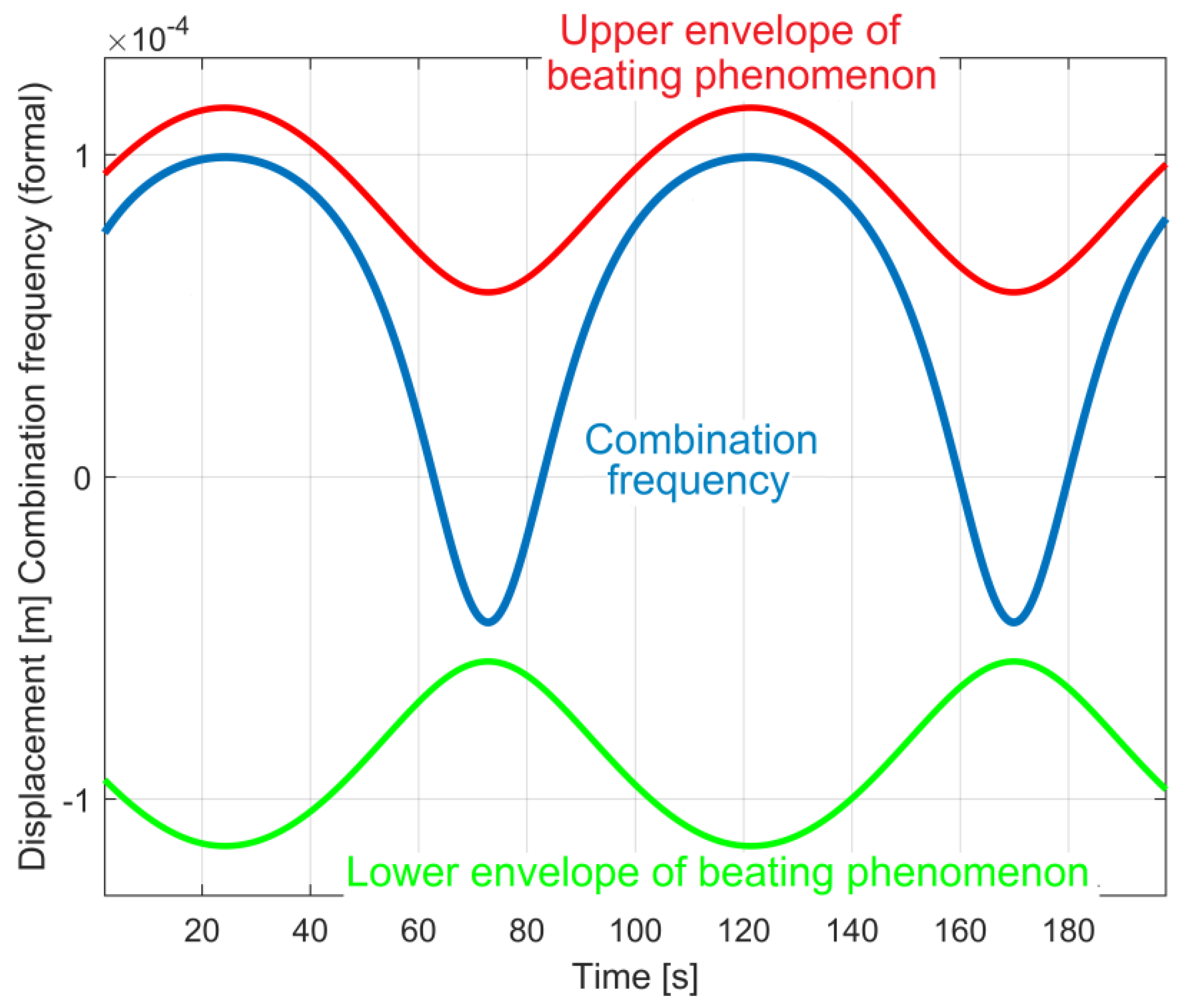
4.2. The Description of the Beating Phenomenon in Vibration Displacement by Numerical Integration

The vibration displacement evolution can be obtained from vibration velocity evolution by numerical integration (antiderivative calculus). Based on the approximate definition of velocity (derivative of displacement) v = ds/dt ≈ Δs/Δt, a current sample of velocity v_i is defined using two successive samples of displacement s_i, s_i−1 (in the displacement interval Δs = s_i − s_i−1) and the values of time t_i, t_i−1 for these samples, in the sampling interval Δt = t_i − t_i−1 (usually this is a constant value) as:

$$v_i = \frac{s_i-s_{i-1}}{\Delta t}$$

(7)

This is an approximation of the first derivative of displacement as backward finite difference, with i > 1 [43]. The current sample of displacement s_i can be simply mathematically extracted from Equation (7) as:

$$s_i = v_i\Delta t+s_{i-1}$$

(8)

Equation (8) describes a sample s_i of displacement related to velocity, this also being our proposal for a description of numerical integration of velocity (antiderivative calculus). According to Equation (8) the sample s_i depends on sampling interval Δt (here Δt is the time t_i − t_i−1 between two consecutive samples of velocity v_i and v_i−1 or two consecutive samples of displacement s_i and s_i−1 as well), the velocity sample v_i and the previous sample of displacement s_i−1, as the result of a previous step of numerical integration. The numerical integration from Equation (8) is available for i > 1. Of course, it is mandatory to know the value of the first sample of displacement s₁, this being an indefinite value because i > 1. This is exactly the constant C of integration (usually an arbitrary value). Pure harmonic signals are numerically integrated, in that case, evidently C = 0.

Figure 5a describes the graphical result of numerical integration of vibration elongation evolution from Figure 3 using Equation (8), with $C = s_1 = 0$. Certainly this evolution is not strictly related to the vibration displacement from the beating phenomenon.

We found that the oscilloscope generates a very small negative constant zero offset. As the theory of integration establishes, the numerical integration of this constant zero offset produces a component with linear evolution, experimentally confirmed in Figure 5a by the evolution with negative slope. The removal of this linear component produces the result from Figure 5b (the evolution emphasized in blue).

It is evident that Figure 5b is not the expected evolution of the vibration displacement in beating phenomenon. Surely, there is not a mistake in the numerical integration proposal in Equation (8) because the numerical derivative of the evolution from Figure 5b using Equation (7) produces exactly the evolution of velocity, as Figure 6 indicates (by comparison with Figure 3).

Our first attempt to explain this deficiency in this result of numerical integration is related by the constant of integration C.

Intuitively it is supposed that somehow the hypothesis that C = 0 is wrong. Perhaps the effect of this wrong hypothesis is mirrored in the evolution from Figure 5b and its effect should be removed (as the influence of negative zero offset was removed before).

It was discovered by numerical simulation that the numerical integration of a computer-generated beating vibration velocity signal (similarly to those depicted in Figure 3) using Equation (8), with C = 0, produces a vertically shifted evolution with a constant nonzero value, which should be mathematically removed.

This approach assumed that in the result of numerical integration of vibration velocity depicted in Figure 5b, a supplementary low frequency component was generated and should be removed. For the time being we unfortunately do not have a consistent explanation for the appearance of this low frequency component. This low frequency component (depicted in Figure 5b in white) was detected by low-pass numerical filtering of the vibration displacement signal (the evolution emphasised in blue).

A computer-generated moving average filter [43] was used, with the first notch frequency equal to the combination frequency f_c = (f₁ + f₂)/2 (assuming that this definition from Equation (6) is accurate), in order to completely remove the variable component from Figure 5b having the resultant vibration frequency, and in order to obtain the low frequency component. The number of points in the average of the filter is defined as integer of the ratio 1/(f_cΔt). The removal of this low frequency component from the result of numerical integration (the vibration displacement signal) depicted in Figure 5b is shown in Figure 7. It is obvious that this evolution properly describes the resultant vibration displacement during the beating phenomenon, previously described in Figure 3, by the velocity of the resultant vibration.

There is a supplementary confirmation of this result: the numerical differentiation of the vibration displacement signal from Figure 7 (using Equation (7)) fits very well with the vibration velocity signal from Figure 3, as a very short detail (15 ms duration) of both evolutions (given in Figure 8a) from the area labelled as A (Figure 3 and Figure 7) indicates. Thus, the absolute velocity vibration sensor together with the proposed numerical signal integration method acts as an absolute displacement vibration sensor.

Figure 8b presents a short detail of the vibration displacement evolution in the area labelled with A in Figure 7. This figure has the same size on the abscissa as Figure 4. By comparison with Figure 4, the evolution is much smoother here, as a consequence of numerical integration, which drastically reduces the amplitudes of high frequency components. The integration acts as a low-pass filter.

In Figure 7 two relationships between the vibrations amplitudes A₁ and A₂ are available (from Equations (1) and (2)) due to the constructive interference in anti-nodes (A₁ + A₂ = 118 μm) and destructive interference in nodes (A₁ − A₂ = 52 μm), so A₁ = 85 μm and A₂ = 33 μm. For the time being A₁ does not necessarily refer to vibration amplitude generated by the main spindle or shaft 1.

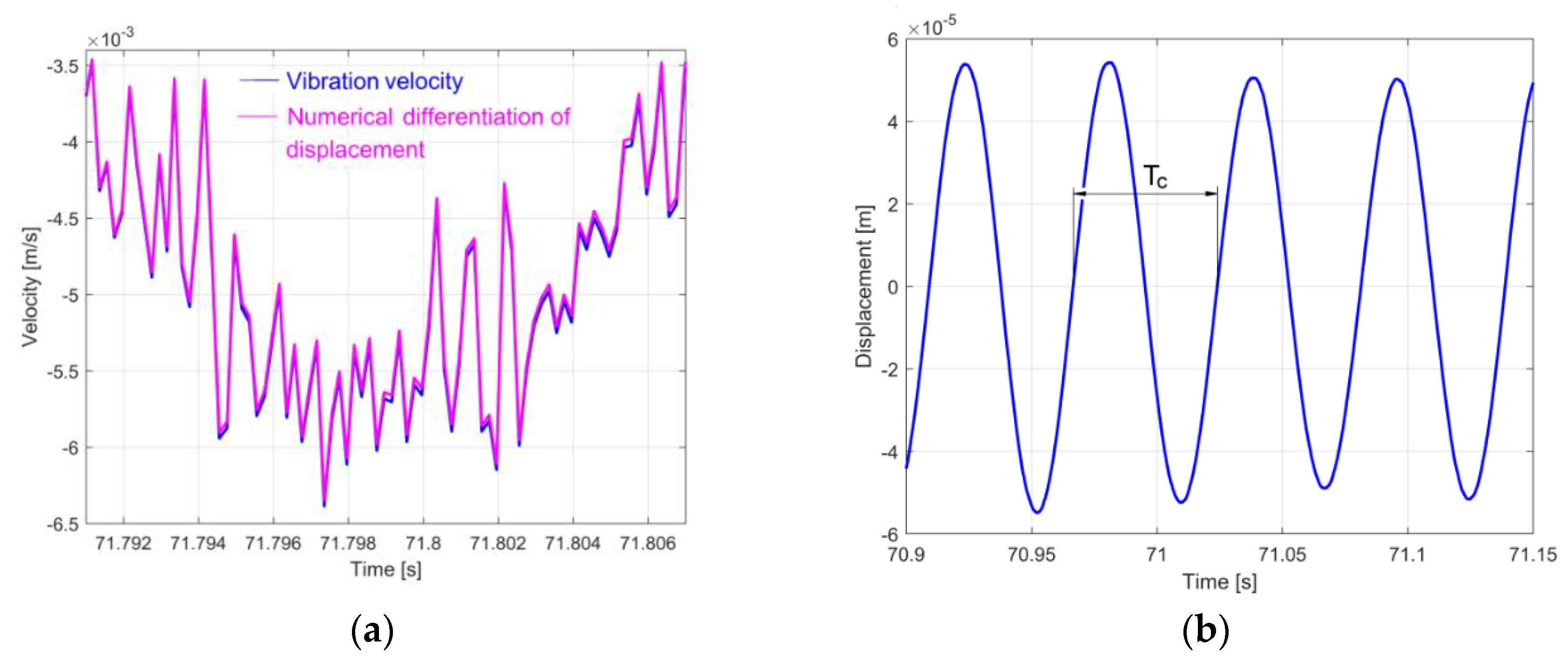
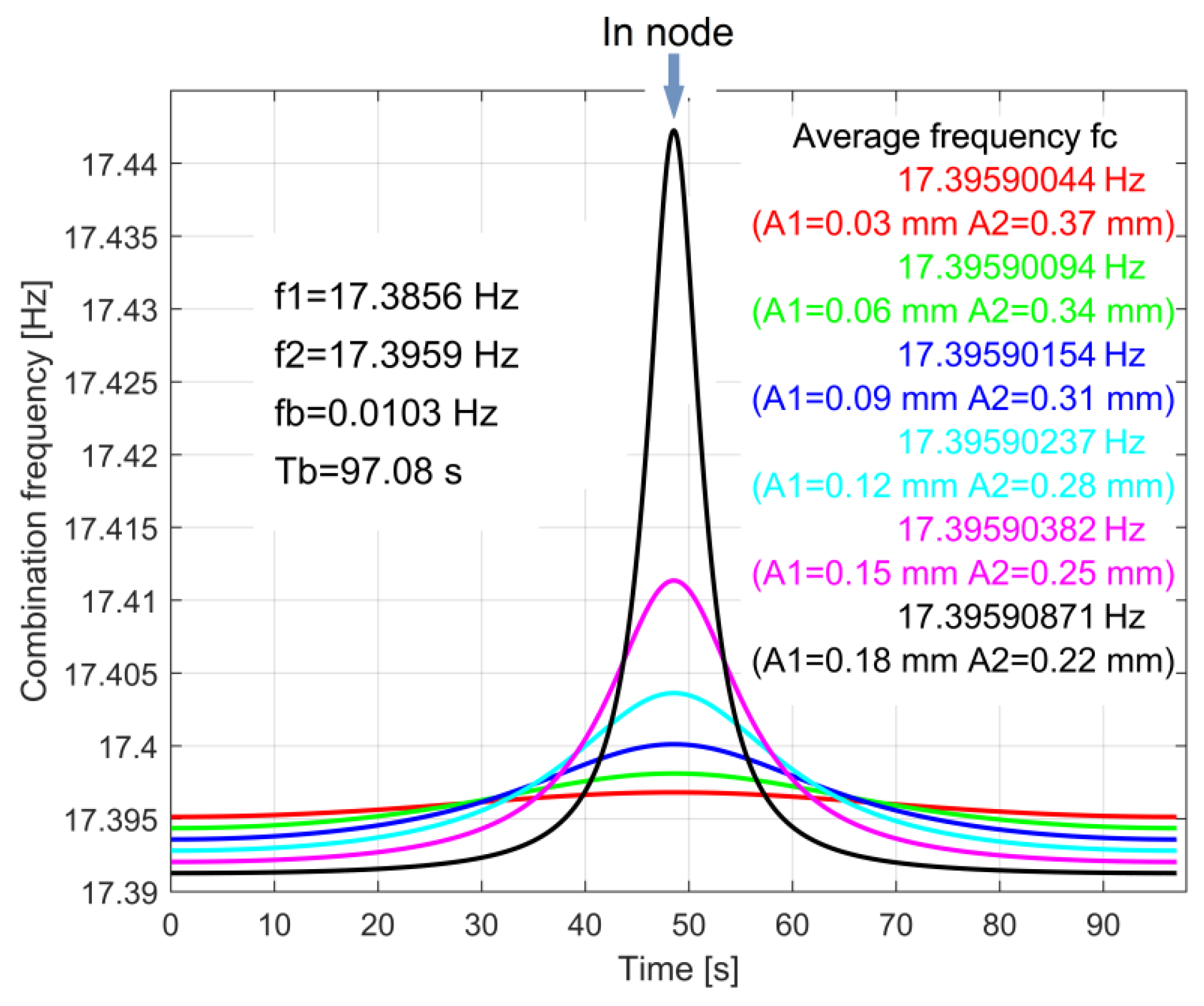
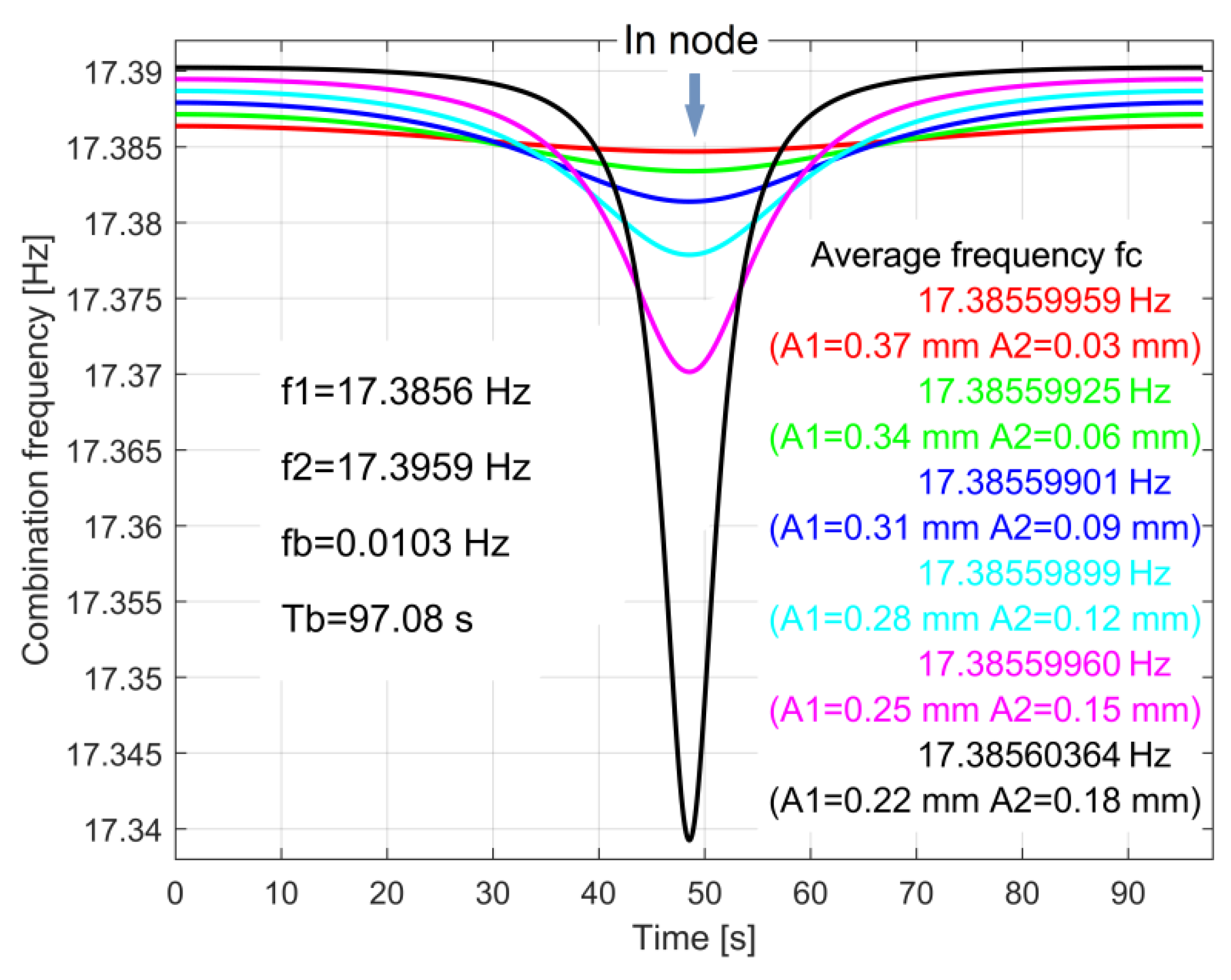
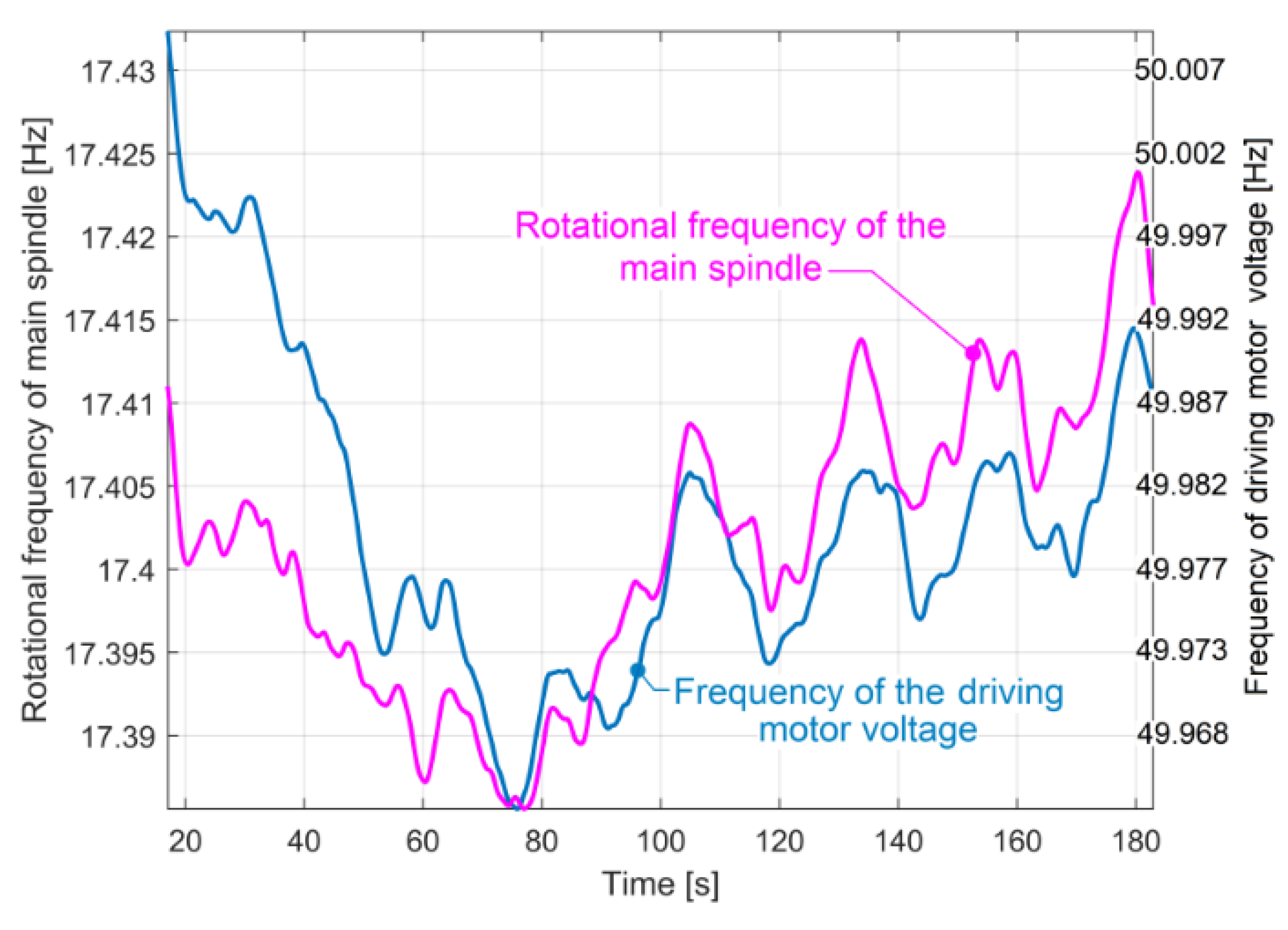
4.3. The Evolution of Frequency for Resultant Vibration in Beating Phenomenon

An interesting item in the beating phenomenon is the evolution of frequency of the resultant vibration f_c (also known as combination frequency or modulation frequency, f_c = 1/T_c, with T_c highlighted in Figure 8b). In [39] this frequency is defined as the average of both frequencies (f₁, f₂) involved in the beating (Equation (6)).

A beating phenomenon was simulated using the sum of two harmonic vibrations displacements y_1s(A₁,f₁) and y_2s(A₂,f₂)—already described in Equations (1) and (2) with different values of amplitudes (A₂ > A₁) and frequencies f₁ and f₂, close to those from the experiment described in Figure 3 and Figure 7 (with f₁ = 17.3856 Hz and f₂ = 17.3959 Hz), for a duration equal to T_b (placed between two anti-nodes).

For six different values of amplitudes (A₁ increases and A₂ decreases), the evolution of the combination frequency f_c and its average value was determined on the vibration beating simulated signal, as Figure 9 indicates, using a high accuracy measurement technique from a previous work [42]. Here each peak describes the value of frequency f_c in vibration beating node. It is obvious that f_c is not constant and, in contradiction with Equation (6) and [39], f_c ≠ (f₁ + f₂)/2. Here, with A₁ > A₂ the average f_c is very close to f₂, with f_c > f₂.

A similar simulation was done in the same conditions, now with A₁ > A₂, as Figure 10 indicates (here A₁ decreases and A₂ increases). Similar to the simulation given in Figure 9, it is obvious that f_c is not constant and again, in contradiction with Equation (6) and [39], f_c ≠ (f₁ + f₂)/2. The average frequency f_c is very close to f₁, with f_c < f₁.

There are two conclusions here, in contradiction with the literature [39]:

-

The combination frequency f_c is not constant over a period T_b (even if its variation is not significant);

-

The average value of the combination frequency f_c over a period T_b is practically the same as the frequency of the input vibration in the beating phenomenon (y_1s(A₁,f₁) or y_2s(A₂,f₂)), whose amplitudes are higher (e.g., if A₂ > A₁ then the average f_c ≈ f₂).

Some supplementary simulations for many other values of frequencies f₁ and f₂ (and consequently T_b) completely confirm these conclusions.

Figure 11 presents the evolution of the instantaneous combination frequency f_c during the vibration beating phenomenon (displacement of headstock) experimentally described in Figure 7.

Apparently, this is a very noisy evolution. The dominant component of the signal from Figure 7 is the displacement of resultant vibration y₁ + y₂. The frequency measurement method [42] is based on detection of zero-crossing moments of this signal (a topic discussed later on). It is obvious that many other additional vibrations of the lathe headstock (some of them with high frequency) disturb the accuracy of the zero-crossing detections, as a main reason for the noisy evolution from Figure 11.

The best information available in Figure 11 is the average value of the combination frequency f_c (${\overline{f}}_c =$17.3830 Hz, very close to the rotational frequency of the main spindle, f₁ = 17.3856 Hz). Based on the previous conclusions from Figure 9 and Figure 10 it is evident that the amplitude A₁ of unbalanced vibration generated by the main spindle (shaft 1) is higher than the amplitude A₂ of shaft 2 (so A₁ = 85 μm and A₂ = 33 μm, an item analysed before). As previously mentioned, the rotational frequency of shaft 2 is f₂ = f₁ − f_b = 17.3752 Hz or f₂ = f₁ + f_b = 17.3959 Hz.

Figure 12 presents a low-pass filtered evolution of the instantaneous combination frequency from Figure 11, (using a multiple moving average filter [43], as a well-known method to attenuate the signal noise).

Despite a relatively strong irregular variation of the combination frequency f_c (due to the variation of experimental conditions: e.g., the small variation of rotational speeds of shafts 1 and 2, caused mainly by the variation of frequency of the supplying voltages applied to the asynchronous driving motor, around a theoretical value of 50 Hz, as Figure 13 clearly indicates), the previous simulations and conclusions are fully experimentally confirmed. Three supplementary identical experiments confirm the evolution presented in Figure 12.

Firstly, in Figure 12 there are two negative peaks (for the two nodes in Figure 3 or Figure 7; each node produces a negative peak on f_c evolution, an item already discussed in the simulation from Figure 10) at a time interval very close to the beat period value T_b, already defined in Figure 3 (96.73 s here, compared with 96.6 s in Figure 3).

Secondly, as shown in Figure 14, a superposition of filtered frequency f_c evolution from Figure 12 (here in a conventional blue coloured description) over the experimental envelopes of vibration displacement in beating (the same as those depicted in Figure 7) indicates that the negative peaks of f_c are placed, as expected, in nodes.

The small displacement to the right of the negative peaks of the filtered combination frequency evolution (as against the nodes on Figure 14) is not related to the numerical filtering. This is proved by the result of the simulation of Figure 14, as given in Figure 15 (with addition of pure harmonic signals y_1s and y_2s in vibration beating simulation).

This periodic pattern of filtered combination frequency f_c evolution experimentally revealed in Figure 12 and Figure 14 (according to the simulations from Figure 10 and Figure 15) is strongly attenuated if the amplitude A₂ becomes significantly lower than A₁ (and vice versa).

An important question is in order here due to a very small variation of filtered frequencies revealed before (less than 50 mHz full scale evolution in Figure 9, Figure 10, Figure 12, Figure 13 and Figure 15): how accurate is this frequency measurement method [42]?

In this measurement method (e.g., the measurement of the combination frequency f_c of vibration displacement signal from Figure 7), the computer-aided detection of the time interval between each two consecutive zero-crossing moments (t_zcj and t_zcj+1) of a periodical signal is used. This time interval defines a semi-period T_c/2 = t_zcj+1 − t_zcj as T_c/2 = 1/2f_c, or a value f_c = 1/T_c. When the result of multiplication of two successive displacements samples s_i and s_i−1 (having the sampling times t_i and t_i−1, with i > 1) is negative or zero (s_i·s_i−1 < 0 or s_i·s_i−1 = 0) a zero-crossing moment is detected (e.g., t_zcj) and calculable as the abscissa of the intersection of a line segment defined by the points of coordinates (t_i, s_i) and (t_i−1,s_i−1) on the t-axis (as x-axis in Figure 8b). The main reason for frequency measurement error ε_f ≠ 0 is a consequence of calculation errors for two successive zero-crossing moments ε_j ≠ 0 (for t_zcj) and ε_j+1 ≠ 0 (for t_zcj+1). These ε_j and ε_j+1 errors are caused by the replacement of a harmonic evolution with a linear evolution between those two successive displacement samples involved in each zero-crossing moment definition. With t_i−1−t_i = Δt (Δt being the sampling interval) the error ε_j = 0 only in three situations: (1) if s_i = 0 (the end of the line segment is placed on the t-axis, with t_j = t_i), (2) if s_i−1 = 0 (the start of line segment is placed on t-axis, with t_j = t_i−1) and (3) if −s_i = s_i−1 (the middle of the line segment is placed on t-axis, with t_j = t_i−1 + Δt/2). A similar approach is available for the next two successive samples (s_i+h and s_i+h−1) involved in the definition of t_zcj+1 moment and ε_j+1 error (with h as the integer part of the ratio T_c/Δt). If simultaneously ε_j and ε_j+1 = 0 then ε_f = 0. Any other definition of sampling times generates frequency measurement errors ε_f ≠ 0.

A computer-aided calculus was performed for frequency measurement error ε_f of a harmonic simulated signal with frequency 17.383 Hz (the average value of the combination frequency f_c) during a semi-period. Here 10,000 different values of sampling time t₁ (between 0 and Δt, with Δt = 200 μs, the same sampling interval as in Figure 3 and Figure 7) and t_{2 =} Δt − t₁ (between Δt and 0) for the first two successive displacement samples involved in the calculus of the first zero-crossing moment t_zc1 was used. Figure 16 describes the evolution of the frequency measurement error ε_f(t₁).

As Figure 16 clearly indicates, the frequency measurement error ε_f of the combination frequency f_c is variable and placed between −0.000935 and +0.0014 mHz. The result of the measured frequency of the simulated signal is ${17.383}_{-0.935 \mathsf{\mu }\mathrm{Hz}}^{+1.4 \mathsf{\mu }\mathrm{Hz}}$ as a description of the accuracy measurement. Very similar limits for the ε_f error are calculated for a harmonic signal with frequency f₁. If the value of the frequency f_c = 1/T_c used in simulation accomplishes the condition T_c = hΔt (with h being an integer), then ε_f = 0 for any value t₁ = 0 ÷ Δt.

4.4. The Influence of the Lathe Suspension Dynamics on Beating Vibrations Amplitude

The relative high vibration displacement amplitude of the headstock during the beating phenomenon (as shown in Figure 7) has an evident explanation: the vibration frequencies f₁, f₂ and f_c as well, are close to the first resonant frequency (vibration mode) of the headstock and lathe on its foundation (as a single body mass–spring–damper vibratory system). This means that the dynamic amplification factors D_af1 and D_af2, (involved in Equations (1) and (2)) are significantly higher than 1 (because of resonant amplification). In order to prove that, the resources of a very simple experiment performed with the same experimental setup are available: the evolution of headstock vibration velocity after an impulse excitation produced with a rubber mallet (hammer) in the same direction with y₁ and y₂ vibrations (as Figure 17 describes).

Here the blue curve partially depicts the free damped vibration velocity v_fd (acquired with the geophone sensor); the red coloured one depicts the best fitting curve of a part of the free response (with 25,000 samples and 500 ns sampling time). The curve fitting [44] was done in Matlab, with an adequate computer program specially designed for this paper, based on a known theoretical model of free viscous damped vibration velocity response [45]:

$$v_{fd}\left(t\right) = a·e^{-bt}sin\left(p_{1}t+\alpha \right)$$

(9)

The best fitting curve (in red in Figure 17) is described with a = 1.170·10⁻³ m/s, b = 5.899 s⁻¹ (as damping constant), p₁ = 117.952 rad/s (as angular frequency of damped harmonic vibration) and α = 4.986 rad (as phase angle at the origin of time t₀ on Figure 17). The angular natural frequency ($p = \sqrt{p_1^2+n^2}$ = 118.099 rad/s) and the damping constant b are useful in the definition [45] of dimensionless dynamic amplification factor D_af from forced vibrations of harmonic excitation (as happens during the beating phenomenon, assuming that the combination frequency is approximately constant):

$$D_{af} = \frac{1}{\sqrt{{\left[1-{\left(\frac{\omega }{p}\right)}^2\right]}^2+{\left(2\frac{\omega }{p}·\frac{b}{p}\right)}^2}}$$

(10)

Here ω = 2πf is the angular frequency of harmonic excitation on frequency f. Based on previous experimental results of curve fitting (with b and p values in Equation (10)) Figure 18 presents the simulated evolution of D_af related to the frequency of excitation (1 ÷ 35 Hz range). Because of a low damping constant b, the system presents resonant amplification, with a maximum value D_af = 10.01 on f = 18.749 Hz frequency.

Based on the previous experimentally determined frequencies f₁ and f₂, with f = f₁ = 17.3856 Hz gives the result D_af1 = 5.831 and with f = f₂ = 17.3752 Hz (or f = f₂ = 17.3959 Hz) the result is D_af2 = 5.803 (or D_af2 = 5.859). For f = ${\overline{f}}_c$ = 17.383 Hz (Figure 12) the result is D_afc = 5.824 (the coordinates of point A on Figure 18). This means that, because of mechanical resonance, the vibration amplitude generated by the beating phenomenon of the headstock and the lathe on its foundation (already revealed in Figure 7) is amplified on average by 5.824 times.

Besides the amplification of the vibration, the resonant behaviour also introduces a significant shift of phase γ between the excitation (unbalancing) force and the vibration displacement, theoretically described [45] as depending on ω (and excitation frequency f as well) with the equation:

$$\gamma = arctan[\frac{2\frac{b}{p}\frac{\omega }{p}}{1-{\left(\frac{\omega }{p}\right)}^2}]$$

(11)

With the b and p values previously determined, the values of shift of phase calculated for each frequency are: γ₁ = 0.5691 rad for f = f₁ = 17.3856 Hz and γ₂ = 0.5656 rad (or γ₂ = 0.5725 rad) for f = f₂ = 17.3752 Hz (or f₂ = 17.3959 Hz). For f = ${\overline{f}}_c$ = 17.383 Hz the result is γ_c = 0.5682 rad.

The knowledge of both of these resonant characteristics (the value of the dynamic amplification factor D_af and especially the phase shift γ) is important for a next approach of the dynamic balancing of these two shafts placed inside the headstock.

As a general comment, we should mention that the resonance behaviour of this low damped vibratory system—as previously mentioned—is a consequence of the disponibility of this system to absorb modal mechanical energy. The system works as a narrow-band modal energy absorber [46].

5. Conclusions and Future Work

Some specific features of the beating vibration phenomenon discovered on a headstock lathe have been revealed in this paper.

An experimental description (with theoretical approaches based on simulations) of this beating vibration phenomenon with very low beat frequency (1/96.6 Hz) was performed. The beating phenomenon occurs due to the addition of vibrations produced by two unbalanced shafts, rotating with very close instantaneous angular speeds (rotating frequencies), with constructive interference in anti-nodes and destructive interference in nodes.

The absolute velocity signal of vibration beating (delivered by a vibration electro-dynamic sensor placed on the headstock) was converted into a displacement signal. For this purpose, a fully confirmed method of numerical integration (antiderivative calculus), with theoretical and experimental approaches was applied. This method is deduced from the approximation of the formula for the first derivative of displacement, as a backward finite difference [43]). An appropriate technique of correction of this numerical antiderivative calculus method was also introduced (mainly by removing the low frequency displacement signal component generated by numerical integration). Thus, an absolute velocity vibration sensor together with a numerical integration procedure plays the role of an absolute vibration displacement sensor.

A consistent part of the research was focused on the resultant vibration displacement signal, mainly on the evolution of frequency (or the combination frequency f_c) related to the nodes and anti-nodes position. It was theoretically discovered (by simulation) and was experimentally proved that, in opposition to the literature reports, the combination frequency is not constant, and the definition of its average value is wrong. The evolution of the combination frequency has a specific periodic pattern (having the same frequency as the beat frequency) with small variation (tens of millihertz) and negative or positive peaks placed in beating nodes. The appearance of these peaks (negative or positive) depends on the relationship between amplitudes and frequencies of vibrations involved in the beating phenomenon. The small variation of frequency inside the pattern and the correlation between the frequencies of different experimental signals (the combination frequency f_c, the rotation frequency f₁ of the main spindle, and the supply voltage frequency of the driving motor) have been correctly described as a result of a high accuracy procedure of frequency measurement, developed in a previous work [42] and successfully applied here. It was proved on a simulated signal (having a frequency of 17.383 Hz, equal to the average value of the combination frequency in vibration beating phenomenon) that this procedure has less than ±1.5 μHz measurement error.

The influence of the behaviour of the headstock and lathe foundation dynamics (as a rigid body placed on a spring–damper system) on the vibration induced by unbalanced rotors and the beating phenomenon was also investigated. Based on computer-aided analysis of free damped viscous response (by curve fitting), the characteristics of foundation dynamics were experimentally revealed (mainly the values of natural angular frequency and the damping constant). Considering these values, the dynamic amplification factors of vibrations (mainly of the resultant vibration) and phase shift between centrifugal forces (as excitation forces produced by unbalanced rotary shafts) and the vibrations generated by these forces were calculated.

For each experiment, numerical simulation and signal processing procedures, several computer programs written in Matlab were successfully used.

In the future, the theoretical and experimental approaches will be focused on the influence of dynamic unbalancing and vibration beating on the active and instantaneous electrical power absorbed by the driving motor of the headstock. There is a logical reasoning for these approaches: the headstock vibration motion (especially during the resonant amplification behaviour revealed in Figure 18) should be mechanically powered. Of course, the instantaneous and active mechanical power (difficult to measure) is delivered by the driving motor as an equivalent of instantaneous and active electric power absorbed from the electrical supply network (easier to measure).

Several theoretical and experimental studies on computer-aided balancing of each rotary shaft inside the lathe headstock will be performed (using two absolute velocity sensors and an appropriate method of computer-assisted experimental balancing). A study on the vibration beating phenomenon produced by more than two unbalanced rotary bodies will be done.