Fragility Curves for RC Structure under Blast Load Considering the Influence of Seismic Demand

Featured Application

The fragility curves can be useful for the early design of strategic RC buildings under blast load.

Abstract

The complex characteristics of explosion load as well as its increasingly high frequency in the civil environment highlight the need to develop models representing the behavior of structures under blast load. This work presents a probabilistic study of the performance of framed reinforced concrete buildings designed according to the current Italian NTC18 and European EC8 technical standards. First, a simplified single degree of freedom model representing the structural system under blast load has been developed. Then, a probabilistic approach based on Monte Carlo simulation analysis highlighted the influence of seismic demand on the behavior of Reinforced Concrete RC buildings subjected to blast load.

1. Introduction

In the last years, structural safety under blast load has become a dramatic problem. Extreme events, such as impacts, explosions, etc., can occur in everyday life with unexpectedly high frequency [1,2]. In fact, the problem of terrorist attacks, important for strategic and military building design [2,3], can be put side by side with civil building explosion accidents [4,5].

Recently, many studies were aimed at assessing the performance of new and advanced materials under blast load: glass [6], fiber reinforced polymer [7,8], layered composite materials [9], and foam [10]. On the other hand, the structural design itself is evolving to a more general framework in which structural elements are designed and assembled to obtain general properties like robustness. The latter is the ability of a structure to withstand extreme loads without being damaged to an extent disproportionate to the cause. When an extreme load is concerned, structural damages are common and robustness is of paramount relevance. See [11] for a current state of the art review and [12] for a detailed analysis of the problem and of the available quantitative indexes.

RC structures designed and built in seismic zones should be robust in order to withstand the extreme earthquake load and many studies on this topic have been developed in the last years: [13,14,15,16,17]. Fewer studies deal with the interaction between earthquake and blast load. Abdollahzadeh and Faghihmaleki [18] evaluated the robustness of a seismic designed RC structure under blast load with deterministic, probabilistic and risk-based methods but did not investigated the influence of seismic demand. The latter risk-based approach has been developed in [19] considering a multi-hazard analysis for seismic and blast critical events.

The uncertainties due to blast load imply the need of a probabilistic approach in order to have an accurate estimation of the structural behavior and integrity [20,21]. Performance based fragility estimates have been adopted to assess the reliability of structures under impact in [22] showing how it is possible to formulate a Bayesian physical model for these kinds of problems.

This paper reports on a probabilistic analysis of the effect of a seismic demand on the structural fragility in case of blast load. Starting from the capacity curves of framed structures designed for different seismic loads in the Italian territory, an equivalent single degree of freedom model is developed in order to perform a probabilistic analysis based on Monte Carlo approach. Fragility curves and performance analysis are obtained with a general methodology that can be extended to many other structures. After this introduction, in Section 2 the blast load model is presented, while Section 3 describes the selected structure. Section 4 depicts the structural model while Section 5 presents the probabilistic framework. Results are in Section 6, while some concluding remarks and prospective developments are stated in Section 7.

2. Load Model

In this work, the case of hemispheric explosion load was considered. The stand-off pressure P_so in MPa was estimated using the Mills’ approach [23]:

$$P_{sO}=1.772\left(\frac{1}{Z^3}\right)-0.114\left(\frac{1}{Z^2}\right)+0.108\left(\frac{1}{Z}\right)$$

(1)

where z is the scaled distance representing the ratio between the distance from the explosive charge to the building and the cubic root of the explosive charge, it is expressed by:

$$z=\frac{R}{W^{\frac{1}{3}}}$$

(2)

where R is the stand-off distance and W is the mass of explosive in kg of equivalent TNT [24,25]. The incident impulse is represented by Held’s [24] equation:

$$I_{sO}=B \frac{W^{2/3}}{R}$$

(3)

where B is a numerical coefficient that has been considered equal to 4.5 × 10⁵ for R > 10 m and 3.5 × 10⁵ for R ≤ 10 m following the indications reported in [24,25]. Instead, the reflected pressure peak can be expressed as [21]:

$$Pr=2·P_{sO }\left(\frac{7P_{atm}+4P_{sO}}{7P_{atm}+P_{sO}}\right)$$

(4)

where P_atm = 0.1 MPa. The positive phase duration t_d can be expressed assuming a triangular impulse:

$$t_d=\frac{2 I_{sO}}{P_{sO}}$$

(5)

The blast load time history is usually expressed with an exponential function of time t as proposed by Friedlander [26] considering $\beta$ = 1.8:

$${\mathrm{P}}_r\left(t\right)=P_r{\left(1-\frac{t}{t_d}\right)}^{\frac{-\beta t}{t_d}}$$

(6)

In this work, in order to reduce the computational cost, the nonlinear Equation (6) can be simplified with an equivalent triangular time-history, as shown in Figure 1:

$${\mathrm{P}}_r\left(t\right)=P_r\left(1-\frac{t}{t_d}\right)$$

(7)

In this linear case, the positive phase duration is obtained by equating the area underneath the two curves in order to have an equivalent impulse for the two models.

3. Case Study

A framed RC structure with squared cross section has been considered as a case study, see Figure 2a for the geometrical sizes. Beam and column characteristics are detailed in Figure 2b. This kind of structure can serve as watchtower in a military environment.

In order to study the influence of the seismic demand in the structural design, the same structure has been designed considering four different locations in Italy: L’Aquila, Catania, Bari and Cagliari characterized by different seismic load, from the highest to the lower, see

Table 1. Location of the considered construction sites for the structure.

Location	Seismic Zone	Max PGA
L’Aquila	1	PGA > 0.25 g
Catania	2	0.15 g < PGA < 0.25 g
Bari	3	0.05 g < PGA < 0.15 g
Cagliari	4	PGA < 0.05 g

and Figure 3. In this way, the reinforcements distributions will be different for each construction site. Clearly, the city with the highest seismic demand is L’Aquila and the highest reinforcement ratio is obtained when the structure is located in this city. At the same time, the lowest reinforcement ratio is obtained for Cagliari, that is the location with the lowest seismic demand.

For the sake of synthesis, the same structure was designed in order to fulfill four different seismic demands corresponding to different Italian locations, see Table 1 and

Table 2. Materials characteristics.

fck (MPa)	εc3‰	εcu‰	fyd (MPa)	εsy‰
28	1.75	3.5	450	2.9

. Consequently, four different structural models are considered in the next sections in order to investigate how the seismic demand can influence also the blast resistance.

4. Structural Model

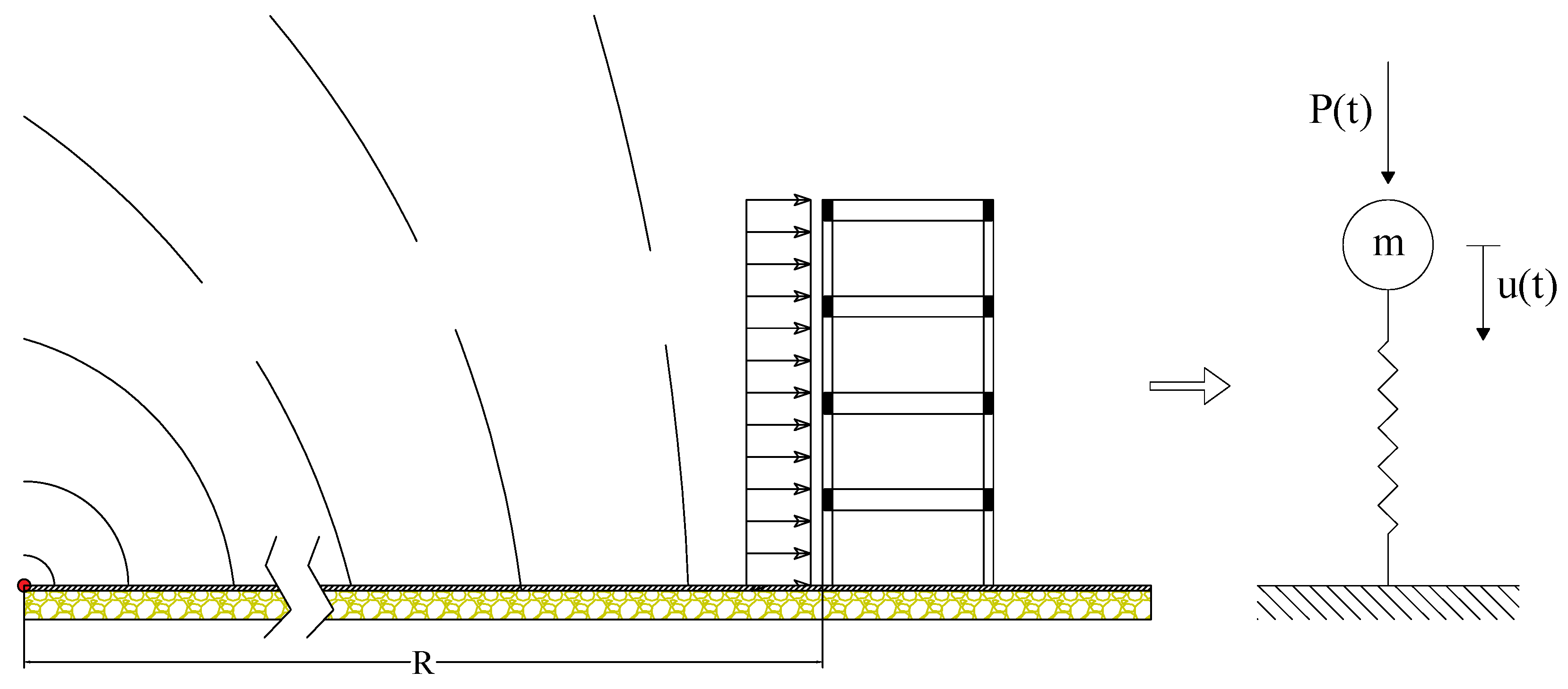
In case of blast load the structural behaviour of a mechanical system can be represented by a single degree of freedom (SDOF) model characterized by a spring denoting the stiffness and a mass expressing the inertia, see Figure 4. Indeed, in this kind of problem damping can be disregarded because the maximum displacement is obtained in the first cycle of loading, see [28]. In fact, the aim of this structural model is to evaluate the maximum displacement of the structure at collapse.

If the mechanical non-linearities are taken into account the SDOF constitutive law can be simplified with load-displacement bilinear diagram, as shown in Figure 5.

For simple structures like beams or columns, it is possible to obtain the bilinear force-displacement diagram quite easily, just by identifying the collapse mechanism and, consequently, yielding and ultimate displacement values. In the case of a complex structure, this process becomes difficult, and in general cases it is not always possible to represent the structural behavior with an equivalent SDOF system. However, in the present case, the framed structure is quite slender and a simple modal analysis (the modal analysis was performed with the numerical model presented in Section 4.2) showed that the first eigenmode is characterized by the 85% of participant mass. For this reason, it is possible to assume that the dynamic behavior of the structure under a uniform blast load pressure can be represented by an equivalent SDOF system. Push-over analysis [29,30,31,32] can produce the force-displacement diagram known as a capacity curve. From this capacity curve it is possible to obtain an equivalent bilinear force–displacement diagram that represents the SDOF constitutive behavior [33,34,35] as shown in Section 4.2.

4.1. Materials and Strain Rate Effects

The materials constitutive laws and characteristics are shown in Figure 6 and Table 2.

The time dependency of the mechanical characteristics of concrete and steel on strain rate is already known. Indeed, in case of blast or impulsive load the characteristics of materials can be strongly influenced by strain rate, see [36,37,38,39]. In the literature, it is possible to find quite advanced analytical models for the strain rate effects [40], but obviously they would increase the computational cost and the complexity of the model. In order to simplify the problem and reduce the computational cost in this paper the approach proposed in [25] has been applied. A set of Dynamic Increase Factors (DIF) equal to the ratio between a dynamic mechanical characteristic f_d and the equivalent static one f has been defined as reported in

Table 3. Dynamic increase factor (DIF) for RC elements, extracted from [25].

Type of Stress	Reinforcing Bars		Concrete
	fdy/fy	fdu/fu	fdc/fc
Bending	1.17	1.05	1.19
Diagonal Tension	1.00	-	1.00
Direct Shear	1.10	1.00	1.10
Bond	1.17	1.05	1.00
Compression	1.10	-	1.12

.

Thus, given the critical internal force for each structural component, the appropriate DIF has been chosen from Table 3 in order to modify the mechanical characteristics of the structural model.

4.2. Capacity Curves

The structure presented in Section 3 has been designed for permanent, service and earthquake load following the Italian [41] and European Standard [42] in each location, see

Table 4. Reinforcements details for columns in each structure, Ac represents the concrete area, As the tensile reinforcement, A’s the compressive reinforcement, r is the reinforcement ratio (r = As/Ac) while the letter x or y denotes the reinforcements for the bending moment around x axis or y axis respectively, see Figure 2.

	Ac	As,x	As,y	r,x	r,y	A’s,x	A’s,y	r’,x	r’,y
Location	[mm2]	[mm2]	[mm2]	[-]	[-]	[mm2]	[mm2]	[-]	[-]
L’Aquila	90,000	770	770	0.0086	0.0086	770	770	0.0086	0.0086
Catania	90,000	616	616	0.0068	0.0068	616	616	0.0068	0.0068
Bari	90,000	462	616	0.0051	0.0068	462	616	0.0051	0.0068
Cagliari	90,000	308	462	0.0034	0.0051	308	462	0.0034	0.0051

. Then a finite element (FE) model of the framed structure has been developed using the commercial software JASP 6.5 [43]. This FE model was used to perform a static non-linear analysis with a uniform horizontal load. The lumped plastic hinge behavior has been modelled by standard approach [42,43,44], as illustrated in Figure 7.

The results in terms of horizontal force and top horizontal displacement (capacity curves) are reported in Figure 8 for the structures designed in the selected locations. The equivalent bilinear SDOF constitutive curves have been calculated equating the area underneath bilinear and capacity curves assuming that the ending point and the first elastic slope should be the same for the two curves.

4.3. Analytical Model

The equations of motion of the equivalent SDOF oscillator in the elastic and plastic regimes have the following forms:

$${\mathrm{M}}_{E,el}\frac{d^2{v}_E\left(t\right)}{d{t}^2}+K_{E,el}{u}_E\left(t\right)=P_E\left(t\right) for 0\le u_E\le u_{Ey}$$

(8a)

$${\mathrm{M}}_{E,pl}\frac{d^2{v}_E\left(t\right)}{d{t}^2}+K_{E,pl}{u}_E\left(t\right)+\left[K_{E,el}-K_{E,pl}\right]u_{Ey}=P_E\left(t\right) for u_{Ey}<u_E\le u_{Eu}$$

(8b)

where $u_E\left(t\right)$ is the model displacement, $P_E\left(t\right)$ is the total load on the structure. ${\mathrm{M}}_{E,el}$ and ${\mathrm{M}}_{E,pl}$ denote the equivalent mass of the oscillator respectively for the elastic and plastic field. In general: ${\mathrm{M}}_E=K_{LM}M$ where M is the structural mass and $K_{LM}$ is a coefficient which accounts for the boundary conditions of the structural element, the type of load and the regime considered (elastic or plastic). The structure presented in Section 3 can be considered similar to a vertical cantilever fixed in the bottom part. Thus, in case of a uniformly distributed load for a cantilever structure M_E,el = 0.65∙M and M_E,pl = 0.66∙M, see [45]. $v_{Ey}$ and $v_{Eu}$ are the equivalent yieding and ultimate model displacement, while $K_{E,el}$ and $K_{E,pl}$ respectively are the equivalent stiffnesses in the elastic and plastic range.

Given the analytical expression of the load time history it is possible to find the close form solution of Equation (8), see [46]. In this work, $P_E\left(t\right)$ is approximated by the linear expression presented in Equation (7).

4.4. Load Scenario

In this paper, only external explosion produced by a terrorist attack has been taken into account. Stewart et al. [47] described some of the possible scenarios that can generate an external hemispheric explosion. It is interesting to distinguish theme by the ways in which a mass of explosives could be transported near the object of the attack: 5 kg body explosive; 25 kg suitcase explosive; 200 kg car explosive.

In this work the load scenario obtained with 200, 300, 400, and 500 kg of TNT has been considered. These situations can be easily obtained considering a car or a truck containing the explosives. Various stand-off distances have been investigated studying the effects of the explosives for the structure described in Section 3.

4.5. Damage Thresolds

In order to measure the structural performance under blast load the drift values proposed by [48] have been adopted, see

Table 5. Assumed drift $x_0$ thresolds for performance levels, extracted from [48].

Slight Damage	Moderate Damage	Severe Damage
0.0012	0.0080	0.011

. It is important to point out that this approach considers the whole structural response given that the stand-off distance is sufficiently large to obtain a planar blast wave acting on the building, see Figure 4. Thus, for the sake of simplicity, localized column or beam collapse has not been considered, in addition, also the harmful damages on secondary elements which can lead to a loss of life are neglected. Instead, the top floor maximum displacement u_MAX related to the building height h=12 m has been considered to define the relative drift:

$$X=\frac{u_{MAX}}{h}$$

(9)

This simplified approach is clearly limited to its assumptions but can be useful in case of preliminary or early design because it can easily provide a synthetic parameter describing the damage condition of a building after the blast load.

5. Probabilistic Analysis

Fragility curves describe the conditional probability of exceedance (P(X > x0|Z)) of the response parameter X (drift in this case) given a demand intensity measure (scaled distance Z in this case). Thus, the structural fragility can be expressed as the cumulative distribution of the probability that a damage threshold $x_0$ is exceeded [21,49]:

$$P\left(X>x_0\right)={{\displaystyle \int }}_{-\infty }^{+\infty }P\left(X>x_0|Z\right) p\left(Z\right)dz\cong {\displaystyle \sum }_{i=0}^{\infty }P{\left(X>x_0|Z\right)}_i p{\left(Z\right)}_i\Delta Z_i$$

(10)

where the discretization of the integral calculation is represented by a discrete sum of conditions in which the scaled distance is varied with a given step $\Delta Z$.

In this paper, the structural characteristics have been considered deterministic while the uncertainties of the load have been modelled considering the explosive mass and stand-off distance as stochastic variables characterized by lognormal distributions whose characteristics are shown in

Table 6. Probabilistic Analysis Input Data.

Symbol	Description	COV	Distribution
R	Stand-off distance	0.05	Lognormal
W	Explosive mass	0.15	Lognormal

.

A Monte Carlo analysis has been developed with the above described SDOF model in order to obtain fragility curves presented in Section 6.2 and the probability of thresholds exceedance shown in Section 6.3. The coefficient of variation (COV) of the maximum drift has been checked in order to define the convergence condition of the analysis.

6. Results and Discussion

6.1. Maximum Drift

In the first load scenario, a 500 kg TNT bomb was blown up at various distance from the structure. The maximum drift values have been plotted as a function of the scaled distance in Figure 9. In the same picture the above-mentioned damage thresholds have been plotted in order to easily find the safety scaled distance for each structure. As expected, the structure designed in L’Aquila with the highest seismic load produced the best performance reaching the damage thresholds with smallest scaled distance in comparison with the other structures. This can be explained given the higher reinforcement ratio (see Table 4) and robustness of this structure in comparison with the others. At the same time, it is clear that 500 kg of TNT represents a huge amount and it is necessary to reach very high scaled distance (higher than 10 /kg^1/3) to avoid any damage.

6.2. Fragility Curves

The fragility curves for the structures designed in the four locations are presented in Figure 10, Figure 11 and Figure 12. In this case the TNT mass has been varied considering a Lognormal distribution with different mean values: 200, 300, 400, and 500 kg. The three damage thresholds have been considered: slight (Figure 10), moderate (Figure 11) and severe (Figure 12). Instead, the stand-off distance has been varied in a deterministic way in order to analyze all the scaled distance values.

As a representative case, the COV of the maximum displacement for the severe damage threshold in case of 500 kg bomb for each structure location has been shown in Figure 13. Also, the other cases present similar trends.

In Figure 10, Figure 11, Figure 12 and Figure 13, the curves corresponding to 500 kg are the ones placed on the far right of each figure highlighting that this is the most severe condition in each case. Instead, if the structure designed in the site with less seismic demand (Cagliari) is compared to the one with the highest (L’Aquila) it is possible to note how the curves are shifted to the left in the latter case and to the right in the former one. This is another proof of the better structural performance of the structure designed in L’Aquila.

6.3. Probability of Thresholds Exceedance

The Monte Carlo analysis has been developed considering both stand-off distance R and mass weight W as stochastic variables following a Lognormal probability distribution as described in Section 5.

Table 7. Percentage probability of thresholds exceedance for L’Aquila location.

	200 Kg	300 Kg	400 Kg	500 Kg
R = 20 m
slight	100	100	100	100
moderate	93.88	100	100	100
severe	64.92	99.8	100	100
R = 25 m
slight	100	100	100	100
moderate	10.72	98.68	100	100
severe	0.02	42.96	98.78	100
R = 30 m
slight	100	100	100	100
moderate	0.02	41.82	96.52	100
severe	0	0.76	48.38	96.78
R = 35 m
slight	100	100	100	100
moderate	0	0.42	37.62	94.18
severe	0	0	2.9	44.6
R = 40 m
slight	100	100	100	100
moderate	0	0	1.88	44.42
severe	0	0	0	1.82
R = 45 m
slight	100	100	100	100
moderate	0	0	0.06	4.74
severe	0	0	0	0.02

,

Table 8. Percentage probability of thresholds exceedance for Catania location.

	200 Kg	300 Kg	400 Kg	500 Kg
R = 20 m
slight	100	100	100	100
moderate	98.54	100	100	100
severe	65.48	99.96	100	100
R = 25 m
slight	100	100	100	100
moderate	25.68	99.74	100	100
severe	0.14	66.32	99.74	100
R = 30 m
slight	100	100	100	100
moderate	0.14	52.68	98.58	100
severe	0	2.48	69.86	99.4
R = 35 m
slight	100	100	100	100
moderate	0	1.48	59.22	98.5
severe	0	0	7.62	61.02
R = 40 m
slight	100	100	100	100
moderate	0	0	6.82	66.26
severe	0	0	0.1	3.86
R = 45 m
slight	100	100	100	100
moderate	0	0	0.18	13.7
severe	0	0	0	0.08

,

Table 9. Percentage probability of thresholds exceedance for Bari location.

	200 Kg	300 Kg	400 Kg	500 Kg
R = 20 m
slight	100	100	100	100
moderate	99.7	100	100	100
severe	68.18	99.98	100	100
R = 25
slight	100	100	100	100
moderate	42.04	99.92	100	100
severe	0.46	81.68	99.96	100
R = 30 m
slight	100	100	100	100
moderate	0.38	62.24	99.62	100
severe	0	7.36	83.88	99.92
R = 35 m
slight	100	100	100	100
moderate	0	4.14	76.38	99.48
severe	0	0.06	14.02	66.04
R = 40 m
slight	100	100	100	100
moderate	0	0.02	16.48	81.3
severe	0	0	0.02	7.5
R = 45 m
slight	100	100	100	100
moderate	0	0	0.46	23.44
severe	0	0	0	0.16

and

Table 10. Percentage probability of thresholds exceedance for Cagliari location.

	200 Kg	300 Kg	400 Kg	500 Kg
R = 20 m
slight	100	100	100	100
moderate	99.96	100	100	100
severe	89.54	100	100	100
R = 25 m
slight	100	100	100	100
moderate	78.12	100	100	100
severe	5.86	97.1	100	100
R = 30 m
slight	100	100	100	100
moderate	2.14	91.96	100	100
severe	0	32.28	95.5	99.86
R = 35 m
slight	100	100	100	100
moderate	0	28	96.18	100
severe	0	0.48	25.64	88.8
R = 40 m
slight	100	100	100	100
moderate	0	1.08	52.24	95.58
severe	0	0	0.92	31.92
R = 45 m
slight	100	100	100	100
moderate	0	0	4.32	55.14
severe	0	0	0	2.02

present the probability of exceedance for each different threshold and for each structure designed in the different location.

Also in this case, it is possible to highlight the better structural performance of the structure designed in L’Aquila in comparison with the others. In addition, it is possible to note how, as the stand-off distance increases, the probability of exceedance for each threshold is reduced. In most cases the safe stand-off distance for a 500 kg TNT bomb is about 40–45 m. Instead, in the case of 200 kg, it is 25 m for L’Aquila, 30 m for Catania and Bari, and 35 m for Cagliari.

7. Conclusions

This paper presented a simplified procedure to evaluate the safety of a framed RC structure under blast load highlighting the seismic design influence. The considered framed building has been designed considering four different seismic demand corresponding to specific locations in Italy characterized by different PGA. Then, a simplified SDOF system has been obtained from a pushover analysis in order to perform several Monte Carlo analyses aimed at highlighting what is the performance of the considered building under blast load in both a deterministic and probabilistic framework.

The structure designed to withstand the highest seismic load (L’Aquila) has been proven to have better performance also in the case of blast load. Thus, the influence of the seismic demand in the building design is evident. Indeed, the structure designed with the lowest seismic demand (Cagliari) presents the worst structural behavior under the blast load. This can be clearly seen from the fragility curves Figure 10, Figure 11 and Figure 12, probability Table 7, Table 8, Table 9 and Table 10, and also from the deterministic maximum drift presented in Figure 9.

The obtained results can be useful for safety evaluation in the case of a terrorist attack. Indeed, the fragility curves and the probability of threshold exceedance can help the designer in evaluating what should be a “safe” distance for the given structure that can be obtained with fence system or bollards.

Further development of this work is expected, applying this method to existing structures, like those described in [50,51]. It is also interesting to merge the proposed method with other assessment approaches and retrofitting techniques considering other kind of structures [52,53,54].