A Multi-Degree of Freedom Tuned Mass Damper Design for Vibration Mitigation of a Suspension Bridge
Abstract
1. Introduction
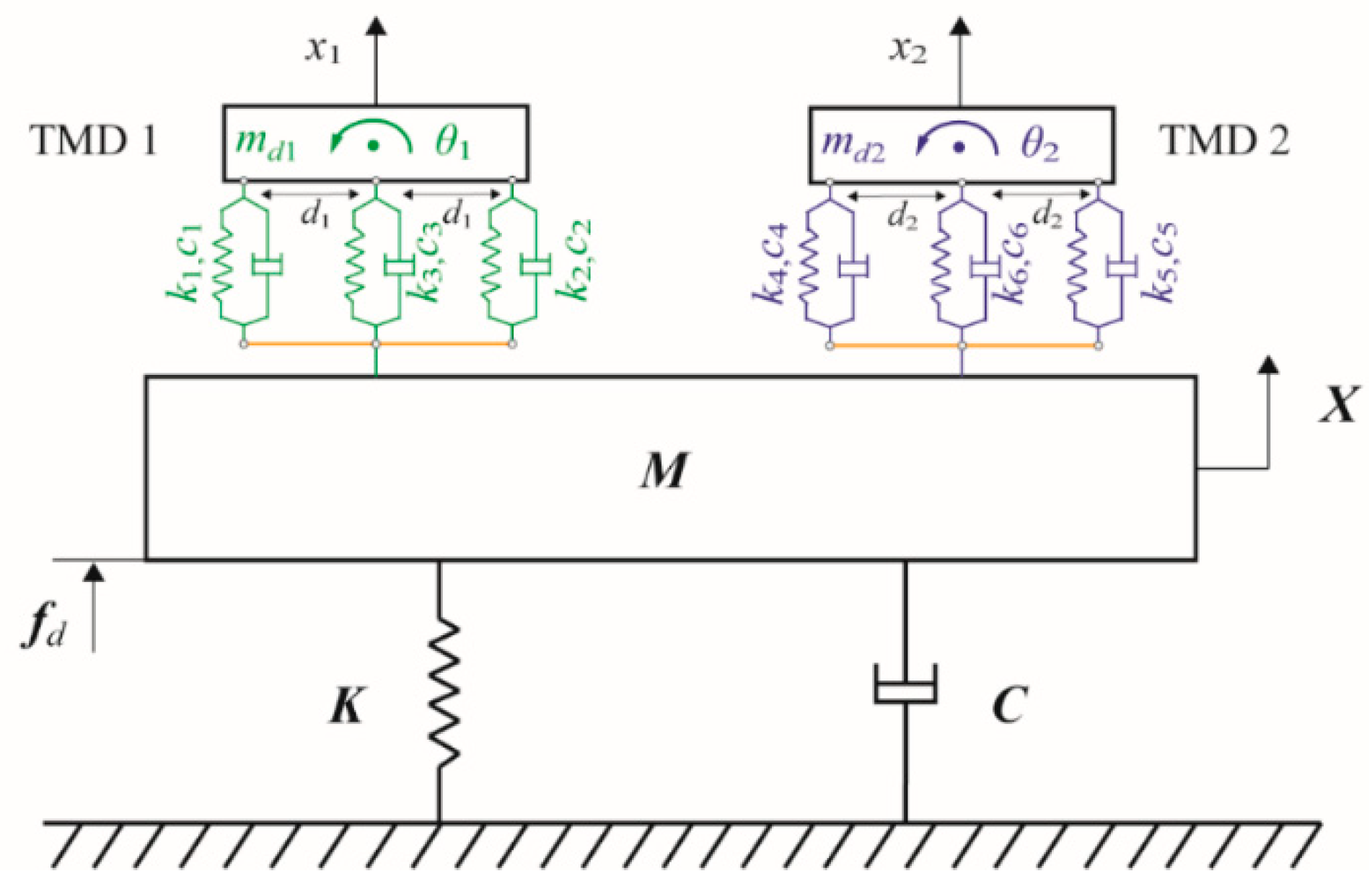
2. Formulation of the Bridge–TMD System
3. Numerical Optimization and Simulation
3.1. Optimization Criteria
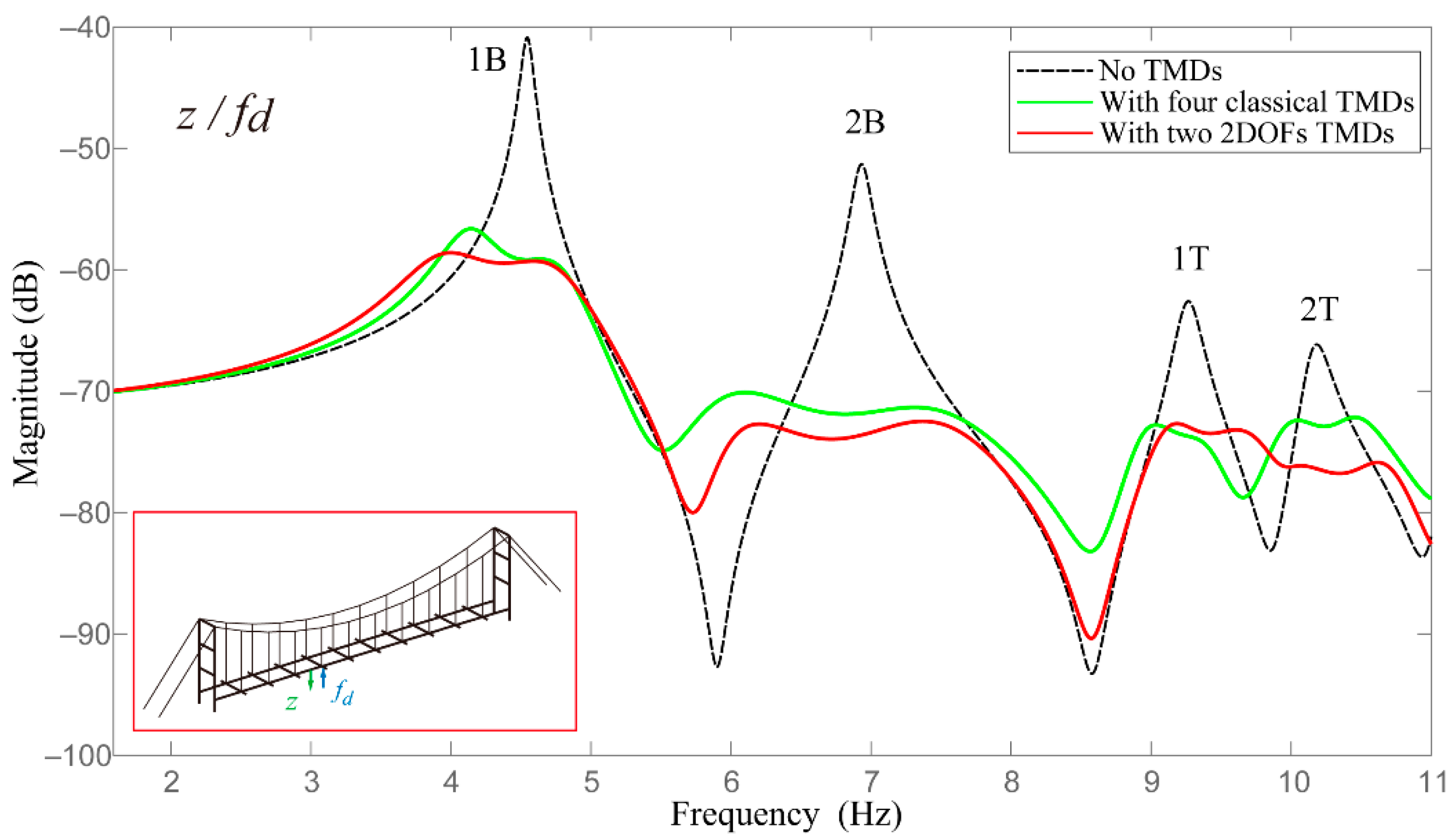
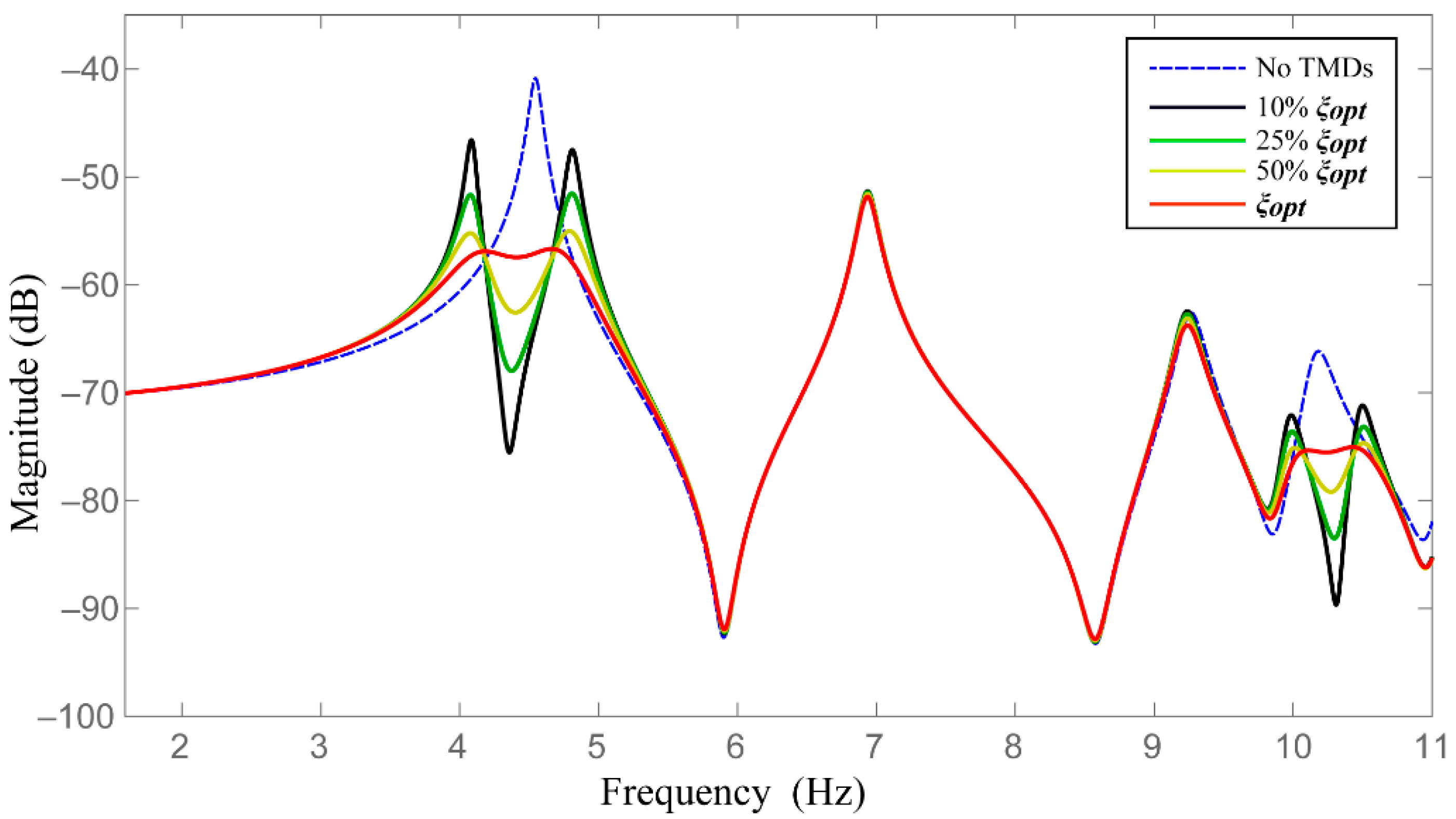
3.2. Numerical Optimization Results
4. Structural Design of 2DOFs TMD
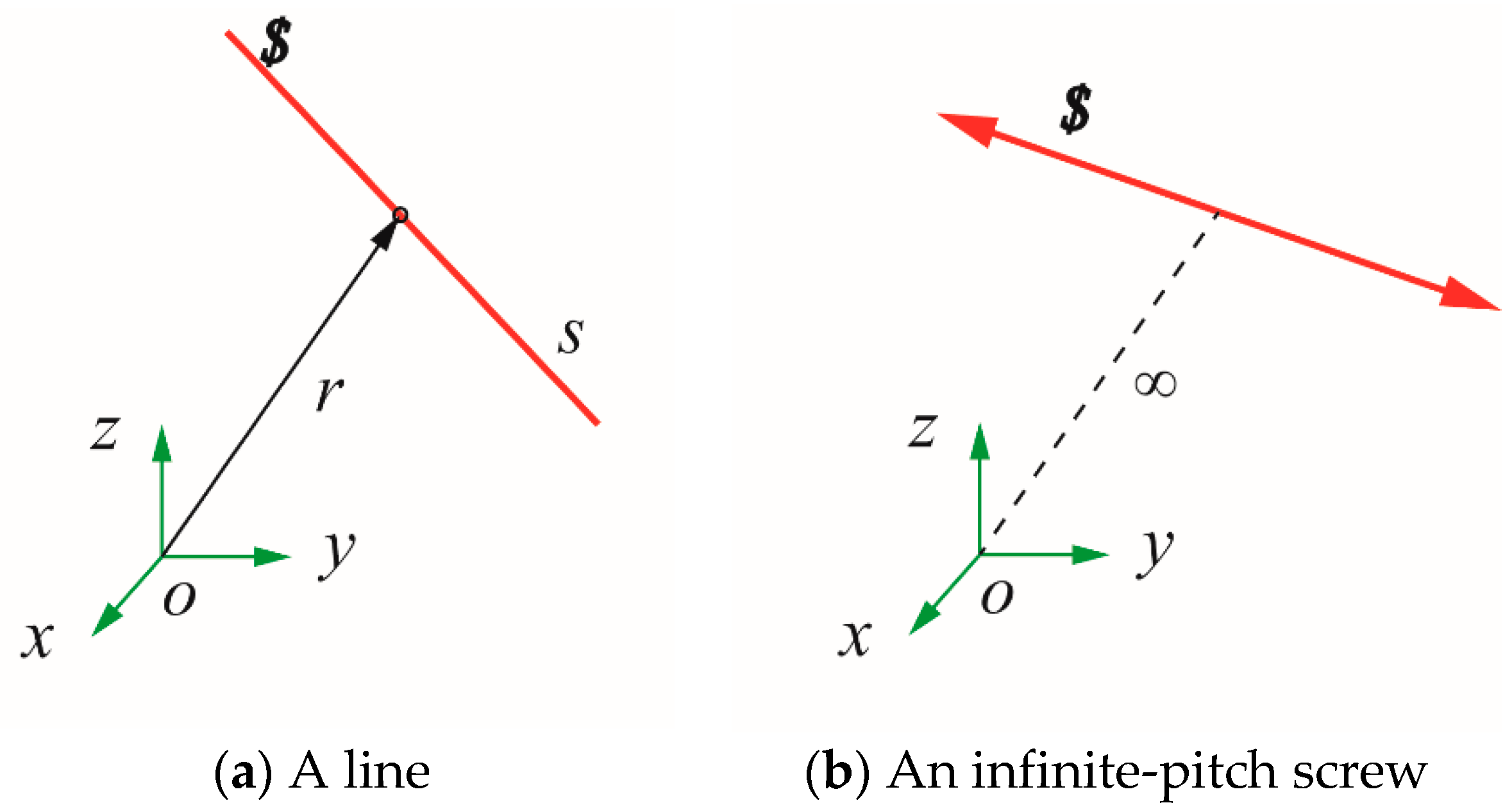
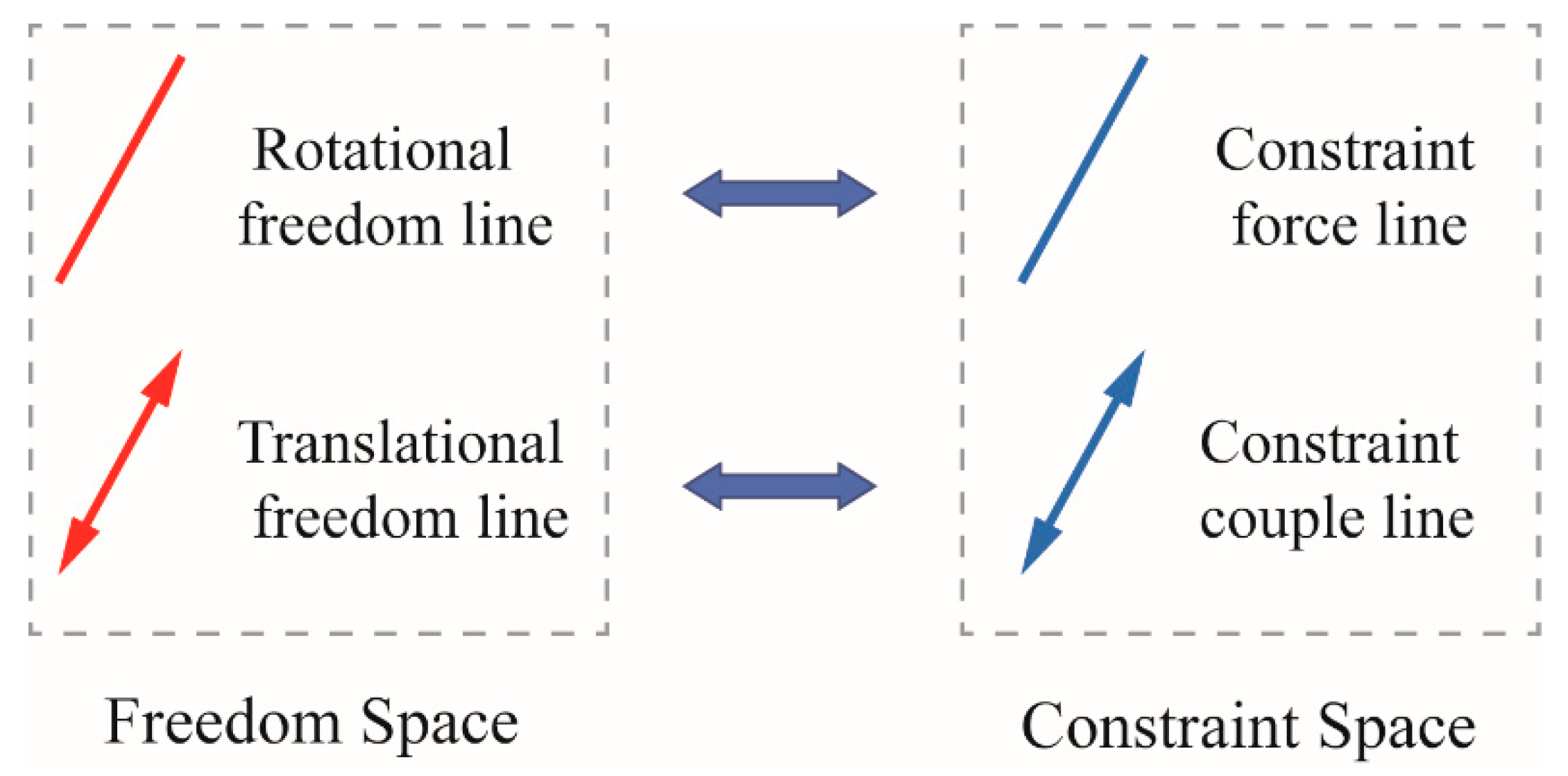
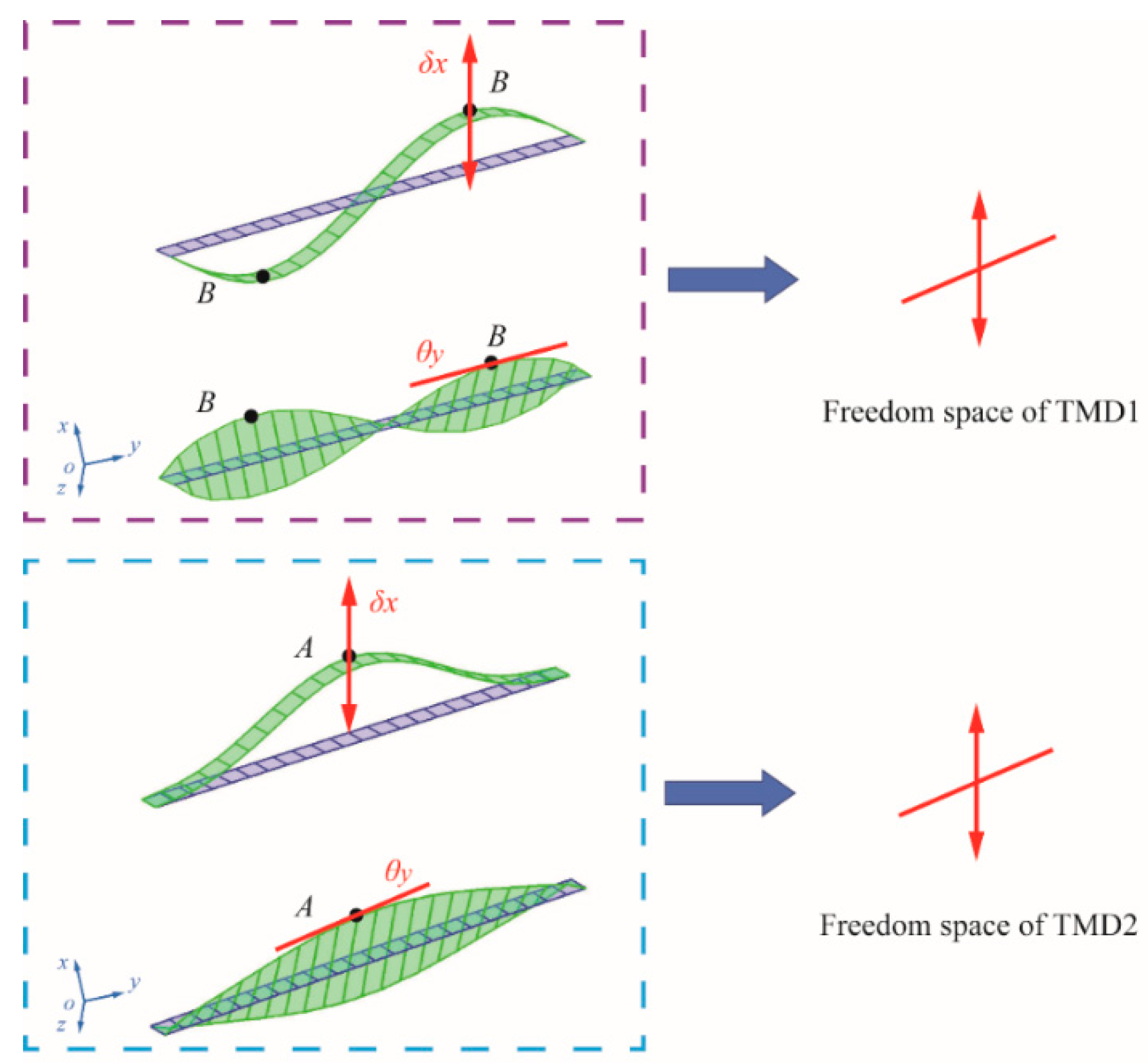
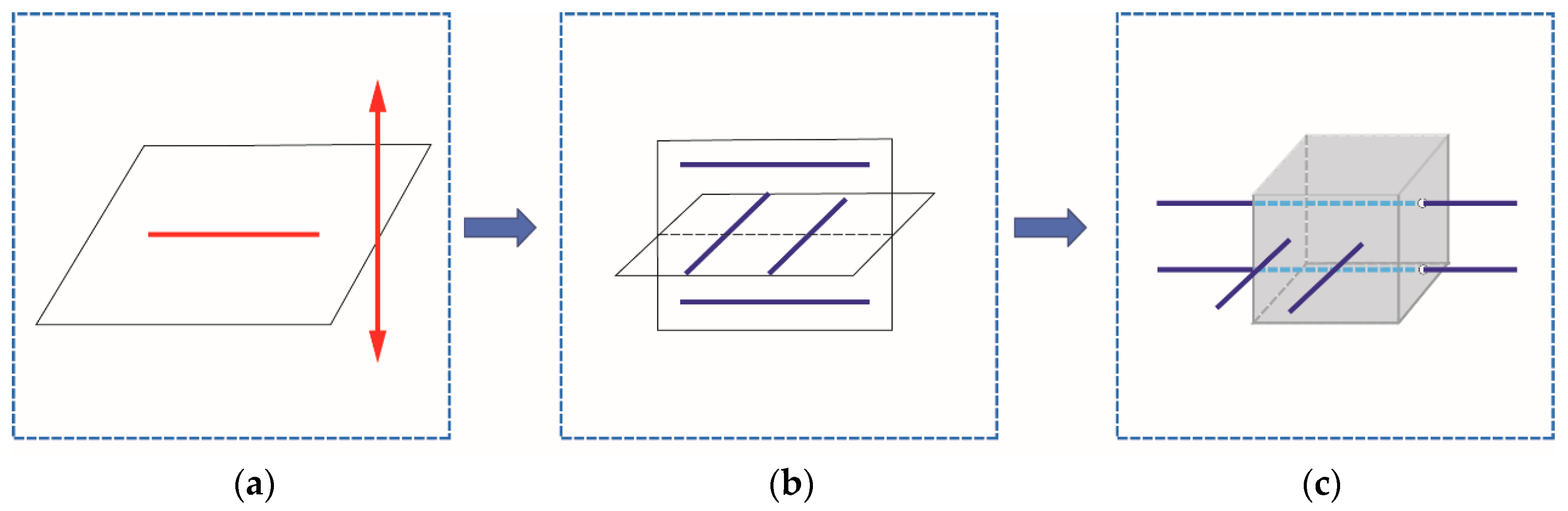
4.1. Graphical Approach
4.2. Conceptual Design of the TMDs
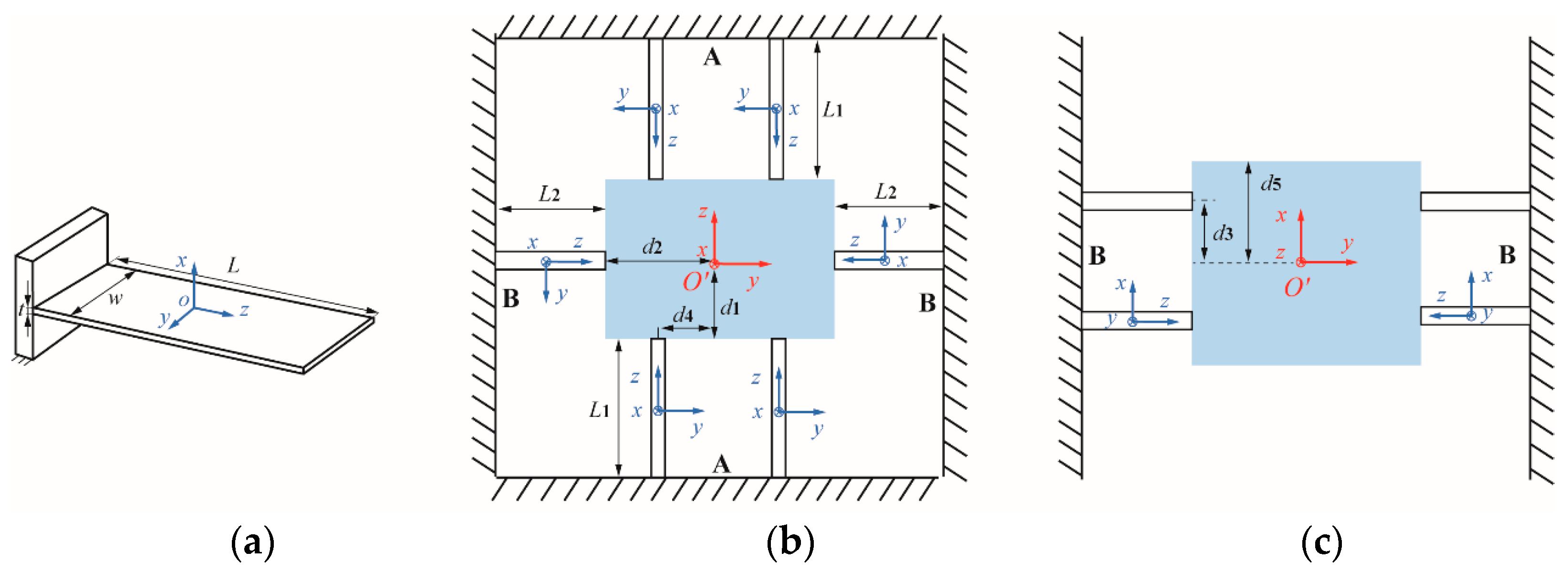
4.3. Parametric Design of 2DOFs TMDs
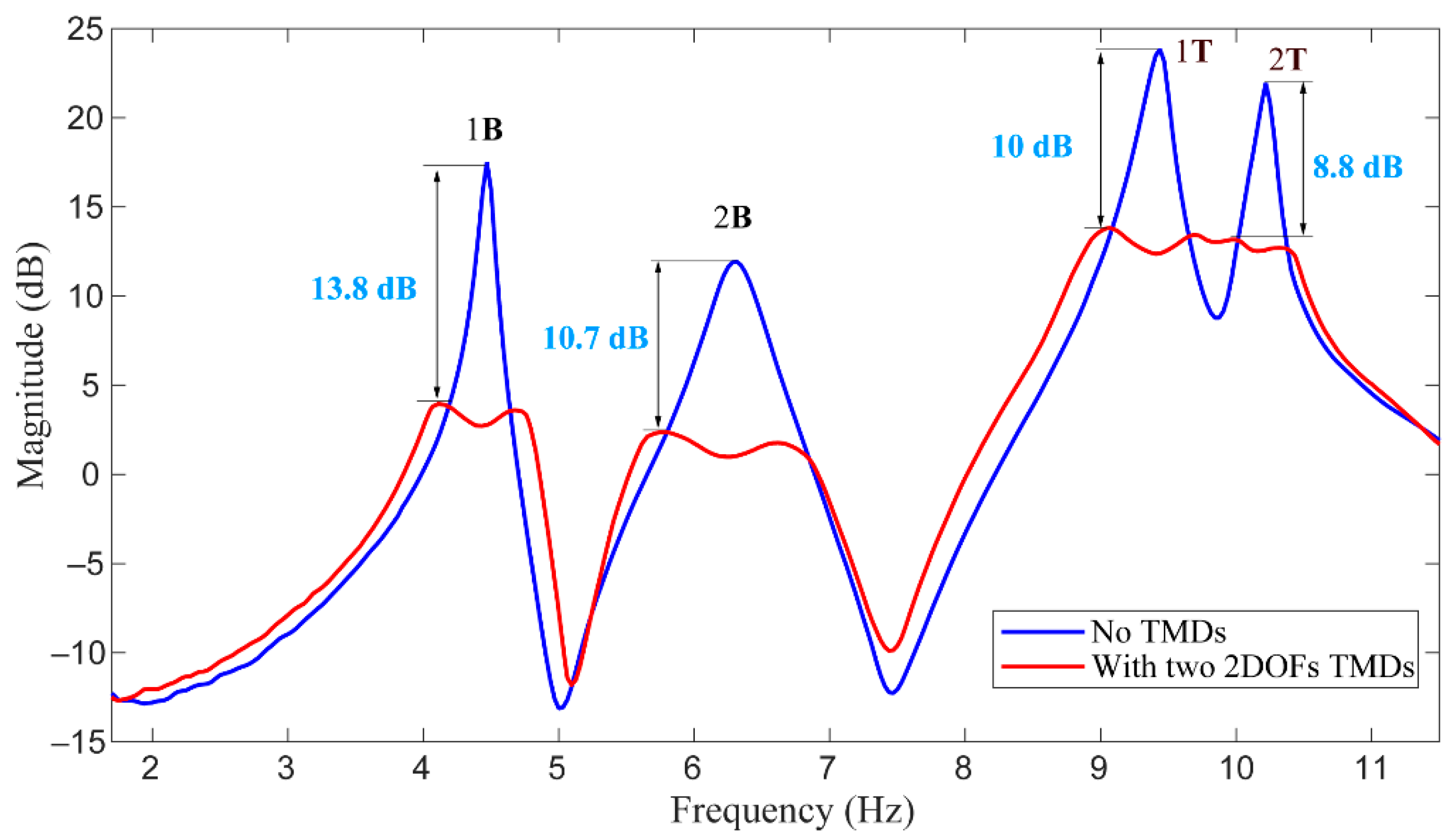
4.4. Results and Discussion
5. Experimental Verification
5.1. Experimental Setup
5.2. Hammer Tests of TMDs
5.3. Vibration Suppression of Bridge with TMDs
6. Conclusions
- The synthetic approach based on both the graphical approach and parameterized compliance is an effective way to design the TMD with the expected DOFs (i.e., 1, 2, …, 6). It is also an effective complement to the empirical design for the multi-DOFs TMD. Comparing with the empirical design, this synthetic approach can design the expected multi-DOFs TMD without much design experience, which can save time and cost. The disadvantage of this method is that the influence of prestress is not taken into account in the theoretical model. Thus, the adjuster is an indispensable part of TMDs.
- This study verifies the feasibility of the two 2DOFs TMDs in vibration reduction of suspension bridges by numerically and experimentally; comparing with the classical configuration of the TMD, the two 2DOFs TMDs can reduce the weight penalty. The experiment demonstrates the ability of the TMDs for suppressing several vibration modes under laboratory conditions. However, their implementation in a full-scale bridge still needs further research.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ubertini, F.; Comanducci, G.; Laflamme, S. A parametric study on reliability-based tuned-mass damper design against bridge flutter. J. Vib. Control. 2017, 23, 1518–1534. [Google Scholar] [CrossRef]
- Wang, Z.; Yue, F.; Gao, H. Free Vibration of a Taut Cable with Two Discrete Inertial Mass Dampers. Appl. Sci. 2019, 9, 3919. [Google Scholar] [CrossRef]
- Shi, W.; Wang, L.; Lu, Z.; Zhang, Q. Application of an Artificial Fish Swarm Algorithm in an Optimum Tuned Mass Damper Design for a Pedestrian Bridge. Appl. Sci. 2018, 8, 175. [Google Scholar] [CrossRef]
- Lievens, K.; Lombaert, G.; De Roeck, G.; Van den Broeck, P. Robust design of a TMD for the vibration serviceability of a footbridge. Eng. Struct. 2016, 123, 408–418. [Google Scholar] [CrossRef]
- Caetano, E.; Cunha, Á.; Moutinho, C.; Magalhães, F. Studies for controlling human-induced vibration of the Pedroe Inês footbridge, Portugal. Part 2: Implementation of tuned mass dampers. Eng. Struct. 2010, 32, 1082–1091. [Google Scholar] [CrossRef]
- Van Nimmen, K.; Verbeke, P.; Lombaert, G.; De Roeck, G.; Van den Broeck, P. Numerical and experimental evaluation of the dynamic performance of a footbridge with tuned mass dampers. J. Bridge Eng. 2016, 21, C4016001. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Improving the dynamic performance of base-isolated structures via tuned mass damper and inerter devices: A comparative study. Struct. Control Health Monit. 2018, 25, e2234. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G.; Takewaki, I. Design strategies of viscous dampers for seismic protection of building structures: A review. Soil Dyn. Earthq. Eng. 2019, 118, 144–165. [Google Scholar] [CrossRef]
- Hao, L.F.; Zhang, R.F. Structural safety redundancy-based design method for structure with viscous dampers. Struct. Eng. Mech. 2016, 59, 821–840. [Google Scholar] [CrossRef]
- Preumont, A.; Voltan, M.; Sangiovanni, A.; Mokrani, B.; Alaluf, D. Active tendon control of suspension bridges. Smart Struct. Syst. 2016, 18, 31–52. [Google Scholar] [CrossRef]
- De Domenico, D.; Deastra, P.; Ricciardi, G.; Sims, N.D.; Wagg, D.J. Novel fluid inerter based tuned mass dampers for optimised structural control of base-isolated buildings. J. Frankl. Inst. 2018, 14, 7626–7649. [Google Scholar] [CrossRef]
- Tian, L.; Rong, K.; Zhang, P.; Liu, Y. Vibration Control of a Power Transmission Tower with Pounding Tuned Mass Damper under Multi-Component Seismic Excitations. Appl. Sci. 2017, 7, 477. [Google Scholar] [CrossRef]
- Zhang, R.F.; Zhao, Z.P.; Dai, K.S. Seismic response mitigation of a wind turbine tower using a tuned parallel inerter mass system. Eng. Struct. 2019, 180, 29–39. [Google Scholar] [CrossRef]
- Mekki, O.B.; Bourquin, F.; Maceri, F.; Merliot, E. Unimodal optimal passive electromechanical damping of elastic structures. Smart Mater. Struct. 2013, 22, 085029. [Google Scholar] [CrossRef]
- Mekki, O.B.; Bourquin, F.; Maceri, F.; Van Phu, C.N. An adaptive pendulum for evolving structures. Struct. Control Health Monit. 2012, 19, 43–54. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V. Research developments in vibration control of structures using passive tuned mass dampers. Annu. Rev. Control 2017, 44, 129–156. [Google Scholar] [CrossRef]
- Casalotti, A.; Arena, A.; Lacarbonara, W. Mitigation of post-flutter oscillations in suspension bridges by hysteretic tuned mass dampers. Eng. Struct. 2014, 69, 62–71. [Google Scholar] [CrossRef]
- Chen, S.R.; Wu, J. Performance enhancement of bridge infrastructure systems: Long-span bridge, moving trucks and wind with tuned mass dampers. Eng. Struct. 2008, 30, 3316–3324. [Google Scholar] [CrossRef]
- Li, Q.; Fan, J.; Nie, J.; Li, Q.; Chen, Y. Crowd-induced random vibration of footbridge and vibration control using multiple tuned mass dampers. J. Sound Vib. 2010, 329, 4068–4092. [Google Scholar] [CrossRef]
- Daniel, Y.; Lavan, O.; Levy, R. Multiple-tuned mass dampers for multimodal control of pedestrian bridges. J. Struct. Eng. 2011, 138, 1173–1178. [Google Scholar] [CrossRef]
- Tubino, F.; Carassale, L.; Piccardo, G. Human-induced vibrations on two lively footbridges in Milan. J. Bridge Eng. 2016, 21, C4015002. [Google Scholar] [CrossRef]
- Wen, Q.; Hua, X.G.; Chen, Z.Q.; Yang, Y.; Niu, H.W. Control of human-induced vibrations of a curved cable-stayed bridge: Design, implementation, and field validation. J. Bridge Eng. 2016, 21, 04016028. [Google Scholar] [CrossRef]
- Lin, C.C.; Wang, J.F.; Chen, B.L. Train-induced vibration control of high-speed railway bridges equipped with multiple tuned mass dampers. J. Bridge Eng. 2005, 10, 398–414. [Google Scholar] [CrossRef]
- Li, J.; Su, M.; Fan, L. Vibration control of railway bridges under high-speed trains using multiple tuned mass dampers. J. Bridge Eng. 2005, 10, 312–320. [Google Scholar] [CrossRef]
- Luu, M.; Zabel, V.; Könke, C. An optimization method of multi-resonant response of high-speed train bridges using TMDs. Finite Elem. Anal. Des. 2012, 53, 13–23. [Google Scholar] [CrossRef]
- Stăncioiu, D.; Ouyang, H. Structural modification formula and iterative design method using multiple tuned mass dampers for structures subjected to moving loads. Mech. Syst. Signal Process. 2012, 28, 542–560. [Google Scholar] [CrossRef]
- Mokrani, B.; Zhui, T.; Alaluf, D.; Meng, F.H.; Preumont, A. Passive damping of suspension bridges using multi-degree of freedom tuned mass dampers. Eng. Struct. 2017, 153, 749–756. [Google Scholar] [CrossRef]
- Zuo, L.; Nayfeh, S.A. The two-degree-of-freedom tuned-mass damper for suppression of single-mode vibration under random and harmonic excitation. J. Vib. Acoust. 2006, 128, 56–65. [Google Scholar] [CrossRef]
- Jang, S.J.; Brennan, M.J.; Rustighi, E.; Jung, H.J. A simple method for choosing the parameters of a two degree-of-freedom tuned vibration absorber. J. Sound Vib. 2012, 331, 4658–4667. [Google Scholar] [CrossRef]
- Yang, Y.; Dai, W.; Liu, Q. Design and implementation of two-degree-of-freedom tuned mass damper in milling vibration mitigation. J. Sound Vib. 2015, 335, 78–88. [Google Scholar] [CrossRef]
- Yang, Y.; Dai, W.; Liu, Q. Design and machining application of a two-DOF magnetic tuned mass damper. Int. J. Adv. Manuf. Technol. 2017, 89, 1635–1643. [Google Scholar] [CrossRef]
- Ma, W.S.; Yang, Y.Q.; Yu, J.J. General routine of suppressing single vibration mode by multi-DOF tuned mass damper: Application of three-DOF. Mech. Syst. Signal Process. 2019, 121, 77–96. [Google Scholar] [CrossRef]
- Meng, F.H.; Mokrani, B.; Alaluf, D.; Yu, J.J.; Preumont, A. Damage detection in active suspension bridges: An experimental investigation. Sensors 2018, 18, 3002. [Google Scholar] [CrossRef]
- Meng, F.H.; Yu, J.J.; Alaluf, D.; Mokrani, B.; Preumont, A. Modal flexibility-based damage detection for suspension bridge hangers: A numerical and experimental investigation. Smart Struct. Syst. 2019, 23, 15–29. [Google Scholar]
- Tubino, F.; Piccardo, G. Tuned mass damper optimization for the mitigation of human-induced vibrations of pedestrian bridges. Meccanica 2015, 50, 809–824. [Google Scholar] [CrossRef]
- Yu, J.J.; Li, S.; Pei, X.; Bi, S.; Zong, G. A unified approach to type synthesis of both rigid and flexure parallel mechanisms. Sci. China Technol. Sci. 2011, 54, 1206–1219. [Google Scholar] [CrossRef]
- Hopkins, J.B.; Culpepper, M.L. Synthesis of multi-degree of freedom, parallel flexure system concepts via Freedom and Constraint Topology (FACT)–Part I: Principles. Precis. Eng. 2010, 34, 259–270. [Google Scholar] [CrossRef]
- Yu, J.J.; Li, S.; Su, H.J.; Culpepper, M.L. Screw theory-based methodology for the deterministic type synthesis of flexure mechanisms. J. Mech. Robot. 2011, 3, 031008. [Google Scholar] [CrossRef]
- Jia, M.; Jia, R.P.; Yu, J.J. A Compliance-Based Parameterization Approach for Type Synthesis of Flexure Mechanisms. J. Mech. Robot. 2015, 7, 031014. [Google Scholar] [CrossRef]












| Mode | Numerical [Hz] | Experimental [Hz] | Experimental Damping | Numerical Mode Shape | Experimental Mode Shape |
|---|---|---|---|---|---|
| 1st B | 4.5 | 4.4 | 0.14% |  |  |
| 2nd B | 6.9 | 6.4 | 2.28% | 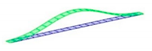 |  |
| 1st T | 9.3 | 9.4 | 0.62% |  |  |
| 2nd T | 10.2 | 10.2 | 0.23% |  | 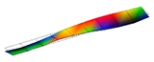 |
| 3rd B | 11.2 | 12.2 | 0.49% | 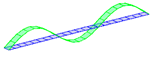 | 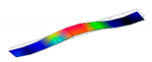 |
| TMD | Optimum Frequency Ratios | Optimum Damping Ratios | ||
|---|---|---|---|---|
| ν1 | ν2 | ξopt1 (%) | ξopt2 (%) | |
| TMD1 | 0.9422 | 1.029 | 13.5 | 10.7 |
| TMD2 | 0.9594 | 1.020 | 17.6 | 9.8 |
| Geometric Condition | Freedom Space ($2) | ||
|---|---|---|---|
| Rotational Freedom Line (h2 = 0) | Translational Freedom Line (h2 = ∞) | ||
| Constraint space ($1) | Constraint force line (h1 = 0) | Coplanar (intersecting or parallel) a12 sinα12 = 0 | Perpendicular α12 = 90° |
| Constraint couple line (h1 = ∞) | Perpendicular α12 = 90° | Arbitrary | |
| TMD | 1st Mode | 2nd Mode |
|---|---|---|
| Bending | Torsion | |
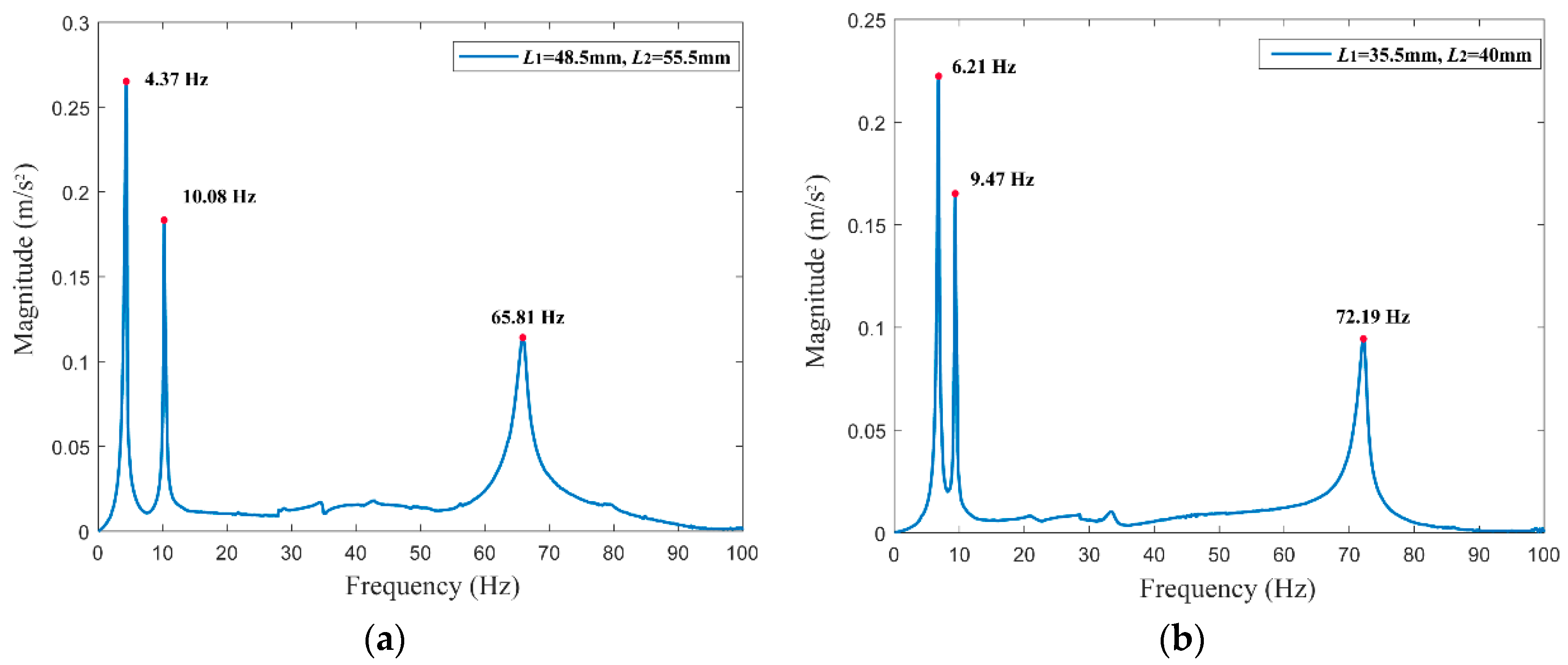
| TMD1 | 4.15 Hz | 10.5 Hz |
| TMD2 | 6.14 Hz | 9.59 Hz |
| TMD | Dimension Parameter (m) | Natural Frequency (Hz) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L1 | L2 | d1 | d2 | d3 | d4 | ω1 | ω2 | ω3 | ω4 | |
| TMD1 | 0.045 | 0.059 | 0.015 | 0.0106 | 0.0075 | 0.0106 | 4.16 | 10.54 | 74.07 | 119.7 |
| TMD2 | 0.0362 | 0.042 | 0.0105 | 0.0105 | 0.008 | 0.0105 | 6.14 | 9.55 | 77.7 | 109.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, F.; Wan, J.; Xia, Y.; Ma, Y.; Yu, J. A Multi-Degree of Freedom Tuned Mass Damper Design for Vibration Mitigation of a Suspension Bridge. Appl. Sci. 2020, 10, 457. https://doi.org/10.3390/app10020457
Meng F, Wan J, Xia Y, Ma Y, Yu J. A Multi-Degree of Freedom Tuned Mass Damper Design for Vibration Mitigation of a Suspension Bridge. Applied Sciences. 2020; 10(2):457. https://doi.org/10.3390/app10020457
Chicago/Turabian StyleMeng, Fanhao, Jiancheng Wan, Yongjun Xia, Yong Ma, and Jingjun Yu. 2020. "A Multi-Degree of Freedom Tuned Mass Damper Design for Vibration Mitigation of a Suspension Bridge" Applied Sciences 10, no. 2: 457. https://doi.org/10.3390/app10020457
APA StyleMeng, F., Wan, J., Xia, Y., Ma, Y., & Yu, J. (2020). A Multi-Degree of Freedom Tuned Mass Damper Design for Vibration Mitigation of a Suspension Bridge. Applied Sciences, 10(2), 457. https://doi.org/10.3390/app10020457






