Jet Noise in Airframe Integration and Shielding
Abstract
:1. Introduction
2. Experimental Observation on Airframe Effect on Jet Noise
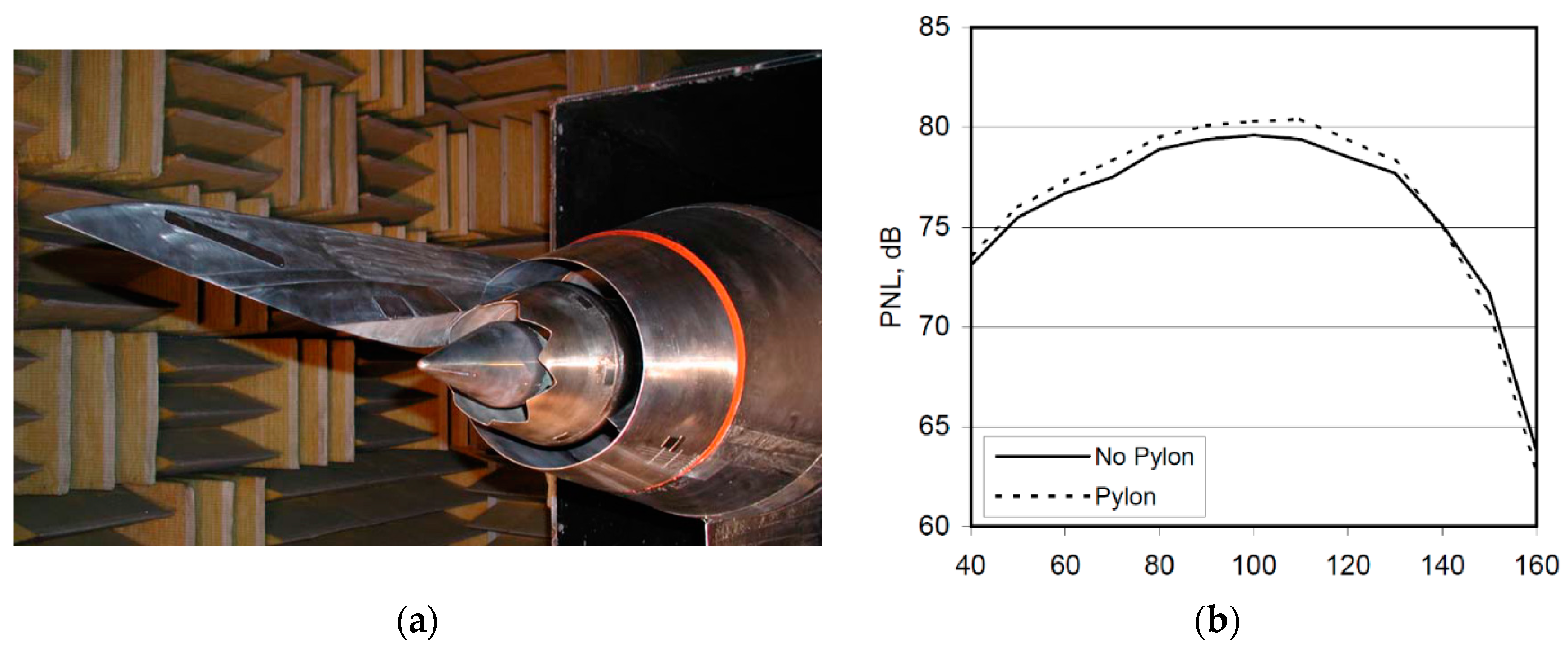
2.1. Jet—Pylon Interactions
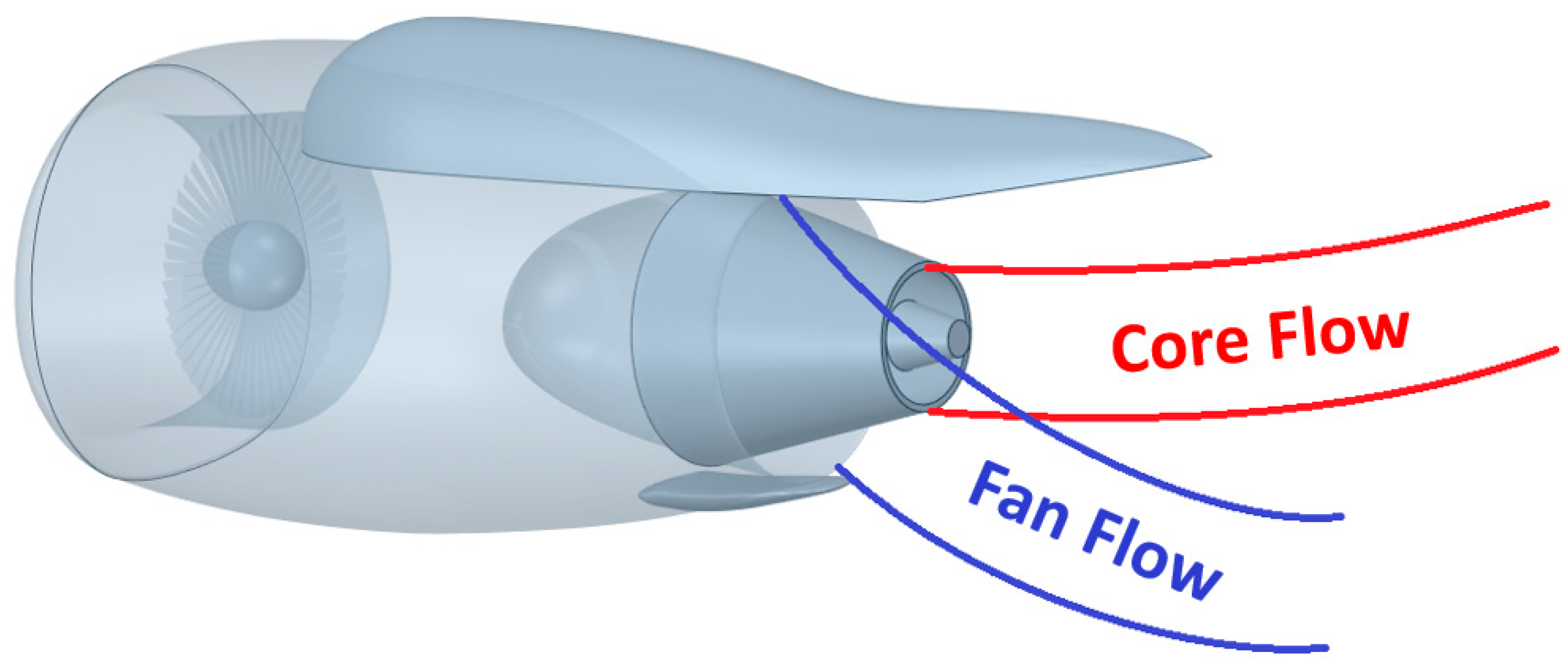
2.2. Jet—Wing Interactions
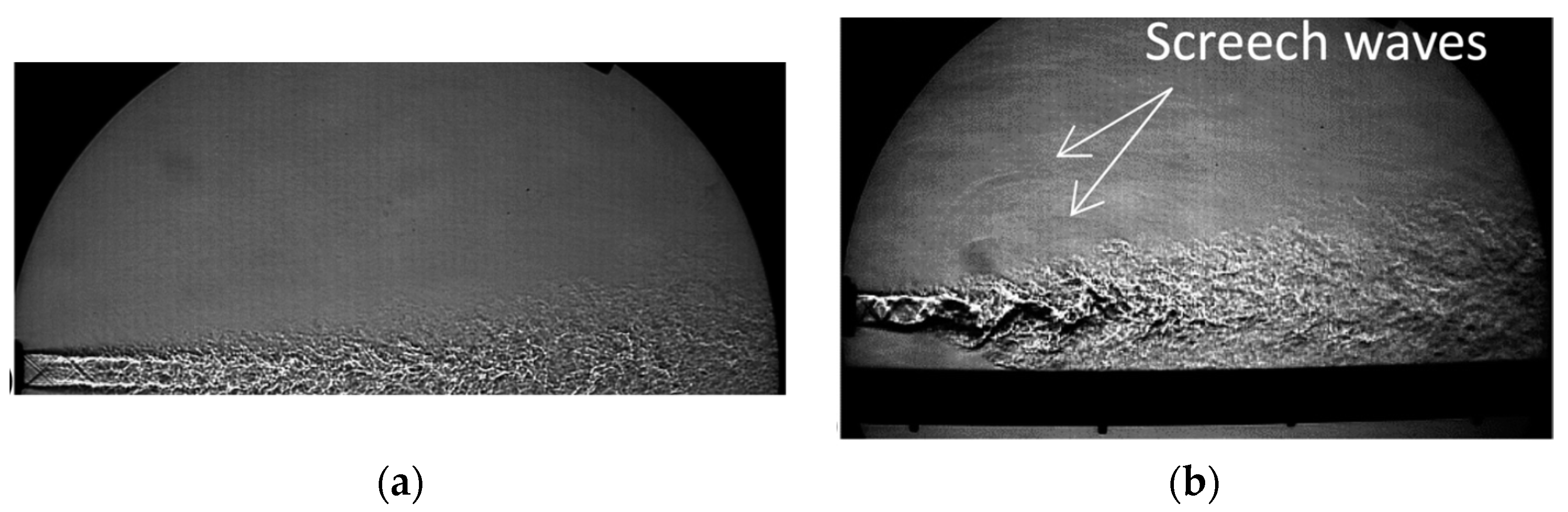
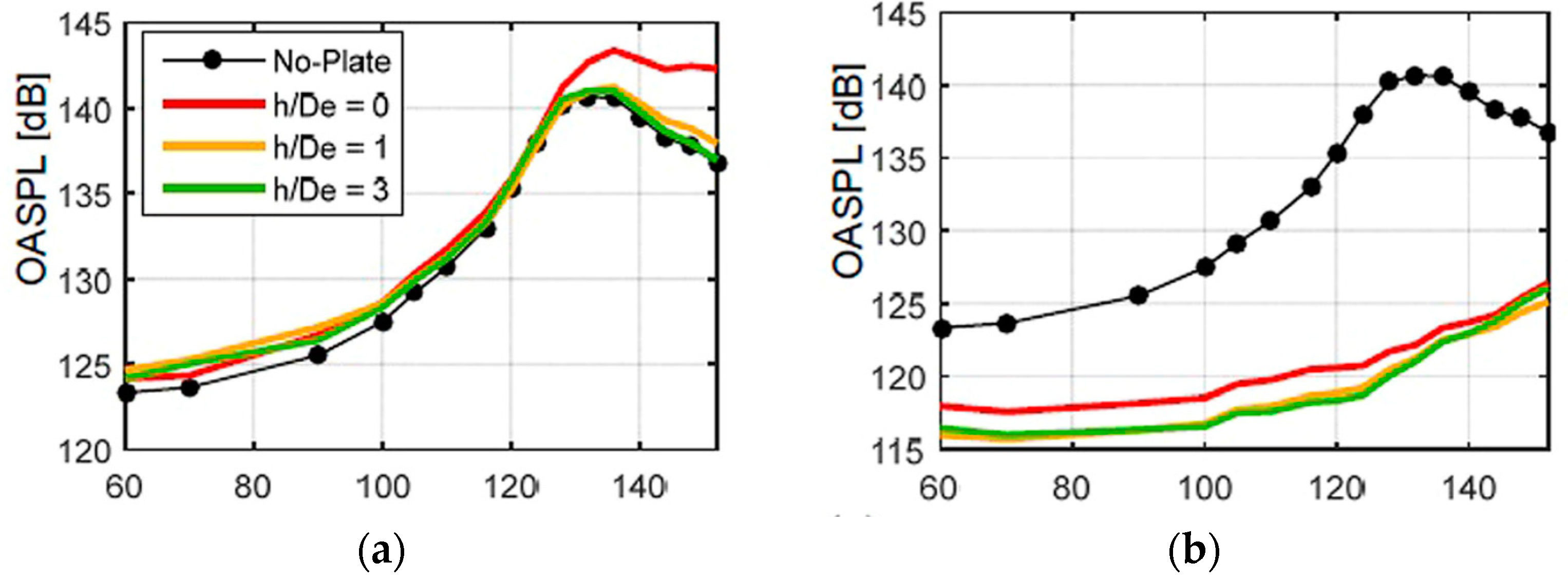
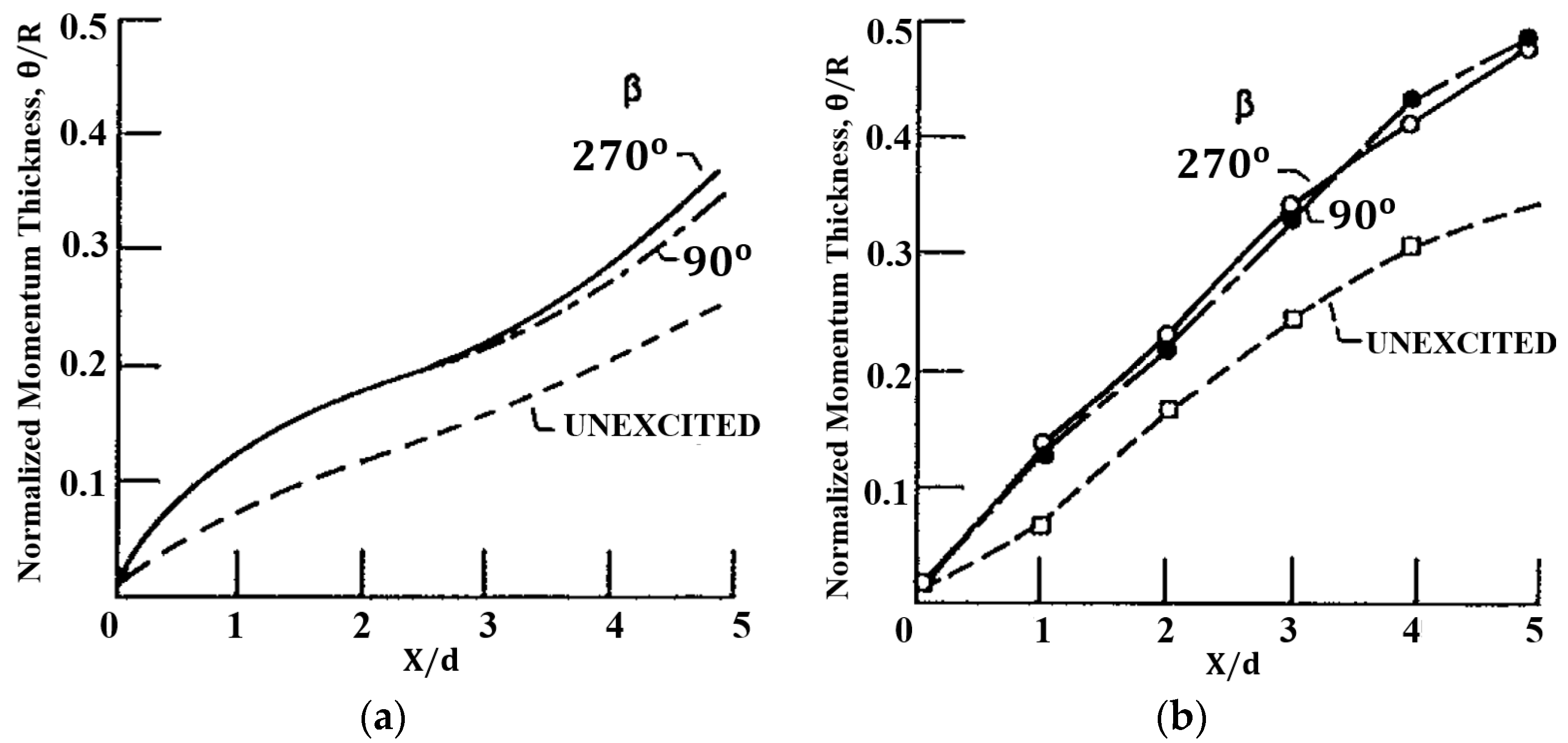
2.3. Jet—Flap Interactions
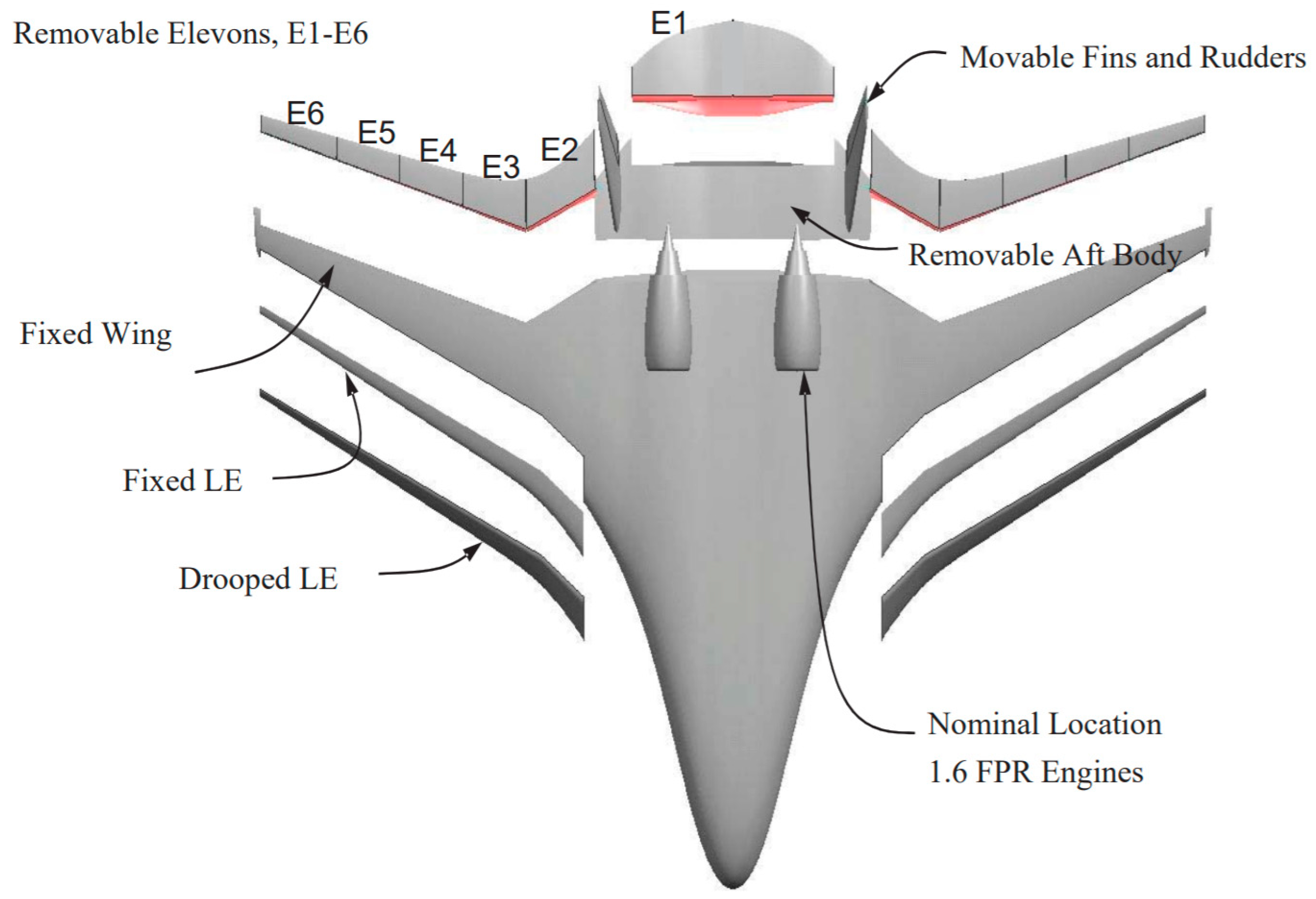
2.4. Hybrid Wing Body Concept
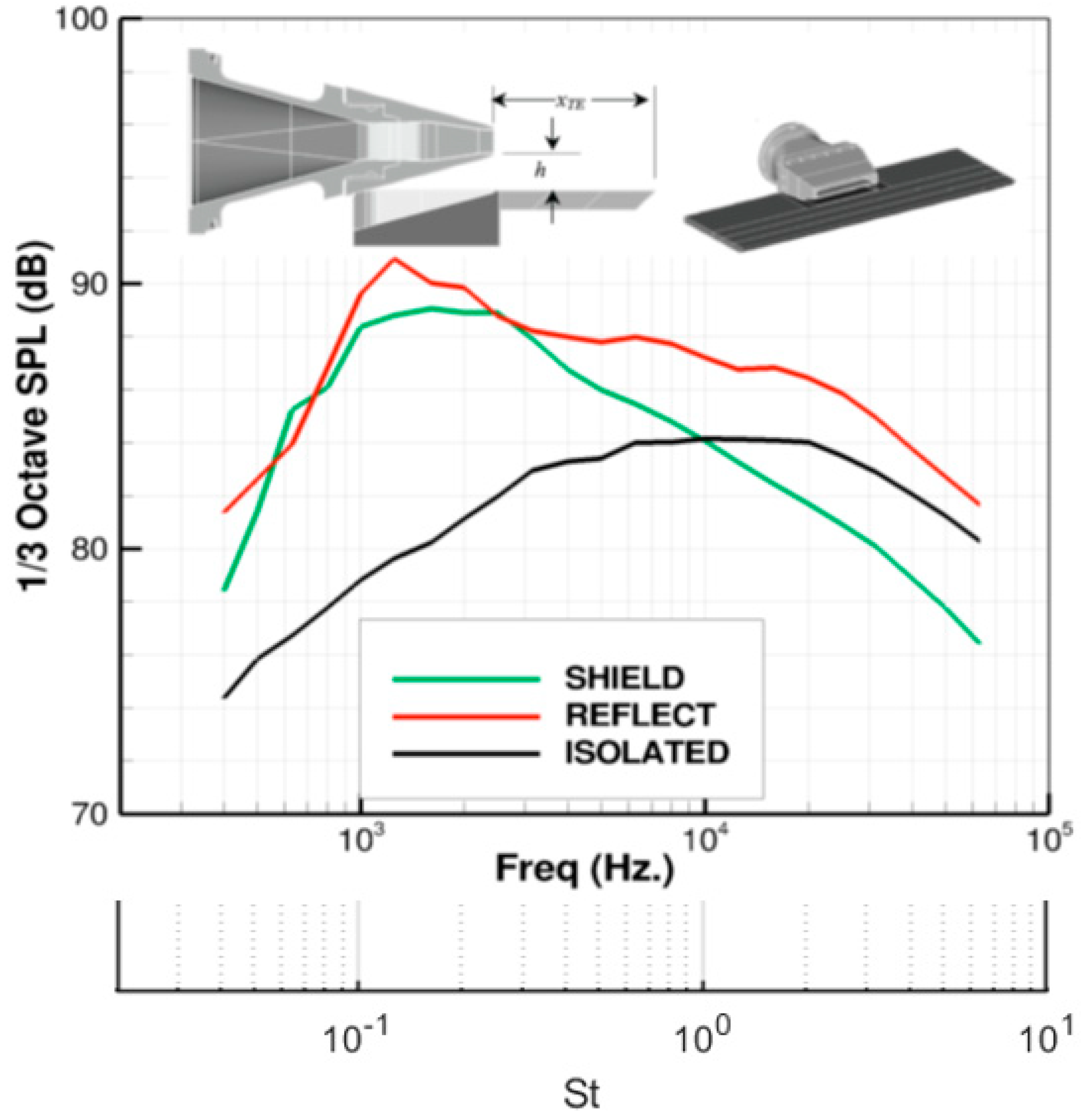
2.5. Shielding Effects
3. Options for Computation of Jet Noise
3.1. Numerical Issues in Capturing the Unsteady Flow and Sound Scales
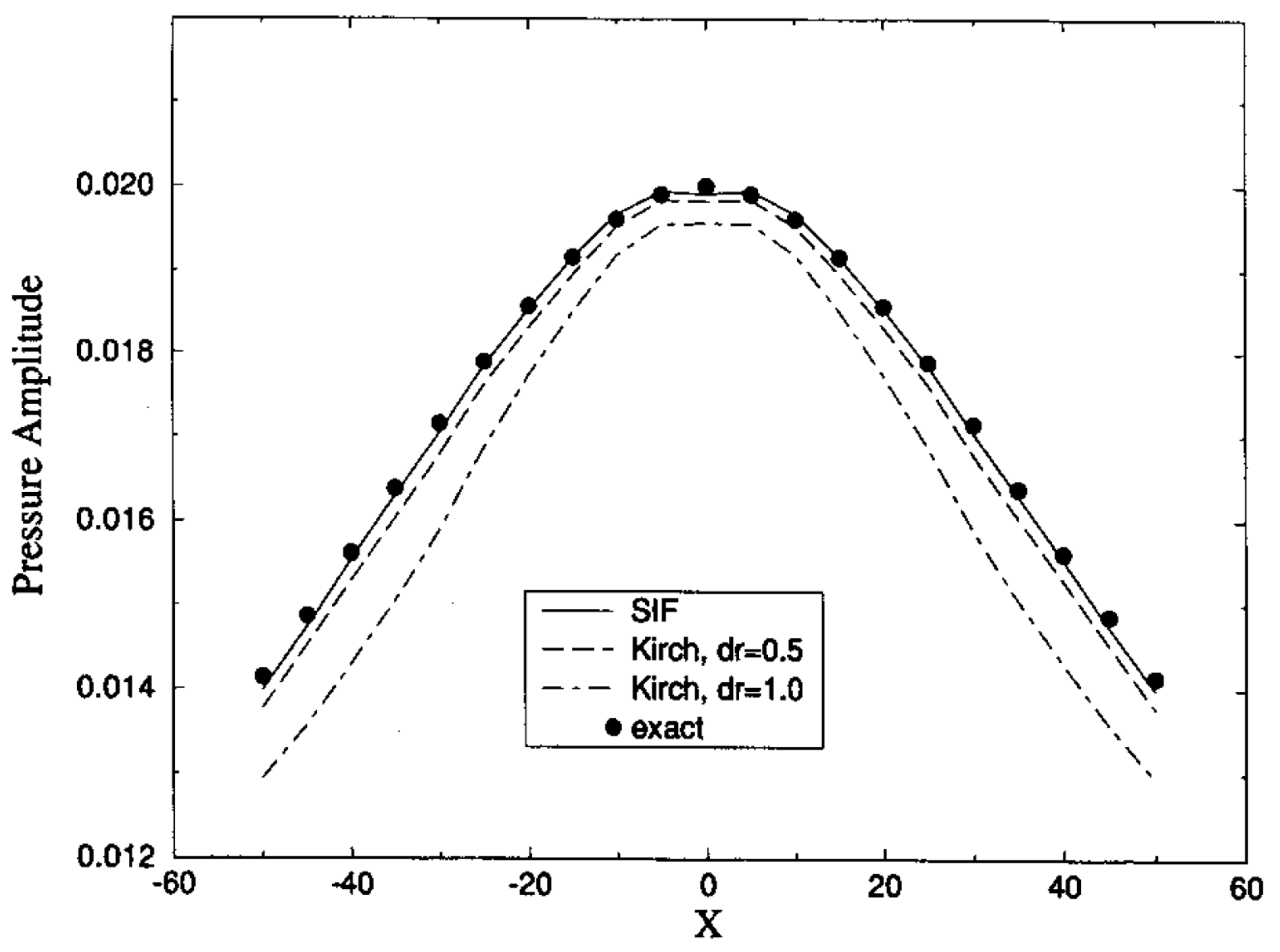
3.2. Extension of the Near Field to the Far Field
3.3. Large-Eddy Simulations
3.4. Faster Simulations Using Linearized Euler Equations
3.5. Very Large-Eddy Simulations
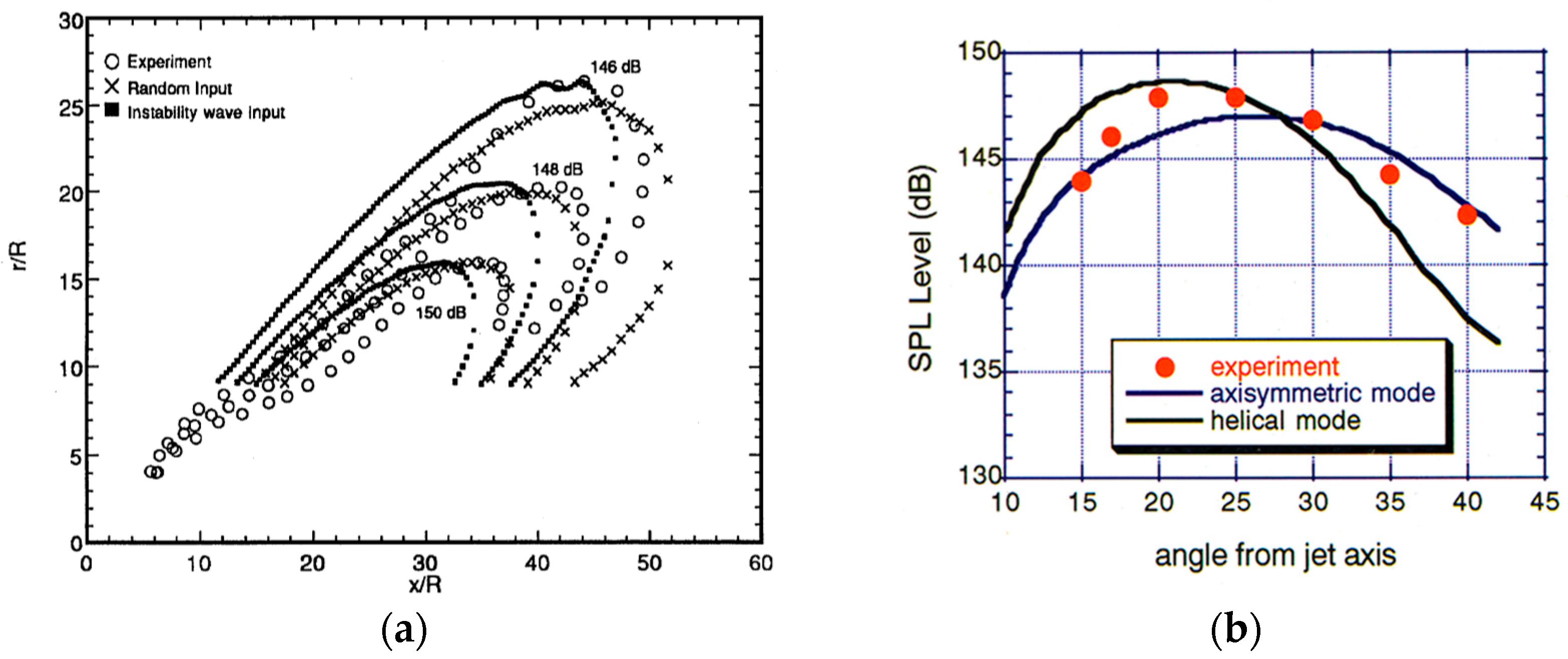
3.6. Active Flow Control for Jet Noise Reduction
4. Numerical Simulation of the Shielding Effect
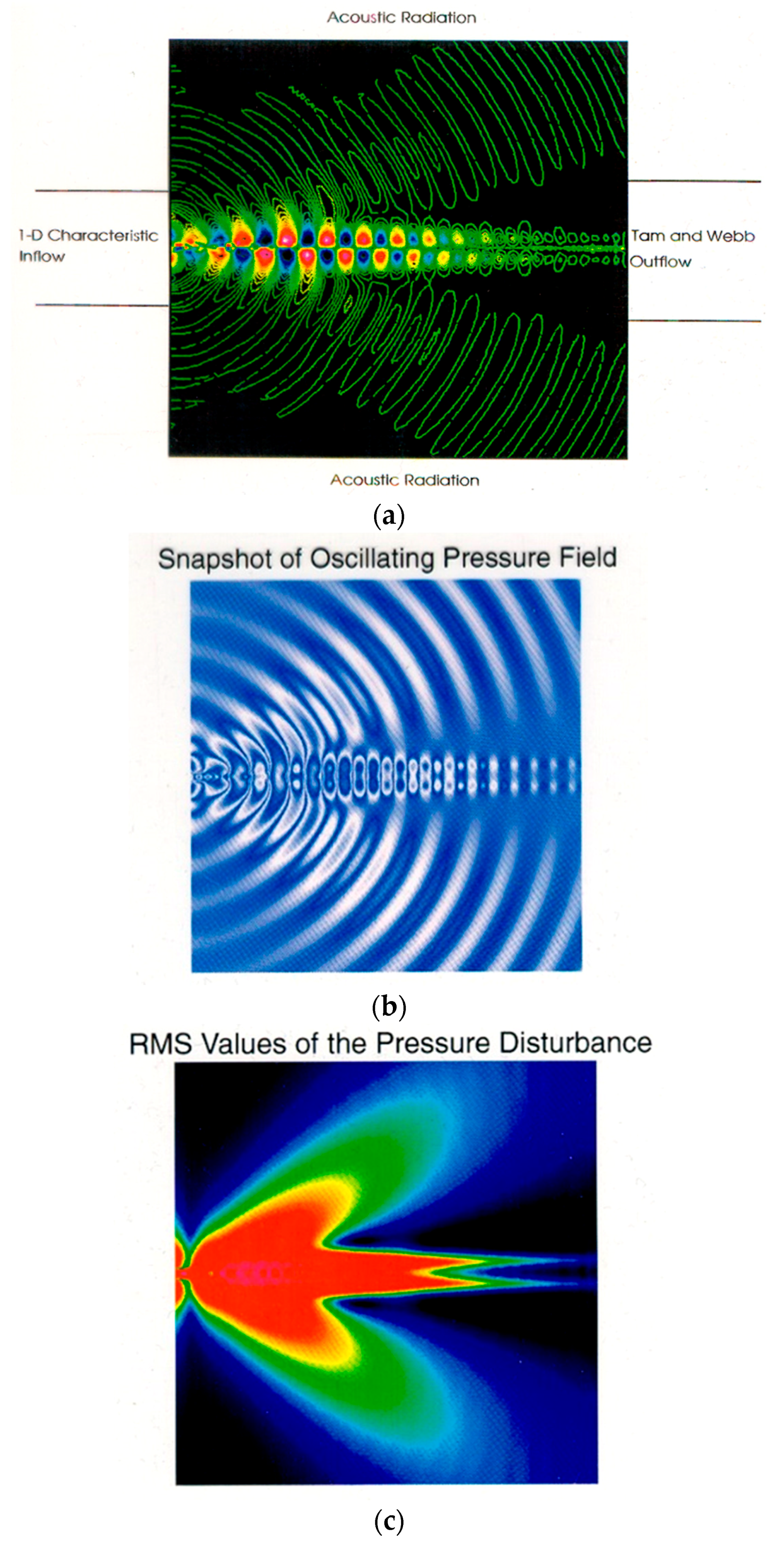
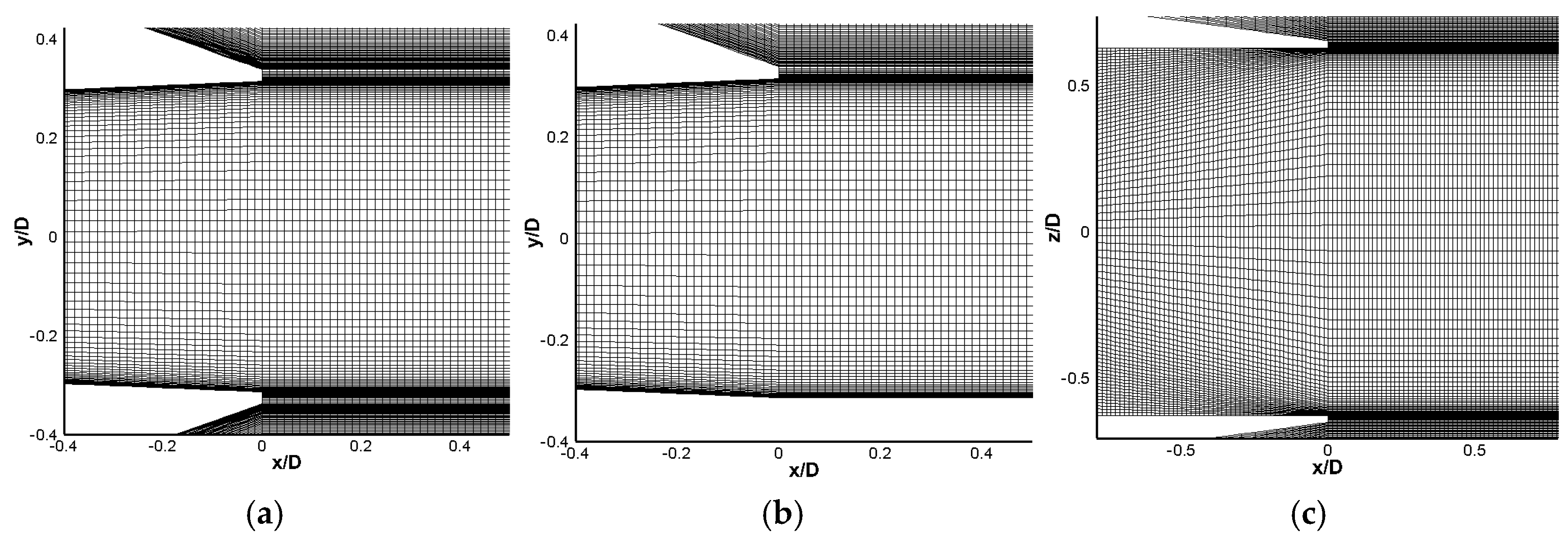
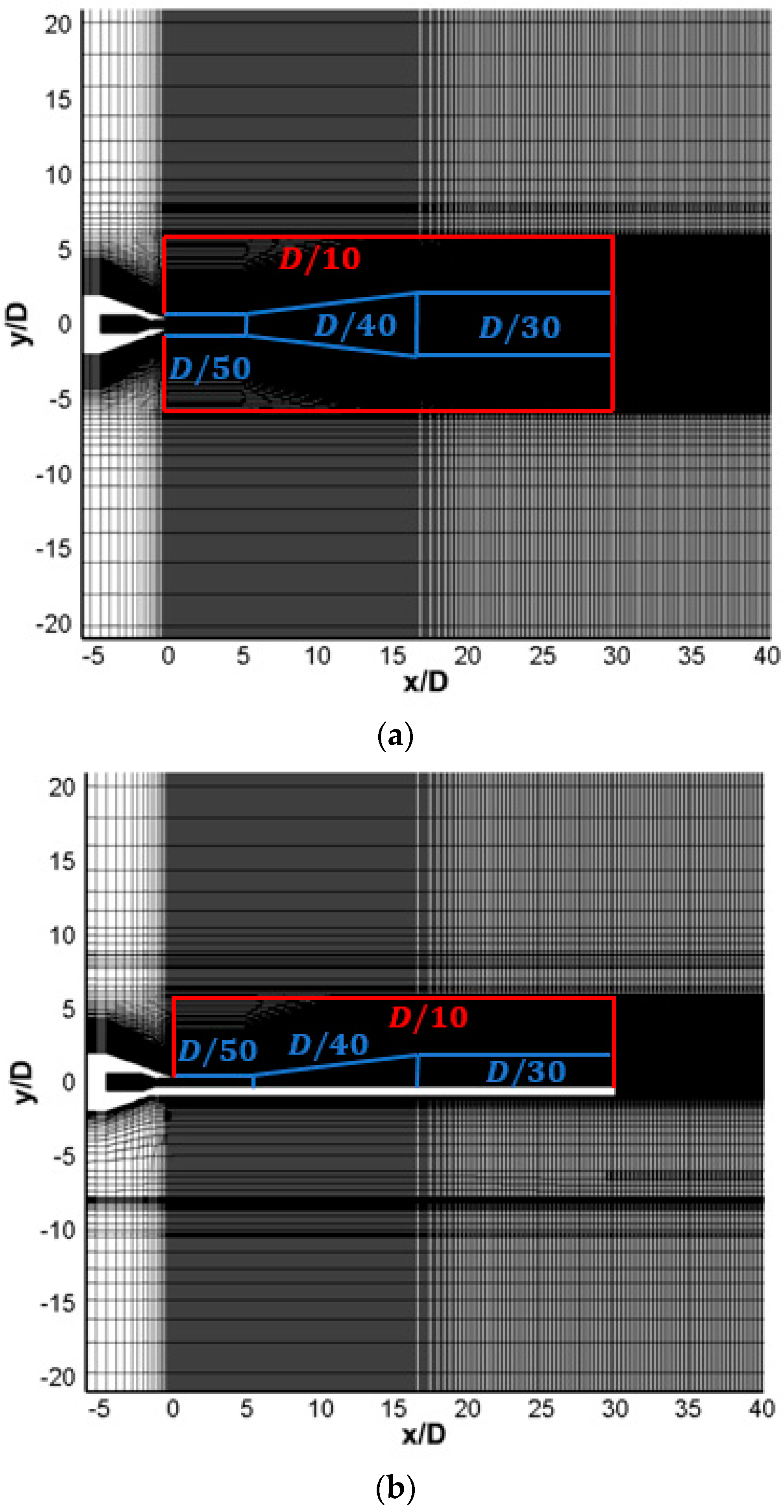
4.1. Numerical Approach
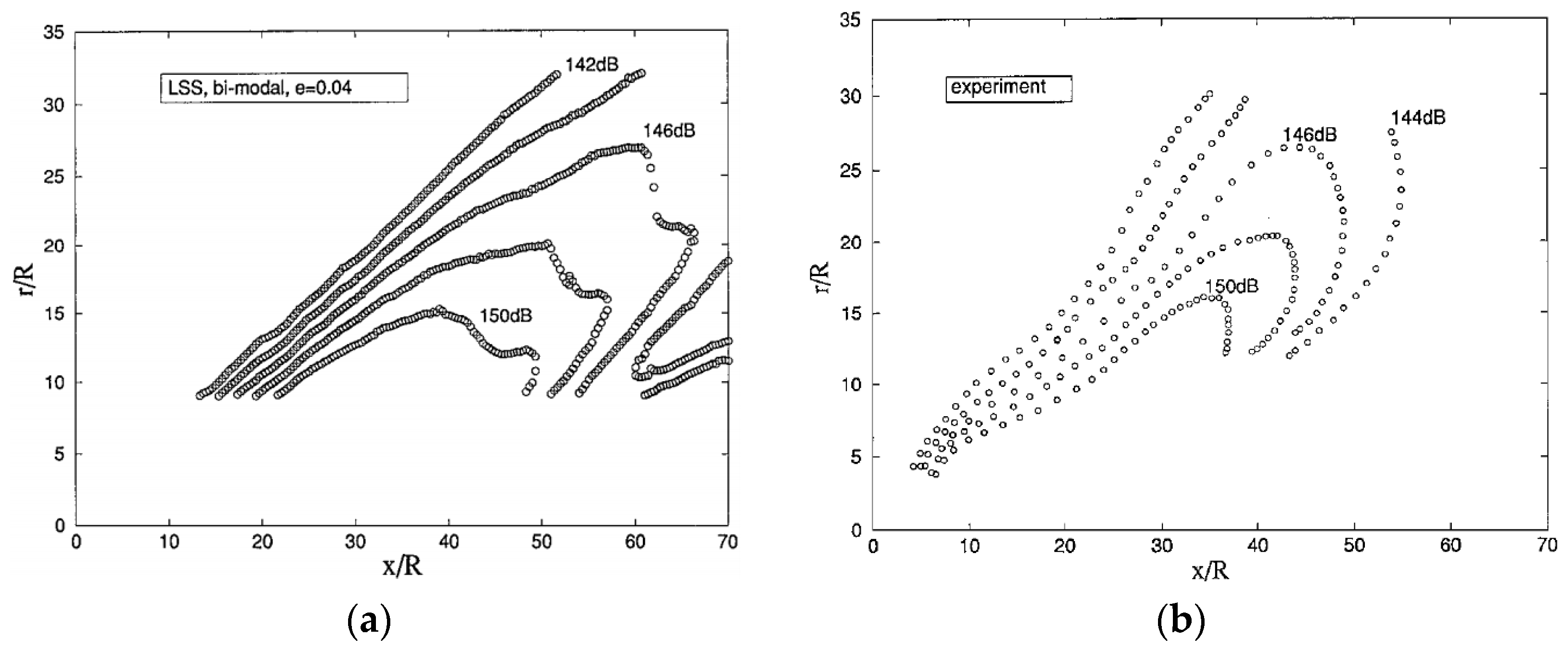
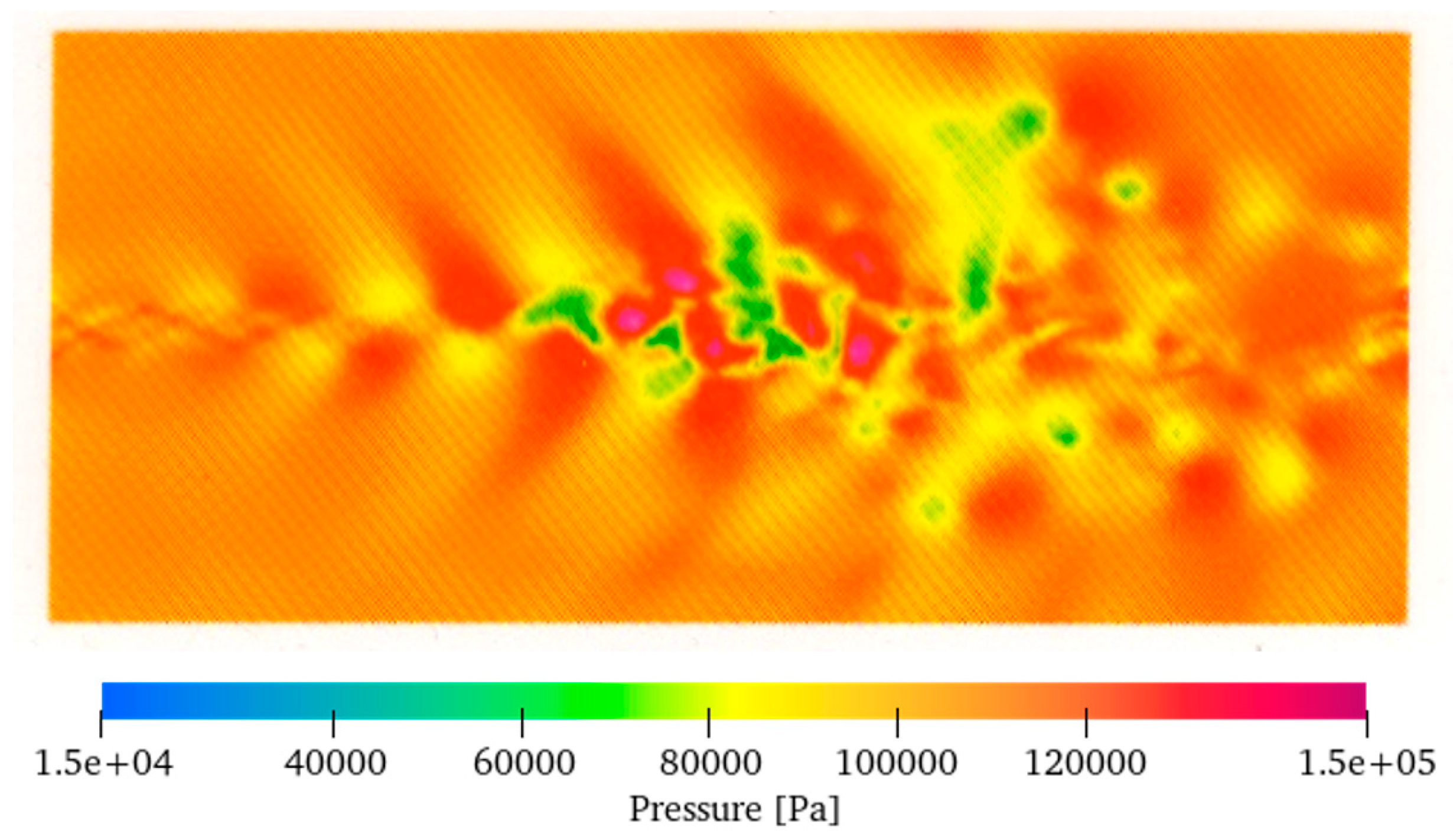
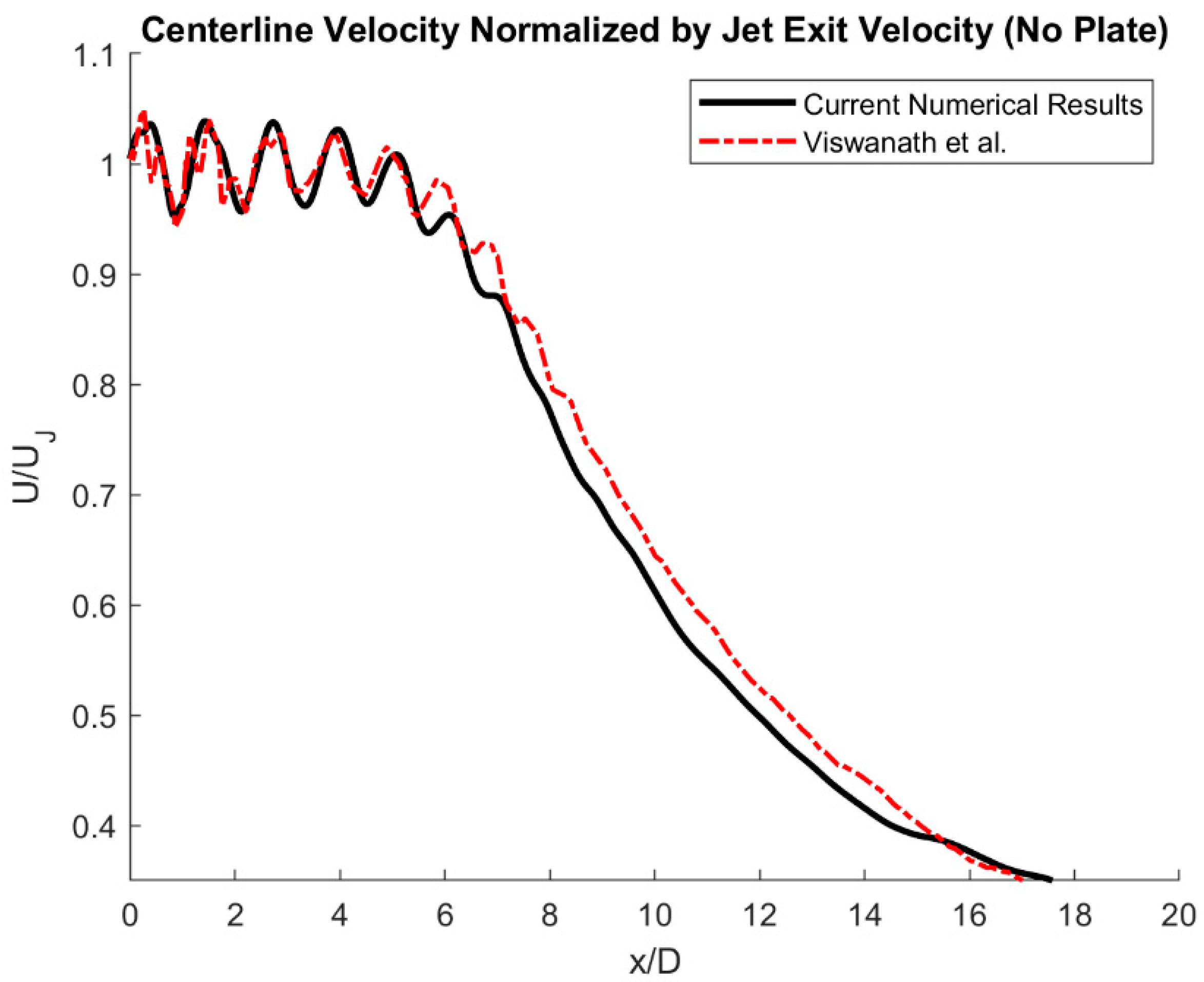
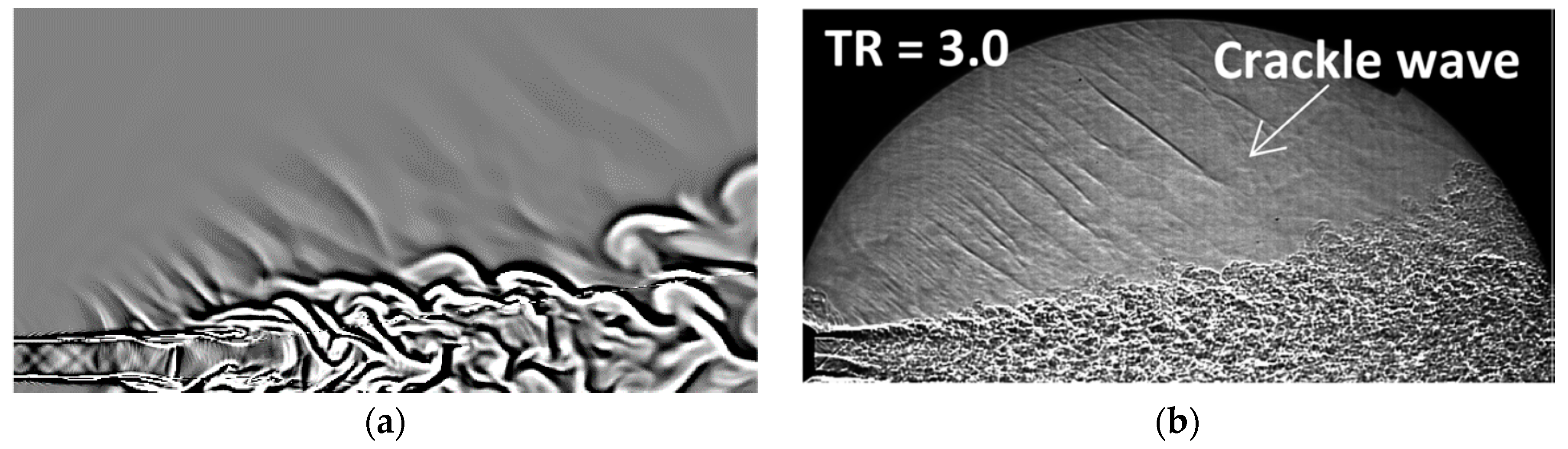
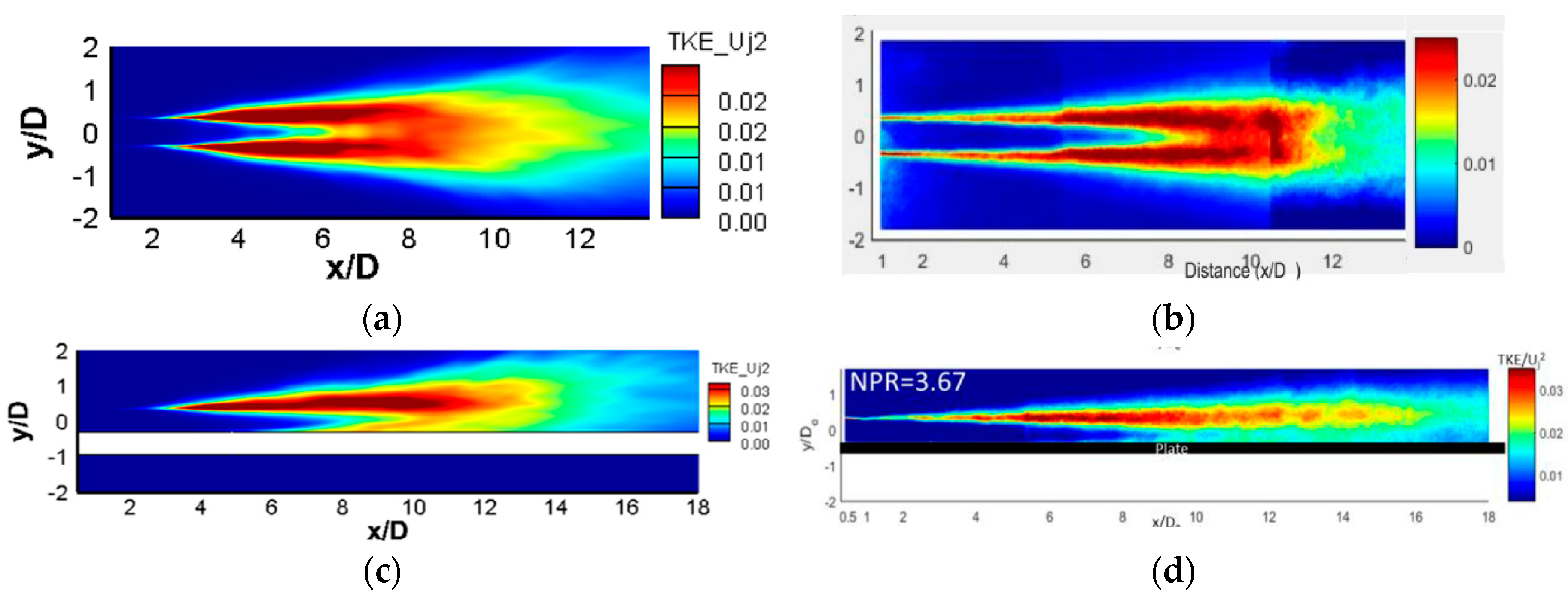
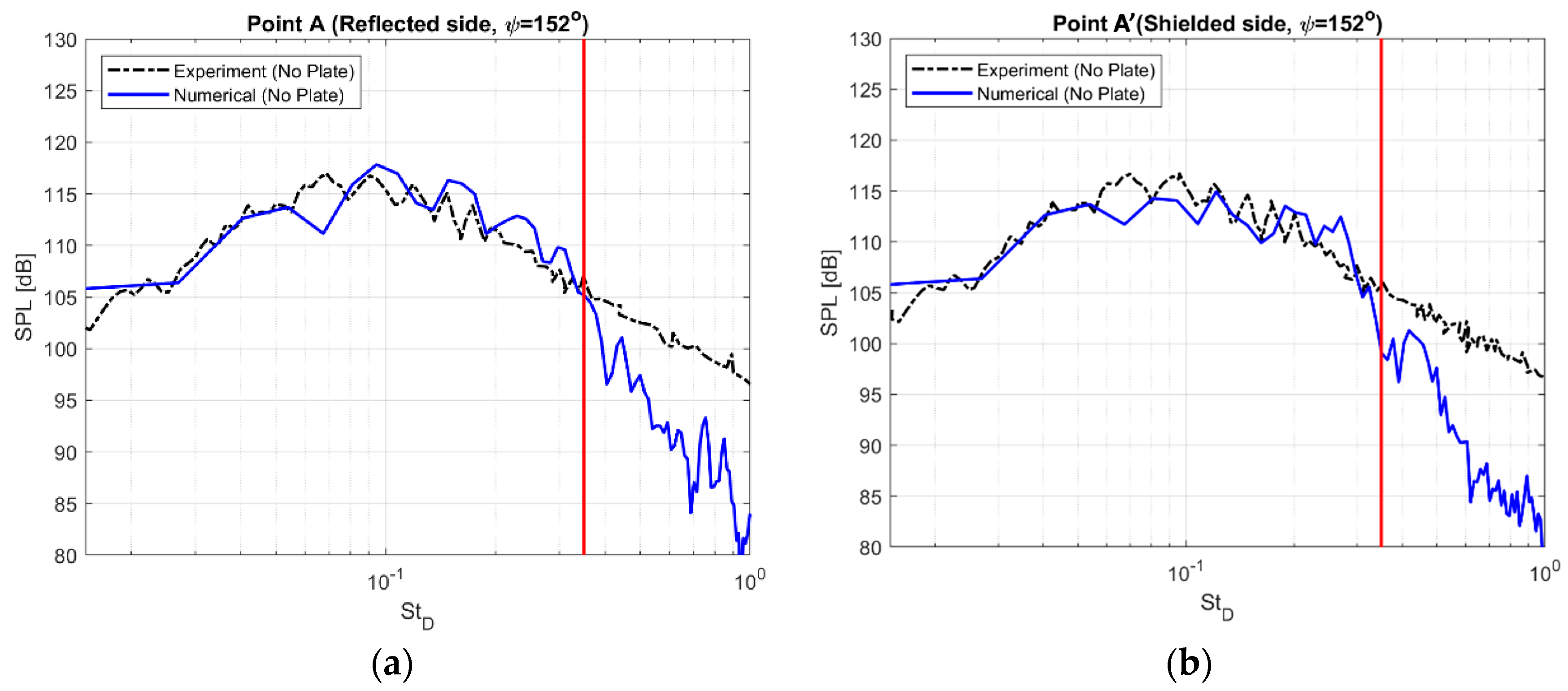
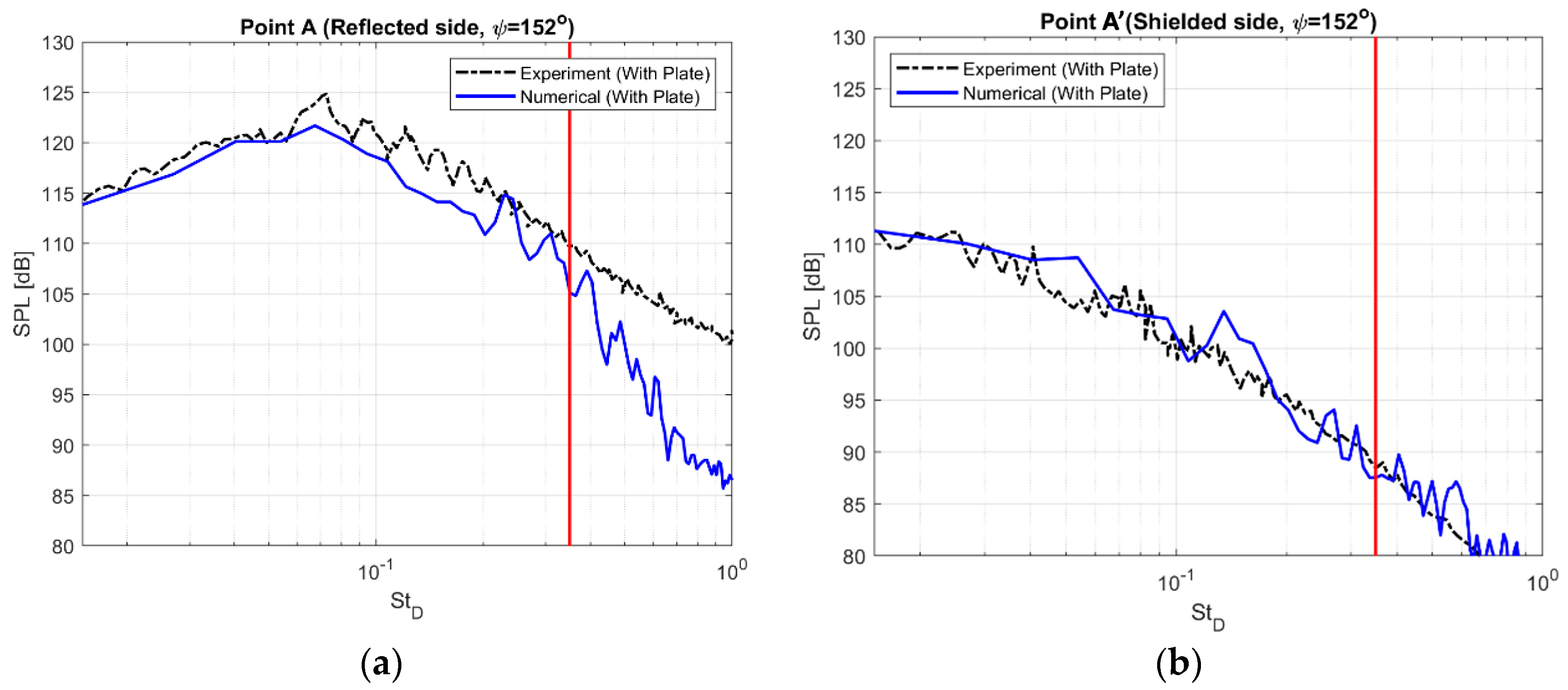
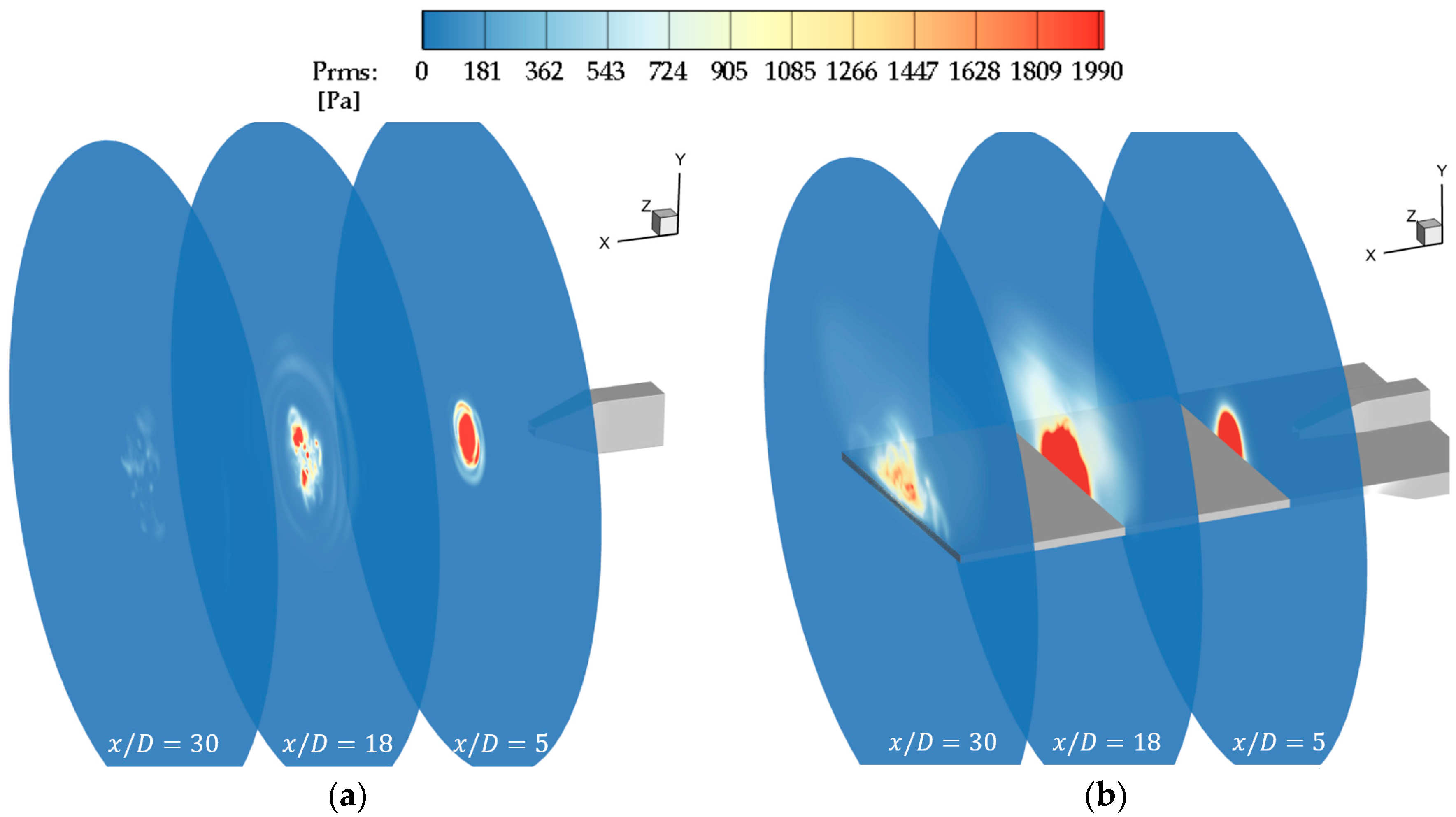
4.2. Numerical Results
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Federal Aviation Regulation 36, Section 5. Federal Aviation Regulation. Noise Standards: Aircraft Type and Airworthiness Certification; US Government Printing Office: Washington, DC, USA, 2005.
- Perrino, M. An Experimental Study into Pylon, Wing, and Flap Installation Effects on Jet Noise Generated by Commercial Aircraft. Ph.D. Thesis, University of Cincinnati, Cincinnati, OH, USA, 2004. [Google Scholar]
- Bhat, T.R.S. Experimental Study of Acoustic Characteristics of Jets from Dual Flow Nozzles. In Proceedings of the 7th AIAA/CEAS Aeroacoustics Conference and Exhibit, Maastricht, The Netherlands, 28–30 May 2001. [Google Scholar] [CrossRef]
- Thomas, R.H.; Kinzie, K.W.; Jet-Pylon, R.H. Interaction of High Bypass Ratio Separate Flow Nozzle Configurations. In Proceedings of the 10th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10–12 May 2004. [Google Scholar]
- Head, R.W.; Fisher, M.J. Jet/surface interaction noise: Analysis of farfield low frequency augmentation of jet noise due to the presence of a solid shield. In Proceedings of the 3rd Aeroacoustics Conference, Palo Alto, CA, USA, 20–23 July 1976. [Google Scholar] [CrossRef]
- Southern, I.S. Exhaust noise in flight: The role of acoustic installation effects. In Proceedings of the 6th Aeroacoustics Conference, Hartford, CT, USA, 4–6 June 1980. [Google Scholar] [CrossRef]
- Brown, W.H.; Ahuja, K.K. Jet and wing/flap interaction noise. In Proceedings of the 9th Aeroacoustics Conference, Williamsburg, VA, USA, 15–17 October 1984. [Google Scholar] [CrossRef]
- Way, D.J.; Turner, B.A. Model tests demonstrating under-wing installation effects on engine exhaust noise. In Proceedings of the 6th Aeroacoustics Conference, Hartford, CT, USA, 4–6 June 1980. [Google Scholar] [CrossRef]
- Wang, M.E. Wing effect on jet noise propagation. J. Aircr. 1981, 18, 295–302. [Google Scholar] [CrossRef]
- Denisov, S.; Faranosov, G.; Ostrikov, N.; Bychkov, O. Theoretical modeling of the excess noise due to jet-wing interaction. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May –1 June 2016. [Google Scholar] [CrossRef]
- Mead, C.J.; Strange, P.J.R. Under-wing installation effects on jet noise at sideline. In Proceedings of the 4th AIAA/CEAS Aeroacoustics Conference, Toulouse, France, 2–4 June 1998. [Google Scholar] [CrossRef]
- Shivashankara, B.N.; Blackner, A.M. Installed jet noise. In Proceedings of the 3rd AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 12–14 May 1997. [Google Scholar] [CrossRef]
- Blackner, A.M.; Bhat, T.R.S. Installation effects on coaxial jet noise—An experimental study. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998. [Google Scholar] [CrossRef]
- Bhat, T.R.S.; Blackner, A.M. Installed jet noise prediction model for coaxial jets. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998. [Google Scholar] [CrossRef]
- Bhat, T.R.S. Jet-Flap Installation Noise; NASA Contractor Final Report on Contract NAS 1-20267, Task 17, Subtask 2; NASA: Washington, DC, USA, 1998.
- Lu, H.Y. An empirical model for prediction of coaxial jet noise in ambient flow. In Proceedings of the 10th Aeroacoustics Conference, Seattle, WA, USA, 9–11 July 1986. [Google Scholar] [CrossRef]
- Mengle, V.G.; Elkoby, R.; Brusniak, L.; Thomas, R.H. Reducing Propulsion Airframe Aeroacoustic Interactions with Uniquely Tailored Chevrons: 3. Jet-Flap Interaction. In Proceedings of the 12th AIAA/CEAS Aeroacoustics Conference (27th AIAA Aeroacoustics Conference), Cambridge, MA, USA, 8–10 May 2006. [Google Scholar] [CrossRef] [Green Version]
- Faranosov, G.; Kopiev, V.; Ostrikov, N.; Kopiev, V.A. The effect of pylon on the excess jet-flap interaction noise. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016. [Google Scholar] [CrossRef]
- Thomas, R.H. Subsonic Fixed Wing Project N+2 Noise Goal Summary. In Proceedings of the NASA Acoustics Technical Working Group, Cleveland, OH, USA, 4–5 December 2007. [Google Scholar]
- Liebeck, R.H. Design of the Blended-Wing-Body Subsonic Transport. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002. [Google Scholar] [CrossRef] [Green Version]
- Khavaran, A. Acoustics of Jet Surface Interaction-Scrubbing Noise. In Proceedings of the 20th AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar] [CrossRef] [Green Version]
- Czech, M.J.; Russell, H.T.; Ronen, E. Propulsion airframe aeroacoustic integration effects for a hybrid wing body aircraft configuration. Int. J. Aeroacoust. 2012, 11, 335–367. [Google Scholar] [CrossRef] [Green Version]
- Henderson, B.; Doty, M. Advanced Jet Noise Exhaust Concepts in NASA’s N+2 Supersonics Validation Study and the Environmentally Responsible Aviation Project’s Upcoming Hybrid Wing Body Acoustics Test. In Proceedings of the Virginia Tech Graduate Seminar, Blacksburg, VA, USA, 17 September 2012. Document ID: 20130000430. [Google Scholar]
- Heath, S.; Brooks, T.; Hutcheson, F.V.; Doty, M.J.; Haskin, H.; Spalt, T.; Bahr, C.J.; Burley, C.L.; Bartram, S.; Humphreys, W.; et al. Hybrid wing body aircraft acoustic test preparations and facility upgrades. In Proceedings of the AIAA Ground Testing Conference, San Diego, CA, USA, 24–27 June 2013. [Google Scholar] [CrossRef]
- Papamoschou, D.; Mayoral, S. Jet Noise Shielding for Advanced Hybrid Wing-Body Configuration. In Proceedings of the 49th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. [Google Scholar] [CrossRef] [Green Version]
- Doty, M.J.; Brooks, T.F.; Burley, C.L.; Bahr, C.J.; Pope, D.S. Jet noise shielding provided by a hybrid wing body aircraft. In Proceedings of the 20th AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar] [CrossRef] [Green Version]
- Brown, C.A. Jet-Surface interaction test: Far-field noise results. Aircraft Engine; Ceramics; Coal, Biomass and Alternative Fuels; Controls, Diagnostics and Instrumentation. In Proceedings of the ASME Turbo Expo: Power for Land, Sea, and Air, Copenhagen, Denmark, 11–15 June 2012; Volume 1. [Google Scholar] [CrossRef] [Green Version]
- Podboy, G.G. Jet-Surface interaction test: Phased array noise source localization results. Aircraft Engine; Ceramics; Coal, Biomass and Alternative Fuels; Controls, Diagnostics and Instrumentation. In Proceedings of the ASME Turbo Expo: Power for Land, Sea, and Air, Copenhagen, Denmark, 11–15 June 2012; Volume 1. [Google Scholar] [CrossRef] [Green Version]
- Bridges, J.E. Noise from Aft Deck Exhaust Nozzles—Differences in Experimental Embodiments. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, Maryland, 13–17 January 2014. [Google Scholar] [CrossRef] [Green Version]
- Zaman, K.Q.; Fagan, A.F.; Bridges, J.E.; Brown, C.A. Investigating the feedback path in a jet-surface resonant interaction. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar] [CrossRef] [Green Version]
- Bridges, J.E.; Wernet, M.P. Noise measurements of high aspect ratio distributed exhaust systems. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar] [CrossRef] [Green Version]
- McLaughlin, D.; Kno, C.W.; Papamoschou, D. Experiments on the Effect of Ground Reflections on Supersonic Jet Noise. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008. [Google Scholar] [CrossRef] [Green Version]
- Brown, C.A.; Clem, M.M.; Fagan, A.F. Investigation of Broadband Shock Noise from a Jet Near a Planar Surface. J. Aircr. 2014, 52, 266–273. [Google Scholar] [CrossRef]
- Clem, M.; Brown, C.; Fagan, A. Background oriented schlieren implementation in a jet-surface interaction test. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar] [CrossRef] [Green Version]
- Mora, P.; Baier, F.; Kailasanath, K.; Gutmark, E.J. Acoustics from a rectangular supersonic nozzle exhausting over a flat surface. J. Acoust. Soc. Am. 2016, 140, 4130–4141. [Google Scholar] [CrossRef]
- Powers, R.W.; McLaughlin, D.K.; Morris, P.J. Noise reduction with fluidic inserts in supersonic jets exhausting over a simulated aircraft carrier deck. J. Aircr. 2018, 55, 310–324. [Google Scholar] [CrossRef]
- Brown, C.A. An Empirical Jet-Surface Interaction Noise Model with Temperature and Nozzle Aspect Ratio Effects. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef] [Green Version]
- Brown, C.A. Empirical Models for the Shielding and Reflection of Jet Mixing Noise by a Surface. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar] [CrossRef] [Green Version]
- Bridges, J.E.; Podboy, G.G.; Brown, C.A. Testing Installed Propulsion For Shielded Exhaust Configurations. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016. [Google Scholar] [CrossRef] [Green Version]
- Mankbadi, R.R.; Liu, J.T.C. Sound Generated Aerodynamically Revisited: Large-Scale Coherent Structure in a Turbulent Jet as a Source of Sound. Philos. Trans. R. Soc. Lond. 1984, 311, 183–217. [Google Scholar] [CrossRef]
- Lush, P.A. Measurements of subsonic jet noise and comparison with theory. J. Fluid Mech. 1971, 46, 477–500. [Google Scholar] [CrossRef]
- Hixon, R. On increasing the accuracy of MacCormack schemes for aeroacoustic applications. In Proceedings of the 3rd AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 12–14 May 1997. [Google Scholar] [CrossRef] [Green Version]
- Lele, S.K. Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]
- Tam, C.K.W.; Webb, J.C. Dispersion-relation-preserving finite difference schemes for computational acoustics. J. Comput. Phys. 1993, 107, 262–281. [Google Scholar] [CrossRef]
- Kurbatskii, K.; Mankbadi, R.R. Review of Computational Aeroacoustics Algorithms. Int. J. Comput. Fluid Dyn. 2004, 18, 533–546. [Google Scholar] [CrossRef]
- Giles, M.B. Nonreflecting Boundary Conditions for Euler Equations Calculations. AIAA J. 1990, 28, 2050–2058. [Google Scholar] [CrossRef]
- Thompson, K.W. Time-dependent boundary conditions for Hyperbolic Systems. J. Comput. Phys. 1990, 89, 439–461. [Google Scholar] [CrossRef]
- Mankbadi, R.R.; Ali, A.A. Evaluation of Subsonic Inflow Treatments for Unsteady Jet Flow. J. Comput. Acoust. 1999, 7, 147–160. [Google Scholar] [CrossRef]
- Hixon, D.R.; Shih, S.H.; Mankbadi, R.R. Evaluation of Boundary Conditions for Computational Aero-Acoustics. AIAA J. 1995, 33, 2006–2012. [Google Scholar] [CrossRef]
- Lighthill’s, M.J. On Sound Generation Aerodynamically: Part I, General Theory. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1952, 211, 564–587. [Google Scholar] [CrossRef]
- Williams, J.F.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Philos. Trans. R. Soc. Lond. A: Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar] [CrossRef]
- Lyrintzis, A.; Mankbadi, R.R. Prediction of the Far-Field Jet Noise Using Kirchhoff Method. AIAA J. 1996, 34, 413–416. [Google Scholar] [CrossRef]
- Mankbadi, R.R.; Shih, S.-H.; Hixon, D.R.; Stuart, J.T.; Povinelli, L.A. A Surface-Integral Formulation for Jet Noise Prediction Based on the Pressure Signal Alone. J. Comput. Acoust. 1998, 6, 307–320. [Google Scholar] [CrossRef]
- Lyrintzis, A. Surface integral methods in computational aeroacoustics—From the (CFD) near-field to the (Acoustic) far-field. Int. J. Aeroacoust. 2003, 2, 95–128. [Google Scholar] [CrossRef]
- Mankbadi, R.R.; Hayer, M.E.; Povinelli, L.A. The Structure of Supersonic Jet Flow and Its Radiated Sound. AIAA J. 1994, 31, 897–906. [Google Scholar] [CrossRef]
- Mankbadi, R.R.; Liu, J.T.C. A Study of the Interactions between Large-Scale Coherent Structures and Fine-Grained Turbulence in a Round Jet. Philos. Trans. R. Soc. Lond. 1981, 298, 54l–602. [Google Scholar] [CrossRef]
- Mankbadi, R.R.; Shih, S.-H.; Hixon, D.R.; Povinelli, L.A. Direct Computation of Jet Noise Produced by Large-Scale Axisymmetric Structures. J. Propuls. Power 2000, 16, 207–215. [Google Scholar] [CrossRef]
- Mankbadi, R. Gas Turbine Engine Noise. Turbomachinery, Parts A, B, and C. In Proceedings of the ASME Turbo Expo: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008; Volume 6. [Google Scholar] [CrossRef]
- Troutt, T.R.; McLaughlin, D.K. Experiments on the Flow and Acoustic Properties of a Moderate-Reynolds-Number Supersonic Jet. J. Fluid Mech. 1982, 116, 123–156. [Google Scholar] [CrossRef]
- Shih, S.-H.; Hixon, D.R.; Mankbadi, R.R. Zonal Approach for Computational Aeroacoustics. AIAA J. Propuls. Power 1997, 13, 745–758. [Google Scholar] [CrossRef] [Green Version]
- Mankbadi, R.R.; Hixon, D.R.; Shih, S.-H.; Povinelli, L.A. Use of Linearized Euler Equations for Supersonic Jet Noise Prediction. AIAA J. 1998, 36, 140–147. [Google Scholar] [CrossRef]
- Mankbadi, R.R.; Hixon, R.; Povinelli, L.A. Very Large Eddy Simulations of Jet Noise. In Proceedings of the 6th AIAA/CEAS Aeroacoustics Conference, Lahaina, HI, USA, 12–14 June 2000. [Google Scholar] [CrossRef]
- Mankbadi, R.R. On the Interaction between Fundamental and Subharmonic Instability Waves in a Turbulent Round Jet. J. Fluid Mech. 1985, 160, 385–419. [Google Scholar] [CrossRef]
- Mankbadi, R.R. The Mechanisms of Mixing Enhancement and Suppression in a Circular Jet Under Excitation Conditions. Phys. Fluids 1985, 28, 2062–2074. [Google Scholar] [CrossRef]
- Mankbadi, R.R. Multifrequency Excited Jets. Phys. Fluids 1991, 3, 595–605. [Google Scholar] [CrossRef]
- Mankbadi, R.; Raman, G.; Rice, E. Phase development and its role on subharmonic control. In Proceedings of the 28th Aerospace Sciences Meeting, Reno, NV, USA, 8–11 January 1989. [Google Scholar] [CrossRef] [Green Version]
- Raman, G.; Rice, E.J.; Mankbadi, R.R. Saturation and the Limit of Jet Mixing Enhancement by Single Frequency Plane Wave Excitation: Experiment and Theory. In Proceedings of the 1st National Fluid Dynamics Conference, Cincinnati, OH, USA, 25–28 June 1988; pp. 1000–1007. [Google Scholar] [CrossRef]
- Zaman, K.B.M.Q.; Hussain, A.K.M.F. Vortex pairing in a circular jet under controlled excitation. Part 1. General jet response. J. Fluid Mech. 1980, 101, 449–491. [Google Scholar] [CrossRef]
- Raman, G.; Rice, E.J. Axisymmetric jet forced by fundamental and subharmonic tones. AIAA J. 1991, 29, 1114–1122. [Google Scholar] [CrossRef]
- Mankbadi, R.R. Transition, Turbulence, and Noise; Kluwer Academic Press: Boston, MI, USA, 1994; Republished by Springer. [Google Scholar]
- Mankbadi, R.R. Review of Computational Aeroacoustics in Propulsion Systems. AIAA J. Propuls. Power 1999, 15, 504–512. [Google Scholar] [CrossRef]
- Arbey, H.; Williams, J.F. Active cancellation of pure tones in an excited jet. J. Fluid Dyn. 1984, 149, 445–454. [Google Scholar] [CrossRef] [Green Version]
- Salehian, S.; Kurbatskii, K.; Golubev, V.V.; Mankbadi, R.R. Numerical Aspects of Rocket Lift-off Noise with Launch-Pad Aqueous Injection. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Kurganov, A.; Noelle, S.; Petrova, G. Semi-Discrete Central-Upwind Schemes for Hyperbolic Conservation Laws and Hamilton-Jacobi Equations. SIAM J. Sci. Comput. 2000, 23, 707–740. [Google Scholar] [CrossRef] [Green Version]
- Kurganov, A.; Tadmor, E. New High-Resolution Central Schemes for Nonlinear Conservation Laws and Convection Diffusion Equations. J. Comput. Phys. 2000, 160, 241–282. [Google Scholar] [CrossRef] [Green Version]
- Van Albada, G.D.; Van Leer, B.; Roberts, W. A comparative study of computational methods in cosmic gas dynamics. In Upwind and High-Resolution Schemes; Springer: Berlin/Heidelberg, Germany, 1997; pp. 95–103. [Google Scholar] [CrossRef] [Green Version]
- Greenshields, C.J.; Weller, H.G.; Gasparini, L.; Reese, J.M. Implementation of semi-discrete, non-staggered central schemes in a colocated, polyhedral, finite volume framework, for high-speed viscous flows. Int. J. Numer. Methods Fluids 2010, 63, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Marcantoni, L.F.G.; Tamagno, J.P.; Elaskar, S.A. High speed flow simulation using openfoam. Mecánica Comput. 2012, 31, 2939–2959. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Education: New York, NY, USA, 2007. [Google Scholar]
- Poinsot, T.J.; Lele, S.K. Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 1992, 101, 104–129. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. In Proceedings of the 4th International Symposium on Turbulence, Heat and Mass Transfer, Antalya, Turkey, 12–17 October 2003; pp. 625–632. [Google Scholar]
- Strelets, M. Detached eddy simulation of massively separated flows. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. [Google Scholar] [CrossRef]
- Epikhin, A.; Evdokimov, I.; Kraposhin, M.; Kalugin, M.; Strijhak, S. Development of a Dynamic Library for computational aeroacoustics applications using the OpenFOAM Open Source Package. Procedia Comput. Sci. 2015, 66, 150–157. [Google Scholar] [CrossRef] [Green Version]
- Viswanath, K.; Johnson, R.; Corrigan, A.; Kailasanath, K.; Mora, P.; Baier, F.; Gutmark, E. Flow Statistics and Noise of Ideally Expanded Supersonic Rectangular and Circular Jets. AIAA J. 2017, 55, 3425–3439. [Google Scholar] [CrossRef]
- Williams, J.F.; Simpson, J.; Virchis, V.J. Crackle: An Annoying Component of Jet Noise. J. Fluid Mech. 1975, 71, 251–271. [Google Scholar] [CrossRef]
- Ffowcs, J.E.W.; Maidanik, G. The Mach wave field radiated by supersonic turbulent shear flows. J. Fluid Mech. 1965, 21, 641–657. [Google Scholar] [CrossRef]
- Baier, F.; Karnam, A.; Gutmark, E.J.; Kailasanath, K. High Temperature Supersonic Flow Measurements of a Rectangular Jet Exhausting over a Flat Surface. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Grapevine, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Baier, F.; Mora, P.A.; Gutmark, E.J.; Kailasanath, K. Flow measurements from a supersonic rectangular nozzle exhausting over a flat surface. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Goldstein, M.E.; Leib, S.J.; Afsar, M.Z. Rapid distortion theory on transversely sheared mean flows of arbitrary cross-section. J. Fluid Mech. 2019, 881, 551–584. [Google Scholar] [CrossRef] [Green Version]










© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salehian, S.; Mankbadi, R. Jet Noise in Airframe Integration and Shielding. Appl. Sci. 2020, 10, 511. https://doi.org/10.3390/app10020511
Salehian S, Mankbadi R. Jet Noise in Airframe Integration and Shielding. Applied Sciences. 2020; 10(2):511. https://doi.org/10.3390/app10020511
Chicago/Turabian StyleSalehian, Saman, and Reda Mankbadi. 2020. "Jet Noise in Airframe Integration and Shielding" Applied Sciences 10, no. 2: 511. https://doi.org/10.3390/app10020511
APA StyleSalehian, S., & Mankbadi, R. (2020). Jet Noise in Airframe Integration and Shielding. Applied Sciences, 10(2), 511. https://doi.org/10.3390/app10020511







