Abstract
This paper presents an investigation of the aerodynamic and aeroacoustic interaction of propellers for distributed electric propulsion applications. The rationale underlying the research is related to the key role that aeroacoustics plays in the establishment of the future commercial aviation scenario. The sustainable development of airborne transportation system is currently constrained by community noise, which limits the operations of existing airports and prevents the building of new ones. In addition, the substantial saturation of the existing noise abatement technologies inhibits the further development of the existing fleet, and imposes the adoption of disruptive configurations in terms of airframe layout and propulsion technology. Simulation-based data may help in clarifying many aspects related to the acoustic impact of such innovative concepts. Blended-wing-body equipped with distributed electric propulsion is one of the most promising, due to the beneficial effect of the substantial shielding induced by its geometry. Nevertheless, the novelty of the layout requires a thorough investigation of specific aspect for which no previous experience is available. Herein, the interaction between propellers is analysed for a fixed propeller geometry, as a function of their mutual distance and compared to the acoustic pattern of the isolated one. The aerodynamic results have been obtained using a boundary integral formulation for unsteady, incompressible, potential flows which accounts for the interaction between free wakes and propellers. For the aeroacoustic analyses, the Farassat 1A boundary integral formulation for the solution of the Ffowcs Williams and Hawkings equation has been used. These results provide an insight into the minimum distance between propellers to avoid aerodynamic/aeroacoustic interaction effects, which is an important starting point for the development of distributed propulsion systems.
1. Introduction
In the last few decades, the efficiency of air transportation has become a primary aspect for aeronautical designers, due to the constant growth of the aviation industry throughout the last century and its expected further increase in the near future []. In turn, the CO emissions due to the aviation industry are foreseen to grow in the next future—a 75% increment was recorded between 1990 and 2012 and it is projected to grow 300% by 2050 []. At this purpose, the international institutions have set quantitative goals for limiting chemical pollution and perceived noise to be fulfilled by the future aviation. Specifically, with respect to the average emissions at 2000, a 75% reduction in , a 90% reduction in and a 65% one in perceived noise of flying aircraft have been settled for 2050 []. As a consequence, two concurring facts are biasing the long-term development of commercial aircraft: the increasing operational constraints to mitigate the environmental impact, and the saturation of the potential development of standard technologies and concepts. These factors impose the identification of breakthrough concepts and highly-innovative technologies to guarantee the air transportation system sustainable development. Most of the solutions currently under analysis present unconventional characteristics in both the aircraft layout and its propulsion system [,,]. It is worth noting that, besides environmental issues, financial interests also drive the aviation industry towards unconventional airframe layouts and novel propulsion systems. As a matter of fact, the typical fluctuation of fuel price make the amount of fuel burnt per flight an uncertain parameter, since in the early design phases.
Differently from the past where structures and propulsion were seen as two different design threads, the challenge nowadays is given by coupling them into a unique subject. Promising concepts are characterised by hybrid-electric power plant configurations with distributed propulsion and novel aircraft configurations such as the Blended-Wing-Body (BWB). The BWB concept seems to be one of the most promising candidates for the future subsonic jetliners. This layout turns out to have a reduced wetted surface to volume ratio, exploiting a greater useful volume compared to the standard configurations. It is characterised by a large centre body surface which lends itself well to mount distributed electric-driven propellers and Boundary-Layer-Injection (BLI) layouts [,,]. Several theoretical studies and experimental campaigns have demonstrated that the BWB aerodynamic efficiency can be considerably improved [], also due to the reduced interference drag. Accordingly, a remarkable reduction of green-house gases emissions and a substantial abatement of the acoustic impact on the community is foreseen []. As a consequence, the BWB layout coupled with the distributed electric-driven propulsion, could lead to strong benefits in terms of fuel efficiency and Direct Operational Costs (DOC).
In Reference [], a general definition of Distributed-Propulsion (DP) can be found, and in particular Distributed-Electric-Propulsion (DEP), which helps the reader to classify these novel architectures. In aviation, DP is used for a propulsion system where the thrust is generated by propeller arrays located on the vehicle. Nevertheless, to be formally classified as DP, the system should have improved efficiency, capabilities, and performance with regards to a classical propulsion system. On the other hand, DEP stands for a particular DP configuration in which multiple devices are powered via an electric transmission system. In some prototypes, the multiple small cores are independently electrically-driven to enhance the vehicle safety (by means of redundant engines) and to allow their use as flight control actuators.
Several concepts of DEP exist in the literature [,,], but most of them are analysed for their applicability in designing BLI configurations [,]. Few studies have been conducted so far on the aeroacoustic properties of interacting propellers and are mainly related to counter-rotating propellers [,] and drones [,,,,], where the distance between rotor hubs is a crucial aspect. In Reference [], numerical aeroacoustic analyses of innovative propeller geometries have been carried out, accounting for a single propeller mounted on a wing. In Reference [] a parametric study for a single open rotor aimed at reducing noise has been reported whereas in Reference [], a new method has been presented to estimate the influence of the number of blades on noise contribution. A further analysis on the installation effect for two consecutive propellers has been presented in Reference []. Despite its lack in the literature, the aerodynamic and aeroacoustic characterisation of an unducted array of propellers is a primary aspect for designing an optimal DEP configuration so as to achieve the targets discussed in Reference [].
Here, the aircraft layout has been optimised and analysed within the in-house Multidisciplinary Conceptual Robust Design Optimisation (MCRDO) framework FRIDA (Framework for Integrated Design of Aircraft) [,,]—the optimised configuration has been tested over the design mission and the flight mechanics variables successfully derived. The initial propeller geometry has been designed using a lifting-line theory method [,]. The main design variables that should be considered to maximise the single propeller efficiency are angular velocity of rotor, radius and chord of blades, and the number of blades per propeller. When it comes to DP sizing, the design of each fan is also constrained by the number of devices chosen for the configuration which, in turn, is a consequence of the optimal distance between propellers in the array. All these factors determine the propeller loading, that is an important aspect for its efficiency. Nowadays, it is of high interest for the optimisation of DP to start analysing how the performances of the entire array are influenced by the distance between propeller and the array installation. After the rotor has been designed, based on the geometrical constraints of encumbrance, the blade pitch angle is verified and corrected, when necessary, by means of an in-house BEM (Boundary-Element-Method) aerodynamic solver, to match the required thrust. Then, the aeroacoustic response of the selected case studies is evaluated through the Farassat 1A boundary integral formulation [].
The paper is organised as follows. A description of the unconventional Hybrid-Electric-Propelled (HEP) aircraft design process is presented in Section 2. Section 3 presents a synthesis of the propeller noise generation. The aerodynamic solver is presented in Section 4, as well as the formulation employed for the aeroacoustic analyses. In Section 5, the numerical results for one isolated propeller and those for the mutual interaction of two or three adjacent rotors are reported. Finally, Section 6 gathers the conclusions.
2. Towards the Unconventional HEP Aircraft Integrated Design
Since the early stage of an aircraft design, optimisation procedures are largely employed to identify the best configuration and, at the same time, guarantee constraints to be satisfied. The design of disruptive airframe layouts coupled with innovative propulsion systems using non-conventional energy sources requires an upgrade of the well-assessed theoretical and numerical techniques used so far to analyse different solutions during the design phase. In particular, safety constrains must be included in the analyses and most of the evaluation methods must be enhanced to account for novel configurations. However, the estimate of the noise maps on the ground must be done taking into account all the operations in the time slot of interest, thus imposing the use of simple prediction models, typically based on the regression of existing data. The lack of such data for innovative concepts makes the evaluation of their impact on the noise mapping extremely time consuming, if not even impossible. Indeed, the unconventionality of the new concepts makes inapplicable the existing aeroacoustic semi-empirical models, thus imposing the inclusion of computationally expensive numerical simulations in the conceptual design frameworks, increasing the computational burden of the entire process by order of magnitudes. For this reason it is extremely important to retrieve a reliable acoustic meta-model to be used in the optimisation procedure so as to reduce the computation timing. At this aim, the number of variables used to build the model should be reduced to those at which the noise footprint is particularly sensitive. As it will be shown in this paper, the investigation on the mutual distance between propellers gives an insight whether to include their distance in the design space.
The MCRDO framework FRIDA has been used for the HEP regional BWB optimised design. The accuracy level of the framework models is such to capture the principal properties along most of the aircraft flight envelope with a computational effort compatible with the high number of evaluations required to converge at an optimised concept: the implemented algorithms used for the aircraft analysis are, whenever possible, prime-principle based, simplified with specific assumptions to reduce the order of complexity. Over the past years, the implemented models have been enhanced, so that the framework can now deeply describe also unconventional aircraft from a multidisciplinary point of view, taking into account the environmental impact estimation (considering both the acoustic and chemical emissions) combined with financial metrics [,]. More recently, within the Horizon 2020 (H2020) program, the four-year research project ARTEM (Aircraft noise Reduction Technologies and related Environmental iMpact [], grant agreement No. 769350) has been instituted in order to explore novel noise reduction technologies for low-noise 2035 and 2050 aircraft concepts. The ARTEM consortium, coordinated by the German Aerospace Centre (DLR), is composed by 24 partners from 10 European countries including Russia (Belgium, France, Germany, Italy, The Netherlands, United Kingdom, Romania, Slovenia, Switzerland, Russian Federation). In this context, important developments of the FRIDA framework have allowed the introduction of HEP and DP within the optimal design process []. Specifically, a revised mass estimation procedure, accounting for the electric components weight has been implemented in addition to nonlinear scaling laws for the distributed propulsion system mass estimate. The optimal hybridisation factor was selected on the basis of an optimisation problem aimed at minimising the fuel and the battery-pack weight at the same time: the specific energy and power have been set to reasonable values foreseen in 2050. In the performance-based optimisation problem, both the cabin layout and the aircraft balance have been imposed as constraints. The main characteristic of the HEP regional BWB aircraft, developed within the ARTEM project, are summarised in Table 1.

Table 1.
Main characteristics of the Hybrid-Electric-Propelled (HEP) regional Blended-Wing-Body (BWB).
A pictorial rendering of the HEP regional BWB aircraft is shown in Figure 1.

Figure 1.
Pictorial rendering of the HEP regional BWB aircraft.
The operating conditions have been derived on the basis of an inverse flight mechanics problem. The design mission is sampled in time and for each sample, the current aircraft weight is evaluated as well as all the flight mechanics variables, including the required thrust (needed for the propeller design). The propeller geometry has been designed by adapting an open source propeller design code [], which makes use of a novel implementation of the lifting-line theory []. The advance ratio J is evaluated starting from the geometrical and operational variables, and then the wake induced velocity components , and are computed (through the Biot-Savart law) to evaluate both the induced and the effective angle of attack ( and respectively). The circulation is evaluated starting from the knowledge of the section aerodynamic coefficients , and (for the prescribed , at the design Mach and Reynolds numbers) by means of the Kutta-Joukowski theorem. Aerodynamic loads distribution in the span-wise direction, torque and power are therefore evaluated, in addition to the thrust. Finally, a first estimate of the rotor angular velocity is addressed by matching the current rotor thrust with the aircraft required thrust, calculated with the inverse flight mechanics problem. The rotor geometrical properties are summarised in Table 2.

Table 2.
Characteristic data of propellers.
3. Propeller Aeroacoustics: Theoretical Background
The design of an optimal propeller involves a large number of design variables to maximise its efficiency. When the design of a propeller array is considered, those variables become an even larger number. Despite the differences on the final design (i.e., blade geometry, number of blades, number of propellers) and its applications, the contributions to the noise-generating process are independent of the configuration type [].
The acoustic signature of a propeller is the combination of a harmonic spectrum and a broadband one. The harmonic noise, also called tonal noise, is the periodic component which repeats itself exactly at each propeller revolution. For an observer not rotating with the blades, the period of the tonal noise, and thus its frequency is linked to the number of blades () and the rotational speed () as follows
where f, called Blade-Passage Frequency (BPF), is the fundamental frequency of the tonal noise. Contrarily, broadband noise has a random characteristic containing components at all frequencies with a shape that depends on the propeller installation and operating condition at the most. However, the broadband amplitude on the spectrum is much lower than the tone signal.
As depicted in Figure 2, the noise mechanisms that contribute to propeller noise spectrum can be classified in three main groups: steady sources, unsteady sources, and random sources.
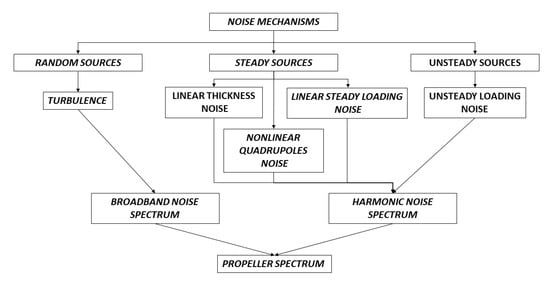
Figure 2.
Noise generation contributions to typical propeller spectrum.
The steady sources are constant in time in the rotating blade system (i.e., a system fixed with the rotating blade), and therefore they are inherently periodic in the non-rotating one. Sources of this type are linear thickness noise, steady loading noise, and the non-linear quadrupoles noise. The thickness noise is associated with the periodic displacement of the air volume due to a passing blade. It is one of the major noise sources in propeller applications, and it can be represented by a monopole source distribution over the blade surface. The magnitude of this noise component is proportional to the blade volume, and its magnitude increases proportionally to the flight speed. The spectrum of the thickness noise strongly depends on the rotor angular velocity and the shape of the blade cross-section.
The linear loading is due to the pressure field acting on the blades during the propeller motion. This noise source is dominant at low to moderate flight speeds. It is generally modelled by dipoles distribution to represent the pressure disturbance that propagates as noise in the medium, with harmonic content at frequencies multiple of the BPF.
Finally, the quadrupoles are mainly used to account for the nonlinear effects that may be significant when the blades are in transonic condition and all the viscous and propagation effects not included in the previously described noise sources. Thus, the presence of volume quadrupoles enhances the noise signature obtained by using loading and thickness like sources.
Non axial-flow conditions (e.g., due to non-axial flight, installation effects, aerodynamic interaction between adjacent propellers, etc.) result in unsteady blade loading which causes another important noise contribution, named the unsteady loading source. These unsteady loads, caused by the inflow distortion that impacts on the blades, can significantly affect the overall noise signature and include both periodic contributions (e.g., pressure bump deriving from the interaction of propeller blades and wing) and random contributions (e.g., trailing edge noise and boundary layer noise). This periodic unsteady-loading noise occurs at harmonics multiple of the blade-passage frequency (for an observer in a non-rotating frame), and it is a contribution that adds/subtracts to the steady-loading noise. Because of the non-axisymmetry of this contribution, the noise directivity may present lobes, whose number is dependent on the entity of the flow distortion and is unrelated to the number of blades.
Random sources are those caused by turbulence phenomena around the blade. They generate a broadband contribution onto the propeller spectrum with components at all frequencies. This contribution is strongly dependent on the operating condition at which the propeller works, but it can generally be neglected compared to the tonal noise generated by the aforementioned noise sources.
In practice, for low-speed operations the contribution given by quadrupoles and random noise sources can be neglected, as the noise level due to thickness and loading sources is dominant. For this reason, in the present work, the authors consider only these major contributions in the aeroacoustic analysis of the propeller arrays.
4. Numerical Solver
In the present section, the aerodynamic and aeroacoustic solvers applied in this work are briefly outlined. The aerodynamic formulation for inviscid incompressible flows around lifting/thrusting bodies is numerically implemented by a zero-th order BEM and provides the input data for the acoustic solver. The noise radiation is based on the solution of the Ffowcs Williams and Hawkings equation through the Farassat 1A boundary integral formulation. Note that, the incompressible flow hypothesis used for the aerodynamic analysis is here fully justified by the low Mach numbers characterizing the analyzed configurations.
4.1. Aerodynamic Solver
The aerodynamic analysis is performed by a solver based on the BEM approach introduced in Reference [] and further improved in Reference []. Considering incompressible, potential flows such that , the potential field, , is assumed to be given by the superposition of an incident potential, , and a scattered potential, (i.e., ). The scattered potential is determined by sources and doublets distribution over the surfaces of the blades, , and by doublets distributed over the wake portion that is very close to the trailing edge from which emanated (near wake, ). The incident potential field is associated to doublets distributed over the complementary wake region that composes the far wake , see Reference []. The incident potential is discontinuous across , whereas the scattered potential is discontinuous across and is represented by []
where , while is the potential jump across the wake surface, known from the history of potential discontinuity at the blade trailing edge through the Kutta-Joukowski condition [,]. In addition, , with representing the body velocity and its outward unit normal, whereas , with denoting the velocity induced by the far wake.
Considering the far wake discretized into panels, assuming the potential jump constant over each panel, and recalling the equivalence between surface distribution of doublets and vortices, the incident velocity field is evaluated through the Biot-Savart law. In order to assure a regular distribution of the induced velocity within the vortex core, the Rankine finite-thickness vortex model is applied []. The shape of the wake surface is determined as part of the solution evaluating the motion of panel vertexes with the velocity field induced by wakes and bodies.
Once the potential field is known, the Bernoulli theorem yields the pressure distribution [] from which, in turn, blade loads can be readily evaluated.
4.2. Aeroacoustic Solver
In the present work the noise radiation is evaluated through the Farassat 1A boundary integral formulation [] for the solution of the Ffowcs Williams and Hawkings equation. Specifically, the acoustic pressure field is given as the superposition of the thickness noise, , depending on body geometry and kinematics,
and the loading noise, , related to the distribution of pressure over body surfaces,
In Equations (3) and (4), denotes the distance between observer position, , and source position, , whereas is the unit vector along the source-observer direction, with . In addition, and are speed of sound and density in the undisturbed medium, respectively, with representing the undisturbed medium pressure, with denoting the body velocity, , , and , where is the outward blade surface unit normal vector. Further, , and denote time derivatives of , and , observed in a frame of reference fixed with the undisturbed medium. Notation indicates that these quantities are evaluated at the emission time, , where is the time taken by the signal started from to arrive in at time t.
5. Results and Discussion
The numerical investigation which pertains to the aerodynamic and aeroacoustic analyses of propeller arrays, assesses the interaction aerodynamic effects on the emitted noise. It is worth noting that, a validation analysis of the presented results has not been performed in this work because of the lack of data to compare with. Indeed, at the Authors knowledge, the most similar results in the literature are those by Zhou [], which however concern the analysis of UAV (Unmanned Aerial Vehicle) rotors in hovering conditions. Anyway, it should be emphasized that both the aerodynamic and the aeroacoustic code used for the present numerical analysis have been widely validated in the past by comparison with numerical and experimental data available in the literature [,].
Two different configurations are analysed, with two and three identical propellers respectively, and their results are compared with those of an isolated rotor, which provides the same thrust of one single rotor of the array. The analysis is aimed at characterising the noise emitted by one of the propellers of the array by taking into account the aerodynamic influence of the others. It is aimed at defining an equivalent noise source of the single propeller to be used within a tool for near-field (and subsequently far-field) propagation. The blade of each rotor is characterised by a rectangular shape with its airfoil profile being a NACA 65A010; the geometric parameters are given in Table 2. The sixteen rotor blades are mounted on a cylindrical hub having radius m and elliptical nose and tail cones with the principal semi-axes of 0.2 m and 0.5 m long, respectively.
The hub distance between two adjacent propellers in the array is defined as the sum of the rotor diameter, d, and the tip-clearance, , as shown in Figure 3. For every analysed configuration, the rotor (#1) spins counterclockwise (if viewed from the front), whereas the other rotors (#2 for the twin-propeller array and #2 and #3 for the three-propeller one) rotate clockwise. In order to perform a sensitivity analysis on the effect of the tip-clearance (and hence of the aerodynamic interaction effects) on the emitted noise, for the twin-propeller configuration four analyses with increasingly tip-clearance distance from m to , with = {0, 0.125d, 0.25d, 0.5d}, are performed, whereas the three-rotor array is analysed only for the tip-clearance . Note that, the additional distance of m is introduced to avoid tips impingement due to the rectangular shape of the blades. All the analysed configurations are in axisymmetric flight condition, with an advance speed of 164 m/s, a blade rotational velocity 2500 rpm, and provide a thrust of 3700 N.
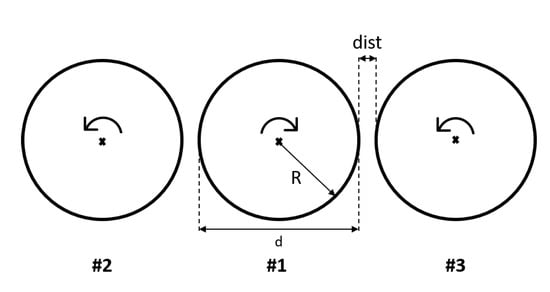
Figure 3.
Sketch of the analysed configurations, front view: twin-propellers configuration (#1 and #2); three-propellers configuration (#1, #2 and #3).
5.1. Aerodynamic Results
The results pertaining to the aerodynamic analysis of the twin- and three-propeller configurations are presented and discussed in this section. All the analyses are performed by meshing the rotor blades with 840 quadrilateral panels (15 along the chord and 28 along the span), the rotor hub with 2160 elements, and the surface of the wake with 5040 elements (180 in the azimuth direction and 28 in the radial direction) distributed on two spirals. As stated before, in all the cases, the rotors have been trimmed to the thrust of the isolated rotor case (3700 N), by minor changes in the blade pitch. The resulting performance in terms of torque (and thus power) vs. thrust has been verified to remain substantially unchanged.
First, Figure 4 shows, for the twin-propeller configuration and the case of minimum tip-clearance ( = 0), the computational grid and the wake shape resulting from the aerodynamic interaction of the two rotors. It is worth noting that, also in the case of the smallest distance between rotors, the aerodynamic interaction effects on the wake shape are negligible (i.e., there is no intersection between the wakes of the two rotors as well as between the wake of a rotor and blades of the other one).
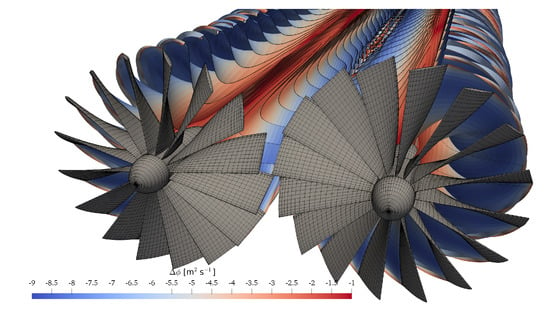
Figure 4.
Twin-propeller computational mesh for the case = 0.
Then, Figure 5a shows the time history over an entire revolution of the perturbation pressure () on each blade of rotor #1 (at the quarter–chord of the blade section located at the radial station ) for = {0, 0.25d, 0.5d, 1.25d}. As expected, as the distance between the rotors diminishes, a growing (in absolute value) pressure peak appears, having its minimum located approximately at the azimuth position where the blade is closer to the second rotor. The aerodynamic interaction becomes negligible for the tip-clearance of the order of magnitude of the rotor diameter. Figure 5b depicts the spectrum of the pressure signals in terms of Discrete Fourier Transform (DFT) module, showing that, for all the configurations considered, the pressure signals are strictly tonal (due to the aerodynamic formulation hypotheses the analysis is based upon), with frequencies multiple of rotor angular velocity, . Moreover, the spectrum of the minimum-distance configuration presents a linear behaviour up to −20 dB, with a very weak, secondary peak at , whereas the linear part of the spectrum for larger distances extends up to about −40 dB, followed by an irregular behaviour at the higher frequencies, probably due to numerical errors (given the low values of harmonics amplitude). As expected, when the distance between rotors increases, the pressure signal tends to become uniform during the rotor revolution, as in the case of an isolated propeller (indeed, the spectrum harmonic content tends to vanish).
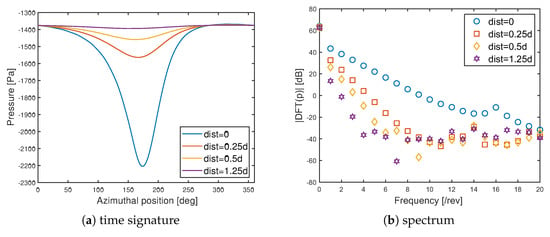
Figure 5.
Aerodynamic pressure evaluated at and on rotor #1 for four different distances between rotor #1 and #2 (twin-propeller configuration).
Finally, for the minimum-distance configuration, Figure 6a shows the comparison of the time history of the pressure at the quarter–chord of the blade section at of the rotor #1 for the twin- and three-propeller configurations. As expected, in the three-propeller configuration two peaks with the same intensity appear, at the azimuth positions at which the blade of rotor #1 is closest to those of the rotors #2 and #3. Furthermore, Figure 6b compares the spectrum of the pressure signals. Also in this case the spectrum of the three-propeller configuration is linear, with harmonic content at the only frequencies multiple of (no odd harmonics are present). Finally, the even tones of the three-propeller configuration are globally more intense than those of twin-propeller case.
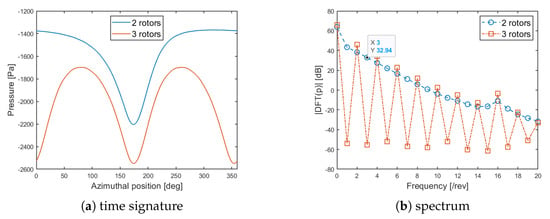
Figure 6.
Aerodynamic pressure evaluated at and on rotor #1: comparison between twin- and three-propeller configurations.
5.2. Aeroacoustic Results
This section presents the acoustic predictions for the twin- and three-propeller configurations and those for the isolated propeller, as well as the sensitivity analysis of the emitted noise of the multi-propeller configurations to the rotors tip-clearance. All the numerical results concern the noise emitted by rotor #1 and are evaluated over a sphere of radius equals to 5 m, centred at the hub of the rotor #1 (depicted in grey in Figure 7). In practical applications, the acoustic characterisation of single elements of an array allows scattering and propagation analysis considering multiple equivalent sources. The underlying assumption is that the equivalent sources may be considered equal, except for those of the first and last element of the array. Thus, obtaining results for each propeller of a three-propeller configuration, allows the evaluation of the noise emitted by an array of arbitrary number of propellers. For all cases shown in the next section, the results have been presented from two views: the northern view (where the sphere is observed from above) depicted in Figure 7a, and the southern view (where the sphere is observed from below) depicted in Figure 7b. For the sake of clearness, in both pictures the flow direction is shown in black (-x direction).
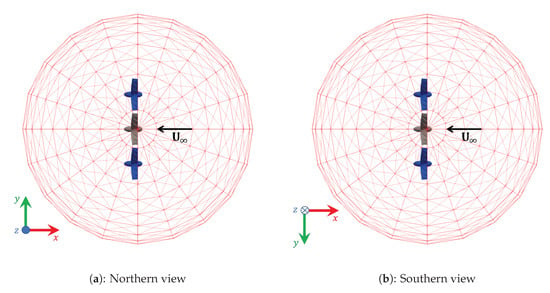
Figure 7.
Convention used to report the acoustic results on the sphere. The coordinate system is right-handed so that, on the left the Northern view is characterised by the z-axis outgoing whereas on the right the Southern view is characterised by the z-axis incoming.
First of all, the sound directivity of the isolated rotor is shown in Figure 8, which depicts (from left to right) the sound pressure levels (SPL) of the first three Blade Passing Frequencies and the overall sound pressure level (OASPL), evaluated by using the first nine BPFs. Due to axisymmetry of the problem, only the southern hemisphere of the radiation pattern is shown. As expected, the noise emitted by the propeller is dominated by thickness contribution (results separately showing thickness and loading contributions are not shown here for the sake of conciseness) and concentrated about the rotation plane.
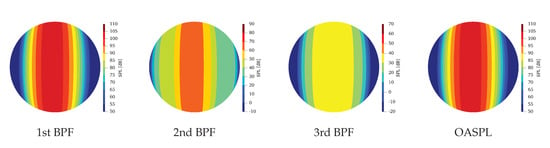
Figure 8.
Sound directivity of isolated rotor.
When a twin-propeller configuration is considered, the axisymmetry of the problem is lost, and hence the acoustic results have to be shown on the whole sphere. Figure 9 shows the noise hemispheres observed from below (southern) and above (northern) for the case of the minimum distance between rotors ( = 0). In the northern hemisphere, the noise directivity, in terms of 1st BPF, is very similar to that of the isolated rotor. Whereas in the southern hemisphere (i.e., the hemisphere where the blades of the two propellers approach), it is really different. In the northern hemisphere, the 1st BPF appears to have a banded shape. Regarding the southern hemisphere, the noise directivity presents two-lobe noise pattern with maximum noise level slightly increased.
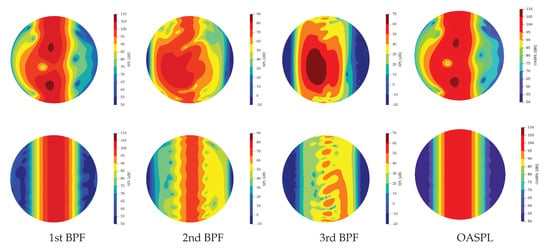
Figure 9.
Sound directivity of rotor #1 for the case dist = 0. The first row shows the noise sphere from below, the second one from above.
These considerations can be extended to the OASPL, which is dominated by the pattern of the 1st BPF (in this case, the maximum noise level on the southern hemisphere is about 2 dB higher than that of the northern). On the contrary, the higher harmonics hemispheres significantly differ with respect to those relative to the isolated rotor, with associated maximum noise levels 10 to 20 dB higher.
Then, results concerning the sensitivity analysis to the distance are summarised in Figure 10, which shows the comparison in terms of OASPL among the isolated rotor and the four twin-propeller configurations analysed (characterised by = {0, 0.125d, 0.25d, 0.5d}).
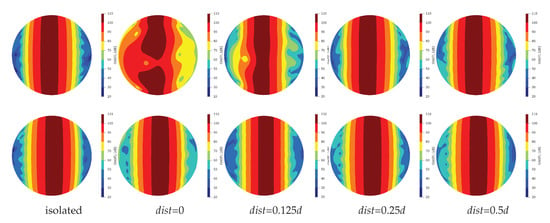
Figure 10.
Sound directivity (OASPL) of rotor #1 for the cases dist = {0, 0.125d, 0.25d, 0.5d}. The first row shows the noise sphere from below, the second one from above.
As expected, the northern hemisphere (second row) remains unaffected by the relative distance between rotors, whereas the southern (first row) hemisphere is significantly modified for . Note that, this threshold might seem to contradict the aerodynamic results shown in Figure 5a, where the effects of rotor proximity are already evident for . This is because the thickness contribution dominates the emitted noise, hiding the loading term, which is the only contribution affected by aerodynamic interaction effects. This concealment effect is also exacerbated because noise is expressed in dB.
Finally, Figure 11 shows the variation of noise emitted by rotor #1 with respect to the isolated rotor in terms of dB, for the two configurations whose noise is more affected by the interaction phenomena ( and ). The main effect is the change in the noise directivity in the forward direction on the southern hemisphere, which increases with the tip-clearance reduction (note that the logarithmic scale hides the variations in the high noise region). The noise level is globally increased, although some regions (located near the south pole) may present lower OASPL values.
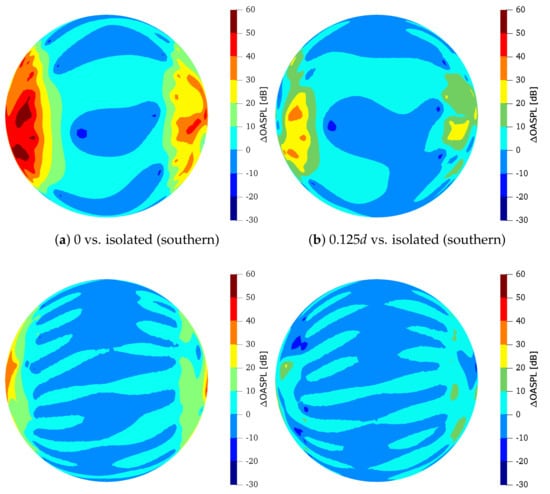
Figure 11.
Variation of OASPL with respect to the isolated rotor.
Furthermore, the three-propeller configuration, with tip-clearance equal to 0, is analysed. Figure 12 shows the directivity pattern on the 5-m sphere, in terms of SPL of the first three BPFs as well as in terms of OASPL, for the southern (first row) and northern (second row) hemispheres.
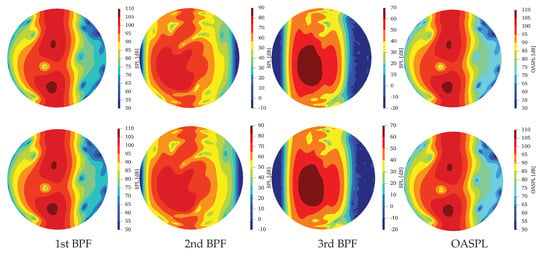
Figure 12.
Sound directivity of rotor #1 for the case dist = 0, for a three rotors configuration. The first row shows the noise sphere from below, the second one from above.
From this analysis two important considerations may be drawn. First, the directivity of the southern hemisphere is practically identical to the northern one. This implies that rotor #2 affects the southern hemisphere of the rotor #1 as the rotor #3 affects the northern one, and vice versa. Besides, comparing southern hemispheres of the three-propeller case with those of the twin-propeller case shown in Figure 9, it is possible to observe that they are really similar, showing that the contribution of the rotor #3 on the southern hemisphere of the rotor #1 is negligible, as well as the contribution of the rotor #2 on the northern one. Hence, each adjacent rotor affects only one of the two hemispheres. Thus, the aeroacoustic characterisation of the three–propeller configuration can be obtained, with an excellent level of approximation, from that of the twin-propeller one through southern hemisphere symmetrisation with respect to the equatorial plane (see Figure 9 and Figure 12).
Finally, Figure 13 shows, for the twin-propeller configuration with tip-clearance equals to and for microphones located on circles in the propeller rotational plane with increasing radius, the comparison between the pressure field directivity pattern at the normalised with the ratio between the reference circle radius (5 m) and the current one. This analysis is aimed at defining the far-field boundary, that is, the distance from the hub centre beyond which the pressure decreases as the inverse of the distance.
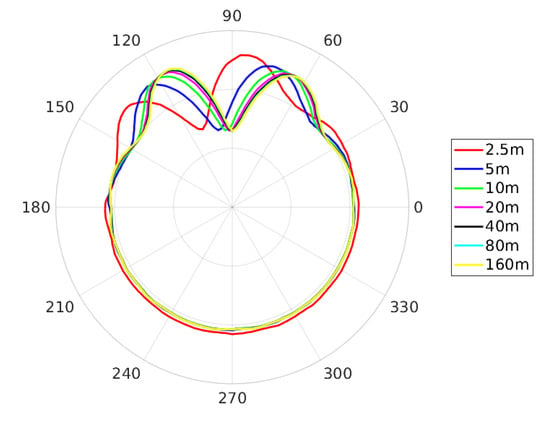
Figure 13.
Directivity pattern at for different observers distances.
As expected, in the near field, the directivity pattern is strongly affected by the distance. For hemisphere radii greater than 20-m, on the contrary, the directivity is almost the same with the magnitude decreasing proportionally to the observer distance. This is confirmed by Figure 14, which shows the trends of: (a) the difference between the azimuth position of the pressure peak evaluated at the current distance and that of the 160 meters circle (considered representative of the far-field conditions and identified by the subscript “ref”); (b) the ratio between the maximum normalised pressure and its value in the far-field conditions; (c) the ratio between the average normalised pressure and its value in the far-field. Once again, up to 20-m the three quantities remarkably change with the distance, whereas they become constant for higher distances. However, the differences between the far-field quantities and those evaluated on the sphere with a radius equal to 5 m (that considered for analyses in Figure 8, Figure 9 and Figure 10 and Figure 12) are quite small, lower than on the pressure peak and average pressure, and about for the azimuth position of the peak.
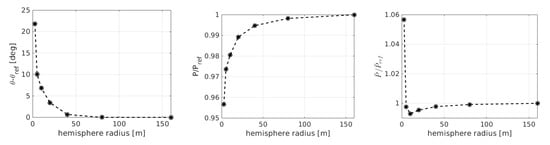
Figure 14.
Convergence analysis as observer distance increases.
6. Conclusions
On the basis of results obtained in this work, it can be concluded that the aerodynamic and the aeroacoustic interaction between small propellers may have a significant impact on the emitted noise in terms of intensity, directivity pattern, and spectral content. The first specific observation that can be made is that the presence of a second rotor introduces a low-frequency disturbance (approximately at 1/rev) on blade pressure which does not exist in a single–rotor signal. This causes the noise signal to include a relevant amount of loading contribution in addition to the dominant thickness term. In addition, there are significant variations when the distance between the rotors tips is closer than one half of the rotor radius. The main modifications concern an increase of the noise that propagates in the forward direction, a noticeable widening of the high-noise region and the increase of the noise peak. The differences are more relevant when the considered frequency is increased. In particular, when the distance between the propellers is lower than , the differences between the noise emitted by the isolated rotor and that emitted in presence of the other one are significant. In the high-noise region of the southern hemisphere, an increase up to 10 dB is observed (depending on the tip-distance). Furthermore, in the region where lower OASPL values are present, the aerodynamic interaction produces an increase of the noise emitted up to 50 dB. Concerning the characteristics of propagation, it can be observed that the far-field condition, where the pressure field decreases proportionally to the distance, is achieved at about 20-m, thus slightly closer than thirty radii. Then, the three-rotors configuration exhibits a symmetric emission which can be advantageously exploited to reduce the computational burden. Indeed, the effect of each side rotor on the noise emitted by the central one is only limited by the hemisphere where the blades of the two propellers approach. As a consequence, the three-propeller directivity pattern can be obtained from the twin-propeller one by mirroring the equatorial plane of the hemisphere affected by the presence of the side rotor. Finally, the numerical investigation confirms the possibility of performing the aeroacoustic analysis of a multi-propeller configuration by characterising each propeller of a three-propeller array and using the central one as an equivalent source for each internal propeller of the multi-propeller array.
In this work, the only design variable considered in the parametric analysis is the distance between consecutive rotors. However, in order to have a wider exploration of the design space (i.e., also in terms of number of blades, chord length, rotational speed and rotational direction for assessing also co-rotating propellers noise), a second numerical campaign has just started.
Author Contributions
Conceptualization, F.C., M.R. and J.S.; methodology, G.B., F.C., C.Pa., C.Po., M.R. and J.S.; software, G.B., F.C., M.G., U.I., C.Pa., C.Po., M.R. and J.S.; validation, F.C., C.Pa., C.Po., M.R. and J.S.; formal analysis, F.C., C.Pa., C.Po., M.R. and J.S.; investigation, F.C., C.Pa., C.Po., M.R. and J.S.; resources, G.B., M.G. and U.I.; data curation, F.C., C.Pa., C.Po., M.R. and J.S.; writing–original draft preparation, F.C., C.Pa., C.Po., M.R. and J.S.; writing–review and editing, G.B., F.C., M.G., U.I., C.Pa., C.Po., M.R. and J.S.; visualization, C.Pa., C.Po. and M.R.; supervision, G.B., F.C., U.I. and J.S.; project administration, U.I.; funding acquisition, U.I. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been partially supported by the European Union’s Horizon 2020 research and innovation programme under project ARTEM (Aircraft noise Reduction Technologies and related Environmental iMpact) grant agreement No. 769350.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BWB | Blended-Wing-Body |
| BLI | Boundary Layer Injection |
| DOC | Direct Operational Costs |
| DP | Distributed Propulsion |
| DEP | Distributed Electric Propulsion |
| MCRDO | Multidisciplinary Conceptual Robust Design Optimisazion |
| FRIDA | Framework for Integrated Design of Aircraft |
| BEM | Boundary-Element-Method |
| HEP | Hybrid-Electric-Propelled |
| SPL | Sound Pressure Level |
| OASPL | OverAll Sound Pressure Level |
| H2020 | Horizon 2020 |
| ARTEM | Aircraft noise Reduction Technologies and related Environmental iMpact |
| DLR | Deutsches Zentrum für Luft- und Raumfahrt |
| BPF | Blade-Passage Frequency |
| NACA | National Advisory Committee for Aeronautics |
| DFT | Discrete Fourier Transform |
| variables | |
| Wake induced velocity components | |
| Induced angle of attack | |
| Effective angle of attack | |
| Lift coefficient | |
| Drag coefficient | |
| Moment coefficient | |
| Number of blades | |
| Hub radius | |
| c | Blade chord |
| Blade root | |
| d | Rotor diameter |
| Blade taper ratio | |
| Pitch angle [deg] | |
| T | Period of the tonal noise |
| Rotational speed | |
| Velocity | |
| Potential | |
| Incident potential | |
| Scattered potential | |
| Body surface | |
| Near wake surface | |
| Far wake surface | |
| G | Fundamental solution |
| Normal velocity | |
| Body velocity | |
| Outward unit normal | |
| Induced normal velocity | |
| Velocity induced by the far wake | |
| Potential jump across the wake surface | |
| Thickness noise | |
| Loading noise | |
| Distance between observer and source | |
| Observer position | |
| Source position | |
| Undisturbed speed of sound | |
| Undisturbed medium density | |
| Undisturbed medium pressure | |
| M | Mach number |
| Emission time | |
| t | Time |
| Delay | |
| Tip-clearance |
References
- AIRBUS. Global Market Forecast, Growing Horizons 2017/2036; Technical Report; AIRBUS: Leiden, The Netherlands, 2017. [Google Scholar]
- International Civil Aviation Organization. 2019 Environmental Report—AVIATION AND ENVIRONMENT; Technical Report; International Civil Aviation Organization: Montreal, QC, Canada, 2019. [Google Scholar]
- European Union. Flightpath 2050; Europe’s Vision for Aviation; Technical Report; European Union: Brussels, Belgium, 2011. [Google Scholar] [CrossRef]
- Ploetner, K.; Rothfeld, R.; Urban, M.; Hornung, M.; Tay, G.; Oguntona, O. Technological and Operational Scenarios on Aircraft Fleet–Level towards ATAG and IATA 2050 Emission Targets. In Proceedings of the 17th AIAA Aviation Technology, Integration and Operations Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Epstein, A. Aeropropulsion for Commercial Aviation in the Twenty-First Century and Research Direction Needed. AIAA J. 2014, 52, 901–911. [Google Scholar] [CrossRef]
- The National Academies of Sciences, Engineering, Medicine. Commercial Aircraft Propulsion and Energy System Research; Technical Report; The National Academies of Sciences, Engineering, Medicine: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Kim, H. Distributed Propulsion Vehicles. In Proceedings of the 27th International Congress of the Aeronautical Sciences, ICAS 2010, Nice, France, 19–24 September 2010. [Google Scholar]
- Centracchio, F.; Rossetti, M.; Iemma, U. Approach to the Weight Estimation in the Conceptual Design of Hybrid-Electric-Powered Unconventional Regional Aircraft. J. Adv. Transp. 2018, 15. [Google Scholar] [CrossRef]
- Qin, N.; Vavalle, A.; Le Moigne, A.; Laban, M.; Hackett, K.; Weinerfelt, P. Aerodynamic considerations of blended wing body aircraft. Prog. Aerosp. Sci. 2004, 40, 321–343. [Google Scholar] [CrossRef]
- Kim, H.; Brown, G.V.; Felder, J.L. Distributed Turboelectric Propulsion for Hybrid Wing Body Aircraft. In Proceedings of the 2008 International Powered Lift Conference, London, UK, 20–24 July 2008. [Google Scholar]
- Kim, H.D.; Perry, A.T.; Ansell, P.J. A Review of Distributed Electric Propulsion Concepts for Air Vehicle Technology. In Proceedings of the 2018 AIAA/IEEE Electric Aircraft Technologies Symposium (EATS), Cincinnati, OH, USA, 12–14 July 2018; pp. 1–21. [Google Scholar]
- Synodinos, A.; Self, R.; Torija, A. Preliminary noise assessment of aircraft with distributed electric propulsion. In Proceedings of the 2018 AIAA/IEEE Aeroacoustics Conference, AIAA AVIATION Forum, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Ko, A.; Schetz, J.A.; Mason, W.H. Assessment of the Potential Advantages of Distributed–Propulsion for Aircraft. Int. J. Sustain. Eng. 2018, 11, 122–134. [Google Scholar] [CrossRef]
- Ko, A.; Schetz, J.; Mason, W. Assessment of the Potential Advantages of Distributes Propulsion for Aircraft. In Proceedings of the 16th International Symposium on Air Breathing Engines—ISABE 2003, Cleveland, OH, USA, 31 August–5 September 2003. [Google Scholar]
- Wick, A.T.; Hooker, J.R.; Hardin, C.J. Integrated Aerodynamic Benefits of Distributed Propulsion. In Proceedings of the 25th AIAA/CEAS Aeroacoustic Conference, Delft, The Netherlands, 20–23 May 2019. [Google Scholar]
- Peters, A.; Spakovszky, Z. Rotor Interaction Noise in Counter-Rotating Propfan Propulsion Systems; ASME International: New York, NY, USA, 2010. [Google Scholar]
- Stuermer, A.; Jianping, Y. Aerodynamic and Aeroacoustic Installation Effects for Pusher–Configuration CROR Propulsion Systems. In Proceedings of the 28th AIAA Applied Aerodynamic Conference, Chicago, IL, USA, 28 June–1 July 2010. [Google Scholar]
- Shukla, D.; Komerath, N. Multirotor Drone Aerodynamic Interaction Investigation. Drones 2018, 2, 43. [Google Scholar] [CrossRef]
- Tinney, C.E.; Sirohi, J. Multirotor Drone Noise at Static Thrust. AIAA J. 2018, 56, 2816–2826. [Google Scholar] [CrossRef]
- Zhongqi, J.; Seongkyu, L. Acoustic Analysis of a Quadrotor eVTOL Design via High–Fedelity Simulations. In Proceedings of the 25th AIAA/CEAS Aeroacoustic Conference, Delft, The Netherlands, 20–23 May 2019. [Google Scholar]
- McKay, R.S.; Kingan, M.J. Multirotor Unmanned Aerial System Propeller Noise Caused by Unsteady Blade Motion. In Proceedings of the 25th AIAA/CEAS Aeroacoustic Conference, Delft, The Netherlands, 20–23 May 2019. [Google Scholar]
- Zhou, W.; Ning, Z.; Li, H.; Hu, H. An experimental investigation on rotor-to-rotor interactions of small UAV propellers. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017; p. 3744. [Google Scholar]
- Chirico, G.; Barakos, G.; Bown, N. Numerical aeroacoustic analysis of propeller design. Aeronaut. J. 2018, 122, 283–315. [Google Scholar] [CrossRef]
- Smith, D.A.; Filippone, A.; Bojdo, N. A Parametric Study of Open Rotor Noise. In Proceedings of the 25th AIAA/CEAS Aeroacoustic Conference, Delft, The Netherlands, 20–23 May 2019. [Google Scholar]
- Yeongmin, J.; Jardin, T.; Jacob, M.C.; Moschetta, J.M. Prediction of Noise from Low Reynolds Number Rotors with Different Number of Blades using Non–Linear Vortex Lattice Method. In Proceedings of the 25th AIAA/CEAS Aeroacoustic Conference, Delft, The Netherlands, 20–23 May 2019. [Google Scholar]
- Roger, M. On combined propeller synchronization and edge scattering for the noise reduction of distributed propulsion systems. In Proceedings of the 26th International Congress on Sound and Vibration, Montreal, QC, Canada, 7–11 July 2019. [Google Scholar]
- Iemma, U.; Pisi Vitagliano, F.; Centracchio, F. Multi-objective design optimization of sustainable commercial aircraft: Performance and costs. Int. J. Sustain. Eng. 2017, 10, 147–157. [Google Scholar] [CrossRef]
- Iemma, U.; Pisi Vitagliano, F.; Centracchio, F. A multi-objective design optimisation of eco-friendly aircraft: The impact of noise fees on airplanes sustainable development. Int. J. Sustain. Eng. 2018, 11, 122–134. [Google Scholar] [CrossRef]
- Adkins, C.; Liebeck, R. Design of Optimum Propellers. J. Propuls. Power 1994, 10, 676–682. [Google Scholar] [CrossRef]
- Falzone, A. Prop Design. Available online: https://propdesign.jimdo.com/ (accessed on 8 April 2020).
- Farassat, F. Derivation of Formulations 1 and 1A of Farassat; Technical Report TM-2007-214853; NASA: Washington, DC, USA, 2007. [Google Scholar]
- Community Research and Development Information Service. ARTEM: Aircraft noise Reduction Technologies and related Environmental iMpact. Available online: https://cordis.europa.eu/project/id/769350 (accessed on 8 April 2020).
- Hubbard, H.H. Aeroacoustics of Flight Vehicles: Theory and Practice. In Noise Sources; Technical Report TR-903052; NASA: Washington, DC, USA, 1991; Volume 1. [Google Scholar]
- Gennaretti, M.; Bernardini, G. Novel boundary integral formulation for blade-vortex interaction aerodynamics of helicopter rotors. AIAA J. 2007, 45, 1169–1176. [Google Scholar] [CrossRef]
- Bernardini, G.; Serafini, J.; Colella, M.M.; Gennaretti, M. Analysis of a structural-aerodynamic fully-coupled formulation for aeroelastic response of rotorcraft. Aerosp. Sci. Technol. 2013, 29, 175–184. [Google Scholar] [CrossRef]
- Gennaretti, M.; Luceri, L.; Morino, L. A unified boundary integral methodology for aerodynamics and aeroacoustics of rotors. J. Sound Vib. 1997, 200, 467–489. [Google Scholar] [CrossRef]
- Morino, L.; Bernardini, G. Singularities in BIEs for the Laplace equation; Joukowski trailing-edge conjecture revisited. Eng. Anal. Bound. Elem. 2001, 25, 805–818. [Google Scholar] [CrossRef]
- Gennaretti, M.; Bernardini, G.; Serafini, J.; Romani, G. Rotorcraft comprehensive code assessment for blade–vortex interaction conditions. Aerosp. Sci. Technol. 2018, 80, 232–246. [Google Scholar] [CrossRef]
- Gennaretti, M.; Bernardini, G.; Hartjes, S.; Scandroglio, A.; Riviello, L.; Paolone, E. Experimental/numerical acoustic correlation of helicopter unsteady MANOEUVRES. In Proceedings of the 42nd European Rotorcraft Forum, Lille, France, 5–8 September 2016. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).