Coverage-Based Classification Using Association Rule Mining ^†

Abstract

Building accurate and compact classifiers in real-world applications is one of the crucial tasks in data mining nowadays. In this paper, we propose a new method that can reduce the number of class association rules produced by classical class association rule classifiers, while maintaining an accurate classification model that is comparable to the ones generated by state-of-the-art classification algorithms. More precisely, we propose a new associative classifier that selects “strong” class association rules based on overall coverage of the learning set. The advantage of the proposed classifier is that it generates significantly smaller rules on bigger datasets compared to traditional classifiers while maintaining the classification accuracy. We also discuss how the overall coverage of such classifiers affects their classification accuracy. Performed experiments measuring classification accuracy, number of classification rules and other relevance measures such as precision, recall and f-measure on 12 real-life datasets from the UCI ML repository (Dua, D.; Graff, C. UCI Machine Learning Repository. Irvine, CA: University of California, 2019) show that our method was comparable to 8 other well-known rule-based classification algorithms. It achieved the second-highest average accuracy (84.9%) and the best result in terms of average number of rules among all classification methods. Although not achieving the best results in terms of classification accuracy, our method proved to be producing compact and understandable classifiers by exhaustively searching the entire example space.

1. Introduction

Association rule mining [1,2] is one of the important data mining tasks that is nowadays applied to solve different kinds of problems in weak formalization fields. The main goal of association rule mining is to find all rules in datasets that satisfy some basic requirements, such as minimum support and minimum confidence. It was initially proposed by Agrawal [3] to solve the market basket problem in transactional datasets and now it has developed to solve many other problems, such as classification, clustering, etc.

Classification and prediction are two important tasks of data mining that can be used to extract the hidden regularities from the given datasets to form accurate models (classifiers). Classification approaches aim to build classifiers (models) to predict the class label of a future data object. Such analysis can help to provide us with a better understanding of the data comprehensively. Classification methods have been widely used in many real-world applications, such as customer relationship management [4], medical diagnosis [5] and industrial design [6].

Associative Classification (AC) is a combination of these two important data mining techniques, namely, classification and association rule mining. AC aims to build accurate and efficient classifiers based on association rules. Researchers have proposed several classification algorithms based on association rules called associative classification methods, such as CBA: Classification-based Association [7], CMAR: Classification based on Multiple Association Rules [8], MCAR: Mining Class Association Rules [9], CPAR: Classification based on Predicted Association Rule [10], MMSCBA: Associative classifier with multiple minimum support [11], CBC: Associative classifier with a small number of rules [12], MMAC: Multi-class, multi-label associative classification [13], ARCID: Association Rule-based Classification for Imbalanced Datasets [14], and others.

Experimental evaluations [7,10,11,12,13,14,15] show that associative classification approaches could achieve higher accuracy than some traditional classification algorithms produced by decision trees [16,17,18,19,20,21], rule induction [22,23,24,25,26] and non-rule-based approaches [27,28,29,30]. Most of the associative classification methods [8,9,31,32,33,34,35,36,37] tend to build accurate and compact classifiers that include a limited number of effective rules by using rule selection or pruning techniques. In comparison with some traditional rule-based classification approaches, associative classification has two main characteristics. Firstly, it generates a large number of association classification rules. Secondly, support and confidence thresholds are applied to evaluate the significance of classification association rules. However, associative classification has some drawbacks. Firstly, it often generates a very large number of classification association rules in association rule mining that is computationally expensive, especially when the training dataset is large. It takes great effort to select a set of high-quality classification rules from among them. Secondly, the accuracy of associative classification depends on the setting of the minimum support and the minimum confidence constraints, that is, unbalanced datasets may heavily affect the accuracy of the classifiers. Although associative classification has some drawbacks, it can achieve higher accuracy than the rule- and tree-based classification algorithms on certain real-life datasets.

Our expected contributions in this research work are:

• To build a compact, accurate and understandable associative classifier (model) based on dataset coverage.
• To solve some of the real-life problems by applying our proposed approach (model).

To achieve these goals, we propose a relatively simple and accurate method to produce a compact and understandable classifier by exhaustively searching the entire example space. More precisely, we select the strong class association rules (CARs) according to their contribution to improving the overall coverage of the learning set. Our proposed classifier has an advantage in that it generates a reasonable fewer number of rules on bigger datasets compared to traditional classifiers, because our method has a stopping criterion in the rule-selection process based on the training dataset’s coverage; that is, our algorithm is not sensitive to the size of the dataset. Once we build the classifier, we compute the relevance measures such as “Precision”, “Recall” and “F-measure”, as well as an overall coverage of the classifier to show how overall coverage affects the accuracy of the classifier [38]. We then perform statistical significance testing by using the paired T-test method between our method and other classification methods.

We have performed experiments on 12 datasets from the UCI Machine Learning Database Repository [39] and compared the experimental result with 8 well-known rule-based classification algorithms (Decision Table (DT) [40], Simple Associative Classifier (SA) [41], PART (PT) [24], C4.5 [18], FURIA (FR) [42], Decision Table and Naïve Bayes (DTNB) [43], Ripple Down Rules (RDR) [44], CBA).

The rest of the paper is organized as follows: Section 2 highlights the related work to our research work. The problem statement is given in detail in Section 3. Section 4 presents how to generate class association rules. In Section 5, our proposed algorithm is widely described. Experimental evaluation (obtained results) is discussed in Section 6. Discussion about this research work is presented in Section 7. Conclusions and future plans are given in Section 8. The Acknowledgement and References close the paper.

2. Related Works

In computer science literature, there are a lot of rule-based, tree-based and probabilistic classification models proposed by prominent researchers. Since we propose associative classification methods based on database coverage, we discuss the performed research works in associative classification fields that were related to our proposed approaches in this section.

CMAR, an associative classification method, also uses multiple association rules for classification [8]. This method first extends FP-growth (an efficient frequent pattern mining) to mine large datasets [45]. Next, CMAR employs a novel data structure to improve the overall accuracy and efficiency, called CR-tree. The main goal of using CR-tree is to store and retrieve a large number of rules compactly and efficiently. In the rule-selection process, CMAR extracts the highly confident, highly related rules based on database coverage and analyzes the correlation between those rules. More precisely, for each rule R, all the examples are found covered by rule R and if R correctly classifies at least one example, then R will be included to a final classifier and cover count (cover count threshold C is applied at the beginning) of those examples covered by R is increased by 1. If the cover count of an example is exceeded by C, then that example is removed. This process continues while both the training dataset and ruleset are not empty.

The key differences are that our approach uses the APRIORI algorithm [3] to generate frequent itemsets, instead of FP-tree and rules being pruned based on minimum support and confidence constraints.

In CBA and MCAR approaches that use the so-called vertical mining approach, the “APRIORI” algorithm is executed first to generate CARs. Then, both algorithms apply greedy pruning based on database coverage to produce predictive rules. They have different rule-selection methods compared to ours—the rule that can classify at least one training example, that is, if the candidate rule’s body and class labels match the training example’s, the body and class labels are selected for the classifier. This step is different in our method since we are trying to increase the overall coverage and accuracy as well as decreasing the size of the classifier: we select the rule as a potential candidate, only if the rule contributes to improving the overall coverage (if the rule’s body matches the training example’s body, we ignore the class label).

The CPAR algorithm proposed by Yin and Han [10] combines the advantages of associative classification and traditional rule-based classification. CPAR utilizes a greedy algorithm to generate rules directly from the training dataset, instead of generating large candidate rules from frequent itemsets as in other associative classification methods. To avoid overfitting, CPAR uses expected accuracy to evaluate each rule and the classification process is also different than traditional classification approaches: First, CPAR selects all rules whose bodies match the testing example, second, it extracts the best k rules for each class among the rules selected in step 1, and finally, CPAR compares the average expected accuracy of the best k rules for each class found in step 2 and predicts the class label which achieves the highest expected accuracy.

The AC method proposed in Reference [46] is based on database coverage associated with test data. During the classification process of the test dataset, this approach considers the class label of rules that are similar to the test data and rule’s position in the classifier. The score of each class label is computed based on the above conditions and the test data is predicted by the class label that has the highest score.

Another AC [37] method aims to build a classifier based on rule-pruning. This method applies the vertical mining (TidList) to generate class association rules. Researchers proposed a new procedure called Active Rule Pruning (APR) to improve predictive accuracy and to reduce rule redundancy. Specifically, in the rule-selecting process, when a rule is being evaluated to be a potential candidate for a classifier, ranking of the remaining untested rules is also updated constantly after removing the training examples covered by that rule. The most important difference between our method and all other similar AC methods is that our approach has the stopping criteria in the rule-evaluation step based on user-defined coverage (for the learning dataset).

In the associative classification method [47], researchers proposed a new measure, called “condenseness” to evaluate the infrequent rule items. Authors argued that infrequent rule items which are not satisfied with the minimum support threshold could produce strong association rules for classification. “Condenseness” of infrequent rule items is the average of lift of all association rules that can be generated from those rule items. A rule item with a high condenseness means that its items are closely related and can produce potential rules for AC, although it does not have enough support. A new associative classifier, CARC—Condensed Association Rules for Classification, is presented based on the concept of “condenseness”. Association rules are generated by using the modified “APRIORI” algorithm and develop the new strategy of rule inference with the condenseness.

A recently proposed associative classifier called ARCID (Association Rule-based Classification for Imbalanced Datasets) aims to extract hidden regularities and knowledge from imbalanced datasets by emphasizing information extracted from minor classes. The key difference between our method and ARCID is in the rule-selection process. ARCID selects the best k rules by using the following interestingness measures: first, rules that have higher accuracy (rules that have higher supports can have higher predictive accuracy) and belong to major classes; second, rare rules that have lower support and belong to minor classes, while our algorithm selects the best rules according to their overall coverage (training dataset coverage) and the number of rules generated by our model depends on the intended_overall_coverage threshold.

Another recent approach [48] aims to produce an optimized associative classifier based on non-trivial data insertion for the incremental dataset. To solve the unattended data insertion and optimization problem, a new technique called “C-NTDI” is used to build a classifier, when there is an insertion of data that takes place in a non-trivial fashion in the initial data that are used for updating the classification rules. In the rule-generation part, PPCE and BAT [49] techniques are applied: PPCE is used to generate the rules, and further Proportion of Frequency Occurrence check with BAT Algorithm (PFOCBA) is applied for pruning the rules that are generated.

The FURIA (Fuzzy Unordered Rule Induction Algorithm) is a rule-based classification method [42] which is a modified and extended version of the RIPPER algorithm [23]. FURIA learns fuzzy rules instead of conventional rules and unordered rulesets (namely a set of rules for each class in a one-vs-rest scheme) instead of rule lists. Moreover, to deal with uncovered examples, it makes use of an efficient rule stretching method. The idea is to generalize the existing rules until they cover the example.

3. Problem Definition and Goals

Associative classification and association rule discovery are two important tasks of association rule mining. There are some differences between them. First, associative classification is supervised learning where the class value is known, while association rule discovery is unsupervised learning. The second and main difference between association rule discovery and AC is that the rule’s consequence in AC can have only the class attribute, however, multiple attribute values are allowed in the rule’s consequence to discover association rules. Overfitting prevention is an important task in AC, but it is really not essential in association rule discovery as in AC. Overfitting problems usually occur with imbalanced datasets, noise datasets or very small learning datasets. We can define the building of an accurate and compact classifier by using AC in the following steps.

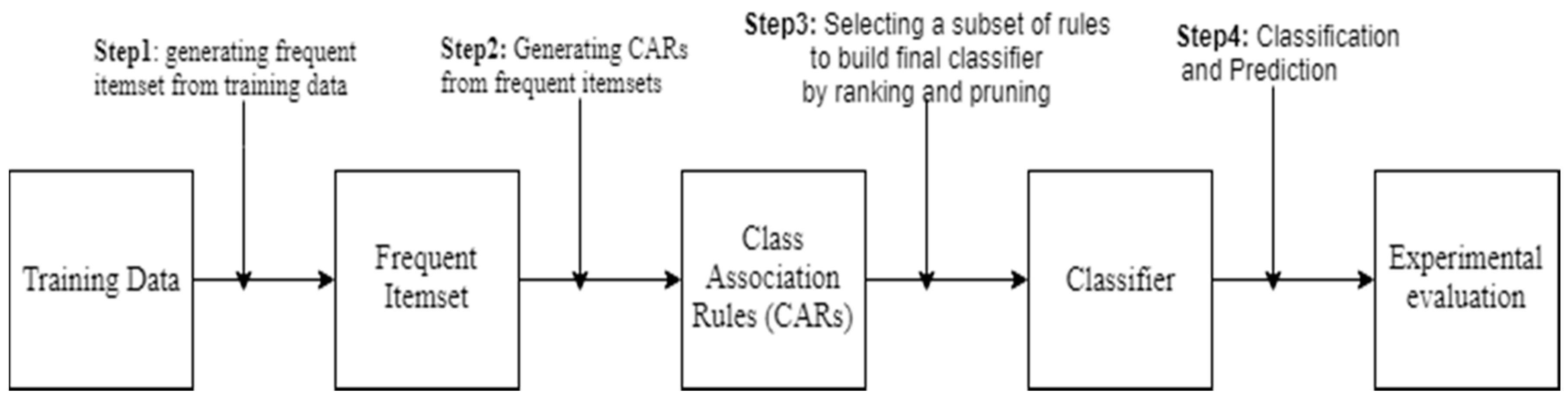
Figure 1 shows the general steps used in the AC approach. The first step is computationally expensive because it is similar to the association rule discovery which exhaustively searches the entire example space to discover the frequent itemsets (Step 1). In the second step, we generate strong class association rules from frequent itemsets that satisfy a user-defined minimum confidence threshold. A single rule is represented in AC by implication X → C, where C is the consequence (class label) and X is antecedent (Itemset) of the rule, that is, the highest frequency of class associated with its antecedent X in the learning dataset. Once the strong class association rules are generated, building an accurate and compact classifier is a straightforward approach, because no support counting or no scanning of the training dataset is required. The most important task is to select the most effective ordered subset of rules to form an intended classifier. In the last step, we measure the quality of the classifier on some independent test datasets.

We assume that we have given a normal relational table which consists of N examples described by L distinct attributes and all examples are classified into M known classes. Attribute type can be categorical (nominal) or continuous (numeric). Our proposed research supports only categorical (nominal) attributes, therefore, we treat all the attributes uniformly. We map the categorical attribute’s values to consecutive positive integers. Numeric attributes are discretized into intervals (bins), and the intervals are also mapped to consecutive positive integers. We use an equal height (frequency) discretization method to discretize the numeric attributes. Discretization methods are not discussed in this work since enough discretization methods are proposed in machine learning literature. Our goals are stated below:

• Our first goal is to generate the complete set of strong class association rules that satisfy the user-specified minimum support and minimum confidence constraints.
• The second and main goal is to build a simple and accurate classifier by straightforward pruning; more precisely, we select the strong rules that have the contribution to the improvement of overall coverage.
• The third goal is to discuss how overall coverage affects the classification accuracy of our proposed classifier.

4. Discovery of Class Association Rules

The step of finding frequent itemsets in associative classification is the most important and computationally expensive step [10,11]. Several different approaches to discover frequent rule items from a dataset have been adopted from association rule discovery. For example, some AC methods [15,50] employ the “APRIORI” candidate generation method. Other AC methods [8,51,52] mainly apply the FP-growth approach [45] to generate association rules. The CPAR algorithm utilizes a greedy strategy produced in FOIL [53]. “Tid-lists” methods of vertical data layout [54,55] are used in References [9,13]. This section focuses on discovering class association rules from frequent itemsets.

Association rule generation is usually split up into two main steps:

• In the first step, the minimum support threshold is applied to find all frequent itemsets from the training dataset.
• A minimum confidence constraint is applied to generate strong class association rules from the frequent itemsets.

In the first step, we use the “APRIORI” algorithm to find frequent itemsets. “APRIORI” utilizes the ‘downward-closure’ property to speed up the searching process by reducing the number of candidate itemsets at any level. The main feature of ‘downward-closure’ is that all subsets of a frequent itemset must be frequent. Infrequent itemsets found at any level are removed, because, it is not possible to “make” a frequent itemset from an infrequent one. “APRIORI” uses this process to prune infrequent itemsets before computing their support at any level. This reduces the time complexity of computing the support for all combinations of items in a dataset.

Once all frequent itemsets are found from a learning dataset in the first step, it is a straightforward approach to generate strong class association rules that satisfy both minimum support and minimum confidence constraints from these frequent itemsets in the second step. This can be done using the following equation for confidence:

$$confidence\left(X\to C\right)=\frac{support\_count\left(X\cup C\right)}{support\_count\left(X\right)}$$

(1)

The Equation (1) is expressed in terms of itemsets support count, where X is antecedent (itemsets that is, left-hand side of the rule), C is a consequence (a class label that is, right-hand side of the rule), support_count ($X\cup C$) is the number of transactions containing the itemsets $X\cup C$, and support_count (X) is the number of transactions containing the itemsets A. Based on this equation, CARs can be generated as follows:

• For each frequent itemsets L and class label C, generate all nonempty subsets of L.
• For every nonempty subset S of L, output the strong rule R in the form of “S→C” if, $\frac{support\_count\left(R\right)}{support\_count\left(S\right)}\ge min\_conf$, where min_conf is the minimum confidence threshold.

5. Our Associative Classification Approach—J&B

Our proposed approach—J&B, can be defined in three steps:

• A complete set of strong class association rules is generated from the training dataset discussed in Section 4.
• We then select strong class association rules that highly contribute to increasing the coverage of the classifier until we meet the stopping criterion to build an accurate, compact and understandable classifier.
• In the last step, we find the overall coverage and accuracy of the intended classifier to show how the overall coverage of the classifier affects its classification accuracy.

5.1. Our Intended Classifier

Once we generated the strong class association rules in Section 4, we propose our classifier by using them. Our proposed method is outlined in Algorithm 1.

Lines 1–2 find all frequent itemsets in the training dataset by using the “APRIORI” algorithm described in Section 4. The third line generates strong class association rules that satisfy the minimum support and confidence constraints from frequent itemsets. Class association rules (generated in line 3) are sorted by confidence and support descending order in the fourth line by the following criteria: Given two rules $R_1$ and $R_2$, R₁ is said to have a higher rank than R₂, denoted as $R_1>R_2$,

• If and only if, $conf\left(R_1\right)>conf\left(R_2\right)$; or
• If $conf\left(R_1\right)=conf\left(R_2\right)$ but, $supp\left(R_1\right)>supp\left(R_2\right)$; or
• If $conf\left(R_1\right)=conf\left(R_2\right)$ and $supp\left(R_1\right)=supp\left(R_2\right),\hspace{1em}{R}_1$ has fewer attribute values in its left-hand side than $R_2$ does;
• If all the parameters of the rules are equal, we can choose any of them.

Initial values of classified_traindata array are filled with false value in line 5. This array is used later to compute the overall coverage of the training data. Basically, the classifier is built in lines 6–17. We scan the training dataset for each rule (lines 6–7): if the rule classifies a new unclassified example 5 (that is, the rule’s body matches the new example’s body), then we increase the contribution (that is, the contribution of the rule to increase the overall coverage) in lines 8–11. If contribution is higher than 0, that is, the rule classified new example(s), then we increase the overall coverage by contribution, and we add that rule to our final classifier in lines 12–14. If the rule can classify training examples, but cannot contribute to the betterment of the overall coverage, then we do not evaluate that rule as a potential rule for our classifier. Lines 15–16 stop the procedure if the classifier achieves the intended overall coverage that is higher than the user-defined intended_coverage threshold, and line 17 returns the proposed classifier.

Algorithm 1: Building a compact and accurate classifier—J&B

Input: A training dataset D, minimum support and confidence constraints, intended coverage

Output: A subset of strong class association rules for classification

1: D = taining_dataset;

2: F = frequent_itemsets(D);

3: Rule = genCARs(F);

4: Rule = sort(R, minconf, minsup);

5: Fill(classified_traindata, false):

6: for i: = 1 to Rule.length do begin

7:  for j: = 1 to D.length do begin

8:   if classified_traindate[j] = false then

9:    if Rule[i].premise classifies D[j].premise then

10:     classified_traindate[j] = true;

11:     contribution = contribution + 1;

12:  if contribution > 0 then

13:   overall_coverage = overall_coverage + contribution;

14:   Classifier = Classifier.add(rule[i]);

15:  if (overall_coverage/D.length) ≥ intended_coverage then

16:   break;

17: return Classifier

The classification process of our method is shown in Algorithm 2.

Algorithm 2: Classification process of J&B

Input: A Classifier and test dataset

Output: Predicted class

1: for each rule y ∈ Classifier do begin

2:  if y classify test_example then

3:   class_count[y.class]++;

4:  if max(class_count) = 0 then

5:   predicted_class = majority_classifier;

6:  else

7:   predicted_class = max_index(class_count);

8: return predicted_class

Algorithm 2 depicts the procedure of using the J&B classifier to find the class label of a (new) test example. For each rule in the J&B classifier (line 1): if the rule can classify the example correctly, then we increase the corresponding class count by one and store it (lines 2–3). If none of the rules can classify the new example correctly, then the algorithm returns the majority class value (lines 4–5); otherwise, it returns the majority class value of correctly classified rules (lines 6–7).

5.2. Overall Coverage and Accuracy

After our classifier is built (as in Section 5.1), it is straightforward to compute the overall coverage and accuracy of the classifier (defined in Algorithm 3). To compute the overall coverage, we count the examples that are covered by the classifier and divide it by the total number of examples in the dataset. For accuracy, we count all the examples that are classified by the classifier and divide it by the total number of examples in the dataset.

The first line finds the length of the dataset. In the second and third lines, we fill all initial values of classified_testdata (to compute the overall coverage) and classified_testdata_withclass (to compute the overall accuracy) arrays as false. Lines 4–11 generally switch the status of the test example, without a class label to compute the overall coverage in lines 6–8 and with a class label to calculate the accuracy in lines 9–11. The number of correctly classified examples by classifier without class labels and with class labels are counted in lines 12–16 to calculate the overall coverage of the classifier, and overall accuracy is computed in lines 17–18. The last line returns the obtained results.

Algorithm 3: Overall coverage and accuracy of the classifier

Input: Dataset D and classifier C

Output: Overall coverage and accuracy of the classifier

1: n = D.length();

2: Fill (classified_testdata, false);

3: Fill (classified_testdata_withclass, false);

4: for i: = 1 to C.length do

5:  for j: = 1 to n do

6:   if C[i].premise classifies D[j].premise then

7:    if classified_testdata[j] = false then

8:     classified_testdata[j] = true;

9:   if C[i] classifies D[j] then

10:    if classified_testdata_withclass[j] = false then

11:     classified_testdata_withclass[j] = true;

12: for i: = 1 to n do

13:  if classified_testdata[i] then

14:   testcoverage++;

15:  if classified_testdata_withclass[i] then

16:   accuracy++;

17: Overallcoverage_testdata = testcoverage/n;

18: Overallaccuracy_testdata = accuracy/n;

19: return Overallaccuracy_testdata, Overallcoverage_testdata

Example 1.

Let us assume we have given the following training dataset that is illustrated in

Table 1. Training dataset.

#	a1	a2	a3	a4	a5	Class
1	3	4	2	1	3	1
2	5	3	1	4	2	2
3	1	5	2	4	2	1
4	3	2	3	1	2	3
5	?	2	?	3	5	1
6	1	3	5	4	3	2
7	2	2	1	2	2	2
8	1	4	4	2	2	1
9	1	?	2	4	3	2
10	1	5	1	1	5	3
11	1	2	1	1	5	2
12	1	4	4	4	2	1
13	1	3	?	?	?	2
14	1	4	5	4	4	3
15	3	2	2	1	2	10

and we apply here minimum coverage threshold as 80%, that is, when our intended classifier covers at least 80% of the training examples, then, we stop.

We have the following class association rules (shown in

Table 2. Generated CARs from the training dataset

CARs	Suppport (%)	Confidence (%)
{a1 = 3, a3 = 2, a4 = 1, a5 = 3} → {1}	4	72
{a1 = 1, a2 = 5} → {3}	5	100
{a1 = 3, a4 = 1} → {1}	8	100
{a1 = 1, a3 = 5, a4 = 4} → {3}	5	100
{a1 = 2, a2 = 2, a3 = 2} → {2}	5	63
{a2 = 3, a3 = 1, a4 = 4, a5 = 2} → {1}	3	80
{a1 = 2, a2 = 3, a3 = 4} → {2}	11	85
{a3 = 1, a5 = 2} → {1}	8	90
{a1 = 1, a2 = 5, a5 = 5} → {3}	6	65
{a1 = 1, a3 = 4, a5 = 2} → {2}	10	85
{a1 = 1, a2 = 2, a3 = 1, a4 = 3, a5 = 1} → {3}	4	64
{a2 = 2, a5 = 5} → {2}	6	100

) (which satisfied the user-specified minimum support and confidence thresholds) that are generated based on minimum support and confidence thresholds which are discussed in the fourth section.

In the second step, we sort the class association rules by confidence and support descending order. The result is shown in

Table 3. Sorted class association rules.

CARs	Suppport (%)	Confidence (%)
{a1 = 3, a4 = 1} → {1}	8	100
{a2 = 2, a5 = 5} → {2}	6	100
{a1 = 1, a2 = 5} → {3}	5	100
{a1 = 1, a3 = 5, a4 = 4} → {3}	5	100
{a3 = 1, a5 = 2} → {1}	8	90
{a1 = 2, a2 = 3, a3 =4} → {2}	11	85
{a1 = 1, a3 = 4, a5 =2} → {2}	10	85
{a2 = 3, a3 = 1, a4 = 4, a5 = 2} → {1}	3	80
{a1 = 3, a3 = 2, a4 = 1, a5 = 3} → {1}	4	72
{a1 = 1, a2 = 5, a5 = 5} → {3}	6	65
{a1 = 1, a2 = 2, a3 = 1, a4 = 3, a5 = 1} → {3}	4	64
{a1 = 2, a2 = 2, a3 = 2} → {2}	5	63

.

In the next step, we form our classifier by selecting the strong rules. We select strong rules which contribute to improving the overall coverage, and we continue until achieving the intended training dataset coverage.

Table 4. Final classifier.

N	Classifier Rules	# Classified Examples
1	{a1 = 3, a4 = 1} → {1}	3
2	{a2 = 2, a5 = 5} → {2}	1
3	{a1 = 1, a2 = 5} → {3}	2
4	{a1 = 1, a3 = 5, a4 = 4} → {3}	2
5	{a3 = 1, a5 = 2} → {1}	2
6	{a1 = 1, a3 = 4, a5 = 2} → {2}	2

illustrates our final classifier.

Our classifier includes 6 rules. In this example, intended coverage is equal to 80% and 6 classification rules in the classifier cover 80% of the learning set. Since our training dataset has some examples with missing values, our classifier covered the whole training dataset (examples without missing values). Other rules also may cover unclassified examples, but we cannot exceed the user-defined training dataset coverage threshold. This is our stopping criterion and we cannot include other rules into our classifier. We cannot also include classification rules which cover only classified examples (this means it does not contribute to the improvement of overall coverage). Now, we classify the following unseen example:

{a1 = 1, a2 = 5, a3 = 5, a4 = 4, a5 = 5}→ ?

So, this example is classified by the third and fourth classification rules. The class values of the rules which correctly classified the new example are 3 and 3. So, our classifier predicts that the class value of the new example is 3 (because majority class value is 3).

6. Experimental Evaluation

We tested our model on 12 real-life datasets taken from the UCI Machine Learning Repository. We evaluated our classifier (J&B) by comparing it with 8 well-known classification methods on the accuracy, relevance measures and the number of classification rules. All differences were tested for statistical significance by performing a paired t-test (with a 95% significance threshold).

J&B was run with default parameters minimum support = 1% and minimum confidence = 60% (on some datasets, however, minimum support was lowered to 0.5% or even 0.1% to ensure enough CARs to be generated for each class value). For all other 8 rule learners, we used their WEKA workbench [56] implementation with default parameters. We applied 90% as a required coverage (training dataset) threshold that is the stopping point of selecting rules to our classifier described in Section 5.1. The description of the datasets and input parameters are shown in

Table 5. Description of datasets and AC algorithm parameters.

Dataset	# of Attributes	# of Classes	# of Records	Min Support	Min Confidence
Breast Can	10	2	286	1%	60%
Balance	5	3	625	1%	50%
Car.Evn	7	4	1728	1%	50%
Vote	17	2	435	1%	60%
Tic-Tac-Toe	10	2	958	1%	60%
Nursery	9	5	12,960	0.5%	50%
Hayes-root	6	3	160	0.1%	50%
Lymp	19	4	148	1%	60%
Spect.H	23	2	267	0.5%	50%
Adult	15	2	45,221	0.5%	60%
Chess	37	2	3196	0.5%	60%
Connect4	43	3	67,557	1%	60%

.

Furthermore, all experimental results were produced by using a 10-fold cross-validation evaluation protocol.

Experimental results on classification accuracies (average values over the 10-fold cross-validation with standard deviations) are shown in

Table 6. The comparison between our method and some classification algorithms on accuracy.

Dataset	DTNB	DT	C4.5	PT	FR	RDR	CBA	SA	J&B	OC
Breast.Can	70.4 $\pm 4.1$	69.2 $\pm 6.7$	75.0 $\pm 6.9$	74.0 $\pm 4.0$	75.1 $\pm 5.3$	71.8 $\pm 5.7$	71.9 $\pm 9.8$	79.3 $\pm 4.4$	80.5 $\pm 4.7$	88.7
Balance	81.4 $\pm 8.1$	66.7 $\pm 5.0$	64.4 $\pm 4.3$	76.2 $\pm 5.6$	77.5 $\pm 7.6$	68.5 $\pm 4.3$	73.2 $\pm 3.8$	74.0 $\pm 4.1$	74.1 $\pm 2.6$	86.3
Car.Evn	95.4 $\pm 0.8$	91.3 $\pm 1.7$	92.1 $\pm 1.7$	94.3 $\pm 1.0$	91.8 $\pm 1.1$	91.0 $\pm 1.8$	91.2 $\pm 3.9$	86.2 $\pm 2.1$	89.4 $\pm 1.4$	94.2
Vote	94.7 $\pm 3.4$	94.9 $\pm 3.7$	94.7 $\pm 4.4$	94.8 $\pm 4.2$	94.4 $\pm 2.8$	95.6 $\pm 4.1$	94.4 $\pm 2.6$	94.7 $\pm 2.3$	94.1 $\pm 1.8$	92.8
Tic-Tac	69.9 $\pm 2.7$	74.4 $\pm 4.4$	85.2 $\pm 2.7$	94.3 $\pm 3.3$	94.1 $\pm 3.1$	94.3 $\pm 2.9$	100.0 $\pm 0.0$	91.7 $\pm 1.5$	95.8 $\pm 2.0$	100.0
Nursery	94.0 $\pm 1.5$	93.6 $\pm 1.2$	95.4 $\pm 1.4$	96.7 $\pm 1.7$	91.0 $\pm 1.4$	92.5 $\pm 1.5$	92.1 $\pm 2.4$	91.6 $\pm 1.2$	89.6 $\pm 1.1$	85.6
Hayes.R	75.0 $\pm 7.2$	53.4 $\pm 8.3$	78.7 $\pm 8.4$	73.1 $\pm 9.7$	77.7 $\pm 8.7$	74.3 $\pm 7.1$	75.6 $\pm 10.9$	73.1 $\pm 6.0$	79.3 $\pm 5.9$	80.7
Lymp	72.9 $\pm 9.0$	72.2 $\pm 8.3$	76.2 $\pm 8.7$	81.7 $\pm 9.0$	80.0 $\pm 8.2$	78.3 $\pm 7.3$	79.0 $\pm 9.7$	73.7 $\pm 5.1$	80.6 $\pm 5.7$	90.1
Spect.H	79.3 $\pm 2.7$	79.3 $\pm 1.6$	80.0 $\pm 9.0$	80.4 $\pm 5.6$	80.4 $\pm 2.2$	80.4 $\pm 2.2$	79.0 $\pm 1.6$	79.1 $\pm 2.1$	79.7 $\pm 3.1$	94.8
Adult	73.0 $\pm 4.1$	82.0 $\pm 2.3$	82.4 $\pm 4.7$	82.1 $\pm 4.7$	75.2 $\pm 3.2$	80.8 $\pm 2.7$	81.8 $\pm 3.4$	80.8 $\pm 2.6$	80.8 $\pm 2.9$	91.7
Chess	93.7 $\pm 3.0$	97.3 $\pm 3.1$	98.9 $\pm 3.6$	98.9 $\pm 3.1$	96.4 $\pm 2.1$	95.8 $\pm 3.3$	95.4 $\pm 2.9$	92.2 $\pm 3.8$	94.6 $\pm 2.7$	100.0
Connect4	78.8 $\pm 5.9$	76.7 $\pm 7.7$	80.0 $\pm 6.8$	81.1 $\pm 7.9$	80.6 $\pm 7.1$	80.0 $\pm 6.4$	80.9 $\pm 8.1$	78.7 $\pm 6.0$	81.2 $\pm 5.2$	90.6
Avg (%):	81.5 $\pm$ 4.4	79.3 $\pm$ 4.5	83.6 $\pm 5.2$	85.6 $\pm 4.9$	84.5 $\pm 4.4$	83.6 $\pm$4.1	84.5 $\pm 4.9$	82.3 $\pm 3.4$	84.9 $\pm 3.3$	91.3

(OC: Overall Coverage).

Our observations (Table 6) on selected datasets show that our proposed classifier (J&B) achieved better performance than Decision Table (DT), C4.5, Decision Table and Naïve Bayes (DTNB), Ripple Down Rules (RDR) and Simple Associative Classifier (SA) (84.9% and 79.3%, 83.6%, 81.5%, 83.6%, 82.3%) on average accuracy. Our proposed method achieved the best accuracy on “Breast Cancer”, “Hayes.R” and “Connect4” datasets.

Standard deviations ranged around 4.0 in all classification methods and were higher for all methods on “Breast cancer”, “Hayes.R”, “Lymp” and “Connect4” datasets (above 4); that is, the differences between accuracies fluctuated and were reasonably high in 10-fold cross-validation experiments. When the overall coverage is above 90%, our proposed method tends to get reasonably high accuracy on all datasets. On the other hand, overall coverage of “J&B” was lower than its accuracy on “Vote” and “Nursery” datasets. This fact is not surprising since uncovered examples get classified by the majority classifier.

Statistically significant testing (wins/losses counts) on accuracy between J&B and other classification models is shown in

Table 7. Statistically significant wins/losses counts of J&B method on accuracy.

	DTNB	DT	C4.5	PT	FR	RDR	CBA	SA
W	6	6	4	2	2	4	2	6
L	3	2	3	4	2	1	2	1
W-L	3	4	5	6	8	7	8	5

. W: our approach was significantly better than compared algorithms, L: selected rule-learning algorithm significantly outperformed our algorithm, W-L: no significant difference has been detected in the comparison.

Table 7 illustrates that the performance of the J&B method on accuracy was better than DTNB, DT, RDR and SA methods. Although J&B obtained a similar result with FR and CBA (there is no statistical difference on 8 datasets out of 12), it is beaten by the PT algorithm according to win/losses counts. However, on average, the classification accuracies of J&B are not much different from those of the other 8 rule-learners.

Results show (

Table 8. The number of classification rules generated by the classifiers.

Dataset	DTNB	DT	C4.5	PT	FR	RDR	CBA	SA	J&B
Breast.Can	122	22	10	20	13	13	63	20	47
Balance	31	35	35	27	44	22	77	45	79
Car.Evn	144	432	123	62	100	119	72	160	41
Vote	270	24	11	8	17	7	22	30	13
Tic-Tac-Toe	258	121	88	37	21	13	23	60	14
Nursery	1240	804	301	172	288	141	141	175	109
Hayes-root	5	8	22	14	11	10	34	45	34
Lymp	129	19	20	10	17	11	23	60	29
Spect.H	145	2	9	13	17	12	4	50	11
Adult	737	1571	279	571	150	175	126	130	97
Chess	507	101	31	29	29	30	12	120	24
Connect4	3826	4952	3973	3973	403	341	349	600	273
Average (%)	618	674	409	411	93	75	79	125	64

) that J&B generates a reasonably smaller number of compact rules which is not sensitive to the size of the training datasets, while the number of rules produced by traditional classification methods such as “DT”, “C4.5”, “PT” and “DTNB” algorithms depend on the dataset’s size. Even though not achieving the best classification accuracies on “Nursery” and “Adult” datasets, it produced the lowest number of rules on those datasets among all classification models.

Statistically significant counts (wins/losses) of J&B against other rule-based classification models on classification rules is shown in

Table 9. Statistically significant wins/losses counts of J&B method on rules.

	DTNB	DT	C4.5	PT	FR	RDR	CBA	SA
W	10	7	6	6	8	5	7	10
L	2	5	4	6	4	5	3	2
W-L	0	0	2	0	0	2	2	0

.

Table 9 proves that J&B produced a statistically smaller classifier than DTNB and SA methods on 10 datasets, and DT, FR and CBA methods on 7 (or more than 7) datasets out of 12. The most importantly, J&B generated statistically smaller classifiers than all other models on bigger datasets, which was our main goal in this research. Experimental evaluations on bigger datasets (over 10,000 samples) are shown in Figure 2.

Figure 2 proves the advantage of the J&B method: it produced the smallest classifier among all rule-based classification models on selected datasets.

Our experiment on relevance measures (average results) such as “Precision”, “Recall” and “F-measure”, is highlighted in Figure 3. The detailed result for each dataset can be found in Appendix A.

7. Discussion

J&B produces classifiers that have on average far fewer rules than those produced by the “classical” rule-learning methods and slightly smaller number of rules comparing to associative classification models included in the comparison. J&B generated a reasonably smaller number of rules on bigger datasets compared to all other classification methods. J&B achieved the best accuracy on “Breast cancer”, “Hayes-root” and “Connect4” datasets among all methods (80.5%, 79.3% and 81.2% respectively), while it got a slightly worse result on “Nursery” and “Car.Evn” datasets. On other datasets, J&B achieved almost similar results with all rule-based classification methods.

We used the “WEKA” software to generate class association rules and to explore other classification algorithms because “WEKA” is open-source software that includes all the necessary classification approaches and it is relatively easy to use and program. Our proposed algorithm has some limitations:

• To get “enough” class association rules (“enough” means at least 5–10 rules for each class value—this situation mainly happens with imbalanced datasets) for each class value and achieve a reasonable overall coverage, we need to apply appropriate minimum support and minimum confidence thresholds. That is, we should take into consideration the class distribution of each dataset.
• In this research work, one of the novel approaches is to apply the intended coverage constraint which becomes the stopping criteria of selecting rules for our classifier. Here, we aimed to show that it is possible to achieve reasonably high accuracy without covering the whole dataset (especially when the dataset has some missing or noisy examples). This criterion becomes an advantage of our method that produces significantly smaller classification rules on bigger datasets.
• The J&B produced an accurate and compact classifier on a dataset which has a large number of attributes and records (especially, with balanced datasets on class-distribution), while the performance of J&B will be slightly worse with the datasets having a small number of attributes and a large number of records (as proven on “Nursery” and “Car.Evn” datasets).
• It is unnecessary to remove the missing values from the dataset because all “classical” classification algorithms and our method can handle missing values directly.
• J&B generates a smaller number of classification rules compared to all other traditional and associative classifiers on bigger datasets.
• We tried to solve the outer-class overlapping problem (that means some samples from different classes have very similar characteristics) by grouping the CARs according to their class value, and the inter-class overlapping problem (several rules that belong to the same class may cover the same samples) by selecting the rules based on database coverage.
• Our method may get slightly worse results in terms of classification accuracy than other traditional classification methods on imbalanced datasets, because unbalanced class distribution may affect the rule-generation part of our algorithm.
• The time complexity of the APRIORI algorithm is potentially exponential but, on the other hand, we gain in more exhaustively exploring the entire search space and in part, this issue can be solved by trying to use more efficient data representation and parallelization of the algorithm, which is what we plan to do in future work.

8. Conclusions and Future Work

Our experiments on accuracy and number of rules show that our method is compact, accurate and comparable with 8 other well-known classification methods. Although it did not achieve the best average classification accuracy, it produced significantly smaller rules on bigger datasets compared to other classification algorithms. Our proposed classifier achieved reasonably high average coverage with 91.3%.

Statistical significance testing shows that our method was statistically better than or equal to other classification methods on some datasets, while it obtained worse results than those methods on some other datasets. The most important achievement in this research was that J&B got significantly better results in terms of an average number of classification rules than all other classification methods, while it had comparable results to those methods on accuracy.

This research was the first and main step for our future goal, where we plan to cluster class association rules by their similarity and thus further reduce their number and increase the accuracy and understandability of the classifier.