Experimental Study on Seismic Retrofitting of Reinforced Concrete Frames Using Welded Concrete-Filled Steel Tubes
Abstract
:1. Introduction
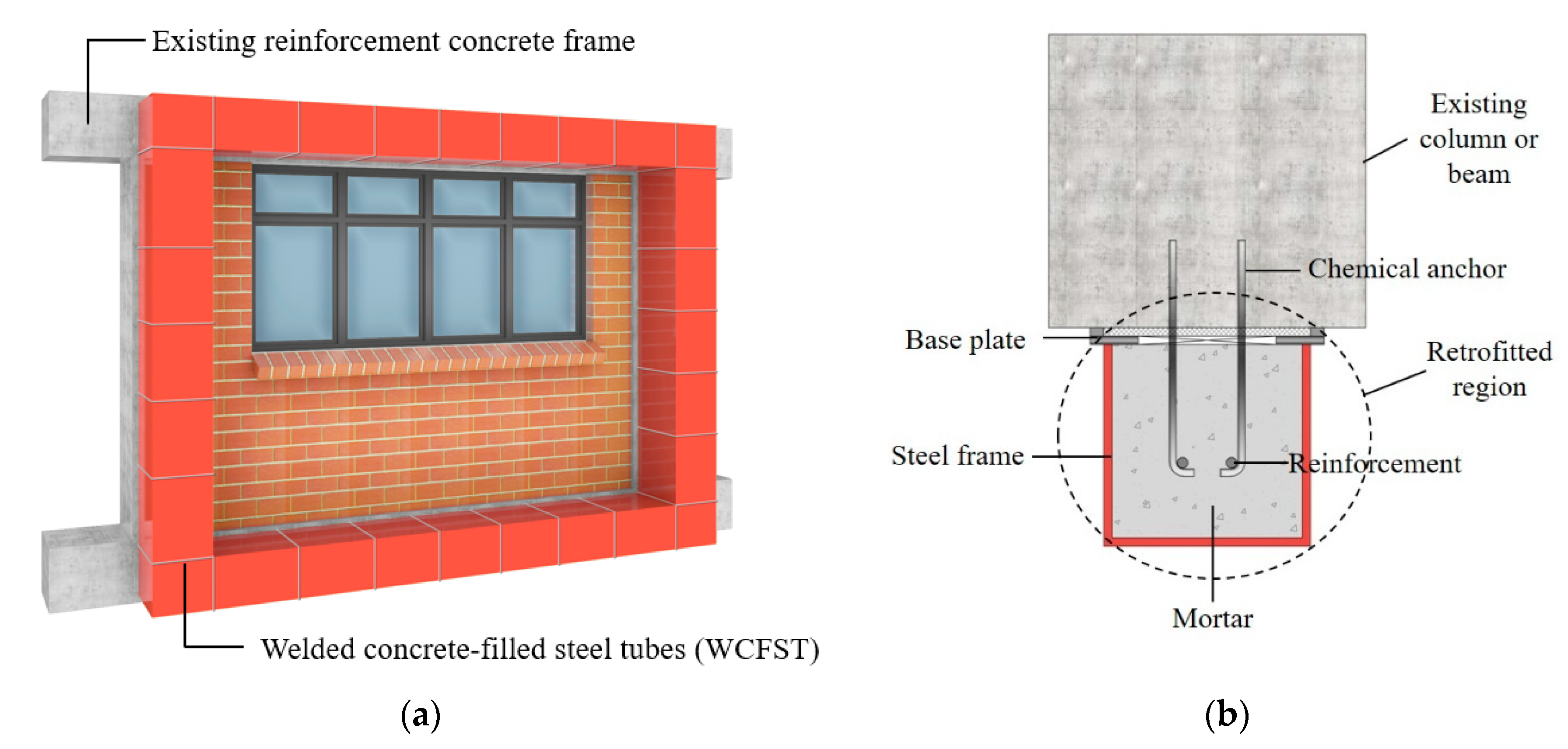
2. Seismic Retrofitting Method Using Welded Concrete-Filled Steel Tubes
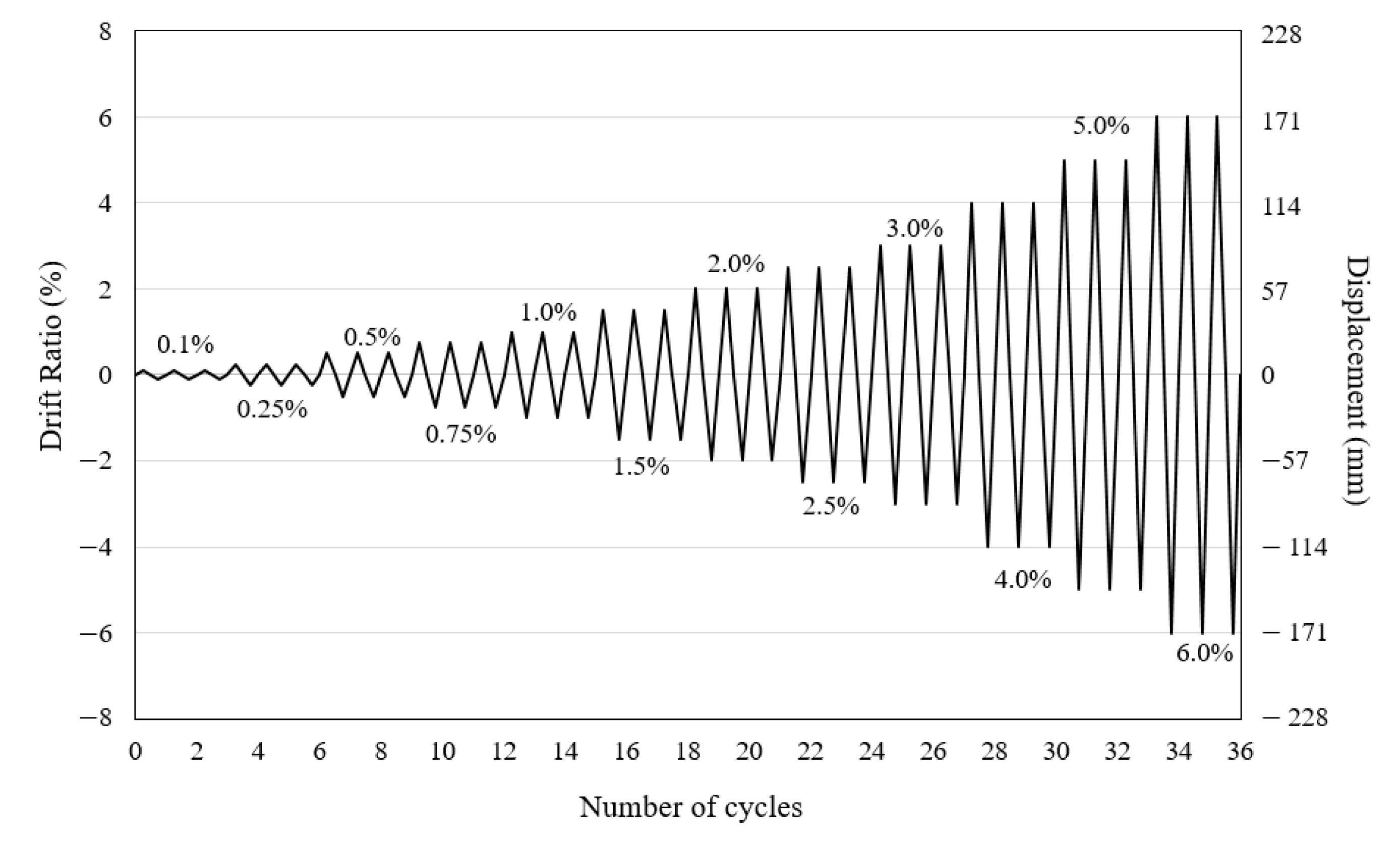
3. Experimental Program
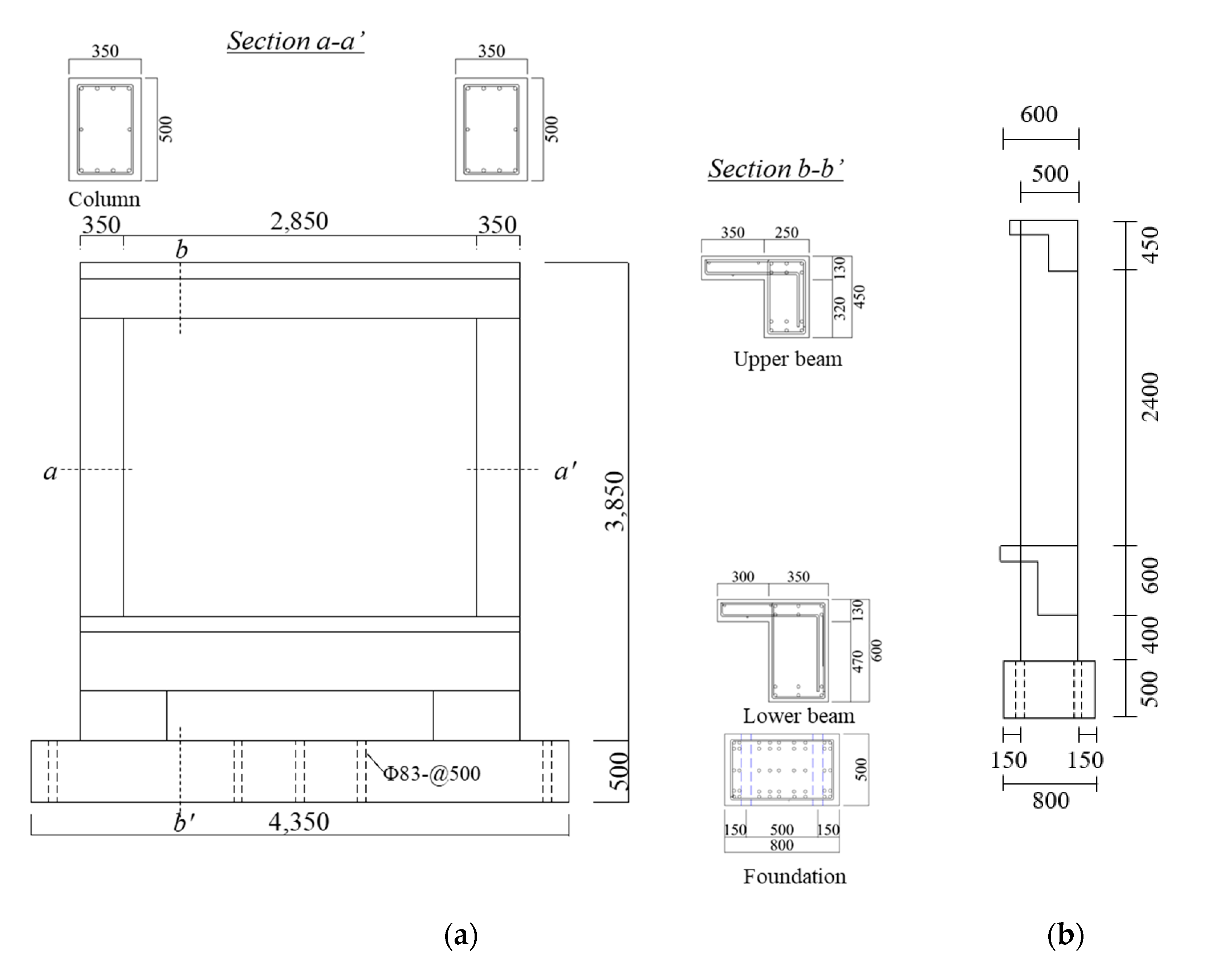
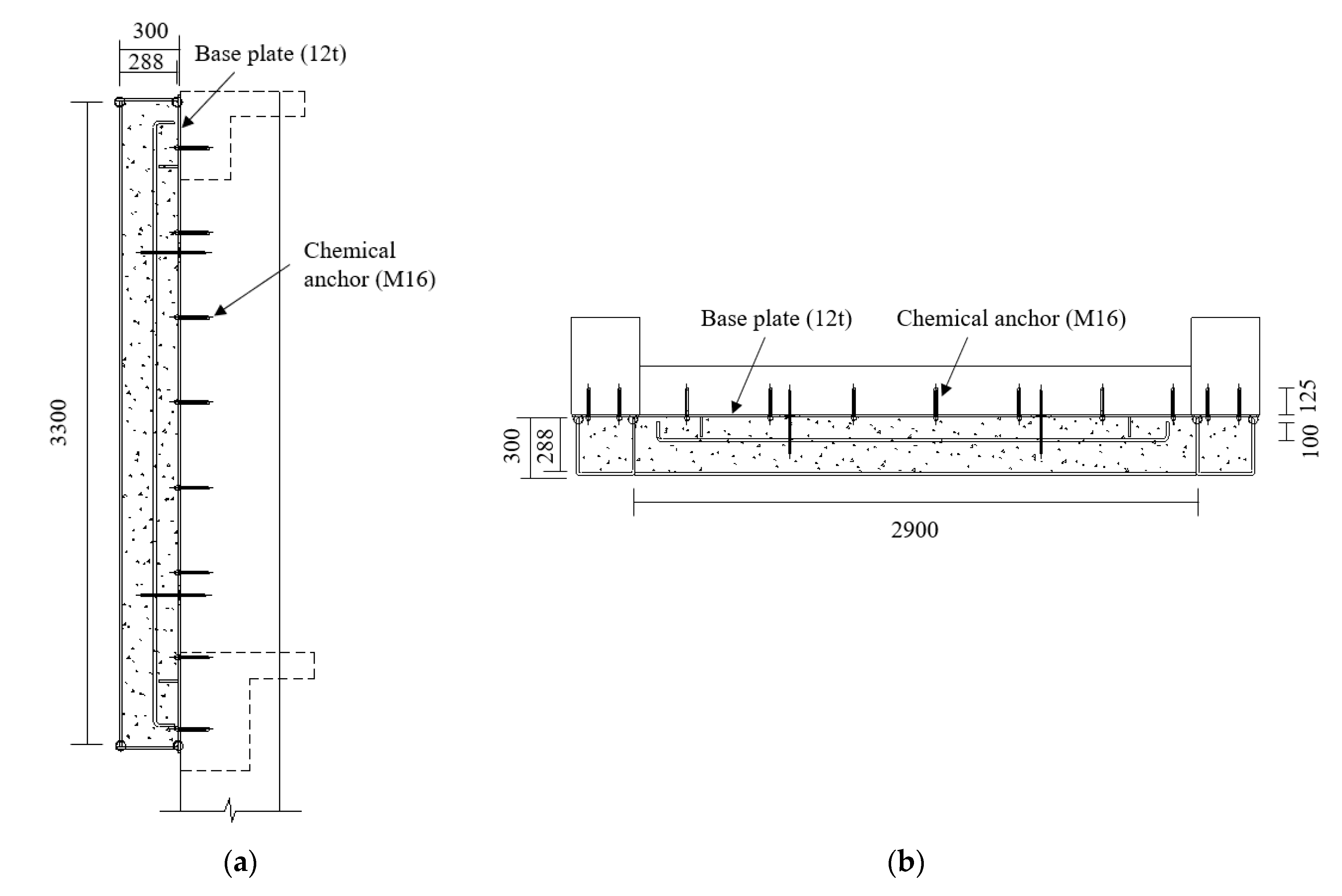
3.1. Specimen Details
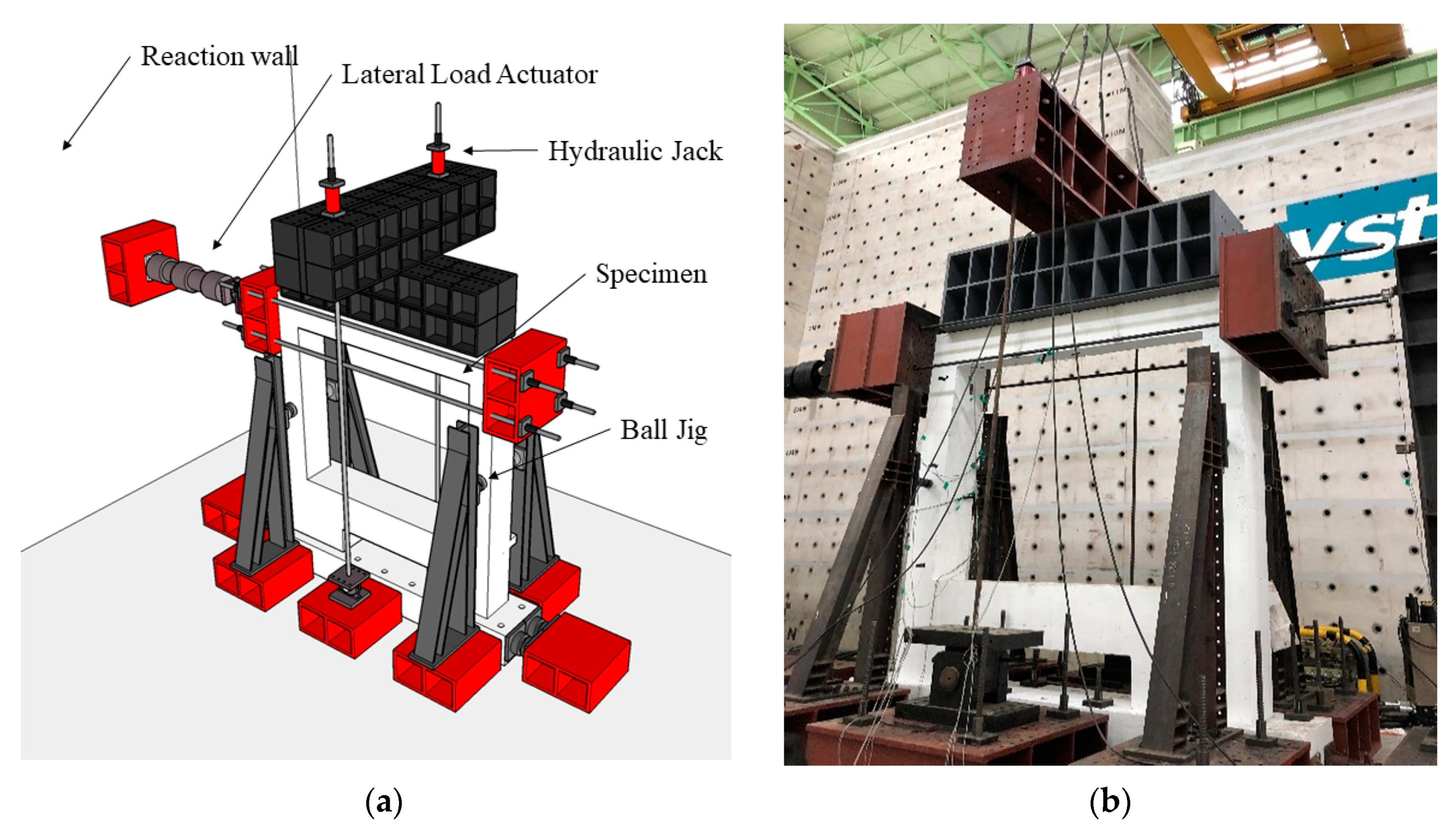
3.2. Test Setup
4. Experimental Results and Analysis
4.1. Cracks and Failure Modes of Specimens
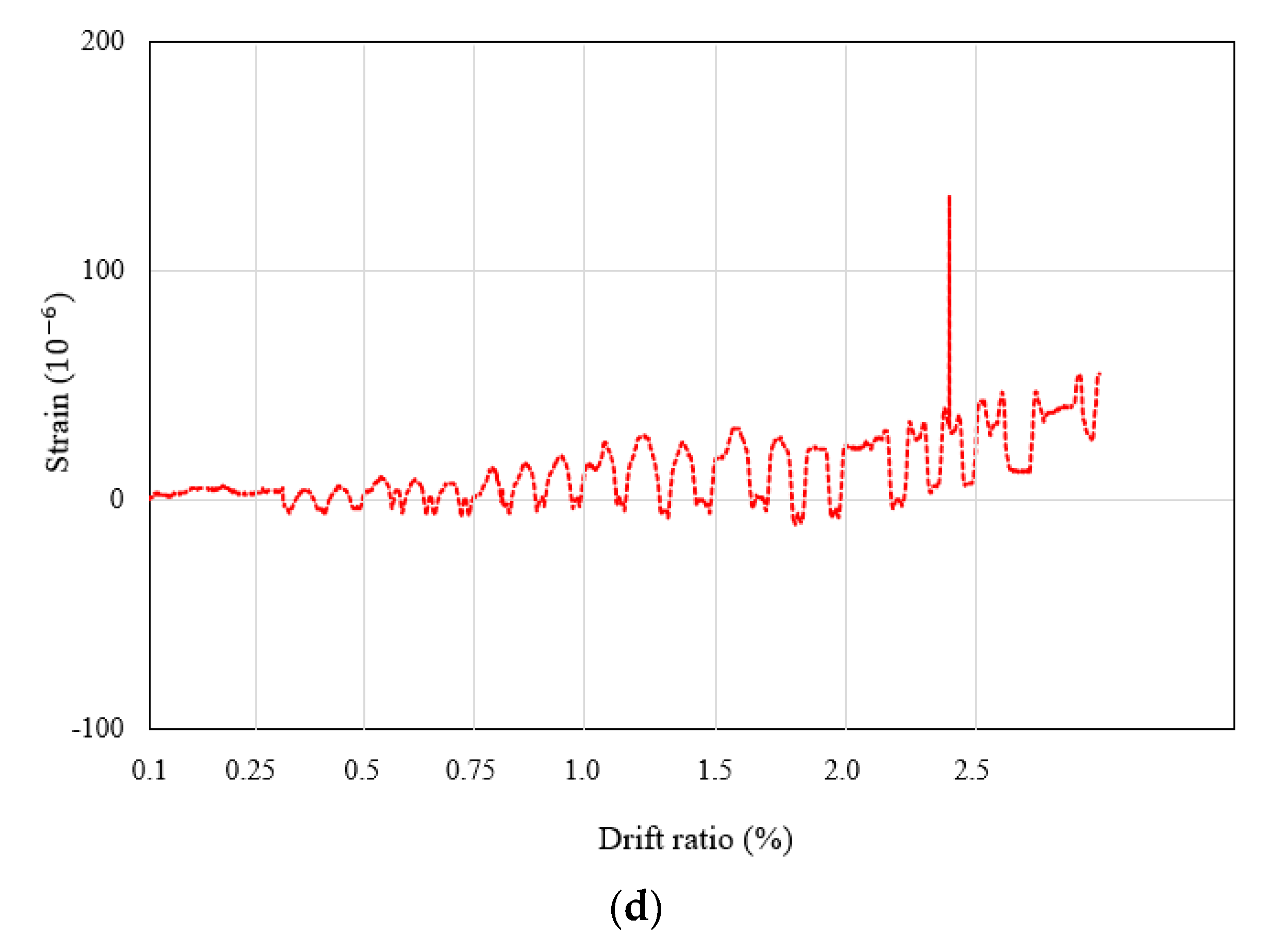
4.2. Load–Displacement Relationships and Strains
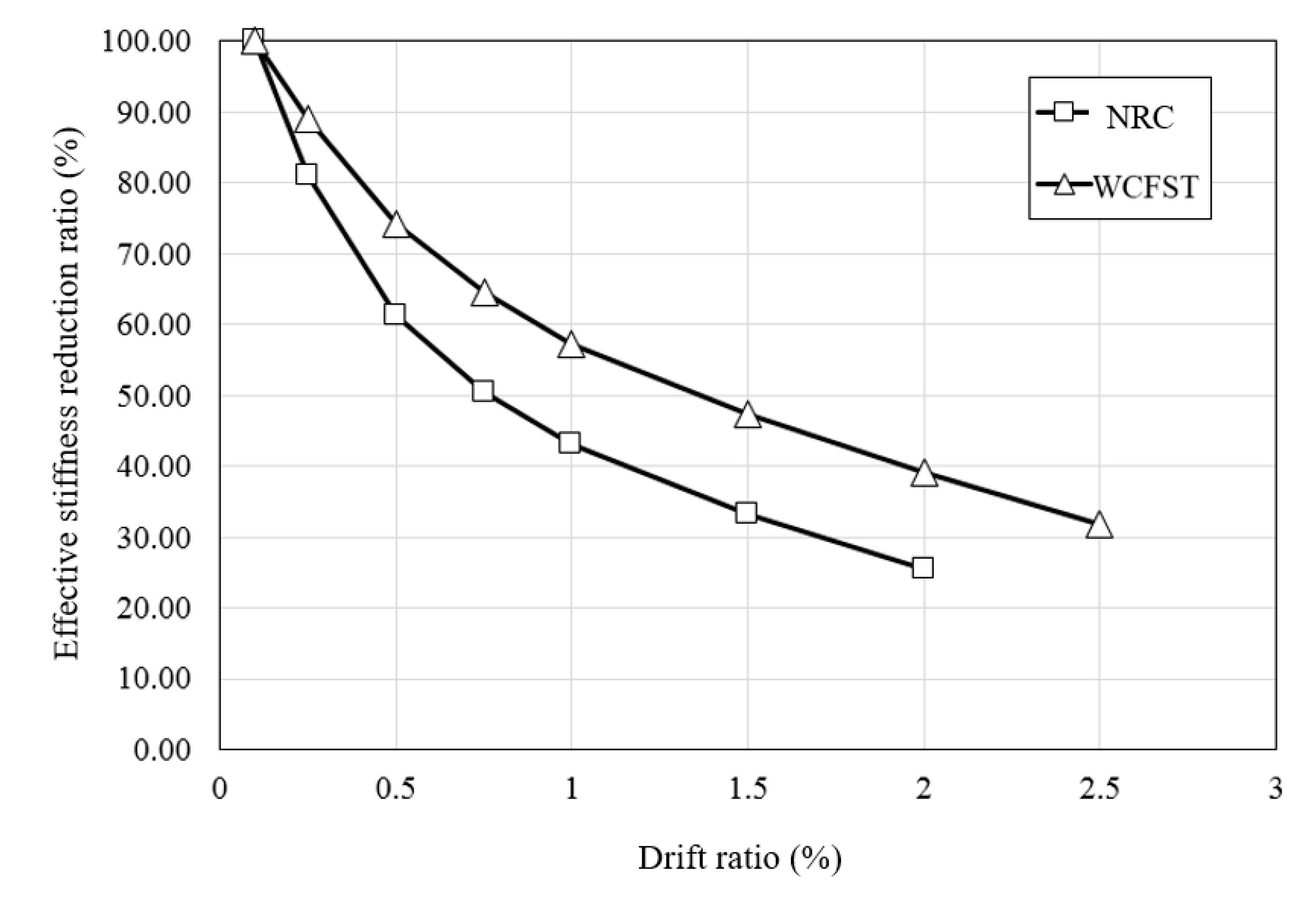
4.3. Effective Stiffness
4.4. Energy Dissipation
5. Conclusions
- All of the specimens showed initial cracking at the bottom of the column at a drift ratio of 1%; the number and width of cracks at the beam-column joint and column increased as the load increased. As the drift ratio increased, the width of the shear cracks on the column increased, concrete spalling occurred, and failure of the specimens was observed at a drift ratio of 2.5%. For the NRC specimen without seismic details, the loading experiment was terminated after shear cracks were observed in the column, as the crack in the column and the overall number of cracks rapidly increased and the lateral reinforcement of the left column buckled. In the case of the WCFST specimen retrofitted according to the proposed method, the increase in shear crack width was not significant (unlike the case of the NRC specimen) and some concrete spalling was observed only at the bottom of the column. No deformation or elimination of the CFST frame was evident when the experiment was terminated.
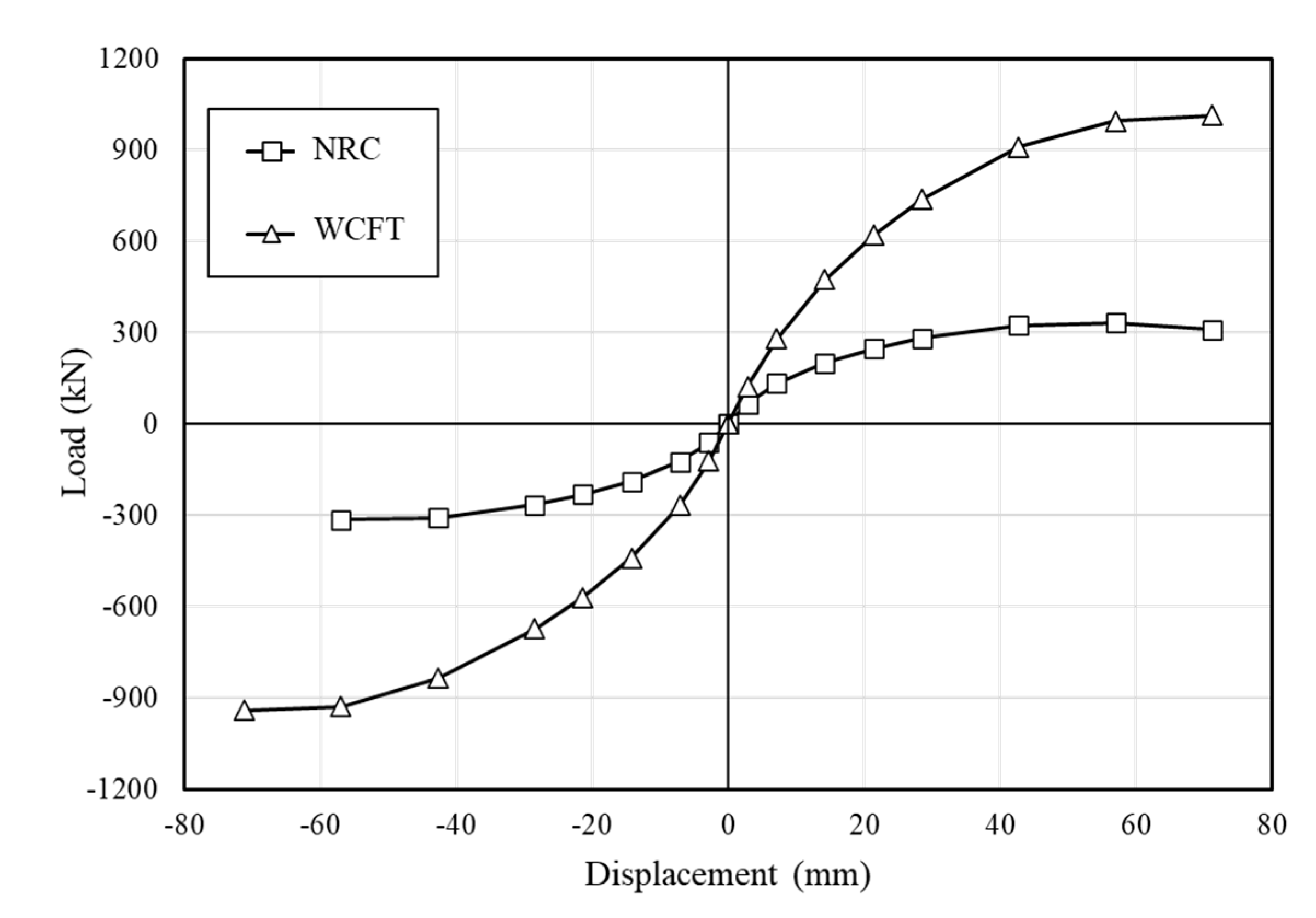
- The maximum loads of the NRC and WCFST specimens were 332 kN and 1013.32 kN in the positive direction, and −314.2 kN and −940.5 kN in the negative direction, respectively. When the proposed seismic retrofitting method was applied, the ability to resist lateral forces increased by about three times when compared with the existing reinforced concrete structure.
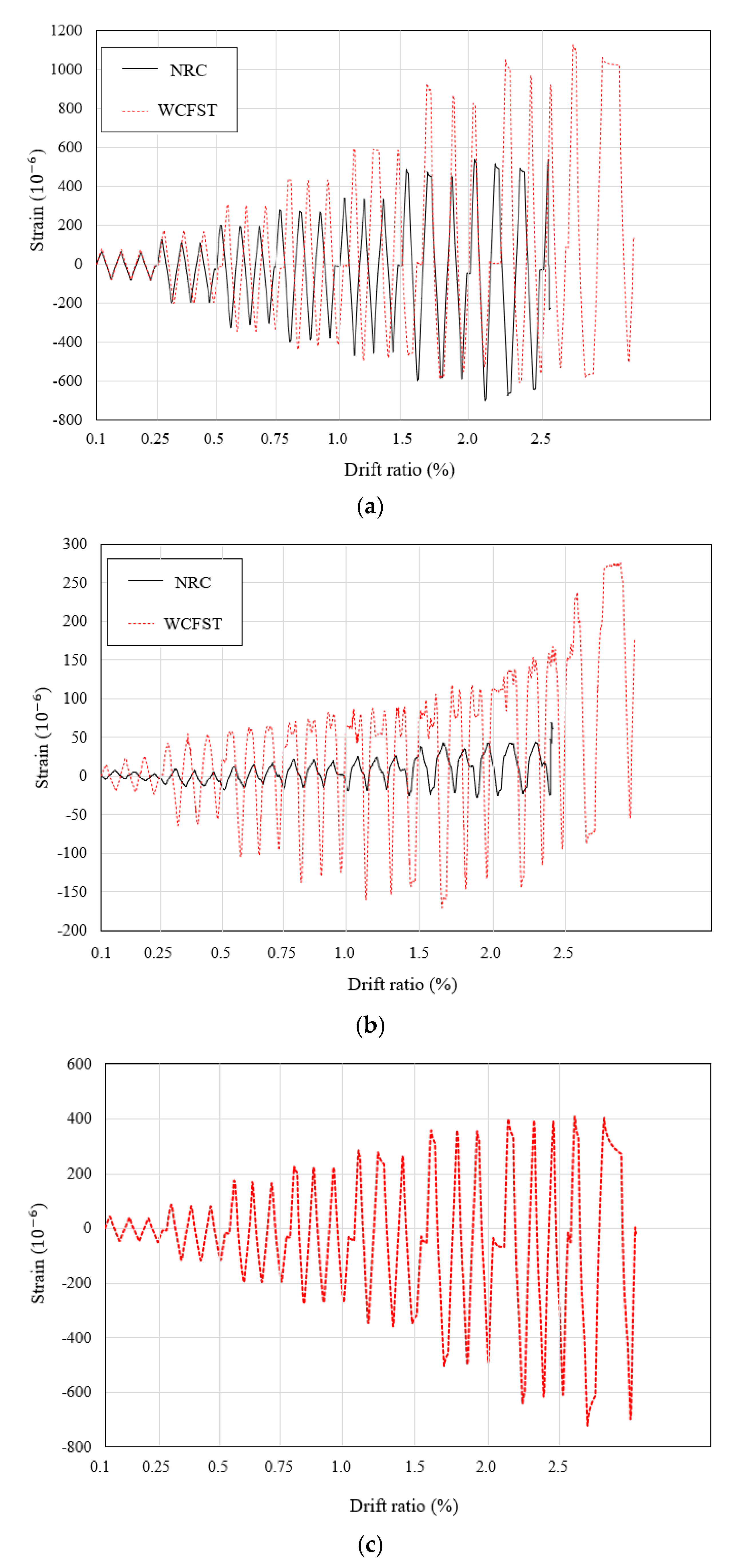
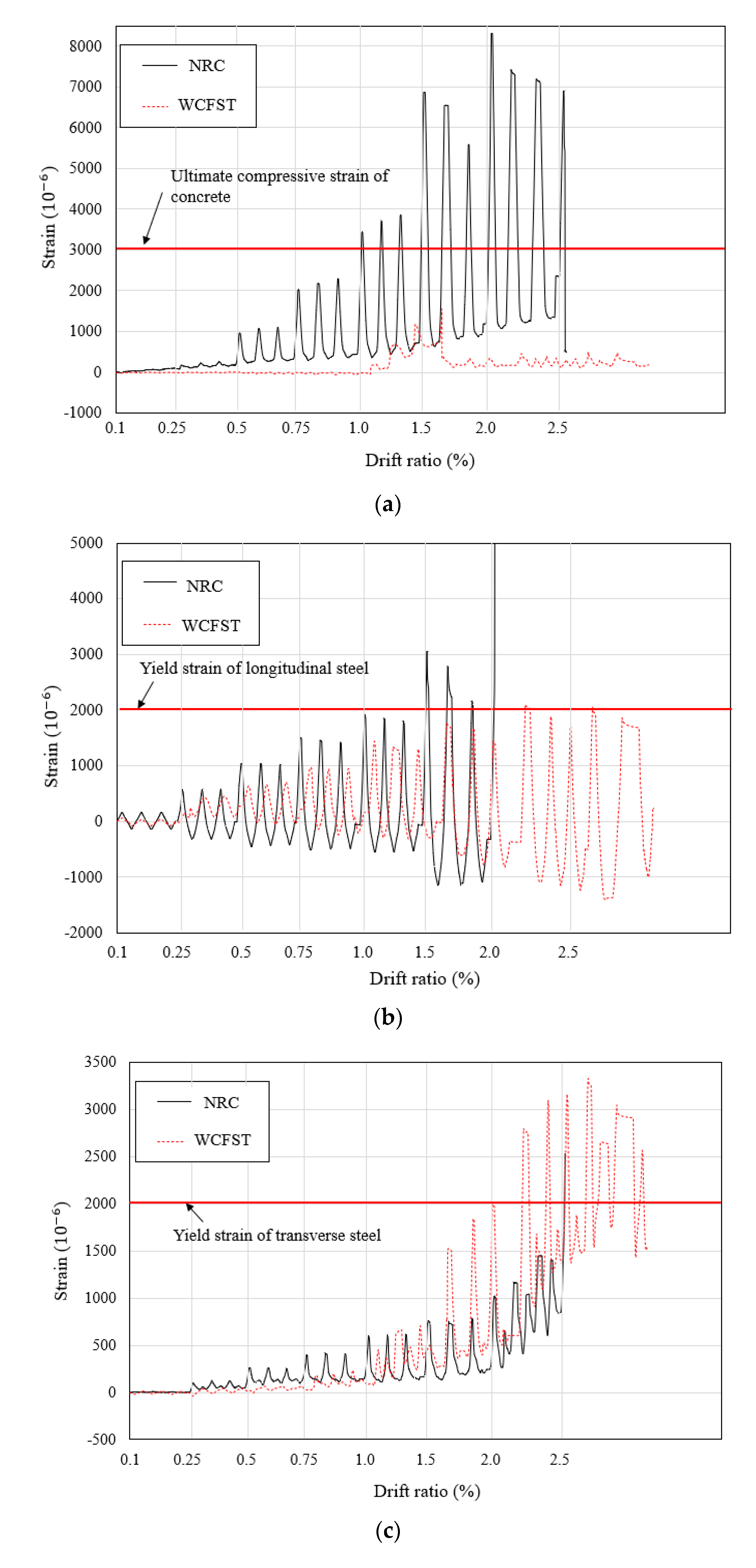
- Unlike the NRC specimen, where the strain at the end of the beams did not increase significantly despite the increase in drift ratio, the strain of the WCFST specimen continuously increased from a drift ratio of 0.75% until failure of the specimen occurred. Such a result confirmed that the stress of the test specimen retrofitted by the WCFST system was not concentrated on the columns, but distributed throughout the specimen. When the concrete strain values of the column lateral reinforcement were examined, the NRC specimen exceeded the ultimate compressive strain of the concrete after a drift ratio of 1% was reached. The longitudinal and transverse reinforcement for both specimens yielded at drift ratios of 1.5% and 2%, respectively. In the NRC specimen, the strain increased rapidly after yield of the reinforcement and, thus, the experiment was terminated. However, in the case of the WCFST specimen, the strain gradually increased to the drift ratio at which final failure occurred after yield of the reinforcement. This observation indicated that the seismic retrofitting method using the WCFST system can distribute stress concentrated on the column evenly on the test specimen, and can increase the lateral resistance capacity of the column.
- The test specimen with the WCFST system was confirmed to have an effective stiffness two times greater than that of the NRC specimen without seismic details. When the effective stiffness relative to the initial stiffness of each specimen reached 50%, the drift ratio was 0.75% and 1.5% for the NRC and WCFST specimens, respectively, indicating that the reduction rate of the effective stiffness for the NRC test specimen was greater than that for the WCFST specimen. The stiffness of the test specimen was increased by the WCFST seismic system retrofitting method, and the reduction rate in the effective stiffness after cracking was confirmed to be moderate.
- The energy dissipation capacity of each test specimen was evaluated. It was found that the test specimen with the WCFST system had an energy dissipation capacity that was 2.5 times larger than that of the NRC test specimen without seismic details. Therefore, the seismic retrofitting strategy utilizing the WCFST system was also effective in enhancing strength, and was considered to be an effective retrofitting method for improving seismic performance by significantly dissipating seismic energy when compared to the existing reinforced concrete structure.
- The proposed seismic retrofitting methods using WCFST have an economic advantage because it is possible to utilize the space during the construction period. In the case of a full building, economic loss may increase when vacancy occurs as a result of construction; therefore, the economic advantages of this proposed method can be emphasized even more. In addition, the experimental results indicate that the proposed seismic retrofitting method is expected to be effective in improving seismic performance. To provide design guidelines for the proposed method, more analytical and experimental studies are needed.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- FEMA-547. Techniques for the Seismic Rehabilitation of Existing Buildings; Building Seismic Safety Council for the Federal Emergency Management Agency: Washington, DC, USA, 2006.
- Choi, S.W. Investigation on the seismic retrofit positions of FRP jackets for RC frames using multi-objective optimization. Compos. Part. B Eng. 2017, 123, 34–44. [Google Scholar] [CrossRef]
- Ahn, N.; Kim, M.S.; Song, S.E.; Lee, Y.H. Seismic performance of reinforced concrete frames retrofitted with inserted steel frame and adhered waved steel panel. J. Vibroeng. 2016, 18, 1041–1051. [Google Scholar]
- Al-Salloum, Y.A.; Siddiqui, N.A.; Elsanadedy, H.M.; Abadel, A.A.; Aqel, M.A. Textile-reinforced mortar versus FRP as strengthening material for seismically deficient RC beam-column joints. J. Compos. Constr. 2011, 15, 920–933. [Google Scholar] [CrossRef]
- Shin, J.; Scott, D.W.; Stewart, L.K.; Yang, C.S.; Wright, T.R.; Des Roches, R. Dynamic response of a full-scale reinforced concrete building frame retrofitted with FRP column jackets. Eng. Struct. 2016, 125, 244–253. [Google Scholar] [CrossRef] [Green Version]
- Attari, N.; Youcef, Y.S.; Amziane, S. Seismic performance of reinforced concrete beam–column joint strengthening by frp sheets. Structures 2019, 20, 353–364. [Google Scholar] [CrossRef]
- Cosgun, C.; Cömert, M.; Demir, C.; İlki, A. Seismic Retrofit of Joints of a Full-Scale 3D Reinforced concrete Frame with FRP Composites. J. Compos. Constr. 2019, 23, 04019004. [Google Scholar] [CrossRef]
- Pohoryles, D.A.; Melo, J.; Rossetto, T.; Varum, H.; Bisby, L. Seismic retrofit schemes with FRP for deficient RC beam-column joints: State-of-the-art review. J. Compos. Constr. 2019, 23, 03119001. [Google Scholar] [CrossRef] [Green Version]
- Ozcelik, R.; Akpınar, U.; Binici, B. Seismic retrofit of deficient RC structures with internal steel frames. Adv. Struct. Eng. 2011, 14, 1205–1222. [Google Scholar] [CrossRef]
- Tafakori, E.; Banazadeh, M.; Jalali, S.A.; Tehranizadeh, M. Risk-based optimal retrofit of a tall steel building by using friction dampers. Struct. Des. Tall Spec. Build. 2013, 22, 700–717. [Google Scholar] [CrossRef]
- Lee, C.H.; Ryu, J.; Kim, D.H.; Ju, Y.K. Improving seismic performance of non-ductile reinforced concrete frames through the combined behavior of friction and metallic dampers. Eng. Struct. 2018, 172, 304–320. [Google Scholar] [CrossRef]
- Dong, Y.R.; Xu, Z.D.; Li, Q.Q.; Xu, Y.S.; Chen, Z.H. Seismic behavior and damage evolution for retrofitted RC frames using haunch viscoelastic damping braces. Eng. Struct. 2019, 199, 109583. [Google Scholar] [CrossRef]
- Eldin, M.N.; Dereje, A.J.; Kim, J. Seismic retrofit of RC buildings using self-centering PC frames with friction-dampers. Eng. Struct. 2020, 208, 109925. [Google Scholar] [CrossRef]
- Vafaei, M.; Sheikh, A.M.O.; Alih, S.C. Experimental study on the efficiency of tapered strip dampers for the seismic retrofitting of damaged non-ductile RC frames. Eng. Struct. 2019, 199, 109601. [Google Scholar] [CrossRef]
- Han, L.H.; Liao, F.Y.; Tao, Z.; Hong, Z. Performance of concrete filled steel tube reinforced concrete columns subjected to cyclic bending. J. Constr. Steel Res. 2009, 65, 1607–1616. [Google Scholar] [CrossRef]
- Lee, C.H.; Kang, T.H.K.; Kim, J.W.; Song, J.K.; Kim, S. Seismic Performance of Concrete-Filled Tube Column-Reinforced Concrete Slab Connections with Shearhead Keys. ACI Struct. J. 2019, 116, 233–244. [Google Scholar]
- Tsonos, A.G. Lateral load response of strengthened reinforced concrete beam-to-column joints. ACI Struct. J. 1999, 96, 46–56. [Google Scholar]




| Elements | Dimension (mm) | Reinforcement | |
|---|---|---|---|
| Longitudinal | Transverse | ||
| Column | 350 × 500 × 2850 | 8-D19, 2-D16 | D10@300 mm |
| Upper beam | 250 × 450 × 3200 | 6-D22 | Mid: D10@300 mm End: D10@200 mm |
| Lower beam | 350 × 600 × 3200 | 6-D22 | Mid: D10@300 mm End: D10@200 mm |
| Foundation | 800 × 500 × 4350 | 45-D22 | D16@130 mm |
| Drift Ratio (%) | Specimens | |
|---|---|---|
| NRC | WCFST | |
| 1.5 | 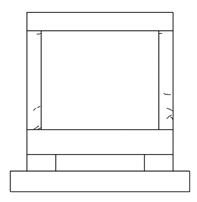 | 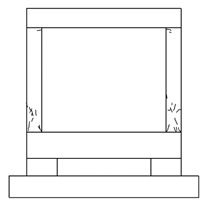 |
| 2.0 | 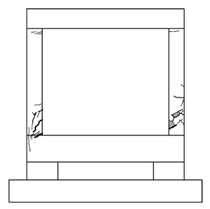 | 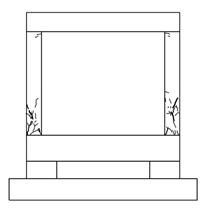 |
| 2.5 | 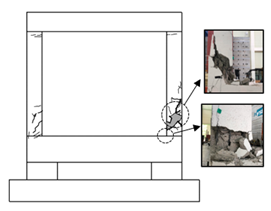 | 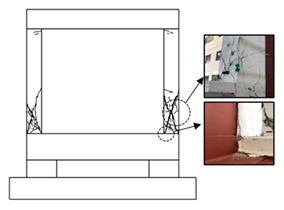 |
| Drift Ratio (%) | Load (kN) | Load Ratio of WCFST to NRC | ||||
|---|---|---|---|---|---|---|
| NRC | WCFST | |||||
| Positive Loading | Negative Loading | Positive Loading | Negative Loading | Positive Loading | Negative Loading | |
| 0.1 | 67.70 | −59.47 | 124.86 | −121.62 | 1.84 | 2.05 |
| 0.25 | 134.25 | −123.20 | 280.65 | −267.54 | 2.09 | 2.17 |
| 0.5 | 201.80 | −187.75 | 475.00 | −440.11 | 2.35 | 2.34 |
| 0.75 | 248.33 | −231.71 | 621.8 | −569.58 | 2.50 | 2.46 |
| 1.0 | 283.10 | −265.51 | 738.58 | −673.65 | 2.61 | 2.54 |
| 1.5 | 323.96 | −308.32 | 910.77 | −836.07 | 2.81 | 2.71 |
| 2.0 | 332.00 | −314.21 | 995.88 | −929.29 | 3.00 | 2.96 |
| 2.5 | 311.39 | - | 1013.32 | −940.5 0 | 3.25 | - |
| Drift Ratio (%) | Effective Stiffness (kN/mm) | Effective Stiffness Ratio of WCFST to NRC | |
|---|---|---|---|
| NRC | WCFST | ||
| 0.1 | 22.31 | 43.24 | 1.94 |
| 0.25 | 18.07 | 38.47 | 2.13 |
| 0.5 | 13.67 | 32.11 | 2.35 |
| 0.75 | 11.23 | 27.87 | 2.48 |
| 1.0 | 9.62 | 24.78 | 2.58 |
| 1.5 | 7.40 | 20.43 | 2.76 |
| 2.0 | 5.67 | 16.89 | 2.98 |
| 2.5 | - | 13.71 | - |
| Drift Ratio (%) | Cumulative Energy Dissipation (kN·mm) | Cumulative Energy Dissipation Ratio of WCFST to NRC | |
|---|---|---|---|
| NRC | WCFST | ||
| 0.1 | - | - | - |
| 0.25 | 246.26 | 453.45 | 1.84 |
| 0.5 | 962.21 | 1883.78 | 1.96 |
| 0.75 | 2176.84 | 4641.06 | 2.13 |
| 1.0 | 3956.35 | 8805.30 | 2.23 |
| 1.5 | 8147.52 | 18,723.15 | 2.30 |
| 2.0 | 13,864.04 | 33,974.65 | 2.45 |
| 2.5 | - | 55,261.46 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ro, K.M.; Kim, M.S.; Lee, Y.H. Experimental Study on Seismic Retrofitting of Reinforced Concrete Frames Using Welded Concrete-Filled Steel Tubes. Appl. Sci. 2020, 10, 7061. https://doi.org/10.3390/app10207061
Ro KM, Kim MS, Lee YH. Experimental Study on Seismic Retrofitting of Reinforced Concrete Frames Using Welded Concrete-Filled Steel Tubes. Applied Sciences. 2020; 10(20):7061. https://doi.org/10.3390/app10207061
Chicago/Turabian StyleRo, Kyong Min, Min Sook Kim, and Young Hak Lee. 2020. "Experimental Study on Seismic Retrofitting of Reinforced Concrete Frames Using Welded Concrete-Filled Steel Tubes" Applied Sciences 10, no. 20: 7061. https://doi.org/10.3390/app10207061
APA StyleRo, K. M., Kim, M. S., & Lee, Y. H. (2020). Experimental Study on Seismic Retrofitting of Reinforced Concrete Frames Using Welded Concrete-Filled Steel Tubes. Applied Sciences, 10(20), 7061. https://doi.org/10.3390/app10207061





