Abstract
3D printing allows the fabrication of ceramic implants, making a personalized approach to patients’ treatment a reality. In this work, we have tested the applicability of the Function Representation (FRep) method for geometric simulation of implants with complex cellular microstructure. For this study, we have built several parametric 3D models of 4 mm diameter cylindrical bone implant specimens of four different types of cellular structure. The 9.5 mm long implants are designed to fill hole defects in the trabecular bone. Specimens of designed ceramic implants were fabricated at a Ceramaker 900 stereolithographic 3D printer, using a commercial 3D Mix alumina (Al2O3) ceramic paste. Then, a single-axis compression test was performed on fabricated specimens. According to the test results, the maximum load for tested specimens constituted from 93.0 to 817.5 N, depending on the size of the unit cell and the thickness of the ribs. This demonstrates the possibility of fabricating implants for a wide range of loads, making the choice of the right structure for each patient much easier.
1. Introduction
Ceramic materials demonstrate excellent mechanical performance, high dimensional stability, high wear and corrosion resistance, and exceptional chemical stability. Current advances in 3D printing can potentially solve the problem of efficient production of custom made complex ceramic parts of arbitrary geometry [1,2,3,4]. Today, 3D printing is used to manufacture complex shaped ceramic parts for various applications, such as integrated ceramic casting molds [5,6], cutting tools [7], sensors [8,9,10], structural parts [11,12,13], photonic crystals [14,15], and dental components [16,17]. Besides, 3D printing is used to manufacture ceramic implants for various applications [18,19,20,21,22,23], mostly for the replacement of lost bones or restoration of damaged bone tissues [24].
Various porous structures (scaffolds) can be used to ensure successful proliferation of cells, demonstrating good biocompatibility and adhesion of live cultures. Scaffolds can have an irregular [25] or regular structure formed by way of 3D printing processes [26]. 3D printing allows the fabrication of scaffold structures with dimensions varying from several nanometers to several meters [27]. As was already shown in the previous studies, synthetic scaffolds can be designed based on various unit cell models, such as cube, gyroid, diamond, dispheroid, and others [26]. These models make it possible to obtain materials with different mechanical properties and biological activity. Such scaffolds can be used to splice both bone [28] and soft tissues [29] such as nerves. Pores in such scaffolds should have a certain size to ensure effective splicing of tissues. The effect of the pore size on bone tissue splicing efficiency is studied in [30], using 3D printed scaffolds with various pore sizes, fabricated from Al2O3-based materials. The optimal pore size for bone tissue proliferation was shown to constitute 390 to 590 μm.
Alumina-based ceramics are biologically inert and resistant materials [31]. High compression strength and wear resistance make these materials an ideal choice for use in stomatology and hip joint surgery. Ceramic parts are produced by sintering at high temperatures (1600–1700 °C) and have residual porosity of about 1–3%. The size of the pores depends on thermal treatment conditions and on the micromorphology of feedstock powders, and usually does not exceed dozens of microns [32], which impedes the growth of tissues, blood vessels, and other nutrient ducts. Alumina-based ceramics can perform a supporting function in the defected bone or in joining two broken bone parts, but they cannot be used for full bone remodeling during treatment. A macroporous architecture is suggested to stimulate bone tissue ingrowth in the region of implant placement. There are several methods of producing highly porous ceramic materials, allowing a trade-off between ceramics porosity and the strength of implants. These are, in particular, the use of foaming [33] and burnt-out additives, and the method of replicas [34]. However, these methods are difficult to control. 3D printing allows the fabrication of parts of any shape [35], implementing a personalized approach to patients’ treatment [36] that involves the use of computerized tomography, while controlling porosity and the size of pores (from 400 μm and higher) [37], necessary for better implant acceptance within the damaged area. Considering this, the design and fabrication of 3D printed ceramic implants with complex tailored porous structure becomes an urgent issue.
In this work, we use a promising stereolithographic (SLA) method of 3D printing of ceramic parts, based on the layer-by-layer polymerization of photocurable ceramic suspension or paste [38], consisting of photocurable multicomponent binder and ceramic powder. Each layer (slice) of a 3D model is solidified by laser hatching in a working area and then, a new layer of paste is applied by spreading blades. Figure 1 shows an illustration of the stereolithographic printing process. The process allows fabrication of materials with high spatial resolution (about 40 μm in the printing plane, and 10 μm in the direction perpendicular to the printing plane). Printed green parts are then heated for several hours to remove polymer binder. Further on, the parts are sintered to impart the final shape and desired mechanical properties. Both these processes are traditional for ceramics manufacturing.
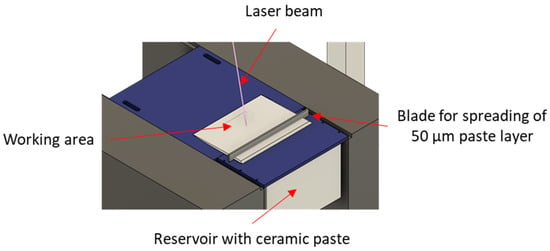
Figure 1.
Stereolithographic printing process.
There are multiple applications of SLA and a large variety of commercially available 3D printers and ceramic pastes. This method is used for 3D printing of ceramics for at least 20 years. SLA (and its modification, a Digital Light Processing (DLP) method is considered one of the best methods for ceramics manufacturing due to the high precision, low defects, and high density and strength of the produced parts. Other methods, such as Fused Deposition Modeling (FDM) or Selective Laser Sintering (SLS), produce inferior results in terms of resolution and microstructural properties of the material. A video demonstrating the 3D printing process of ceramic parts based on the SLA process can be found at the 3D Ceram company website [39].
In practice, all fabricated ceramic implants would be customized, i.e., tailored to individual patient needs. This raises the question of the quick design of parts with complex porous structure. Traditional methods of geometric modeling based on surface representation of a model cannot be applied here due to a very large amount of computations required to build models with complex internal structure [40]. Considering the above, we used the Function Representation (FRep) approach for geometric modeling of complex shapes with porous, cellular, and irregular microstructure [41]. This approach defines any geometrical object by non-negative values of a real continuous function procedurally evaluated at any given point of coordinate space. Whether a point belongs to an object depends on the sign of the defining function evaluated at that point. Typically, points with positive and zero function values are included in a set, while a zero-level subset is considered a boundary. Basically, FRep modeling is the “extended” implicit modeling [42] with explicitly introduced elementary objects (primitives).
Compared to boundary representation-based Computer-aided design (CAD) systems, the FRep approach offers significant advantages for microstructure modeling. First, the FRep format always ensures the accuracy of the obtained model, as opposed to traditional polygonal representation used in CAD systems where the probability of ending up with cracks or nonmatching edges in a model is rather high, even in simple operations such as offsetting. Second, the FRep has the advantage of complete parametrization of obtained microstructures, giving high flexibility in fast generation of variable 3D models. Third, the FRep offers a wide variety of tools to model various meshed structures, including periodic functions, Triply Periodic Minimal Surfaces (TMPS) [43,44], and replication of a unit cell, based on the method of skeleton-based surfaces [45]. In addition, FRep-based software makes it possible to use controlled blending versions of set-theoretic operations on geometric primitives. It is important for most applications to be able to combine a microstructure with the given external shape of an object or with a rigid platform.
In this study, we investigated the applicability of 3D printing for fabrication of easily modified cellular ceramic structures. While FRep is not a novel method, there are no publications on such application of this approach. Here, we used the FRep method to design 4 mm diameter cylindrical implants. The designed 9.5 mm long implants are intended to fill hole-like defects in the trabecular bone. The implants reproduce the structure of the trabecular bone, having a dense cylindrical base similar to the structure of cortical bone tissue, and porous main body similar to the structure of cancellous bone tissue. Besides, the dense base improves the adhesion of an implant to the building platform during the 3D printing process. The implants were designed on the request of a local medical research institute for the testing of bone substitute materials on rabbits under laboratory conditions. The primary loading mechanism in the implants was specified as compression. Only small tensile or flexural loads were expected for the implants. The cubic diamond-type cell was used as a basis for modeling the cellular microstructure. In the design, we varied the diameter of ribs (from 500 to 700 μm, with 100 μm increment) and the distance between ribs (from 500 to 1000 μm, with 250 μm increment). The size of cells was selected so as to ensure optimal conditions for bone tissues proliferation after sintering and shrinkage. Ceramic implant specimens were fabricated by a stereolithographic 3D printing process at a Ceramaker 900 printer, using a commercial 3DMix alumina feedstock paste. Then, implant specimens were tested in axial compression.
2. Materials and Methods
2.1. Design
In the FRep approach, the geometry of an object can be represented by the real function, and a general model can be represented as a certain ensemble (M, Φ, W), where M—the set of geometric objects; Φ—the set of geometric operations; W—the set of relationships over the set of objects [46]. Generally, geometric objects of a given model represent closed subsets of the N-dimensional space, . In our case, a 3D Euclidean space, , will be considered. The geometry of an object is specified by the function of 3 variables; by using various rules of points classification, we can obtain surfaces or geometric solids. Thus, expression (1) specifies the boundary surface and expression (2) specifies a geometric solid:
In each point in space , the classification is done by the value of function , such that , if the point P is located within the object; , if the point P is located at the object’s boundary; , if the point P is located outside the object.
FRep uses R-functions as set-theoretic operations [46]. The controlled blending versions of set-theoretic operations are applicable to FRep objects. The bounded blending operation [47] is useful for combining a microstructure with the other primitives. This operation allows for the addition or removal of material to/from specified regions of a 3D object, using expression (3) for the bounded blending operation.
where —the implicit functions of 2 geometric primitives; —the implicit function of a primitive restricting the region of blending operations; —the R-function; —blending operation parameters controlling the symmetry and a resulting shape.
In the course of 3D modeling, we used Function Representation of 3D objects and, particularly, the skeleton-based surfaces approach in combination with the definition of a scalar field and a distance function [48]. As the unit cell, we take a tetrahedral structure built as a crystal lattice of a diamond, where each atom (red points in Figure 2) forms bonds with its 4 nearest neighbors (blue points in Figure 2), with angles between the bonds constituting 109.47°.
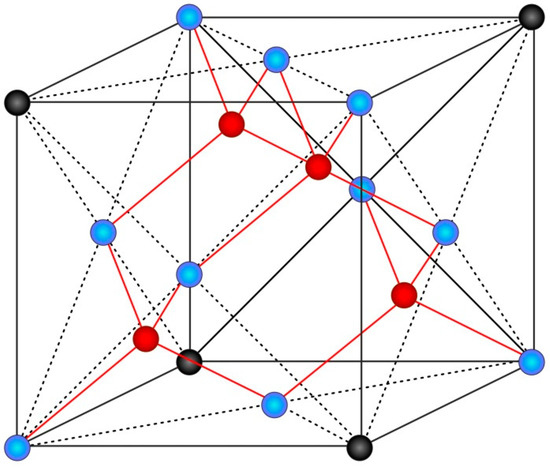
Figure 2.
Tetrahedral structure of a diamond.
Implant models were built in Rhinoceros suite (version 5), using the Symvol FRep plugin for Rhino version 1.5. Figure 3 shows the workflow of the modeling process consisting of 7 general steps: 1. Construction of the wireframe of the unit cell; 2. Replication of the unit cell; 3. Trimming the frame to its external form (cylinder); 4. Removing unnecessary parts; 5. Application of vTube operation; 6. Adding a cylindrical base plate; 7. Applying the bounded blending operation.

Figure 3.
Workflow of the modeling process with Symvol FRep plugin for Rhino version 1.5.
2.2. Fabrication
To analyze the possibility of fabricating Al2O3 ceramic implants by 3D printing, we conducted several experiments to fabricate cylindrical specimens. As a ceramic feedstock, we used 3DMix alumina paste produced by 3DCeram (Limoges, France). The weight fraction of the alumina powder in the paste constitutes 84%. We used a Ceramaker 900 (3DCeram, Limoges, France) stereolithographic printer to print green body specimens. The printing scene was prepared in the Netfabb suite (Autodesk, San Rafael, USA). Slicing of the model was done with a slicer tool of DMC software (Direct Machining Control, Vilnius, Lithuania). Processing parameters for the 3D printer were provided by the 3DCeram company in the form of an encrypted formulation file, together with the feedstock material. The precise parameters of the laser system are proprietary information not disclosed by the manufacturer.
After printing, we cleaned all specimens from the excess uncured ceramic feedstock at the CeraKleaner cleaning station (3DCeram, Limoges, France), using the pulverized proprietary solvent provided by 3DCeram. Then, printed specimens were debinded in the Kittec CLL-15 laboratory kiln (Kittec, Rosenheim, Germany). Specimens were gradually heated to 500 °C in the course of 6 h to remove organic binder, constituting over 30% of the volume of the green body. To improve the mechanical strength of the material for further processing, specimens were additionally heated for an hour at a temperature of 1100 °C in the same kiln without prior cooling, for presintering.
Then, specimens were further sintered in the ThermConcept HTL 20/17 furnace (ThermConcept, Bremen, Germany), using the procedure proposed by the furnace manufacturer. After placing the specimens in the kiln, a dome of ceramic bricks was constructed around specimens in order to mitigate spatial temperature gradients. The specimens were heated to a temperature of 1700 °C and held at this temperature for 1.5 h and then, cooled down. The heat up and cooldown rate constituted 3 °C/min.
2.3. Scanning Electron Microscopy
After sintering, we analyzed the shape and microstructure of implants using the Apreo scanning electron microscope (SEM) from Thermo Fisher Scientific (Waltham, MA, USA). No additional surface treatments were applied to the specimens before the SEM study. For the SEM study, we used the following parameters: working distance of 13 mm, accelerating voltage of 5 kV, and beam current of 50 pA. Secondary electrons were collected with the in-lens detector.
2.4. Mechanical Testing
Fabricated implant specimens were tested under axial compression. Such type of implants can be used for compression tests because the top and the bottom contact faces of the implants are parallel. The bottom face has a tight contact with the compression plate of the mechanical press. The top surface contacts the compression plate at a number of points.
We tested specimens at the Instron 5969 electromechanical testing machine equipped with a 50 kN load cell. We used two 150 mm diameter hardened, polished compression plates, with an adjustable upper plate. Before the test, the plates were brought together with a small load and the upper plate was adjusted so as to ensure parallelism. To avoid premature failure of the ceramic specimens at spots of contact with the metal, thin cardboard pads were glued onto both compression plates with double-sided adhesive tape. For full-field strain measurements, we applied speckles of black acrylic paint onto the specimens, using a spray bottle.
The upper plate was brought to the position of approx. 5 mm above a specimen, then the load was balanced, and the test started with the constant traverse speed of 0.2 mm/min. Tests were stopped manually, on visible signs of specimen fracture. We used a Digital Image Correlation (DIC) system from Correlated Solutions, taking one photograph a second from a 5 MP camera with a Tokina 100 mm F2.8 Macro D lens with simultaneous recording of force via a National Instruments Data acquisition (DAQ). Speckle correlation was performed in the VIC-2D-2009 program. After obtaining the strain field, we applied a virtual extensometer incorporated in the program to extract the tabulated data of engineering strain vs. force relationship.
In this study, we do not consider the testing of specimens with cylindrical base plates at both faces of a cylinder due to the following reasons. The proposed design with a single base plate represents a real implant to be used in further clinical testing. As the mechanical performance of such items is a very important part of the engineering design for biomedical applications, the real implants need to be tested “as is”, without artificial parallelization of surfaces.
2.5. Mechanical Simulation
For mechanical simulation of implant specimens under compression testing, we used the Abaqus finite element analysis (FEA) suite (version 6.14) [49]. To build the finite element model of the implant, we used its geometrical model in STL format. The model was built with quadratic tetrahedral elements of C3D10-type. To model the printed ceramic material, we used a linear elastic material with elastic modulus of E = 350 GPa and Poisson’s ratio of .
3. Results
3.1. Design
Four different types of parametric models of bioimplants were built, using four different types of unit cells and filling. Implant models were built by replicating unit cells along three coordinate axes (X,Y,Z) to obtain a wire frame with the addition of a cylindrical base plate. The following unit cells were constructed (see Figure 4): UC001—the cell built on the basis of tetrahedral diamond structure, with rib thickness of 0.4 mm, cell length (L) of 2.3 mm, cell width (W) of 2.3 mm, and cell height (H) of 1.7 mm; UC002—the cell built on the basis of the UC001 unit cell by removing dangling ribs, with rib thickness of 0.7 mm, L = 1.6 mm, W = 1.6 mm, H = 2.3 mm; UC003—the cell built by duplicating the UC002 unit cell along the X and Y axes, with the offset along the Z-axis by H/2, and along the X-axis by W/2, with rib thickness of 0.7 mm, L = 3.5 mm, W = 3.5 mm, H = 3.8 mm; UC004—the cell built by compressing the UC003 unit cell along X and Y axes by a factor of 2, with rib thickness of 0.3 mm, L = 2.0 mm, W = 2.0 mm, H = 4.1 mm. Based on the unit cells data, we modeled the bioimplants with the following wireframe (mesh) types: BI001—the wireframe built by replicating the UC001 unit cell along three coordinate axes—by a factor of 3 along X and Y axes, and by a factor of 5 along Z axis; BI002—the UC002 unit cell is replicated by a factor of 2 along X and Y axes, and by a factor of 4 along Z axis; BI003—the UC003 unit cell is replicated by a factor of 1 along X and Y axes, and by a factor of 3 along Z axis; BI004—the UC004 unit cell is replicated by a factor of 3 along X, Y, and Z axes. The above structures were limited by a 5 mm thick cylinder of 3.8 mm in diameter. These structures were then trimmed by using the SelBoundary operation. Dangling ribs in the structures were also deleted. A 2.5 mm thick cylinder of 4 mm in diameter was modeled as the implant base plate, allowing: (a) better adhesion of a part to a modeling base for 3D printing; (b) tight closure of the inlet hole of a bone defect; (c) machining of a part to the shape of the bone for better implantation into the defect. Modeling and unit cell replication parameters are given in Table 1. Implant models are shown in Figure 5.
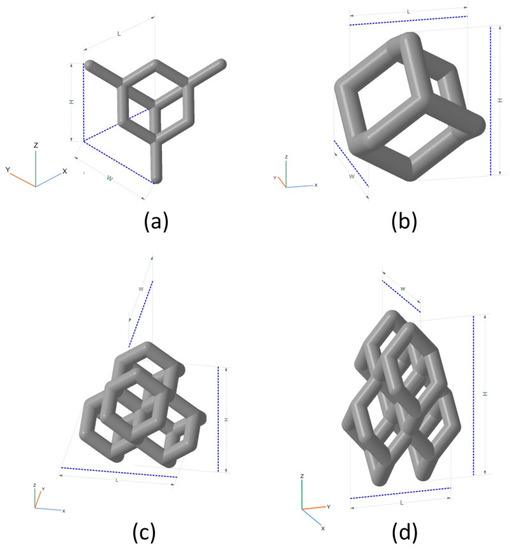
Figure 4.
Unit cells used for implant modeling: (a) UC001—the unit cell built on the basis of tetrahedral diamond structure (rib thickness = 0.4 mm, cell length (L) = 2.3 mm, cell width (W) = 2.3 mm, cell height (H) = 1.7 mm); (b) UC00202—the cell built on the basis of the UC001 unit cell by removing open ribs (rib thickness = 0.7 mm, L = 1.6 mm, W = 1.6 mm, H = 2.3 mm); (c) UC003—the cell built by replicating the UC002 unit cell along the X and Y axes by a factor of 2, with the offset along Z-axis by H/2, and along X-axis by W/2 (rib thickness of 0.7 mm, L = 3.5 mm, W = 3.5 mm, H = 3.8 mm); (d) UC004—the cell built by compressing the UC003 unit cell along X and Y axes by the factor of 2 (rib thickness =0.3 mm, L = 2.0 mm, W = 2.0 mm, H = 4.1 mm).

Table 1.
Implants modeling parameters.
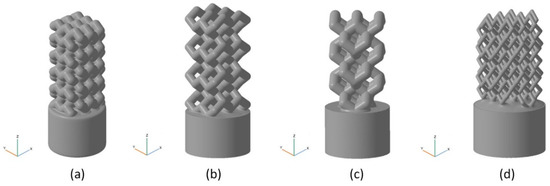
Figure 5.
The models of implants. Combination of a wireframe with a cylindrical base plate: (a) BI001—the wireframe built by replicating the UC001 unit cell along three coordinate axes, by a factor of 3 along X and Y axes, and by a factor of 5 along Z-axis; (b) BI002—the UC002 unit cell is replicated by a factor of 2 along X and Y axes, and by the factor of 4 along Z axis; (c) BI003—the UC003 unit cell is replicated by a factor of 1 along X and Y axes, and by a factor of 3 along Z-axis; (d) BI004—the UC004 unit cell is replicated by a factor of 3 along X,Y, and Z axes.
To improve stiffness of the structure, we added an extra material between the cylindrical base plate and the wireframe, using the bounded blending operation. Figure 6 shows the result of the bounded blending operation applied to assign stiffness to the implant structure. In our case, the bounded blending operation includes the implicit functions of two geometric primitives: the cylindrical base plate and the wireframe; the R-function is union.

Figure 6.
Application of bounded blending operation to assign stiffness to the implant structure.
The files of the BI001–BI004 models designed in Rhino software with the Symvol plugin can be found in the Supplementary Materials. The screenshots of the executed operations are also shown in the Supplementary Materials. File sizes of the models in various formats are given in Table 2.

Table 2.
File sizes of the models in various formats are given in MB.
Table 3 shows porosity values for the models built both with and without account for the cylindrical base plate.

Table 3.
Porosity of the models with and without account for the cylindrical base plate (%).
To demonstrate the capabilities of the method described here, we have built an array of 20 × 20 BI004 models (see Figure 7), consisting of 10,800 unit cells. The file size of the array model built in Symvol format constitutes 0.201 Mb (see the Supplementary Materials).

Figure 7.
The array of 20 × 20 BI004 models.
3.2. Fabrication
Four cylindrical implant specimens with dimensions of d = 4 mm, h = 9.5 mm were fabricated for the study. The structure of the implants is described in Table 1. Implant models were additionally scaled to account for shrinkage, using standard shrinkage coefficients for 3DMix alumina paste ( = 1.159, = 1.146, = 1.187). To prepare the models for printing and to set up printing parameters (laser power, slicing, etc.), we used the Ceramaker software (3DCeram, Limoges, France). With a slice thickness of 50 μm, the printing of the specimens took approximately 5 h. Specimens were printed at 71% of the power of the laser system, which is equivalent to 120 mW/cm2. To remove excess uncured ceramic feedstock, we used a CeraKleaner cleaning station. Due to the complex macroporous geometry of the implants, an ultrasonic cleaning bath was used to speed up the cleaning process. Figure 8 shows photographs of the obtained specimens after printing.

Figure 8.
Photographs of printed implants fabricated from models developed earlier and shown in Figure 5.
Parts were debinded in the Kittec CLL-15 laboratory kiln at a temperature of 550 °C, using the multistep procedure, and presintered at 1100 °C. Presintered specimens were then placed in the Thermoconcept HTL 20/17 high temperature furnace and heated for 1.5 h at a temperature of 1700 °C for final sintering. Figure 9 shows BI002 model specimens after printing (left) and after sintering (right).

Figure 9.
BI002 model specimens after printing (left) and after sintering (right).
Thus, the full manufacturing cycle for the porous Al2O3 implant (see Figure 10) constituted approximately 7 days.
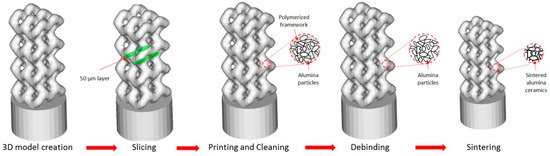
Figure 10.
Fabrication of Al2O3 ceramic implant at the Ceramaker 900 stereolithographic 3D printer.
We manufactured 11 specimens of each type. Ten specimens were given to a local medical institute for bone substitute testing on rabbits. The remaining specimens were subjected to mechanical testing. The authors also intend to conduct biomedical testing including cytotoxicity and osteogenic studies. The results of those studies will be reported in future publications.
3.3. Scanning Electron Microscopy
According to the SEM images, fabricated structures feature pore sizes of 440 to 700 μm, which is in good agreement with the results obtained earlier [6]. Such structures feature the optimal morphology for bone tissue proliferation. Figure 11 shows the typical example of BI004 structure: (а) scaffold; (b) and (с) pores and ribs after sintering, enlarged view; (d) ceramic microstructure. The average size of grains constitutes several micrometers and the surface of the structure has no pronounced pores and defects. The density of the obtained structures was studied in our previous work and constitutes approximately 3.8 g/cm3 [50]. The porosity of the sintered ceramic material does not exceed 5%.

Figure 11.
SEM images of the BI004 implant after sintering: (a) scaffold; (b) enlarged view of a pore; (c) enlarged view of a rib; (d) sintered ceramics.
3.4. Mechanical Testing
Figure 12 shows loading curves for implants tested under axial compression. The testing machine crosshead travel (mm) is plotted on a horizontal axis; the testing load (N) is plotted on the vertical axis. Shown also are the photographs of implant specimens after fracture. Table 2 shows maximum load values for specimens under axial compression. The results show that the BI001 specimen is almost three times stronger, compared to the other three specimens. This can be explained by a denser packing of a wireframe, resulting from the use of the UC001 unit cell with rib thickness of 0.4 mm and dimensions of L = 2.3 mm, W = 2.3 mm, H = 1.7 mm. Moreover, the BI001 specimen features three rows of contact surfaces in the upper part of the model, thus forming a larger area of contact with the loading plate and providing more uniform and less intense redistribution of load from the testing machine. At the same time, the BI004 specimen also features three rows of contact surfaces at the upper part of the model; however, the thinner and longer ribs of the UC004 unit cell (thickness = 0.3 mm, L = 2.0 mm, W = 2.0 mm, H = 4.1 mm) make the structure susceptible to premature local buckling and result in a significantly lower strength of the implant. The BI002 specimen has two rows of contact surfaces in the upper part of the model and features higher strength compared to that of the BI004 specimen, due to the higher thickness of the ribs of the UC002 unit cell (rib thickness = 0.7 mm, L = 1.6 mm, W = 1.6 mm, H = 2.3 mm). The lowest strength was demonstrated by the BI003 specimen, having only one row of contact surfaces. The increase in unit cell dimensions (from UC001 to UC004) results in lower maximum load the specimen can carry and in significantly lower physical permeability of an implant, which is necessary for successful integration of the implant into the patient organism. Reducing unit cell dimensions while keeping the thickness of the ribs the same or lower is currently impossible with the SLA printing process. Due to the low strength of the printed layers, they tend to be destroyed by a printer spreading blade when applying new layers of ceramic paste (see Figure 1). Smaller unit cell dimensions in combination with an increase in rib thickness result in a collapse of gaps between neighboring ribs, thus making the removal of excess feedstock from printed parts almost impossible (even in an ultrasound bath).
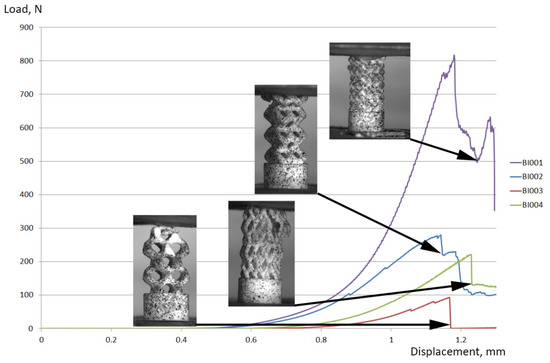
Figure 12.
Loading curves for implant specimens tested under axial compression. The crosshead travel (mm) during testing is plotted on the horizontal axis; the load (N) is plotted on the vertical axis.
Table 4 also shows the effective compressive strength of implants, calculated by division of the maximum load by the area of a cylindrical base plate of 4 mm in diameter. According to the available data, the ultimate compression strength in the longitudinal direction constitutes 193 MPa for a cortical bone and ~50 MPa for a trabecular bone [51], which is comparable to the effective compressive strength of the BI001 implant (65.1 MPa) shown in Table 4.

Table 4.
Implants modeling parameters.
Figure 13 shows the distribution of vertical strains at the surface of the BI002 specimen during testing at the 185.7 N load, obtained by digital image correlation. We also measured strains between reference points A and B, located at the cylindrical base plate and in the lower part of the wireframe, respectively (see Figure 13). Before loading, the distance between points constituted 7.26 mm. At the load of 185.7 N, the distance between reference points A and B decreased by mm; thus, the resulting strain constituted .

Figure 13.
The distribution of vertical strains at the surface of the BI002 specimen during testing at the 187.5 N load, obtained by digital image correlation (DIC).
3.5. Mechanical Simulation
Figure 14 shows the compression test simulation results for the BI002 specimen. The computational model includes the implant model and the discrete rigid plane (see Figure 14a) located at the distance of 0.45 mm from the edge of the wireframe part of the implant. The number of C3D10-type finite elements in the model constitutes 432265. General contact conditions are imposed between the implant model and the discrete rigid plane. The implant model is fixed to the foundation of the cylindrical base plate. The loading of the implant is given by the displacement of the discrete rigid plane.
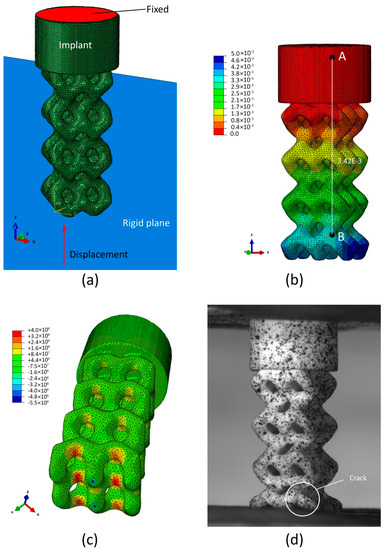
Figure 14.
Compression test simulation results for the BI002 specimen: (a) Computational model; (b) distribution of vertical displacements (mm) at the load of 185.7 N; (c) distribution of maximal principal stress (Pa) at the load of 279.9 N; (d) initial fracture of the specimen during compression test.
Figure 14b shows the distribution of vertical displacements at the load of 185.7 N. Calculated displacement of the reference points B relative to the point A constituted mm. Thus, the difference between predicted and measured changes in distance between reference points A and B does not exceed 5%. Figure 14c shows the distribution of maximum principal stresses at the load of 279.9 N (see Table 4). The region with maximum principal stress is located in the bridged area between lateral and central rows of pillars. Stresses in this area constitute 400 MPa, exceeding the tensile strength of Al2O3-based ceramics. During tests, the initial fracture was also observed in this area (see Figure 14d).
4. Discussion
The FRep approach allows an engineer to build parametric 3D models of implants, while providing flexibility in the generation of variable 3D objects for further fabrication. The FRep provides an analytical description of models, reducing the volume of data necessary to describe a single model to several hundred kilobytes of a source file, which is several dozen times less compared to the traditional definition of a model that uses boundary representation and a polygonal format (such as STL, for example).
After modeling, the models should be exported to the polygonal STL format suitable for 3D printers for further slicing and 3D printing. The size of the obtained STL files constitutes approximately 20 Mbytes. Polygonization of a model is a time-consuming operation and is often the cause of errors in generated surfaces of 3D objects. However, Jamieson and Hacker in [52] have proposed a method of direct 3D printing, which was further modified and tested for FRep models in [53,54]. The method makes it possible to slice an FRep-model and prepare the job for a 3D printer directly, without the intermediate stage of polygonization, thus reducing the total time required for 3D processing and eliminating the errors related to polygonization. Therefore, the further developments in this field may include the application of a direct 3D printing method.
The ultimate compressive stress of implants studied here corresponds to the strength of porous ceramics and lies between the compressive strength of trabecular (0.1–50 MPa) and cortical (150–200 MPa) bone tissues. Therefore, by varying the size of a unit cell and the thickness of ribs, we can obtain implants with effective strength in the range of 7.4 to 65.1 MPa, making it easier to choose the right material for each patient.
Advantages of studied structures are their high porosity and sufficient distance between ribs, optimal for the ingrowth of bone tissue during treatment. The combination of chemical composition (alumina) and macroporous 3D structure makes it possible to obtain highly porous, permeable, strong bone implants.
In future research, we intend to conduct biomedical testing of fabricated implants, including cytotoxicity and osteogenic studies. The results of these studies will be reported in further publications.
The authors also intend to conduct in-depth finite element analysis of the experimental data in order to obtain a validated computational model. This model will be used for the topological optimization [55] of bioimplants with account for geometric requirements, loading conditions, and anisotropy of mechanical properties of printed ceramics.
5. Conclusions
In this study, four types of macroporous ceramic implants based on Al2O3 have been designed and printed. The BI001 type implant has demonstrated effective compressive strength comparable to that of the trabecular bone, making it a promising bone substitute able to withstand high operating loads.
Supplementary Materials
The following are available online at https://www.mdpi.com/2076-3417/10/20/7138/s1, Models.zip: the files of the models designed in Rhino software with the Symvol plugin, Description.docx: the description of the modeling process in Rhino software with the Symvol plugin.
Author Contributions
Conceptualization, A.S. and E.M.; methodology, A.P. and E.M.; software, D.P.; validation, A.P., E.M. and S.C.; formal analysis, S.C.; investigation, A.T. and E.M.; resources, S.C.; data curation, S.K. and S.E.; writing—original draft preparation, A.S., A.T. and E.M.; writing—review and editing, E.M., S.E. and A.T.; visualization, E.M. and A.T.; supervision, A.S.; project administration, A.S.; funding acquisition, I.A. All authors have read and agreed to the published version of the manuscript.
Funding
S.C. and I.A. acknowledge financial support by the Ministry of Science and Higher Education of the Russian Federation in the framework of the project with a unique identifier RFMEFI61820X0006.
Acknowledgments
The authors would like to express their sincere gratitude to the handling editor Joy Sun for the invaluable help in preparation of the manuscript. The authors also would like to thank the anonymous reviewers for their thoughtful and detailed comments on our paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Travitzky, N.; Bonet, A.; Dermeik, B.; Fey, T.; Filbert-Demut, I.; Schlier, L.; Schlordt, T.; Greil, P. Additive Manufacturing of Ceramic-Based Materials. Adv. Eng. Mater. 2014, 16, 729–754. [Google Scholar] [CrossRef]
- Zocca, A.; Colombo, P.; Gomes, C.M.; Günster, J. Additive Manufacturing of Ceramics: Issues, Potentialities, and Opportunities. J. Am. Ceram. Soc. 2015, 98, 1983–2001. [Google Scholar] [CrossRef]
- Deckers, J.; Vleugels, J.; Kruth, J.-P. Additive manufacturing of ceramics: A review. J. Ceram. Sci. Technol. 2014, 5, 245–260. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Z.; Li, J.; Liu, C.; Lao, C.; Fu, Y.; Liu, C.; Li, Y.; Wang, P.; He, Y. 3D printing of ceramics: A review. J. Eur. Ceram. Soc. 2019, 39, 661–687. [Google Scholar] [CrossRef]
- Zhou, W.Z.; Li, D.; Chen, Z.W.; Chen, S. Direct fabrication of an integral ceramic mould by stereolithography. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2010, 224, 237–243. [Google Scholar] [CrossRef]
- Chen, Z.; Li, D.; Zhou, W. Process parameters appraisal of fabricating ceramic parts based on stereolithography using the Taguchi method. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2012, 226, 1249–1258. [Google Scholar] [CrossRef]
- Zhou, M.; Liu, W.; Wu, H.; Song, X.; Chen, Y.; Cheng, L.; He, F.; Chen, S.; Wu, S. Preparation of a defect-free alumina cutting tool via additive manufacturing based on stereolithography—Optimization of the drying and debinding processes. Ceram. Int. 2016, 42, 11598–11602. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Delhote, N.; Ettorre, M.; Baillargeat, D.; Le Coq, L.; Sauleau, R. Design and Characterization of 60-GHz Integrated Lens Antennas Fabricated Through Ceramic Stereolithography. IEEE Trans. Antennas Propag. 2010, 58, 2757–2762. [Google Scholar] [CrossRef]
- Leigh, S.J.; Purssell, C.P.; Bowen, J.; Hutchins, D.A.; Covington, J.A.; Billson, D.R. A miniature flow sensor fabricated by micro-stereolithography employing a magnetite/acrylic nanocomposite resin. Sens. Actuators A Phys. 2011, 168, 66–71. [Google Scholar] [CrossRef]
- Tian, Z.; Yang, Y.; Wang, Y.; Wu, H.; Liu, W.; Wu, S. Fabrication and properties of a high porosity h-BN–SiO2 ceramics fabricated by stereolithography-based 3D printing. Mater. Lett. 2019, 236, 144–147. [Google Scholar] [CrossRef]
- Wu, H.; Liu, W.; He, R.; Wu, Z.; Jiang, Q.; Song, X.; Chen, Y.; Cheng, L.; Wu, S. Fabrication of dense zirconia-toughened alumina ceramics through a stereolithography-based additive manufacturing. Ceram. Int. 2017, 43, 968–972. [Google Scholar] [CrossRef]
- Liu, W.; Wu, H.; Tian, Z.; Li, Y.; Zhao, Z.; Huang, M.; Deng, X.; Xie, Z.; Wu, S. 3D printing of dense structural ceramic microcomponents with low cost: Tailoring the sintering kinetics and the microstructure evolution. J. Am. Ceram. Soc. 2018, 102, 2257–2262. [Google Scholar] [CrossRef]
- He, R.; Liu, W.; Wu, Z.; An, D.; Huang, M.; Wu, H.; Jiang, Q.; Ji, X.; Wu, S.; Xie, Z. Fabrication of complex-shaped zirconia ceramic parts via a DLP- stereolithography-based 3D printing method. Ceram. Int. 2018, 44, 3412–3416. [Google Scholar] [CrossRef]
- Chen, W.; Kirihara, S.; Miyamoto, Y. Fabrication and Measurement of Micro Three-Dimensional Photonic Crystals of SiO2Ceramic for Terahertz Wave Applications. J. Am. Ceram. Soc. 2007, 90, 2078–2081. [Google Scholar] [CrossRef]
- Kirihara, S.; Niki, T. Three-Dimensional Stereolithography of Alumina Photonic Crystals for Terahertz Wave Localization. Int. J. Appl. Ceram. Technol. 2015, 12, 32–37. [Google Scholar] [CrossRef]
- Sarment, D.P.; Al-Shammari, K.; Kazor, C.E. Stereolithographic surgical templates for placement of dental implants in complex cases. Int. J. Periodontics Restor. Dent. 2003. [Google Scholar] [CrossRef]
- Lian, Q.; Sui, W.; Wu, X.; Yang, F.; Yang, S. Additive manufacturing of ZrO2 ceramic dental bridges by stereolithography. Rapid Prototyp. J. 2018, 24, 114–119. [Google Scholar] [CrossRef]
- Scalera, F.; Corcione, C.E.; Montagna, F.; Sannino, A.; Maffezzoli, A. Development and characterization of UV curable epoxy/hydroxyapatite suspensions for stereolithography applied to bone tissue engineering. Ceram. Int. 2014, 40, 15455–15462. [Google Scholar] [CrossRef]
- Du, D.; Asaoka, T.; Ushida, T.; Furukawa, K.S. Fabrication and perfusion culture of anatomically shaped artificial bone using stereolithography. Biofabrication 2014, 6, 045002. [Google Scholar] [CrossRef]
- Ribas, R.G.; Schatkoski, V.M.; Montanheiro, T.L.D.A.; De Menezes, B.R.C.; Stegemann, C.; Leite, D.M.G.; Thim, G.P. Current advances in bone tissue engineering concerning ceramic and bioglass scaffolds: A review. Ceram. Int. 2019, 45, 21051–21061. [Google Scholar] [CrossRef]
- Yelten, A.; Yilmaz, S. A novel approach on the synthesis and characterization of bioceramic composites. Ceram. Int. 2019, 45, 15375–15384. [Google Scholar] [CrossRef]
- Liu, Z.; Liang, H.; Shi, T.; Xie, D.; Chen, R.; Han, X.; Shen, L.; Wang, C.; Tian, Z. Additive manufacturing of hydroxyapatite bone scaffolds via digital light processing and in vitro compatibility. Ceram. Int. 2019, 45, 11079–11086. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, C.; Wang, J.; Zou, B. Development of a novel aqueous hydroxyapatite suspension for stereolithography applied to bone tissue engineering. Ceram. Int. 2019, 45, 3902–3909. [Google Scholar] [CrossRef]
- Samavedi, S.; Whittington, A.R.; Goldstein, A.S. Calcium phosphate ceramics in bone tissue engineering: A review of properties and their influence on cell behavior. Acta Biomater. 2013, 9, 8037–8045. [Google Scholar] [CrossRef]
- Evlashin, S.; Dyakonov, P.; Tarkhov, M.; Dagesyan, S.; Rodionov, S.; Shpichka, A.; Kostenko, M.; Konev, S.; Sergeichev, I.; Timashev, P.; et al. Flexible Polycaprolactone and Polycaprolactone/Graphene Scaffolds for Tissue Engineering. Materials 2019, 12, 2991. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, G.; Liang, H.; Gao, C.; Peng, S.; Shen, L.; Shuai, C. Additive manufacturing of bone scaffolds. Int. J. Bioprinting 2019, 5, 148. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.W.; Stucker, B. Additive Manufacturing Technologies; Springer: New York, NY, USA, 2010. [Google Scholar]
- Zhou, X.; Nowicki, M.; Cui, H.; Zhu, W.; Fang, X.; Miao, S.; Lee, S.-J.; Keidar, M.; Zhang, L.G. 3D bioprinted graphene oxide-incorporated matrix for promoting chondrogenic differentiation of human bone marrow mesenchymal stem cells. Carbon 2017, 116, 615–624. [Google Scholar] [CrossRef]
- Jakus, A.E.; Secor, E.B.; Rutz, A.L.; Jordan, S.W.; Hersam, M.C.; Shah, R.N. Three-Dimensional Printing of High-Content Graphene Scaffolds for Electronic and Biomedical Applications. ACS Nano 2015, 9, 4636–4648. [Google Scholar] [CrossRef]
- Entezari, A.; Roohani, I.; Li, G.; Dunstan, C.R.; Rognon, P.; Li, Q.; Jiang, X.; Zreiqat, H. Architectural Design of 3D Printed Scaffolds Controls the Volume and Functionality of Newly Formed Bone. Adv. Healthc. Mater. 2019, 8, 8. [Google Scholar] [CrossRef]
- Piconi, C.; Porporati, A.A. Bioinert Ceramics: Zirconia and Alumina. In Handbook of Bioceramics and Biocomposites; Springer: Berlin/Germany, Germany, 2016; ISBN 9783319124605. [Google Scholar]
- Ben-Nissan, B.; Choi, A.H.; Cordingley, R. Alumina ceramics. In Bioceramics and Their Clinical Applications; Woodhead Publishing: Cambridge, UK, 2008; ISBN 9781845692049. [Google Scholar]
- Su, B.; He, X.; Dhara, S.; Mansell, J.P. Porous and bioactive alumina ceramics for bone grafts and tissue engineering scaffolds. In Key Engineering Materials; Trans Tech Publications Ltd.: Stafa, Switzerland, 2007; Volumes 330–332. [Google Scholar]
- Ohji, T.; Fukushima, M. Macro-porous ceramics: Processing and properties. Int. Mater. Rev. 2012, 57, 115–131. [Google Scholar] [CrossRef]
- Galante, R.; Figueiredo-Pina, C.G.; Serro, A.P. Additive manufacturing of ceramics for dental applications: A review. Dent. Mater. 2019, 35, 825–846. [Google Scholar] [CrossRef]
- Jariwala, S.H.; Lewis, G.S.; Bushman, Z.J.; Adair, J.H.; Donahue, H.J. 3D Printing of Personalized Artificial Bone Scaffolds. 3D Print. Addit. Manuf. 2015, 2, 56–64. [Google Scholar] [CrossRef]
- Gulan, G.; Jurdana, H.; Gulan, L. Personalized Total Knee Arthroplasty: Better Fit for Better Function. In Personalized Medicine in Healthcare Systems; Springer: Cham, Switzerland, 2019; pp. 307–314. [Google Scholar]
- Safonov, A.; Chugunov, S.; Tikhonov, A.; Gusev, M.; Akhatov, I. Numerical simulation of sintering for 3D-printed ceramics via SOVS model. Ceram. Int. 2019, 45, 19027–19035. [Google Scholar] [CrossRef]
- Ceramic 3D Printing Solutions. Available online: https://3dceram.com/en/ (accessed on 5 August 2020).
- Pasko, A.; Fryazinov, O.; Vilbrandt, T.; Fayolle, P.-A.; Adzhiev, V. Procedural function-based modelling of volumetric microstructures. Graph. Model. 2011, 73, 165–181. [Google Scholar] [CrossRef]
- Shapiro, V. Real functions for representation of rigid solids. Comput. Aided Geom. Des. 1994, 11, 153–175. [Google Scholar] [CrossRef]
- Bloomenthal, J.; Bajaj, C.; Blinn, J.; Wyvill, B.; Cani, M.P.; Rockwood, A.; Wyvill, G. (Eds.) Introduction to Implicit Surfaces; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1997; ISBN 978-1-55860-233-5. [Google Scholar]
- Kapfer, S.C.; Hyde, S.T.; Mecke, K.; Arns, C.H.; Schröder-Turk, G.E. Minimal surface scaffold designs for tissue engineering. Biomaterials 2011, 32, 6875–6882. [Google Scholar] [CrossRef]
- Tikhonov, A.A.; Evdokimov, P.V.; Putlyaev, V.I.; Safronova, T.V.; Filippov, Y.Y. On the Choice of the Architecture of Osteoconductive Bioceramic Implants. Inorg. Mater. Appl. Res. 2019, 10, 242–247. [Google Scholar] [CrossRef]
- Fryazinov, O.; Vilbrandt, T.; Pasko, A. Multi-scale space-variant FRep cellular structures. CAD Comput. Aided Des. 2013, 45, 26–34. [Google Scholar] [CrossRef]
- Pasko, A.; Adzhiev, V.; Sourin, A.; Savchenko, V. Function representation in geometric modeling: Concepts, implementation and applications. Vis. Comput. 1995, 11, 429–446. [Google Scholar] [CrossRef]
- Pasko, G.; Pasko, A.; Ikeda, M.; Kunii, T. Bounded blending operations. In Proceedings of the SMI 2002: Shape Modeling International 2002, Banff, AB, Canada, 17–22 May 2002; pp. 95–103. [Google Scholar]
- Sanchez, M.; Fryazinov, O.; Fayolle, P.-A.; Pasko, A. Convolution Filtering of Continuous Signed Distance Fields for Polygonal Meshes. Comput. Graph. Forum 2015, 34, 277–288. [Google Scholar] [CrossRef]
- Abaqus Analysis User Manual, Version 6.14. 2014. Available online: https://www.3ds.com/products-services/ (accessed on 5 August 2020).
- Chugunov, S.; Adams, N.A.; Akhatov, I.S. Evolution of SLA-Based Al2O3 Microstructure during Additive Manufacturing Process. Materials 2020, 13, 3928. [Google Scholar] [CrossRef] [PubMed]
- Hart, N.H.; Nimphius, S.; Rantalainen, T.; Ireland, A.; Siafarikas, A.; Newton, R.U. Mechanical basis of bone strength: Influence of bone material, bone structure and muscle action. J. Musculoskelet. Neuronal Interact. 2017, 17, 114–139. [Google Scholar] [PubMed]
- Jamieson, R.; Hacker, H. Direct slicing of CAD models for rapid prototyping. Rapid Prototyp. J. 1995, 1, 4–12. [Google Scholar] [CrossRef]
- Song, Y.; Yang, Z.; Liu, Y.; Deng, J. Function representation based slicer for 3D printing. Comput. Aided Geom. Des. 2018, 62, 276–293. [Google Scholar] [CrossRef]
- Popov, D.; Maltsev, E.; Fryazinov, O.; Pasko, A.; Akhatov, I. Efficient contouring of functionally represented objects for additive manufacturing. Comput. Des. 2020, 129, 102917. [Google Scholar] [CrossRef]
- Safonov, A.A. 3D topology optimization of continuous fiber-reinforced structures via natural evolution method. Compos. Struct. 2019, 215, 289–297. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).