Area-Efficient Short-Time Fourier Transform Processor for Time–Frequency Analysis of Non-Stationary Signals

Abstract

In this paper, we propose an area-efficient short-time Fourier transform (STFT) processor that can perform time–frequency analysis of non-stationary signals in real time, which is essential for voice or radar-signal processing systems. STFT processors consist of a windowing module and a fast Fourier transform processor. The length of the window function is related to the time–frequency resolution, and the required window length varies depending on the application. In addition, the window function needs to overlap the input data samples to minimize the data loss in the window boundary, and overlap ratios of 25%, 50%, and 75% are generally used. Therefore, the STFT processor should ideally support a variable window length and overlap ratio and be implemented with an efficient hardware architecture for real-time time–frequency analysis. The proposed STFT processor is based on the radix-4 multi-path delay commutator (R4MDC) pipeline architecture and supports a variable length of 16, 64, 256, and 1024 and overlap ratios of 25%, 50%, and 75%. Moreover, the proposed STFT processor can be implemented with very low complexity by having a relatively lower number of delay elements, which are the ones that increase complexity in the most STFT processors. The proposed STFT processor was designed using hardware description language (HDL) and synthesized to gate-level circuits using a standard cell library in a 65 nm CMOS process. The proposed STFT processor results in logic gates of 197,970, which is 63% less than that of the conventional radix-2 single-path delay feedback (R2SDF) based STFT processor.

1. Introduction

Short-time Fourier transform (STFT) is a time–frequency analysis technique for non-stationary signals. The STFT segments a time-domain input signal into several separated or overlapped frames by multiplying the signal with a window function and then applies the fast Fourier transform (FFT) to each frame. Because Fourier transforms are performed while moving the window, this technique can measure the frequency content changes of a signal over time [1,2,3]. Owing to these characteristics, the STFT is widely used in various fields that require frequency measurement over time, such as radar systems and voice-signal processing systems. In particular, to carry out these measurements in real-time, it is necessary to implement the STFT algorithm into a hardware processor [4,5,6,7,8,9,10].

An STFT processor consists of a windowing module and an FFT processor. The available types of FFT hardware architectures that can be considered for designing an STFT processor are the single butterfly architecture, the pipeline architecture, and the parallel architecture. Among them, the pipeline architecture offers a good tradeoff between hardware complexity and throughput rate; therefore, it is an attractive option for implementing the FFT processor in an STFT processor. Pipeline architectures are classified as single-path delay feedback (SDF) architecture and multi-path delay commutator (MDC) architecture. The SDF pipeline architecture is the more commonly used out of the two because it provides the lowest number of nontrivial multiplications, which are the most complex operations to perform in a single channel [11]. However, when using multiple data channels, the SDF FFT processor must be implemented in each channel. Thus, there is a problem in that hardware complexity increases linearly with the number of data channels. In the case of multi-channel FFT, Sansaloni et al. suggested that the MDC FFT processor could be implemented in a lower area than the SDF FFT processor [12].

The windowing module multiplies the non-stationary signal with the window function to add a time dimension and reduces the side lobes in the spectrum, thereby reducing the spectral leakage caused by noise. In addition, the type and length of the window function used in the windowing module are closely related to performance. Consequently, the type and length of the window function appropriate for each application are different [13].

The length of the window function in the STFT is related to the resolution of the signal. Long windows provide higher frequency resolution but lower time resolution. Analogously, short windows provide higher time resolution but lower frequency resolution. Because the required time and frequency resolutions vary between applications using STFT processors, the window length should ideally be variable to support various time and frequency resolutions [14,15,16]. STFT processors generally use several types of tapering windows, such as Hamming, Hanning, and Kaiser, to reduce the side lobes in the spectrum and mitigate spectral leakage due to noise. However, tapering windows are usually very small or zero at the beginning and end, resulting in data loss near the boundary. To solve this problem, we need to minimize the loss of data by overlapping window functions. The overlap ratio that minimizes data loss varies depending on the type of window function used. According to Heinzel et al., to minimize data loss when using a window function, it is typically used with a 0%, 25%, 50%, or 75% overlap [17]. Therefore, depending on the type of window used, the STFT processor should be capable of changing the overlap ratio to the one that minimizes data loss.

Various studies have been conducted to improve the performance of STFT processors. Zhang et al. implemented an STFT processor that uses several SDF FFT processors in parallel to support a high overlap ratio, but this increases complexity [18]. In addition, Srinivas et al. implemented the STFT processor as a single SDF FFT processor and reused the FFT calculation results to reduce hardware area and latency [19]. However, this STFT processor can only use a rectangular window and supports a 50% overlap only.

Therefore, in this paper, we propose an STFT processor that provides a 0/25/50/75% variable overlap ratio to minimize data loss depending on the type of window used and 16/64/256/1024-point variable window lengths to support various time–frequency resolutions. In particular, because the proposed STFT processor is based on a radix-4 MDC (R4MDC) architecture, it has lower complexity than architectures using several SDF FFT processors.

The remainder of this paper is organized as follows. Section 2 describes the STFT algorithm and general hardware architectures. Section 3 presents the hardware architecture of the proposed STFT processor. Section 4 presents the design and implementation results of the proposed STFT processor. Finally, Section 5 concludes the paper.

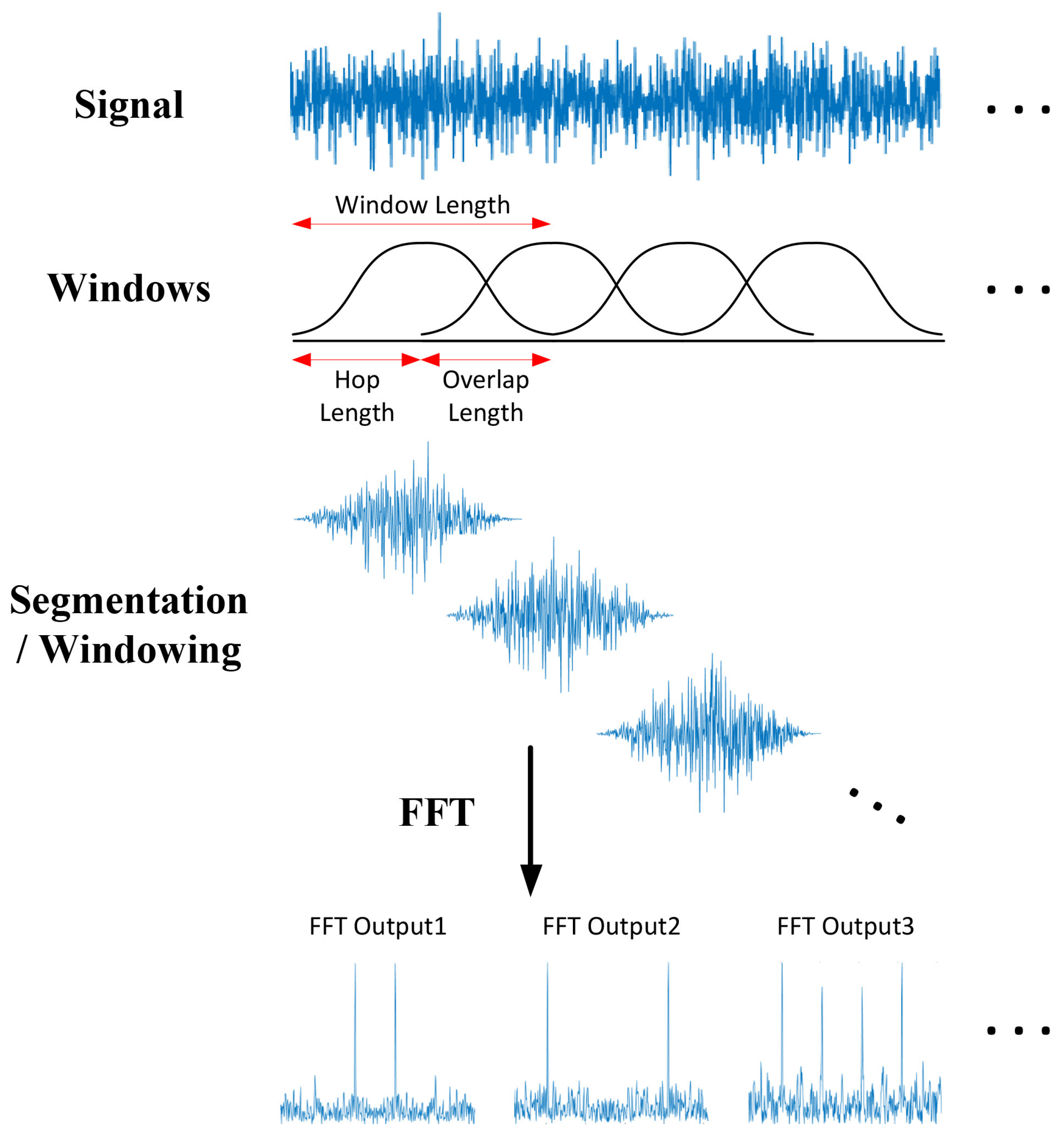
2. STFT Algorithm and Hardware Architecture

The STFT is defined as

$$X_{STFT}\left[k,n\right]=\sum _{m=0}^{N-1}x\left[m+nH\right]w\left[m\right]W_N^{km},0\le k\le N-1,1\le H\le N$$

(1)

where $\mathit{x}\left[m\right]$ is the input signal, $\mathit{w}\left[m\right]$ is the window function, $\mathit{N}$ is the length of the window, $\mathit{n}$ is the time frame index, and $\mathit{k}$ is the frequency index. Here, $\mathit{H}$ denotes the hop length, and the overlap length between adjacent frames is $\mathit{N}-H$. In addition, the overlap ratio between consecutive frames is $(N-H)/N$. At a specific time $\mathit{n}H$, the signal $\mathit{x}\left[m\right]$ is multiplied by the window function $\mathit{w}\left[m\right]$. Therefore, Equation (1) can be defined as the FFT operation of $\mathit{x}[m+nH]w\left[m\right]$. The STFT processor measures the frequency over time by moving the window function $\mathit{w}\left[m\right]$ along the signal $\mathit{x}\left[m\right]$ according to the hop length and performing the FFT operation on samples inside the window. The flow of the algorithm is shown in Figure 1.

The STFT processor should be capable of varying the overlap ratio according to the window type to minimize the data loss due to the tapering window. Therefore, the STFT processor needs a windowing module that overlaps the input data stream at a certain overlap ratio and multiplies the signal by the window function. Figure 2 shows how windows are overlapped at ratios of 0%, 25%, 50%, and 75% in the windowing module. Figure 2b,c shows window overlaps at ratios of 25% and 50%, respectively, and that the windowing module requires at least two output channels to overlap a single data stream by 25% and 50%. Figure 2d shows a window overlap of 75%. In this case, the windowing module requires at least four output channels to overlap a single data stream by 75% overlap ratio. In addition, when the windowing module supports a 75% overlap ratio, channels 1 and 3 of the windowing module have a 50% overlap ratio, channels 1 and 4 have a 25% overlap ratio, and channel 1 has a 0% overlap ratio. In other words, a windowing module that supports a 75% overlap ratio also includes 0%, 25%, and 50% overlap ratios. Therefore, to support a variable overlap ratio, the windowing module should be able to receive a single data stream and create four data streams overlapped by 75% between each channel.

The 75% overlapped data streams are output through the four channels of the windowing module as input to the FFT processor, which performs the FFT operation to measure the frequency content changes over time. As previously stated, current FFT hardware architectures that can be considered for designing an STFT processor are generally classified as single butterfly architectures, pipeline architectures, and parallel architectures. The parallel architecture has the most significant advantage in terms of throughput rate but has high hardware complexity. The single butterfly architecture has the lowest hardware complexity, but offers a low throughput rate. In contrast, the pipeline architecture offers a good tradeoff between throughput and complexity and is consequently used in many fields [20,21,22].

Pipeline architectures in FFT processors are classified as SDF and MDC. In the SDF architecture, the input sequence goes through a single channel and is reordered by a modified butterfly computational unit. Since this architecture requires only one complex multiplier per butterfly unit, it has low complexity and is commonly used in STFT processors. However, as shown in Figure 3, four FFT processors are required to design an STFT processor with a variable overlap ratio of maximum 75% using an SDF FFT processor. Thus, a large hardware area is required. In contrast, MDC FFT processors process data through multiple channels and perform an alignment of the data according to a signal-flow graph (SFG) using delay elements [23]. In the case of four-channel FFT, the R4MDC FFT processor can be implemented in a lower area than four radix-2 SDF (R2SDF) FFT processors [24]. Therefore, designing an STFT processor that supports a variable overlap ratio using an MDC FFT processor requires a single FFT processor instead of four SDF FFT processors, as shown in Figure 4.

3. Hardware Architecture of the Proposed STFT Processor

3.1. Variable Overlap Ratio of the Proposed STFT Processor

Because a single data stream is input to the STFT processor, we need a windowing module (WM) that receives a single data stream and creates four data streams that overlap by 75% between each channel. For a window length of $\mathit{N}$, the input and output data flows of the WM are as shown in Figure 5. The output data of channel 1 is delayed by $\mathit{3}N/4$ cycles of the input data stream, and the output data of channel 2 is delayed by $\mathit{N}/2$ cycles of the input data stream. The output data of channel 3 is delayed by $\mathit{N}/4$ cycles of the input data stream. Finally, the output data stream of channel 4 is output without delaying the input data stream. The FFT operation starts after the first data of channel 1 is delayed by $\mathit{3}N/4$ cycles. That is, the FFT operation starts when the data on channel 1 and channel 2, channel 2 and channel 3, channel 3 and channel 4 overlap by 75% each and are input into the FFT processor.

As previously stated, it is possible to change the overlap ratio by approximately selecting output channels of the FFT processor. For example, we can obtain 50% overlapped STFT result by selecting output channels along to blue arrow in Figure 6, because channels 1 and 3 overlap by 50%. Similarly, 25% and 75% overlapped STFT results can be obtained along to red and green arrows, respectively. If only channel 1 is selected, we can obtain STFT result of the non-overlapped data streams.

3.2. Hardware Architecture of the Proposed STFT Processor

Figure 7 shows the hardware architecture of the proposed STFT processor, which supports a 0/25/50/75% variable overlap ratio to minimize the loss of information depending on the type of window used. It also supports 16/64/256/1024-point variable window lengths to provide various time–frequency resolutions. The hardware architecture of the proposed STFT processor consists of a WM, four data mapping modules (DMM1, DMM2, DMM3, DMM4), a data reordering module (DRM), five radix-4 butterfly modules (R4BM1, R4BM2, R4BM3, R4BM4, R4BM5). The principle of operation is as follows. The input single data stream is reconstructed according to the length of the predefined window by the WM and converted into four overlapped data streams. Moreover, the four data streams are multiplied by the predefined window and input to the next stage. In the case of 1024-point STFT, the four-channel data streams reconstructed by the WM are input to R4BM1 by a multiplexer to perform the 1024-point STFT operation. In the case of 256-point STFT, the four-channel data streams are input to R4BM2. In the case of 64-point STFT, the four-channel data streams are input to R4BM3. In the 16-point STFT, four channels of data streams are input to R4BM4.

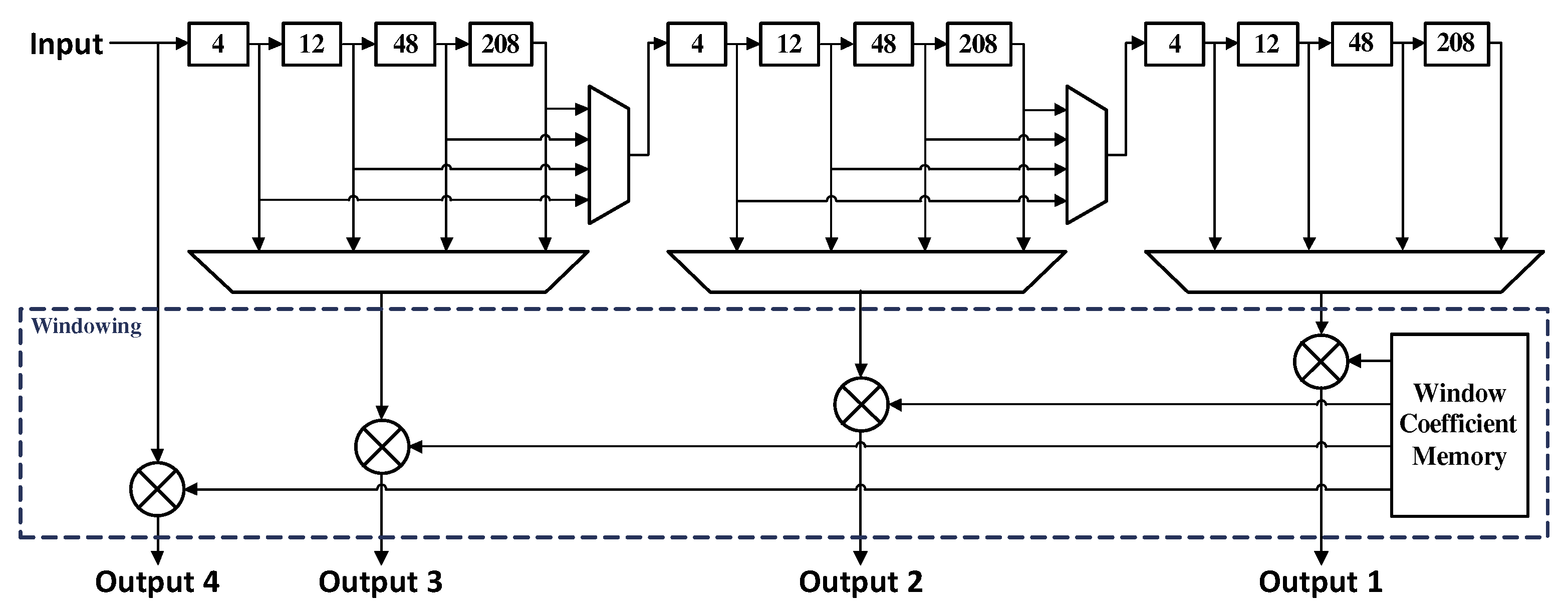
3.2.1. Windowing Module (WM)

If the conventional R4MDC architecture is applied to the STFT processor, there is a problem in that the area required is higher owing to the first DMM that reconstructs the data before the first R4BM input [25]. In the case of 1024-point R4MDC FFT, 3072 delay elements are required for the subsequent R4BM (R4BM1). However, in the proposed STFT processor, the WM converts the input single data stream into four 75% overlapped data streams and reconstructs the data with an alignment pattern corresponding to that required by the first R4BM as shown in Figure 8. Therefore, in the proposed architecture, a DMM for performing data alignment for the first R4BM was not used. In this way, the required number of delay elements is only 768, thereby enabling an implementation with lower complexity. In addition, since the proposed WM should support variable lengths of 16/64/256/1024 points, we use multiplexers to determine the required data alignment pattern for 16/64/256/1024 points.

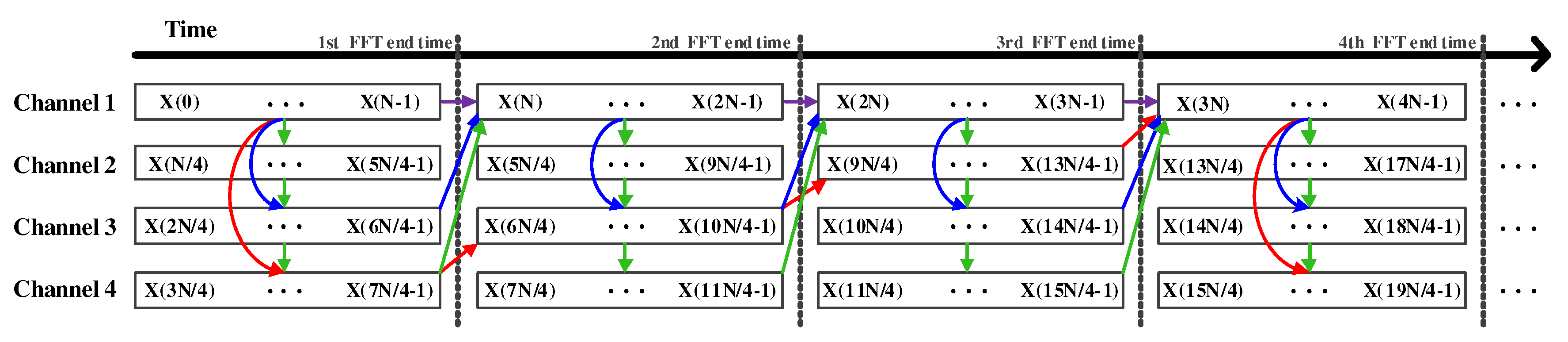
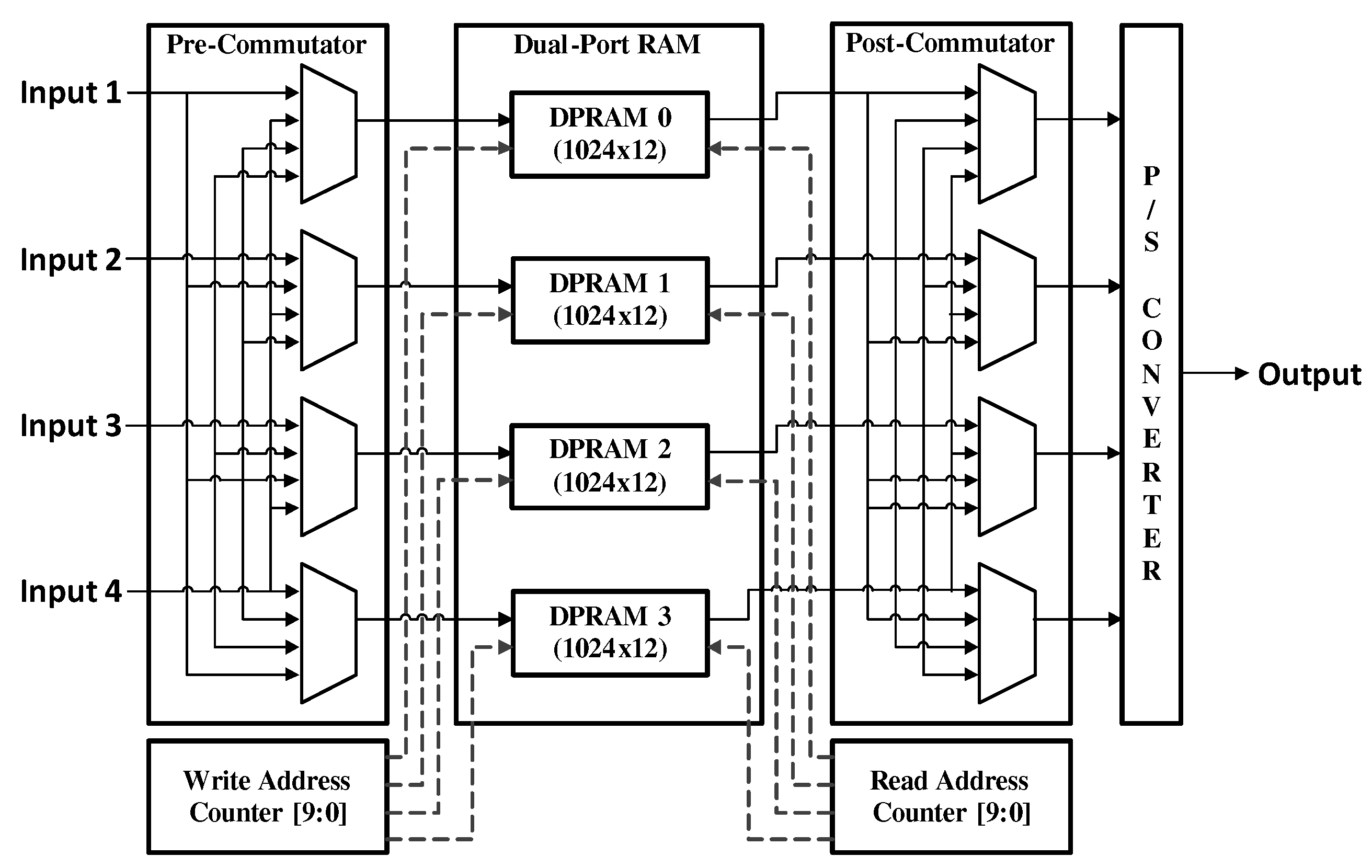
3.2.2. Data Reordering Module (DRM)

The DRM makes the four-channel data after the FFT operation match the predefined overlap ratio, as shown in Figure 6, and then outputs it. In this paper, the DRM is implemented using the architecture proposed in [26], and Figure 9 shows the hardware architecture of the proposed DRM. The pre-commutator reconstructs four-channel input data for the dual-port RAM (DPRAM). Because we need to support 16/64/256/1024-point variable lengths, we use multiplexers to enforce the necessary data alignment pattern for the 16/64/256/1024-point FFTs, respectively. The output of DPRAM is reconstructed and used as the input of the post-commutator, which uses multiplexers to reconstruct the data so that it matches the MDC data structure. The parallel-to-serial (P/S) converter selects data from the four-channel output of the post-commutator in the order that matches the predefined overlap ratio and outputs it as a single stream.

4. Implementation Results

To verify that the proposed STFT processor architecture is efficient in terms of hardware complexity, we implemented STFT processors using R2SDF, R4MDC, and the proposed architectures. A 12-bit word for the real and imaginary data paths was selected to satisfy the requirement for a signal-to-quantization-noise ratio (SQNR) of 40 dB. Three STFT processors were designed using hardware description language (HDL) and synthesized for an operating frequency of 200 MHz with a 65 nm CMOS standard cell library using Synopsys Design Compiler tool [27].

Table 1. Comparison of the logic synthesis results between the proposed and conventional STFT processors.

Block Name	R2SDF Based	R4MDC Based	Proposed	Reduction (%)
				R2SDF	R4MDC
Butterfly Unit	30,072	15,036	15,036	50	0
Multiplier	141,138	47,046	47,046	67	0
Delay Elements	369,360	369,360	135,888	63	63
Total	540,670	431,442	197,970	63	54

summarizes the comparison results in terms of the number of logic gates. As shown in the Table, the proposed STFT processor architecture reduces the number of logic gates by 54% compared with the conventional R4MDC-based STFT processor and by 63% compared with the R2SDF-based STFT processor.

Table 2. Comparison of the proposed STFT processor with previous research results.

Circuit	Tech (nm)	FFT Architecture	Window Length (N)	Overlap Ratio $\left(\mathit{\alpha }\right)$	Frequency (MHz)	Operating Time (ns)	Area (mm${}^2$)	A${}_{\mathit{norm}}$
[18]	180	R2SDF	32	max. 94	180	N.A.	7.74	2.15
Proposed	65	R4MDC	16/64/ 256/1024	0/25/ 50/75	200	175/665/ 2596/10,285	0.27	0.93

shows the comparison results between the proposed STFT processor and the STFT processor described in [18]. To make a fair comparison, we normalized the area as

$$A_{norm}=\frac{Area\times {10}^3}{{\left(Tech/65nm\right)}^2\times {log}_2\left(N\right)\times \alpha }$$

(2)

where $\mathit{N}$, $\alpha$, and $\mathit{T}ech$ are the window length, maximum overlap ratio, and the process technology in nanometers, respectively. Even though the design of [18] can support a higher overlap ratio than the proposed STFT processor, it only supports a window length of 32. It also requires an approximately 2.3 times larger area than the proposed STFT processor.

5. Conclusions

In this paper, we propose the design of an STFT processor architecture that supports a variable overlap ratio of 0/25/50/75% to minimize the data loss depending on the type of window used as well as variable window lengths of 16/64/256/1024 to provide various time–frequency resolutions. In the proposed WM architecture for our R4MDC-based STFT processor, the single-channel data stream is converted into four overlapped data streams by 75%, greatly reducing the number of delay elements needed, which occupy the largest portion of the device’s area. To assess the complexity of the proposed STFT processor, we implemented the conventional R2SDF-based and R4MDC-based STFT processors as well as the proposed STFT processor. Our comparison results indicate that the proposed processor architecture can reduce the logic gates by 63% compared with the R2SDF-based STFT processor. It can also be implemented with 54% fewer gates compared with the conventional R4MDC-based STFT processor. We have thereby demonstrated that the proposed architecture is efficient for the implementation of STFT processors, which are widely used in many fields to measure the changes in a signal’s frequency over time.