Novel Cost Reduction Method for Wind Farms Associated with Energy Storage Systems by Optimal Kinetic Energy Control
Abstract
:1. Introduction
2. System Description
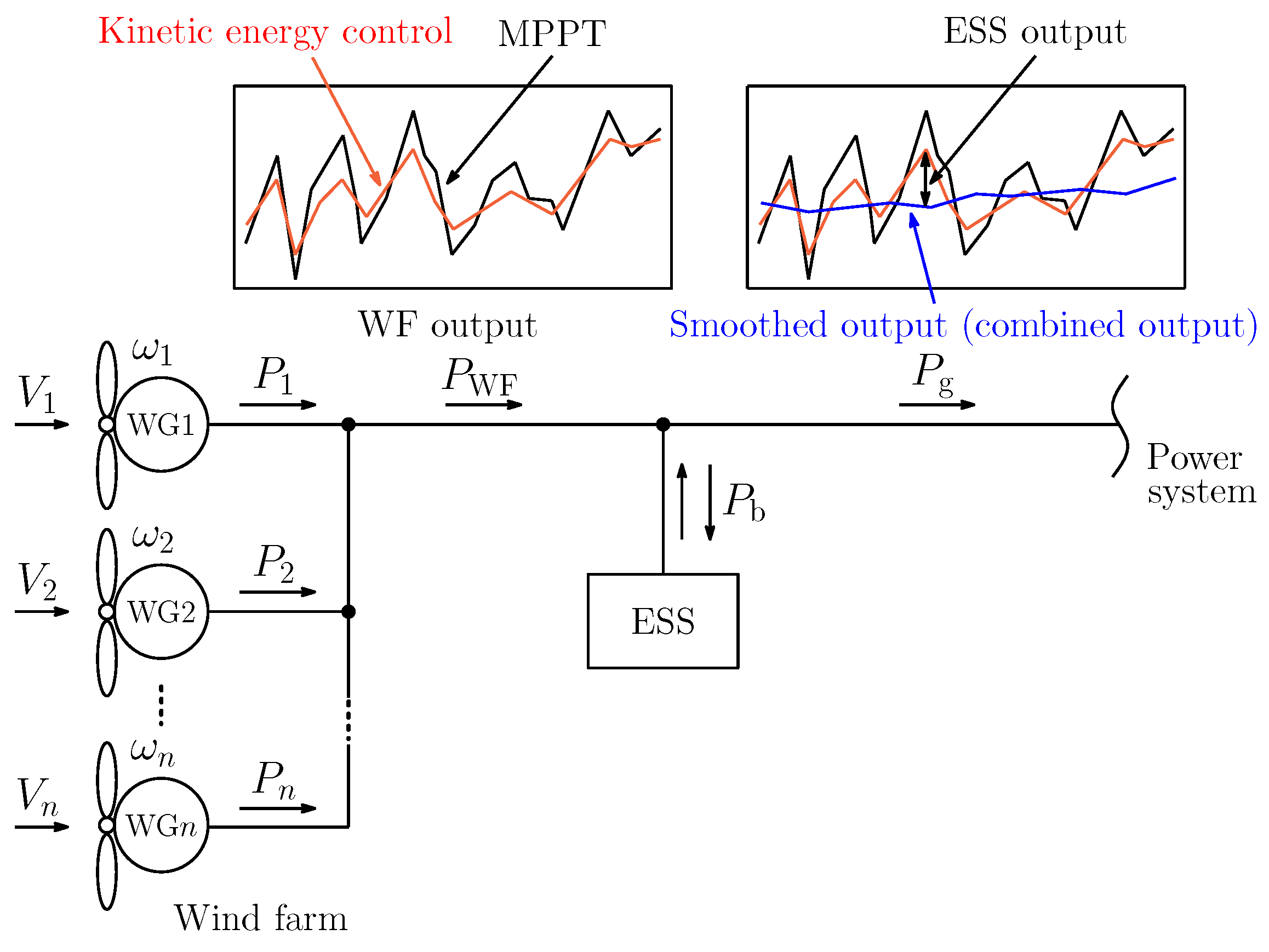
2.1. System Configuration
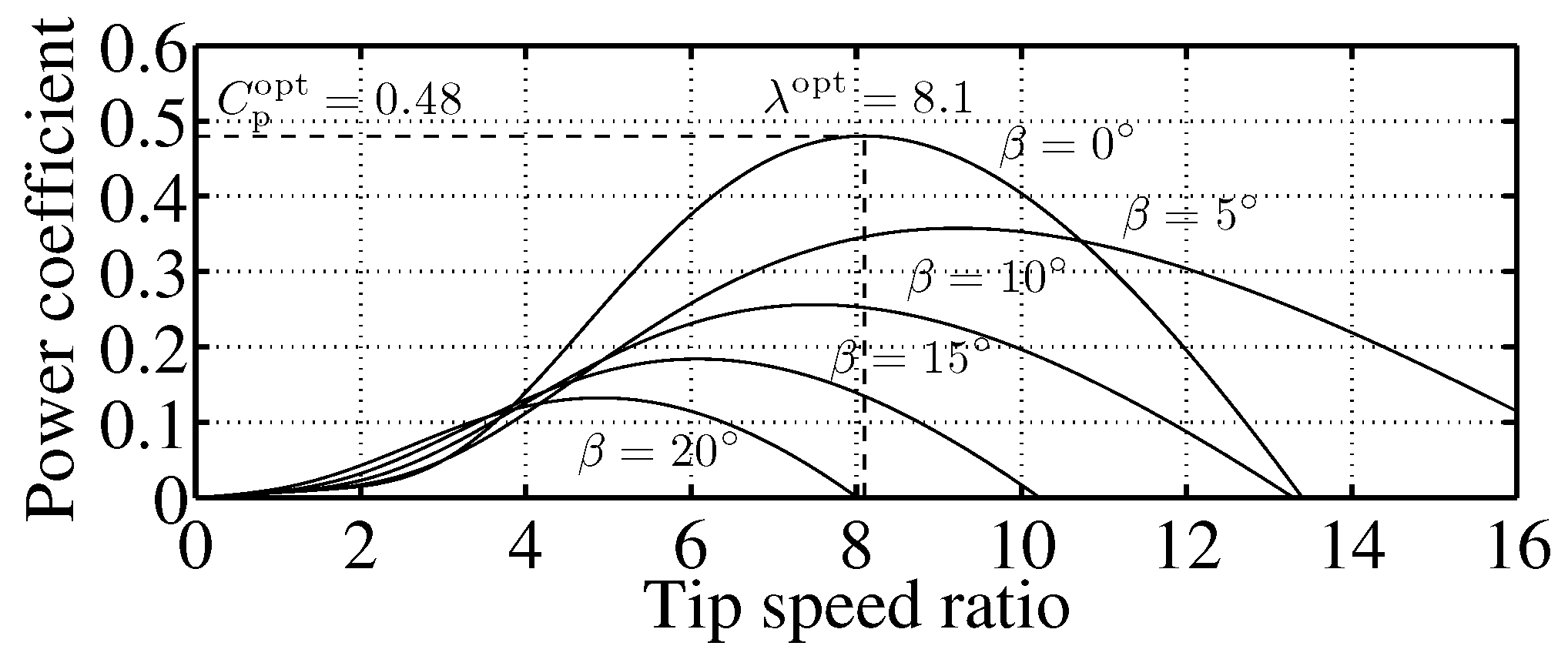
2.2. Wind Turbine Model
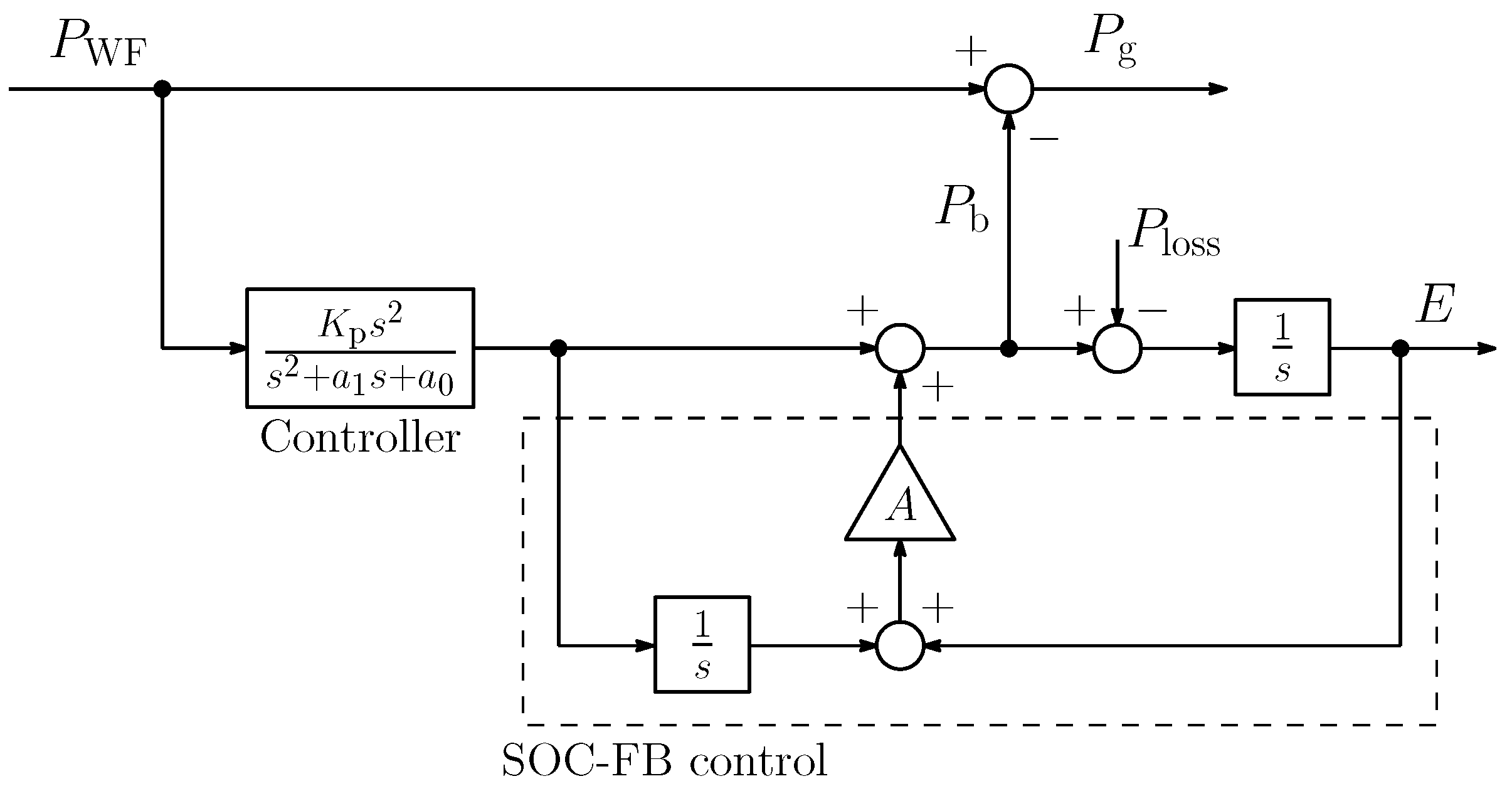
2.3. ESS Control System
2.4. Fluctuation of Combined Output and Technical Requirement
- The maximum power change per minute is within 10% of the WF power rating.
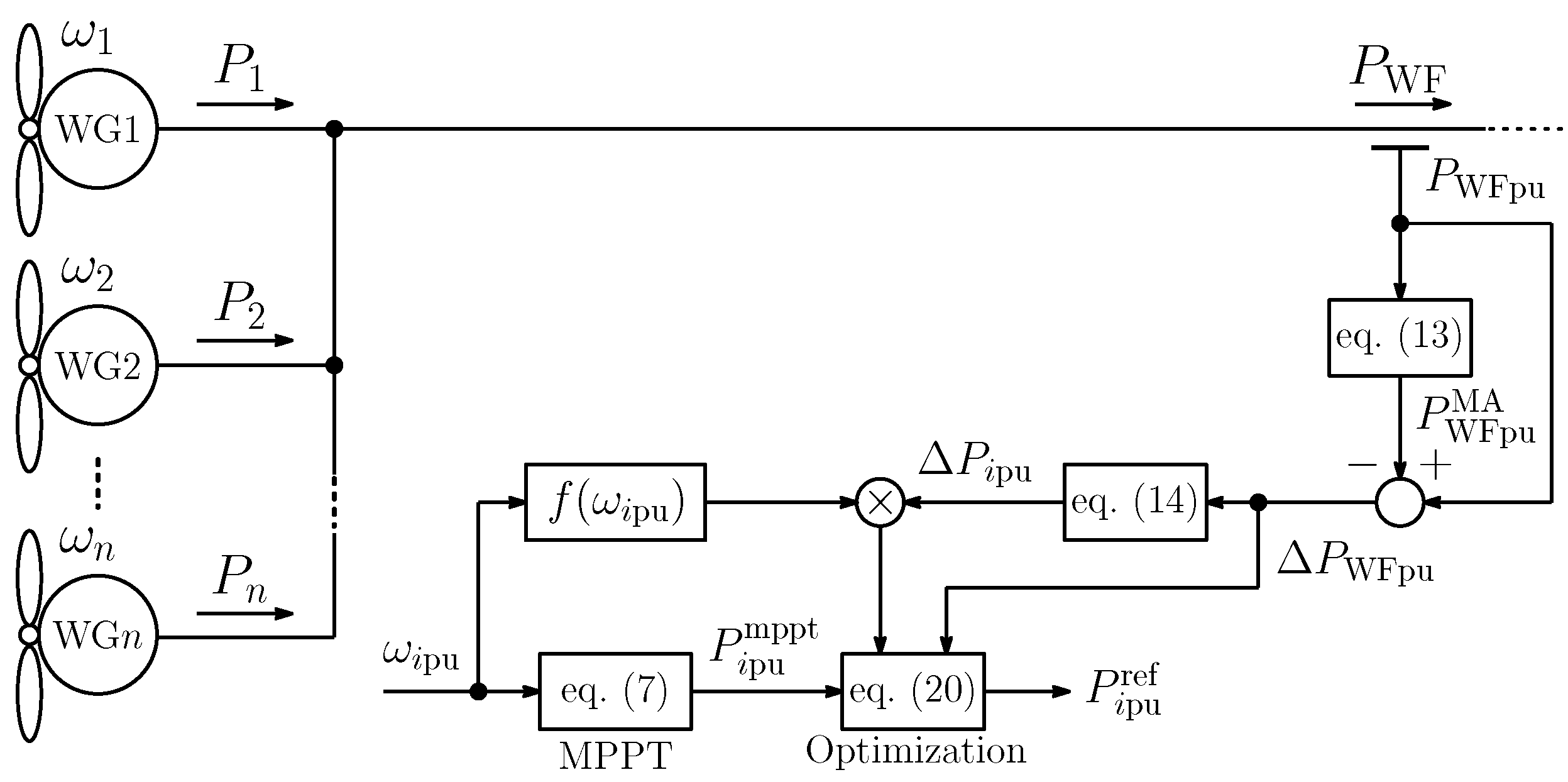
3. Kinetic Energy Control
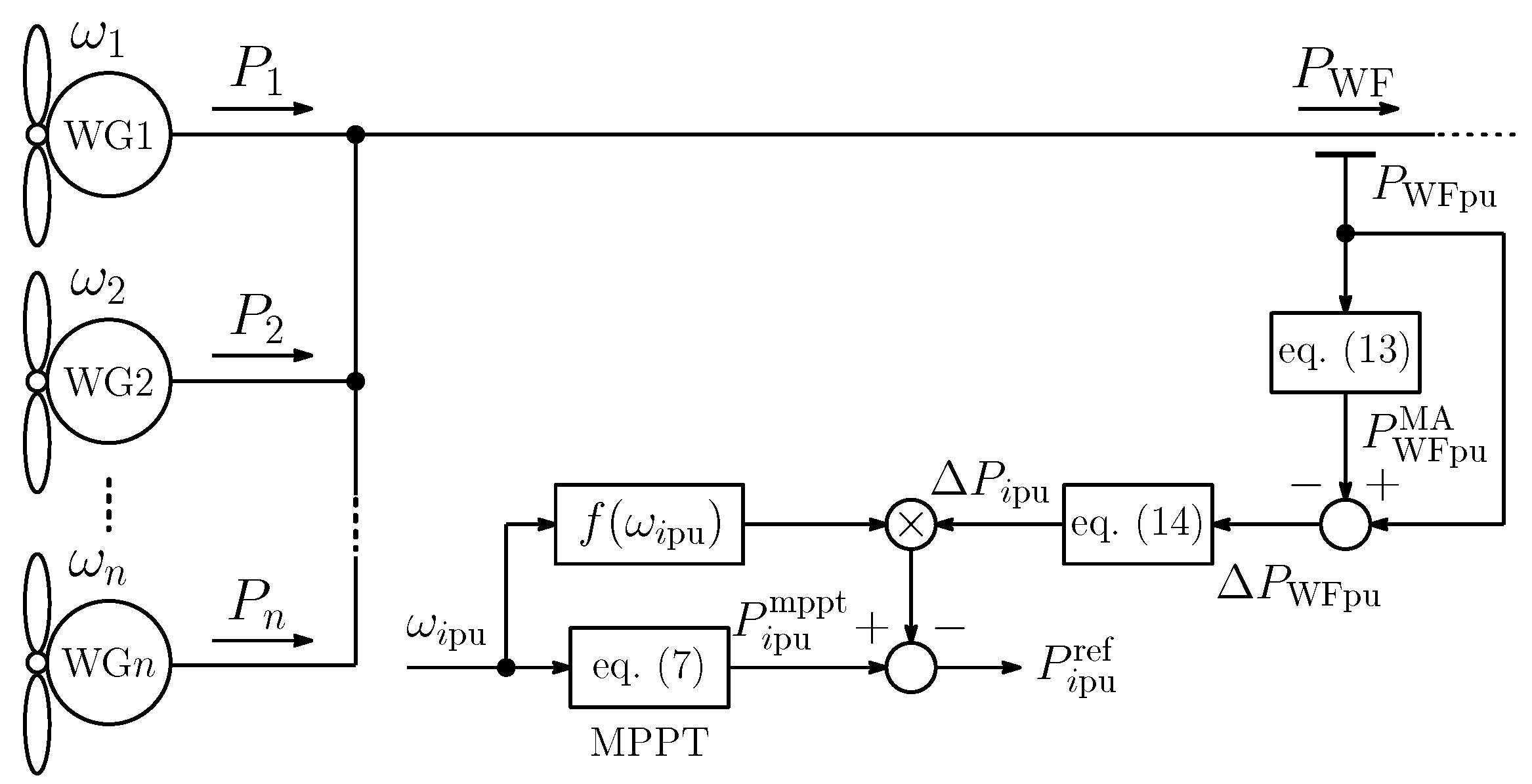
3.1. Standard Moving Average Kinetic Energy Control
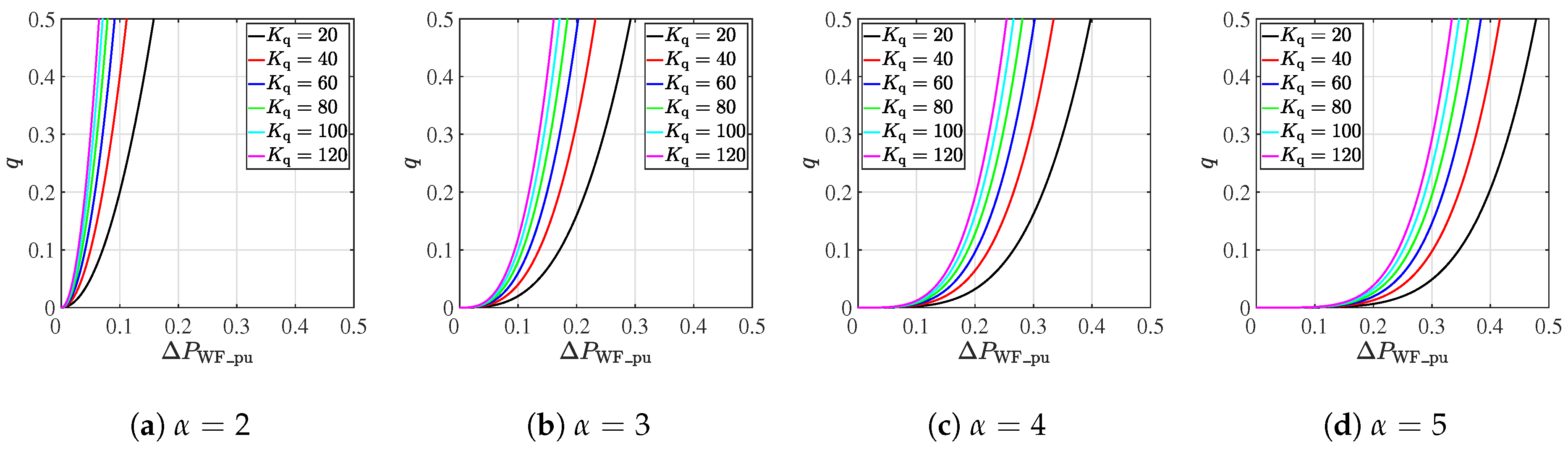
3.2. Optimal Kinetic Energy Control
4. Cost Calculation Method
- Installation cost of WF:
- Opportunity loss of WF:
- Installation cost of ESS:
- Opportunity loss of ESS:
- Cost of PCS:
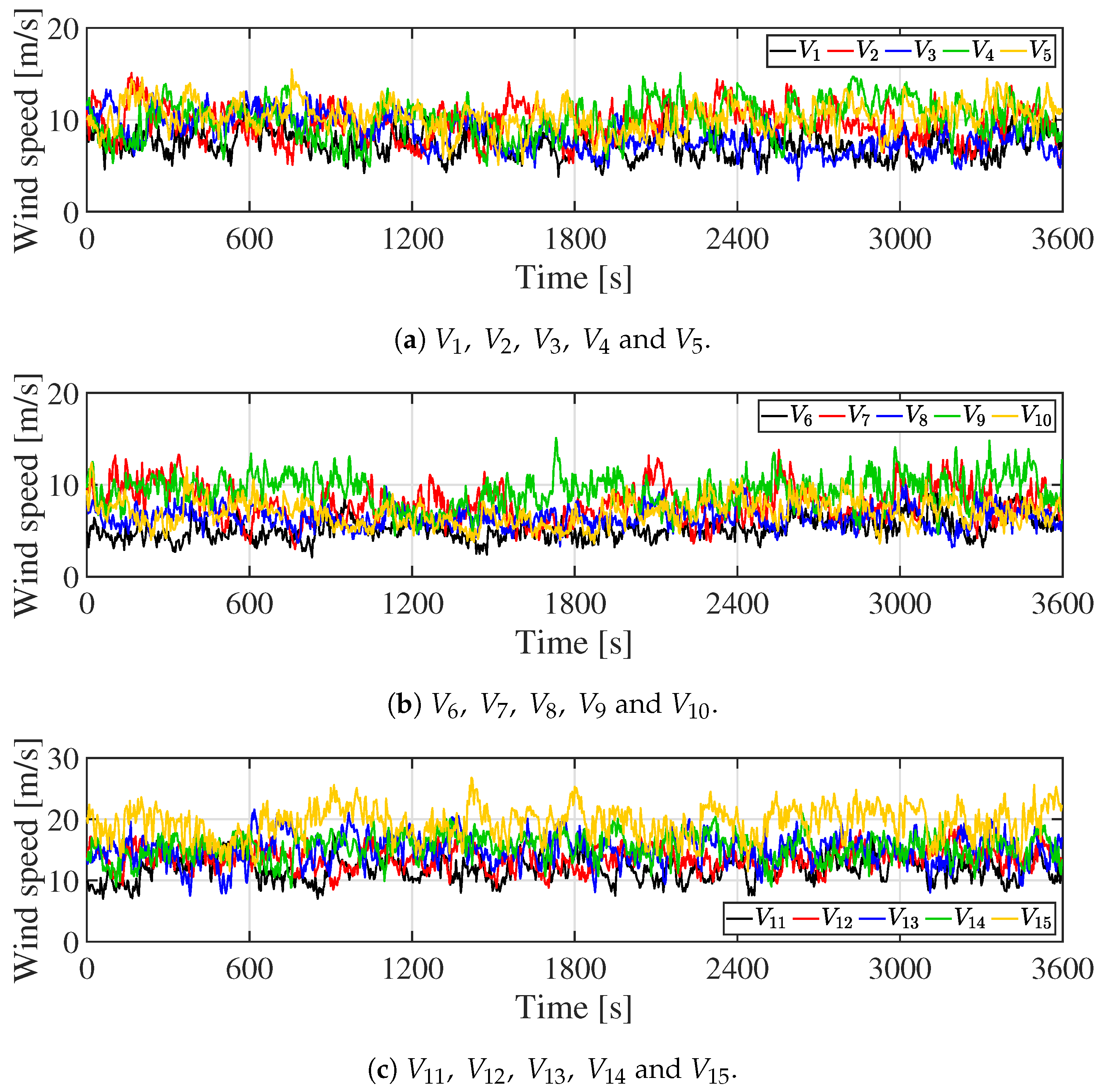
5. Simulations and Discussions
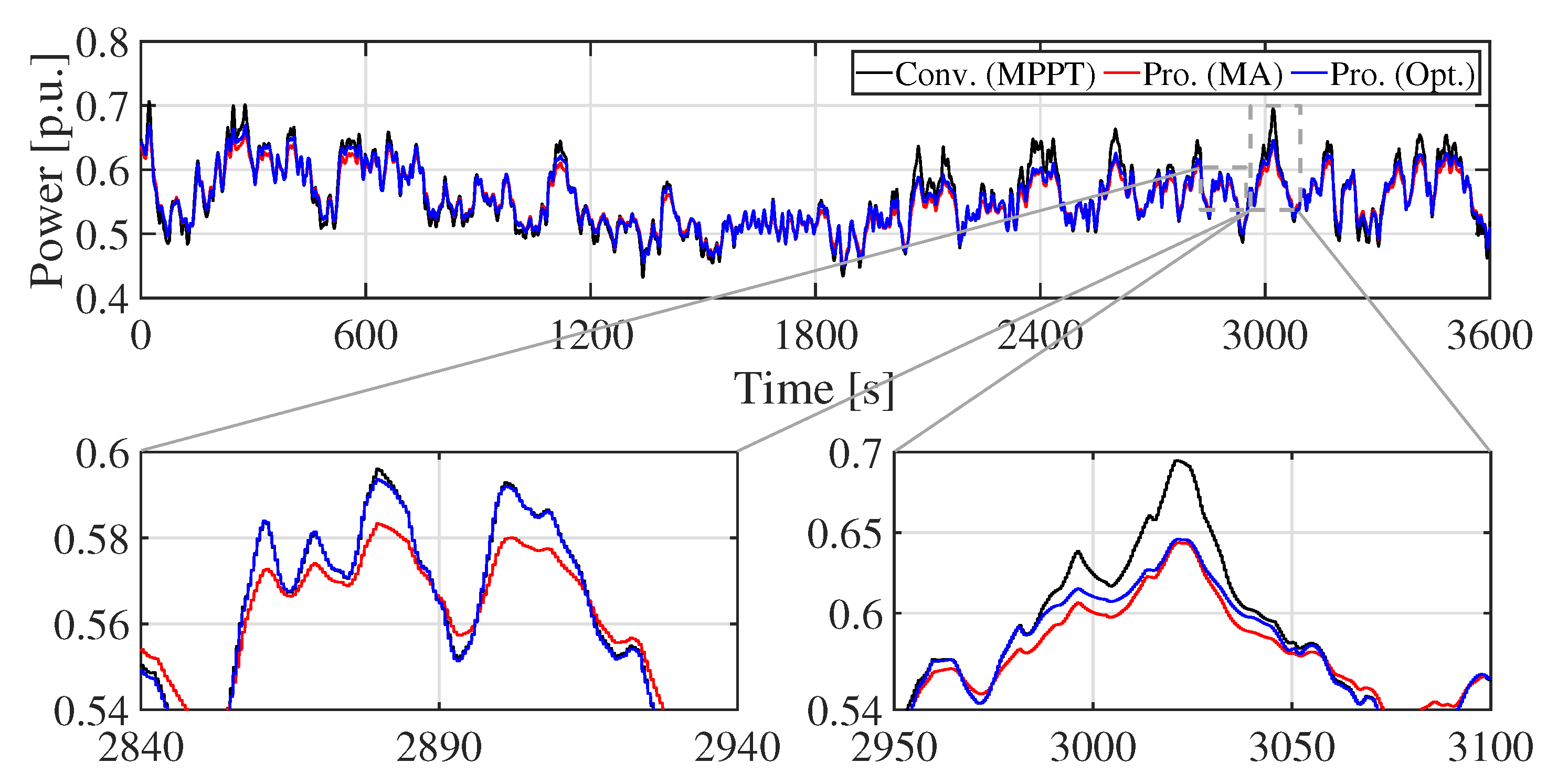
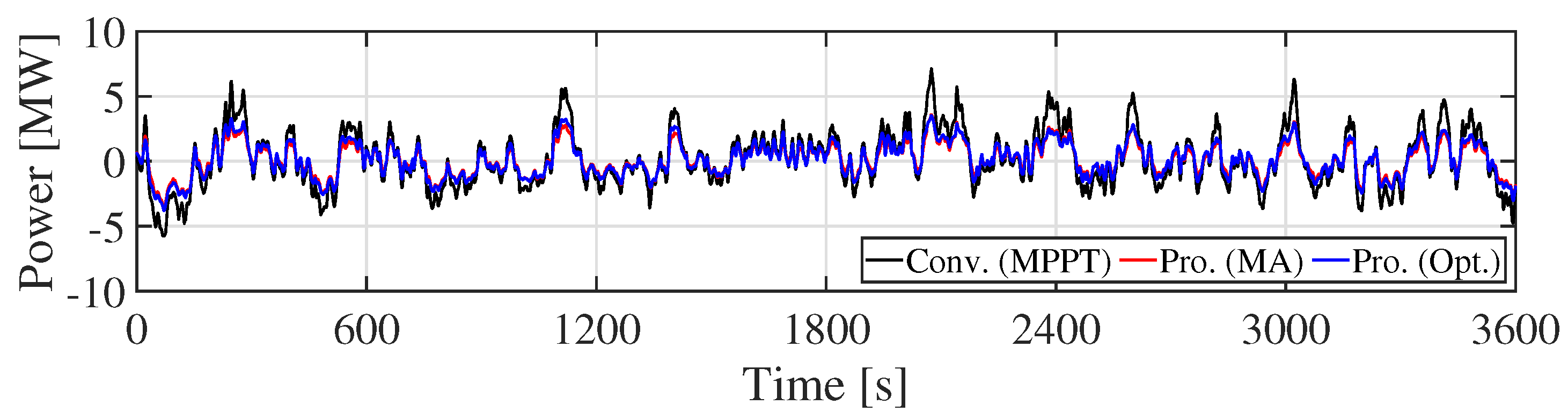
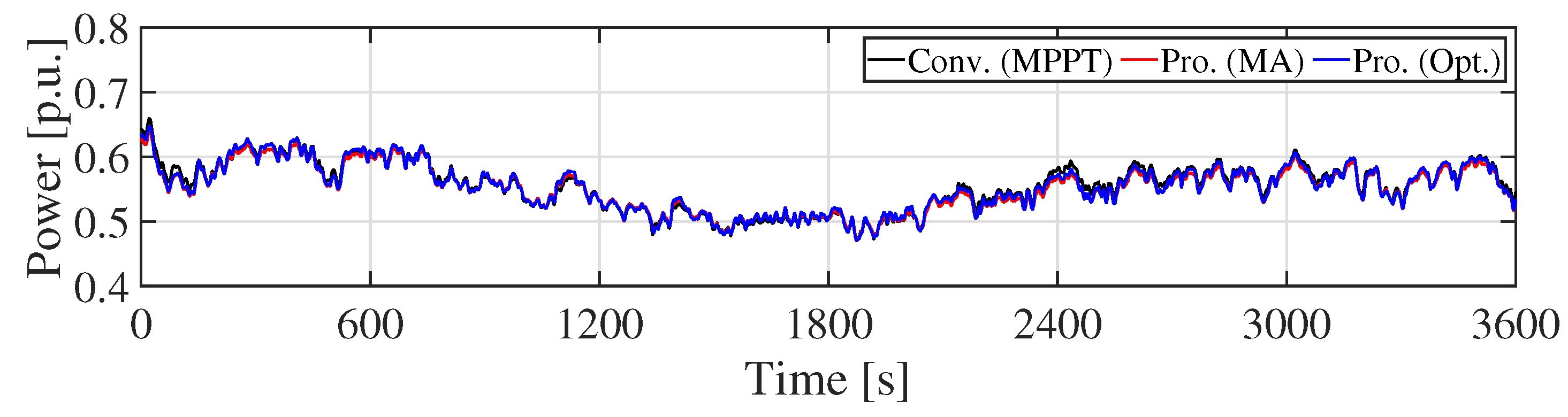
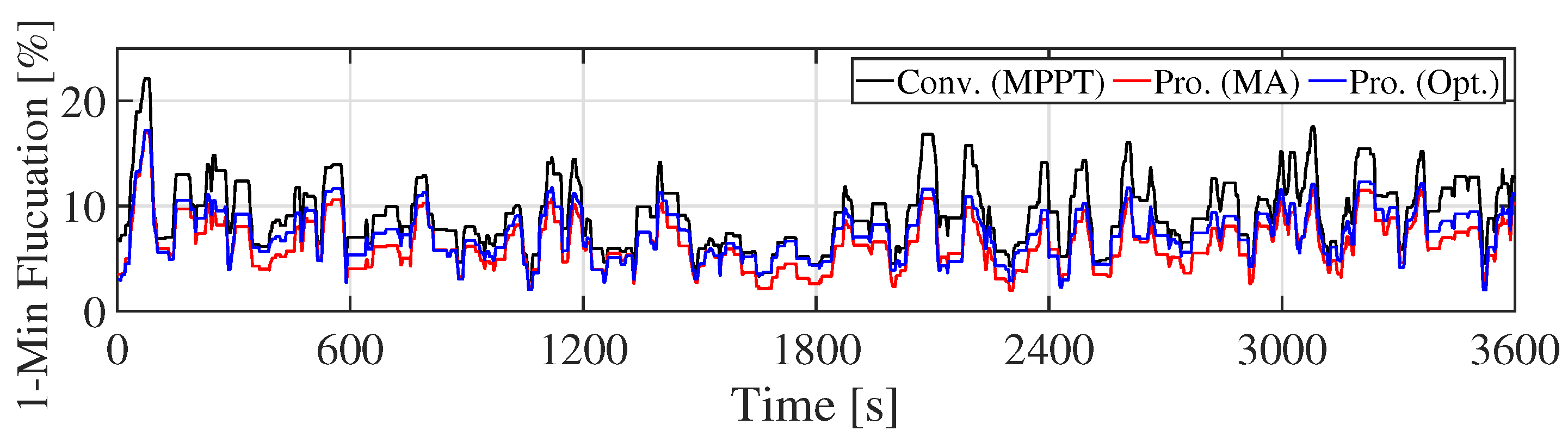
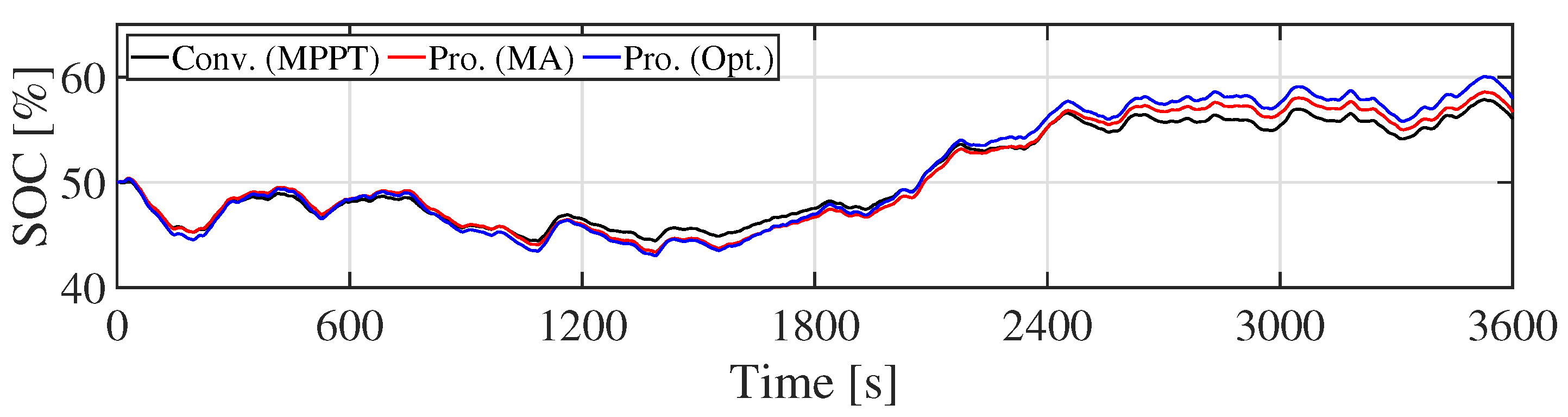
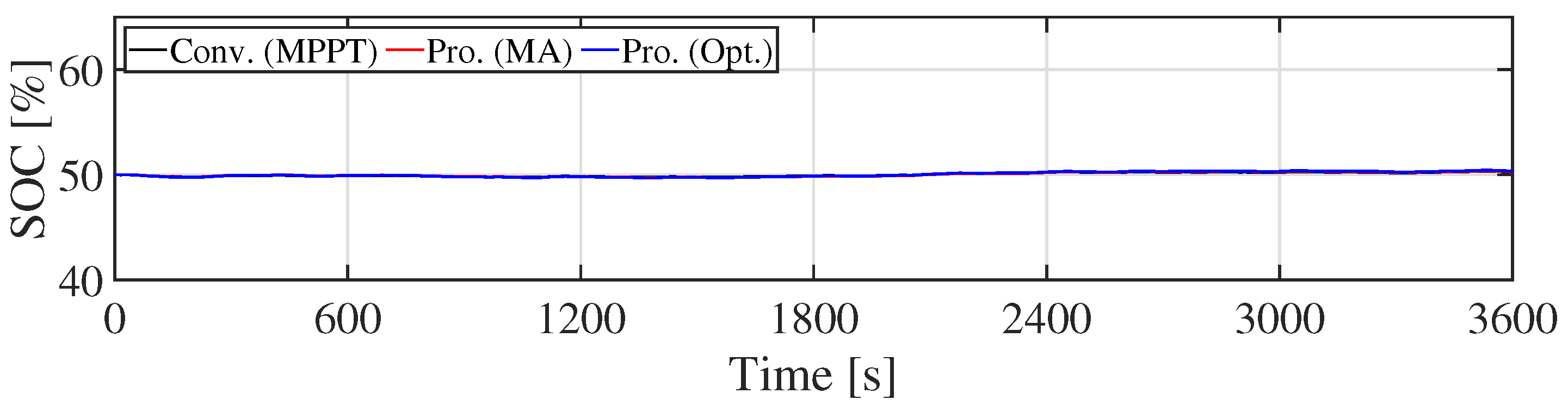
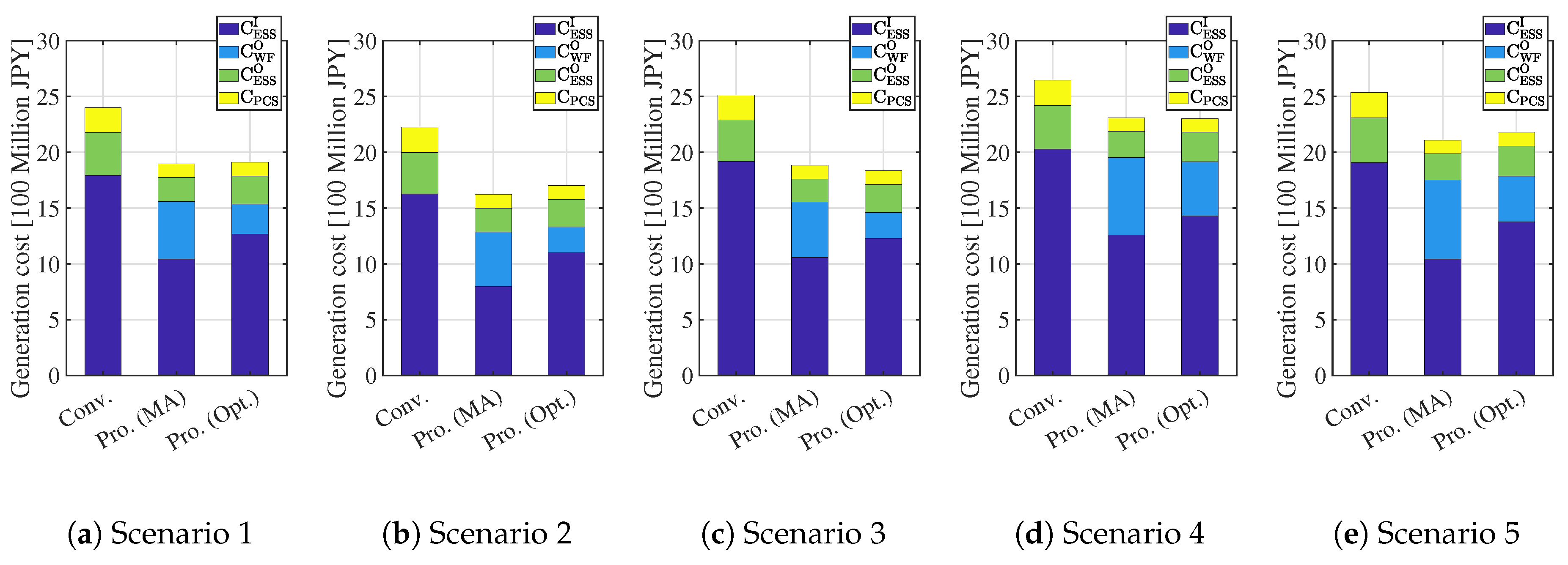
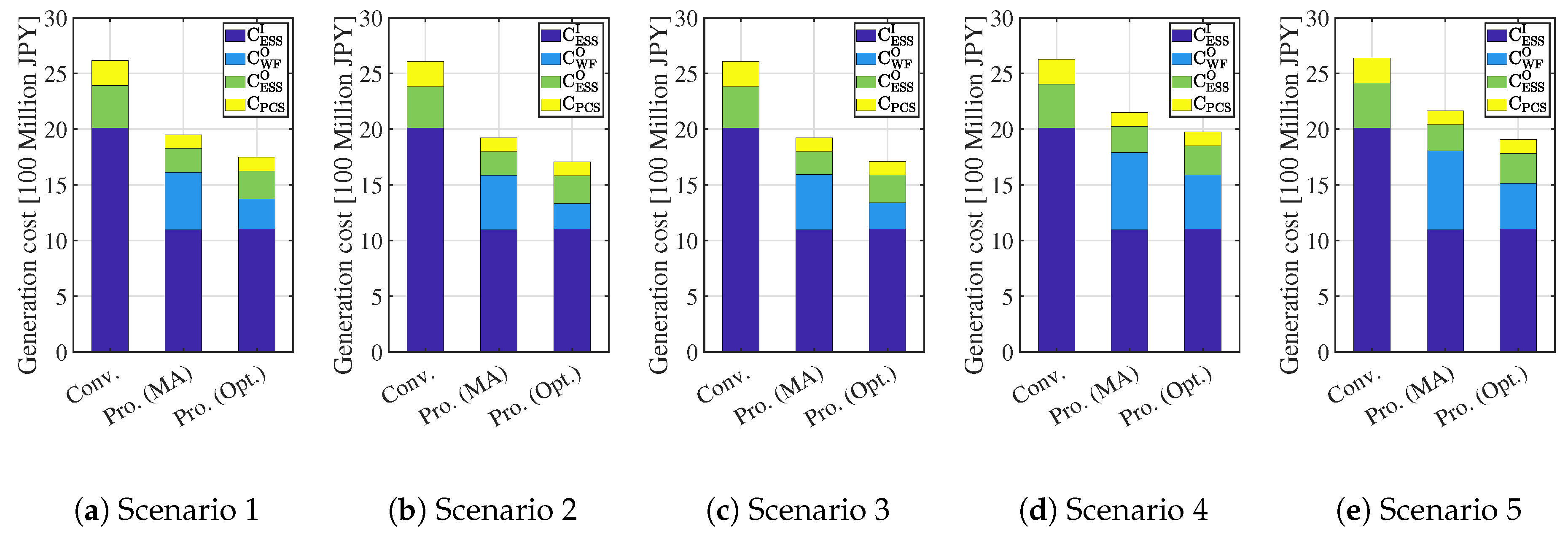
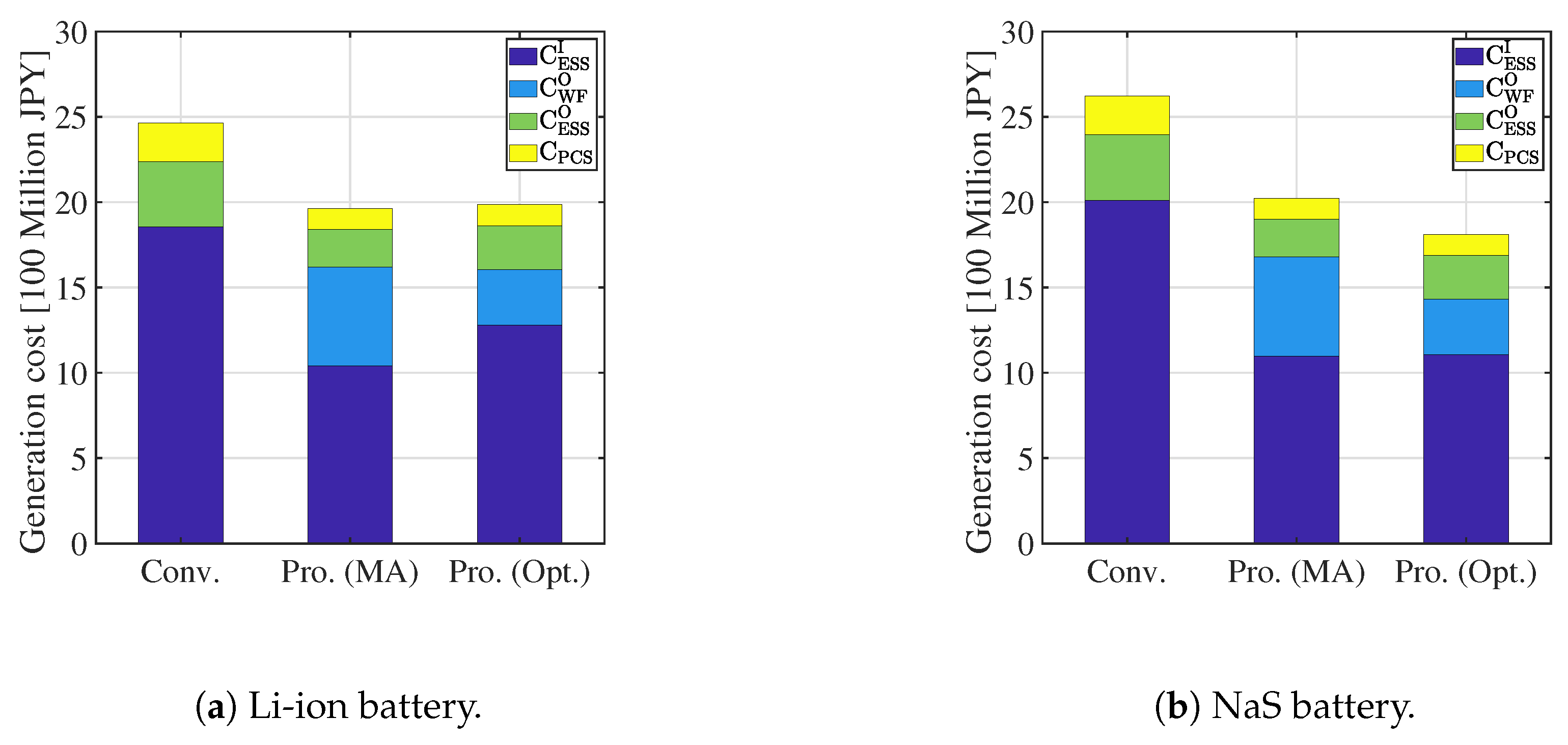
5.1. Simulations Results
5.2. Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ESS | Energy storage system |
| WF | Wind farm |
| KE | Kinetic energy |
| MA | Moving average |
| FLF | First-order low-pass filter |
| WG | Wind generator |
| MPPT | maximum power point tracking |
| SOC | State-of-charge |
| PCS | Power converter system |
| JPY | Japanese yen |
| DOD | Depth of discharge |
| SD | Standard deviation |
Nomenclature
| n | Number of WGs |
| V | Wind speed |
| Mechanical rotor angular frequency | |
| P | WG output |
| WF output | |
| ESS output | |
| Combined output power | |
| Air-density | |
| R | Radius of rotor blade |
| Tip speed ratio | |
| Blade pitch angle | |
| Power coefficien | |
| H | Inertia constant of WG |
| Mechanical torque | |
| Electrical torque | |
| MPPT output reference | |
| Charge/discharge loss of the ESS | |
| A | SOC-FB gain |
| Gain of ESS controller | |
| Parameter of ESS controller | |
| Fluctuation ratio of combined output | |
| E | Remaining energy of ESS |
| Short-period components of the WF output | |
| MA of | |
| Fluctuation component of WG | |
| q | Nonlinear weight |
| Weight | |
| Exponent weight | |
| Installation cost of WF | |
| Opportunity loss of WF | |
| Installation cost of ESS | |
| Opportunity loss of ESS | |
| Cost of PCS | |
| Energy loss by KE control | |
| C-rate | |
| Integral of the charge/discharge loss | |
| Calendar life | |
| Cycle life | |
| Subscript | |
| pu | Per-unit |
| n | rated value |
| Superscript | |
| ref | Reference value |
References
- Global Wind Energy Council. Global Wind Report 2018. 2019. Available online: http://www.gwec.net/ (accessed on 24 September 2020).
- Liu, Y.; Du, W.; Xiao, L.; Wang, H.; Cao, J. A Method for Sizing Energy Storage System to Increase Wind Penetration as Limited by Grid Frequency Deviations. IEEE Trans. Power Syst. 2016, 31, 729–737. [Google Scholar] [CrossRef]
- Cao, J.; Du, W.; Wang, H.; McCulloch, M. Optimal Sizing and Control Strategies for Hybrid Storage System as Limited by Grid Frequency Deviations. IEEE Trans. Power Syst. 2018, 33, 5486–5495. [Google Scholar] [CrossRef]
- Koiwa, K.; Liu, K.; Tamura, J. Analysis and Design of Filters for the Energy Storage System: Optimal Tradeoff Between Frequency Guarantee and Energy Capacity/Power Rating. IEEE Trans. Ind. Electron. 2018, 65, 6560–6570. [Google Scholar] [CrossRef]
- Tsili, M.; Papathanassiou, S. A review of grid code technical requirements for wind farms. IET Renew. Power Gener. 2009, 3, 308–332. [Google Scholar] [CrossRef]
- Nguyen, C.; Lee, H. Optimization of power dispatch to minimize battery storage capacity in wind farm. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 420–427. [Google Scholar]
- Nguyen, C.; Lee, H. Power Management Approach to Minimize Battery Capacity in Wind Energy Conversion Systems. IEEE Trans. Ind. Appl. 2017, 53, 4843–4854. [Google Scholar] [CrossRef]
- Yoshimoto, K.; Nanahara, T.; Koshimizu, G. New Control Method for Regulating State-of- Charge of a Battery in Hybrid Wind Power/Battery Energy Storage System. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006; pp. 1244–1251. [Google Scholar]
- Kurose, N.; Takahashi, R.; Tamura, J.; Fukushima, T.; Sasano, E.; Shinya, K. A consideration on the determination of power rating of Energy Storage System for smoothing wind generator output. In Proceedings of the Electrical Machines and Systems (ICEMS), Incheon, Korea, 10–13 October 2010; pp. 622–627. [Google Scholar]
- Zhao, H.; Wu, Q.; Hu, S.; Xu, H.; Rasmussen, C.N. Review of energy storage system for wind power integration support. Appl. Energy 2015, 137, 545–553. [Google Scholar] [CrossRef]
- Zou, J.; Peng, C.; Shi, J.; Xin, X.; Zhang, Z. State-of-charge optimising control approach of battery energy storage system for wind farm. IET Renew. Power Gener. 2015, 9, 647–652. [Google Scholar] [CrossRef] [Green Version]
- Lin, F.; Chiang, H.; Chang, J.; Chang, Y. Intelligent wind power smoothing control with BESS. IET Renew. Power Gener. 2017, 11, 398–407. [Google Scholar] [CrossRef]
- Lamsal, D.; Sreeram, V.; Mishra, Y.; Kumar, D. Achieving a minimum power fluctuation rate in wind and photovoltaic output power using discrete Kalman filter based on weighted average approach. IET Renew. Power Gener. 2018, 12, 633–638. [Google Scholar] [CrossRef]
- Koiwa, K.; Ishii, T.; Liu, K.; Zanma, T.; Tamura, J. On the Reduction of the Rated Power of Energy Storage System in Wind Farms. IEEE Trans. Power Syst. 2020, 35, 2586–2596. [Google Scholar] [CrossRef]
- Senjyu, T.; Sakamoto, R.; Urasaki, N.; Funabashi, T.; Fujita, H.; Sekine, H. Output power leveling of wind turbine Generator for all operating regions by pitch angle control. IEEE Trans. Energy Convers. 2006, 21, 467–475. [Google Scholar] [CrossRef]
- Chowdhury, M.A.; Hosseinzadeh, N.; Shen, W. Fuzzy logic systems for pitch angle controller for smoothing wind power fluctuations during below rated wind incidents. In Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011; pp. 1–7. [Google Scholar]
- Chowdhury, M.; Hosseinzadeh, N.; Shen, W. Smoothing wind power fluctuations by fuzzy logic pitch angle controller. Renew. Energy 2012, 38, 224–233. [Google Scholar] [CrossRef]
- Sato, D.; Saitoh, H. Smoothing Control of Wind Farm Output by Using Kinetic Energy of Variable Speed Wind Power Generators. IEEJ Trans. Power Energy 2009, 129, 580–590. [Google Scholar] [CrossRef]
- Varzaneh, S.G.; Gharehpetian, G.; Abedi, M. Output power smoothing of variable speed wind farms using rotor-inertia. Electr. Power Syst. Res. 2014, 116, 208–217. [Google Scholar] [CrossRef]
- Howlader, A.M.; Urasaki, N.; Pratap, A.; Senjyu, T.; Saber, A.Y. A fuzzy control strategy for power smoothing and grid dynamic response enrichment of a grid-connected wind energy conversion system. Wind Energy 2014, 17, 1347–1363. [Google Scholar] [CrossRef]
- Zhao, X.; Yan, Z.; Zhang, X. A Wind-Wave Farm System With Self-Energy Storage and Smoothed Power Output. IEEE Access 2016, 4, 8634–8642. [Google Scholar] [CrossRef]
- Rosyadi, M.; Umemura, A.; Takahashi, R.; Tamura, J.; Uchiyama, N.; Ide, K. Simplified Model of Variable Speed Wind Turbine Generator for Dynamic Simulation Analysis. IEEJ Trans. Power Energy 2015, 135, 538–549. [Google Scholar] [CrossRef]
- Hazari, M.R.; Mannan, M.A.; Muyeen, S.M.; Umemura, A.; Takahashi, R.; Tamura, J. Stability Augmentation of a Grid-Connected Wind Farm by Fuzzy-Logic-Controlled DFIG-Based Wind Turbines. Appl. Sci. 2018, 8, 20. [Google Scholar] [CrossRef] [Green Version]
- Rosyadi, M.; Muyeen, S.M.; Takahashi, R.; Tamura, J. New controller design for PMSG based wind generator with LCL-filter considered. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 12 November 2012; pp. 2112–2118. [Google Scholar]
- Koiwa, K.; Sato, H.; Umemura, A.; Takahashi, R.; Tamura, J. Frequency Control of Power System by Output Frequency Band Control of Wind Farm by Variable Speed Wind Generators. IEEJ Trans. Power Energy 2015, 135, 351–361. [Google Scholar] [CrossRef]
- Tamura, S. Economic Analysis of Hybrid Battery Energy Storage Systems Applied to Frequency Control in Power System. Electr. Eng. Jpn. 2016, 195, 24–31. [Google Scholar] [CrossRef]
- Investigating R&D Committee on Application and Control Technology of Battery Energy Storage for Power Systems. In Application and Control Technology of Battery Energy Storage for Power Systems; The Institute of Electrical Engineers of Japan: Tokyo, Japan, 2017.
- Kintner-Meyer, M.C.W.; Balducci, P.J.; Jin, C.; Nguyen, T.B.; Elizondo, M.A.; Viswanathan, V.V.; Guo, X.; Tuffner, F.K. Energy Storage for Power Systems Applications: A Regional Assessment for the Northwest Power Pool (NWPP); Pacific Northwest National Laboratory: Richland, WA, USA, 2010.
- Gee, A.M.; Robinson, F.V.P.; Dunn, R.W. Analysis of Battery Lifetime Extension in a Small-Scale Wind-Energy System Using Supercapacitors. IEEE Trans. Energy Convers. 2013, 28, 24–33. [Google Scholar] [CrossRef]
- Alam, M.J.E.; Saha, T.K. Cycle-life degradation assessment of Battery Energy Storage Systems caused by solar PV variability. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Agency for Natural Resources and Energy. 2019. Available online: https://www.meti.go.jp/shingikai/santeii/pdf/049_01_00.pdf (accessed on 24 September 2020).
- International Renewable Energy Agency. Electricity Storage and Renewables for Island Power: A Guide for Decision Makers. 2012. Available online: https://irena.org/publications/ (accessed on 24 September 2020).
- Mongird, K.; Fotedar, V.; Viswanathan, V.; Koritarov, V.; Balducci, P.; Hadjerioua, B.; Alam, J. Energy Storage Technology and Cost Characterization Report; U.S. Department of Energy’s Water Power Technologies Office by Pacific Northwest National Laboratory: Washington, DC, USA, 2019.


| Method | Cost | Efficiency | Mechanical Stress | Smoothing Effect |
|---|---|---|---|---|
| ESS | Expensive | Good | – | Excellent |
| Pitch angle control | Inexpensive | Poor | Poor | Good |
| Kinetic energy control | Inexpensive | Good | Excellent | Poor |
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | Scenario 5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Avg. | SD | Avg. | SD | Avg. | SD | Avg. | SD | Avg. | SD | |
| 7.30 | 1.36 | 8.45 | 1.61 | 8.34 | 1.72 | 10.4 | 2.15 | 10.4 | 2.15 | |
| 9.59 | 1.81 | 8.93 | 1.78 | 8.66 | 1.85 | 8.09 | 1.79 | 8.09 | 1.79 | |
| 8.36 | 1.84 | 8.90 | 1.37 | 6.51 | 0.95 | 8.51 | 1.18 | 8.51 | 1.18 | |
| 10.13 | 2.03 | 7.62 | 1.68 | 11.12 | 1.83 | 10.40 | 1.55 | 10.39 | 1.55 | |
| 10.34 | 1.60 | 10.11 | 1.60 | 9.96 | 1.59 | 4.82 | 0.77 | 4.82 | 0.77 | |
| 5.26 | 1.99 | 5.16 | 2.19 | 4.56 | 1.93 | 14.55 | 1.92 | 14.55 | 1.93 | |
| 8.02 | 1.79 | 10.96 | 1.74 | 8.96 | 2.27 | 9.82 | 1.70 | 9.82 | 1.70 | |
| 6.46 | 2.32 | 9.60 | 2.08 | 6.35 | 2.35 | 8.68 | 2.00 | 8.68 | 2.00 | |
| 9.33 | 2.02 | 10.64 | 1.83 | 9.85 | 2.53 | 7.02 | 1.44 | 7.02 | 1.44 | |
| 7.00 | 2.56 | 4.87 | 2.12 | 6.35 | 2.33 | 7.15 | 1.44 | 7.15 | 1.44 | |
| 11.99 | 1.15 | 15.47 | 1.17 | 11.5 | 0.99 | 11.97 | 2.61 | 11.97 | 2.61 | |
| 13.68 | 1.92 | 13.54 | 2.16 | 14.55 | 1.98 | 9.12 | 1.48 | 9.12 | 1.48 | |
| 15.01 | 1.09 | 15.39 | 2.49 | 14.68 | 1.54 | 12.10 | 2.16 | 12.10 | 2.16 | |
| 15.45 | 1.72 | 11.77 | 1.78 | 15.6 | 1.84 | 7.05 | 1.50 | 7.05 | 1.50 | |
| 19.48 | 1.38 | 18.66 | 1.34 | 19.45 | 1.20 | 10.42 | 1.52 | 10.42 | 1.52 | |
| Rated power of WG [MW] | 5 |
| Rated wind speed [m/s] | 12 |
| Inertia constant H of WG [s] | 5.05 |
| Number of WG | 15 |
| Lifespan of WG [y] | 20 |
| Wind power price [JPY/kWh] | 8 |
| [100 Million JPY] | 150 |
| Li-Ion Battery | NaS Battery | |
|---|---|---|
| C-rate | 3 | 0.13 |
| Price [JPY/kWh] | 200,000 | 25,000 |
| Efficiency [%] | 85 | 85 |
| [y] | 10 | 15 |
| PCS price [JPY/kW] | 28,800 | 28,800 |
| Con. (MPPT) | Pro. (MA) | Pro. (Opt.) | |
|---|---|---|---|
| Sampling period [s] | 0.5 | 0.5 | 0.5 |
| Number of Steps for MA | – | 1200 | 1200 |
| – | 120 | – | |
| – | 5 | – | |
| 0.65 | 0.5 | 0.5 | |
| A | 1 | 1 | 1 |
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | Scenario 5 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Conv. | Pro. (MA) | Pro. (Opt.) | Conv. | Pro. (MA) | Pro. (Opt.) | Conv. | Pro. (MA) | Pro. (Opt.) | Conv. | Pro. (MA) | Pro. (Opt.) | Conv. | Pro. (MA) | Pro. (Opt.) | |
| Maximum 1-Min fluctuation of [%] | 22.1 | 17.0 | 17.2 | 21.8 | 15.5 | 15.5 | 18.6 | 12.4 | 13.0 | 19.9 | 14.3 | 14.4 | 17.9 | 12.8 | 14.2 |
| Average of 1-Min fluctuation of [%] | 9.33 | 6.42 | 7.37 | 9.31 | 6.34 | 7.35 | 9.60 | 6.61 | 7.66 | 9.96 | 6.96 | 7.78 | 9.88 | 6.78 | 7.70 |
| SD of [p.u.] | 0.0507 | 0.0411 | 0.0445 | 0.0456 | 0.0345 | 0.0387 | 0.0421 | 0.0306 | 0.0353 | 0.0496 | 0.0400 | 0.0424 | 0.0523 | 0.0433 | 0.0461 |
| Maximum 1-Min fluctuation of [%] | 9.86 | 9.65 | 9.97 | 8.24 | 8.21 | 8.35 | 7.28 | 6.72 | 7.25 | 8.50 | 9.10 | 9.19 | 7.22 | 7.20 | 7.68 |
| Average of 1-Min fluctuation of [%] | 3.39 | 3.27 | 3.76 | 3.32 | 3.21 | 3.73 | 3.47 | 3.37 | 3.90 | 3.56 | 3.51 | 3.93 | 3.55 | 3.42 | 3.90 |
| SD of [p.u.] | 0.0373 | 0.0344 | 0.0362 | 0.0257 | 0.0230 | 0.0252 | 0.0198 | 0.0180 | 0.0204 | 0.0307 | 0.0292 | 0.0303 | 0.0367 | 0.0351 | 0.0361 |
| Maximum power of ESS [kW] | 7126.8 | 3592.0 | 3790.7 | 6713.4 | 3577.5 | 3707.3 | 6472.3 | 3294.9 | 3334.7 | 7844.9 | 4283.2 | 4310.5 | 7400.3 | 3902.8 | 3668.0 |
| [kWh/h] | – | 367.1 | 192.0 | – | 349.6 | 162.9 | – | 353.2 | 166.8 | – | 494.7 | 345.3 | – | 505.9 | 292.9 |
| [kWh/h] | 272.1 | 154.0 | 179.8 | 265.1 | 150.6 | 178.3 | 264.3 | 147.3 | 178.4 | 279.65 | 167.9 | 188.6 | 287.9 | 167.1 | 191.9 |
| Integral of WF output [MWh/h] | 41.86 | 41.49 | 41.67 | 44.53 | 44.18 | 44.36 | 41.42 | 41.07 | 41.25 | 37.48 | 37.00 | 37.14 | 42.75 | 42.25 | 42.46 |
| Battery life (Li-ion) [y] | 5.83 | 5.48 | 4.54 | 6.43 | 7.16 | 5.22 | 5.45 | 5.40 | 4.68 | 5.16 | 4.54 | 4.02 | 5.49 | 5.48 | 4.18 |
| Battery life (NaS) [y] | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 |
| Conv. | Pro. (MA) | Pro. (Opt.) | |
|---|---|---|---|
| Maximum 1-Min fluctuation of [%] | 20.1 | 14.4 () | 14.9 () |
| Average of 1-Min fluctuation of [%] | 9.62 | 6.62 () | 7.57 () |
| SD of [p.u.] | 0.0481 | 0.0379 () | 0.0414 () |
| Maximum 1-Min fluctuation of [%] | 8.22 | 8.18 () | 8.49 () |
| Average of 1-Min fluctuation of [%] | 3.46 | 3.36 () | 3.84 () |
| SD of [p.u.] | 0.0300 | 0.0279 () | 0.0296 () |
| [kWh/h] | – | 414.1 | 232.0 |
| [kWh/h] | 273.8 | 157.4 () | 183.4 () |
| Integral of WF output [MWh/h] | 41.61 | 41.20 (%) | 41.38 () |
| Battery life (Li-ion) [y] | 5.67 | 5.61 () | 4.53 () |
| Battery life (NaS) [y] | 15 | 15 | 15 |
| Cost (Li-ion) [100 million JPY] | 22.38 | 18.40 () | 18.62 () |
| Cost (NaS) [100 million JPY] | 24.0 | 19.0 () | 16.9 () |
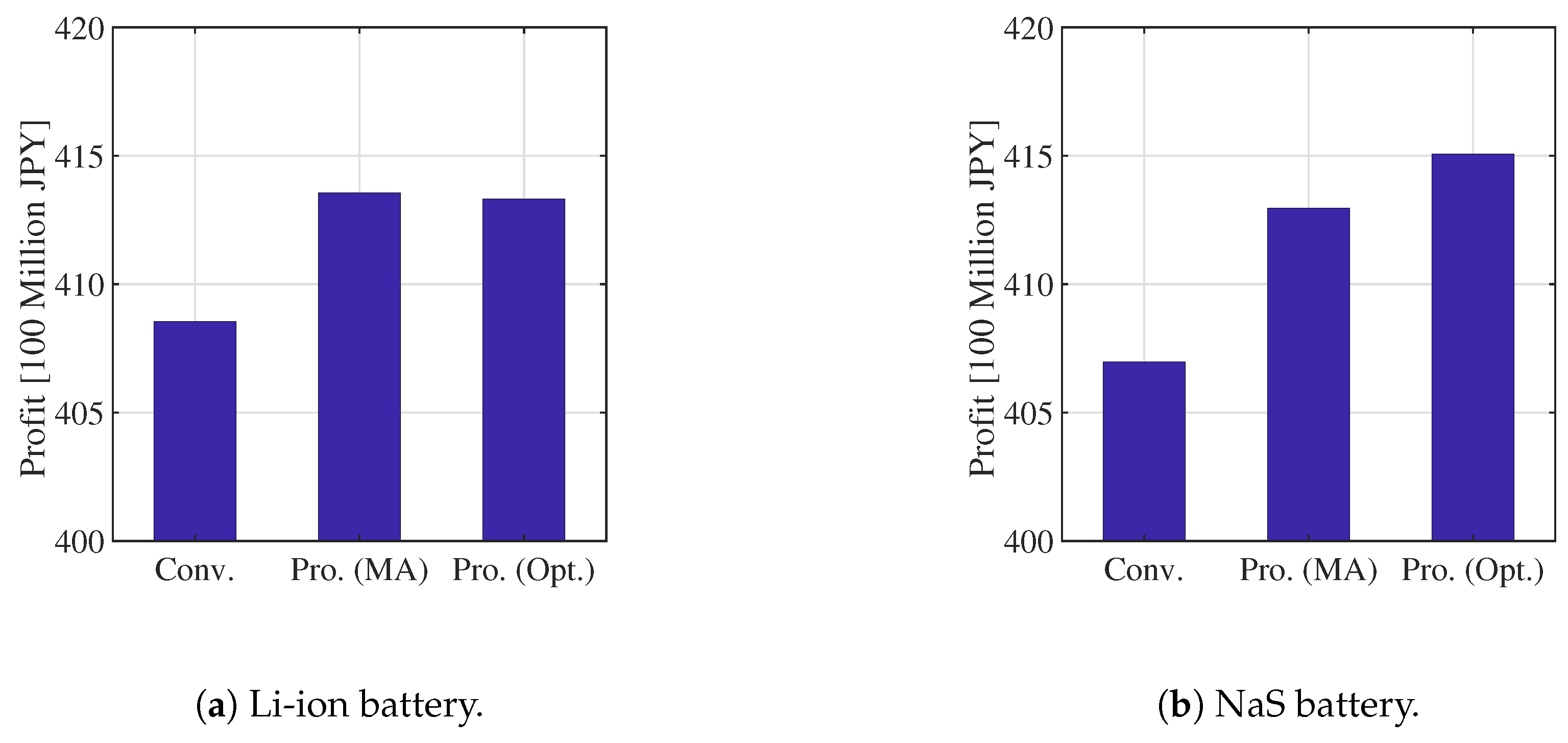
| Profit (Li-ion) [100 million JPY] | 410.81 | 414.79 () | 414.57 () |
| Profit (NaS) [100 million JPY] | 409.24 | 414.20 () | 416.32 () |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koiwa, K.; Tawara, T.; Watanabe, M.; Liu, K.-Z.; Zanma, T.; Tamura, J. Novel Cost Reduction Method for Wind Farms Associated with Energy Storage Systems by Optimal Kinetic Energy Control. Appl. Sci. 2020, 10, 7223. https://doi.org/10.3390/app10207223
Koiwa K, Tawara T, Watanabe M, Liu K-Z, Zanma T, Tamura J. Novel Cost Reduction Method for Wind Farms Associated with Energy Storage Systems by Optimal Kinetic Energy Control. Applied Sciences. 2020; 10(20):7223. https://doi.org/10.3390/app10207223
Chicago/Turabian StyleKoiwa, Kenta, Takuro Tawara, Mizuki Watanabe, Kang-Zhi Liu, Tadanao Zanma, and Junji Tamura. 2020. "Novel Cost Reduction Method for Wind Farms Associated with Energy Storage Systems by Optimal Kinetic Energy Control" Applied Sciences 10, no. 20: 7223. https://doi.org/10.3390/app10207223






