Some Key Aspects in the Mechanics of Stress Transfer Between SRG and Masonry
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Specimen Preparation and Application of SRG Reinforcement
2.3. Single-Lap Direct Shear Test
3. Discussion of Results
3.1. Failure Modes
- Interlaminar failure with debonding at the interface between the internal layer of mortar and steel fibers (MF);
- Rupture of steel fibers (FR);
- Detachment of the SRG strip from the substrate with a thin layer of substrate attached to it in a limited portion (SF).
3.2. Load Responses
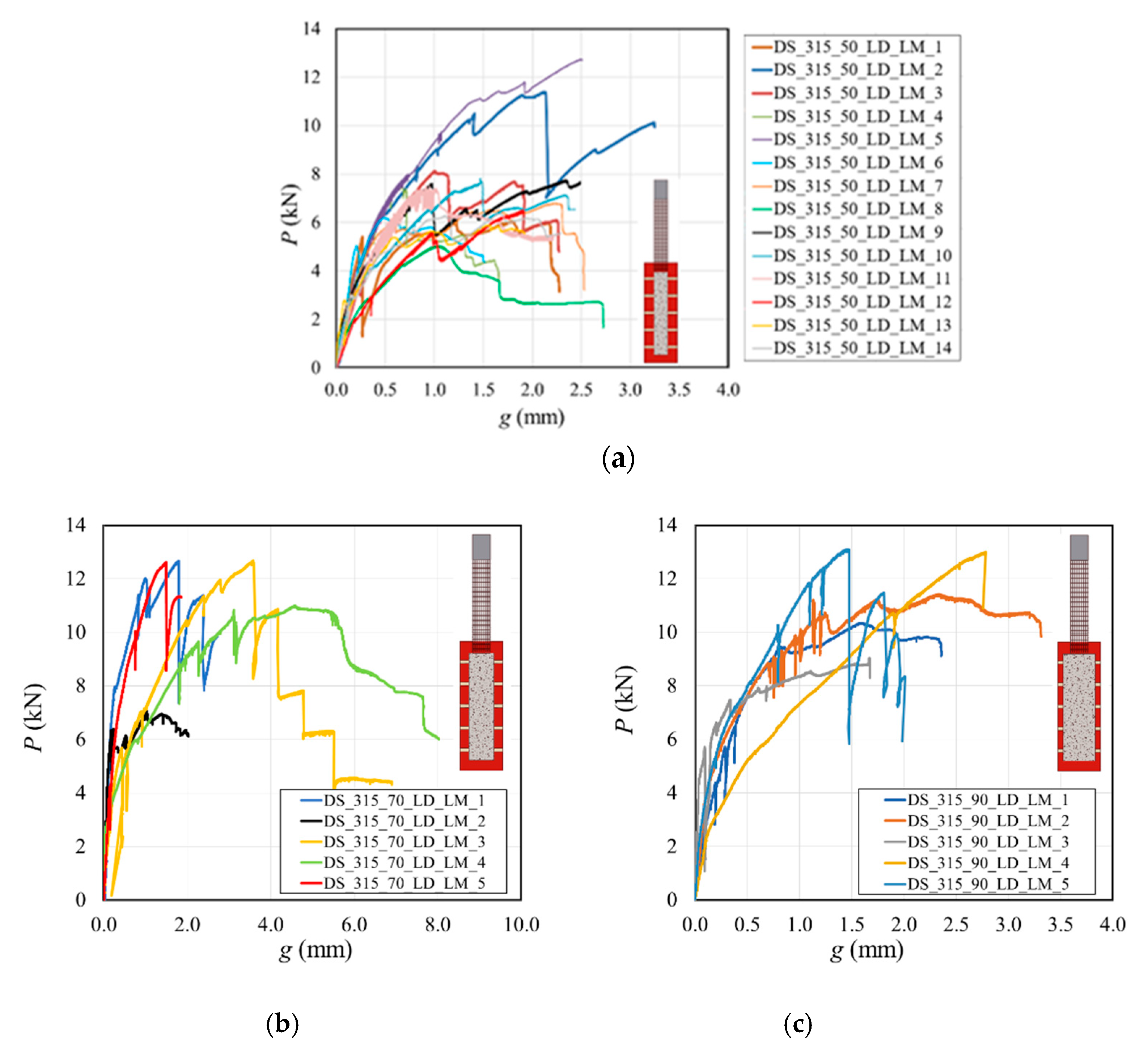
3.2.1. Influence of SRG Matrix Width
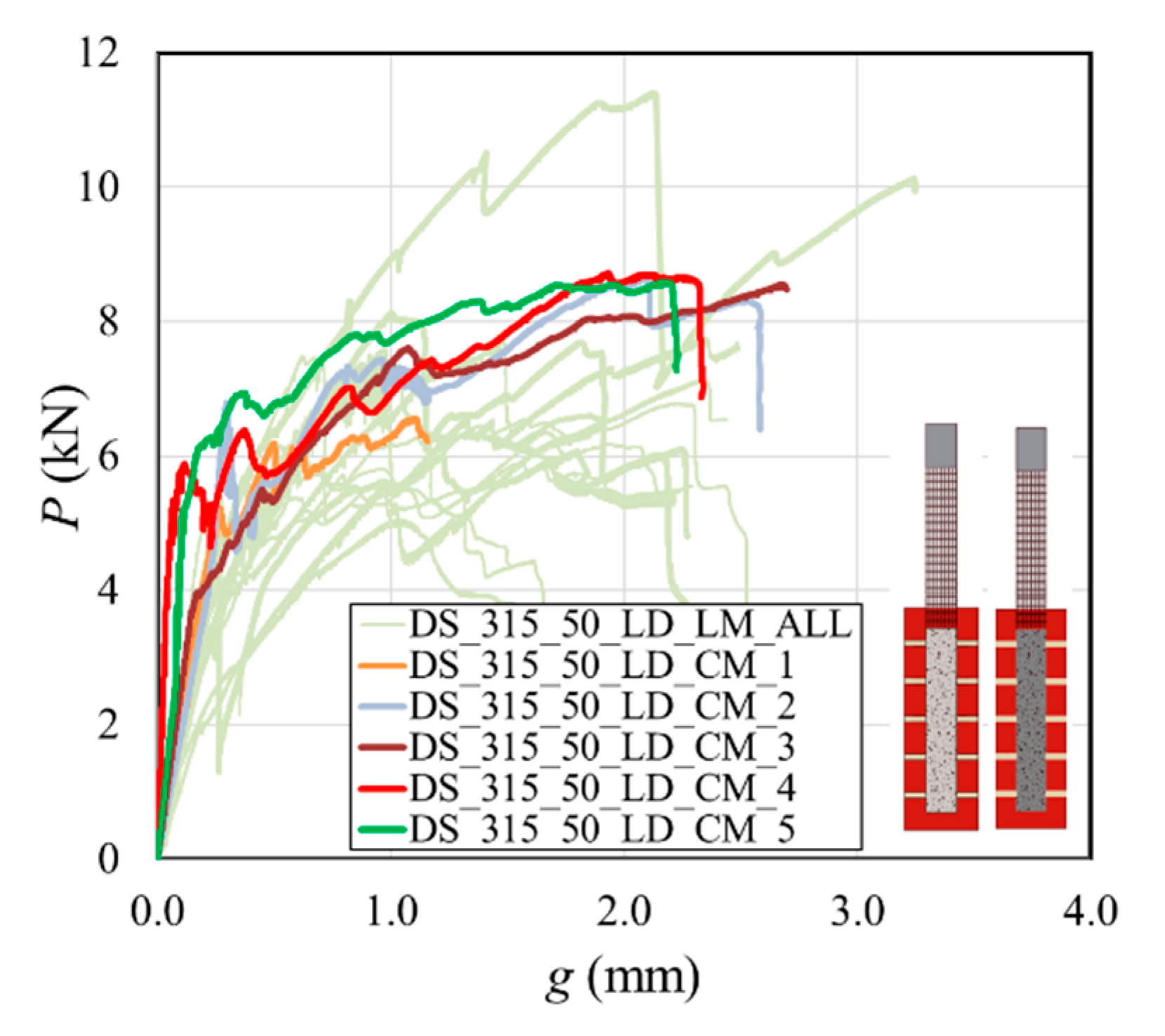
3.2.2. Influence of the Type of Matrix
3.2.3. Influence of the Test Rate
3.2.4. Influence of the Substrate
4. Conclusions
- Increasing the width of the SRG matrix (without increasing the width of the fibers), from 50 mm to 70 and 90 mm, the average load-carrying capacity Pcrit increased by 52% and 69%, respectively, due to a higher amount of energy required for the crack to initiate and propagate.
- Results of masonry blocks strengthened with cement-based mortar SRG were less scattered with respect to blocks strengthened with lime-based mortar SRG. Compared to specimens with the same matrix width but strengthened with lime-based matrix SRG, the average load-carrying capacity (Pcrit) and peak load (P*) of specimens strengthened with cement-based matrix SRG increased by 33% and 20%, respectively.
- The average peak load of SRG-masonry joints tested at a rate ten times the standard rate increased by 37%. Therefore, it appears that for this type of composite a rate effect might be present.
- Comparing masonry and concrete substrate strengthened with the same SRG system, the mode of failure changed: failure of SRG-concrete joints was due to rupture of steel fibers, while SRG-masonry joints exhibited predominantly interlaminar failure. Therefore, for concrete specimens, it was not possible to evaluate Pcrit. When the averages of peak load P* were compared, the highest average value was observed in concrete specimens since rupture of the fibers occurred.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bakis, C.E.; Bank, L.; Brown, V.L.; Cosenza, E.; Davalos, J.F.; Lesko, J.J.; Machida, A.; Rizkalla, S.H.; Triantafillou, T.C. Fiber-Reinforced Polymer Composites for Construction—State-of-the-Art Review. J. Compos. Constr. 2002, 6, 73–87. [Google Scholar] [CrossRef]
- Carrara, P.; Ferretti, D.; Freddi, F. Debonding behavior of ancient masonry elements strengthened with CFRP sheets. Compos. Part B Eng. 2013, 45, 800–810. [Google Scholar] [CrossRef]
- Bilotta, A.; Ceroni, F.; Nigro, E.; Pecce, M. Efficiency of CFRP NSM strips and EBR plates for flexural strengthening of RC beams and loading pattern influence. Compos. Struct. 2015, 124, 163–175. [Google Scholar] [CrossRef]
- American Concrete Institute. Guide to Design and Construction of Externally Bonded Fabric-Reinforced Cementitious Matrix (FRCM) Systems for Repair and Strengthening Concrete and Masonry Structures; ACI 549.4R-13; ACI: Farmington Hills, MI, USA, 2013. [Google Scholar]
- Kouris, L.A.S.; Triantafillou, T.C. State-of-the-art on strengthening of masonry structures with textile reinforced mortar (TRM). Constr. Build. Mater. 2018, 188, 1221–1233. [Google Scholar] [CrossRef]
- Wiberg, A. Strengthening of Concrete Beams Using Cementitious Carbon Fibre Composites. Ph.D. Thesis, Royal Institute of Technology, Stockholm, Sweden, 2003. [Google Scholar]
- Napoli, A.; Realfonzo, R. Reinforced concrete beams strengthened with SRP/SRG systems: Experimental investigation. Constr. Build. Mater. 2015, 93, 654–677. [Google Scholar] [CrossRef]
- Bisby, L.A.; Stratford, T.J.; Roy, E.C.; Ward, M. Fibre Reinforced Cementitious Matrix Systems for Fire-Safe Flexural Strengthening of Concrete: Pilot Testing at Ambient Temperatures. In Advanced Composites in Construction (ACIC) 2009 Conference Proceedings; NetComposites Ltd.: Chesterfield, UK, 2009; pp. 449–460. [Google Scholar]
- Ombres, L.; Verre, S. Shear performance of FRCM strengthened RC beams. In Proceedings of the ACI SP-324, 2017 ACI Spring Convention, Detroit, Detroit, MI, USA, 26–30 March 2017; Gianmarco, d.F., Lesley, H.S., Antonio, N., Eds.; 2017; p. 324. [Google Scholar]
- D’Antino, T.; Focacci, F.; Sneed, L.H.; Pellegrino, C. Shear strength model for RC beams with U-wrapped FRCM composites. J. Compos. Constr. 2020, 24, 04019057. [Google Scholar] [CrossRef]
- Younis, A.; Ebead, U.; Shrestha, K.C. Different FRCM systems for shear-strengthening of reinforced concrete beams. Constr. Build. Mater. 2017, 153, 514–526. [Google Scholar] [CrossRef]
- Trapko, T. Fibre Reinforced Cementitious Matrix confined concrete elements. Mater. Des. 2013, 44, 382–391. [Google Scholar] [CrossRef]
- Donnini, J.; Spagnuolo, S.; Corinaldesi, V. A comparison between the use of FRP, FRCM and HPM for concrete confinement. Compos. Part B 2019, 160, 586–594. [Google Scholar] [CrossRef]
- Cascardi, A.; Aiello, M.A.; Triantafillou, T. Analysis-oriented model for concrete and masonry confined with fiber reinforced mortar. Mater. Struct. 2017, 50, 202. [Google Scholar] [CrossRef]
- Babaeidarabad, S.; De Caso, F.; Nanni, A. URM Walls Strengthened with Fabric-Reinforced Cementitious Matrix Composite Subjected to Diagonal Compression. J. Compos. Constr. 2014, 18, 04013045. [Google Scholar] [CrossRef]
- Dong, Z.; Deng, M.; Zhang, Y.; Zhang, C.; Ma, P. Out-of-plane strengthening of unreinforced masonry walls using textile reinforced mortar added short polyvinyl alcohol fibers. Constr. Build. Mater. 2020, 260, 119910. [Google Scholar] [CrossRef]
- Borri, A.; Castori, G.; Corradi, M. Shear behavior of masonry panels strengthened by high strength steel cords. Constr. Build. Mater. 2011, 25, 494–503. [Google Scholar] [CrossRef]
- Cascardi, A.; Micelli, F.; Aiello, M.A. FRCM-confined masonry columns: Experimental investigation on the effect of the inorganic matrix properties. Constr. Build. Mater. 2018, 186, 811–825. [Google Scholar] [CrossRef]
- Sneed, L.H.; Baietti, G.; Fraioli, G.; Carloni, C. Compressive Behavior of Brick Masonry Columns Confined with Steel-Reinforced Grout Jackets. J. Compos. Constr. 2019, 23, 04019037. [Google Scholar] [CrossRef]
- Krevaikas, T.D. Experimental study on carbon fiber textile reinforced mortar system as a means for confinement of masonry columns. Constr. Build. Mater. 2019, 208, 723–733. [Google Scholar] [CrossRef]
- Alecci, V.; Focacci, F.; Rovero, L.; Stipo, G.; De Stefano, M. Intrados strengthening of brick masonry arches with different FRCM composites: Experimental and analytical investigations. Compos. Struct. 2017, 176, 898–909. [Google Scholar] [CrossRef]
- Ramaglia, G.; Lignola, G.P.; Balsamo, A.; Prota, A.; Manfredi, G. Seismic Strengthening of Masonry Vaults with Abutments Using Textile-Reinforced Mortar. J. Compos. Constr. 2017, 21, 04016079. [Google Scholar] [CrossRef]
- National Research Council. Guide for the Design and Construction of Externally Bonded Fibre Reinforced Inorganic Matrix Systems for Strengthening Existing Structures; CNR-DT 215/2018; CNR: Rome, Italy, 2018. [Google Scholar]
- Calabrese, A.S.; Colombi, P.; D’Antino, T. Analytical solution of the bond behavior of FRCM composites using a rigid-softening cohesive material law. Compos. Part B 2019, 174, 107051. [Google Scholar] [CrossRef]
- Lignola, G.P.; Caggegi, C.; Ceroni, F.; De Santis, S.; Krajewski, P.; Lourenço, P.B.; Morganti, M.; Papanicolaou, C.; Pellegrino, C.; Prota, A.; et al. Performance assessment of basalt FRCM for retrofit applications on masonry. Compos. Part B 2017, 128, 1–18. [Google Scholar] [CrossRef]
- D’Ambrisi, A.; Feo, L.; Focacci, F. Experimental and analytical investigation on bond between Carbon-FRCM materials and masonry. Compos. Part B 2013, 46, 15–20. [Google Scholar] [CrossRef]
- Askouni, P.D.; Papanicolaou, C.G. Experimental investigation of bond between glass textile reinforced mortar overlays and masonry: The effect of bond length. Mater. Struct. 2017, 50, 164. [Google Scholar] [CrossRef]
- Sneed, L.H.; Verre, S.; Carloni, C.; Ombres, L. Flexural behavior of RC beams strengthened with steel-FRCM composite. Eng. Struct. 2016, 127, 686–699. [Google Scholar] [CrossRef]
- De Santis, S.; de Felice, G. Steel reinforced grout systems for the strengthening of masonry structures. Compos. Struct. 2015, 134, 533–548. [Google Scholar] [CrossRef]
- D’Ambrisi, A.; Focacci, F. Flexural Strengthening of RC Beams with Cement-Based Composites. J. Compos. Constr. 2011, 15, 707–720. [Google Scholar] [CrossRef]
- Babaeidarabad, S.; Loreto, G.; Nanni, A. Flexural Strengthening of RC Beams with an Externally Bonded Fabric-Reinforced Cementitious Matrix. J. Compos. Constr. 2014, 18, 04014009. [Google Scholar] [CrossRef]
- Calabrese, A.S.; D’Antino, T.; Colombi, P.; Poggi, C. Study of the influence of interface normal stresses on the bond behavior of FRCM composites using direct shear and modified beam tests. Constr. Build. Mater. 2020, 262, 120029. [Google Scholar] [CrossRef]
- Sneed, L.H.; D’Antino, T.; Carloni, C.; Pellegrino, C. A comparison of the bond behavior of PBO-FRCM composites determined by double-lap and single-lap shear tests. Cem. Concr. Compos. 2015, 64, 37–48. [Google Scholar] [CrossRef]
- European Committee for Standardization. Methods of Test for Masonry Units. Part 1: Determination of Compressive Strength; EN 772-1:2011; CEN: Brussels, Belgium, 2011; ISBN 978-0-580-84584-0. [Google Scholar]
- Santandrea, M.; Focacci, F.; Mazzotti, C.; Ubertini, F.; Carloni, C. Determination of the interfacial cohesive material law for SRG composites bonded to a masonry substrate. Eng. Fail. Anal. 2020, 111, 104322. [Google Scholar] [CrossRef]
- Elices, M.; Guinea, G.V.; Planas, J. Measurement of the fracture energy using three-point bend tests: Part 3-influence of cutting theP-δ tail. Mater. Struct. 1992, 25, 327–334. [Google Scholar] [CrossRef]
- Gerstle, W. Progress in Developing a Standard Fracture Toughness Test for Concrete. In Proceedings of the Structures Congress, Orlando, FL, USA, 12–15 May 2010; pp. 1915–1926. [Google Scholar] [CrossRef]
- Hoover, C.G.; Bažant, Z.P. Comprehensive concrete fracture tests: Size effects of Types 1 & 2, crack length effect and postpeak. Eng. Fract. Mech. 2013, 110, 281–289. [Google Scholar] [CrossRef]
- D’Antino, T.; Santandrea, M.; Carloni, C. Advances in Knowledge of the Fracture Properties of Cohesive Materials: Fired-Clay and Tuff Bricks. J. Eng. Mech. 2020, 146, 04020079. [Google Scholar] [CrossRef]
- German Institute for Standardisation. Testing of Mortars Containing Mineral Binders—Part 9: Hardened Mortars—Determination of the Mortar Compressive Strength in the Bed Joint; DIN 18555-9; German Institute for Standardisation: Berlin, Germany, 1999. [Google Scholar]
- Kerakoll, S.p.a. GeoSteel G600. Available online: https://products.kerakoll.com/it-IT/p/geosteel-g600 (accessed on 29 July 2020).
- European Committee for Standardization. Methods of Test for Mortar for Masonry. Determination of Flexural and Compressive Strength of Hardened Mortar; EN 1015-11:1999; CEN: Brussels, Belgium, 1999; ISBN 058035469. [Google Scholar]
- Santandrea, M. Bond Behavior between Fiber Reinforced Composites and Quasi-Brittle Material Interfaces. Ph.D. Thesis, University of Bologna, Bologna, Italy, 2018. [Google Scholar]
- Subramaniam, K.V.; Carloni, C.; Nobile, L. Width effect in the interface fracture during shear debonding of FRP sheets from concrete. Eng. Fract. Mech. 2007, 74, 578–594. [Google Scholar] [CrossRef]
- D’Antino, T.; Carloni, C.; Sneed, L.H.; Pellegrino, C. Matrix–fiber bond behavior in PBO FRCM composites: A fracture mechanics approach. Eng. Fract. Mech. 2014, 117, 94–111. [Google Scholar] [CrossRef]
- Carloni, C.; Verre, S.; Sneed, L.H.; Ombres, L. Loading rate effect on the debonding phenomenon in fiber reinforced cementitious matrix-concrete joints. Compos. Part B 2017, 108, 301–314. [Google Scholar] [CrossRef]
- Carloni, C.; Santandrea, M.; Imohamed, I.A.O. Determination of the interfacial properties of SRP strips bonded to concrete and comparison between single-lap and notched beam tests. Eng. Fract. Mech. 2017, 186, 80–104. [Google Scholar] [CrossRef]







| Property | Value from the Manufacturer |
|---|---|
| Area of chord (mm2) | 0.538 |
| Number of cords/cm | 1.57 |
| Tensile strength (MPa) | >3000 |
| Elastic modulus (GPa) | >190 |
| Ultimate tensile strain (%) | >1.5 |
| Equivalent thickness (mm) | 0.084 |
| Material | Mechanical Property Evaluated | Results |
|---|---|---|
| Brick | Compressive strength (MPa) | 20.3 |
| Tensile strength (MPa) | 3.16 | |
| Elastic modulus (GPa) | 7.3 | |
| Fracture energy (N/m) | 29.5 | |
| LM matrix | Flexural strength (MPa) | 5 |
| Compressive strength (MPa) | 12.3 | |
| Fracture energy (N/m) | 30.3 | |
| CM matrix | Flexural strength (MPa) | 7.6 |
| Compressive strength (MPa) | 46.4 | |
| Fracture energy (N/m) | 101 |
| Specimen | g1 | g2 | Pcrit (kN) | P* (kN) | Failure Mode | ||
|---|---|---|---|---|---|---|---|
| DS_315_50_LD_LM_1 | 1.33 | 2.18 | 5.8 | 5.8 (0.178) | 6.1 | 7.6 (0.278) | MF |
| DS_315_50_LD_LM_2 | \ | \ | \ | 11.4 | MF | ||
| DS_315_50_LD_LM_3 | 1.15 | 2.26 | 6.7 | 8.1 | MF | ||
| DS_315_50_LD_LM_4 | 0.73 | 1.30 | 5.3 | 7.5 | MF | ||
| DS_315_50_LD_LM_5 | \ | \ | \ | 12.7 | FR | ||
| DS_315_50_LD_LM_6 | \ | \ | \ | 6.2 | MF | ||
| DS_315_50_LD_LM_7 | 1.00 | 2.30 | 6.3 | 6.8 | MF | ||
| DS_315_50_LD_LM_8 | 1.03 | 2.70 | 3.3 | 5.1 | MF | ||
| DS_315_50_LD_LM_9 | 1.03 | 2.49 | 6.9 | 7.8 | MF | ||
| DS_315_50_LD_LM_10 | 1.54 | 2.35 | 6.7 | 7.8 | MF | ||
| DS_315_50_LD_LM_11 | 1.12 | 2.22 | 5.8 | 7.5 | MF | ||
| DS_315_50_LD_LM_12 | \ | \ | \ | 6.5 | MF | ||
| DS_315_50_LD_LM_13 | 0.58 | 1.92 | 5.5 | 5.9 | MF | ||
| DS_315_50_LD_LM_14 | 1.18 | 2.29 | 5.8 | 6.4 | MF | ||
| DS_315_70_LD_LM_1 | \ | \ | \ | 8.8 (0.321) | 12.7 | 11.2 (0.219) | FR |
| DS_315_70_LD_LM_2 | 1.08 | 1.58 | 6.8 | 7.0 | MF | ||
| DS_315_70_LD_LM_3 | \ | \ | \ | 12.7 | FR | ||
| DS_315_70_LD_LM_4 | 3.68 | 5.52 | 10.8 | 11.0 | MF * | ||
| DS_315_70_LD_LM_5 | \ | \ | \ | 12.6 | FR | ||
| DS_315_90_LD_LM_1 | 1.17 | 2.22 | 9.9 | 9.8 (0.118) | 10.3 | 11.4 (0.155) | MF * |
| DS_315_90_LD_LM_2 | 1.45 | 2.13 | 10.9 | 11.4 | MF * | ||
| DS_315_90_LD_LM_3 | 1.11 | 1.53 | 8.6 | 9.0 | MF * | ||
| DS_315_90_LD_LM_4 | \ | \ | \ | 13.0 | FR | ||
| DS_315_90_LD_LM_5 | \ | \ | \ | 13.1 | FR | ||
| DS_315_50_LD_LM_10TR_1 | \ | \ | \ | \ | 8.46 | 10.4 (0.192) | MF |
| DS_315_50_LD_LM_10TR_2 | \ | \ | \ | 10.31 | MF | ||
| DS_315_50_LD_LM_10TR_3 | \ | \ | \ | 12.46 | MF | ||
| DS_315_50_LD_CM_1 | 0.65 | 1.10 | 6.2 | 7.7 (0.109) | 10.9 | 9.1 (0.111) | SF |
| DS_315_50_LD_CM_2 | 0.98 | 2.55 | 7.9 | 8.7 | MF | ||
| DS_315_50_LD_CM_3 | 1.20 | 2.60 | 7.9 | 8.6 | MF | ||
| DS_315_50_LD_CM_4 | 0.90 | 2.30 | 8.0 | 8.7 | MF | ||
| DS_315_50_LD_CM_5 | 0.98 | 2.20 | 8.3 | 8.6 | MF | ||
| Nomenclature | 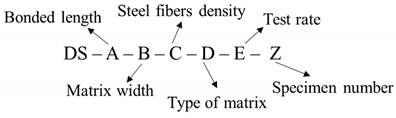 | ||||||
| Specimen | g1 | g2 | Pcrit (kN) | P* (kN) | Failure Mode | ||
|---|---|---|---|---|---|---|---|
| DS_200_50_LD_CM_1 | \ | \ | \ | \ | 13.15 | 13.2 (0.006) | FR |
| DS_200_50_LD_CM_2 | \ | \ | \ | \ | 13.23 | FR | |
| DS_200_50_LD_CM_3 | \ | \ | \ | \ | 13.31 | FR | |
| Nomenclature | 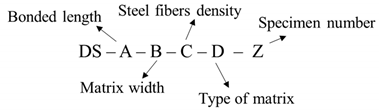 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baietti, G.; D’Antino, T.; Carloni, C. Some Key Aspects in the Mechanics of Stress Transfer Between SRG and Masonry. Appl. Sci. 2020, 10, 7303. https://doi.org/10.3390/app10207303
Baietti G, D’Antino T, Carloni C. Some Key Aspects in the Mechanics of Stress Transfer Between SRG and Masonry. Applied Sciences. 2020; 10(20):7303. https://doi.org/10.3390/app10207303
Chicago/Turabian StyleBaietti, Giulia, Tommaso D’Antino, and Christian Carloni. 2020. "Some Key Aspects in the Mechanics of Stress Transfer Between SRG and Masonry" Applied Sciences 10, no. 20: 7303. https://doi.org/10.3390/app10207303
APA StyleBaietti, G., D’Antino, T., & Carloni, C. (2020). Some Key Aspects in the Mechanics of Stress Transfer Between SRG and Masonry. Applied Sciences, 10(20), 7303. https://doi.org/10.3390/app10207303





