Slot Design Optimization for Copper Losses Reduction in Electric Machines for High Speed Applications
Abstract
:1. Introduction
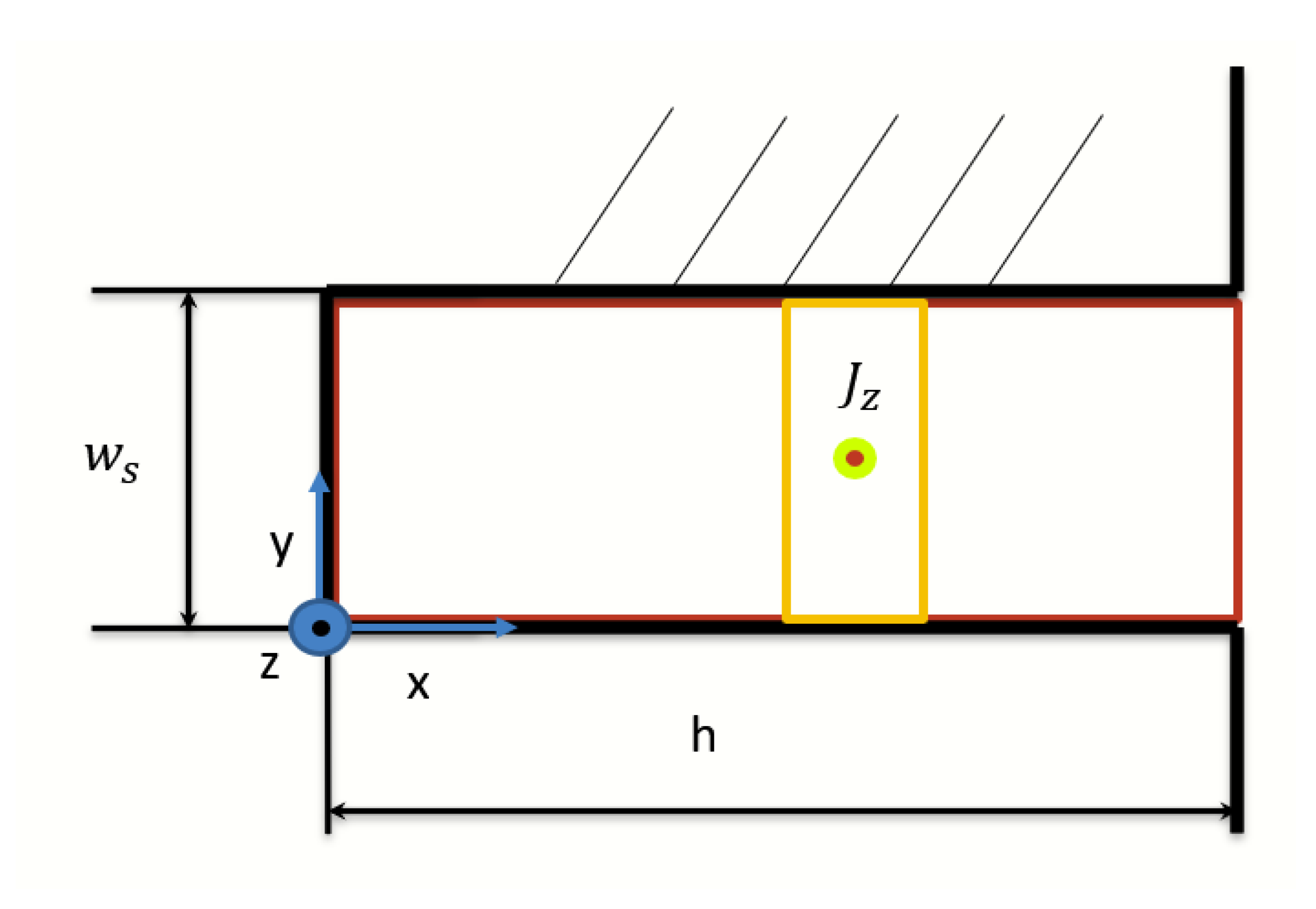
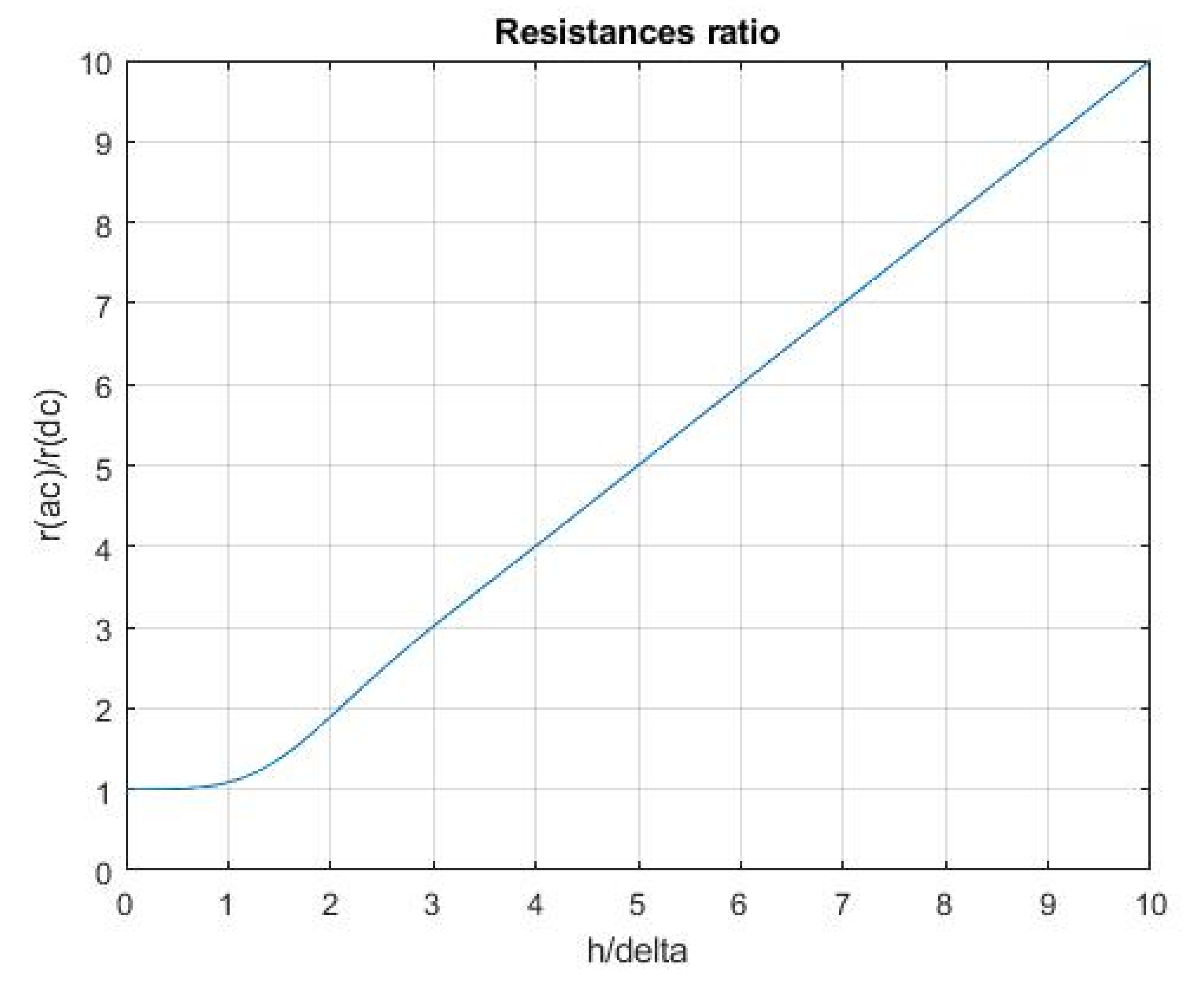
2. Analytical Approach
3. Finite Element Analyses
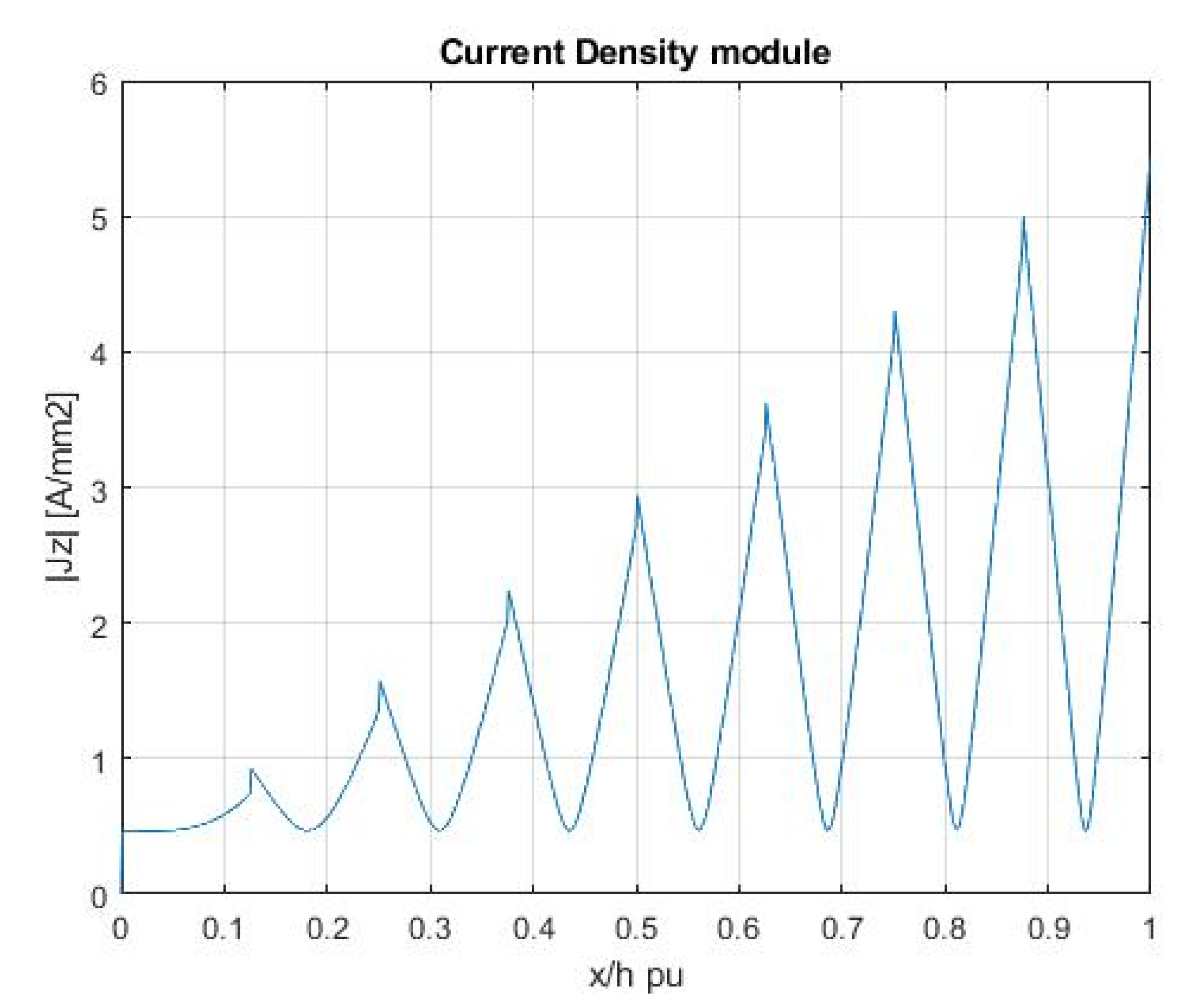
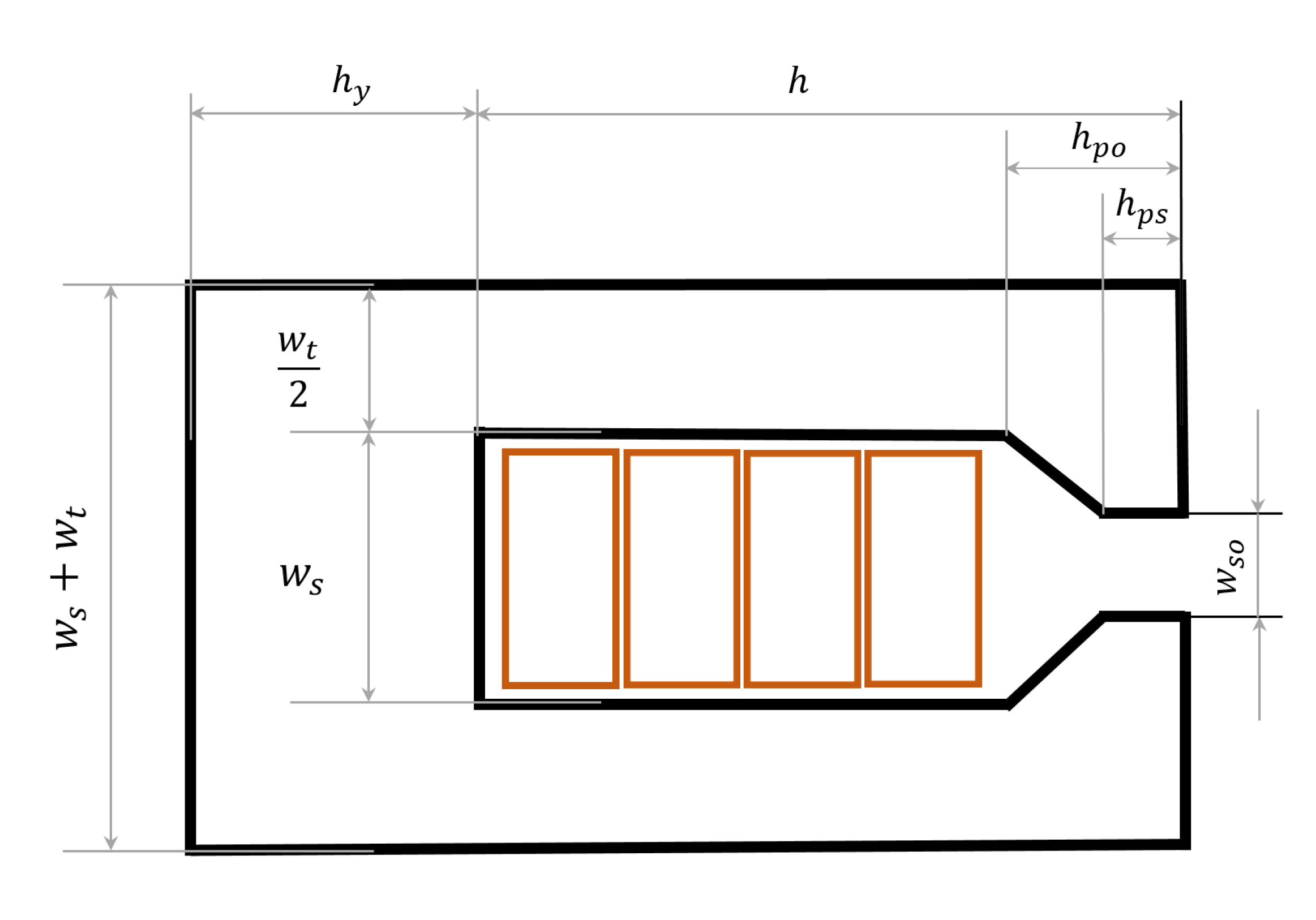
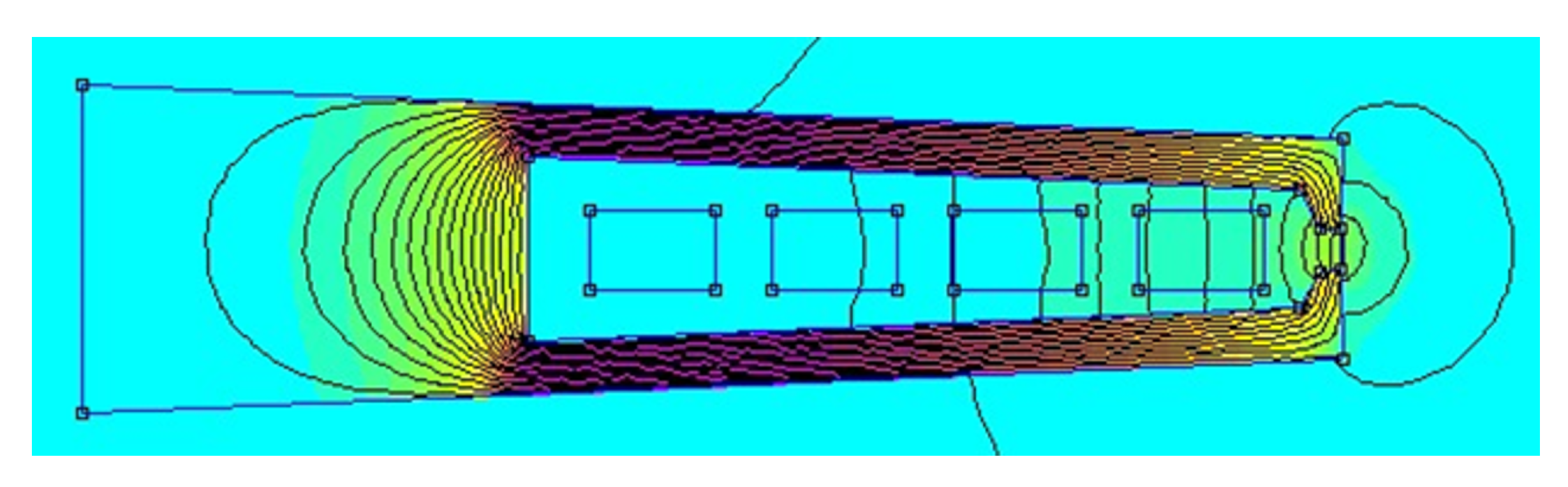
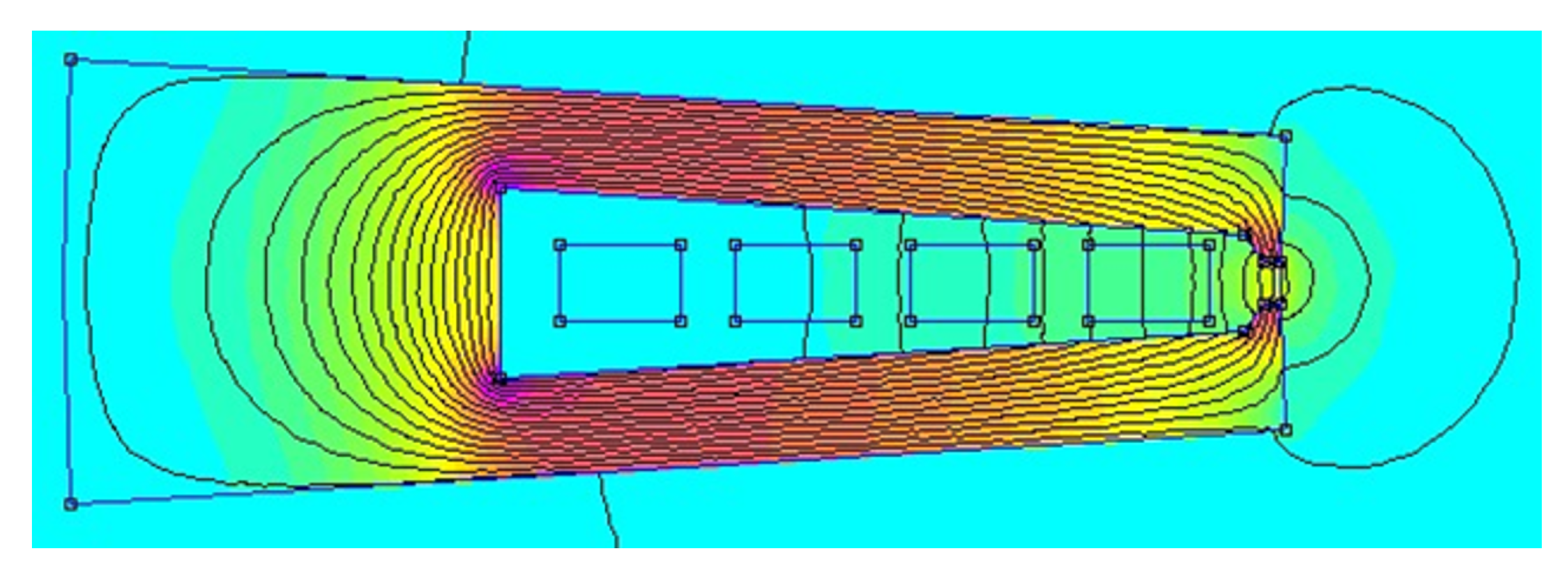
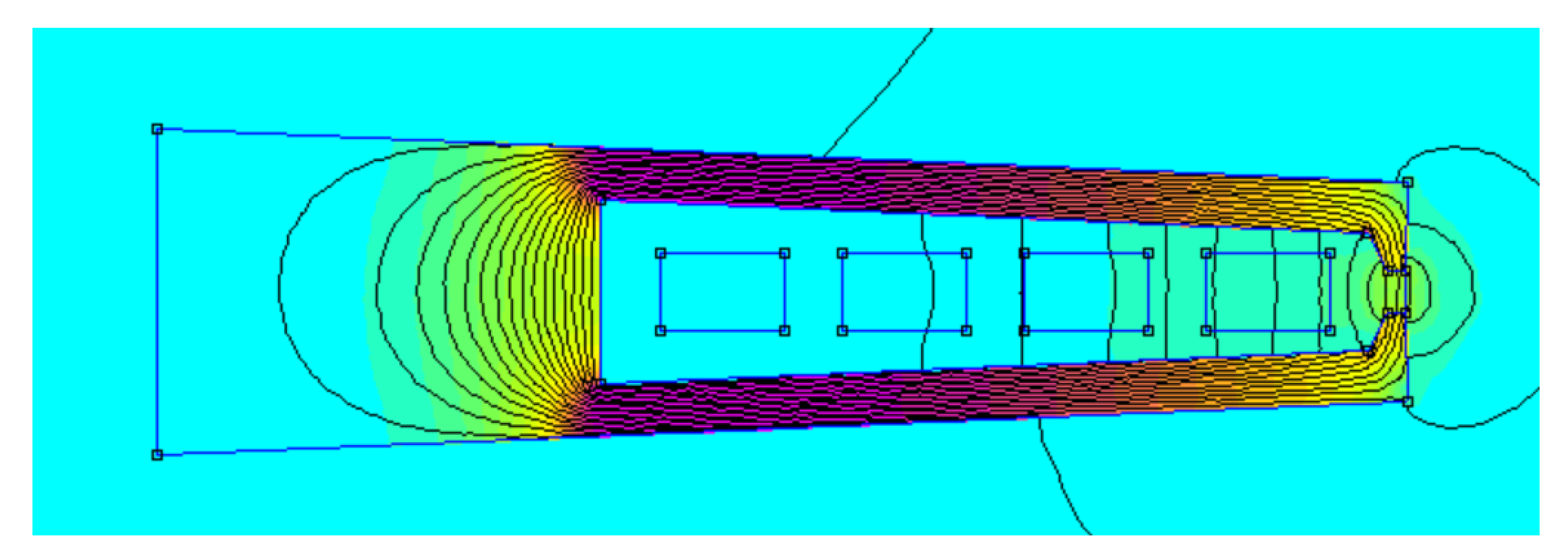
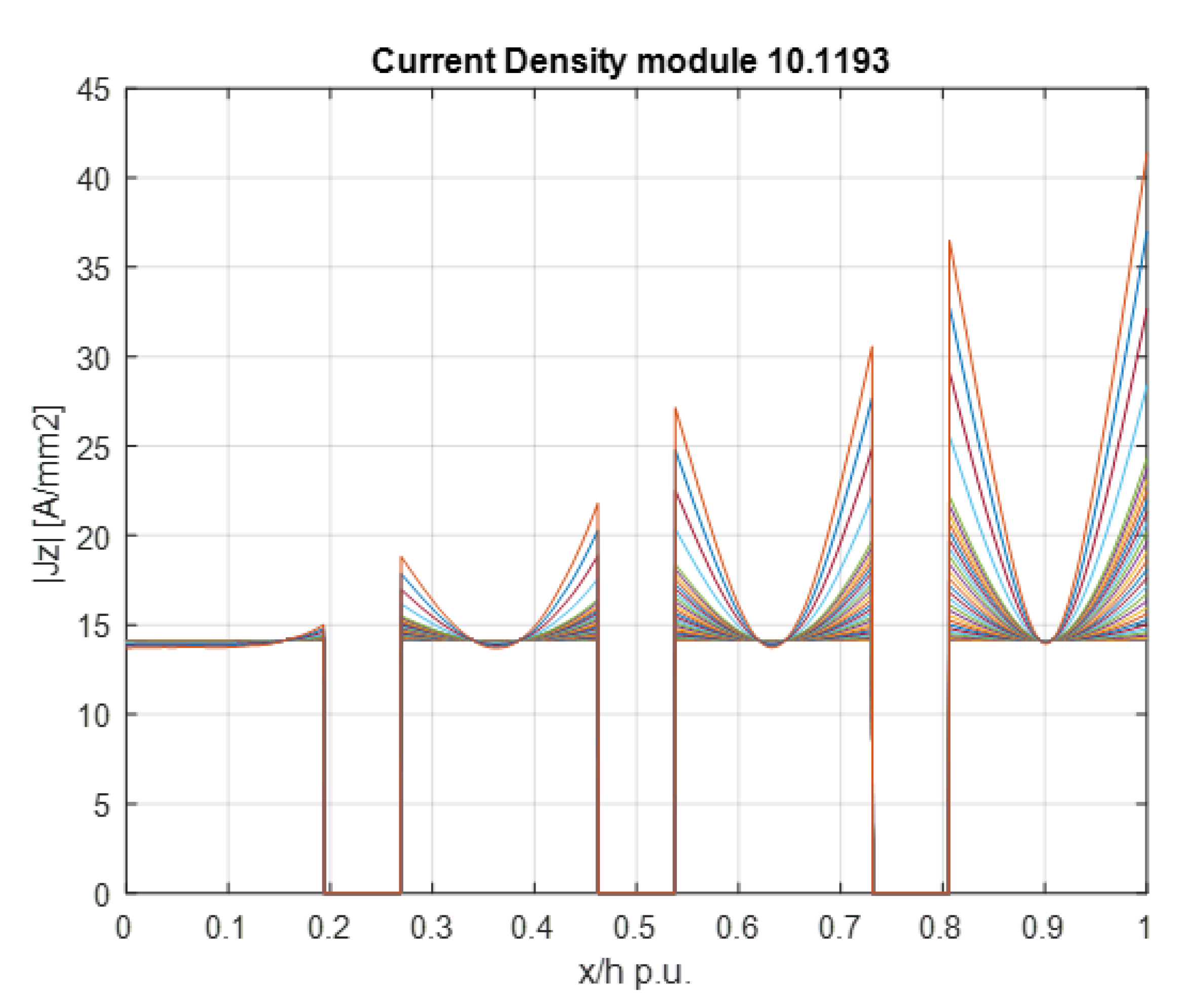
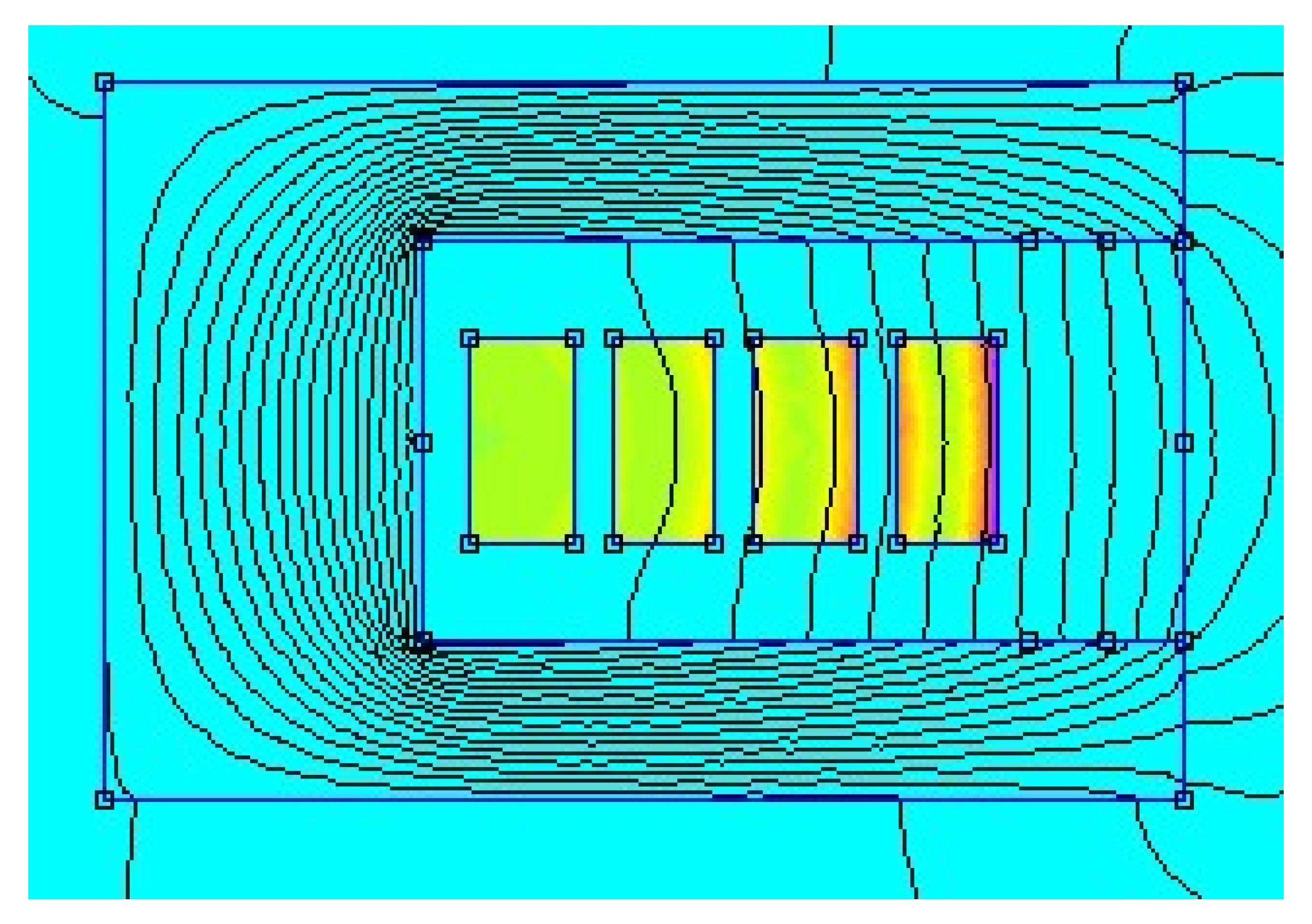
3.1. Introduction to the Analyses
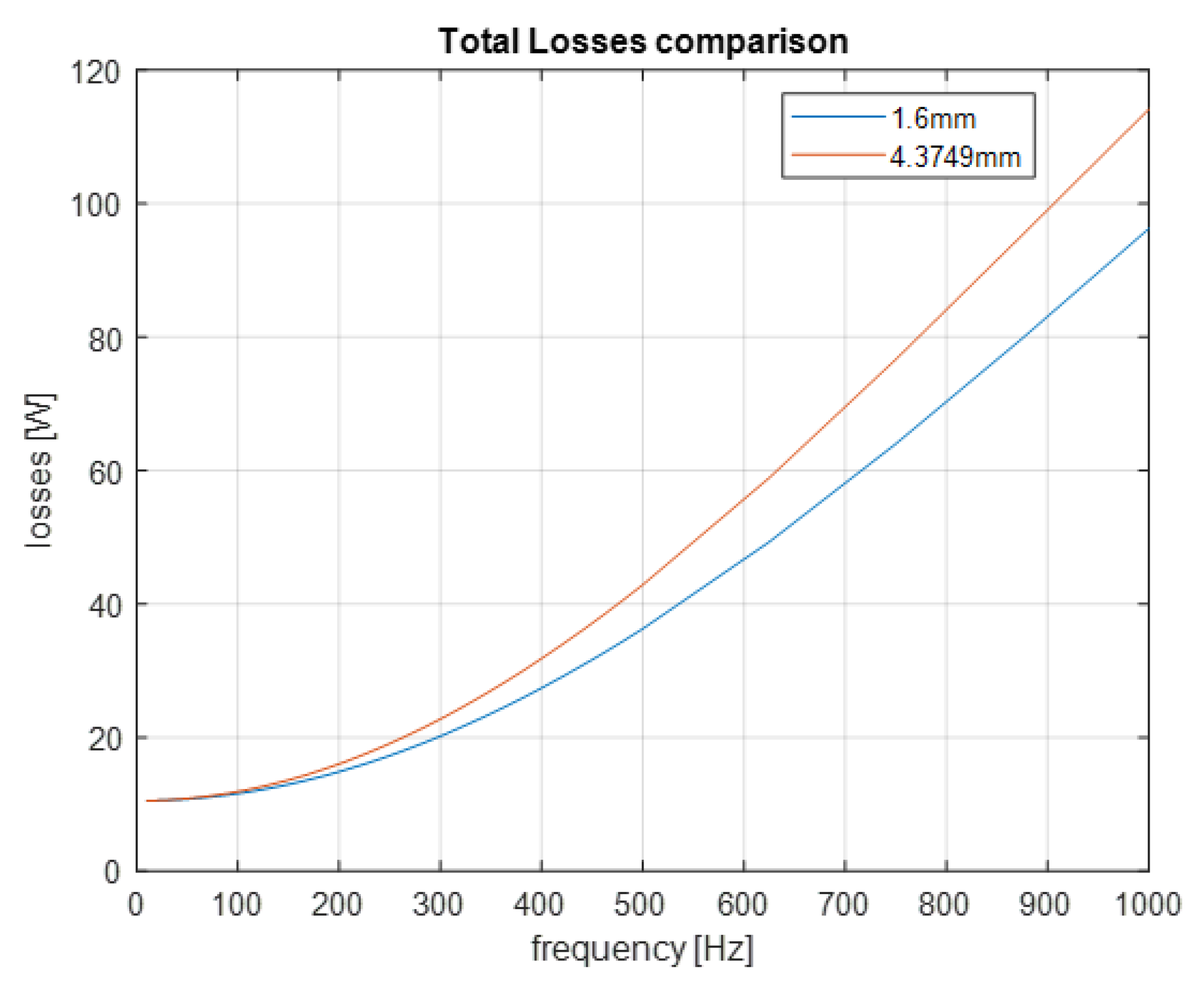
- The percentage reduction, or the increment, in the total power losses;
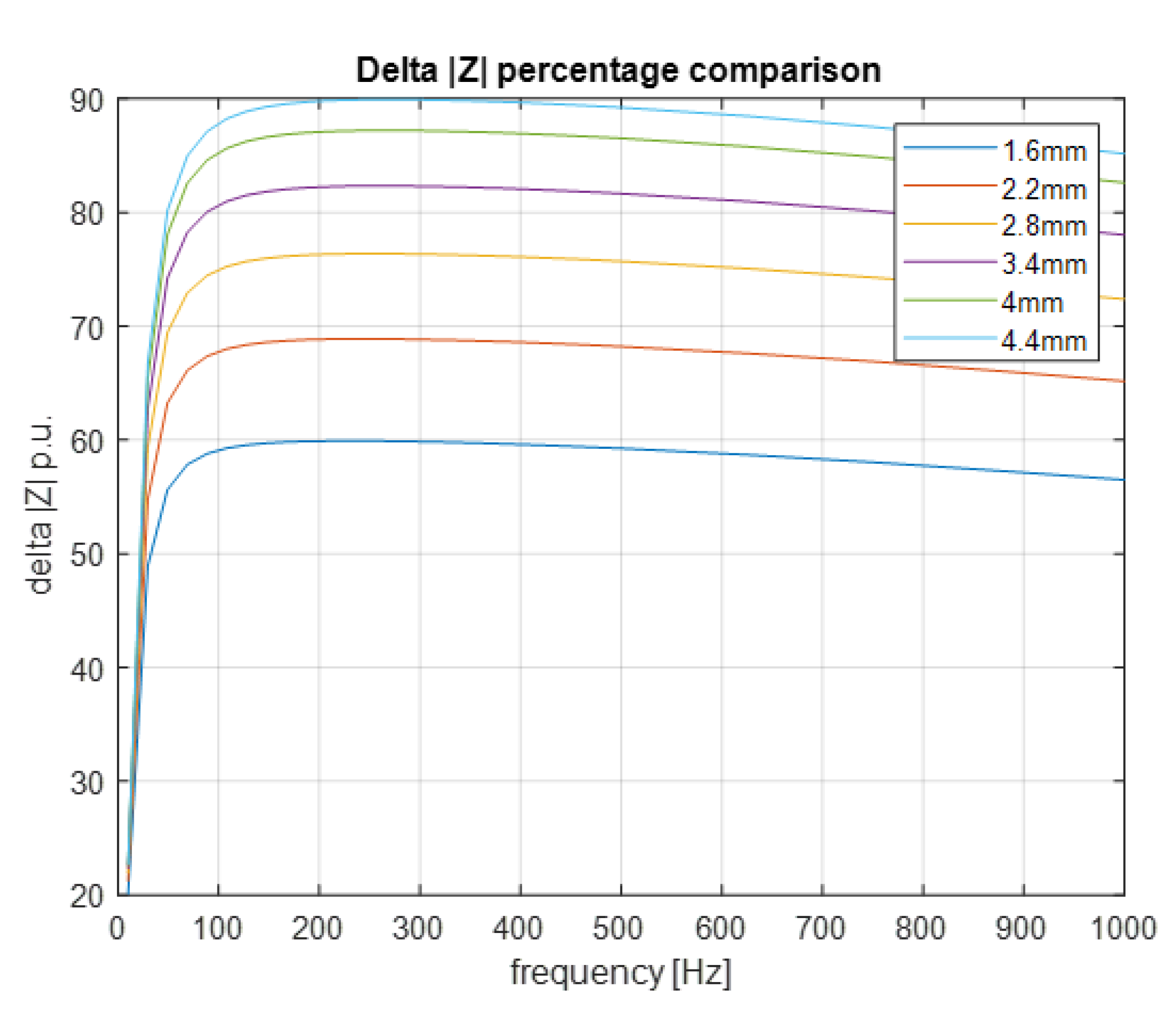
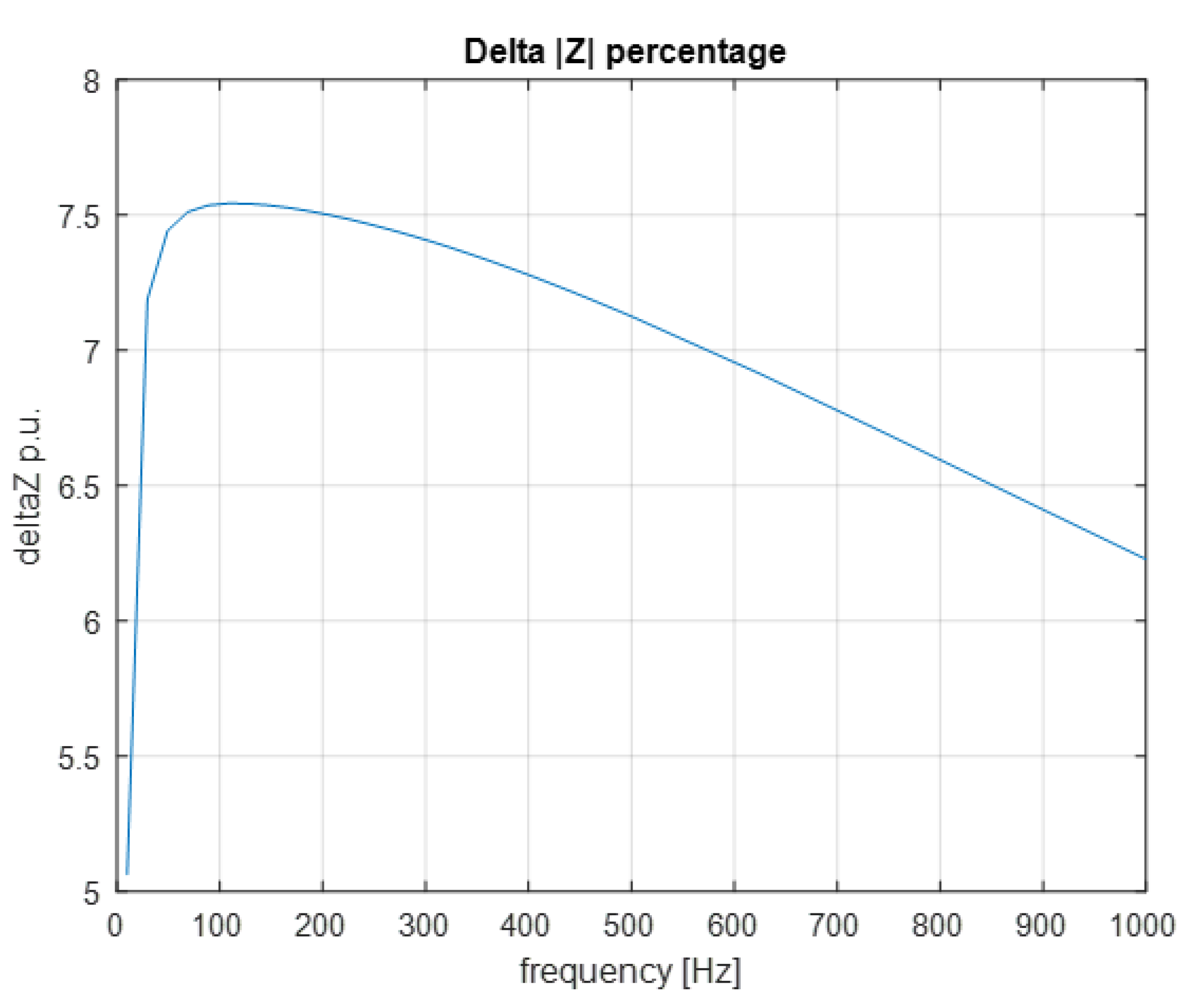
- The percentage difference between the greatest and the smallest impedance between the conductors inside the slot, see Equation (13).
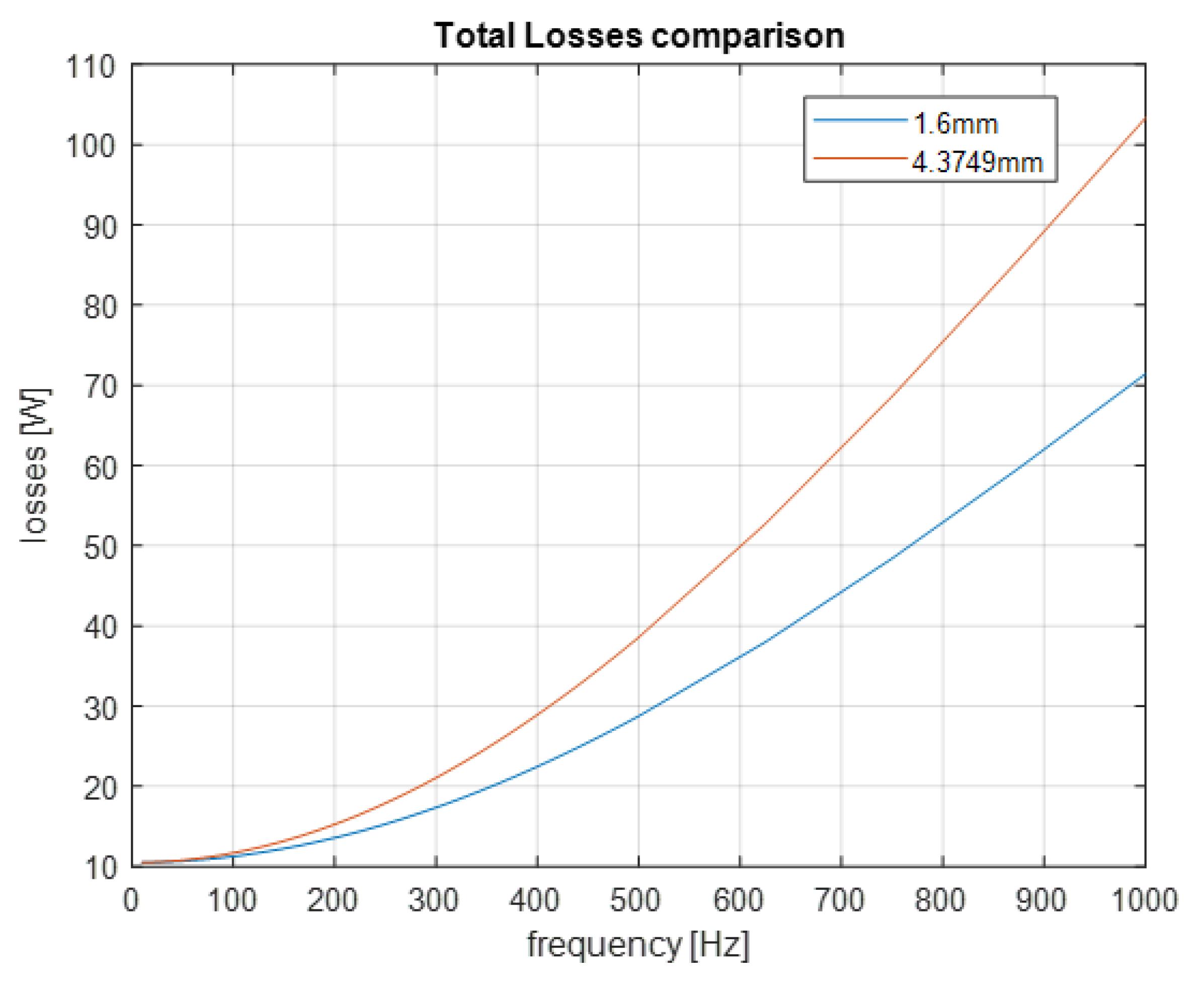
3.2. Slot Opening Width Analysis
3.2.1. Rectangular Slot
3.2.2. Trapezoidal Slot
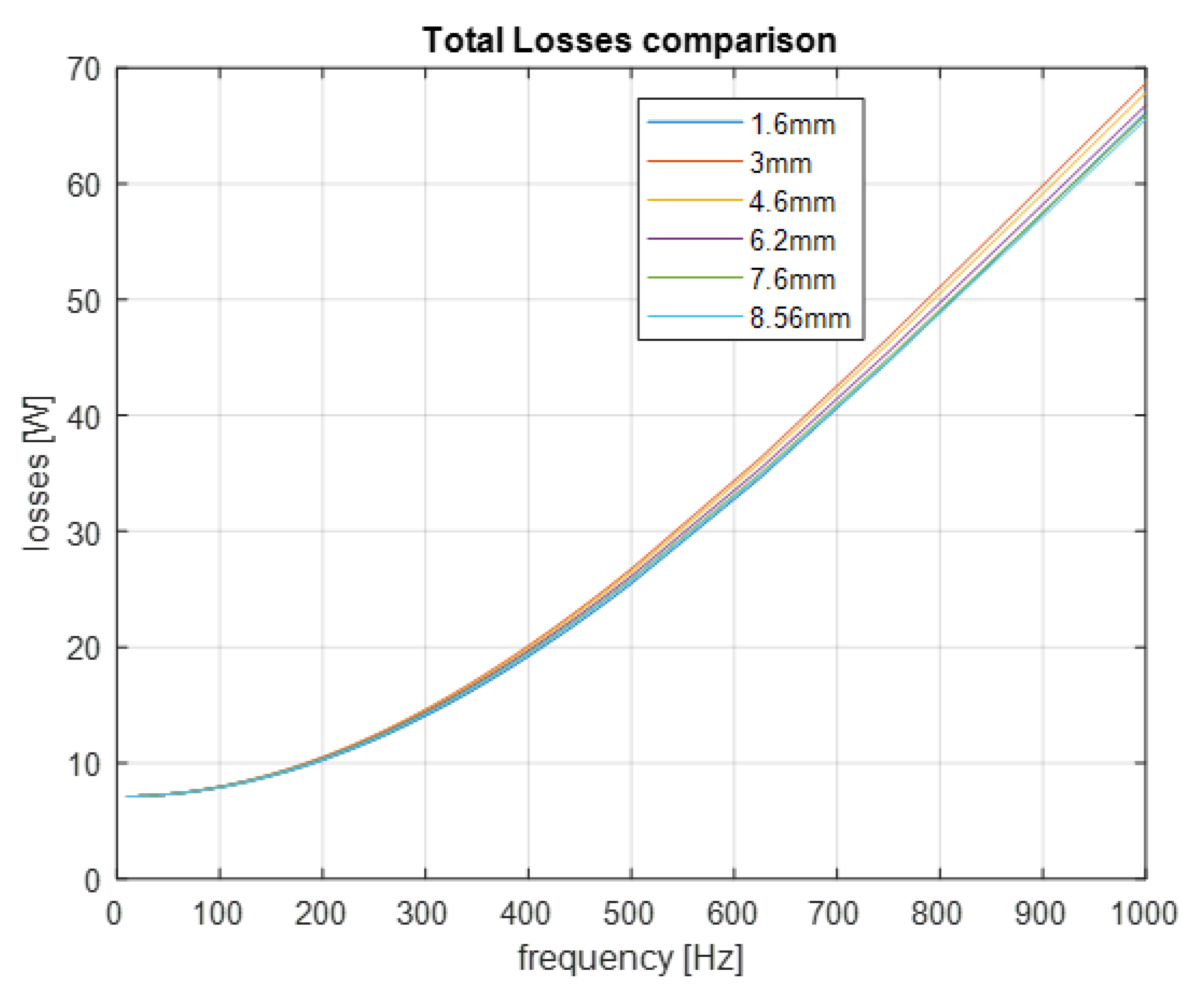
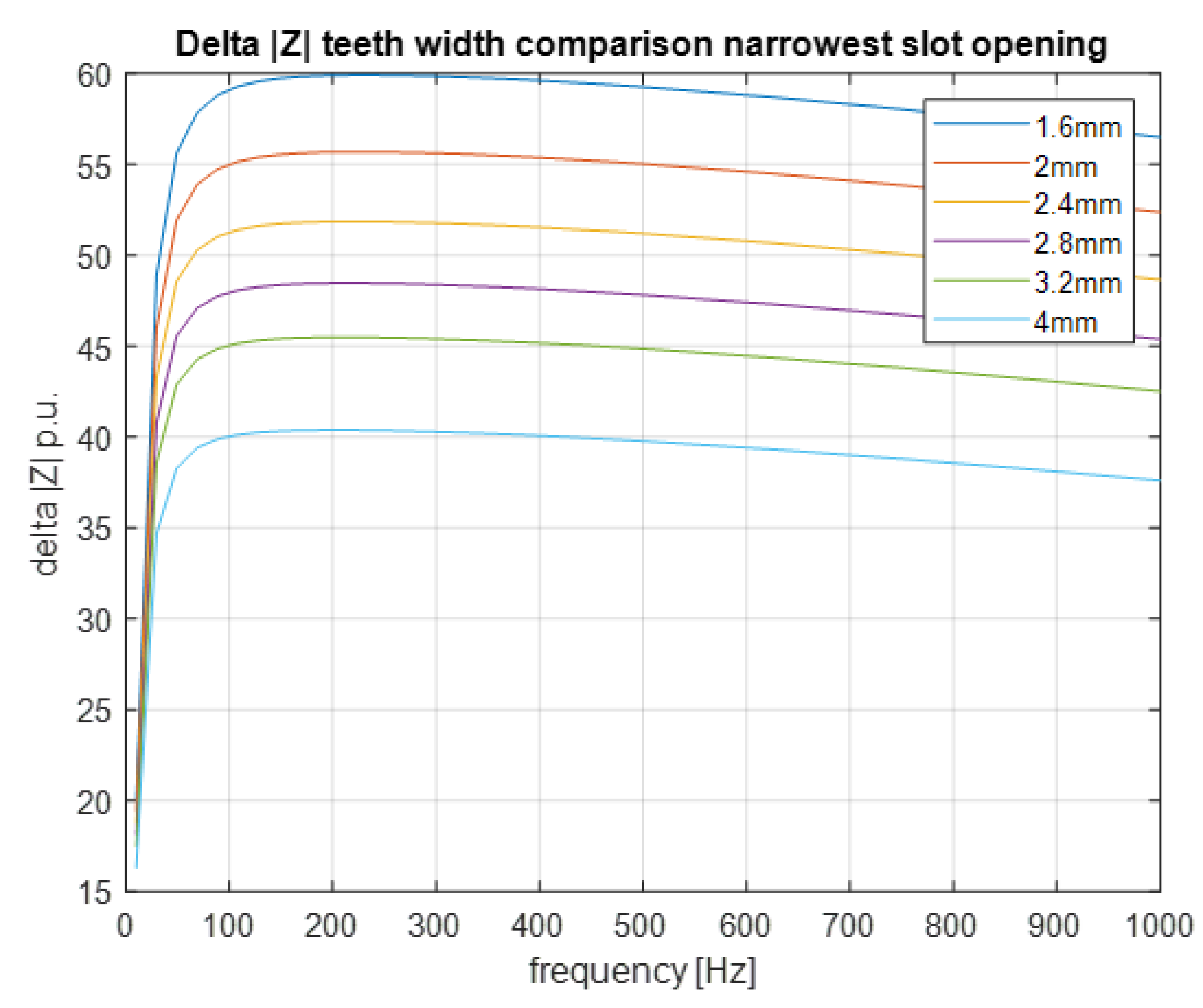
3.3. Tooth Width Analysis
Trapezoidal Slot
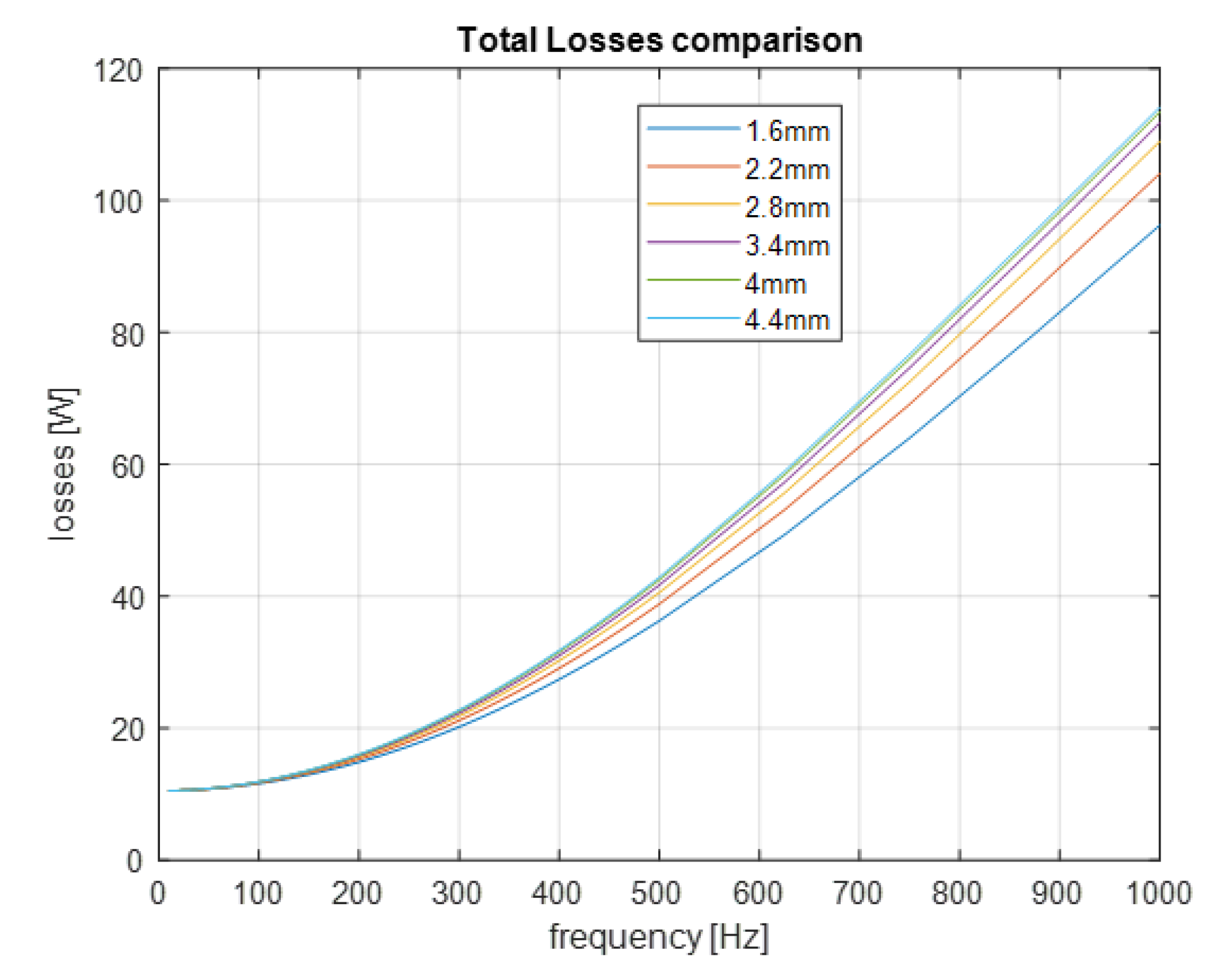
3.4. Polar Shoe Depths Analysis
Trapezoidal Slot
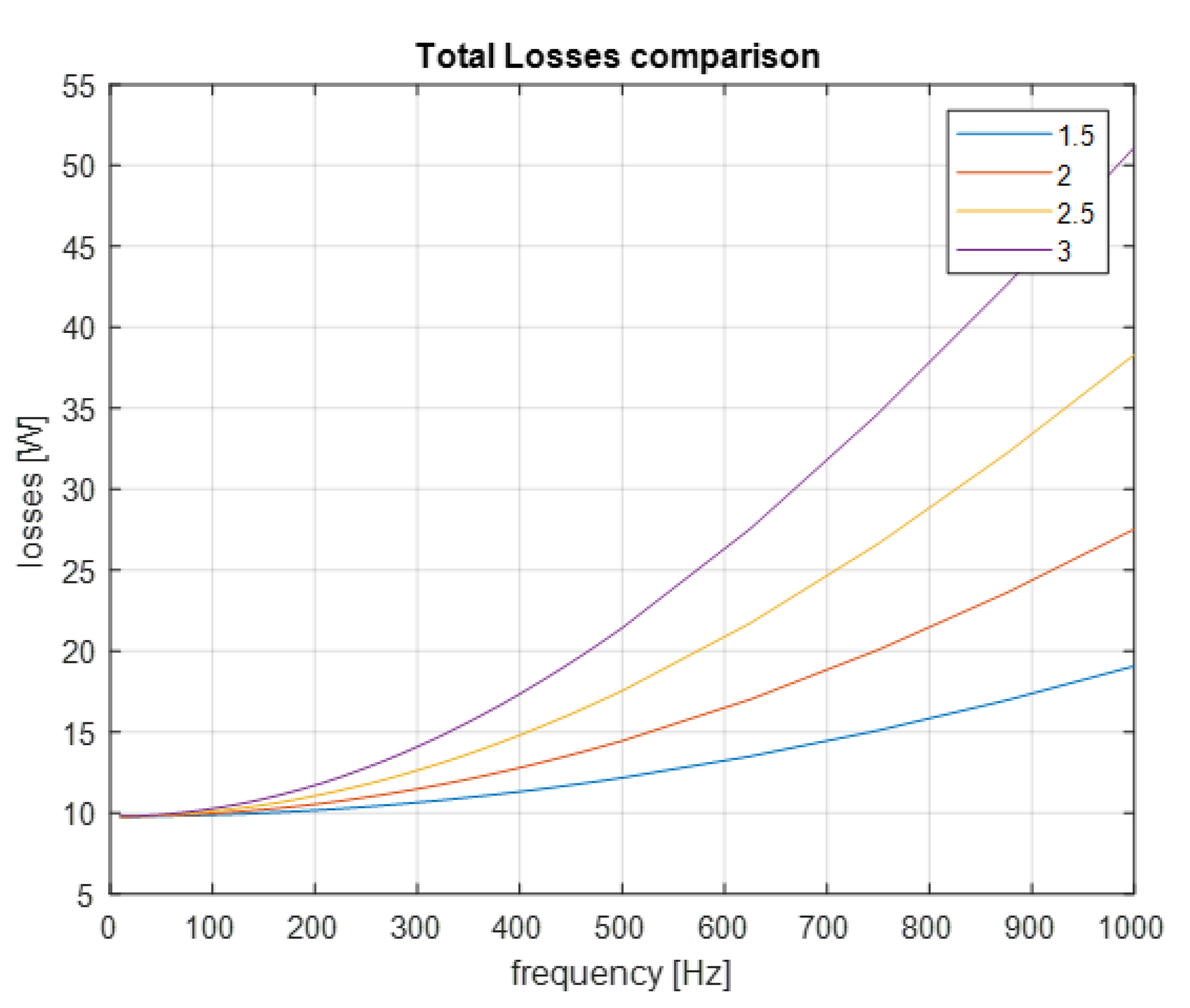
3.5. Slot Depth to Width Ratio Analysis
Rectangular Slot
4. Conclusions
- Narrow stator teeth;
- Great polar shoes, in order to create the best flux density paths;
- Narrow slot-opening.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BEV | Battery Electric Vehicles |
| HEV | Hybrid Electric Vehicles |
| FEA | Finite Element Analysis |
| KPI | Key Performance Indicator |
References
- Popescu, M.; Goss, J.; Staton, D.A.; Hawkins, D.; Chong, Y.C.; Boglietti, A. Electrical Vehicles—Practical Solutions for Power Traction Motor Systems. IEEE Trans. Ind. Appl. 2018, 54, 2751–2762. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Li, D.; Pei, T.; Qu, R. Overview of the rectangular wire windings AC electrical machine. CES Trans. Electr. Mach. Syst. 2019, 3, 160–169. [Google Scholar] [CrossRef]
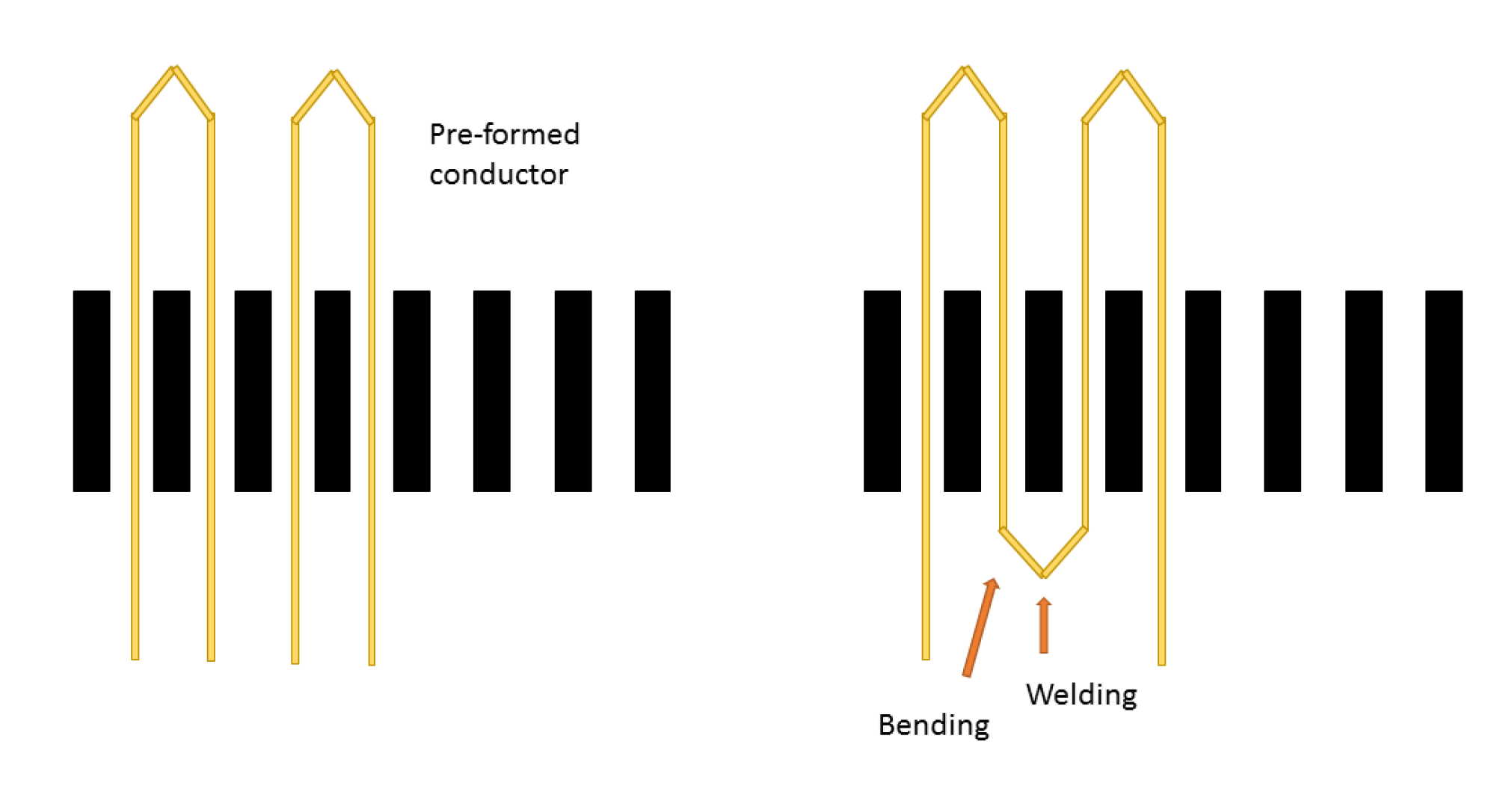
- Riedel, A.; Masuch, M.; Weigelt, M.; Tobias, G.; Kühl, A.; Reinstein, S. Challenges of the Hairpin Technology for Production Techniques. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea, 7–10 October 2018; pp. 2471–2476. [Google Scholar] [CrossRef]
- Glaessel, T.; Seefried, J.; Masuch, M.; Riedel, A.; Mayr, A.; Kuehl, A.; Franke, J. Process Reliable Laser Welding of Hairpin Windings for Automotive Traction Drives. In Proceedings of the 2019 International Conference on Engineering, Science, and Industrial Applications (ICESI), Tokyo, Japan, 22–24 August 2019. [Google Scholar]
- Ishigami, T.; Tanaka, Y.; Homma, H. Motor Stator with Thick Rectangular Wire Lap Winding for HEVs. In Proceedings of the International Power Electronics Conference (IPEC—Hiroshima 2014—ECCE ASIA), Hiroshima, Japan, 18–21 May 2014. [Google Scholar]
- Bianchi, N.; Berardi, G. Approach to Design Hairpin Windings in High Performance Electric Vehicle Motors. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 4398–4405. [Google Scholar]
- Arzillo, A.; Braglia, P.; Nuzzo, S.; Barater, D.; Franceschini, G.; Gerada, D.; Gerada, C. Challenges and Future opportunities of Hairpin Technologies. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 277–282. [Google Scholar]
- Ferreira, J.A. Electromagnetic Modeling for Power Electronics Converters; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Ferreira, J.A. Improved Analytical Modeling of Conductive Losses in Magnetic Components. IEEE Trans. Power Electron. 1994, 9, 127–131. [Google Scholar] [CrossRef]
- Kazimierczuk, M.K. High-Frequency Magnetic Components, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Du-Bar, C.; Wallmark, C.O. Eddy Current Losses in Hairpin Windings for an Automotive Application. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018. [Google Scholar]
- Montgomery, D.C. Introduction to Statistical Quality Control, 6th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2009. [Google Scholar]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bianchini, C.; Vogni, M.; Torreggiani, A.; Nuzzo, S.; Barater, D.; Franceschini, G. Slot Design Optimization for Copper Losses Reduction in Electric Machines for High Speed Applications. Appl. Sci. 2020, 10, 7425. https://doi.org/10.3390/app10217425
Bianchini C, Vogni M, Torreggiani A, Nuzzo S, Barater D, Franceschini G. Slot Design Optimization for Copper Losses Reduction in Electric Machines for High Speed Applications. Applied Sciences. 2020; 10(21):7425. https://doi.org/10.3390/app10217425
Chicago/Turabian StyleBianchini, Claudio, Mattia Vogni, Ambra Torreggiani, Stefano Nuzzo, Davide Barater, and Giovanni Franceschini. 2020. "Slot Design Optimization for Copper Losses Reduction in Electric Machines for High Speed Applications" Applied Sciences 10, no. 21: 7425. https://doi.org/10.3390/app10217425
APA StyleBianchini, C., Vogni, M., Torreggiani, A., Nuzzo, S., Barater, D., & Franceschini, G. (2020). Slot Design Optimization for Copper Losses Reduction in Electric Machines for High Speed Applications. Applied Sciences, 10(21), 7425. https://doi.org/10.3390/app10217425






