Modeling of a Village-Scale Multi-Energy System for the Integrated Supply of Electric and Thermal Energy †
Abstract
:Featured Application
Abstract
1. Introduction
2. Case Study and Scenario Characterization
3. Modeling Approach
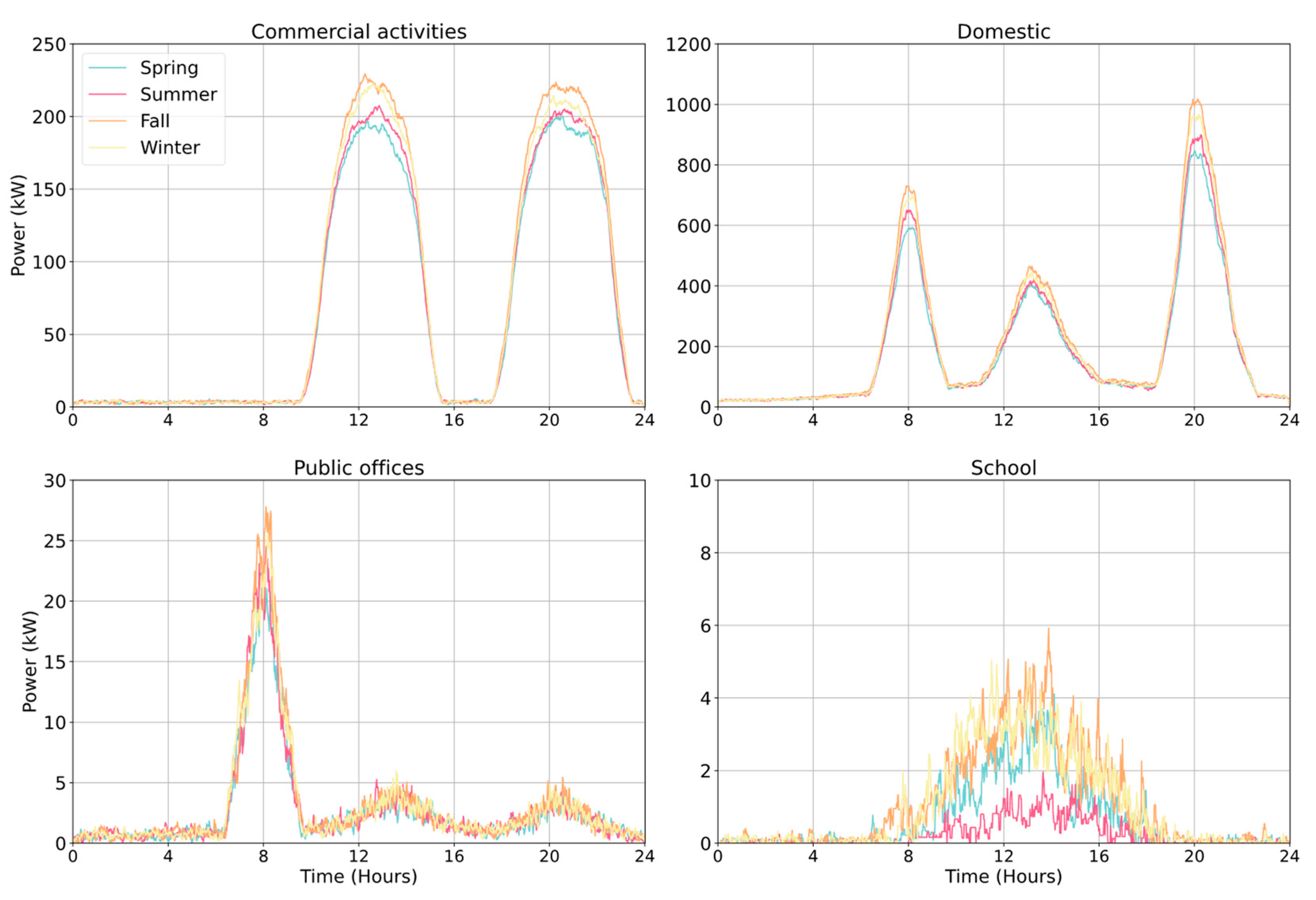
3.1. Load Profiles
3.1.1. Electric Load Curves
3.1.2. Thermal Load Curves
- is the groundwater temperature;
- is the progressive number of the considered day of the year;
- is the yearly average ambient temperature;
- is the progressive number of the day with the lowest temperature of the year.
- is the power required to heat the water for the operation of the task;
- is the water isobaric specific heat;
- is the groundwater temperature.
- (i)
- commercial activities,
- (ii)
- domestic,
- (iii)
- public offices,
- (iv)
- school.
3.2. Multi-Energy System
3.2.1. Electric Components
3.2.2. Thermal Components
Solar Thermal Collectors
Hot-Water Tanks
- The energy stored in the tank is constrained not to exceed the maximum capacity of the tank, for each class k.
- The energy stored in the tank is constrained to be kept above a minimum value (defined as depth of discharge, ), defined as a percentage of the nominal tank capacity.
- The thermal energy flow out of the tank () is constrained to be lower than the tank maximum power of discharge () multiplied by a delta time () calibrated on the time-step.
Electric Resistance Heating Elements
LPG Boilers
3.2.3. Optimization
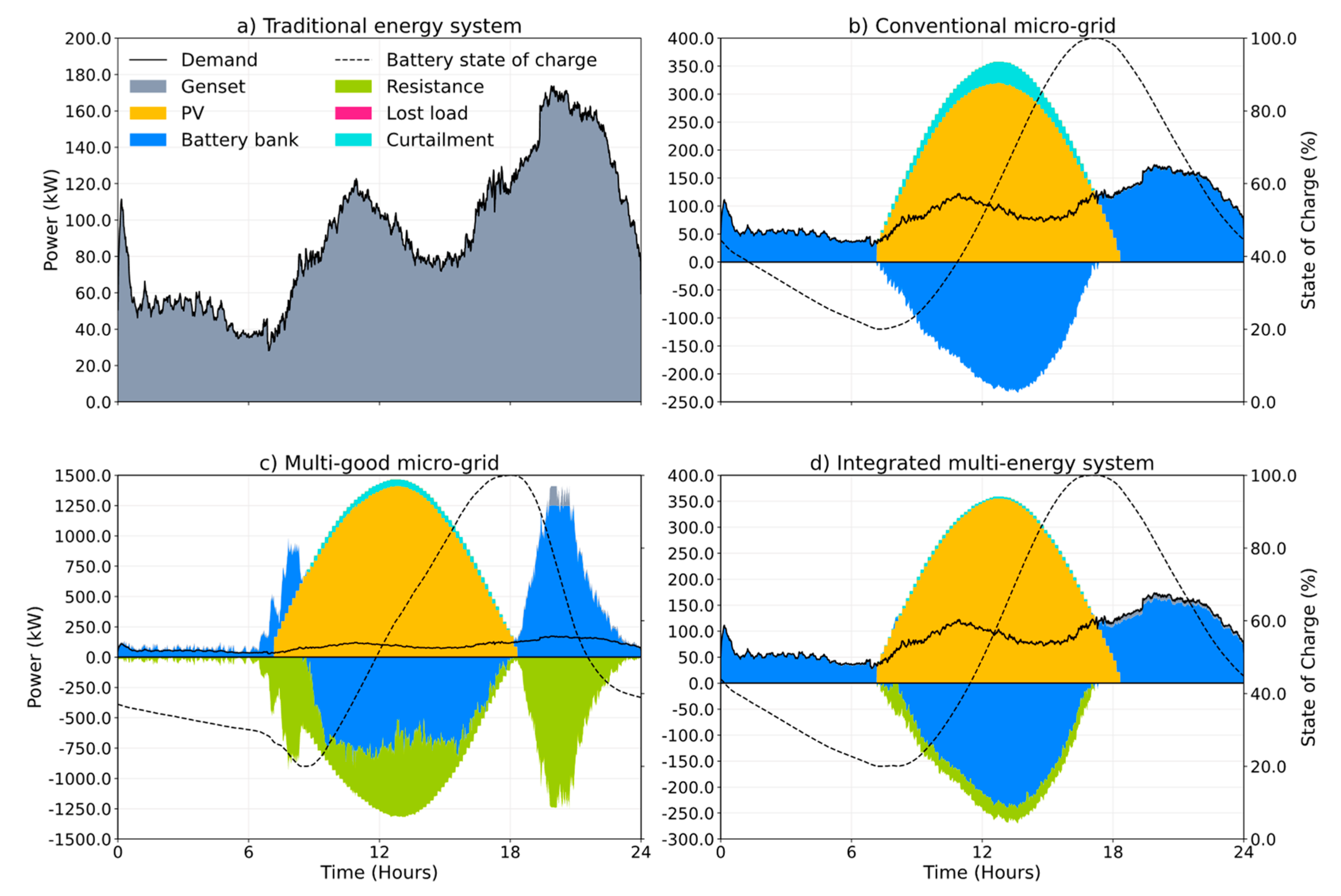
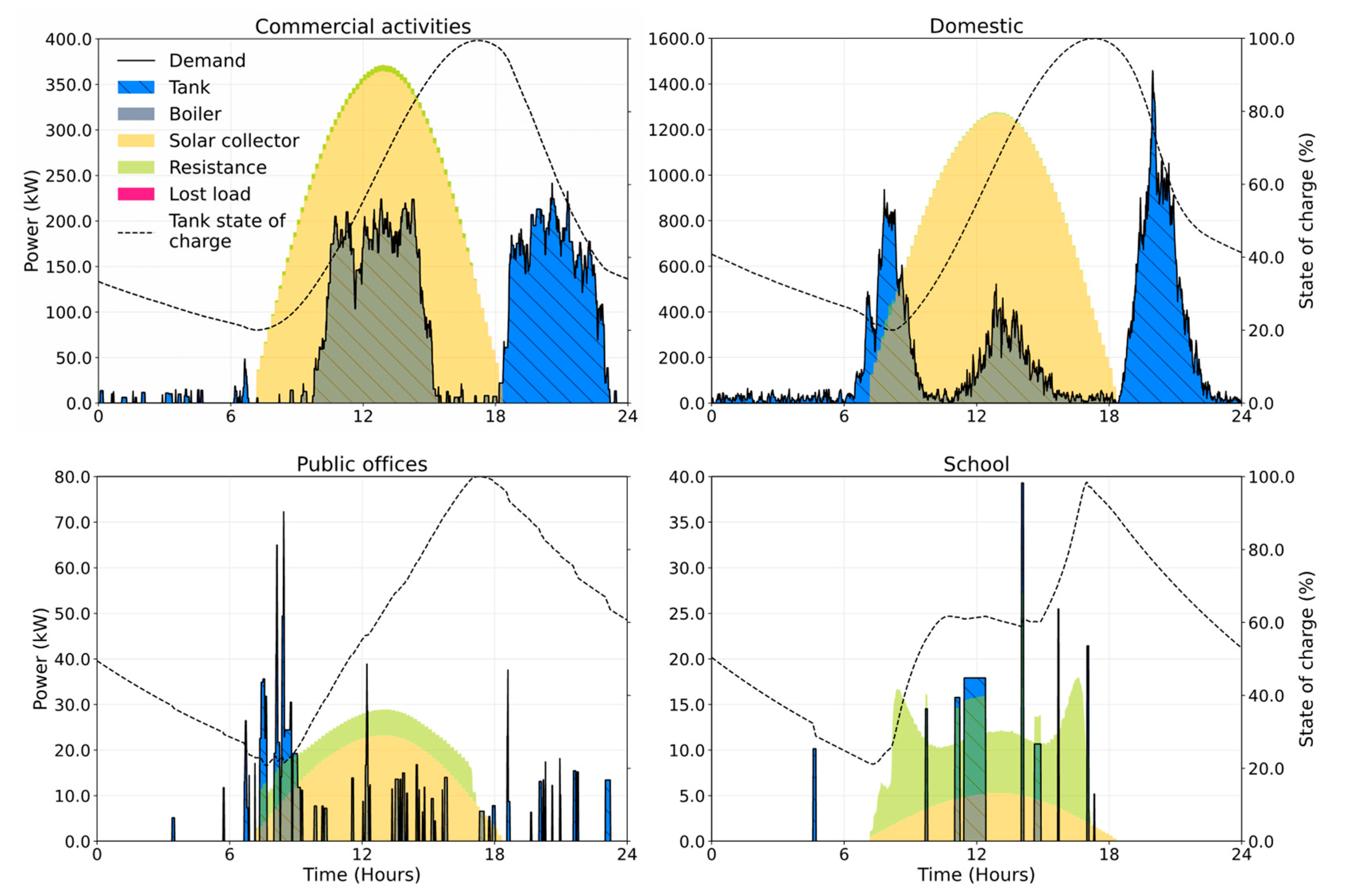
4. Results and Discussion
4.1. Generated Load Profiles
4.2. Optimization Results
5. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MES | Multi-Energy System |
| LPG | Liquid Propane Gas |
| DHW | Domestic Hot Water |
| TPES | Total Primary Energy Supply |
| TFC | Total Final (energy) Consumption |
| NPC | Net Present Cost |
| LCOE | Levelized Cost of Energy |
| LP | Linear Programming |
| MILP | Mixed-Integer Linear Programming |
| BESS | Battery Energy Storage System |
Nomenclature
| Groundwater temperature | K | |
| Progressive number of the considered day of the year | - | |
| Yearly average ambient temperature | K | |
| Progressive number of the day with the lowest temperature of the year | - | |
| Power required to heat the water for the operation of the task | W | |
| Water mass flow required by the task | l/s | |
| Water isobaric specific heat | ||
| Thermal energy demand | Wh | |
| Energy supplied by the boiler | Wh | |
| Energy exiting the hot-water tank | Wh | |
| Fraction of the excess energy produced by solar collectors that cannot be stored in the tank | Wh | |
| Allowed fraction of unmet thermal load | Wh | |
| Electricity demand of the study area | Wh | |
| Energy produced by the PV panels | Wh | |
| Energy produced by the generator | Wh | |
| Flow of energy into the battery | Wh | |
| Flow of energy out of the battery | Wh | |
| Electric energy that is curtailed | Wh | |
| Energy supplied to the thermal storage through electric resistance heating elements | Wh | |
| Cumulative energy absorbed by the electric resistance heating elements of all n thermal classes | Wh | |
| Allowed fraction of unmet electric load | Wh | |
| Total thermal energy provided by the solar collectors | Wh | |
| Energy generated by a single solar collector | Wh | |
| Number of solar collectors in the class | - | |
| Thermal energy stored in the tank at the time step t | Wh | |
| Thermal energy stored in the tank at the timestep t–1 | Wh | |
| Coefficient accounting for energy losses due to the heat transfer between thermal storage and environment | - | |
| Thermal efficiency of the electric resistances | - | |
| Depth of discharge | - | |
| Tank maximum power of discharge | W | |
| LPG consumption | l | |
| Boiler efficiency | - | |
| Lower heating value of the LPG | ||
| Total investment cost | ||
| Yearly constant cost of the project | ||
| Discount rate | - | |
| Interest rate | - | |
| Cost of components replacement | ||
| Number of installed PV panels | - | |
| Capacity of a PV unit | kW | |
| Specific cost of PV unit | $/kW | |
| Capacity of installed battery bank | kWh | |
| Specific cost of battery bank | $/kWh | |
| Capacity of installed generator | kW | |
| Specific cost of generator | $/kW | |
| Number of solar collectors installed | - | |
| Capacity of a solar collector | kW | |
| Specific cost of solar collector | $/kW | |
| Capacity of the installed hot-water tank | kWh | |
| Specific cost of the hot-water tank | $/kWh | |
| Capacity of the installed boiler | kW | |
| Specific cost of the boiler | $/kW | |
| Capacity of the installed electric resistance | kW | |
| Specific cost of the electric resistance | $/kW | |
| Percentage of the investment financed by a bank | - | |
| Cost of operation and maintenance of the system | ||
| Fixed-rate loan payment | ||
| Cost of the used diesel | ||
| Cost of the used LPG | ||
| Cost of the actually unmet load | ||
| Total energy demand (electric and thermal) of the system | kWh | |
| Net (i.e., after subtracting the lost load) total energy demand | kWh | |
| Total energy supplied by each j-th energy supply technology | kWh | |
| Overall system efficiency | - |
References
- Collier, U. Renewable Heat Policies—Delivering Clean Heat Solutions for the Energy Transition; International Energy Agency: Paris, France, 2018. [Google Scholar]
- Lund, H.; Østergaard, P.A.; Connolly, D.; Mathiesen, B.V. Smart energy and smart energy systems. Energy 2017, 137, 556–565. [Google Scholar] [CrossRef]
- Mancarella, P. MES ( multi-energy systems): An overview of concepts and evaluation models. Energy 2014, 65, 1–17. [Google Scholar] [CrossRef]
- International Energy Agency. World Energy Outlook 2018; Organisation for Economic Co-Operation and Development (OECD): Paris, France, 2018. [Google Scholar]
- Riva, F.; Ahlborg, H.; Hartvigsson, E.; Pachauri, S.; Colombo, E. Electricity access and rural development: Review of complex socio-economic dynamics and casual diagrams for more appropriate energy modelling. Energy Sustain. Dev. 2018, 43, 203–223. [Google Scholar] [CrossRef]
- Sahn, D.; Stifel, D. Urban-Rural Inequality in Living Standards in Africa. J. Afr. Econ. 2003, 12, 564–597. [Google Scholar] [CrossRef] [Green Version]
- Mandelli, S.; Barbieri, J.; Mereu, R.; Colombo, E. Off-grid systems for rural electrification in developing countries: Definitions, classification and a comprehensive literature review. Renew. Sustain. Energy. Rev. 2016, 58, 1621–1646. [Google Scholar] [CrossRef]
- Kaygusuz, K. Energy services and energy poverty for sustainable rural development. Renew. Sustain. Energy Rev. 2011, 15, 936–947. [Google Scholar] [CrossRef]
- Ravindra, K.; Agarwal, N.; Kaur-Sidhu, M.; Mor, S. Appraisal of thermal comfort in rural household kitchens of Punjab, India and adaptation strategies for better health. Environ. Int. 2019, 124, 431–440. [Google Scholar] [CrossRef]
- WHO. Household Air Pollution and Health; WHO: Geneva, Switzerland, 2018. [Google Scholar]
- Mathiesen, B.V.; Lund, H.; Connolly, D.; Wenzel, H.; Ostergaard, P.A.; Moller, B.; Nielsen, S.; Ridjan, I.; Karnoe, P.; Sperling, K.; et al. Smart Energy Systems for coherent 100% renewable energy and transport solutions. Appl. Energy 2015, 145, 139–154. [Google Scholar] [CrossRef]
- Lund, H.; Østergaard, P.A.; Connolly, D.; Ridjan, I.; Mathiesen, B.V.; Hvelplund, F. Energy Storage and Smart Energy Systems. Int. J. Sustain. Energy Plan. Manag. 2016, 11, 3–14. [Google Scholar] [CrossRef]
- Good, N.; Mancarella, P. Flexibility in Multi-Energy Communities with Electrical and Thermal Storage: A Stochastic, Robust Approach for Multi-Service Demand Response. IEEE Trans. Smart Grid 2017, 10, 503–513. [Google Scholar] [CrossRef]
- International Energy Agency. Energy Access Outlook 2017—From Poverty to Prosperit; International Energy Agency: Paris, France, 2017. [Google Scholar]
- Moretti, L.; Astolfi, M.; Vergara, C.; Macchi, E.; Pérez-Arriaga, J.I.; Manzolini, G. A design and dispatch optimization algorithm based on mixed integer linear programming for rural electrification. Appl. Energy 2019, 234, 1104–1121. [Google Scholar] [CrossRef]
- Balderrama, S.; Lombardi, F.; Riva, F.; Canedo, W.; Colombo, E.; Quoilin, S. A two-stage linear programming optimization framework for isolated hybrid microgrids in a rural context: The case study of the “El Espino” community. Energy 2019, 188, 116073. [Google Scholar] [CrossRef]
- Ciller, P.; De Cuadra, F.; Lumbreras, S. Optimizing Off-Grid Generation in Large-Scale Electrification-Planning Problems: A Direct-Search Approach. Energies 2019, 12, 4634. [Google Scholar] [CrossRef] [Green Version]
- Hirsch, A.; Parag, Y.; Guerrero, J. Microgrids: A review of technologies, key drivers, and outstanding issues. Renew. Sustain. Energy Rev. 2018, 90, 402–411. [Google Scholar] [CrossRef]
- Peters, J.; Sievert, M.; Toman, M.A. Rural electrification through mini-grids: Challenges ahead. Energy Policy 2019, 132, 27–31. [Google Scholar] [CrossRef] [Green Version]
- Balderrama, J.G.P.; Subieta, S.B.; Lombardi, F.; Stevanato, N.; Sahlberg, A.; Howells, M.; Colombo, E.; Quoilin, S. Incorporating high-resolution demand and techno-economic optimization to evaluate micro-grids into the Open Source Spatial Electrification Tool (OnSSET). Energy Sustain. Dev. 2020, 56, 98–118. [Google Scholar] [CrossRef]
- Sinha, S.; Chandel, S. Review of software tools for hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2014, 32, 192–205. [Google Scholar] [CrossRef]
- Stevanato, N.; Lombardi, F.; Guidicini, G.; Rinaldi, L.; Balderrama, S.L.; Pavičević, M.; Quoilin, S.; Colombo, E. Long-term sizing of rural microgrids: Accounting for load evolution through multi-step investment plan and stochastic optimization. Energy Sustain. Dev. 2020, 58, 16–29. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, X.; Li, P.; Wang, K.; Xue, M.; Wang, C. Optimal sizing, operating strategy and operational experience of a stand-alone microgrid on Dongfushan Island. Appl. Energy 2014, 113, 1656–1666. [Google Scholar] [CrossRef]
- Díaz, P.; Arias, C.; Pena, R.; Sandoval, D. FAR from the grid: A rural electrification field study. Renew. Energy 2010, 35, 2829–2834. [Google Scholar] [CrossRef]
- Energy Sector Management Assistance Program. Mini Grids for Half a Billion People: Market Outlook and Handbook for Decision Makers; ESMAP Technical Report 014/19 2019; The World Bank: Washington, DC, USA, 2019. [Google Scholar]
- International Renewable Energy Agency (IRENA). Policies and Regulations for Renewable Mini-Grids; International Renewable Energy Agency: Abu Dhabi, UAE, 2018. [Google Scholar]
- Mendes, G.; Ioakimidis, C.; Ferrão, P. On the planning and analysis of Integrated Community Energy Systems: A review and survey of available tools. Renew. Sustain. Energy Rev. 2011, 15, 4836–4854. [Google Scholar] [CrossRef]
- Van Ruijven, B.J.; Van Vuuren, D.P.; De Vries, B.J.; Isaac, M.; Van Der Sluijs, J.P.; Lucas, P.L.; Balachandra, P. Model projections for household energy use in India. Energy Policy 2011, 39, 7747–7761. [Google Scholar] [CrossRef] [Green Version]
- McKenna, E.; Thomson, M. High-resolution stochastic integrated thermal–electrical domestic demand model. Appl. Energy 2016, 165, 445–461. [Google Scholar] [CrossRef] [Green Version]
- Pfenninger, S.; Decarolis, J.; Hirth, L.; Quoilin, S.; Staffell, I. The importance of open data and software: Is energy research lagging behind? Energy Policy 2017, 101, 211–215. [Google Scholar] [CrossRef]
- HOMER Energy LLC. HOMER Energy n.d. Available online: https://www.homerenergy.com/ (accessed on 25 September 2020).
- Mashayekh, S.; Stadler, M.; Cardoso, G.; Heleno, M. A mixed integer linear programming approach for optimal DER portfolio, sizing, and placement in multi-energy microgrids. Appl. Energy 2017, 187, 154–168. [Google Scholar] [CrossRef] [Green Version]
- Dufo-López, R.; Bernal-Agustín, J.L.; Yusta-Loyo, J.M.; Domínguez-Navarro, J.A.; Ramírez-Rosado, I.J.; Lujano, J.; Aso, I. Multi-objective optimization minimizing cost and life cycle emissions of stand-alone PV–wind–diesel systems with batteries storage. Appl. Energy 2011, 88, 4033–4041. [Google Scholar] [CrossRef]
- Dufo-López, R.; Cristóbal-Monreal, I.R.; Yusta, J.M. Stochastic-heuristic methodology for the optimisation of components and control variables of PV-wind-diesel-battery stand-alone systems. Renew. Energy 2016, 99, 919–935. [Google Scholar] [CrossRef]
- Karavas, C.-S.; Kyriakarakos, G.; Arvanitis, K.G.; Papadakis, G. A multi-agent decentralized energy management system based on distributed intelligence for the design and control of autonomous polygeneration microgrids. Energy Convers. Manag. 2015, 103, 166–179. [Google Scholar] [CrossRef]
- Karavas, C.-S.; Arvanitis, K.; Papadakis, G. A Game Theory Approach to Multi-Agent Decentralized Energy Management of Autonomous Polygeneration Microgrids. Energies 2017, 10, 1756. [Google Scholar] [CrossRef] [Green Version]
- Karavas, C.-S.; Arvanitis, K.; Kyriakarakos, G.; Piromalis, D.D.; Papadakis, G. A novel autonomous PV powered desalination system based on a DC microgrid concept incorporating short-term energy storage. Sol. Energy 2018, 159, 947–961. [Google Scholar] [CrossRef]
- Ministerio de Energía. Anuario Estadístico de Energía 2018; CNE: Santiago, Chile, 2018.
- International Energy Agency (IEA). Energy Statistics Manual; International Energy Agency: Paris, France, 2005. [Google Scholar] [CrossRef]
- Stevanato, N.; Lombardi, F.; Colmbo, E.; Balderrama, S.; Quoilin, S. Two-Stage Stochastic Sizing of a Rural Micro-Grid Based on Stochastic Load Generation. In Proceedings of the 13th IEEE PowerTech Conference, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Lombardi, F.; Balderrama, S.; Quoilin, S.; Colombo, E. Generating high-resolution multi-energy load profiles for remote areas with an open-source stochastic model. Energy 2019, 177, 433–444. [Google Scholar] [CrossRef]
- Fischer, D.; Wolf, T.; Scherer, J.; Wille-Haussmann, B. A stochastic bottom-up model for space heating and domestic hot water load profiles for German households. Energy Build. 2016, 124, 120–128. [Google Scholar] [CrossRef]
- Caleffi, M. Produzione di acqua calda ad accumulo. In Idraulica; Caleffi: Novara, Italy, 1999; Volume 16. [Google Scholar]
- ASHRAE. 2015 ASHRAE Handbook–Heating, Ventilation and Air-Conditioning Applications; ASHRAE: Peachtree Corners, GA, USA, 2015. [Google Scholar]
- Stevanato, N.; Pistolese, S.; Lombardi, F.; Rinaldi, L. Multi-Energy Systems Py. 2020. Available online: https://github.com/Stevogallo/MicroGridsPy-MultiEnergy_Paper (accessed on 25 September 2020).
- Dumont, O.; Carmo, C.; Dickes, R.; Emelines, G.; Quoilin, S.; Lemort, V. Hot water tanks : How to select the optimal modelling approach? In Clima 2016; Heiselberg, P.K., Ed.; Aalborg University: Aalborg, Denmark, 2016. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]

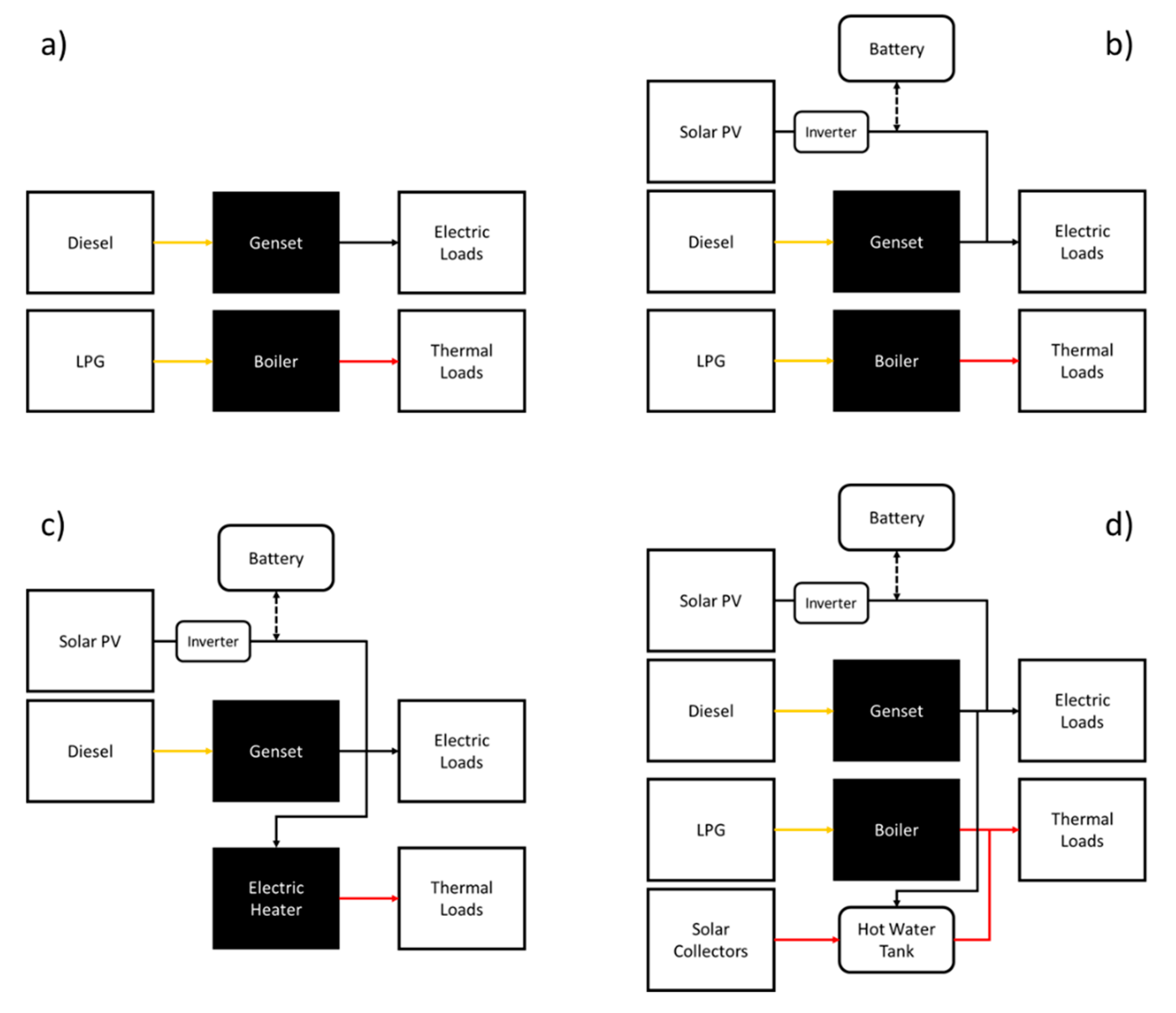


| Inputs | Outputs |
|---|---|
| PV panel output | Optimal system size |
| Solar collector output | Net Present Cost (NPC) |
| Electric load profile | Levelized Cost of Energy (LCOE) |
| Thermal load profile | Electric dispatch strategy |
| Economic parameters | Thermal dispatch strategy |
| Traditional Energy System (Baseline) | Conventional Micro-Grid | Multi-Good Micro-Grid | Integrated Multi-Energy System | |
|---|---|---|---|---|
| TPES [ktoe] | 467.8 | 322.2 | 362.3 | 442.9 |
| Imports [%TPES] | 100% | 77.0% | 16.2% | 6.3% |
| Renewables [%TPES] | 0% | 23.0% | 83.8% | 93.7% |
| BESS Use [%TFC_el] | 0% | 67.8% | 61.0% | 53.8% |
| LCOE [USD/kWh] | 0.259 | 0.220 | 0.198 | 0.090 |
| Traditional Energy System (Baseline) | Conventional Micro-Grid | Multi-Good Micro-Grid | Integrated Multi-Energy System | |
|---|---|---|---|---|
| PV panels [kW] | - | 320 | 1312 | 321 |
| Battery storage [kWh] | - | 1621 | 6257 | 1563 |
| Diesel gensets [kW] | 181 | 19 | 159 | 42 |
| Solar collectors [kW] | - | - | - | 1703 |
| Hot-water tanks [kWh] | - | - | - | 8533 |
| LPG boilers [kW] | 1417 | 1417 | - | 1 |
| Electric heaters [kW] | - | - | 1467 | 229 |
| Total investment cost [MUSD] | 0.18 | 1.68 | 6.24 | 2.56 |
| Total O&M cost [MUSD] | 11.55 | 8.31 | 2.74 | 1.53 |
| Net Present Cost [MUSD] | 11.73 | 9.98 | 8.98 | 4.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stevanato, N.; Rinaldi, L.; Pistolese, S.; Balderrama Subieta, S.L.; Quoilin, S.; Colombo, E. Modeling of a Village-Scale Multi-Energy System for the Integrated Supply of Electric and Thermal Energy. Appl. Sci. 2020, 10, 7445. https://doi.org/10.3390/app10217445
Stevanato N, Rinaldi L, Pistolese S, Balderrama Subieta SL, Quoilin S, Colombo E. Modeling of a Village-Scale Multi-Energy System for the Integrated Supply of Electric and Thermal Energy. Applied Sciences. 2020; 10(21):7445. https://doi.org/10.3390/app10217445
Chicago/Turabian StyleStevanato, Nicolo, Lorenzo Rinaldi, Stefano Pistolese, Sergio Luis Balderrama Subieta, Sylvain Quoilin, and Emanuela Colombo. 2020. "Modeling of a Village-Scale Multi-Energy System for the Integrated Supply of Electric and Thermal Energy" Applied Sciences 10, no. 21: 7445. https://doi.org/10.3390/app10217445
APA StyleStevanato, N., Rinaldi, L., Pistolese, S., Balderrama Subieta, S. L., Quoilin, S., & Colombo, E. (2020). Modeling of a Village-Scale Multi-Energy System for the Integrated Supply of Electric and Thermal Energy. Applied Sciences, 10(21), 7445. https://doi.org/10.3390/app10217445







