Measurement of Wafer Focus by Grating Shearing Interferometry

Abstract

A method applied for improving the measurement precision and efficiency of wafer focusing in an optical lithography instrument (OLI) is introduced. Based on grating shearing interferometry, the defocus and tilt of the wafer are measured by testing the phase difference in the interference pattern. To validate the feasibility, an experiment is implemented, of which the measurement precision is indicated as 30 nm due to the high precision of phase-resolving arithmetic after analyzing the measurement uncertainty and indicating the precision by interferometer.

1. Introduction

The wafer focusing technique (WFT) [1,2] is a pivotal section in optical lithography instruments (OLIs) [3], which affects the image quality and exposure effect [4]. In traditional OLIs, charge coupled device (CCD) sensors [5] and position sensitive detectors (PSDs) [6] are applied and wafer defocus with micron precision is measured by analyzing the image removement of the gap in the WFT system based on a triangle method.

With the improvement of the exposure field of view (FOV) and resolution in new-fashioned OLI [7], the WFT needs higher measurement precision and thus the WFT is widely investigated [8,9]. Based on the Talbot-moiré effect [10] and interferometric spatial-phase imaging [11], a diffractive grating [12,13] is applied for wafer defocus measurement to improve the precision; another technique based on a probe beam scanner [14,15] is also introduced. By complicated analyzation and calculation, these two WFTs have nanometer measurement precision.

To improving the measurement efficiency of WFT with nanometer measurement precision, a simple WFT based on grating shearing interferometry is proposed in this paper. The defocus of the wafer is immediately detected by measuring the phase difference in the interference pattern at meridian position through the measurement system, which is simply composed of a diffractive grating and a CCD sensor. Like traditional grating interferometry [16,17], the advantages of grating shearing interferometry are its high precision and simple setup, while its calculation is complex. This paper proposes a spatial domain phase shift technique for calculating the phase difference in the interferometry fringe between the focus and defocus positions of the wafer.

In summary, a novel WFT based on grating shearing interferometry and a spatial domain phase shift technique is introduced to improve the measuring precision and efficiency. An experiment is carried out to verify the feasibility and calibrate the measurement precision of this technology in this paper.

2. Methodology

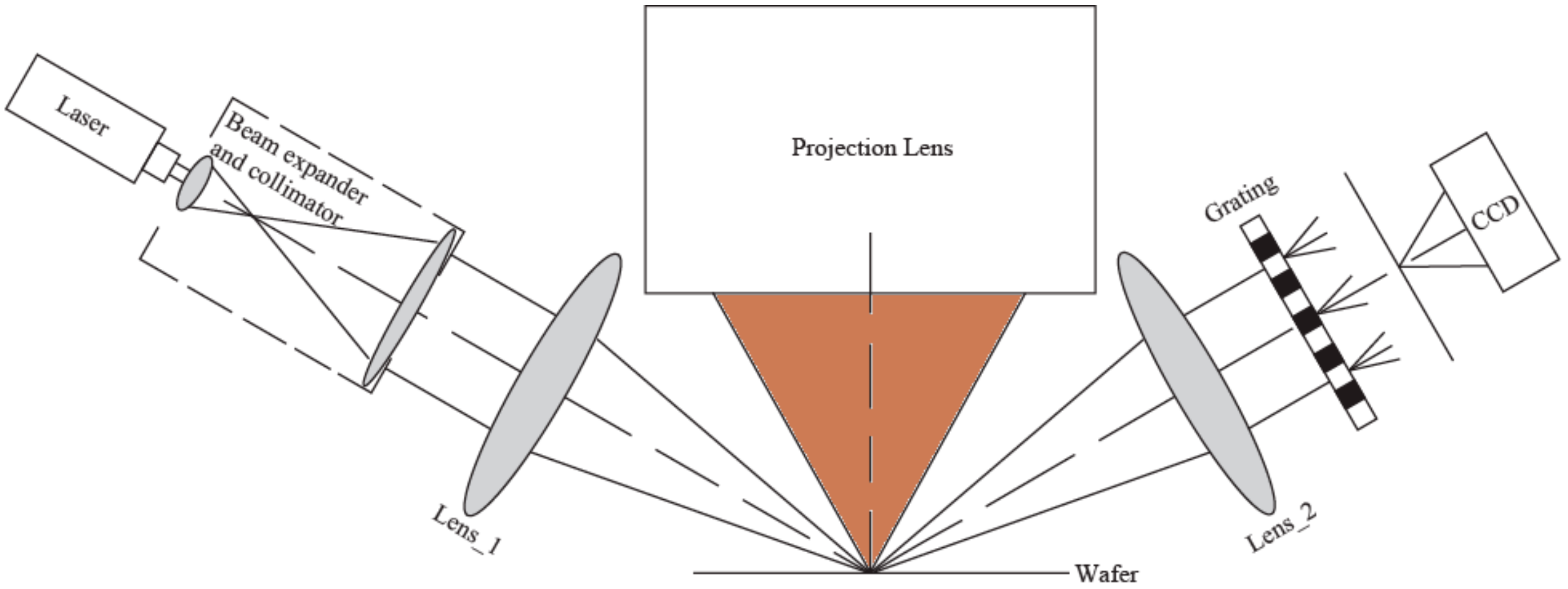
The measurement system for the WFT introduced in this paper is simply composed of a laser, beam expander and collimator, 4f optical lenses, a diffractive grating and CCD (charge coupled device), as shown in Figure 1.

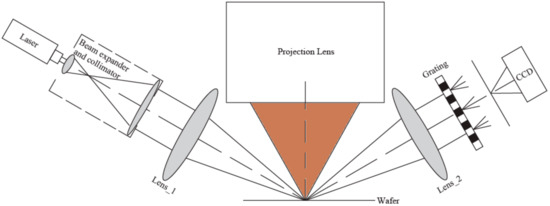
Figure 1. Illustration of focus measurement system (CCD: charge coupled device).

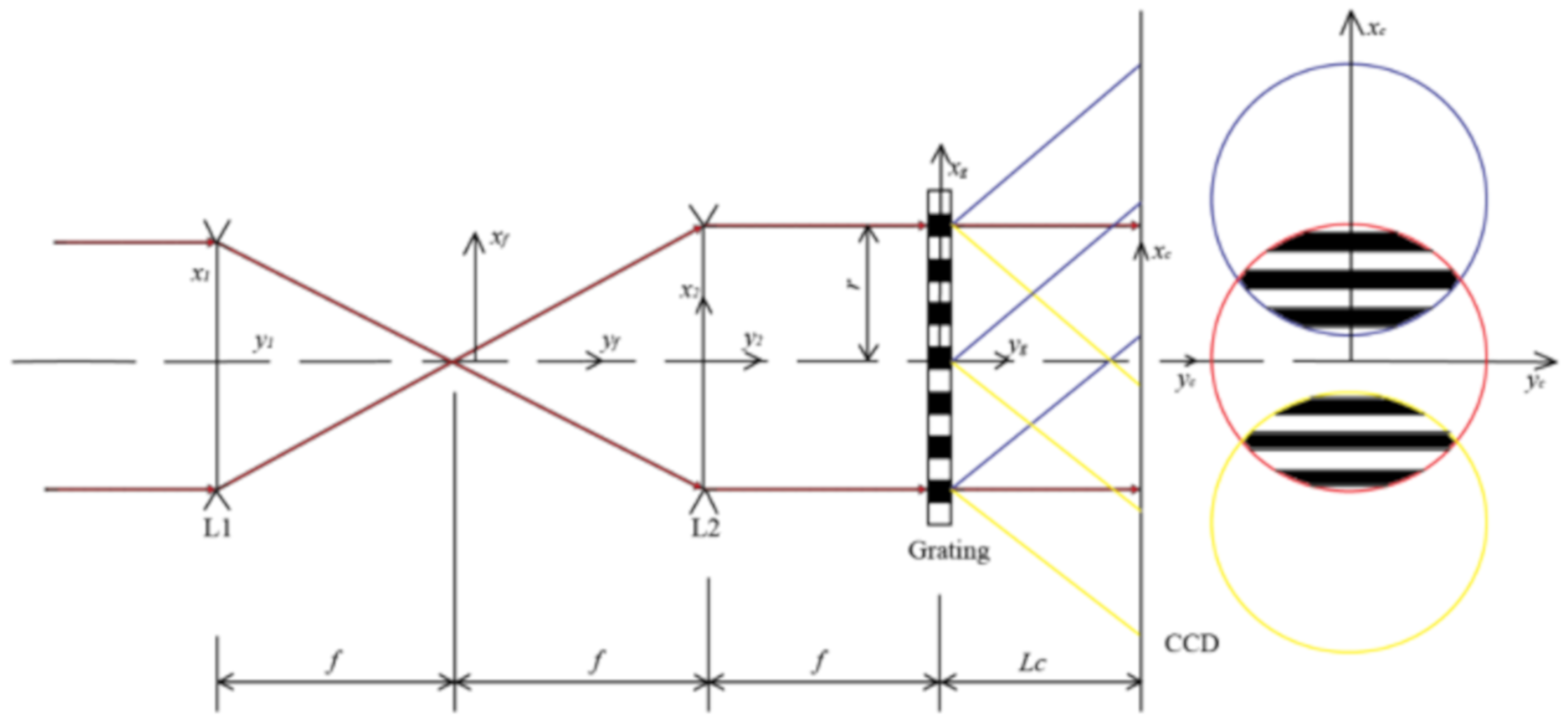
The plane wavefront formed by the beam expander and collimator is transformed by lenses and sheared by the diffractive grating. The diffractive wavefront of the grating and the coordinates of the measuring system are illustrated in Figure 2.

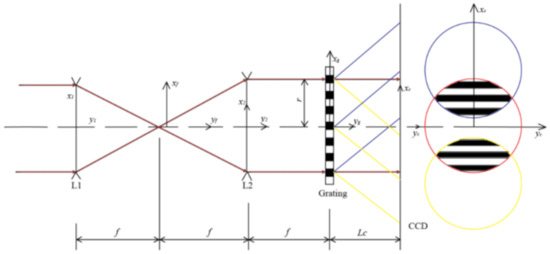
Figure 2. Illustration of grating diffractive wavefront.

When the wafer under investigation is positioned at the co-focal plane lenses, the distribution of diffractive light intensity in the CCD sensor can be calculated as:

$$E_0\left(x_{\mathrm{g}},y_g\right)=E_0{c}_0+E_0{c}_1\exp \left(j2\pi \frac{x_g}{d}\right)+E_0{c}_1\exp \left(-j2\pi \frac{x_g}{d}\right)$$

(1)

In this equation, d is the period of the Ronchi grating, E₀ is the plural amplitude of the plane wavefront and c₀/c₁ is the diffractive factor of the grating. The distribution of plural amplitude, imaged by the CCD sensor, can be calculated as:

$$\begin{array}{l}{E}_0\left(x_{\mathrm{c}},y_c\right)=\frac{\exp \left(ik{L}_c\right)}{i\lambda L_c}\exp \left[\frac{ik\left(x_c^2+y_c^2\right)}{2L_c}\right]{\displaystyle \underset{\Sigma }{\iint }E\left(x_g,y_g\right)\exp \left[-ik\left(\frac{x_g{x}_{\mathrm{c}}+y_g{y}_{\mathrm{c}}}{L_c}\right)\right]}d{x}_{g}d{y}_{\mathrm{g}}\\ \approx E_0{c}_{0}cir\left(\frac{\sqrt{x_g^2+y_g^2}}{r}\right)+E_1{c}_{1}cir\left(\frac{\sqrt{{\left(x_g-\raisebox{1ex}{$\lambda L_c$}\!\left/ \!\raisebox{-1ex}{$d$}\right.\right)}^2+y_g^2}}{r}\right)\exp \left(2\pi i\frac{x_g-\raisebox{1ex}{$\lambda L_c$}\!\left/ \!\raisebox{-1ex}{$d$}\right.}{d}\right)\\ +E_1{c}_{1}cir\left(\frac{\sqrt{{\left(x_g+\raisebox{1ex}{$\lambda L_c$}\!\left/ \!\raisebox{-1ex}{$d$}\right.\right)}^2+y_g^2}}{r}\right)\exp \left(-2\pi i\frac{x_g+\raisebox{1ex}{$\lambda L_c$}\!\left/ \!\raisebox{-1ex}{$d$}\right.}{d}\right)\end{array}$$

(2)

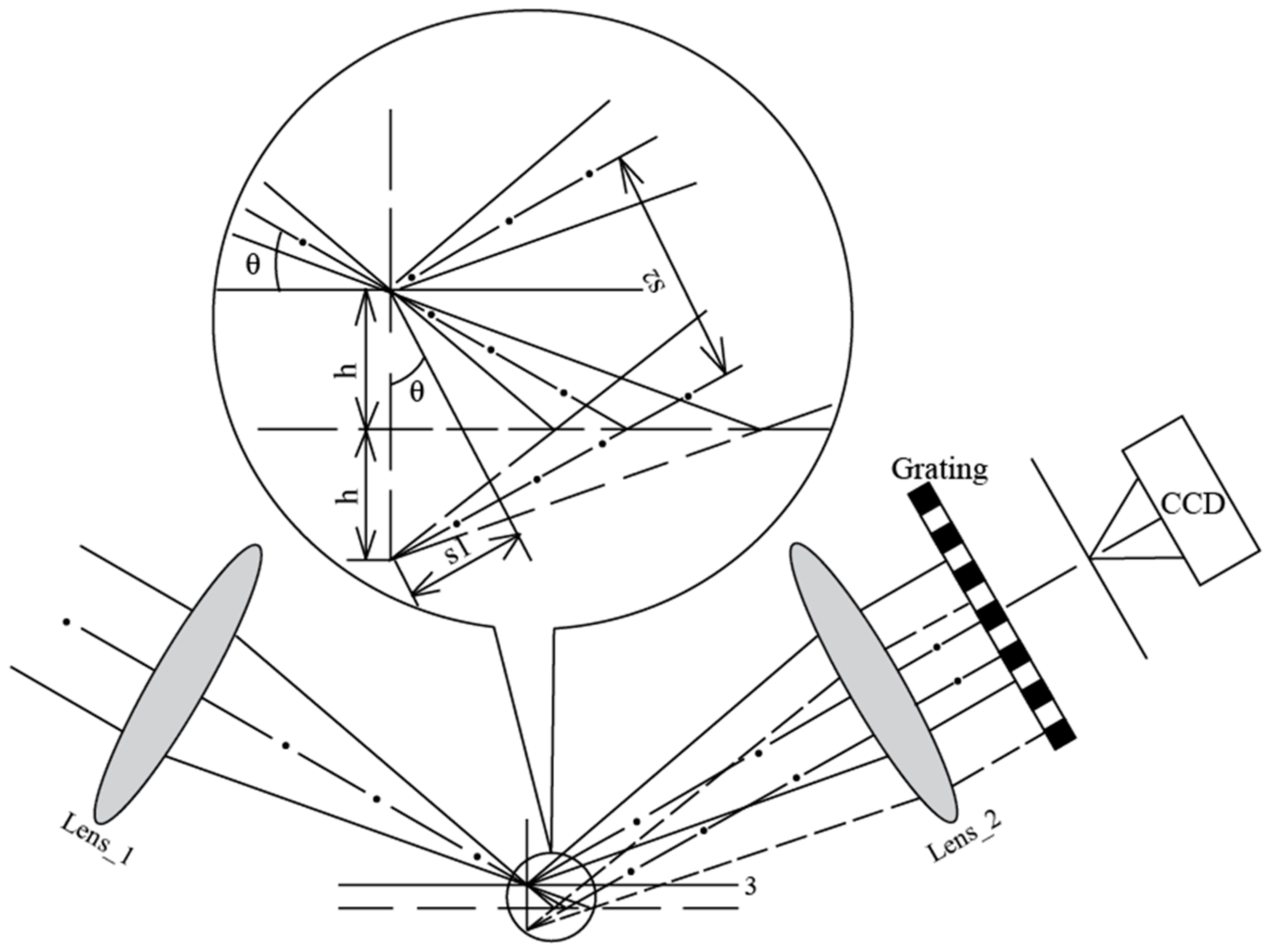
In Equation (2), r is the semi-diameter of diaphragm and L_c is the distance between the grating and the CCD sensor when the wafer is placed at a defocus position in relation to the projection lens, as shown in Figure 3.

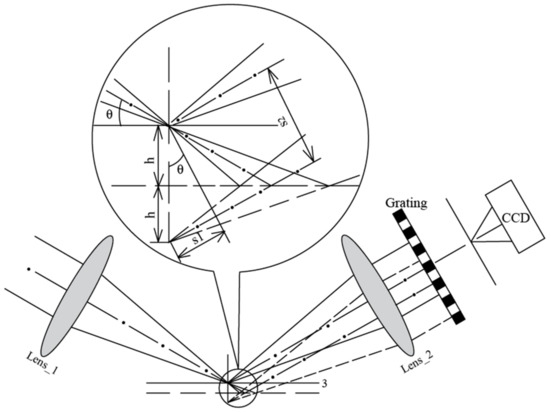
Figure 3. Illustration of defocus measurement system.

Based on the triangle principle, the defocus of wafer can be calculated in measuring system coordinates:

$$\left\{\begin{array}{l}{s}_1=2h\sin \theta \\ s_2=2h\cos \theta \end{array}\right.$$

(3)

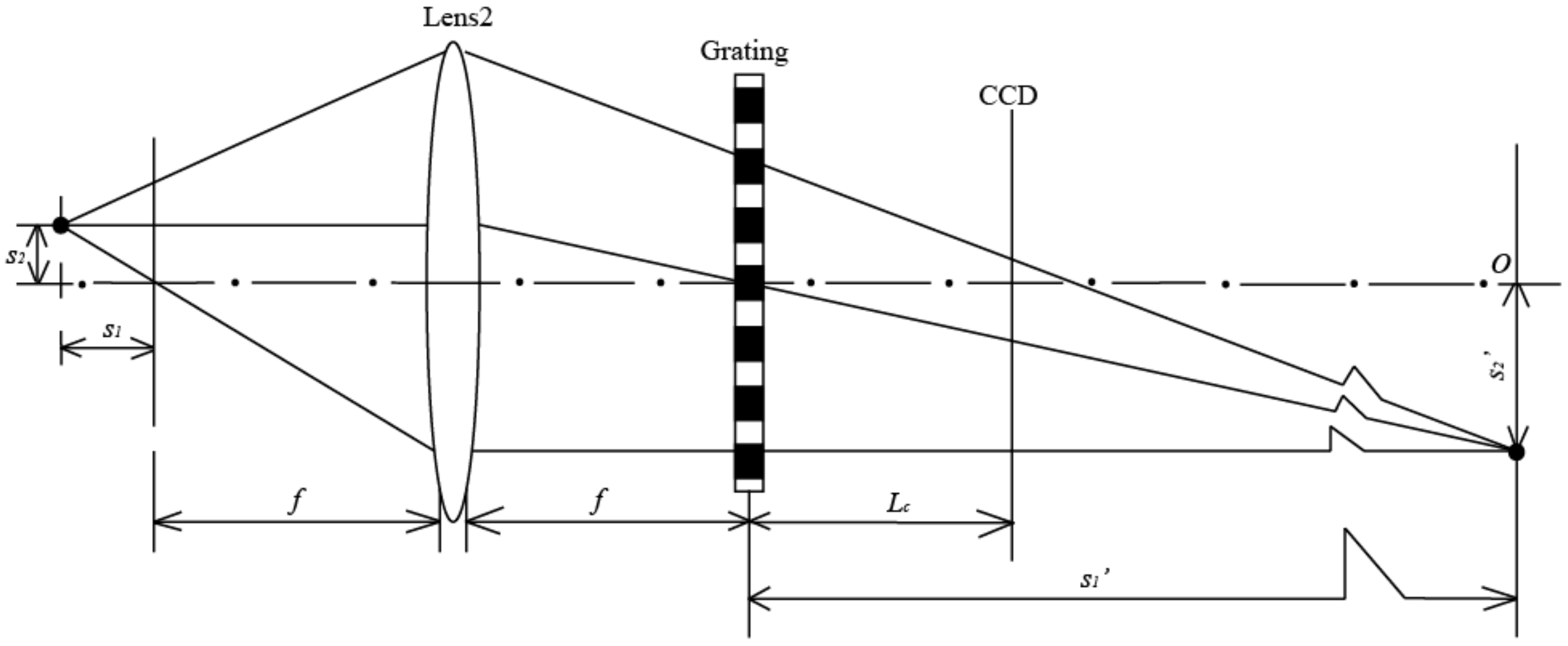
In this equation, s₁ and s₂ are axis defocus and vertical axis defocus, respectively. Defocus s₁ transforms the plane wavefront into a spherical wavefront in the 4f optical system and defocus s₂ engenders a phase shift in the measurement system, as shown in Figure 4.

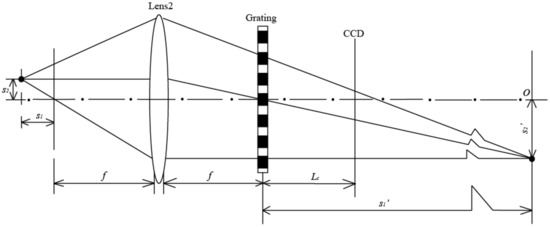
Figure 4. Element location of focus measurement system.

To simplify the analysis, the spherical wavefront is approximated as plane wavefront ($s_1$ << f). We calculated the intensity of the shearing interference area between the 0-order and ±1-order wavefronts of the grating diffractive:

$$\begin{array}{l}{E}_{\mathrm{s}}\left(x_g,y_g\right)=E_0{c}_0\exp \left(i2\pi \frac{s_2}{f}\right)+E_1{c}_1\exp \left[i2\pi \frac{\left(x_g+d\frac{s_2}{f}\right)}{d}\right]\\ \begin{array}{cc}& \end{array}+E_1{c}_1\exp \left[-i2\pi \frac{\left(x_g-d\frac{s_2}{f}\right)}{d}\right]\end{array}$$

(4)

The distribution of plural amplitude, imaged by the CCD sensor, can be calculated as:

$$\begin{array}{l}{E}_{\mathrm{s}}\left(x_{\mathrm{c}},y_c\right)=E_0{c}_{0}cir\left[\frac{\sqrt{{\left(x_c+\raisebox{1ex}{$s_2{L}_c$}\!\left/ \!\raisebox{-1ex}{$f$}\right.\right)}^2+y_c^2}}{r}\right]+\\ E_0{c}_{1}cir\left[\frac{\sqrt{{\left(x_c-\raisebox{1ex}{$\lambda L_c$}\!\left/ \!\raisebox{-1ex}{$d$}\right.+\raisebox{1ex}{$s_2{L}_c$}\!\left/ \!\raisebox{-1ex}{$f$}\right.\right)}^2+y_c^2}}{r}\right]\exp \left[i2\pi \frac{\left(x_c-\raisebox{1ex}{$\lambda L_c$}\!\left/ \!\raisebox{-1ex}{$d$}\right.+d\frac{s_2}{f}{L}_c\right)}{d}\right]\\ +E_0{c}_{1}cir\left[\frac{\sqrt{{\left(x_c+\raisebox{1ex}{$\lambda L_c$}\!\left/ \!\raisebox{-1ex}{$d$}\right.+\raisebox{1ex}{$s_2{L}_c$}\!\left/ \!\raisebox{-1ex}{$f$}\right.\right)}^2+y_c^2}}{r}\right]\exp \left[-i2\pi \frac{\left(x_c+\raisebox{1ex}{$\lambda L_c$}\!\left/ \!\raisebox{-1ex}{$d$}\right.+d\frac{s_2}{f}{L}_c\right)}{d}\right]\end{array}$$

(5)

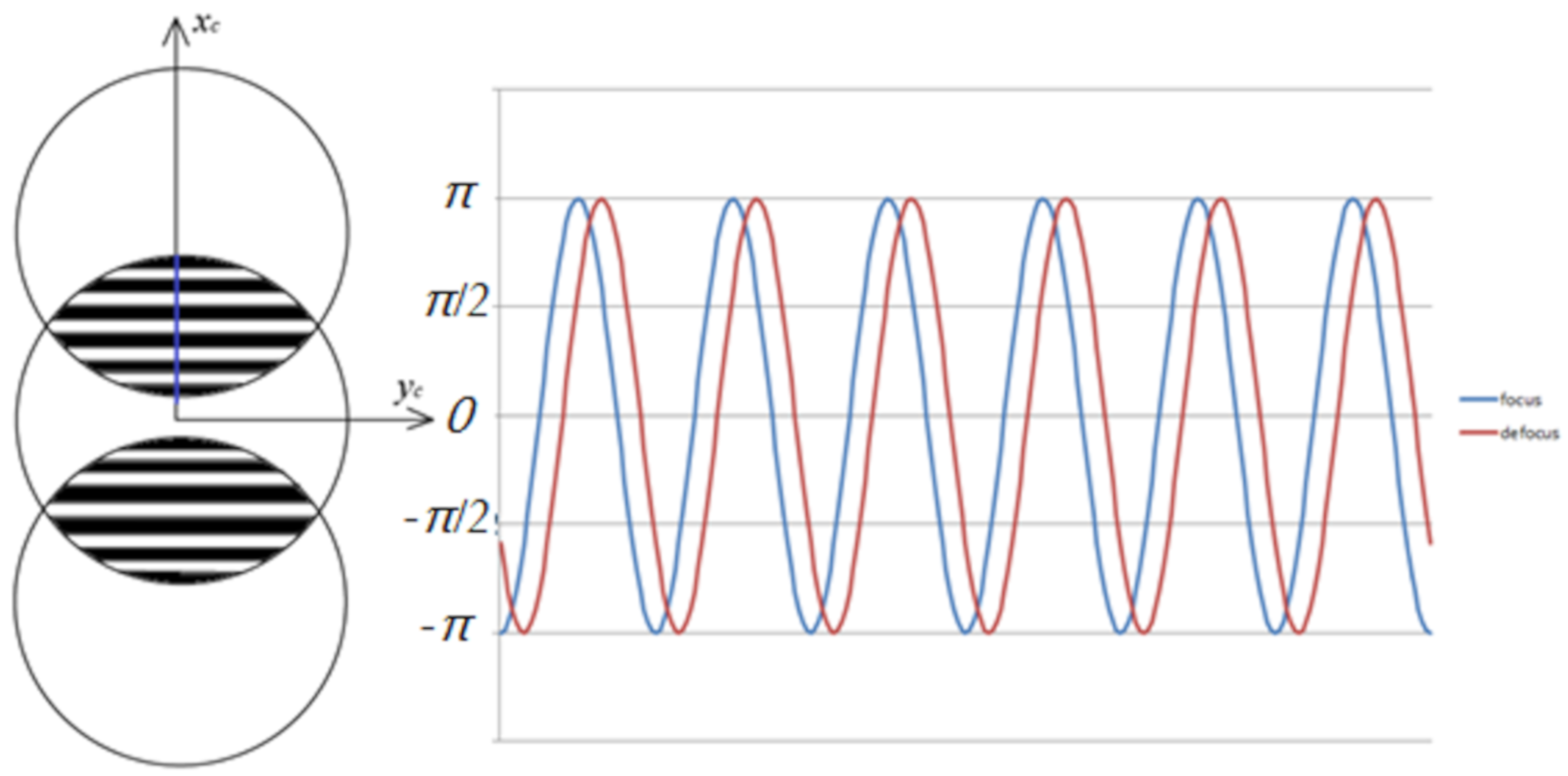
By contrasting Equations (2) and (5), we note that the defocus of the wafer is calculated in this system by measuring the phase shift of the interference pattern between the 0-order and ±1-order diffractive wavefronts, showed in Figure 5.

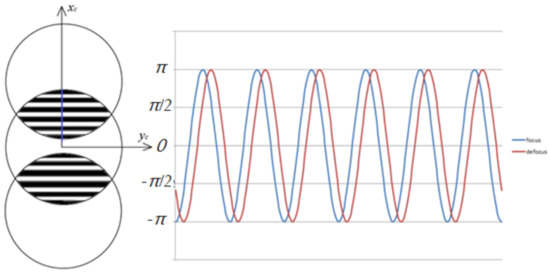
Figure 5. Simulation of phase shift at focus and defocus position.

By contrasting the phase shift δ between the focus and defocus positions, the defocus of wafer h can be calculated:

$$\delta =\frac{2\pi }{\mathrm{d}}\frac{L_c{s}_2}{f}=\frac{2\pi }{\mathrm{d}}\frac{2L_{c}h\cos \theta }{f}$$

(6)

As the parameters of the measuring system (focal length of lens f, distance between the grating and CCD sensor L_c, and the period of grating d) are fixed, the defocus of the wafer is measured by the phase extraction between the focus and defocus positions.

3. Experiment

An experiment is proceeded to verify the feasibility and calculate the measurement precision of this technology, which is conducted by the measurement system shown in Figure 6.

Figure 6. Measurement system for wafer focusing technique (WFT).

When analyzed by Equation (6), the defocus of wafer can be calculated as (light way θ is 30°):

$$\mathrm{h}=\frac{df\delta }{2\sqrt{3}\pi L_c}$$

(7)

The measuring uncertainty can be calculated by:

$${\mathrm{u}}_h=\sqrt{{\left(\frac{\partial h}{\partial d}{u}_d\right)}^2+{\left(\frac{\partial h}{\partial \delta }{u}_{\delta }\right)}^2+{\left(\frac{\partial h}{\partial L_c}{u}_{Lc}\right)}^2+{\left(\frac{\partial h}{\partial f}{u}_f\right)}^2}$$

(8)

In this equation, the measuring uncertainty is impacted by the phase extraction precision and the parameters of the measuring system (focal length of lens f, distance between the grating and CCD sensor L_c, and the period of grating d). The measurement parameter and uncertainty factor in this system are analyzed in Table 1.

Table 1. Measurement uncertainty in the system.

Parameter	Uncertainty Factor
d: 16.67 μm period of grating measured by microscope Ud as 0.1 μm	0.06
δ: 1.1 rad (1 μm defocus) phase extracted by wavelet transform Uδ as 0.02 rad	0.92
Lc: 50 mm distance is measured by rangefinder ULc as 0.01 mm	0.02
f: 30 mm focal length is calibrated Uf as 0.1 mm	0.03
Complex measuring uncertainty Uh is calculated as 19.7 nm

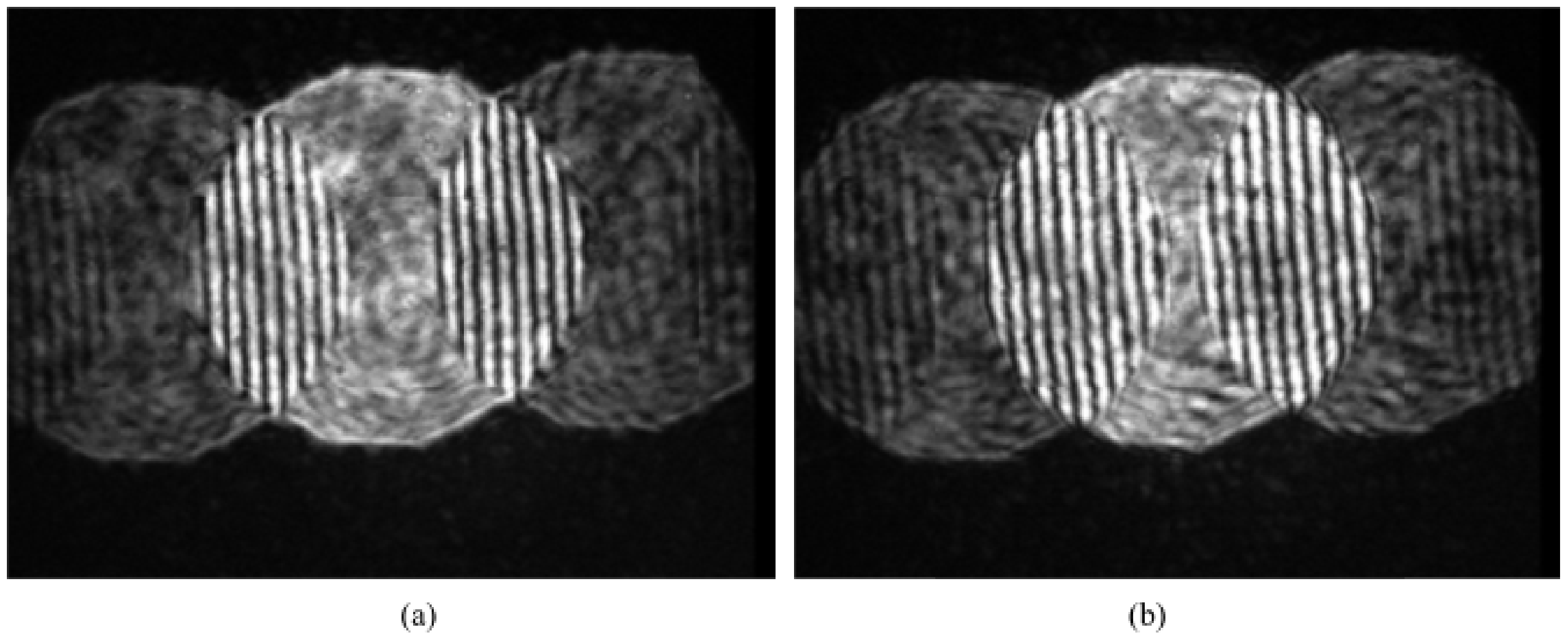
The main measuring uncertainty is impacted by phase extraction precision. Instead of the wafer, a reflex lens is applied and controlled by an electronic driver and an interferometer is also applied for reference. As the Reflex lenses are driven, they form a 1000-nm defocus to focus position; the interferometry pattern detected by CCD is shown in Figure 7.

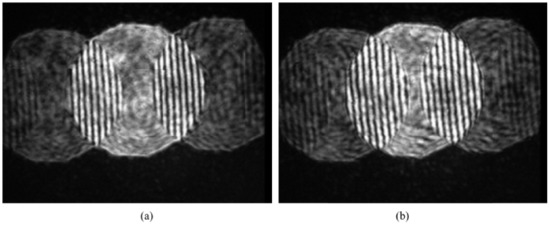
Figure 7. Distribution of interferometry pattern detected by CCD sensor: (a) wafer at focus position; (b) wafer at defocus position.

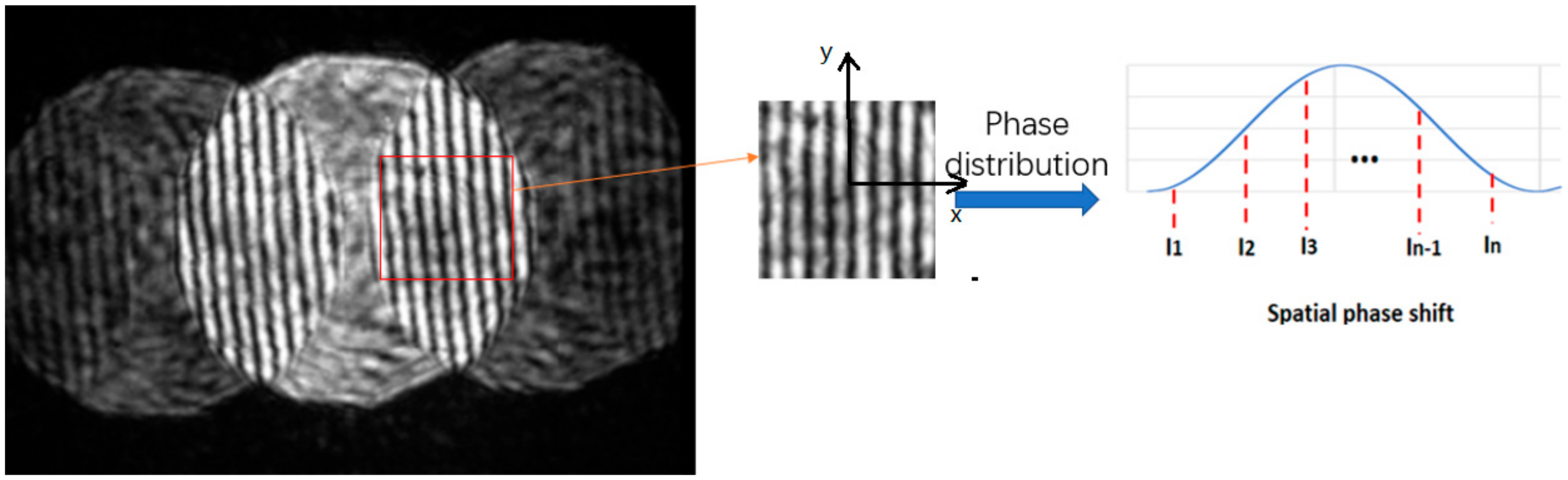
To indicate the precision of this technique, the reflex lens, instead of the wafer, is driven by a piezo driver 1 μm from the focus to defocus position detected by the interferometer. A method based on the spatial domain phase shift technique is applied for the phase parsing of the shearing interferometry fringe.

The phase distribution is calculated by the light intensity of a nearby pixel (n = 5 in Figure 8):

$$\delta (x,y)=\arctan (\frac{2(I_1-I_3)}{2I_2-I_0-I_4}\sqrt{1-{\left[\frac{I_0-I_4}{2(I_1-I_3)}\right]}^2})$$

(9)

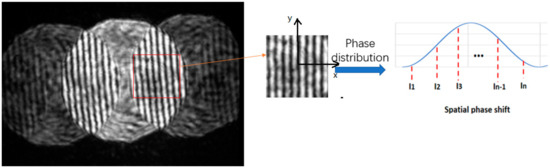
Figure 8. Phase parsing by spatial domain phase shift technique.

We chose ten optional pixels to calculate the phase difference in the interferometry fringe between the focus and defocus positions of the wafer.

Tens of measurement results are calculated by a single shot of CCD; this method ensures measurement precision and efficiency. The measurement result is shown in Table 2.

Table 2. Measurement result contrasted with interferometer.

Shearing: 988.2 995.3 1013.5 996.3 1003.5 985.4 991.4 986.2 1002.8 1009.7 Interferometer: detected as 1000 nm

Statistics: PV 28.1 nm, RMS: 9.8 nm

After analyzing and contrasting these measurement errors using the interferometer, the final measurement precision precedes 30 nm.

4. Conclusions

On the whole, a novel WFT based on grating shearing interferometry and the spatial domain phase shift technique is introduced in detail and the measurement system is simply composed of a diffractive grating. By calibration, using an interferometer, an experiment is proposed to verify the measurement feasibility, which indicates the outstanding advantages of this WFT, including its simple setup and high measurement accuracy (30 nm).