Snake Robot with Driving Assistant Mechanism
Abstract
1. Introduction
2. Materials and Methods
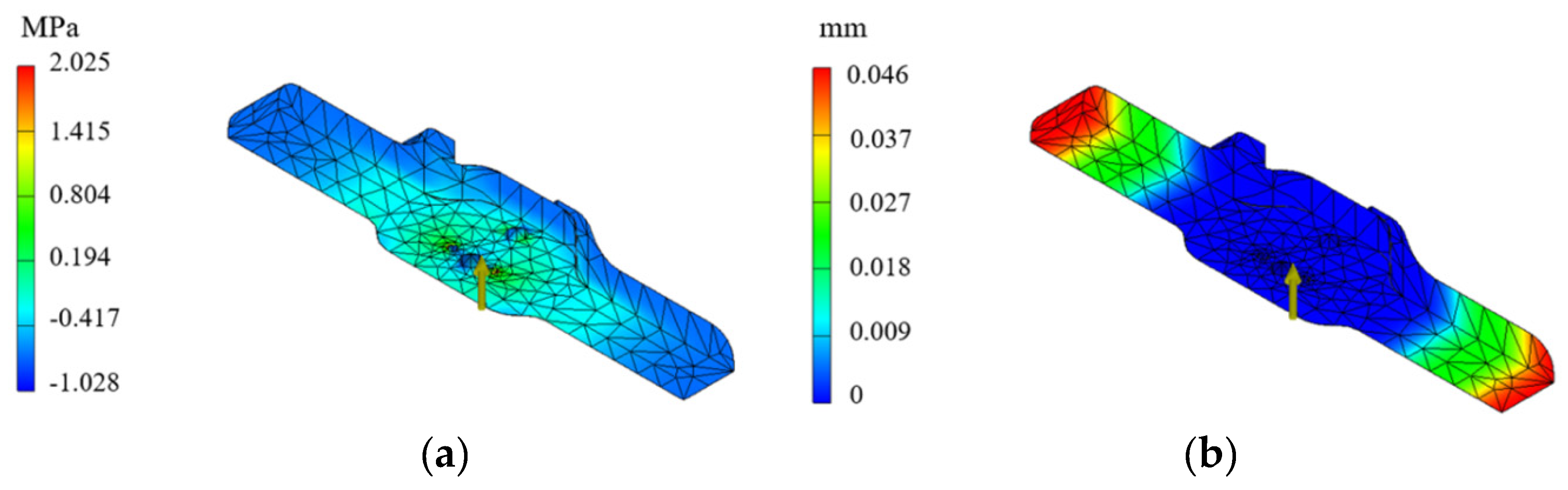
2.1. Design of the Snake Robot with a DAM
2.2. Dynamic Modeling of Driving Assistant Mechanism
2.3. Experiment of Slope Condition
2.4. Locomotion Experiment for Various Gait Types
2.5. Friction Experiment of the DAM and the Frame
2.6. Locomotion Experiment for Various Terrains
3. Results
3.1. Experiment Results of Slope Condition
3.2. Locomotion Experiment Results for Various Gait Types
3.3. Friction Experiment of the DAM and the Frame
3.4. Locomotion Experiment Results on Various Terrains
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sanfilippo, F.; Azpiazu, J.; Marafioti, G.; Transeth, A.A.; Stavdahl, Ø.; Liljebäck, P. Perception-driven obstacle-aided locomotion for snake robots: The state of the art, challenges and possibilities. Appl. Sci. 2017, 7, 336. [Google Scholar] [CrossRef]
- Yun, D. Development of a mobile robot mimicking the frilled lizard. J. Mech. Sci. Technol. 2018, 32, 1787–1792. [Google Scholar] [CrossRef]
- Ariizumi, R.; Matsuno, F. Dynamic analysis of three snake robot gaits. IEEE Trans. Robot. 2017, 33, 1075–1087. [Google Scholar] [CrossRef]
- Liljeback, P.; Pettersen, K.Y.; Stavdahl, Ø.; Gravdahl, J.T. Controllability and stability analysis of planar snake robot locomotion. IEEE Trans. Autom. Control 2010, 56, 1365–1380. [Google Scholar] [CrossRef]
- Takemori, T.; Tanaka, M.; Matsuno, F. Gait design for a snake robot by connecting curve segments and experimental demonstration. IEEE Trans. Robot. 2018, 34, 1384–1391. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q.; Shen, D.; Chen, J. A Novel Rescue Robot: Hybrid Soft and Rigid Structures for Narrow Space Searching. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, Yunnan, China, 6–8 December 2019; pp. 2207–2213. [Google Scholar]
- Manzoor, S.; Khan, U.; Ullah, I. Serpentine and Rectilinear Motion Generation in Snake Robot Using Central Pattern Generator with Gait Transition. Iran. J. Sci. Technol. Trans. Electr. Eng. 2019, 44, 1–11. [Google Scholar] [CrossRef]
- Huq, N.M.L.; Khan, M.R.; Shafie, A.A.; Billah, M.M.; Ahmmad, S.M. Motion Investigation of a Snake Robot with Different Scale Geometry and Coefficient of Friction. Robotics 2018, 7, 18. [Google Scholar] [CrossRef]
- Liljebäck, P.; Pettersen, K.Y.; Stavdahl, Ø.; Gravdahl, J.T. A review on modelling, implementation, and control of snake robots. Robot. Auton. Syst. 2012, 60, 29–40. [Google Scholar] [CrossRef]
- Selvarajan, A.; Kumar, A.; Sethu, D.; bin Ramlan, M.A. Design and Development of a Snake-Robot for Pipeline Inspection. In Proceedings of the 2019 IEEE Student Conference on Research and Development (SCOReD), Bandar Seri Iskandar, Malaysia, 15–17 October 2019; pp. 237–242. [Google Scholar]
- Whitman, J.; Zevallos, N.; Travers, M.; Choset, H. Snake robot urban search after the 2017 Mexico City earthquake. In Proceedings of the 2018 IEEE international symposium on safety, security, and rescue robotics (SSRR), Philadelphia, PA, USA, 6–8 August 2018; pp. 1–6. [Google Scholar]
- Chang, A.H.; Vela, P.A. Shape-centric modeling for control of traveling wave rectilinear locomotion on snake-like robots. Robot. Auton. Syst. 2020, 124, 103406. [Google Scholar] [CrossRef]
- Manzoor, S.; Cho, Y.G.; Choi, Y. Neural oscillator based CPG for various rhythmic motions of modular snake robot with active joints. J. Intell. Robot. Syst. 2019, 94, 641–654. [Google Scholar] [CrossRef]
- Yun, D.; Fearing, R.S. Cockroach Milli-Robot With Improved Load Capacity. J. Mech. Robot. 2019, 11, 1. [Google Scholar] [CrossRef]
- Yun, D.; Kim, K.-S.; Kim, S.; Kyung, J.; Lee, S. Note: Dynamic analysis of a robotic fish motion with a caudal fin with vertical phase differences. Rev. Sci. Instrum. 2013, 84, 036108. [Google Scholar] [CrossRef] [PubMed]
- Gong, C.; Tesch, M.; Rollinson, D.; Choset, H. Snakes on an inclined plane: Learning an adaptive sidewinding motion for changing slopes. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 1114–1119. [Google Scholar]
- Koopaee, M.J.; Bal, S.; Pretty, C.; Chen, X. Design and Development of a Wheel-less Snake Robot with Active Stiffness Control for Adaptive Pedal Wave Locomotion. J. Bionic Eng. 2019, 16, 593–607. [Google Scholar] [CrossRef]
- Sanfilippo, F.; Helgerud, E.; Stadheim, P.A.; Aronsen, S.L. Serpens, a low-cost snake robot with series elastic torque-controlled actuators and a screw-less assembly mechanism. In Proceedings of the 2019 5th International Conference on Control, Automation and Robotics (ICCAR), Beijing, China, 19–22 April 2019; pp. 133–139. [Google Scholar]
- Transeth, A.A.; Leine, R.I.; Glocker, C.; Pettersen, K.Y.; Liljebäck, P. Snake robot obstacle-aided locomotion: Modeling, simulations, and experiments. IEEE Trans. Robot. 2008, 24, 88–104. [Google Scholar] [CrossRef]
- Fjerdingen, S.A.; Liljebäck, P.; Transeth, A.A. A snake-like robot for internal inspection of complex pipe structures (PIKo). In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 5665–5671. [Google Scholar]
- Mori, M.; Hirose, S. Three-dimensional serpentine motion and lateral rolling by active cord mechanism ACM-R3. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002; pp. 829–834. [Google Scholar]
- McKenna, J.C.; Anhalt, D.J.; Bronson, F.M.; Brown, H.B.; Schwerin, M.; Shammas, E.; Choset, H. Toroidal skin drive for snake robot locomotion. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 1150–1155. [Google Scholar]
- Ma, S.; Tadokoro, N. Analysis of creeping locomotion of a snake-like robot on a slope. Auton. Robot. 2006, 20, 15–23. [Google Scholar] [CrossRef]
- Bing, Z.; Cheng, L.; Knoll, A.; Zhong, A.; Huang, K.; Zhang, F. Slope angle estimation based on multi-sensor fusion for a snake-like robot. In Proceedings of the 2017 20th International Conference on Information Fusion (Fusion), Xi’an, China, 10–13 July 2017; pp. 1–6. [Google Scholar]
- Li, D.; Wang, C.; Deng, H.; Wei, Y. Motion Planning Algorithm of a Multi-Joint Snake-Like Robot Based on Improved Serpenoid Curve. IEEE Access 2020, 8, 8346–8360. [Google Scholar] [CrossRef]

























| Symbol | Description | Value | Unit |
|---|---|---|---|
| L | Length of the DAM (Length of the Servo Motor) | 0.09, 0.12, 0.15, 0.18 (0.045) | m |
| Lcm | Y coordinate of the one module’s center of mass | 0.034 | m |
| L1 | Distance between rotational axis and gravity force | - | m |
| L2 | Distance between rotational axis and action force | - | m |
| L3 | Distance between rotational axis and gravity force | - | m |
| θ1 | Degree of the inclined plane | - | rad |
| m | Mass of the one module of the snake robot | 0.175 | kg |
| I | Moment of inertia without DAM (with DAM) | 0.00097 (0.0012) | kg·m2 |
| KT | Motor torque constant | 1.23 | A/N·m |
| i0 | No load current | 0.07 | A |
| g | Acceleration of gravity | 9.81 | m/s2 |
| Fm2 | Magnitude of substitution force of | - | N |
| Fm3 | Magnitude of reaction force of | - | N |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bae, J.; Kim, M.; Song, B.; Jin, M.; Yun, D. Snake Robot with Driving Assistant Mechanism. Appl. Sci. 2020, 10, 7478. https://doi.org/10.3390/app10217478
Bae J, Kim M, Song B, Jin M, Yun D. Snake Robot with Driving Assistant Mechanism. Applied Sciences. 2020; 10(21):7478. https://doi.org/10.3390/app10217478
Chicago/Turabian StyleBae, Junseong, Myeongjin Kim, Bongsub Song, Maolin Jin, and Dongwon Yun. 2020. "Snake Robot with Driving Assistant Mechanism" Applied Sciences 10, no. 21: 7478. https://doi.org/10.3390/app10217478
APA StyleBae, J., Kim, M., Song, B., Jin, M., & Yun, D. (2020). Snake Robot with Driving Assistant Mechanism. Applied Sciences, 10(21), 7478. https://doi.org/10.3390/app10217478







