Three-Dimensional Magnetic Inversion Based on an Adaptive Quadtree Data Compression
Abstract
:1. Introduction
2. Methods
2.1. Inversion Method
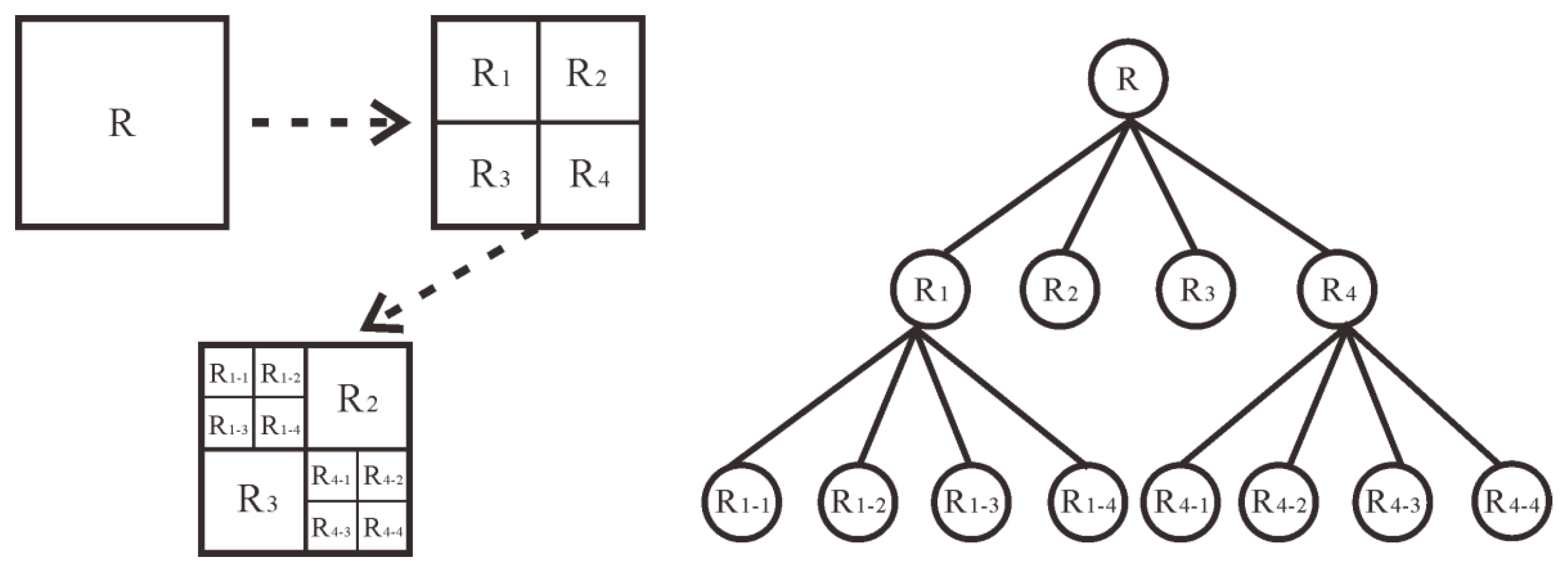
2.2. Adaptive Quadtree Data Compression Algorithm
2.3. Synthetic Model Test
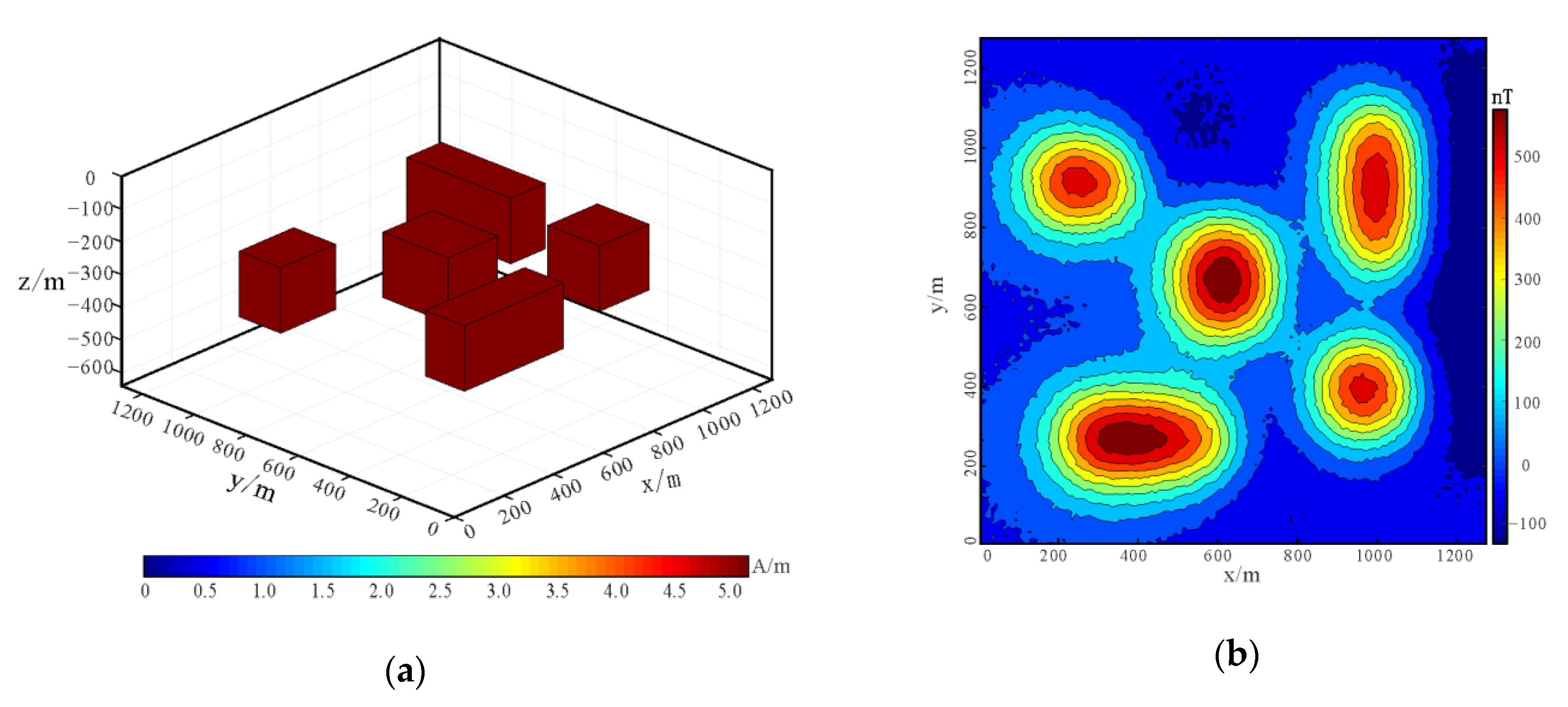
3. Application in Mineral Exploration
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nabighian, M.N.; Hansen, R.O.; Lafehr, T.R.; Li, Y.; Peirce, J.W.; Phillips, J.D.; Ruder, M.E. The historical development of the magnetic method in exploration. Geophysics 2005, 70, 33ND–61ND. [Google Scholar] [CrossRef]
- Yan, H.-F.; Liu, G.-F. A extension of probability tomography of gravity data. Prog. Geophys. 2014, 29, 1837–1842. [Google Scholar]
- Mauriello, P.; Patella, D. Localization of magnetic sources underground by a data adaptive tomographic scanner. arXiv 2005, arXiv:0511192v2. [Google Scholar]
- Mauriello, P.; Patella, D. Localization of magnetic sources underground by a probability tomography approach. Prog. Electromagn. Res. M 2008, 3, 27–56. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Shi, L.; Meng, X. 3D correlation imaging of magnetic total field anomaly and its vertical gradient. J. Geophys. Eng. 2011, 8, 287–293. [Google Scholar] [CrossRef] [Green Version]
- Boschetti, F.; Dentith, M.; List, R. Inversion of potential field data by genetic algorithms. Geophys. Prospect. 1997, 45, 461–478. [Google Scholar] [CrossRef]
- Guan, Z.-N.; Hou, J.-S.; Huang, L.-P.; Yao, C.-L. Inversion of gravity and magnetic anomalies using pseduo-BP neural network method and its application. Chin. J. Geophys. 1998, 41, 242–251. [Google Scholar]
- Pilkington, M. 3-D magnetic imaging using conjugate gradients. Geophysics 1997, 62, 1132–1142. [Google Scholar] [CrossRef]
- Li, Y.; Melo, A.; Martinez, C.; Sun, J. Geology differentiation: A new frontier in quantitative geophysical interpretation in mineral exploration. Lead. Edge 2019, 38, 60–66. [Google Scholar] [CrossRef]
- Zhdanov, M.S.; Alfouzan, F.; Cox, L.H.; Alotaibi, A.M.; Alyousif, M.M.; Sunwall, D.; Endo, M. Large-Scale 3D Modeling and Inversion of Multiphysics Airborne Geophysical Data: A Case Study from the Arabian Shield, Saudi Arabia. Minerals 2018, 8, 271. [Google Scholar] [CrossRef] [Green Version]
- Green, W.R. Inversion of Gravity Profiles by Use of a Backus-Gilbert Approach. Geophysics 1975, 40, 763–772. [Google Scholar] [CrossRef]
- Last, B.J.; Kubik, K. Compact gravity inversion. Geophysics 1983, 48, 713–721. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of magnetic data. Geophysics 1996, 61, 394–408. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of gravity data. Geophysics 1998, 63, 109–119. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M.S. 3-D magnetic inversion with data compression and image focusing. Geophysics 2000, 67, 1532–1541. [Google Scholar] [CrossRef] [Green Version]
- Portniaguine, O. Image Focusing and Data Compression in the Solution of Geophysical Inverse Problems. Ph.D. Thesis, The University of Utah, Salt Lake City, UT, USA, 1999. [Google Scholar]
- Zhdanov, M.S.; Ellis, R.G.; Mukherjee, S. Three-dimensional regularized focusing inversion of gravity gradient tensor component data. Geophysics 2004, 69, 925–937. [Google Scholar] [CrossRef]
- Sun, J.; Li, Y. Geophysical inversion using petrophysical constraints with application to lithology differentiation. In Proceedings of the 2011 SEG Annual Meeting, San Antonio, TX, USA, 18–23 September 2011. [Google Scholar]
- Sun, J.; Li, Y. Multidomain petrophysically constrained inversion and geology differentiation using guided fuzzy c-means clustering. Geophysics 2015, 80, ID1–ID18. [Google Scholar] [CrossRef]
- Silva, J.B.C.; Medeiros, W.E.; Barbosa, V.C.F. Potential-field inversion: Choosing the appropriate technique to solve a geologic problem. Geophysics 2001, 66, 511–520. [Google Scholar] [CrossRef]
- Pilkington, M. 3D magnetic data-space inversion with sparseness constraints. Geophysics 2008, 74, L7–L15. [Google Scholar] [CrossRef]
- Commer, M. Three-dimensional gravity modeling and focusing inversion using rectangular meshes. Geophys. Prospect. 2011, 59, 966–979. [Google Scholar]
- Paoletti, V.; Ialongo, S.; Florio, G.; Fedi, M.; Cella, F. Self-constrained inversion of potential fields. Geophys. J. Int. 2013, 195, 854–869. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Li, Y. Adaptive Lp inversion for simultaneous recovery of both blocky and smooth features in a geophysical model. Geophys. J. Int. 2014, 197, 882–899. [Google Scholar] [CrossRef] [Green Version]
- Uieda, L.; Barbosa, V.C.F. Robust 3D gravity gradient inversion by planting anomalous densities. Geophysics 2012, 77, G55–G66. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. Fast inversion of large-scale magnetic data using wavelet transforms and a logarithmic barrier method. Geophys. J. Int. 2003, 152, 251–265. [Google Scholar] [CrossRef] [Green Version]
- Yao, C.; Hao, T.; Guan, Z.; Zhang, J. High-speed calculation and effective storage method and technology in 3D inversion of gravity and magnetic genetic algorithm. Chin. J. Geophys. 2003, 46, 252–258. [Google Scholar] [CrossRef]
- Cuma, M.; Wilson, G.A.; Zhdanov, M.S. Large-scale 3D inversion of potential field data. Geophys. Prospect. 2012, 60, 1186–1199. [Google Scholar] [CrossRef]
- Čuma, M.; Zhdanov, M.S. Massively parallel regularized 3D inversion of potential fields on CPUs and GPUs. Comput. Geoences 2014, 62, 80–87. [Google Scholar] [CrossRef]
- Hou, Z.; Huang, D. Multi-GPU parallel algorithm design and analysis for improved inversion of probability tomography with gravity gradiometry data. J. Appl. Geophys. 2017, 144, 18–27. [Google Scholar] [CrossRef]
- Ascher, U.M.; Haber, E. Grid refinement and scaling for distributed parameter estimation problems. Inverse Probl. 2001, 17, 571–590. [Google Scholar] [CrossRef] [Green Version]
- Davis, K.; Li, Y. Fast solution of geophysical inversion using adaptive mesh, space-filling curves and wavelet compression. Geophys. J. Int. 2011, 185, 157–166. [Google Scholar] [CrossRef] [Green Version]
- Davis, K.; Li, Y. Efficient 3D inversion of magnetic data via octree-mesh discretization, space-filling curves, and wavelets. Geophys. J. Soc. Explor. Geophys. 2013, 78, J61–J73. [Google Scholar] [CrossRef]
- Yang, M.; Wang, W.; Welford, J.K.; Farquharson, C. 3D gravity inversion with optimized mesh based on edge and center anomaly detection. Geophysics 2019, 84, 1–62. [Google Scholar] [CrossRef]
- Foks, N.L.; Krahenbuhl, R.; Li, Y. Adaptive sampling of potential-field data: A direct approach to compressive inversion. Geophysics 2014, 79, 1–9. [Google Scholar] [CrossRef]
- Vatankhah, S.; Renaut, R.A.; Ardestani, V.E. Total variation regularization of the 3-D gravity inverse problem using a randomized generalized singular value decomposition. Geophys. J. Int. 2018, 213, 695–705. [Google Scholar] [CrossRef] [Green Version]
- Toushmalani, R.; Saibi, H. Fast 3D inversion of gravity data using Lanczos bidiagonalization method. Arab. J. Geosci. 2015, 8, 4969–4981. [Google Scholar] [CrossRef]
- Meng, Z.; Li, F.; Zhang, D.; Xu, X.; Huang, D. Fast 3D inversion of airborne gravity-gradiometry data using Lanczos bidiagonalization method. J. Appl. Geophys. 2016, 132, 211–228. [Google Scholar] [CrossRef]
- Rezaie, M.; Moradzadeh, A.; Kalate, A.N.; Aghajani, H. Fast 3D Focusing Inversion of Gravity Data Using Reweighted Regularized Lanczos Bidiagonalization Method. Pure Appl. Geophys. 2017, 174, 359–374. [Google Scholar] [CrossRef]
- Klinger, A.; Dyer, C.R. Experiments on Picture Representation Using Regular Decomposition. Comput. Graph. Image Process. 1976, 5, 68–105. [Google Scholar] [CrossRef]
- Yerry, M.A.; Shephard, M.S. A Modified Quadtree Approach To Finite Element Mesh Generation. IEEE Comput. Graph. Appl. 1983, 3, 39–46. [Google Scholar] [CrossRef]
- Jackson, D.J.; Mahmoud, W.; Stapleton, W.A.; Gaughan, P.T. Faster fractal image compression using quadtree recomposition. Image Vis. Comput. 1997, 15, 759–767. [Google Scholar] [CrossRef]
- Zeng, Z.; Cumming, I. SAR image data compression using a tree-structured wavelet transform. IEEE Trans. Geosci. Remote Sens. 2001, 39, 546–552. [Google Scholar] [CrossRef] [Green Version]
- Tikhonov, A.N.; Arsenin, V.Y. Solutions of ill-posed problems. Math. Comput. 1977, 32, 491. [Google Scholar]
- Li, Y. 3-D Inversion of gravity gradiometer data. In Proceedings of the SEG Int’l Exposition and Annual Meeting, San Antonio, TX, USA, 9–14 September 2001. [Google Scholar]
- Bertrand, L.; Gavazzi, B.; Mercier de Lépinay, J.; Diraison, M.; Géraud, Y.; Munschy, M. On the Use of Aeromagnetism for Geological Interpretation: 2. A Case Study on Structural and Lithological Features in the Northern Vosges. J. Geophys. Res. Solid Earth 2020, 125, 5. [Google Scholar] [CrossRef]
- Pilkington, M.; Boulanger, O. Potential field continuation between arbitrary surfaces—Comparing methods. Geophysics 2017, 82, J9–J25. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, D.; Zeng, Z.; Zhou, S.; Guan, Y.; Lin, T.; Lu, P. Three-Dimensional Magnetic Inversion Based on an Adaptive Quadtree Data Compression. Appl. Sci. 2020, 10, 7636. https://doi.org/10.3390/app10217636
Jiang D, Zeng Z, Zhou S, Guan Y, Lin T, Lu P. Three-Dimensional Magnetic Inversion Based on an Adaptive Quadtree Data Compression. Applied Sciences. 2020; 10(21):7636. https://doi.org/10.3390/app10217636
Chicago/Turabian StyleJiang, Dandan, Zhaofa Zeng, Shuai Zhou, Yanwu Guan, Tao Lin, and Pengyu Lu. 2020. "Three-Dimensional Magnetic Inversion Based on an Adaptive Quadtree Data Compression" Applied Sciences 10, no. 21: 7636. https://doi.org/10.3390/app10217636




