DM: Dehghani Method for Modifying Optimization Algorithms

Abstract

In recent decades, many optimization algorithms have been proposed by researchers to solve optimization problems in various branches of science. Optimization algorithms are designed based on various phenomena in nature, the laws of physics, the rules of individual and group games, the behaviors of animals, plants and other living things. Implementation of optimization algorithms on some objective functions has been successful and in others has led to failure. Improving the optimization process and adding modification phases to the optimization algorithms can lead to more acceptable and appropriate solution. In this paper, a new method called Dehghani method (DM) is introduced to improve optimization algorithms. DM effects on the location of the best member of the population using information of population location. In fact, DM shows that all members of a population, even the worst one, can contribute to the development of the population. DM has been mathematically modeled and its effect has been investigated on several optimization algorithms including: genetic algorithm (GA), particle swarm optimization (PSO), gravitational search algorithm (GSA), teaching-learning-based optimization (TLBO), and grey wolf optimizer (GWO). In order to evaluate the ability of the proposed method to improve the performance of optimization algorithms, the mentioned algorithms have been implemented in both version of original and improved by DM on a set of twenty-three standard objective functions. The simulation results show that the modified optimization algorithms with DM provide more acceptable and competitive performance than the original versions in solving optimization problems.

1. Introduction

The purpose of optimization is to determine the best solution among the available solutions for an optimization problem according to the constraints of problem [1]. Each optimization problem is designed with three parts: constraints, objective functions, and decision variables [2]. There are many optimization problems in different sciences that should be optimized using the appropriate method. Stochastic search-based optimization algorithms have always been of interest to researchers in solving optimization problems [3]. Optimization algorithms are able to provide a quasi-optimal solution based on random scan of the search space instead of a full scan. The quasi-optimal solution is not the best solution, but it is close to the global optimal solution of the problem [1]. In this regard, optimization algorithms have been applied by scientists in various fields such as energy [4,5,6], protection [7], electrical engineering [8,9,10,11,12,13], topology optimization [14] and energy carriers [15,16,17] to achieve the quasi-optimal solution.

Table 1. Optimization algorithms.

Optimization Algorithms	Swarm-based	General description: Designed based on simulation of the living thing behavior processes of the plants, and other swarm-based phenomena.
		Particle Swarm Optimization (PSO) [18], Ant Colony Optimization (ACO) [19,20], Spotted Hyena Optimizer (SHO) [21], Group Optimization (GO) [22], Artificial Bee Colony (ABC) [23], Following Optimization Algorithm (FOA) [24], Rat Swarm Optimizer (RSO) [2], Multi Leader Optimizer (MLO) [1], Bat-inspired Algorithm (BA) [25], Emperor Penguin Optimizer (EPO) [26], Cuckoo Search (CS) [27], Donkey Theorem Optimization (DTO) [28], Teaching-Learning-Based Optimization (TLBO) Algorithm [29], Grasshopper Optimization Algorithm (GOA) [30], Doctor and Patient Optimization (DPO) [31], Gray Wolf Optimizer (GWO) [32]	Ref. [18] The most widely used algorithm in this group, which is designed based on modeling the movement of birds. Refs. [19,20] It is based on the modeling the discovery of the shortest path by ants. Ref. [29] It has gained wide acceptance among the optimization researchers. This algorithm is a teaching-learning process inspired algorithm and is based on the effect of influence of a teacher on the output of learners in a class. Ref. [31] It is designed by simulating the process of treating patients by a physician. The treatment process has three phases, including vaccination, drug administration, and surgery. Ref. [32] It mimics the leadership hierarchy and hunting mechanism of grey wolves in nature. Four types of grey wolves such as alpha, beta, delta, and omega are employed for simulating the leadership hierarchy.
	Game-based	General description: Designed based on simulation of different processes and rules of individual and group games.
		Football Game-Based Optimization (FGBO) [3], Hide Objects Game Optimization (HOGO) [33], Orientation Search Algorithm (OSA) [34,35], Dice Game Optimizer (DGO) [36], Shell Game Optimization (SGO) [37], Darts Game Optimizer (DGO) [38]	Ref. [3] It is designed based on mathematical modeling of football league rules and behaviors of football players and clubs. Ref. [33] It is based on the simulation of the players behaviors and their trying to find a hidden object in the hide object game.
	Physics-based	General description: Designed based on the ideation of various laws of physics.
		Spring Search Algorithm (SSA) [39,40], Curved Space Optimization (CSO) [41], Black Hole (BH) [42], Ray Optimization (RO) [43] algorithm, Artificial Chemical Reaction Optimization Algorithm (ACROA) [44], Galaxy-based Search Algorithm (GbSA) [45], and Small World Optimization Algorithm (SWOA) [46]	Refs. [39,40] The simulation of the Hooke’s law between a number of weights and springs is used.
	Evolutionary-based	General description: They have involved evolution of a population in order to create new generations of genetically superior individuals [47].
		Biogeography-based Optimizer (BBO) [48], Differential Evolution (DE) [49], Genetic Algorithm (GA) [50], Evolution Strategy (ES) [51], and Genetic Programming (GP) [52].	Ref. [50] It has found wide acceptance in many disciplines, with application to environmental science problems. This algorithm is an optimization tool that mimics natural selection and genetics.

shows the optimization algorithms grouped according to the main design idea.

Each optimization problem has a definite solution called a global solution. Optimization algorithms provide a solution based on random search of the search space, which is not necessarily a universal solution, but because it is close to the optimal solution, it is an acceptable solution. The solution that is provided by optimization algorithms is called quasi-optimal solution. Therefore, an optimization algorithm that offers a better quasi-optimal solution than another algorithm is a better optimizer algorithm. In this regard, many optimization algorithms have been proposed by researchers to solve optimization problems and achieve to the better quasi-optimal solution.

Although optimization algorithms have been successful in solving many optimization problems, improving the equations of optimization algorithms and adding modification phases to optimization algorithms can lead to better quasi-optimal solutions. In fact, the purpose of improving an optimization algorithm is to increase the ability of that algorithm to more accurately scan the problem search space and thus provide a more appropriate quasi-optimal solution and closer to the global optimal solution.

In this paper, a new modification method called Dehghani method (DM) is proposed to improve the performance of optimization algorithms. DM is designed based on the use of the algorithm population members information. In the proposed DM, the information of each population member can improve the situation of the new generation. The main idea of DM is to amplify the best population member of an optimization algorithm using population member information. The proposed method is fully described in the next section.

The continuation of the present article is organized in such a way that in Section 2, the DM is fully explained and modeled. Following this, Section 3 explains how to implement the proposed method on several algorithms. The simulation of the proposed method for solving optimization problems is presented in Section 4. Finally, conclusions and several suggestions for future studies are presented in Section 5.

2. Dehghani Method (DM)

In this section, first DM is explained and then its mathematical modeling is presented. DM shows that all population members of the optimization algorithm, even the worst one, can contribute to the development of the population of algorithm.

Each population-based optimization algorithm has a matrix called the population matrix, which each row of this matrix represents a population member. Each member of the population is actually a vector which represents the values of the problem variables. Given that each member of the population is a random vector in the problem search space, it is a suggested solution (SS) to the problem. After the formation of the population matrix, the values proposed by each population member for the problem variables are evaluated in the objective function (OF). The population matrix and values of the objective functions are defined in Equation (1).

$$\mathrm{SS}=X=\left[\begin{array}{ccccccc}S{S}_1=X_1& x_1^1& \cdots & x_1^d& \cdots & x_1^m& O{F}_1\\ ⋮& ⋮& \ddots & ⋮& ⋰& ⋮& ⋮\\ S{S}_i=X_i& x_i^1& \cdots & x_i^d& \cdots & x_i^m& O{F}_i\\ ⋮& ⋮& ⋰& ⋮& \ddots & ⋮& ⋮\\ S{S}_N=X_N& x_N^1& \cdots & x_N^d& \cdots & x_N^m& O{F}_N\end{array}\right],$$

(1)

where, $\mathrm{SS}$ is the suggested solutions matrix, $X$ is the population matrix, ${\mathrm{SS}}_{\mathrm{i}}$ is the i’th suggested solution, $X_i$ is the i’th population member, $x_i^d$ is the value of d’th variables of optimization problem suggested by i’th population member, $N$ is the number of population members or suggested solutions, $m$ is the number of variables, and $O{F}_i$ is the value of objective function for the i’th suggested solution.

Different values for the objective function are obtained based on the values proposed for the variables by the population members. The member that offers the best-suggested solution (BSS) to the optimization problem plays an important role in improving the algorithm population. The row number of this member in the population matrix is determined using Equation (2).

$$best=\left\{\begin{array}{c}the row number of X matrix with\min OF, for minimization problems\\ the row number of X matrix with\max OF, for maximization problems\end{array}\right.,$$

(2)

where, $best$ is the row number of the member with BSS. The BSS and it’s OF are specified by Equations (3) and (4).

$$X_{best} :variables value of\min objective function,$$

(3)

$$F_{best} :value of\min objective function,$$

(4)

where, $X_{best}$ is the BSS or best population member and $F_{best}$ is the value of OF for BSS.

As mentioned, the best member of the population plays an important role in improving the population of the algorithm and thus the performance of the optimization algorithm. Optimization algorithms update the status of its population members according to its own process to achieve a quasi-optimal solution. Accordingly, with the improvement of the best member of the population, is expected that the population be updated more effectively and the performance of the algorithm in solving the optimization problem is improved.

DM is designed with the idea of modifying the best population member with the aim of improving the performance of an optimization algorithm.

In DM, just as the best member is influential in updating the population members, the population members even the worst member can influence to modification the best member. The measurement criterion for suggested solutions is the value of the objective function. However, a suggested solution that is not the best solution may provide appropriate values for some problem variables. The proposed DM modifies the best member considering this issue and using the values suggested by other of the population members. This concept is mathematically simulated in Equations (5) and (6).

$$X_{DM}=X_{DM}^{i,d}= \left[x_{best}^1 \cdots x_i^d \cdots x_{best}^m\right],$$

(5)

$$X_{best}^{new}=\left\{\begin{array}{l}{X}_{DM}, OF(X_{DM}^{i,d})<F_{best}\\ X_{best}, else\end{array}\right.,$$

(6)

where, $X_{DM}$ is the modified best member by DM, $X_{DM}^{i,d}$ is the modified best member based on the suggested value for d’th variable by i’th SS, $X_{best}^{new}$ is the new status for best member based on DM, and $OF(X_{DM}^{i,d})$ is the objective function value for modified best member by DM.

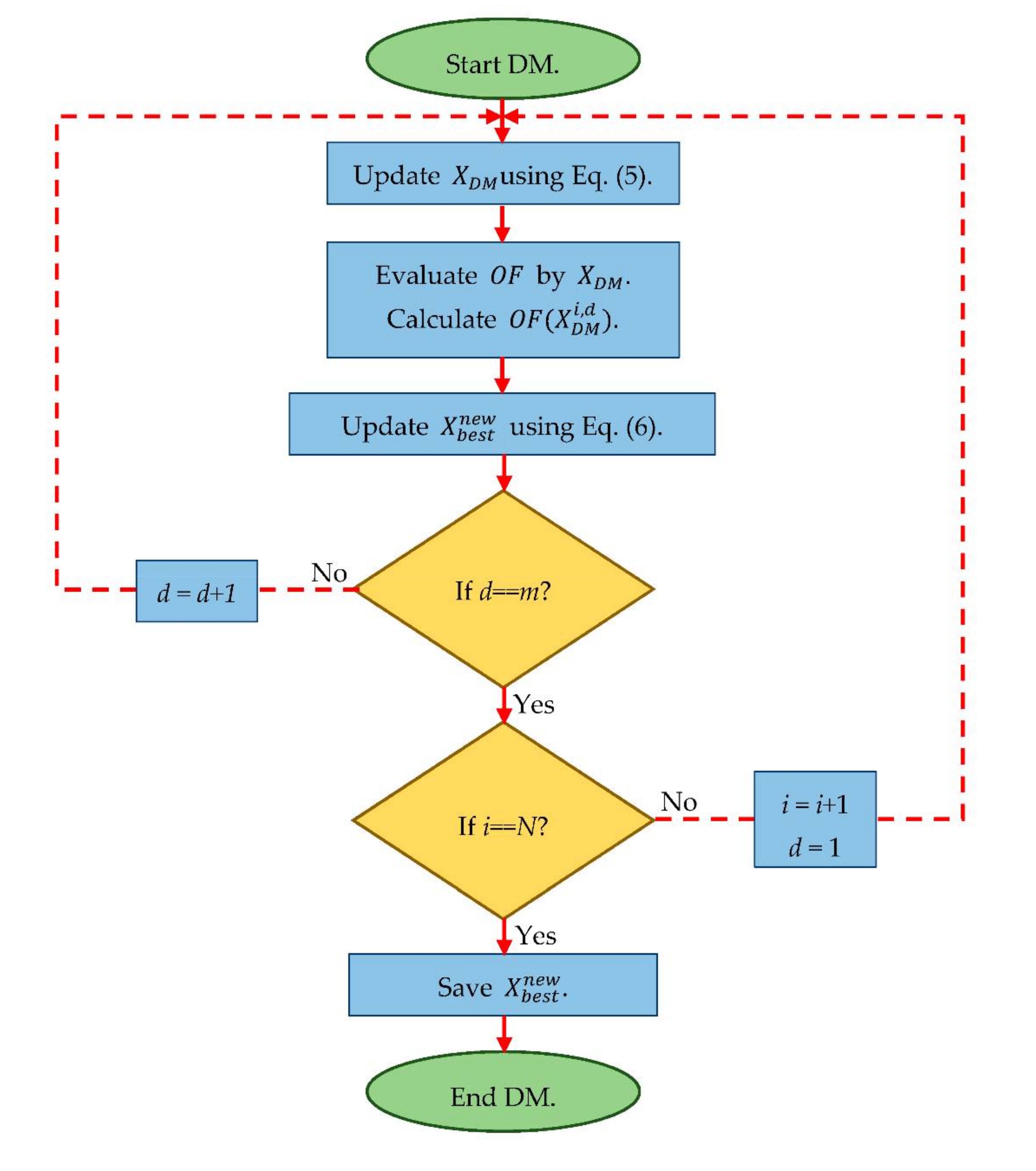
The pseudo code of DM is presented in Algorithm 1. In addition, the different stages of the proposed method with the aim of improving the best member are shown as a flowchart in Figure 1.

Algorithm 1. Pseudo code of DM
1.	For i = 1:Npopulaion	Npopulaion: number of population members.
2.	For d = 1:m	m: number of variables.
3.	Update $X_{DM}$ using Equation (5).
4.	Calculate $OF(X_{DM}^{i,d})$.
5.	Update $X_{best}^{new}$ using Equation (6):
6.	If $OF(X_{DM}^{i,d})<F_{best}$
7.	$X_{best}^{new}$ = $X_{DM}$
8.	End if
9.	End for d
10.	End: for i

3. DM Implantation on Optimization Algorithms

This section describes how to implement the proposed DM on optimization algorithms. The proposed DM is applicable to modify population-based optimization algorithms. Although the idea of designing optimization algorithms is different, the procedure is the same. These algorithms provide a quasi-optimal solution starting from a random initial population and following a process based on repetition and population updates in each iteration.

The pseudo code of implantation of the DM for modifying optimization algorithms is presented in Algorithm 2. The steps of the modified version of the optimization algorithms using DM are shown in Figure 2.

Algorithm 2. Pseudo code of implantation of the DM for modifying optimization algorithms
Start.
1.	Set parameters.
2.	Input: m, OF, constraints.
3	Create initial population.
4.	Create another matrix (if there are).
5.	For t = 1: iterationmax	iterationmax: maximum number of iterations.
6.	Calculate OF.
7.	Find $X_{best}$.
8.	DM toolbox:
9.	Update $X_{best}^{new}$ based on DM.
10.	Continue the processes of optimization algorithm.
11.	Update population.
12.	End for t
13.	Output: BSS.
End.

4. Simulation and Discussion

In this section, the performance of the proposed DM in improving optimization algorithms is evaluated. Thus, the present work and the optimization algorithms described in [18,29,32,50,53] are developed using the same computational platform: Matlab R2014a (8.3.0.532) version in the environment of Microsoft Windows 10 with 64 bits on Core i-7 processor with 2.40 GHz and 6 GB memory. To generate and report the results, for each objective function, optimization algorithms utilize 20 independent runs where each run employs 1000 times of iterations.

4.1. Algorithms Used for Comparisons and Benchmark Test Functions

To evaluate the performance of the proposed DM, the following methodology is applied:

(1)

Find in the literature five well-known optimization algorithms, such as: genetic algorithm (GA) [50], particle swarm optimization (PSO) [18], gravitational search algorithm (GSA) [53], teaching learning based optimization (TLBO) [29] and grey wolf optimizer (GWO) [32].

(2)

Modify the optimization algorithms implementing the proposed DM.

(3)

Define the set of twenty-three objective functions and divide it into three main categories: unimodal [53,54], multimodal [31,54], and fixed-dimension multimodal [54] functions (see Appendix A).

(4)

Implement the present work and the optimization algorithms in the same computational platform.

(5)

Compare the performance of the modified and the original optimization algorithms using the following metrics: the average and the standard deviation of the best obtained optimal solution till the last iteration is computed.

4.2. Results

Optimization algorithms in the original version and the modified version, using the proposed DM, are implemented on the objective functions. The simulation results are presented from

Table 2. Optimization results of genetic algorithm (GA) for original and “modified by DM” versions.

Unimodal				Multimodal				Fixed-Dimension Multimodal
		Original	DM			Original	DM			Original	DM
F1	Avg	13.2405	1.6151 × 10−11	F8	Avg	−8184.4142	−12569.4850	F14	Avg	0.9986	0.9980
	std	4.7664 × 10−15	1.1560× 10−26		std	8.3381 × 10−12	1.2202 × 10−21		std	1.5640 × 10−15	3.4755 × 10−16
F2	Avg	2.4794	4.5161 × 10−35	F9	Avg	62.4114	0.0019	F15	Avg	5.3952 × 10−2	3.3882 × 10−03
	std	2.2342 × 10−15	7.1717 × 10−51		std	2.5421 × 10−14	3.8789 × 10−19		std	7.0791 × 10−18	2.0364 × 10−18
F3	Avg	1536.8963	2.0620 × 10−16	F10	Avg	3.2218	0.0127	F16	Avg	−1.0316	−1.0316
	std	6.6095 × 10−13	6.6148 × 10−32		std	5.1636 × 10−15	0		std	7.9441 × 10−16	5.9580 × 10−16
F4	Avg	2.0942	6.6058 × 10−15	F11	Avg	1.2302	0.0272	F17	Avg	0.4369	0.3984
	std	2.2342 × 10−15	8.1141 × 10−30		std	8.4406 × 10−16	3.1031 × 10−18		std	4.9650 × 10−17	4.9650 × 10−17
F5	Avg	310.4273	5.9802	F12	Avg	0.0470	8.2396 × 10−7	F18	Avg	4.3592	3.0000
	std	2.0972 × 10−13	6.3552 × 10−25		std	4.6547 × 10−18	3.3145 × 10−22		std	5.9580 × 10−16	2.0853 × 10−15
F6	Avg	14.55	0	F13	Avg	1.2085	2.8065 × 10−5	F19	Avg	-3.85434	−3.8627
	std	3.1776 × 10−15	0		std	3.2272 × 10−16	2.1213 × 10−20		std	9.9301 × 10−17	9.9301 × 10−16
F7	Avg	5.6799 × 10−03	2.6009 × 10−5					F20	Avg	−2.8239	−3.2387
	std	7.7579 × 10−19	1.6364 × 10−29						std	3.97205 × 10−16	1.7874 × 10−15
								F21	Avg	−4.3040	−10.1522
									std	1.5888 × 10−15	1.5888 × 10−15
								F22	Avg	−5.1174	−10.4016
									std	1.2909 × 10−15	1.6682 × 10−14
								F23	Avg	−6.5621	−10.5362
									std	3.8727 × 10−15	7.5469 × 10−15

,

Table 3. Optimization results of particle swarm optimization (PSO) for original and “modified by DM” versions.

Unimodal				Multimodal				Fixed-Dimension Multimodal
		Original	DM			Original	DM			Original	DM
F1	Avg	1.7740 × 10−5	6.746 × 10−218	F8	Avg	−6908.6558	−12516.1893	F14	Avg	2.1735	0.9980
	std	6.4396 × 10−21	0		std	1.0168 × 10−12	9.3549 × 10−19		std	7.9441 × 10−16	5.4615 × 10−19
F2	Avg	0.3411	2.9565 × 10−111	F9	Avg	57.0613	1.5631 × 10−13	F15	Avg	0.0535	0.0034
	std	7.4476 × 10−17	1.0736 × 10−126		std	6.3552 × 10−15	0		std	3.8789 × 10−19	2.0849 × 10−18
F3	Avg	589.4920	1.9627 × 10−70	F10	Avg	2.1546	4.7784 × 10−14	F16	Avg	−1.0316	−1.0316
	std	7.1179 × 10−13	5.0357 × 10−86		std	7.9441 × 10−16	1.1289 × 10−29		std	3.4755 × 10−16	4.4685 × 10−21
F4	Avg	3.9634	1.5239 × 10−97	F11	Avg	0.0462	0.0214	F17	Avg	0.7854	0.4076
	std	1.9860 × 10−16	5.8112 × 10−113		std	3.1031 × 10−18	3.1031 × 10−23		std	4.9650 × 10−17	0
F5	Avg	50.26245	2.3706 × 10−13	F12	Avg	0.4806	1.5705 × 10−32	F18	Avg	3	3
	std	1.5888 × 10−14	1.9191 × 10−28		std	1.8619 × 10−16	1.2239 × 10−47		std	3.6741 × 10−15	2.5818 × 10−19
F6	Avg	20.25	0	F13	Avg	0.5084	1.3497 × 10−32	F19	Avg	−3.8627	−3.8627
	std	0	0		std	4.9650 × 10−17	1.2239 × 10−47		std	8.9371 × 10−15	9.0364 × 10−21
F7	Avg	0.1134	0.0110					F20	Avg	−3.2619	−3.2744
	std	4.3444 × 10−17	1.2412 × 10−27						std	2.9790 × 10−16	3.9720 × 10−21
								F21	Avg	−5.3891	−10.1532
									std	1.4895 × 10−15	3.4755 × 10−15
								F22	Avg	−7.6323	−10.4029
									std	1.5888 × 10−15	1.2909 × 10−15
								F23	Avg	−6.1648	−10.5364
									std	2.7804 × 10−15	7.6462 × 10−15

,

Table 4. Optimization results of gravitational search algorithm (GSA) for original and “modified by DM” versions.

Unimodal				Multimodal				Fixed-Dimension Multimodal
		Original	DM			Original	DM			Original	DM
F1	Avg	2.0255 × 10−17	1.6060 × 10−157	F8	Avg	−2849.0724	−12532.65497	F14	Avg	3.5913	0.9980
	std	1.1369 × 10−32	0		std	1.0168 × 10-12	2.84717 × 10-12		std	7.9441 × 10−16	4.2203 × 10−16
F2	Avg	2.3702 × 10−08	2.4203 × 10−80	F9	Avg	16.2675	0	F15	Avg	0.0024	8.0939 × 10−4
	std	5.1789 × 10−24	8.3748 × 10−96		std	3.1776 × 10−15	0		std	2.9092 × 10−19	3.5153 × 10−28
F3	Avg	279.3439	1.4902 × 10−30	F10	Avg	3.5673 × 10−09	4.3396 × 10−13	F16	Avg	−1.0316	−1.0316
	std	1.2075 × 10−13	5.4834 × 10−46		std	3.6992 × 10−25	9.0314 × 10−29		std	5.9580 × 10−16	6.4545 × 10−34
F4	Avg	3.2547 × 10−9	7.1301 × 10−71	F11	Avg	3.7375	0.0311	F17	Avg	0.3978	0.3978
	std	2.0346 × 10−24	3.5969 × 10−87		std	2.7804 × 10−15	0		std	9.9301 × 10−17	0
F5	Avg	36.10695	23.1212	F12	Avg	0.0362	2.319 × 10−27	F18	Avg	3	3
	std	3.0982 × 10−14	5.5608 × 10−15		std	6.2063 × 10−18	1.0829 × 10−42		std	6.9511 × 10−16	1.2909 × 10−35
F6	Avg	0	0	F13	Avg	0.0020	2.5758 × 10−26	F19	Avg	−3.8627	−3.8627
	std	0	0		std	4.2617 × 10−14	7.7006 × 10−42		std	8.3413 × 10−15	6.3248 × 10−29
F7	Avg	0.0206	7.4501 × 10−4					F20	Avg	−3.0396	−3.3219
	std	2.7152 × 10−18	1.9394 × 10−29						std	2.1846 × 10−14	1.9860 × 10−25
								F21	Avg	−5.1486	−10.1531
									std	2.9790 × 10−16	1.1916 × 10−24
								F22	Avg	−9.0239	−10.4029
									std	1.6484 × 10−12	1.3505 × 10−34
								F23	Avg	−8.9045	−10.5364
									std	7.1497 × 10−14	5.95808 × 10−45

,

Table 5. Optimization results of teaching learning based optimization (TLBO) for original and “modified by DM” versions.

Unimodal				Multimodal				Fixed-Dimension Multimodal
		Original	DM			Original	DM			Original	DM
F1	Avg	8.3373 × 10−60	1.1627 × 10−157	F8	Avg	−7408.6107	−12569.4866	F14	Avg	2.2721	0.9980
	std	4.9436 × 10−76	0		std	3.0505 × 10−12	1.6269 × 10−11		std	1.9860 × 10−16	0
F2	Avg	7.1704 × 10−35	1.9426 × 10−80	F9	Avg	10.2485	0	F15	Avg	0.0033	3.9560 × 10−4
	std	6.6936 × 10−50	1.2562 × 10−96		std	5.5608 × 10−15	0		std	1.2218 × 10−17	0
F3	Avg	2.7531 × 10−15	1.0076 × 10−30	F10	Avg	0.2757	4.7961 × 10−15	F16	Avg	−1.0316	−1.0316
	std	2.6459 × 10−31	5.8751 × 10−46		std	2.5641 × 10−15	1.4111 × 10−30		std	1.4398 × 10−15	9.9301 × 10−19
F4	Avg	9.4199 × 10−15	5.6754 × 10−71	F11	Avg	0.6082	0.0182	F17	Avg	0.3978	0.4085
	std	2.1167 × 10−30	2.8775 × 10−86		std	1.9860 × 10−16	6.2063 × 10−18		std	7.4476 × 10−17	9.9301 × 10−17
F5	Avg	146.4564	21.4361	F12	Avg	0.0203	1.5705 × 10−32	F18	Avg	3.0009	3
	std	1.9065 × 10−14	2.0654 × 10−21		std	7.7579 × 10−19	1.2239 × 10−47		std	1.5888 × 10−15	1.3902 × 10−26
F6	Avg	0.4435	0	F13	Avg	0.3293	1.3497 × 10−32	F19	Avg	−3.8609	−3.8627
	std	4.2203 × 10−16	0		std	2.1101 × 10−16	1.2239 × 10−47		std	7.3483 × 10−15	9.9301 × 10−45
F7	Avg	0.0017	3.4102 × 10−4					F20	Avg	−3.2014	−3.3104
	std	3.87896 × 10−19	2.4849 × 10−27						std	1.7874 × 10−15	9.9301 × 10−18
								F21	Avg	−9.1746	−10.1531
									std	8.5399 × 10−15	0
								F22	Avg	−10.0389	−10.4029
									std	1.5292 × 10−14	0
								F23	Avg	−9.2905	−10.5364
									std	1.1916 × 10−15	0

and

Table 6. Optimization results of grey wolf optimization (GWO) for original and “modified by DM” versions.

Unimodal				Multimodal				Fixed-Dimension Multimodal
		Original	DM			Original	DM			Original	DM
F1	Avg	1.09 × 10−58	2.84 × 10−278	F8	Avg	−5885.1172	−11901.9832	F14	Avg	3.7408	1.3948
	std	5.1413 × 10−74	0		std	2.0336 × 10−12	4.8808 × 10−14		std	6.4545 × 10−15	8.44062 × 10−16
F2	Avg	1.2952 × 10−34	1.6523 × 10−137	F9	Avg	8.5265 × 10−15	0	F15	Avg	0.0063	0.0043
	std	1.9127 × 10−50	1.2275 × 10−152		std	5.6446 × 10−30	0		std	1.1636 × 10−18	3.10317 × 10−28
F3	Avg	7.4091 × 10−15	1.0362 × 10−30	F10	Avg	1.7053 × 10−14	1.0835 × 10−14	F16	Avg	−1.0316	−1.0316
	std	5.6446 × 10−30	1.2533 × 10−45		std	2.7517 × 10−29	2.8223 × 10−30		std	3.9720 × 10−16	5.9580 × 10−26
F4	Avg	1.2599 × 10−14	2.5914 × 10−47	F11	Avg	0.0037	0.0014	F17	Avg	0.3978	0.3978
	std	1.0583 × 10−29	2.1742 × 10−63		std	1.2606 × 10−18	0		std	8.6888 × 10−17	1.2412 × 10−19
F5	Avg	26.8607	4.9282	F12	Avg	0.0372	1.0468 × 10−09	F18	Avg	3.0000	3.0000
	std	0	0		std	4.3444 × 10−17	3.2368 × 10−25		std	2.0853 × 10−15	2.0853 × 10−18
F6	Avg	0.6423	9.6762 × 10−09	F13	Avg	0.5763	9.4403 × 10−09	F19	Avg	−3.8621	−3.8627
	std	6.2063 × 10−17	7.3985 × 10−24		std	2.4825 × 10−16	3.6992 × 10−24		std	2.4825 × 10−15	0
F7	Avg	0.0008	0.0005					F20	Avg	−3.2523	−3.2982
	std	7.2730 × 10−20	1.9394 × 10−29						std	2.1846 × 10−15	1.8867 × 10−30
								F21	Avg	-9.6452	−10.1531
									std	6.5538 × 10−15	1.1916 × 10−32
								F22	Avg	−10.4025	−10.4029
									std	1.9860 × 10−15	1.1519 × 10−25
								F23	Avg	−10.1302	−10.5364
									std	4.5678 × 10−15	2.7804 × 10−20

for three different categories: unimodal, multimodal, and fixed-dimension multimodal functions. The first category consists of seven objective functions, F₁ to F₇, the second category consists of six objective functions, F₈ to F₁₃, and the third category consists of ten objective functions, F₁₄ to F₂₃.

To further analyze the simulation results, the convergence curves of the optimization algorithms for the twenty-three objective functions are shown from Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7. In these figures, the convergence curves for the original and the modified versions are plotted simultaneously.

Computational time analysis in accessing the optimal solution is presented in

Table 7. Computational time analysis on unimodal objective functions (second).

		GA	MGA	PSO	MPSO	GSA	MGSA	TLBO	MTLBO	GWO	MGWO
F1	P.I.	0.0025	0.0079	0.0011	0.0039	0.0105	0.0129	0.0055	0.0063	0.0025	0.0042
	P.C.R.	2.5218	7.9613	1.1309	3.9634	10.5790	12.9160	5.5465	6.3235	2.5969	4.2516
	O.T.S.	0.8699		0.2407		2.5412		2.3713		1.8153
F2	P.I.	0.0024	0.0103	0.0019	0.0050	0.0107	0.0138	0.0056	0.0057	0.0027	0.0031
	P.C.R.	2.4125	10.3794	1.1945	5.0867	10.7194	13.8475	5.6229	5.7781	2.7101	3.1541
	O.T.S.	0.1031		0.2148		4.2400		2.1668		1.1421
F3	P.I.	0.0071	0.1630	0.0035	0.0784	0.0126	0091	0.0115	0.0851	0.0075	0.0918
	P.C.R.	7.1174	163.0316	3.5810	78.4169	12.5987	91.2295	11.53338	85.1981	7.5661	91.8338
	O.T.S.	3.7623		3.5364		5.5923		44.5162		37.2164
F4	P.I.	0.0023	0.0082	0.0090	0.0038	0.0102	0.0133	0.0035	0.0065	0.0026	0.0075
	P.C.R.	2.3254	8.2181	0.9058	3.8641	10.2537	13.3495	3.5392	6.5216	2.6966	7.5614
	O.T.S.	0.2793		0.0721		3.5859		1.5757		1.2614
F5	P.I.	0.0031	0.0300	0.0012	0.0138	0.0106	0.0218	0.0041	0.0177	0.0035	0.0015
	P.C.R.	3.1018	30.0027	1.2819	13.8921	10.6810	21.8228	4.1720	17.7407	3.5823	15.2196
	O.T.S.	0.2677		0.2105		9.8639		0.2629		6.1547
F6	P.I.	0.0024	0.0114	0.0007	0.0048	0.0101	0.0146	0.0032	0.0069	0.0027	0.0114
	P.C.R.	2.4156	11.4786	0.7947	4.8365	10.1832	14.6262	3.2010	6.9231	2.7229	11.4774
	O.T.S.	0.1558		0.0870		0.5940		0.8843		0.2376
F7	P.I.	0.0047	0.0785	0.0020	0.0381	0.0107	0.0493	0.0067	0.0428	0.0049	0.0390
	P.C.R.	4.7185	78.5709	2.0728	38.1957	10.7416	49.3055	6.7193	42.8670	4.9646	39.0686
	O.T.S.	4.3080		0.1156		0.9553		6.5309		25.3156

,

Table 8. Computational time analysis on multimodal objective functions (second).

		GA	MGA	PSO	MPSO	GSA	MGSA	TLBO	MTLBO	GWO	MGWO
F8	P.I.	0.0037	0.0320	0.0015	0.0145	0.0108	0.0261	0.0049	0.0175	0.0034	0.0260
	P.C.R.	3.7004	32.0411	1.5194	14.5251	10.8230	26.1593	4.9084	17.5273	3.4282	26.0069
	O.T.S.	0		0		0		0		0
F9	P.I.	0.0029	0.0128	0.0011	0.0057	0.0103	0.0160	0.0041	0.0084	0.0031	0.0154
	P.C.R.	2.9477	12.8883	1.1813	5.7547	10.3758	16.0688	4.1855	8.4233	3.1391	15.3918
	O.T.S.	0		0.0404		0.4220		0.1464		0.3783
F10	P.I.	0.0028	0.0149	0.0014	0.0069	0.0105	0.0168	0.0036	0.0092	0.0031	0.0145 3.9092
	P.C.R.	2.8721	14.9436	1.4455	6.9011	10.5083	16.8567	3.6440	9.2561	3.1046	14.5384
	O.T.S.	0.1703		0.0755		5.2755		0.4661		1.3942
F11	P.I.	0.0038	0.0403	0.0015	0.0196	0.0110	0.0288	0.0049	0.0212	0.0039	0.0289
	P.C.R.	3.8680	40.3218	1.5616	19.6877	11.0021	28.8871	4.9292	21.2885	3.9092	28.9343
	O.T.S.	0.3821		0.6098		0.6825		0.3316		1.7435
F12	P.I.	0.0102	0.2506	0.0047	0.1188	0.0135	0.1307	0.0148	0.1294	0.0111	0.1383
	P.C.R.	10.2150	250.5924	4.7914	118.8262	13.5497	130.7448	14.8773	129.4573	11.1936	138.3059
	O.T.S.	0.8169		0.1446		3.1468		1.3416		1.5073
F13	P.I.	0.0099	0.2358	0.0046	0.1201	0.0141	0.1276	0.0145	0.1311	0.0104	0.1414
	P.C.R.	9.9011	235.8891	4.6563	120.1492	14.1304	127.6587	14.5221	131.1560	10.4009	141.4475
	O.T.S.	1.0468		0.3086		2.0328		0.9692		1.2553

and

Table 9. Computational time analysis on fixed-dimension multimodal objective functions (second).

		GA	MGA	PSO	MPSO	GSA	MGSA	TLBO	MTLBO	GWO	MGWO
F14	P.I.	0.0010	0.0472	0.0082	0.0249	0.0104	0.0264	0.0269	0.0434	0.0161	0.0328
	P.C.R.	1.0468	47.2794	8.2528	24.9162	10.4771	26.4766	26.9827	43.4908	16.1510	32.8053
	O.T.S.	0.6287		0.1399		0.4855		0.2652		0.3096
F15	P.I.	0.0023	0.0034	0.0007	0.0013	0.0038	0.0047	0.0038	0.0039	0.0014	0.0029
	P.C.R.	2.3853	3.4227	0.7764	1.3148	3.8712	4.7457	3.8933	3.9249	1.4375	2.9109
	O.T.S.	0.1309		0		0.9101		0.3985		0.1430
F16	P.I.	0.0020	0.0031	0.0006	0.0008	0.0035	0.0038	0.0029	0.0033	0.0011	0.0018
	P.C.R.	2.0042	3.1025	0.6528	0.8631	3.5103	3.8281	2.9861	3.3501	1.1685	1.8361
	O.T.S.	0.2672		0.0442		0.5542		0.1176		0.1103
F17	P.I.	0.0019	0.0021	0.0005	0.0006	0.0033	0.0038	0.0027	0.0029	0.0010	0.0014
	P.C.R.	1.9120	2.1799	0.5358	0.5988	3.3251	3.8600	2.7069	2.9407	1.0611	1.4350
	O.T.S.	0.1188		0		0.6116		0.2421		0.2306
F18	P.I.	0.0018	0.0025	0.0004	0.0006	0.0035	0.0037	0.0029	0.0030	0.0010	0.0015
	P.C.R.	1.8757	2.5166	0.4211	0.6029	3.4917	3.7297	2.9081	3.0689	1.0903	1.5060
	O.T.S.	0.0979		0.0576		1.1963		0.1772		0.2609
F19	P.I.	0.0025	0.0037	0.0008	0.0014	0.0037	0.0048	0.0035	0.0041	0.0016	0.0026
	P.C.R.	2.5233	3.7541	0.8540	1.4255	3.7397	4.8479	3.5075	4.1393	1.6122	2.6632
	O.T.S.	0.4878		0.0811		1.4218		0.0983		0.4146
F20	P.I.	0.0028	0.0051	0.0009	0.0021	0.0045	0.0056	0.0036	0.0083	0.0017	0.0042
	P.C.R.	2.8411	5.1640	0.9246	2.1016	4.5773	5.6775	3.6700	4.8358	1.7797	4.2165
	O.T.S.	0		0.0846		0		0.1673		0.1526
F21	P.I.	0.0027	0.0056	0.0010	0.0023	0.0044	0.0057	0.0041	0.0054	0.0020	0.0045
	P.C.R.	2.7466	5.6009	1.0173	2.3777	4.4041	5.7909	4.1728	5.4967	2.0670	4.5858
	O.T.S.	0.1158		0.0913		0		2.1696		0.5408
F22	P.I.	0.0030	0.0071	0.0010	0.0030	0.0041	0.0064	0.0048	0.0065	0.0022	0.0050
	P.C.R.	3.0287	7.1416	1.0454	3.0463	4.1996	6.4820	4.8034	6.5908	2.2729	5.0265
	O.T.S.	0.1123		0.3930		1.2738		0.4395		0.6946
F23	P.I.	0.0035	0.0089	0.0012	0.0039	0.0045	0.0075	0.0051	0.0080	0.0026	0.0065
	P.C.R.	3.5326	8.9343	1.2184	3.9863	4.5094	7.5026	5.1003	8.0755	2.6291	6.5630
	O.T.S.	2.0295		0.0757		1.2981		0.2980		0.7469

. This analysis shows computational time for per iteration, per complete run, and the overall time required for the original and modified algorithm to achieve similar objective function value. In these tables, P.I. means per iteration, P.C. means per complete run, and the O.T.S. means overall time required for the original and modified algorithm to achieve similar objective function value.

4.3. Discussion

Exploitation and exploration abilities are two important indicators in evaluating optimization algorithms. The exploitation ability of an optimization algorithm means its power to provide a quasi-optimal solution. An algorithm that offers a better quasi-optimal solution than another algorithm has a higher exploitation ability. The unimodal objective functions F₁ to F₇, which have only one global optimal solution without local solutions, are applied to analyze the exploitation ability of optimization algorithms. The results presented in Table 2, Table 3, Table 4, Table 5 and Table 6 show that the proposed DM by modifying the optimization algorithms is able to increase the exploitation ability of the optimization algorithms and as a result more suitable quasi-optimal solutions are provided by the modified version.

The exploration ability means the power of the optimization algorithm to scan the search space of an optimization problem. Given that the basis of optimization algorithms is random scanning of the search space, an algorithm that scans the search space more accurately is able move towards a quasi-optimal solution by escape from local optimal solutions. In the second and third category of objective functions F₈ to F₂₃, there are multiple local solutions besides the global optimum which are useful to analyze the local optima avoidance and an explorative ability of an algorithm. Table 2, Table 3, Table 4, Table 5 and Table 6 show that the modified version with the DM of optimization algorithms has a higher exploration ability than the original version.

The convergence curves shown in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 visually show the effect of the proposed DM on the modifying the optimization algorithms. In these figures it is clear that the modified version moves with more convergence towards the quasi-optimal solution.

The simulation results of optimization algorithms to solve the optimization problems show that the modified version of the optimization algorithms with the DM are much more competitive than the its original version. Therefore, the proposed method has the ability to be implemented on a variety of optimization algorithms in order to solve various optimization problems.

The result of computational time analysis for both original and modified by DM versions is presented in Table 7, Table 8 and Table 9. In these tables, three different time criteria are presented, which are the average time per iteration (P.I.), the average time per complete run (P.C.R.), and overall time required for the original and modified algorithm to achieve similar objective function value (O.T.S.). Due to the addition of a correction phase based on proposed DM, P.I. and P.C.R. have been increased compared to the original version. Table 7 shows that except for four cases (TLBO: F₃, GWO: F₃, F₅, and F₇), in all unimodal objective functions, the modified version provides the final solution of the original version in less time. Table 8 and Table 9 show that the modified version of the studied algorithms for all F₈ to F₂₃ objective functions provides the final solution of the original version in less time.

5. Conclusions

There are various optimization problems in different sciences that should be optimized using the appropriate method. The optimization algorithm is one method to solve such problems, and it can provide a quasi-optimal solution by random scanning in the search space. Many optimization algorithms have been proposed by researchers which have been applied by scientists to solve optimization problems. The performance of optimization algorithms in achieving quasi-optimal solutions is improved by modifying optimization algorithms. In this paper, a new modification method has been presented for optimization algorithms called Dehghani method (DM). The main idea of the proposed DM is to improve and strengthen the best member of the population using the information of the population members. In DM, all members of a population, even the worst one, can contribute to the development of the population. The various stages of DM have been described and then has been modeled mathematically. The DM has been implemented on five different optimization algorithms including GA, PSO, GSA, TLBO, and GWO. The effect of the proposed method on modifying the performance of optimization algorithms in solving optimization problems has been evaluated on a set of twenty-three standard objective functions. In this evaluation, the results of optimizing the objective functions set has been presented for both the original and the modified by DM version of the optimization algorithms. The results of simulation and implementation of DM on the mentioned optimization algorithms with the aim of optimizing the optimization problems show that the proposed method improves the performance of the optimization algorithms. The optimization of different objective functions in the three groups unimodal, multimodal, and fixed-dimension multimodal functions indicates that the modified version with the proposed method is much more competitive than the original version. Moreover, the convergence curves visually show that the modified version moves with more convergence towards the quasi-optimal solution.

The authors suggest several ideas and proposals for future studies and perspectives of this study to researchers. The main potential for these ideas is to be found in modifying various optimization algorithms using DM. DM may also be used to overcome many objective real-life optimizations as well as multi-objective problems.