Development of Mathematical Models in Explicit Form for Design and Analysis of Axial Flux Permanent Magnet Synchronous Machines
Abstract
:1. Introduction
- outer dimensions of the machine and its mass and
- current density in the windings.
2. Materials and Methods
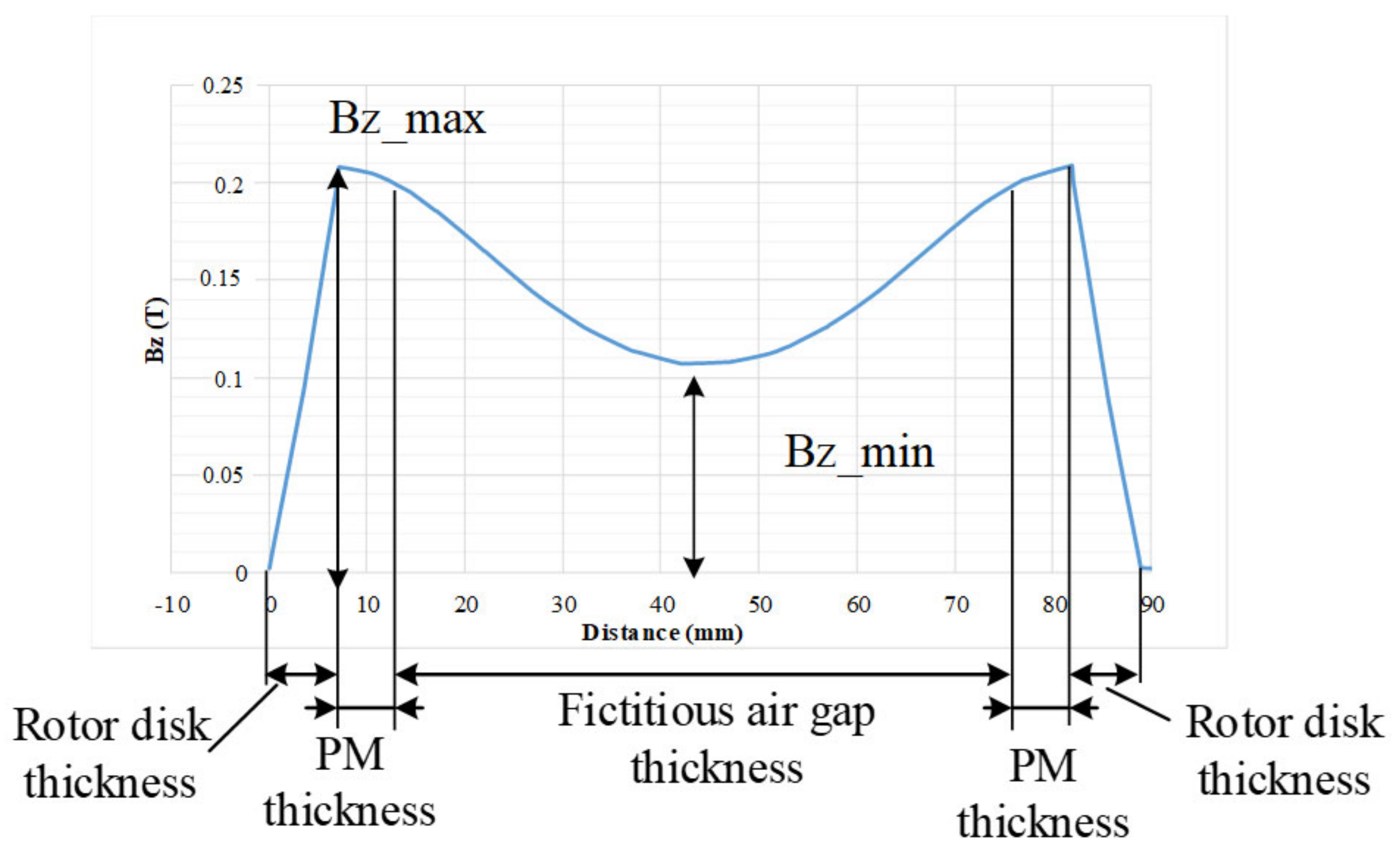
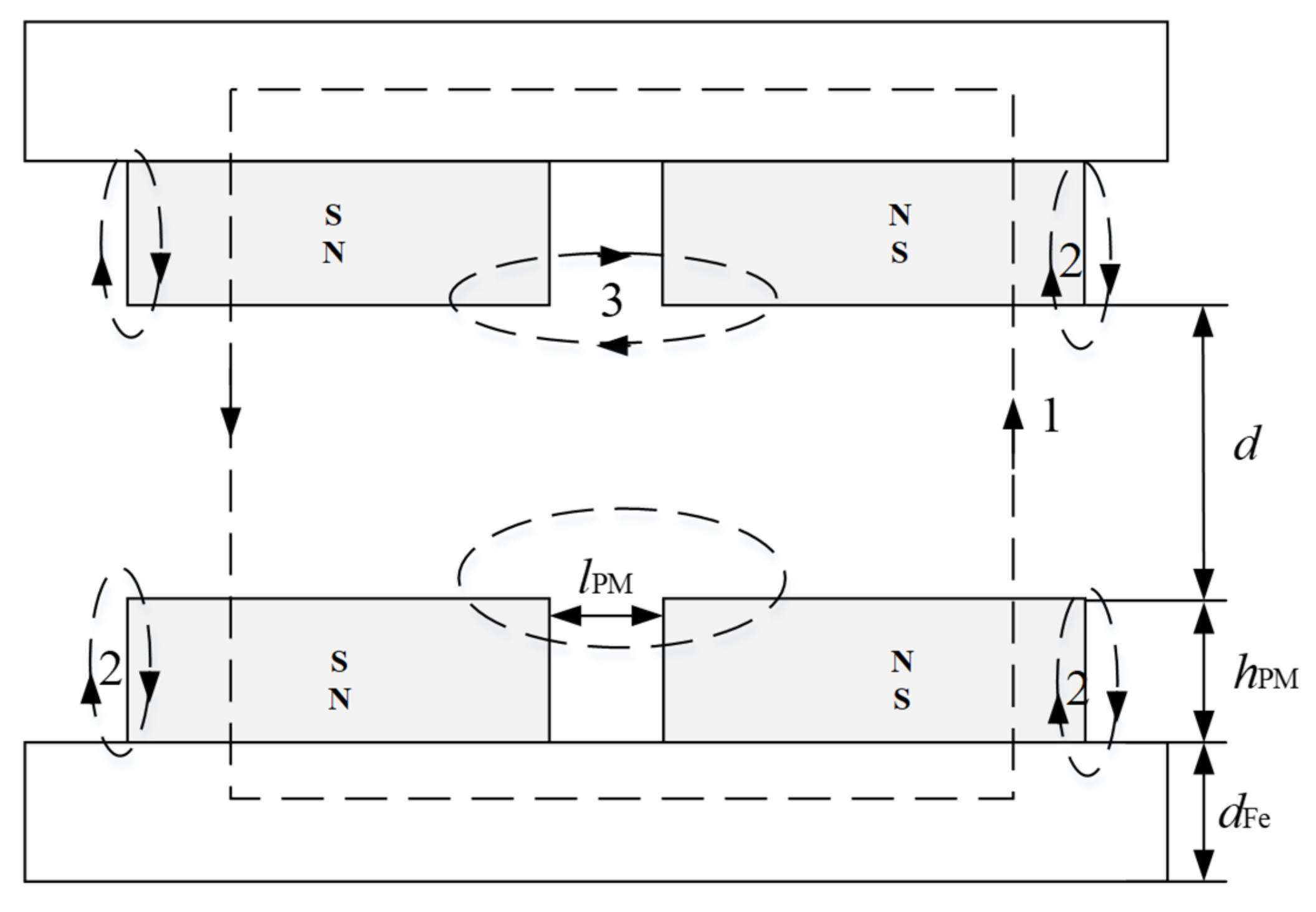
2.1. Simplified FEM Calculations
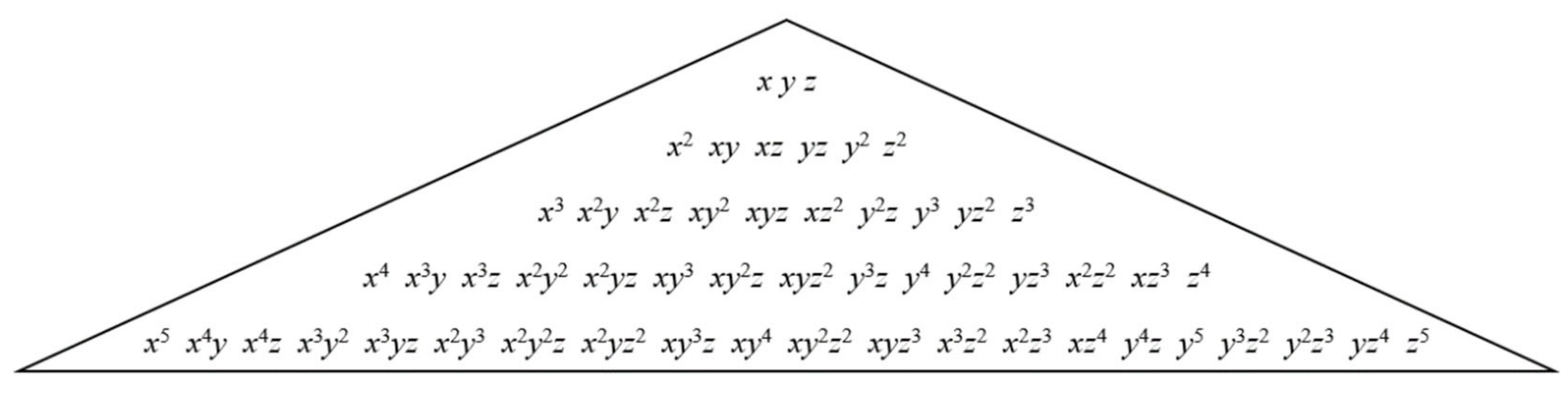
2.2. Least Square Approximation Method
2.3. Design and Analysis of AFPMSM
3. Results and Discussions
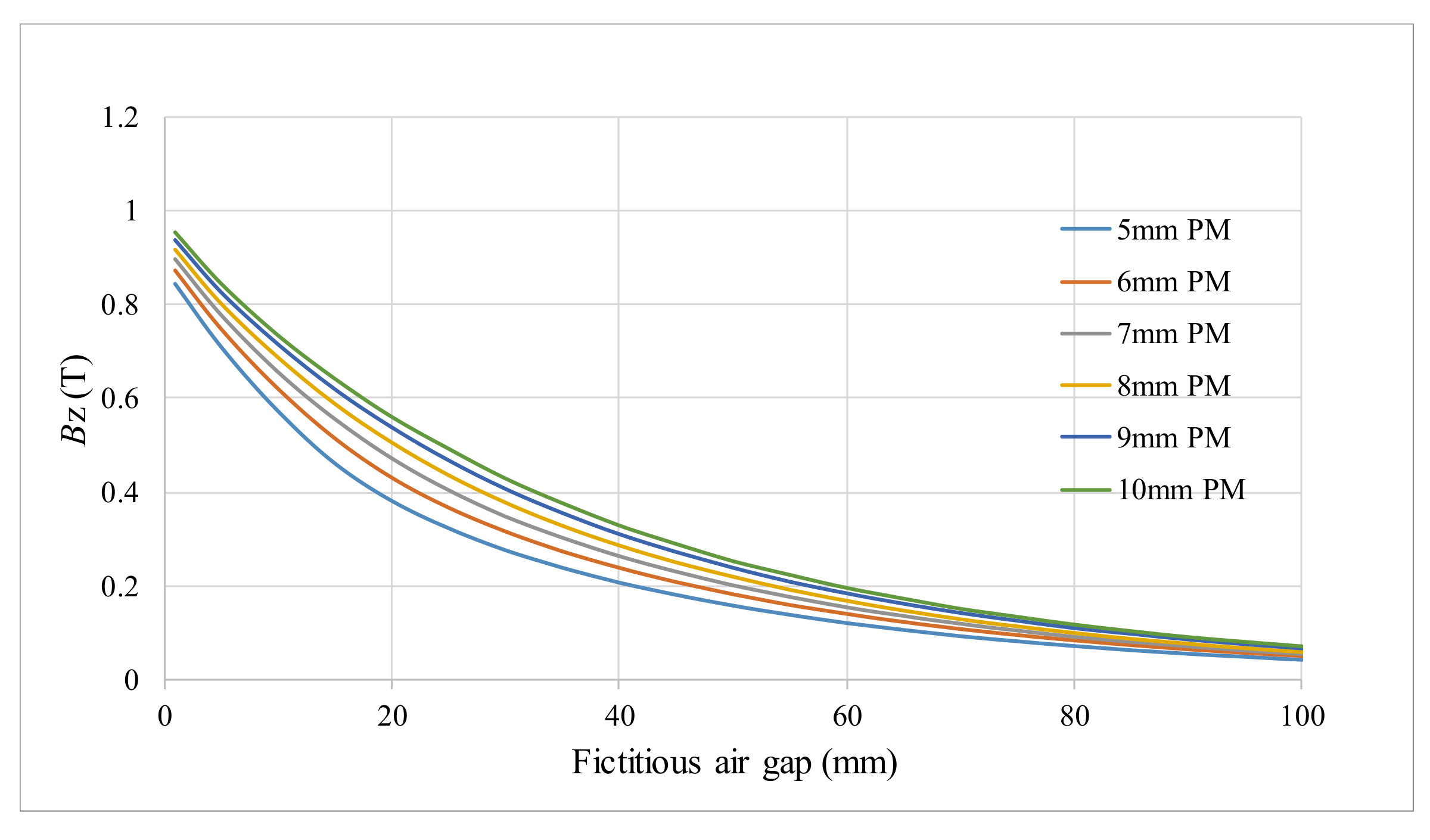
3.1. Influence of Different Geometrical Parameters on Characteristics of the Machine
3.2. Design and Analysis of AFPMSM
3.3. Laboratory Measurements
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mirsalim, M.; Yazdanpanah, R.; Hekmati, P. Design and analysis of double-sided slotless axial-flux permanent magnet machines with conventional and new stator core. IET Electr. Power Appl. 2015, 9, 193–202. [Google Scholar] [CrossRef]
- Caricchi, F.; Crescimbini, F.; Mezzetti, F.; Santini, E. Multistage axial-flux PM machine for wheel direct drive. IEEE Trans. Ind. Appl. 1996, 32, 882–888. [Google Scholar] [CrossRef]
- Virtic, P.; Pisek, P.; Marcic, T.; Hadziselimovic, M.; Stumberger, B. Analytical Analysis of Magnetic Field and Back Electromotive Force Calculation of an Axial-Flux Permanent Magnet Synchronous Generator with Coreless Stator. IEEE Trans. Magn. 2008, 44, 4333–4336. [Google Scholar] [CrossRef]
- Lombard, N.; Kamper, M.J. Analysis and performance of an ironless stator axial flux PM machine. IEEE Trans. Energy Convers. 1999, 14, 1051–1056. [Google Scholar] [CrossRef]
- Daghigh, A.; Javadi, H.; Torkaman, H. Improved design of coreless axial flux permanent magnet synchronous generator with low active material cost. In Proceedings of the 6th Power Electronics, Drive Systems & Technologies Conference (PEDSTC2015), Tehran, Iran, 3–4 February 2015; pp. 532–537. [Google Scholar] [CrossRef]
- Javadi, S.; Mirsalim, M. A Coreless Axial-Flux Permanent-Magnet Generator for Automotive Applications. IEEE Trans. Magn. 2008, 44, 4591–4598. [Google Scholar] [CrossRef]
- Chen, A.; Nilssen, R.; Nysveen, A. Performance comparisons among radial flux, multi-stage axial flux and three-phase transverse flux PM machines for downhole applications. In Proceedings of the IEEE International Electric Machines and Drives Conference, Miami, FL, USA, 3–6 May 2009; pp. 1010–1017. [Google Scholar]
- Hanselman, D. Brushless Permanent Magnet Motor Design; The Writers’ Collective: Cranston, RI, USA, 2003. [Google Scholar]
- Gieras, J.F.; Wang, R.J.; Kamper, M.J. Axial Flux Permanent Magnet Brushless Machines; Kluwer Academic Publishers: Dordrecht, Germany, 2004. [Google Scholar]
- Mueller, M.A.; McDonald, A.S.; MacPherson, D.E. Structural analysis of low-speed axial-flux permanent-magnet machines. IEE Proc. Electr. Power Appl. 2005, 152, 1417–1426. [Google Scholar] [CrossRef]
- Jara, W.; Martín, A.; Tapia, J.A. Axial flux PM machine for low wind power generation. In Proceedings of the XIX International Conference on Electrical Machines—ICEM 2010, Rome, Italy, 6–8 September 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Daghigh, A.; Javadi, H.; Javadi, A. Improved Analytical Modeling of Permanent Magnet Leakage Flux in Design of the Coreless Axial Flux Permanent Magnet Generatorx. Can. J. Electr. Comput. Eng. 2017, 40, 3–11. [Google Scholar]
- Caricchi, F.; Crescimbini, F.; Honorzti, O.; Bianco, G.L.; Santini, E. Performance of coreless-winding axial-flux permanent-magnet generator with power output at 400 Hz-3000 rev/min. In Proceedings of the IAS ’97 Conference Record of the 1997 IEEE Industry Applications Conference Thirty-Second IAS Annual Meeting, New Orleans, LA, USA, 5–9 October 1997; Volume 1, pp. 61–66. [Google Scholar]
- Wang, Y.; Chen, W.X.C.; Dong, Z. A parametric magnetic network model for axial flux permanent magnet machine with coreless stator. In Proceedings of the 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 1108–1113. [Google Scholar] [CrossRef]
- Chan, T.F.; Lai, L.L.; Xie, S. Field Computation for an Axial Flux Permanent-Magnet Synchronous Generator. IEEE Trans. Energy Convers. 2009, 24, 1–11. [Google Scholar] [CrossRef]
- Bumby, J.R.; Martin, R.; Mueller, M.A.; Spooner, E.; Brown, N.L.; Chalmers, B.J. Electromagnetic design of axial-flux permanent magnet machines. Proc. Inst. Elect. Eng. Elect. Power Appl. 2004, 151, 151–160. [Google Scholar] [CrossRef]
- Azzouzi, J.; Barakat, G.; Dakyo, B. Quasi-3D analytical modeling of the magnetic field of an axial flux permanent magnet synchronous machine. In Proceedings of the IEEE International Electric Machines and Drives Conference, IEMDC’03, Madison, WI, USA, 1–4 June 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 3, pp. 1941–1947. [Google Scholar] [CrossRef]
- Virtic, P.; Pisek, P.; Hadziselimovic, M.; Marcic, T.; Stumberger, B. Torque Analysis of an Axial Flux Permanent Magnet Synchronous Machine by Using Analytical Magnetic Field Calculation. IEEE Trans. Magn. 2009, 45, 1036–1039. [Google Scholar] [CrossRef]
- Tiegna, H.; Bellara, A.; Amara, Y.; Barakat, G. Analytical Modeling of the Open-Circuit Magnetic Field in Axial Flux Permanent-Magnet Machines with Semi-Closed Slots. IEEE Trans. Magn. 2012, 48, 1212–1226. [Google Scholar] [CrossRef]
- Marignetti, F.; Di Stefano, R. Electromagnetic Analysis of Axial-Flux Permanent Magnet Synchronous Machines with Fractional Windings with Experimental Validation. IEEE Trans. Ind. Electron. 2011, 59, 2573–2582. [Google Scholar] [CrossRef]
- Caricchi, F.; Crescimbini, F.; Honorati, O.; Di Napoli, A.; Santini, E. Compact wheel direct drive for EVs. IEEE Ind. Appl. Mag. 1996, 2, 25–32. [Google Scholar] [CrossRef]
- Pranjić, F.; Virtič, P. Determination of an Optimum Fictitious Air Gap and Rotor Disk Thickness for a Coreless AFPMM. Teh. Vjesn. 2018, 25, 1731–1738. [Google Scholar] [CrossRef]
- Pranjic, F.; Virtic, P. Designing Rotor Disks of a Coreless Axial Flux Permanent Magnet Machines by Using Simplified FEM and an Approximation Method. IEEE Trans. Energy Convers. 2020, 35, 1505–1512. [Google Scholar] [CrossRef]
- Kahourzade, S.; Mahmoudi, A.; Rahim, N.A.; Ping, H.W. Sizing equation and Finite Element Analysis optimum design of axial-flux permanent-magnet motor for electric vehicle direct drive. In Proceedings of the IEEE International Power Engineering and Optimization Conference, Melaka, Malaysia, 6–7 June 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Rallabandi, V.; Taran, N.; Ionel, D.M.; Eastham, J.F. On the feasibility of carbon nanotube windings for electrical machines—Case study for a coreless axial flux motor. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–7. [Google Scholar]
- Kalender, O.; Ege, Y.; Nazlibilek, S. Design and determination of stator geometry for axial flux permanent magnet free rod rotor synchronous motor. Measurement 2011, 44, 1753–1760. [Google Scholar] [CrossRef]
- Huang, S.; Luo, J.; Leonardi, F.; Lipo, T.A. A comparison of power density for axial flux machines based on general purpose sizing equations. IEEE Trans. Energy Convers. 1999, 14, 185–192. [Google Scholar] [CrossRef]
- Aydin, M.; Gulec, M.; Demir, Y.; Akyuz, B.; Yolacan, E. Design and validation of a 24-pole coreless axial flux permanent magnet motor for a solar powered vehicle. In Proceedings of the XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 1493–1498. [Google Scholar] [CrossRef]
- Xie, H.; Wei, X.; Yang, K. A novel modular multistage axial-flux permanent magnet machine for electric vehicles. In Proceedings of the 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 206–211. [Google Scholar] [CrossRef]
- Capponi, F.G.; De Donato, G.; Caricchi, F. Recent Advances in Axial-Flux Permanent-Magnet Machine Technology. IEEE Trans. Ind. Appl. 2012, 48, 2190–2205. [Google Scholar] [CrossRef]
- Seo, J.M.; Jung, I.S.; Jung, H.K.; Ro, J.S. Analysis of Overhang Effect for a Surface-Mounted Permanent Magnet Machine Using a Lumped Magnetic Circuit Model. IEEE Trans. Magn. 2014, 50, 1–7. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Rahim, N.A.; Hew, W.P. Axial-flux permanent-magnet machine modeling, design, simulation and analysis. Sci. Res. Essays 2011, 6, 2525–2549. [Google Scholar]
- Taran, N.; Ardebili, M. A novel approach for efficiency and power density optimization of an Axial Flux Permanent Magnet generator through genetic algorithm and finite element analysis. In Proceedings of the IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 709–714. [Google Scholar]
- Egea, A.; Almandoz, G.; Poza, J.; Gonzalez, A. Axial flux machines modelling with the combination of 2D FEM and analytic tools. In Proceedings of the XIX International Conference on Electrical Machines—ICEM, Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar]
- Choi, J.Y.; Lee, S.H.; Ko, K.J.; Jang, S.M. Improved Analytical Model for Electromagnetic Analysis of Axial Flux Machines with Double-Sided Permanent Magnet Rotor and Coreless Stator Windings. IEEE Trans. Magn. 2011, 47, 2760–2763. [Google Scholar] [CrossRef]
- Mohammadi, S.; Mirsalim, M. Analytical Design Framework for Torque and Back-EMF Optimization, and Inductance Calculation in Double-Rotor Radial-Flux Air-Cored Permanent-Magnet Synchronous Machines. IEEE Trans. Magn. 2013, 50, 1–16. [Google Scholar] [CrossRef]
- Radwan-Pragłowska, N.; Borkowski, D.; Wegiel, T. Model of coreless axial flux permanent magnet generator. In Proceedings of the International Symposium on Electrical Machines (SME), Naleczow, Poland, 18–21 June 2017; pp. 1–6. [Google Scholar]
- Mulyaseputra, P.S.; Hadi, S.P.; Wijaya, F.D.; Suharyanto, S. Analysis of ferrite effect in Axial Flux Permanent Magnet Generator using magnetic circuit approach. In Proceedings of the 3rd International Conference on Science and Technology—Computer (ICST), Yogyakarta, Indonesia, 11–12 July 2017; pp. 45–50. [Google Scholar]
- Mulyaseputra, P.S.; Wijaya, F.D.; Hadi, S.P.; Suharyanto, S. Magnetic field distribution simulation on two permanent magnet rotor discs with twelve pole pairs. In Proceedings of the 3rd International Conference on Instrumentation, Communications, Information Technology and Biomedical Engineering (ICICI-BME), Bandung, Indonesia, 7–8 November 2013; pp. 178–183. [Google Scholar]
- Joss, A.; Randewijk, P.J. Design and optimisation of an Ironless Double-rotor Radial Flux Permanent Magnet machine. In Proceedings of the XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 1473–1479. [Google Scholar]
- Virtič, P. Načrtovanje in Analiza Sinhronskih Strojev s Trajnimi Magneti in Aksialnim Magnetnim Pretokom. Ph.D. Thesis, University of Maribor, Maribor, Slovenia, 2009. [Google Scholar]
- Weisstein, E.W. Least Squares Fitting. MathWorld—Wolfram Web Resource. Available online: http://mathworld.wolfram.com/LeastSquaresFitting.html (accessed on 20 March 2019).
- Kenney, J.F.; Keeping, E.S. Linear Regression and Correlation. In Mathematics of Statistics, 3rd ed.; Van Nostrand: Princeton, NJ, USA, 1962; Chapter 15, Part 1; pp. 252–285. [Google Scholar]
- Pyrhonen, J.; Jokinen, T.; Hrabovcova, V. Design of Rotating Electrical Machines; Wiley and Sons: Hoboken, NJ, USA, 2009; Wiley Online. [Google Scholar]
- Spooner, E.; Chalmers, B. ‘TORUS’: A slotless, toroidal-stator, permanent-magnet generator. Proc. Inst. Elect. Eng. Elect. Power Appl. 1992, 139, 497. [Google Scholar] [CrossRef] [Green Version]
- Caricchi, F.; Chalmers, B.; Crescimbini, F.; Spooner, E. Advances in the design of TORUS machines. In Proceedings of the International Conference on Power Electronic Drives and Energy Systems for Industrial Growth, Perth, WA, Australia, 1–3 December 1998; pp. 516–522. [Google Scholar]







| Symbol | Quantity | Value/Unit |
|---|---|---|
| dFe | Rotor disk thickness | 7 mm |
| hPM | Permanent magnet thickness | 5 mm |
| τm | Magnetic pitch | 25° |
| Di | Inner diameter of PM | 80 mm |
| Do | Outer diameter of PM | 150 mm |
| τp | Pole pitch | 36° |
| I | Electrical current | 2 × 10 A |
| Number of windings | 6 | |
| ds | Winding thickness | 15 mm |
| dc | Coil width | 20 mm |
| Sw | Copper wire cross section | 1.23 mm2 |
| dag | Air gap thickness | 1 mm |
| kw | Winding factor | 0.966 |
| p | Number of pole pairs | 5 |
| Symbol | Quantity | Value/Unit |
|---|---|---|
| dFe | Rotor disk thickness | 7 mm |
| hPM | Permanent magnet thickness | 5 mm |
| τm | Magnetic pitch | 12° |
| Di | Inner diameter of PM | 80 mm |
| Do | Outer diameter of PM | 150 mm |
| τp | Pole pitch | 18° |
| I | Electrical current | 2 × 10 A |
| Number of windings | 12 | |
| ds | Winding thickness | 15 mm |
| dc | Coil width | 15 mm |
| Sw | Copper wire cross section | 1.23 mm2 |
| dag | Air gap thickness | 1 mm |
| kw | Winding factor | 0.966 |
| p | Number of pole pairs | 10 |
| ds (mm) | hPM (mm) | dFe (mm) | Nf | ksat | Bz (T) | Φ (Wb) | Tem (Nm) | E (V) |
|---|---|---|---|---|---|---|---|---|
| 15 | 5 | 7 | 107 | 1.011 | 0.4298 | 0.001509746 | 29.80 | 34.67 |
| 20 | 5 | 7 | 142 | 1.011 | 0.3610 | 0.001268166 | 33.22 | 38.64 |
| 15 | 7 | 7 | 107 | 1.011 | 0.5274 | 0.00185257 | 36.57 | 42.54 |
| 20 | 7 | 7 | 142 | 1.011 | 0.4520 | 0.00158751 | 41.59 | 48.37 |
| 25 | 7 | 7 | 178 | 1.011 | 0.3954 | 0.001388804 | 45.61 | 53.05 |
| 20 | 10 | 8 | 142 | 1.010 | 0.5574 | 0.001958025 | 51.30 | 59.66 |
| 30 | 10 | 7 | 214 | 1.011 | 0.4468 | 0.001569545 | 61.97 | 72.08 |
| 40 | 10 | 7 | 285 | 1.011 | 0.3730 | 0.001310093 | 68.89 | 80.12 |
| ds (mm) | hPM (mm) | dFe (mm) | Nf | Bz (T) | Φ (Wb) | Tem (Nm) | E (V) |
|---|---|---|---|---|---|---|---|
| 15 | 5 | 7 | 107 | 0.4319 | 0.001517 | 29.95 | 34.83 |
| 20 | 5 | 7 | 142 | 0.3628 | 0.0012743 | 33.38 | 38.83 |
| 15 | 7 | 7 | 107 | 0.5183 | 0.0018205 | 35.94 | 41.80 |
| 20 | 7 | 7 | 142 | 0.4437 | 0.0015585 | 40.83 | 47.49 |
| 25 | 7 | 7 | 178 | 0.3827 | 0.0013442 | 44.14 | 51.35 |
| 20 | 10 | 8 | 142 | 0.5368 | 0.0018855 | 49.40 | 57.45 |
| 30 | 10 | 7 | 214 | 0.4051 | 0.0014229 | 56.18 | 65.34 |
| 40 | 10 | 7 | 285 | 0.3168 | 0.0011128 | 58.51 | 68.05 |
| Analytical Method | FEM | Analytical Method and Mathematical Models | |||||
|---|---|---|---|---|---|---|---|
| hPM | ds | Tem | E | Tem | E | Tem | E |
| (mm) | (mm) | (Nm) | (V) | (Nm) | (V) | (Nm) | V |
| 5 | 15 | 29.80 | 34.67 | 29.94 | 33.85 | 29.95 | 34.83 |
| 20 | 33.22 | 38.64 | 33.43 | 37.69 | 33.38 | 38.83 | |
| 7 | 15 | 36.57 | 42.54 | 35.96 | 38.21 | 35.94 | 41.80 |
| 20 | 41.59 | 48.37 | 41.22 | 46.41 | 40.83 | 47.49 | |
| 25 | 45.61 | 53.05 | 44.56 | 50.5 | 44.14 | 51.35 | |
| 10 | 20 | 51.30 | 59.66 | 49.69 | 55.27 | 49.40 | 57.45 |
| 30 | 61.97 | 72.08 | 57.57 | 65.73 | 56.18 | 65.34 | |
| 40 | 68.89 | 80.12 | 62.63 | 71.29 | 58.51 | 68.05 | |
| Analytical Method | FEM | Analytical Method and Mathematical Models | Matching (%) | |||
|---|---|---|---|---|---|---|
| hTM (mm) | ds (mm) | Tem (Nm) | Tem (Nm) | Tem (Nm) | FEM/ Model | FEM/ Analytical |
| 5 | 15 | 42.78 | 36.78 | 38.87 | 105.68 | 116.31 |
| 20 | 48.07 | 40.00 | 40.26 | 100.67 | 120.18 | |
| 7 | 15 | 52.50 | 43.17 | 45.91 | 106.33 | 121.60 |
| 20 | 60.17 | 47.58 | 48.02 | 100.93 | 126.47 | |
| 25 | 65.43 | 50.19 | 46.87 | 93.38 | 130.35 | |
| 10 | 20 | 74.21 | 54.76 | 55.25 | 100.89 | 135.52 |
| 30 | 88.96 | 60.26 | 51.69 | 85.78 | 147.62 | |
| 40 | 99.31 | 62.44 | 43.59 | 69.82 | 159.05 | |
| Average | 95.43 | 132.14 | ||||
| n (min−1) | E1 (V) | E2 (V) | E3 (V) | Eaverage (V) |
|---|---|---|---|---|
| 200 | 11.31 | 11.52 | 11.48 | 11.33 |
| 300 | 16.8 | 17.12 | 17.1 | 16.99 |
| 400 | 22.5 | 22.88 | 22.67 | 22.65 |
| 500 | 28.14 | 28.47 | 28.34 | 28.31 |
| 600 | 33.84 | 34.18 | 33.96 | 33.97 |
| 700 | 39.44 | 39.83 | 39.6 | 39.62 |
| 800 | 45.04 | 45.53 | 45.23 | 45.27 |
| 900 | 50.68 | 51.22 | 50.89 | 50.92 |
| n | Eaverage | f | Emodel | Eaverage/Emodel |
|---|---|---|---|---|
| (min−1) | (V) | (Hz) | (V) | (%) |
| 200 | 11.33 | 16.67 | 10.85 | 104.42 |
| 300 | 16.99 | 25 | 16.28 | 104.36 |
| 400 | 22.65 | 33.33 | 21.7 | 104.38 |
| 500 | 28.31 | 41.67 | 27.13 | 104.35 |
| 600 | 33.97 | 50 | 32.55 | 104.36 |
| 700 | 39.62 | 58.33 | 37.98 | 104.32 |
| 800 | 45.27 | 66.67 | 43.41 | 104.28 |
| 900 | 50.92 | 75 | 48.83 | 104.28 |
| I | Tmeasured | Tmodel | Tmeasured/Tmodel |
|---|---|---|---|
| (A) | (Nm) | (Nm) | (%) |
| 10.21 | 16.72 | 15.29 | 109.35 |
| 11.00 | 17.97 | 16.48 | 109.04 |
| 12.03 | 19.52 | 18.01 | 108.38 |
| 13.06 | 21.05 | 19.55 | 107.67 |
| 13.98 | 22.41 | 20.93 | 107.07 |
| 15.08 | 23.94 | 22.57 | 106.07 |
| 16.14 | 25.48 | 24.16 | 105.46 |
| 17.18 | 26.91 | 25.72 | 104.63 |
| 18.16 | 28.27 | 27.19 | 103.97 |
| 19.3 | 29.8 | 28.89 | 103.15 |
| 20.19 | 30.97 | 30.22 | 102.48 |
| hTM (mm) | d (ds + 2 dag) (mm) | dFe (mm) | Bz_FEM (T) | Bz_Model (T) | Bz_Meas (T) | Bz_FEM/Bz_Meas (%) | Bz_Model/Bz_Meas (%) |
|---|---|---|---|---|---|---|---|
| 5 | 17 | 5 | 0.4401 | 0.4367 | 0.4490 | 98.02 | 97.27 |
| 5 | 17 | 6 | 0.4581 | 0.4551 | 0.4720 | 97.06 | 96.41 |
| 5 | 17 | 10 | 0.4671 | 0.4700 | 0.4790 | 97.52 | 98.12 |
| 5 | 17 | 11 | 0.4676 | 0.4687 | 0.4800 | 97.41 | 97.64 |
| 5 | 17 | 15 | 0.4686 | 0.4718 | 0.4830 | 97.02 | 97.68 |
| 5 | 22 | 5 | 0.3758 | 0.3737 | 0.3870 | 97.10 | 96.57 |
| 5 | 22 | 6 | 0.3810 | 0.3842 | 0.3950 | 96.45 | 97.27 |
| 5 | 22 | 10 | 0.3851 | 0.3838 | 0.4020 | 95.79 | 95.46 |
| 5 | 22 | 11 | 0.3856 | 0.3820 | 0.4020 | 95.92 | 95.02 |
| 5 | 22 | 15 | 0.3861 | 0.3929 | 0.4020 | 96.04 | 97.74 |
| Average | 96.83 | 96.92 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pranjić, F.; Virtič, P. Development of Mathematical Models in Explicit Form for Design and Analysis of Axial Flux Permanent Magnet Synchronous Machines. Appl. Sci. 2020, 10, 7695. https://doi.org/10.3390/app10217695
Pranjić F, Virtič P. Development of Mathematical Models in Explicit Form for Design and Analysis of Axial Flux Permanent Magnet Synchronous Machines. Applied Sciences. 2020; 10(21):7695. https://doi.org/10.3390/app10217695
Chicago/Turabian StylePranjić, Franjo, and Peter Virtič. 2020. "Development of Mathematical Models in Explicit Form for Design and Analysis of Axial Flux Permanent Magnet Synchronous Machines" Applied Sciences 10, no. 21: 7695. https://doi.org/10.3390/app10217695
APA StylePranjić, F., & Virtič, P. (2020). Development of Mathematical Models in Explicit Form for Design and Analysis of Axial Flux Permanent Magnet Synchronous Machines. Applied Sciences, 10(21), 7695. https://doi.org/10.3390/app10217695





