Scaling Law, Confined and Surface Modes in Photonic Fibonacci Stub Structures: Theory and Experiment
Abstract
:1. Introduction
2. Theoretical Approach: Green’s Function
- (i)
- when the magnetic field vanishes on both sides of the FS structure (i.e., or equivalently ), one obtains:
- (ii)
- When the electric field vanishes on the side of the structure which will be grafted on the waveguide and the magnetic field vanishes on the free surface (i.e., or ), one obtains:
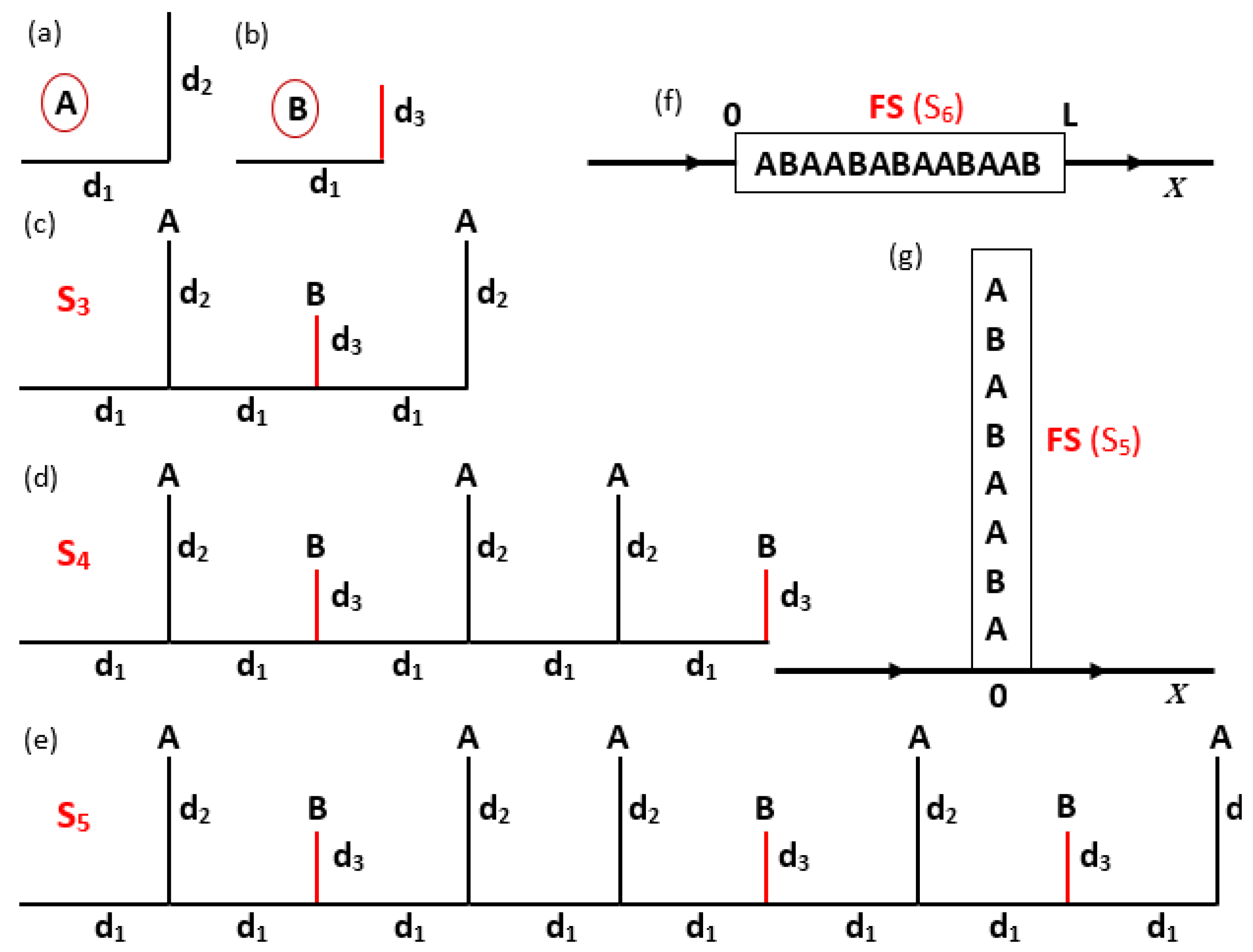
3. Experimental Procedure
4. Numerical and Experimental Results
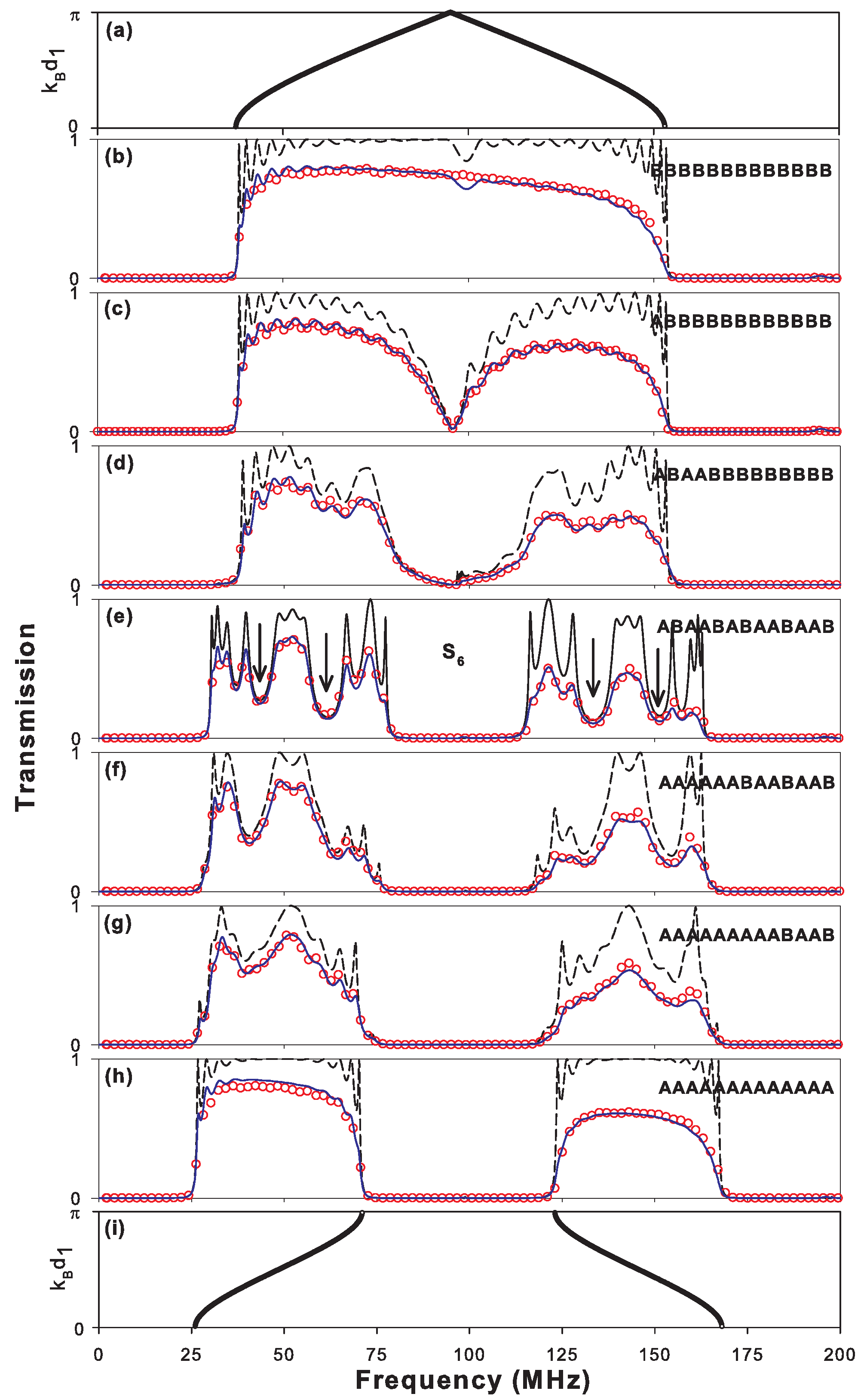
4.1. From Periodic to Fibonacci Sequence and Vice Versa
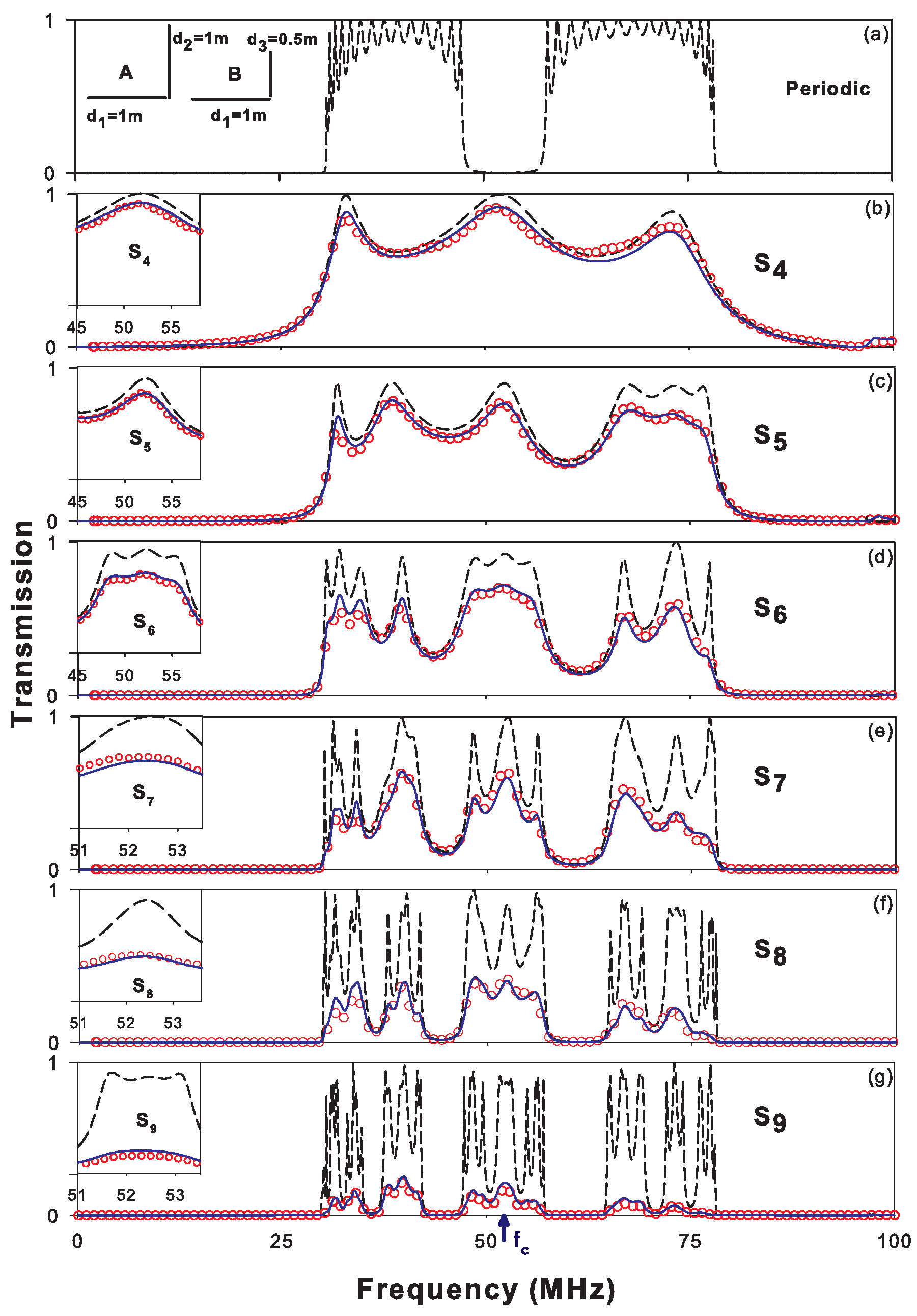
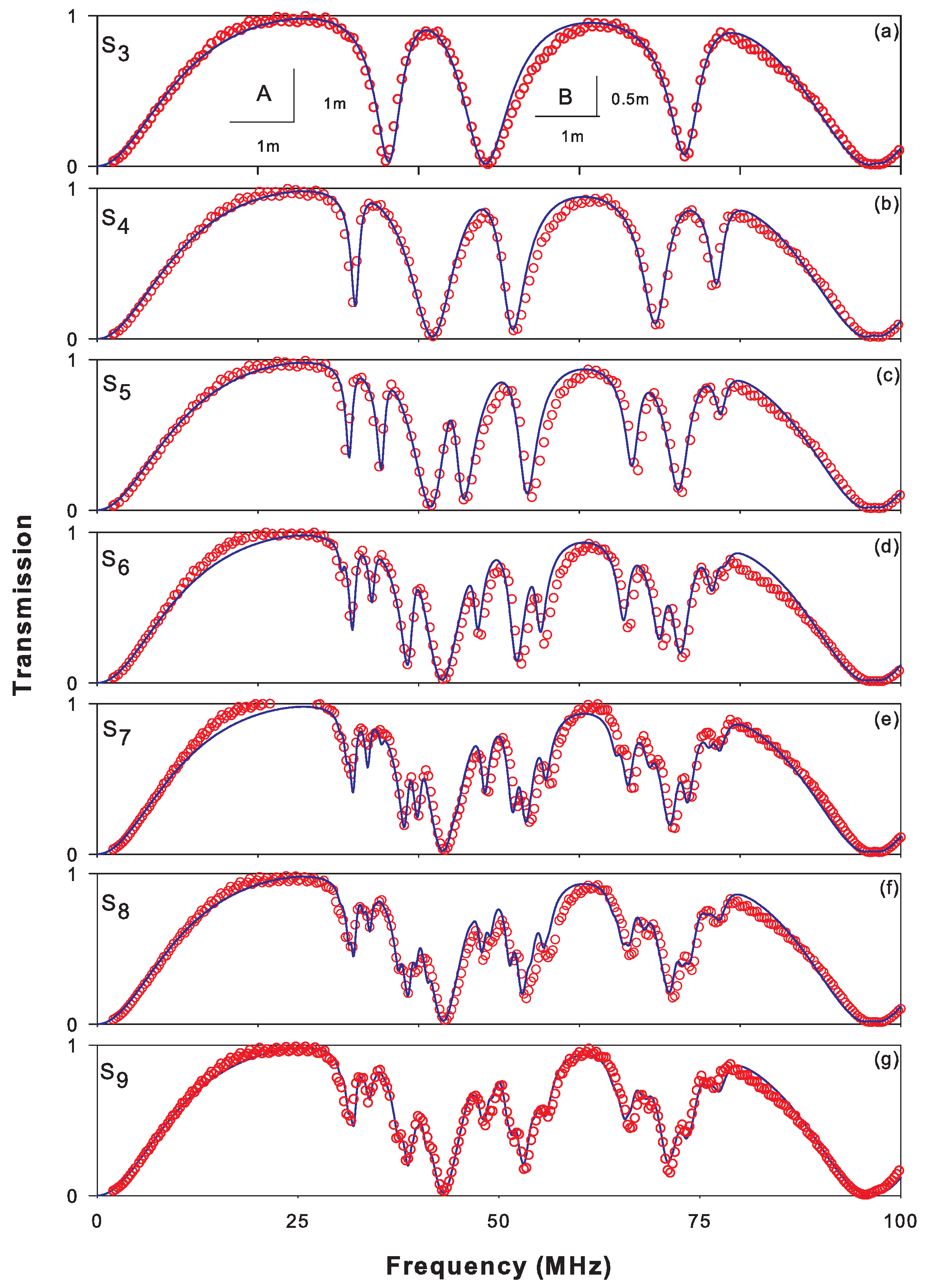
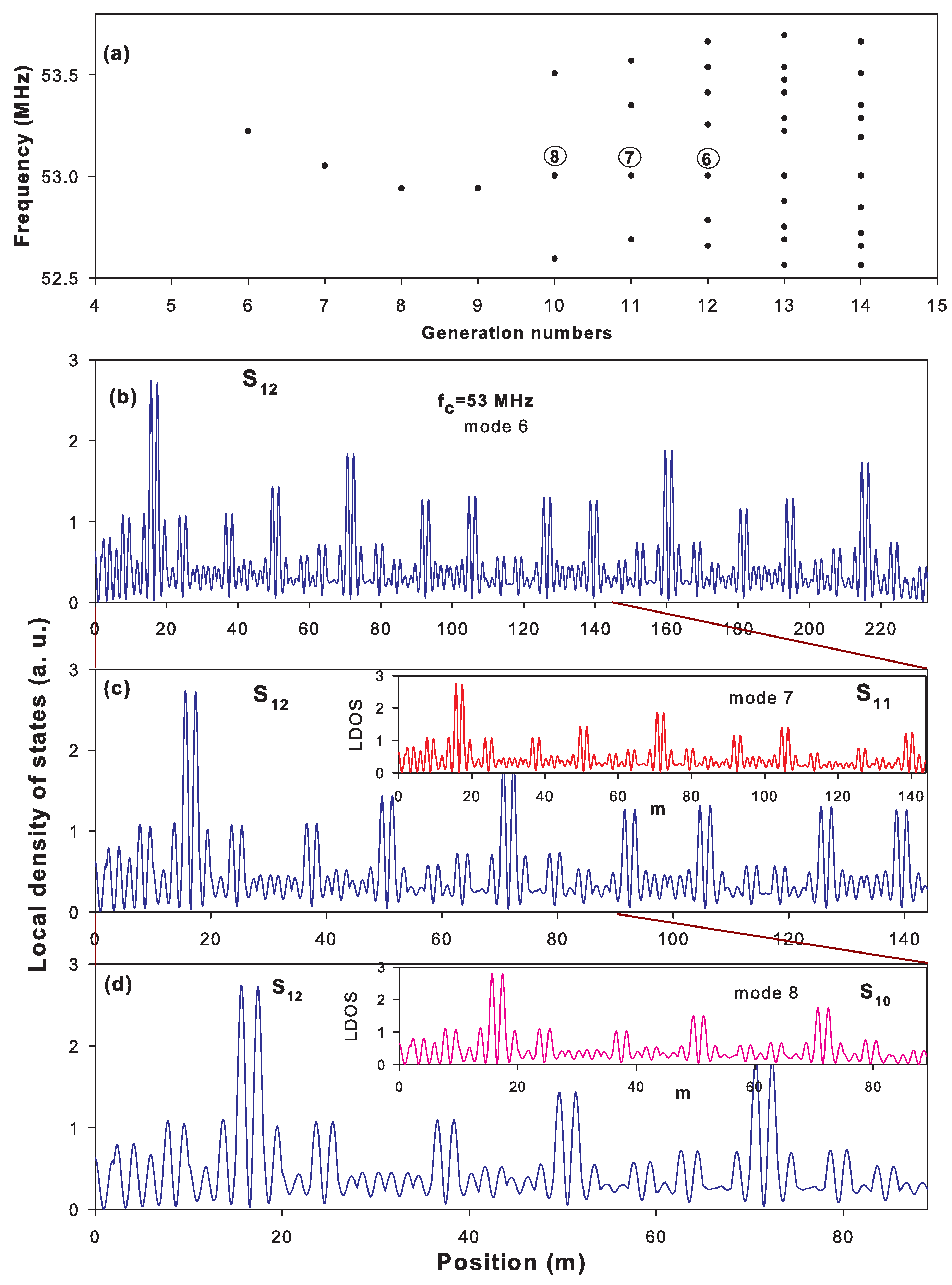
4.2. Horizontal Fibonacci Sequence: Scaling Law
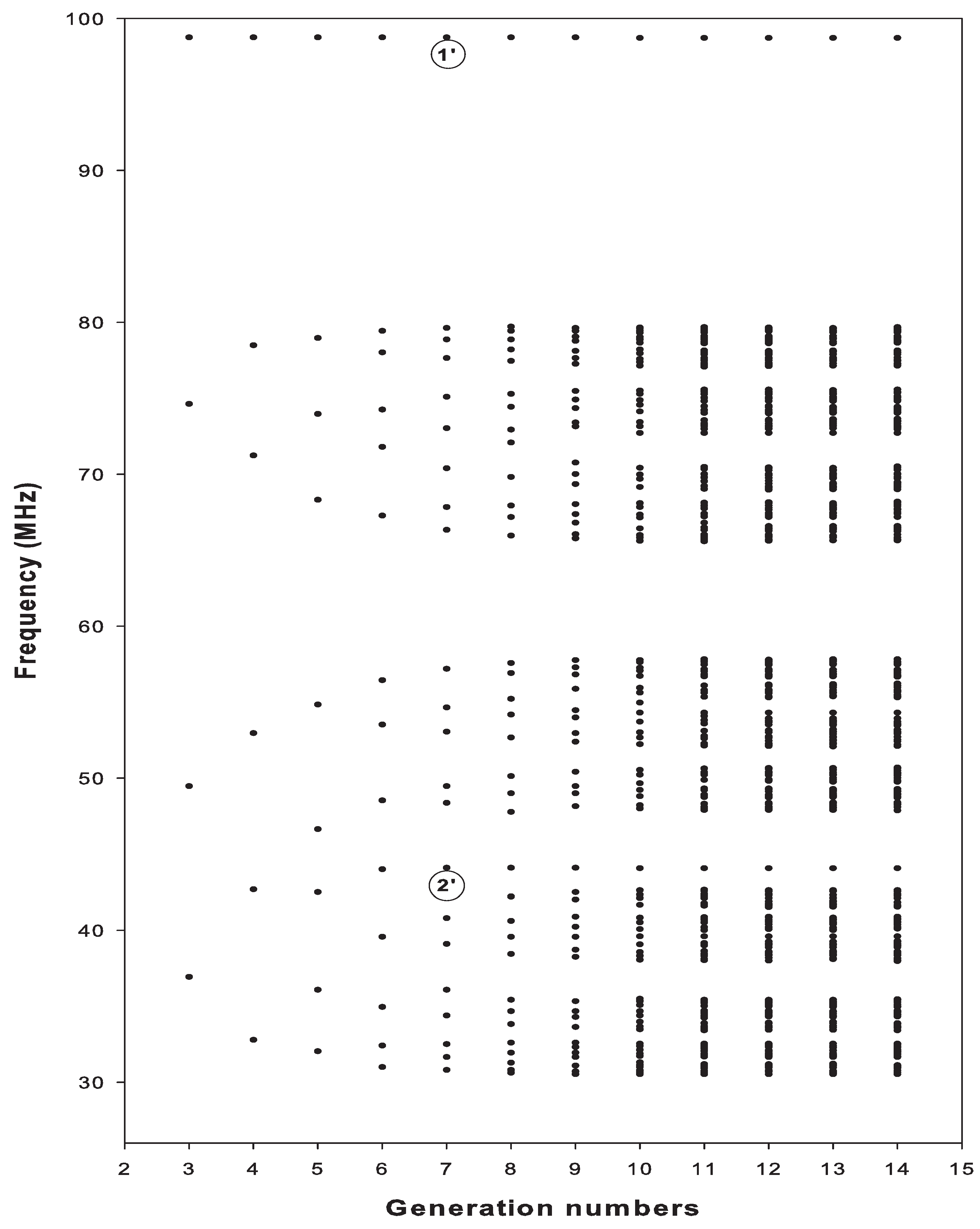
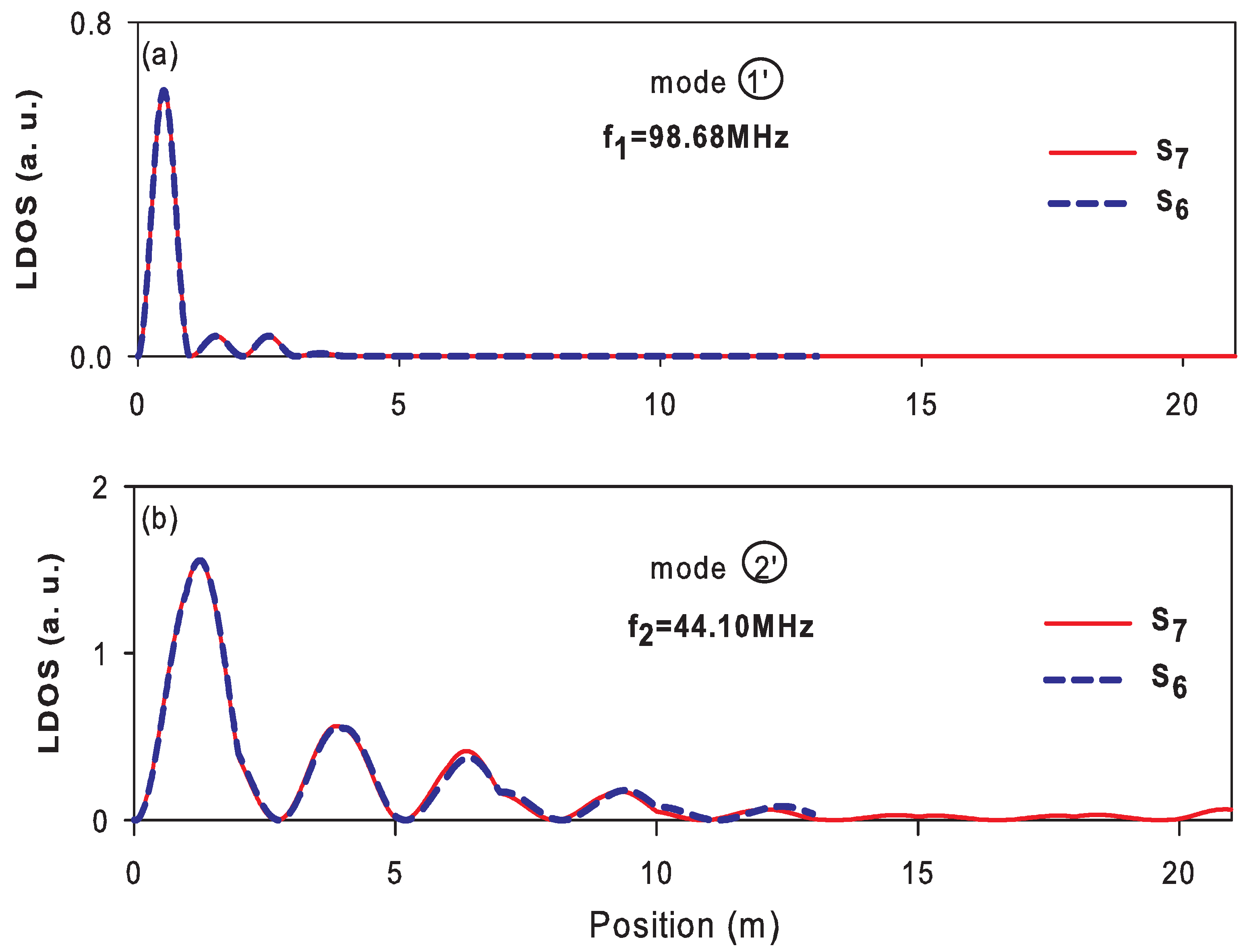
4.3. Vertical Fibonacci Sequence: Confined and Surface Modes
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Inverse Surface Green’s Function of the Fibonacci Sequence
References
- Shechtman, D.; Bletch, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951. [Google Scholar] [CrossRef] [Green Version]
- Levine, D.; Steinhardt, P.J. Quasicrystals: A new class of ordered structures. Phys. Rev. Lett. 1984, 53, 2477. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Ji, A.; Cao, Z. Stressed Fibonacci spiral patterns of definite chirality. Appl. Phys. Lett. 2007, 90, 164102. [Google Scholar] [CrossRef] [Green Version]
- Maciá, E. Aperiodic Structures in Condensed Matter: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Vardeny, Z.V.; Nahata, A.; Agrawal, A. Optics of photonic quasicrystal. Nat. Photonics 2013, 7, 177. [Google Scholar] [CrossRef]
- Negro, L.D. Optics of Aperiodic Structures: Fundamentals and Device Applications; Pan Stanford Publishing: Singapore; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Zhao, Y.F.; Wang, Z.M.; Jiang, Z.J.; Chen, X.; Yue, C.X.; Wang, J.Z.; Liu, J.J. Add-drop filter with compound structures of photonic crystal and photonic quasicrysta. J. Infrared Millim. Waves 2017, 36, 342–348. [Google Scholar]
- Ren, J.; Sun, X.; Wang, S. A narrowband filter based on 2D 8-fold photonic quasicrystal. Superlattices Microstruct. 2018, 116, 221. [Google Scholar] [CrossRef]
- Trabelsi, Y.; Ali, N.B.; Elhawil, A.; Krishnamurthy, R.; Kanzari, M.; Amiri, I.S.; Yupapin, P. Design of structural gigahertz multichanneled filter by using generalized Fibonacci superconducting photonic quasicrystals. Results Phys. 2019, 13, 102343. [Google Scholar] [CrossRef]
- Liu, E.; Tan, W.; Yan, B.; Xie, J.L.; Ge, R.; Liu, J.J. Broadband ultra-flattened dispersion, ultra-low confinement loss and large effective mode area in an octagonal photonic quasi-crystal fiber. J. Opt. Soc. Am. A 2018, 35, 431. [Google Scholar] [CrossRef] [PubMed]
- Yan, B.; Wang, A.; Liu, E.; Tan, W.; Xie, J.; Ge, R.; Liu, J. Polarization filtering in the visible wavelength range using surface plasmon resonance and a sunflower-type photonic quasi-crystal fiber. J. Phys. D Appl. Phys. 2018, 51, 155105. [Google Scholar] [CrossRef]
- Vitiello, M.S.; Nobile, M.; Ronzani, A.; Tredicucci, A.; Castellano, F.; Talora, V.; Li, L.; Linfield, E.H.; Davies, A.G. Photonic quasi-crystal terahertz lasers. Nat. Commun. 2014, 5, 5884. [Google Scholar] [CrossRef] [Green Version]
- Notomi, M.; Suzuki, H.; Tamamura, T.; Edagawa, K. Lasing action due to the two-dimensional quasiperiodicity of photonic quasicrystals with a Penrose lattic. Phys. Rev. Lett. 2004, 92, 123906. [Google Scholar] [CrossRef] [PubMed]
- Mahler, L.; Tredicucci, A.; Beltram, F.; Walther, C.; Faist, J.; Beere, H.E.; Ritchie, D.A.; Wiersma, D.S. Quasi-periodic distributed feedback laser. Nat. Photonics 2010, 4, 165. [Google Scholar] [CrossRef]
- Ren, J.; Sun, X.; Wang, S. A low threshold nanocavity in a two-dimensional 12-fold photonic quasicrysta. Opt. Laser Technol. 2018, 101, 42. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, J.; Fang, Z.; An, D.; Zhao, X. Visible light metasurfaces assembled by quasiperiodic dendritic cluster sets. Adv. Mater. Interfaces 2019, 6, 1801834. [Google Scholar] [CrossRef]
- Liu, J.J.; Fan, Z.G. Size limits for focusing of two-dimensional photonic quasicrystal lenses. IEEE Photonics Technol. Lett. 2018, 30, 1001. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, L.; Zhao, T.; Liu, X.; Feng, S.; Chen, X.; Guo, H.; Li, C.; Wang, Y. High-sensitivity quasi-periodic photonic crystal biosensor based on multiple defective modes. Appl. Opt. 2019, 58, 2860. [Google Scholar] [CrossRef]
- Lee, S.Y.; Amsden, J.J.; Boriskina, S.V.; Gopinath, A.; Mitropolous, A.; Kaplan, D.L.; Omenetto, F.G.; Negro, L.D. Spatial and spectral detection of protein monolayers with deterministic aperiodic arrays of metal nanoparticles. Proc. Natl. Acad. Sci. USA 2010, 107, 12086. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mauriz, P.W.; Vasconcelos, M.S.; Albuquerque, E.L. Optical transmission spectra in symmetrical Fibonacci photonic multilayers. Phys. Lett. A 2009, 373, 496. [Google Scholar] [CrossRef]
- Negro, L.D.; Yi, J.H.; Nguyen, V.; Michel, Y.Y.J.; Kimerling, L.C. Spectrally enhanced light emission from aperiodic photonic structures. Appl. Phys. Lett. 2005, 86, 261905. [Google Scholar] [CrossRef]
- Boriskina, S.V.; Gopinath, A.; Negro, L.D. Optical gap formation and localization properties of optical modes in deterministic aperiodic photonic structures. Opt. Express 2008, 16, 18813. [Google Scholar] [CrossRef]
- Hiltunen, M.; Negro, L.D.; Ning-Ning, F.; Kimerling, L.C.; Michel, J. Modeling of aperiodic fractal waveguide structures for multifrequency light transport. J. Light. Technol. 2007, 25, 1841. [Google Scholar] [CrossRef] [Green Version]
- Zotov, N.; Feydt, J.; Walther, T.; Ludwig, A. Structure of PtFe/Fe double-period multilayers investigated by X-ray diffraction, reflectivity, diffuse scattering and TEM. Appl. Surf. Sci. 2006, 253, 128. [Google Scholar] [CrossRef]
- Lambropoulos, K.; Simserides, C. Periodic, quasiperiodic, fractal, Kolakoski, and random binary polymers: Energy structure and carrier transport. Phys. Rev. E 2019, 99, 032415. [Google Scholar] [CrossRef] [Green Version]
- Esaki, K.; Sato, M.; Kohmoto, M. Wave propagation through Cantor-set media: Chaos, scaling, and fractal structures. Phys. Rev. E 2009, 79, 056226. [Google Scholar] [CrossRef] [Green Version]
- Sakaguchi, H.; Ogawana, T. Scaling laws of reflection coefficients of quantum waves at a Cantor-like potential. Phys. Rev. E 2017, 95, 032214. [Google Scholar] [CrossRef]
- Ogawana, T.; Sakaguchi, H. Transmission coefficient from generalized Cantor-like potentials and its multifractality. Phys. Rev. E 2018, 97, 012205. [Google Scholar] [CrossRef]
- Albuquerque, E.L.; Cottam, M.G. Polaritons in Periodic and Quasiperiodic Structures; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Merlin, R.; Bajema, K.; Clarke, R.; Juang, F.Y.; Bhattacharya, P.K. Quasiperiodic GaAs-AlAs Heterostructures. Phys. Rev. Lett. 1985, 55, 1768. [Google Scholar] [CrossRef]
- Kohmoto, M.; Sutherland, B.; Tang, C. Critical wave functions and a Cantor-set spectrum of a one-dimensional quasicrystal model. Phys. Rev. B 1987, 35, 1020. [Google Scholar] [CrossRef] [Green Version]
- Tamura, S.; Wolfe, J.P. Acoustic-phonon transmission in quasiperiodic superlattices. Phys. Rev. B 1987, 36, 3491. [Google Scholar] [CrossRef]
- Aynaou, H.; El Boudouti, E.H.; Djafari-Rouhani, B.; Akjouj, A.; Velasco, V.R. Propagation and localization of acoustic waves in Fibonacci phononic circuits. J. Phys. Condens. Matter 2005, 17, 4245. [Google Scholar] [CrossRef]
- Aynaou, H.; Velasco, V.R.; Nougaoui, A.; El Boudouti, E.H.; Bria, D. Properties of elastic waves in quasiregular structures with planar defects. Superlattices Microstruct. 2002, 32, 35. [Google Scholar] [CrossRef]
- Ma, B.; Liu, T.; Liu, W.; Xue, J.; Tao, Z. Non-Bragg Bands in Acoustic Quasi-Periodic Fibonacci Waveguides. Phys. Status Solidi 2019, 13, 1900203. [Google Scholar] [CrossRef]
- Kohmoto, M.; Sutherland, B.; Iguchi, K. Localization of optics: Quasiperiodic media. Phys. Rev. Lett. 1987, 58, 2436. [Google Scholar] [CrossRef]
- Hattori, T.; Tsurumachi, N.; Kawato, S.; Nakatsuka, H. Photonic dispersion relation in a one-dimensional quasicrystal. Phys. Rev. B 1994, 50, 4220. [Google Scholar] [CrossRef]
- Costa, C.H.O.; Vasconcelos, M.S.; Albuquerque, E.L. Band structures of exchange spin waves in one-dimensional bi-component magnonic crystals. J. Appl. Phys. 2011, 109, 07D319. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Nahata, A.; Vardeny, Z.V. Measurement of surface plasmon correlation length differences using Fibonacci deterministic hole arrays. Opt. Express 2012, 20, 15222. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.W.; Fung, K.; Chan, C.; Wang, H.Z. Localization characteristics of two-dimensional quasicrystals consisting of metal nanoparticles. Phys. Rev. B 2009, 80, 155118. [Google Scholar] [CrossRef] [Green Version]
- Dallapiccola, R.; Gopinath, A.; Stellacci, F.; Negro, L.D. Quasi-periodic distribution of plasmon modes in two-dimensional Fibonacci arrays of metal nanoparticles. Opt. Express 2008, 16, 5544. [Google Scholar] [CrossRef] [PubMed]
- Bajema, K.; Merlin, R. Raman scattering by acoustic phonons in Fibonacci GaAs-AIAs superlattices. Phys. Rev. B 1987, 36, 4555. [Google Scholar] [CrossRef]
- Hurley, D.C.; Tamura, S.; Wolfe, J.P.; Ploog, K.; Nagle, J. Angular dependence of phonon transmission through a Fibonacci superlattice. Phys. Rev. B 1988, 37, 8829. [Google Scholar] [CrossRef]
- Maciá, E.; Domínguez-Adame, F. Electrons, Phonons and Excitons in Low Dimensional Aperiodic Systems; Editorial Complutense: Madrid, Sapin, 2000. [Google Scholar]
- King, P.D.C.; Cox, T.J. Acoustic band gaps in periodically and quasiperiodically modulated waveguides. J. Appl. Phys. 2007, 102, 014902. [Google Scholar] [CrossRef]
- Bellingeri, M.; Chiasera, A.; Kriegel, I.; Scotognella, F. Optical properties of periodic, quasi-periodic, and disordered one-dimensional photonic structures. Opt. Mat. 2017, 72, 403. [Google Scholar] [CrossRef] [Green Version]
- Gellermann, W.; Kohmoto, M.; Sutherland, B.; Taylor, P.C. Localization of light waves in Fibonacci dielectric multilayers. Phys. Rev. Lett. 1994, 72, 633. [Google Scholar] [CrossRef]
- Pelster, R.; Gasparian, V.; Nimtz, G. Propagation of plane waves and of waveguide modes in quasiperiodic dielectric heterostructures. Phys. Rev. E 1997, 55, 7645. [Google Scholar] [CrossRef] [Green Version]
- Peng, R.W.; Liu, Y.M.; Huang, X.Q.; Qin, F.; Wang, M.; Hu, A.; Jiang, S.S.; Feng, D.; Ouyang, L.Z.; Zou, J. Dimerlike positional correlation and resonant transmission of electromagnetic waves in aperiodic dielectric multilayers. Phys. Rev. B 2004, 69, 165109. [Google Scholar] [CrossRef] [Green Version]
- Ghulinyan, M.; Oton, C.J.; Negro, L.D.; Pavesi, L.; Sapienza, R.; Colocci, M.; Wiersma, D.S. Light-pulse propagation in Fibonacci quasicrystals. Phys. Rev. B 2005, 71, 094204. [Google Scholar] [CrossRef] [Green Version]
- Peng, R.W.; Wang, M.; Hu, A.; Jiang, S.S.; Jin, G.J.; Feng, D. Photonic localization in one-dimensional k-component Fibonacci structures. Phys. Rev. B 1998, 57. [Google Scholar] [CrossRef]
- Sibilia, C.; Nefedov, I.S.; Scolara, M.; Berlotti, M. Electromagnetic mode density for finite quasi-periodic structures. J. Opt. Soc. Am. B 1998, 15, 1947. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Y.; Gong, C. Numerical investigation of light-wave localization in optical Fibonacci superlattices with symmetric internal structure. J. Phys. Condens. Matter 1999, 11, 7645. [Google Scholar] [CrossRef]
- Liu, N.H. Propagation of light waves in Thue-Morse dielectric multilayers. Phys. Rev. B 1997, 55, 3543. [Google Scholar] [CrossRef]
- Lavrinenko, A.V.; Zhukovsky, S.V.; Sandmirski, K.S.; Gaponenko, S.V. Propagation of classical waves in nonperiodic media: Scaling properties of an optical Cantor filter. Phys. Rev. E 2002, 65, 036621. [Google Scholar] [CrossRef] [Green Version]
- Macia, E. Exploiting quasiperiodic order in the design of optical devices. Phys. Rev. B 2001, 63, 205421. [Google Scholar] [CrossRef] [Green Version]
- Lusk, D.; Abdulhalim, I.; Placido, F. Omnidirectional reflection from Fibonacci quasi-periodic one-dimensional photonic crystal. Opt. Commun. 2001, 198, 273. [Google Scholar] [CrossRef]
- Segovia-Chaves, F.; Vinck-Posada, H. Transmittance spectrum of a superconductor-semiconductor quasiperiodic one-dimensional photonic crystal. Physica C 2019, 563, 10. [Google Scholar] [CrossRef]
- Elsayed, H.A.; Abadla, M.M. Transmission investigation of one-dimensional Fibonacci-based quasi-periodic photonic crystals including nanocomposite material and plasma. Phys. Scr. 2020, 95, 035504. [Google Scholar] [CrossRef]
- Aynaou, H.; El Boudouti, E.H.; El Hassouani, Y.; Akjouj, A.; Djafari-Rouhani, B.; Vasseur, J.; Benomar, A.; Velasco, V.R. Propagation and localization of electromagnetic waves in quasiperiodic serial loop structures. Phys. Rev. E 2005, 72, 056601. [Google Scholar] [CrossRef]
- El Boudouti, E.H.; El Hassouani, Y.; Aynaou, H.; Djafari-Rouhani, B.; Akjouj, A.; Velasco, V.R. Electromagnetic wave propagation in quasi-periodic photonic circuits. J. Phys. Condens. Matter 2007, 19, 246217. [Google Scholar] [CrossRef] [PubMed]
- El Hassouani, Y.; Aynaou, H.; El Boudouti, E.H.; Djafari-Rouhani, B.; Akjouj, A.; Velasco, V.R. Surface electromagnetic waves in Fibonacci superlattices: Theoretical and experimental results. Phys. Rev. B 2006, 74, 035314. [Google Scholar] [CrossRef]
- Sánchez-Lopez, M.M.; Sánchez Mero no, A.; Arias, J.; Davis, J.A.; Moreno, I. Observation of superluminal and negative group velocities in a Mach-Zehnder interferometer. Appl. Phys. Lett. 2008, 93, 074102. [Google Scholar] [CrossRef]
- Jin, G.J.; Wang, Z.D.; Hu, A.; Jiang, S.S. Quantum waveguide theory of serial stub structures. J. Appl. Phys. 1999, 85, 1597. [Google Scholar] [CrossRef] [Green Version]
- Nomata, A.; Horie, S. Self-similarity appearance conditions for electronic transmission probability and Landauer resistance in a Fibonacci array of T stubs. Phys. Rev. B 2007, 76, 235113. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Chakrabarti, A. Electronic transmission in quasiperiodic serial stub structures. J. Phys. Condens. Matter 2004, 16, 313. [Google Scholar] [CrossRef]
- Vasseur, J.O.; Akjouj, A.; Djafari-Rouhani, B.; Dobrzynski, L.; El Boudouti, E.H. Photon, electron, magnon, phonon and plasmon mono-mode circuits. Surf. Sci. Rep. 2004, 54, 1. [Google Scholar] [CrossRef]
- Dobrzynski, L.; Akjouj, A.; Djafari-Rouhani, B.; Vasseur, J.O.; Zemmouri, J. Giant gaps in photonic band structures. Phys. Rev. B 1998, 57, R9388. [Google Scholar] [CrossRef]
- Vasseur, J.O.; Djafari-Rouhani, B.; Dobrzynski, L.; Akjouj, A.; Zemmouri, J. Defect modes in one-dimensional comblike photonic waveguides. Phys. Rev. B 1999, 49, 13446. [Google Scholar] [CrossRef]
- El Boudouti, E.H.; El Hassouani, Y.; Djafari-Rouhani, B.; Aynaou, H. Two types of modes in finite size one-dimensional coaxial photonic crystals: General rules and experimental evidence. Phys. Rev. E 2007, 76, 026607. [Google Scholar] [CrossRef]
- Djafari-Rouhani, B.; El Boudouti, E.H.; Akjouj, A.; Dobrzynski, L.; Vasseur, J.O.; Mir, A.; Fettouhi, N.; Zemmouri, J. Surface states in one-dimensional photonic band gap structures. Vacuum 2001, 63, 177. [Google Scholar] [CrossRef]
- Harper, P.G. Single Band Motion of Conduction Electrons in a Uniform Magnetic Field. Proc. Phys. Soc. Lond. Sect. A 1955, 68, 874. [Google Scholar] [CrossRef]
- Kraus, Y.E.; Zilberberg, O. Topological equivalence between the Fibonacci quasicrystal and the Harper model. Phys. Rev. Lett. 2012, 109, 116404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verbin, M.; Zilberberg, O.; Lahini, Y.; Kraus, Y.E.; Silberberg, Y. Topological pumping over a photonic Fibonacci quasicrystal. Phys. Rev. B 2015, 91, 064201. [Google Scholar] [CrossRef] [Green Version]
- Dobrzynski, L. Interface response theory of continuous composite systems. Surf. Sci. Rep. 1990, 11, 139. [Google Scholar] [CrossRef]
- Wadell, B.C. Transmission Line Design Handbook; Artech House, Inc.: Norwood, MA, USA, 1991; Chapter 3. [Google Scholar]
- Mouadili, A.; El Boudouti, E.H.; Soltani, A.; Talbi, A.; Djafari-Rouhani, B.; Akjouj, A.; Haddadi, K. Electromagnetically induced absorption in detuned stub waveguides: A simple analytical and experimental model. J. Phys. Condens. Matter 2014, 26, 505901. [Google Scholar] [CrossRef]
- Khattou, S.; Amrani, M.; Mouadili, A.; El Boudouti, E.H.; Talbi, A.; Akjouj, A.; Djafari-Rouhan, B. Comparison of density of states and scattering parameters in coaxial photonic crystals: Theory and experiment. Phys. Rev. B 2020, 102, 165310. [Google Scholar] [CrossRef]
- Kohmoto, M.; Kadanoff, L.P.; Tang, C. Localization problem in one dimension: Mapping and escape. Phys. Rev. Lett. 1983, 50, 1870. [Google Scholar] [CrossRef]
- Macia, E.; Dominguez-Adame, F. Physical nature of critical wave functions in Fibonacci systems. Phys. Rev. Lett. 1996, 76, 2957. [Google Scholar] [CrossRef] [Green Version]
- Fijiwara, T.; Komoto, M.; Tokihito, T. Multifractal wave functions on a Fibonacci lattice. Phys. Rev. B 1989, 40, 7413. [Google Scholar] [CrossRef]
- Jin, D.; Jin, G. Matrix maps for substitution sequences in the biquaternion representation. Phys. Rev. B 2005, 71, 014212. [Google Scholar] [CrossRef]
- Peng, R.W.; Jin, G.J.; Wang, M.; Hu, A.; Jiang, S.S.; Feng, D. Electronic transport in k-component Fibonacci quantum waveguides. J. Phys. Condens. Matter 2000, 12, 5701. [Google Scholar] [CrossRef]
- Negro, L.D.; Oton, C.J.; Gaburro, Z.; Pavesi, L.; Johnson, P.; Lagendijk, A.; Righini, R.; Colocci, M.; Wiersma, D.S. Light transport through the band-edge states of Fibonacci quasicrystals. Phys. Rev. Lett. 2003, 90, 055501. [Google Scholar] [CrossRef]
- Wiersma, D.; Sapienza, R.; Mujumdar, S.; Colocci, M.; Ghulinyan, M.; Pavesi, L. Optics of nanostructured dielectrics. J. Opt. A Pure Appl. Opt. 2005, 7, S190. [Google Scholar] [CrossRef]
- Mouadili, A.; El Boudouti, E.H.; Soltani, A.; Talbi, A.; Haddadi, K.; Akjouj, A.; Djafari-Rouhani, B. Photonic demultiplexer based on electromagnetically induced transparency resonances. J. Phys. D Appl. Phys. 2018, 52, 075101. [Google Scholar] [CrossRef]
- Amrani, M.; Khattou, S.; Noual, A.; El Boudouti, E.H.; Djafari-Rouhani, B. Plasmonic Demultiplexer Based on Induced Transparency Resonances: Analytical and Numerical Study. Lect. Notes Electr. Eng. 2020, 681, 239. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aynaou, H.; Mouadili, A.; Ouchani, N.; El Boudouti, E.H.; Akjouj, A.; Djafari-Rouhani, B. Scaling Law, Confined and Surface Modes in Photonic Fibonacci Stub Structures: Theory and Experiment. Appl. Sci. 2020, 10, 7767. https://doi.org/10.3390/app10217767
Aynaou H, Mouadili A, Ouchani N, El Boudouti EH, Akjouj A, Djafari-Rouhani B. Scaling Law, Confined and Surface Modes in Photonic Fibonacci Stub Structures: Theory and Experiment. Applied Sciences. 2020; 10(21):7767. https://doi.org/10.3390/app10217767
Chicago/Turabian StyleAynaou, Hassan, Abdelkader Mouadili, Noama Ouchani, El Houssaine El Boudouti, Abdellatif Akjouj, and Bahram Djafari-Rouhani. 2020. "Scaling Law, Confined and Surface Modes in Photonic Fibonacci Stub Structures: Theory and Experiment" Applied Sciences 10, no. 21: 7767. https://doi.org/10.3390/app10217767





