Experimental Investigations on Nonlinear Flutter Behaviors of a Bridge Deck with Different Leading and Trailing Edges
Abstract
:1. Introduction
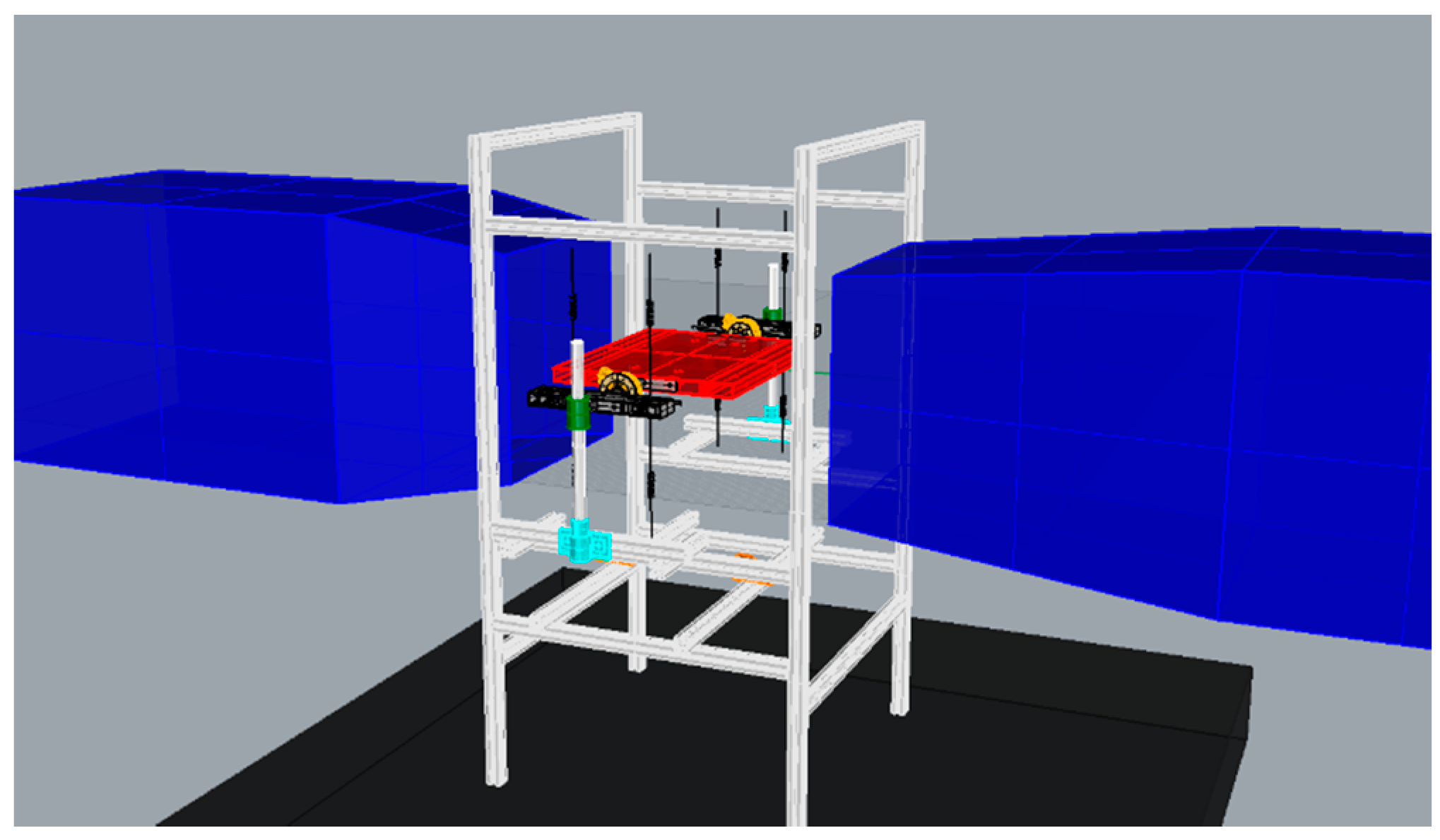
2. Experiment Setup
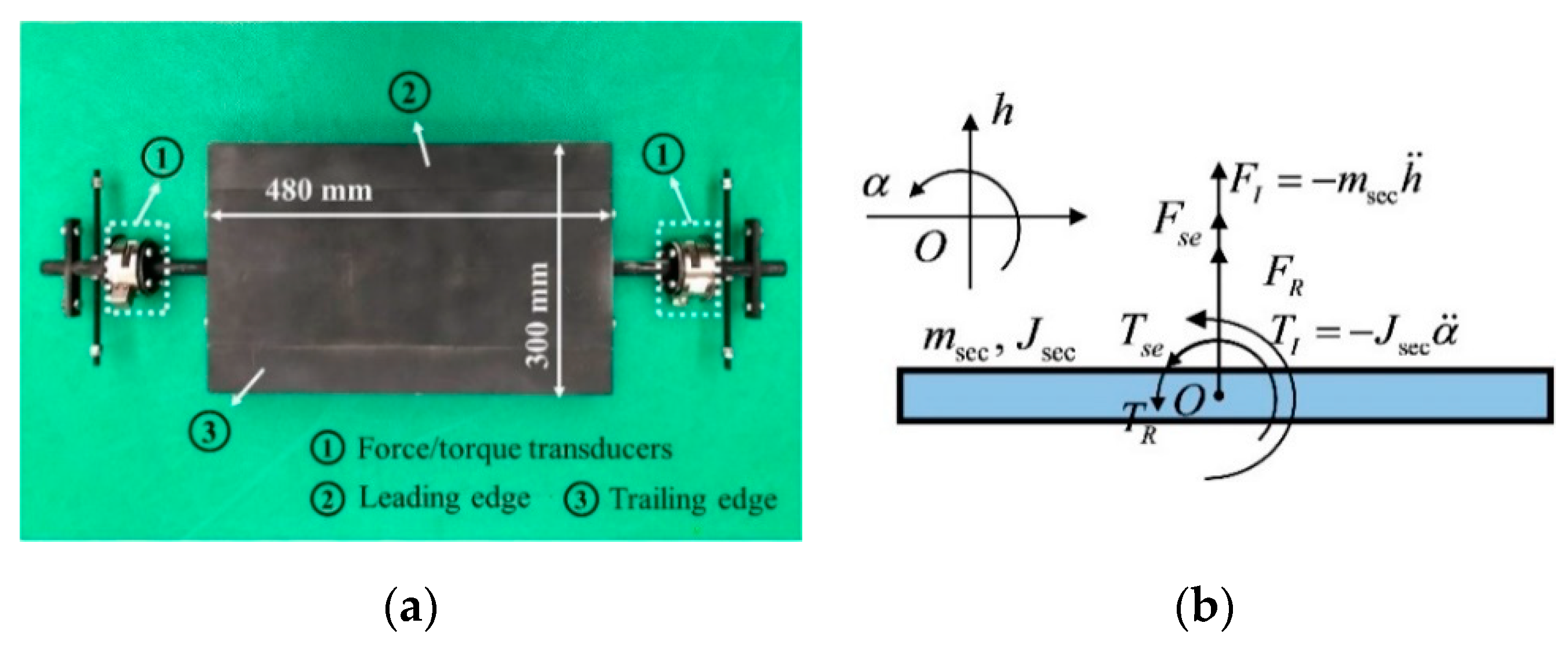
2.1. Test Device and Model Aerodynamic Configuration
2.2. Displacement and Aerodynamic Force Measurement
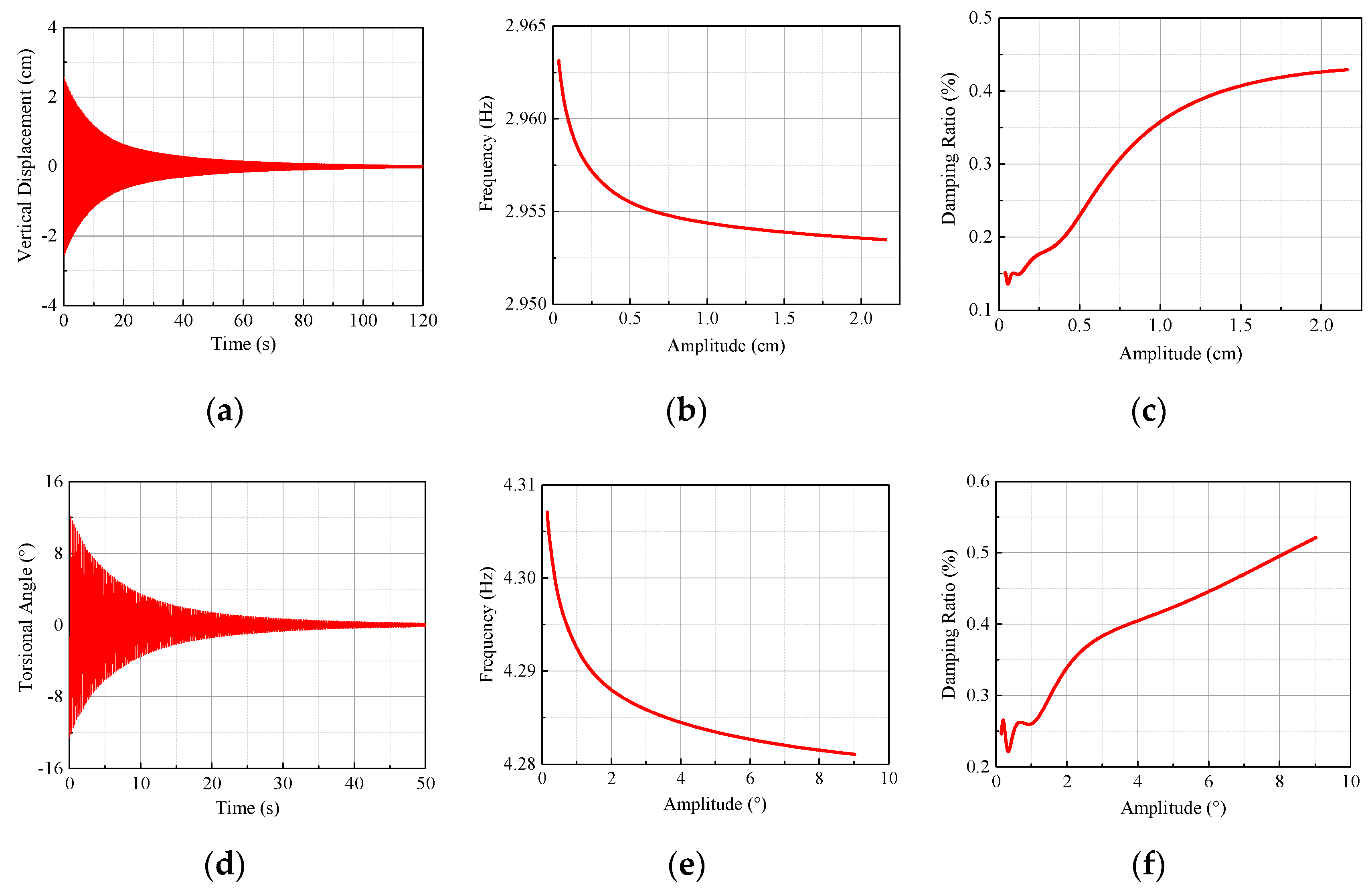
2.3. Structural Dynamic Parameters
3. Results and Discussion
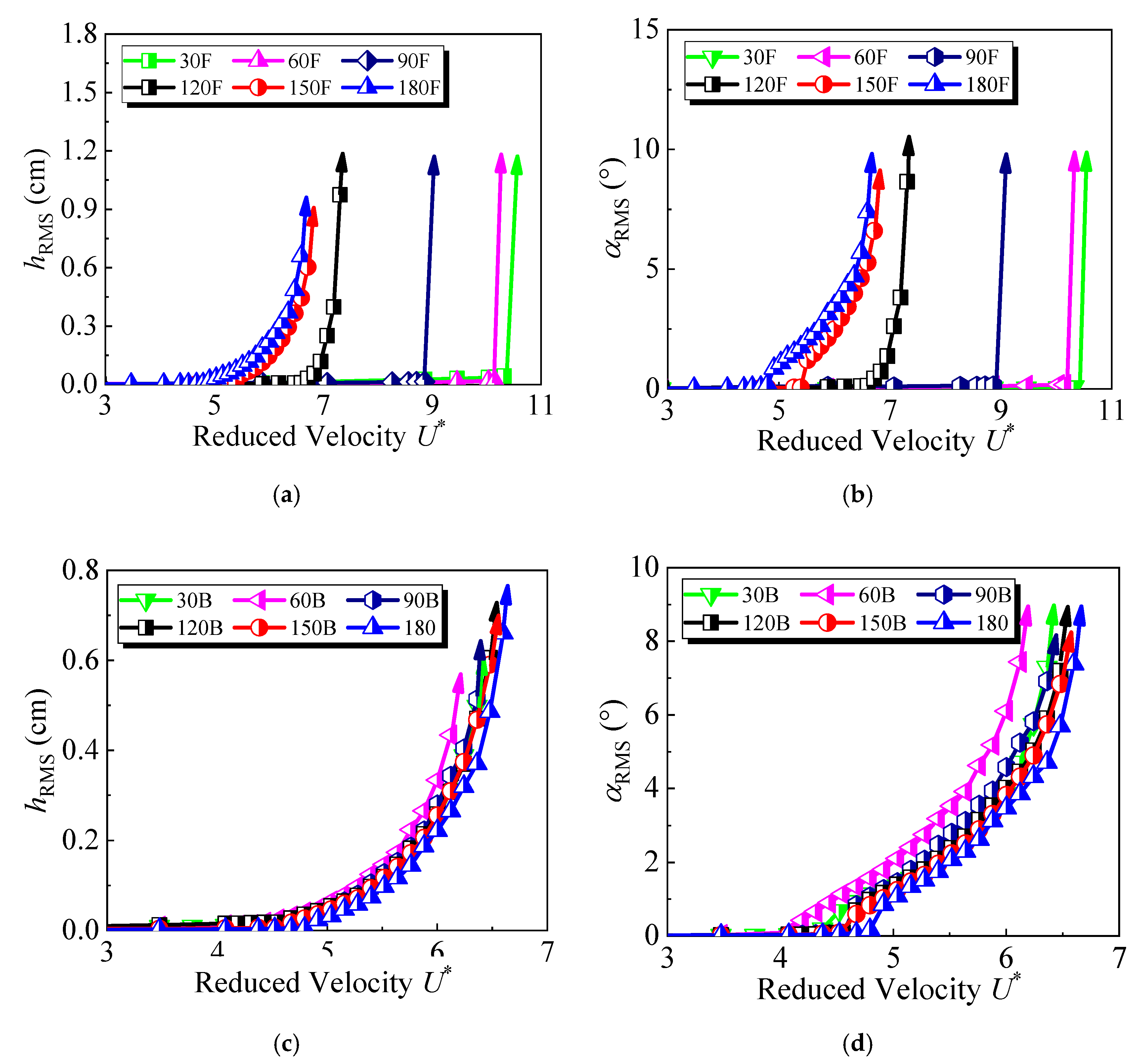
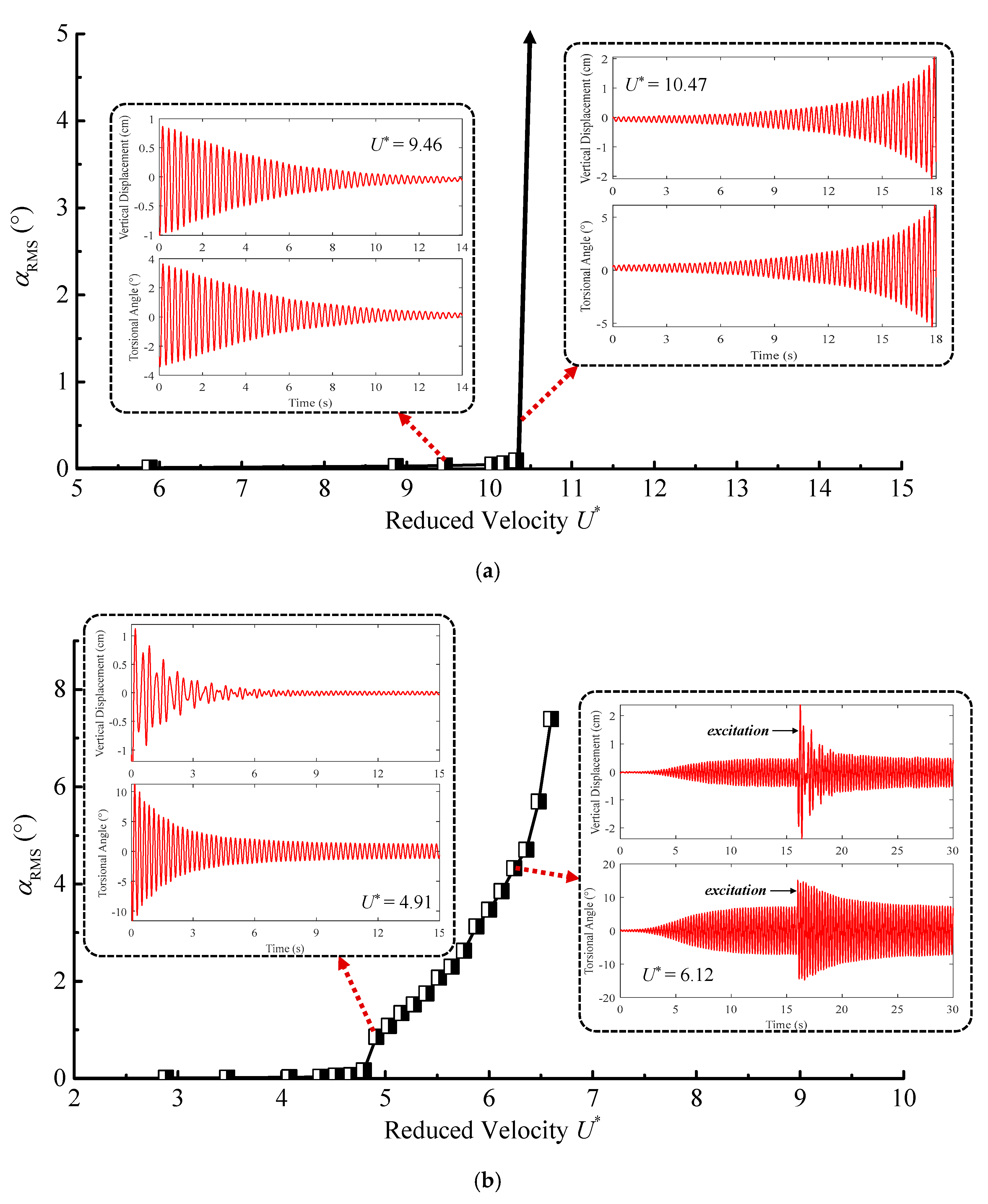
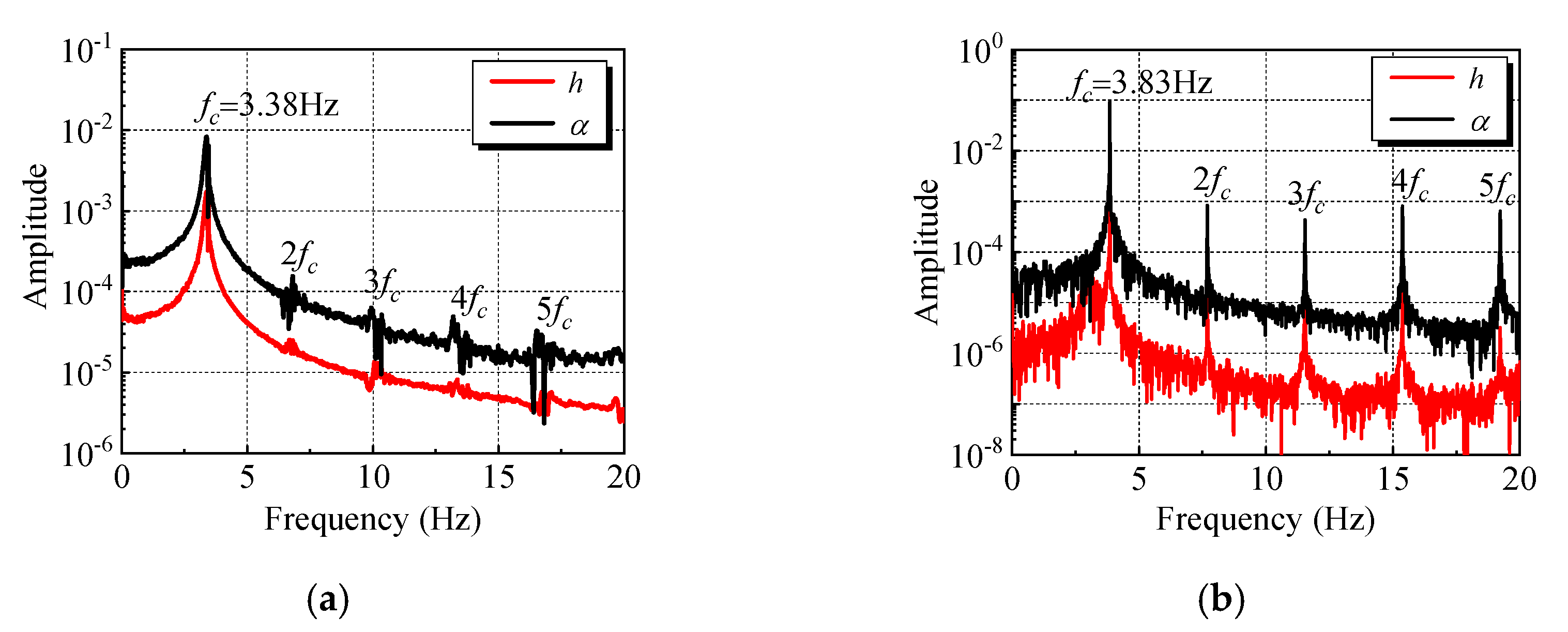
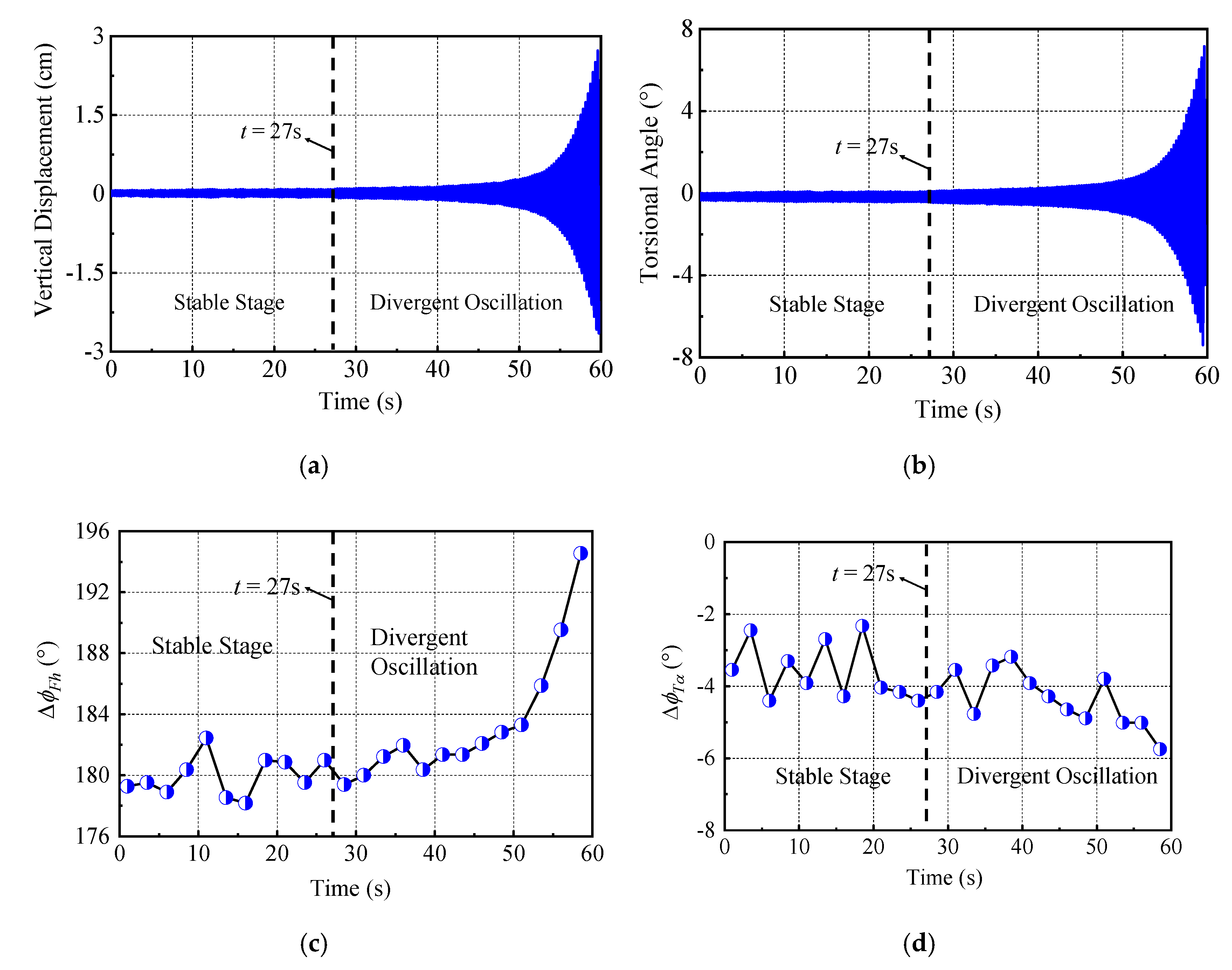
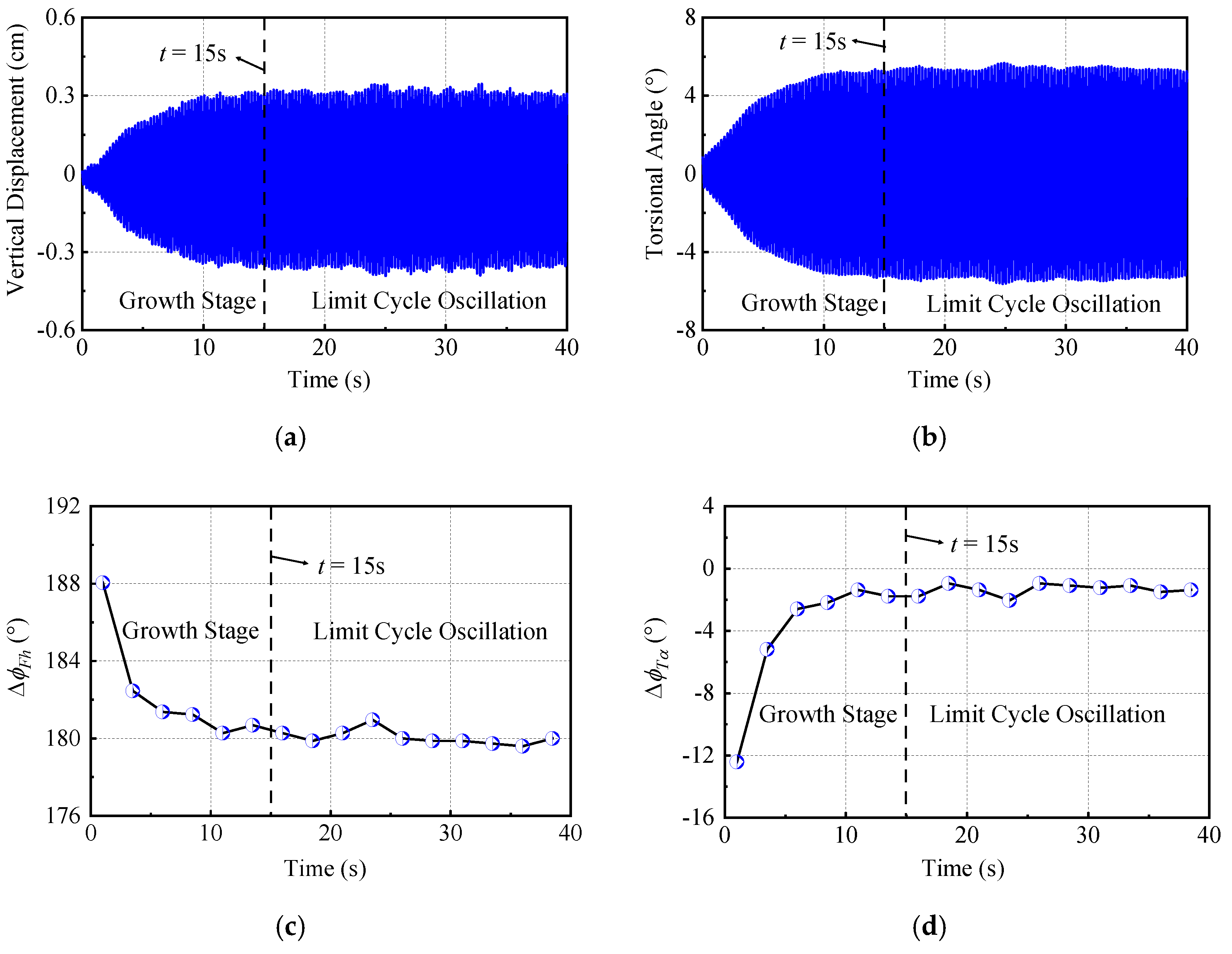
3.1. Characteristics of Flutter Responses under Different Leading and Trailing Edges
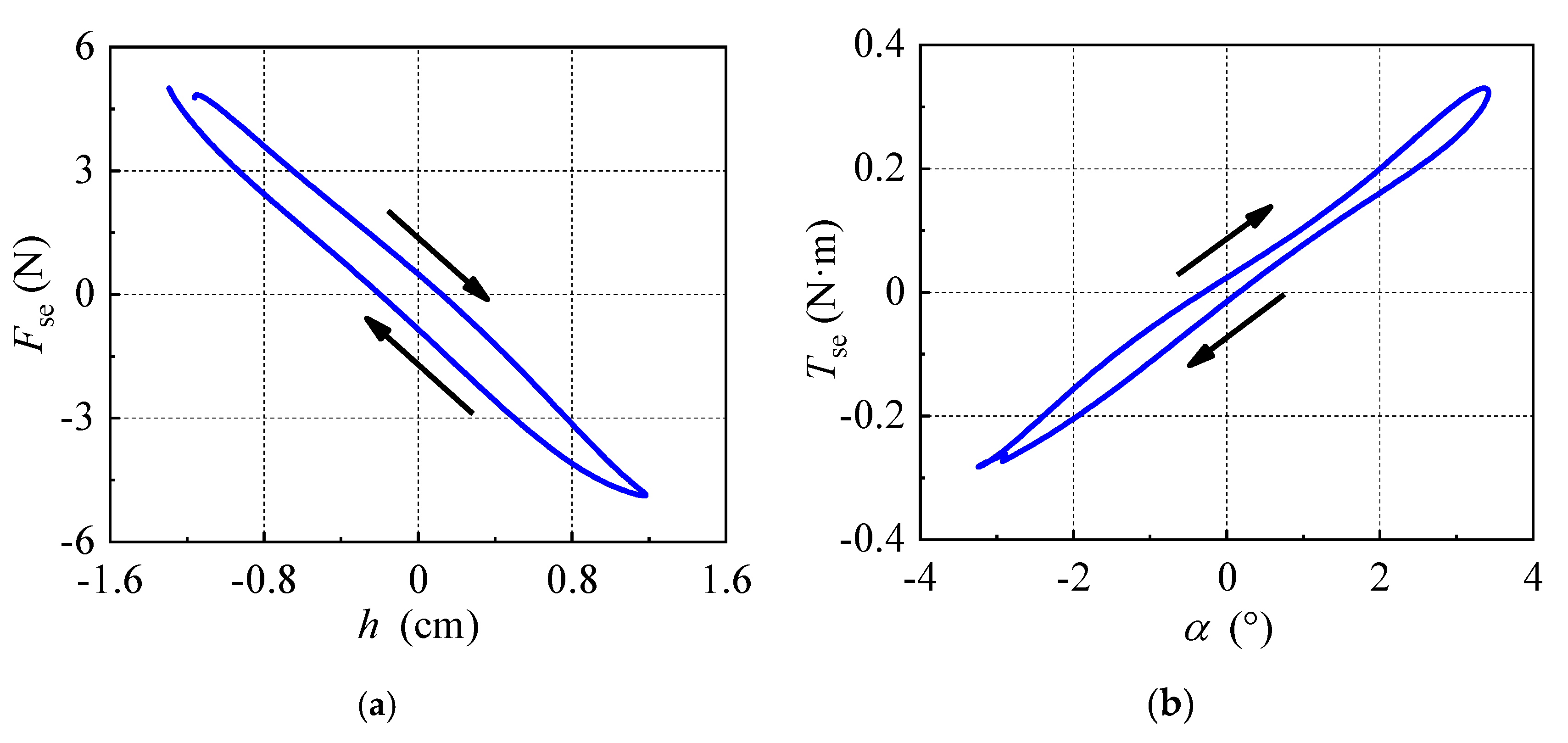
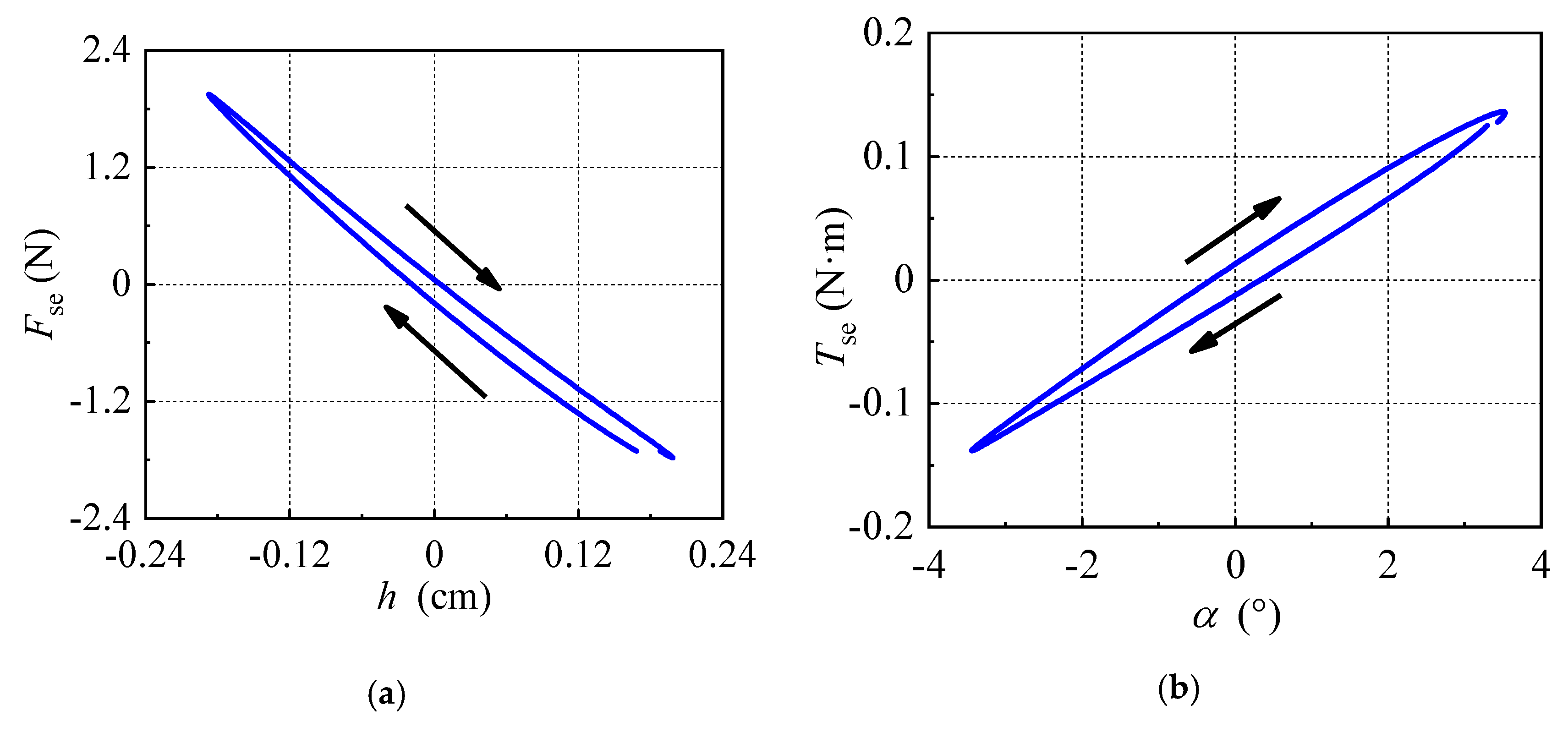
3.2. Hysteresis of Unsteady Aerodynamic Forces
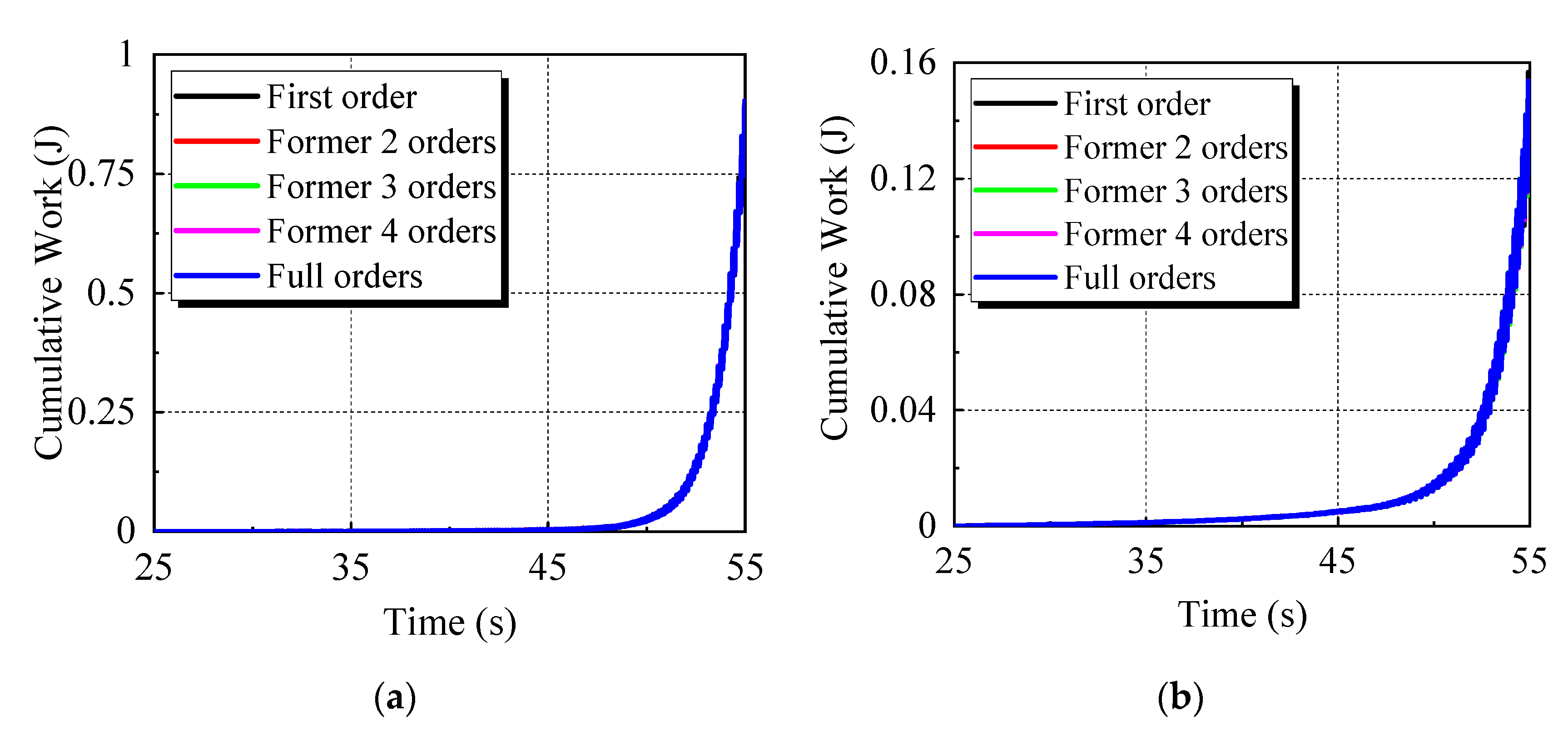
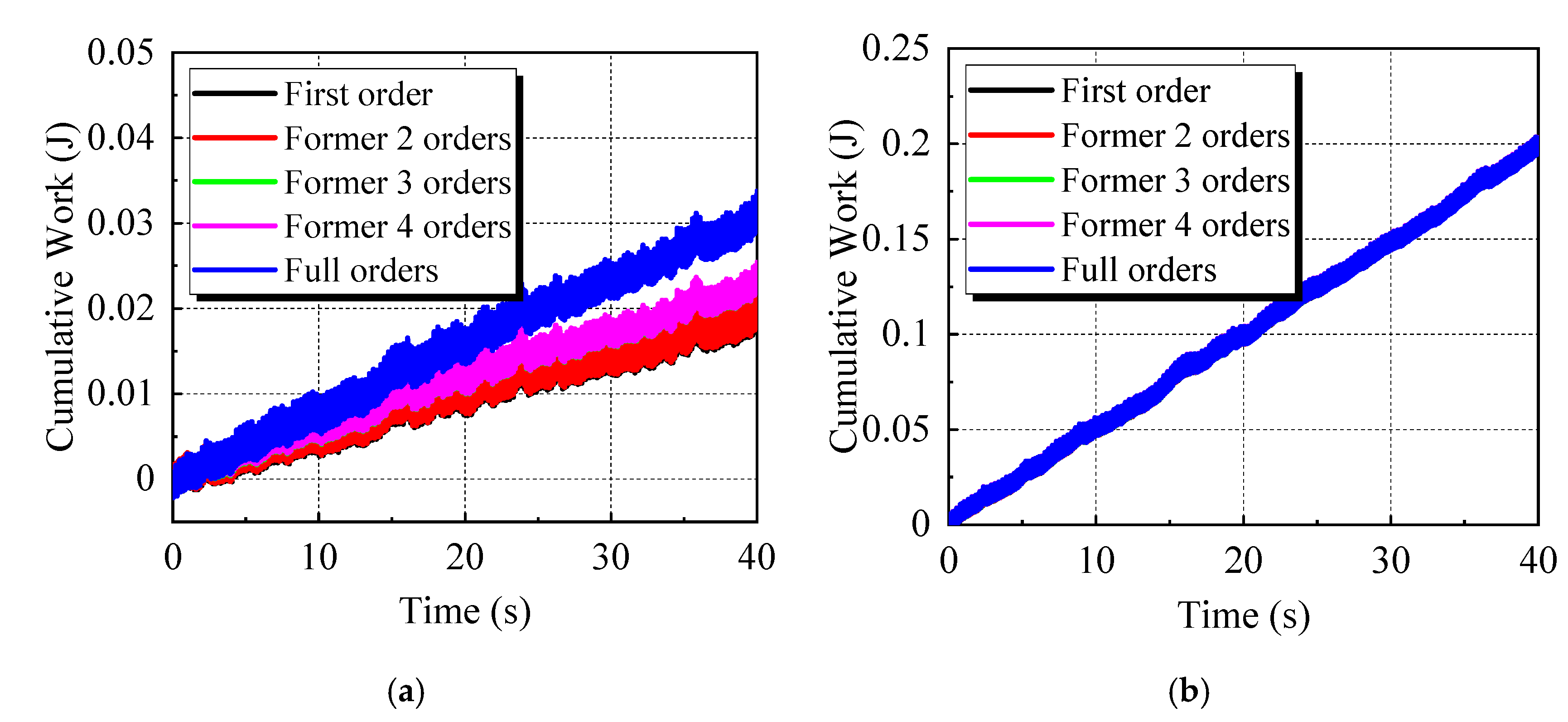
3.3. Work Analysis of Unsteady Aerodynamic Force
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Diana, G.; Fiammenghi, G.; Belloli, M.; Rocchi, D. Wind tunnel tests and numerical approach for long span bridges: The Messina bridge. J. Wind. Eng. Ind. Aerodyn. 2013, 122, 38–49. [Google Scholar] [CrossRef]
- Scanlan, R.H.; Tomko, J.J. Airfoil and bridge deck flutter derivatives. J. Eng. Mech. Div. 1971, 97, 1717–1737. [Google Scholar]
- Iwamoto, M.; Fujino, Y. Identification of flutter derivatives of bridge deck from free vibration data. J. Wind. Eng. Ind. Aerodyn. 1995, 54, 55–63. [Google Scholar] [CrossRef]
- Larsen, A.; Walther, J.H. Discrete vortex simulation of flow around five generic bridge deck sections. J. Wind. Eng. Ind. Aerodyn. 1998, 77, 591–602. [Google Scholar] [CrossRef]
- Gu, M.; Zhang, R.; Xiang, H. Identification of flutter derivatives of bridge decks. J. Wind. Eng. Ind. Aerodyn. 2000, 84, 151–162. [Google Scholar] [CrossRef]
- Brusiani, F.; De Miranda, S.; Patruno, L.; Ubertini, F.; Vaona, P. On the evaluation of bridge deck flutter derivatives using RANS turbulence models. J. Wind. Eng. Ind. Aerodyn. 2013, 119, 39–47. [Google Scholar] [CrossRef]
- Sarkar, P.P.; Jones, N.; Scanlan, R.H. Identification of Aeroelastic Parameters of Flexible Bridges. J. Eng. Mech. 1994, 120, 1718–1742. [Google Scholar] [CrossRef]
- Chen, A.; He, X.; Xiang, H. Identification of 18 flutter derivatives of bridge decks. J. Wind. Eng. Ind. Aerodyn. 2002, 90, 2007–2022. [Google Scholar] [CrossRef]
- Watanabe, S.; Fumoto, K. Aerodynamic study of slotted box girder using computational fluid dynamics. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1885–1894. [Google Scholar] [CrossRef]
- Sato, H.; Hirahara, N.; Fumoto, K.; Hirano, S.; Kusuhara, S. Full aeroelastic model test of a super long-span bridge with slotted box girder. J. Wind. Eng. Ind. Aerodyn. 2002, 90, 2023–2032. [Google Scholar] [CrossRef]
- Nieto, F.; Montoya, M.C.; Hernández, S.; Kusano, I.; Casteleiro, A.; Álvarez, A.J.; Jurado, J.Á.; Fontán, A. Aerodynamic and aeroelastic responses of short gap twin-box decks: Box geometry and gap distance dependent surrogate based design. J. Wind. Eng. Ind. Aerodyn. 2020, 201, 104147. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, R.; Ge, Y.; Zou, X.; Zhang, L. Flutter characteristics of twin-box girder bridges with vertical central stabilizers. Eng. Struct. 2017, 133, 33–48. [Google Scholar] [CrossRef] [Green Version]
- Mei, H.; Wang, Q.; Liao, H.; Fu, H. Improvement of Flutter Performance of a Streamlined Box Girder by Using an Upper Central Stabilizer. J. Bridg. Eng. 2020, 25, 04020053. [Google Scholar] [CrossRef]
- Li, K.; Ge, Y.; Zhao, L. Cfd simulation of the feedback controlled twin-winglet system for flutter suppression of long-span suspension bridges. In Proceedings of the 14th International Conference on Wind Engineering (ICWE), Porto Alegre, Brazil, 21–26 June 2015. [Google Scholar]
- Bakis, K.N.; Massaro, M.; Williams, M.S.; Limebeer, D.J.N. Aeroelastic control of long-span suspension bridges with controllable winglets. Struct. Control. Heal. Monit. 2016, 23, 1417–1441. [Google Scholar] [CrossRef]
- Sangalli, L.A.; Braun, A.L. A fluid-structure interaction model for numerical simulation of bridge flutter using sectional models with active control devices. Preliminary results. J. Sound Vib. 2020, 477, 115338. [Google Scholar] [CrossRef]
- Náprstek, J.; Pospíšil, S.; Hračov, S. Analytical and experimental modelling of non-linear aeroelastic effects on prismatic bodies. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 1315–1328. [Google Scholar] [CrossRef]
- Arena, A.; Lacarbonara, W. Nonlinear parametric modeling of suspension bridges under aeroelastic forces: Torsional divergence and flutter. Nonlinear Dyn. 2012, 70, 2487–2510. [Google Scholar] [CrossRef]
- Amandolese, X.; Michelin, S.; Choquel, M. Low speed flutter and limit cycle oscillations of a two-degree-of-freedom flat plate in a wind tunnel. J. Fluids Struct. 2013, 43, 244–255. [Google Scholar] [CrossRef] [Green Version]
- Král, R.; Pospíšil, S.; Náprstek, J. Wind tunnel experiments on unstable self-excited vibration of sectional girders. J. Fluids Struct. 2014, 44, 235–250. [Google Scholar] [CrossRef]
- Arena, A.; Lacarbonara, W.; Marzocca, P. Post-Critical Behavior of Suspension Bridges Under Nonlinear Aerodynamic Loading. J. Comput. Nonlinear Dyn. 2015, 11, 011005. [Google Scholar] [CrossRef]
- Ying, X.; Xu, F.; Zhang, Z. Study on numerical simulation and mechanism of soft flutter of a bridge deck. In Proceedings of the 2016 World Congress, Advances in Civil, Environmental, and Materials Research (ACEM16), Daejeon, Korea, 28 August–1 September 2016. [Google Scholar]
- Zhang, M.; Xu, F.; Ying, X. Experimental Investigations on the Nonlinear Torsional Flutter of a Bridge Deck. J. Bridg. Eng. 2017, 22, 04017048. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, F.; Zhang, Z.; Ying, X. Energy budget analysis and engineering modeling of post-flutter limit cycle oscillation of a bridge deck. J. Wind. Eng. Ind. Aerodyn. 2019, 188, 410–420. [Google Scholar] [CrossRef]
- Tang, H.; Shum, K.; Li, Y. Investigation of flutter performance of a twin-box bridge girder at large angles of attack. J. Wind. Eng. Ind. Aerodyn. 2019, 186, 192–203. [Google Scholar] [CrossRef]
- Matsumoto, M.; Daito, Y.; Yoshizumi, F.; Ichikawa, Y.; Yabutani, T. Torsional flutter of bluff bodies. J. Wind. Eng. Ind. Aerodyn. 1997, 69, 871–882. [Google Scholar] [CrossRef]
- Ying, X.; Xu, F.; Zhang, M.; Zhang, Z. Numerical explorations of the limit cycle flutter characteristics of a bridge deck. J. Wind. Eng. Ind. Aerodyn. 2017, 169, 30–38. [Google Scholar] [CrossRef]
- Gao, G.; Zhu, L.; Han, W.; Li, J. Nonlinear post-flutter behavior and self-excited force model of a twin-side-girder bridge deck. J. Wind. Eng. Ind. Aerodyn. 2018, 177, 227–241. [Google Scholar] [CrossRef]
- Scanlan, R.H. Amplitude and Turbulence Effects on Bridge Flutter Derivatives. J. Struct. Eng. 1997, 123, 232–236. [Google Scholar] [CrossRef]
- Noda, M.; Utsunomiya, H.; Nagao, F.; Kanda, M.; Shiraishi, N. Effects of oscillation amplitude on aerodynamic derivatives. J. Wind. Eng. Ind. Aerodyn. 2003, 91, 101–111. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Li, Y. Nonlinear self-excited forces and aerodynamic damping associated with vortex-induced vibration and flutter of long span bridges. J. Wind. Eng. Ind. Aerodyn. 2020, 204, 104207. [Google Scholar] [CrossRef]
- Gao, G.; Zhu, L. Nonlinearity of mechanical damping and stiffness of a spring-suspended sectional model system for wind tunnel tests. J. Sound Vib. 2015, 355, 369–391. [Google Scholar] [CrossRef]
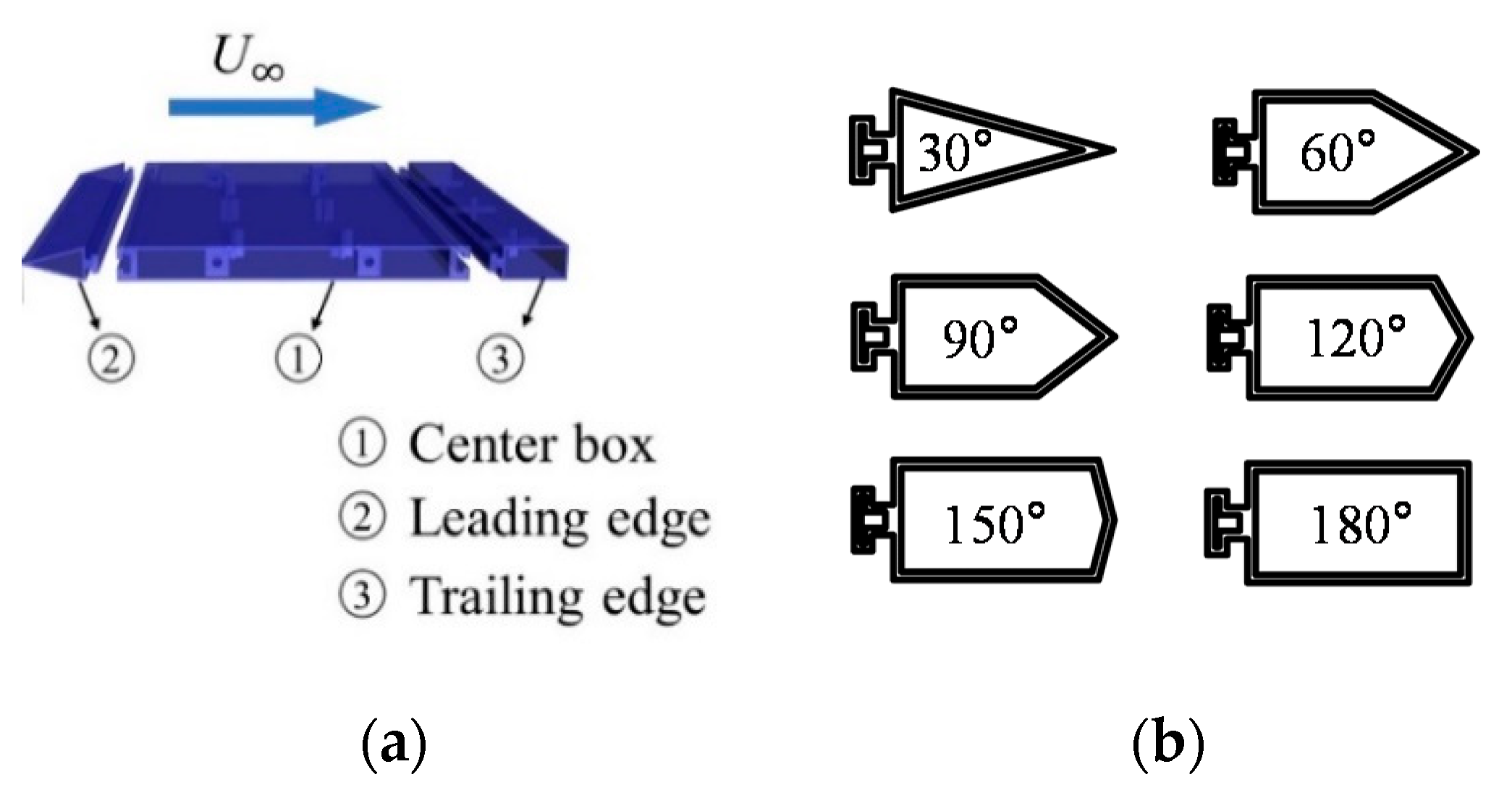

| Case | L30 | L60 | L90 | L120 | L150 | L180/T180 | T30 | T60 | T90 | T120 | T150 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Leading edge | 30° | 60° | 90° | 120° | 150° | 180° | 180° | 180° | 180° | 180° | 180° |
| Trailing edge | 180° | 180° | 180° | 180° | 180° | 180° | 30° | 60° | 90° | 120° | 150° |
| Case | (Hz) | (%) | (Hz) | (%) | Case | (Hz) | (%) | (Hz) | (%) |
|---|---|---|---|---|---|---|---|---|---|
| L30 | 2.965 | 0.174 | 4.307 | 0.282 | T30 | 2.970 | 0.191 | 4.317 | 0.268 |
| L60 | 2.976 | 0.190 | 4.287 | 0.312 | T60 | 2.972 | 0.193 | 4.314 | 0.259 |
| L90 | 2.981 | 0.202 | 4.272 | 0.265 | T90 | 2.970 | 0.187 | 4.286 | 0.288 |
| L120 | 2.984 | 0.204 | 4.264 | 0.283 | T120 | 2.968 | 0.175 | 4.287 | 0.234 |
| L150 | 2.980 | 0.210 | 4.267 | 0.263 | T150 | 2.964 | 0.163 | 4.283 | 0.273 |
| L180/T180 | 2.966 | 0.171 | 4.274 | 0.260 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Laima, S. Experimental Investigations on Nonlinear Flutter Behaviors of a Bridge Deck with Different Leading and Trailing Edges. Appl. Sci. 2020, 10, 7781. https://doi.org/10.3390/app10217781
Li W, Laima S. Experimental Investigations on Nonlinear Flutter Behaviors of a Bridge Deck with Different Leading and Trailing Edges. Applied Sciences. 2020; 10(21):7781. https://doi.org/10.3390/app10217781
Chicago/Turabian StyleLi, Wenjie, and Shujin Laima. 2020. "Experimental Investigations on Nonlinear Flutter Behaviors of a Bridge Deck with Different Leading and Trailing Edges" Applied Sciences 10, no. 21: 7781. https://doi.org/10.3390/app10217781
APA StyleLi, W., & Laima, S. (2020). Experimental Investigations on Nonlinear Flutter Behaviors of a Bridge Deck with Different Leading and Trailing Edges. Applied Sciences, 10(21), 7781. https://doi.org/10.3390/app10217781




