Multi-Scale Demodulation for Fault Diagnosis Based on a Weighted-EMD De-Noising Technique and Time–Frequency Envelope Analysis
Abstract
:1. Introduction
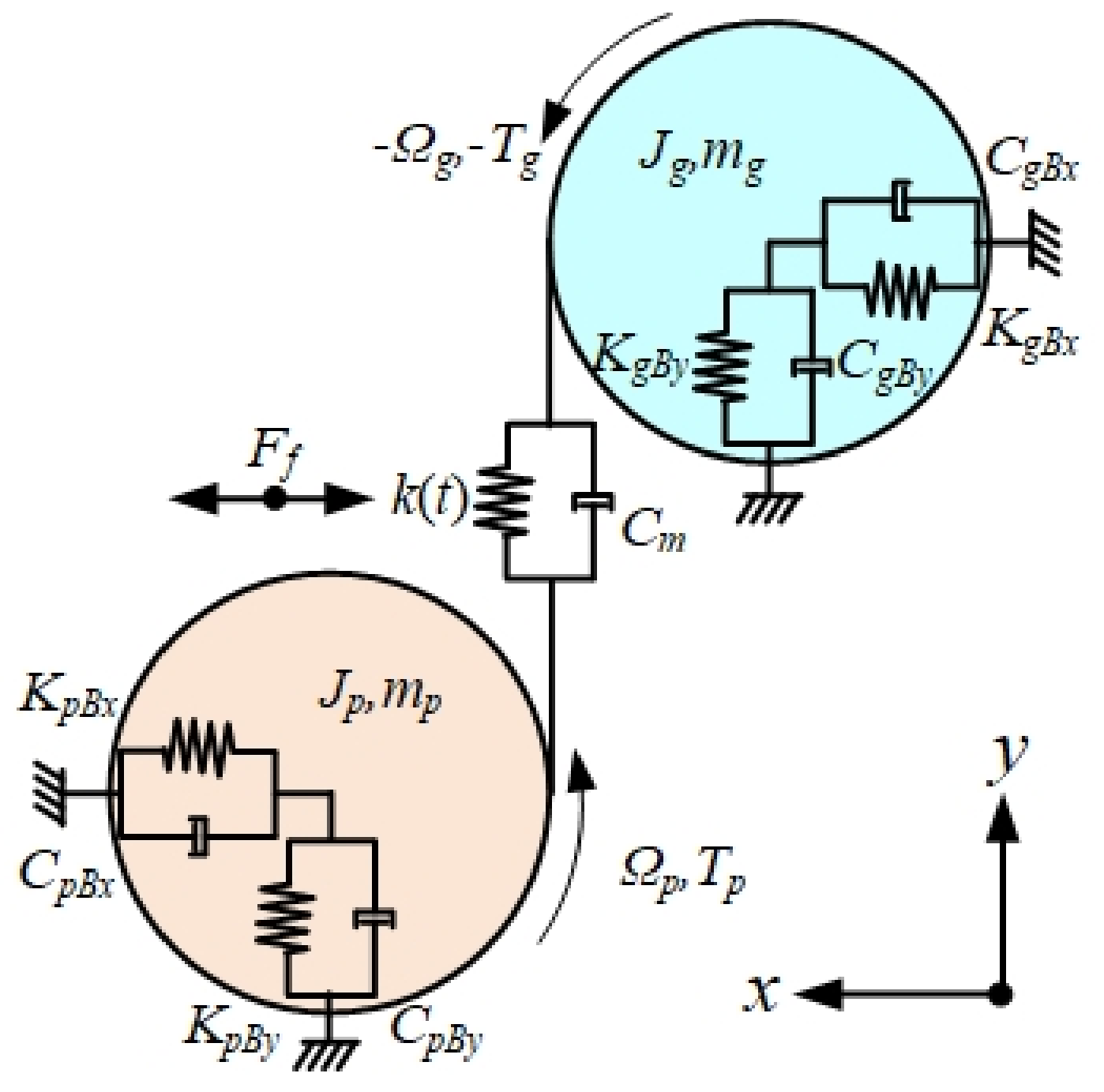
2. Problem Formulation
3. The Proposed Multi-Scale Demodulation Method
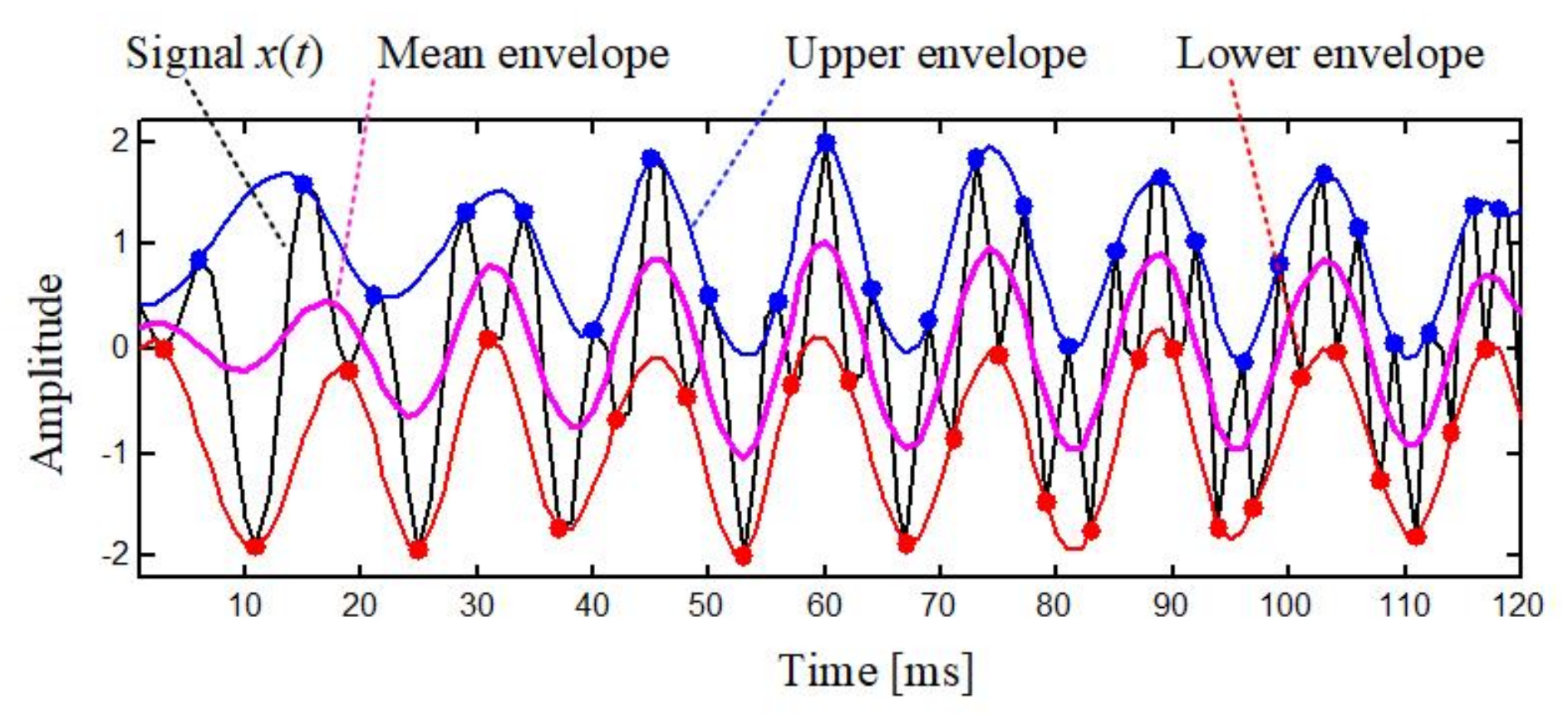
3.1. Adaptive Signal Decomposition Based on EMD
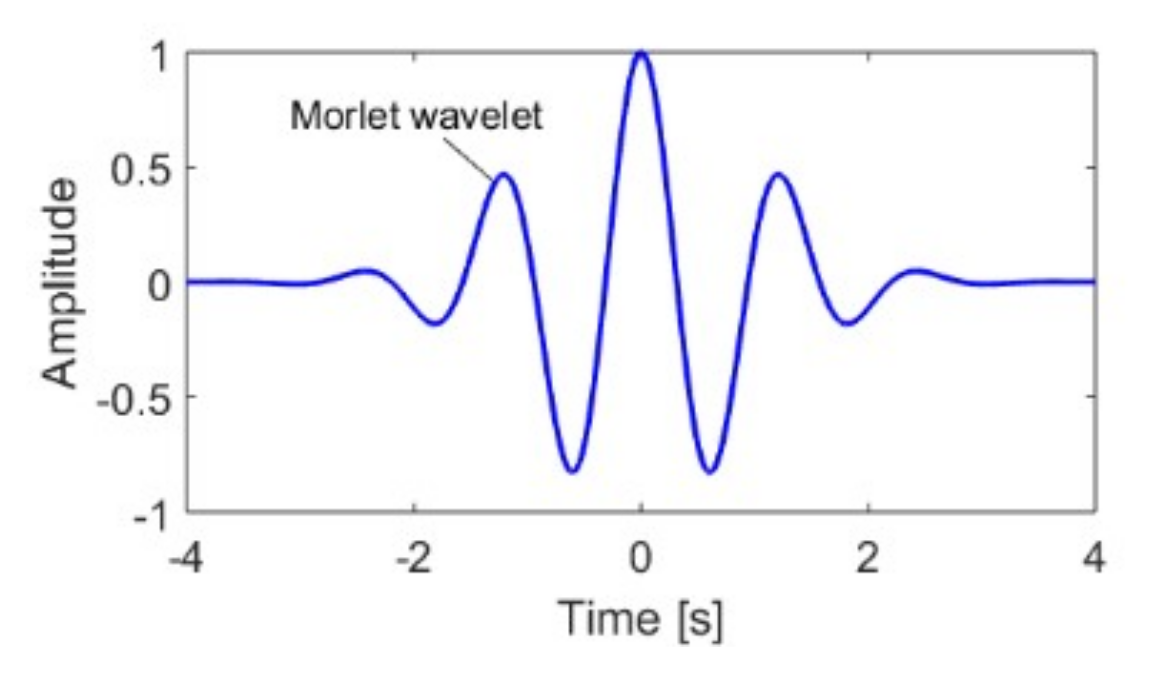
3.2. Time–Frequency Representation (TFR) Calculation Based on Continuous Wavelet Transformation (CWT)
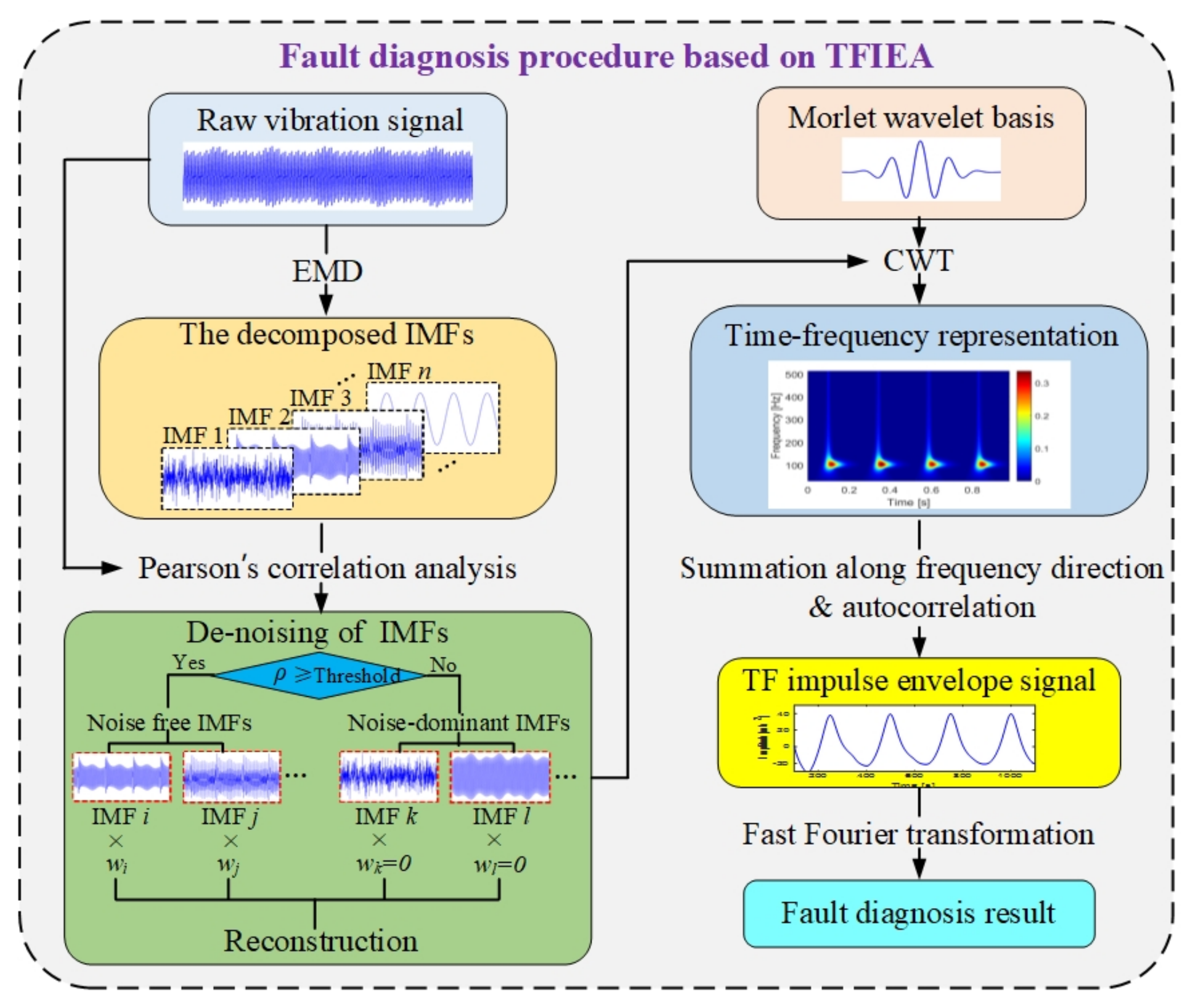
3.3. Fault Diagnosis Procedure Based on the Proposed Method
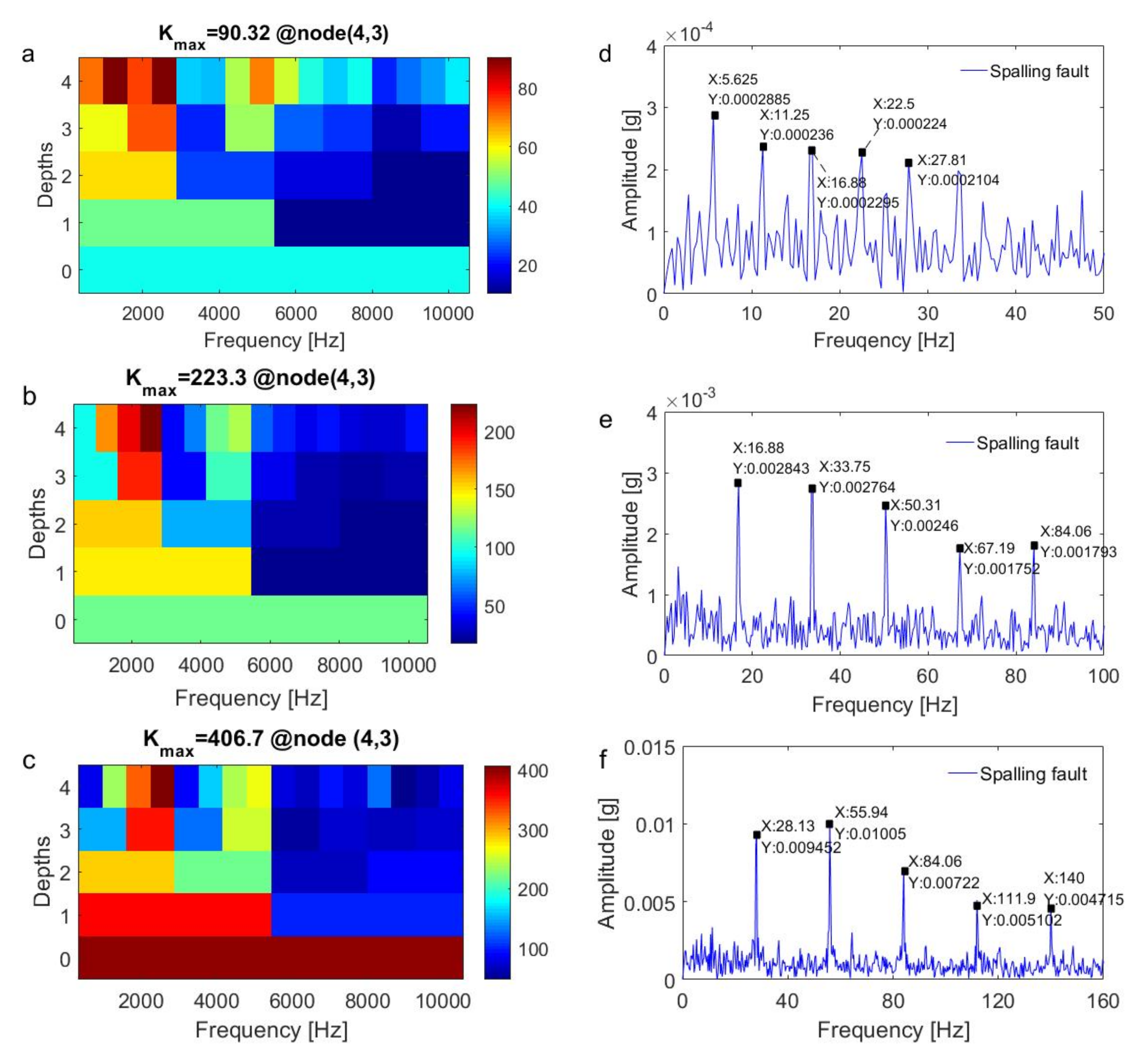
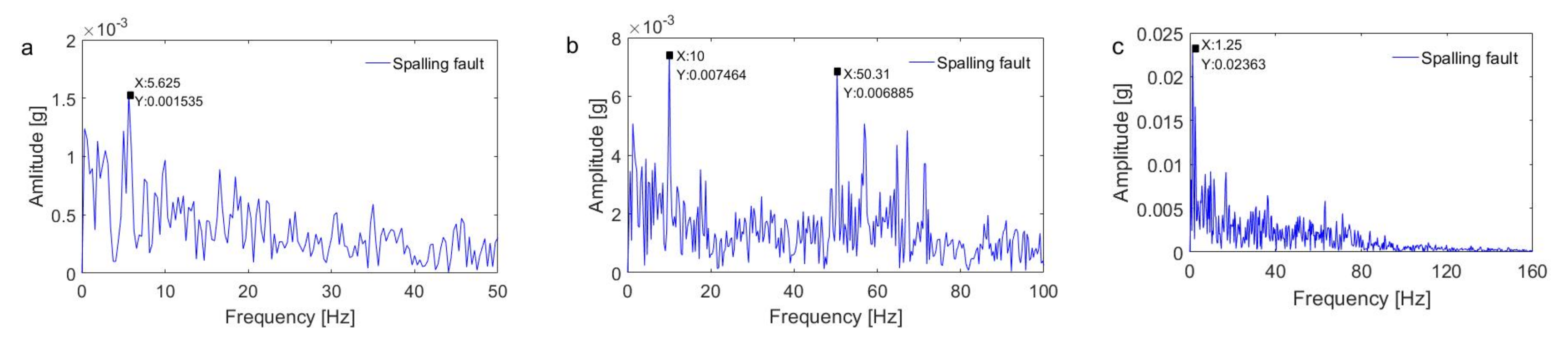
4. Validation of the Proposed Method by the Fault Diagnosis of a Planetary Gearbox with a Sun Gear Spalling Fault
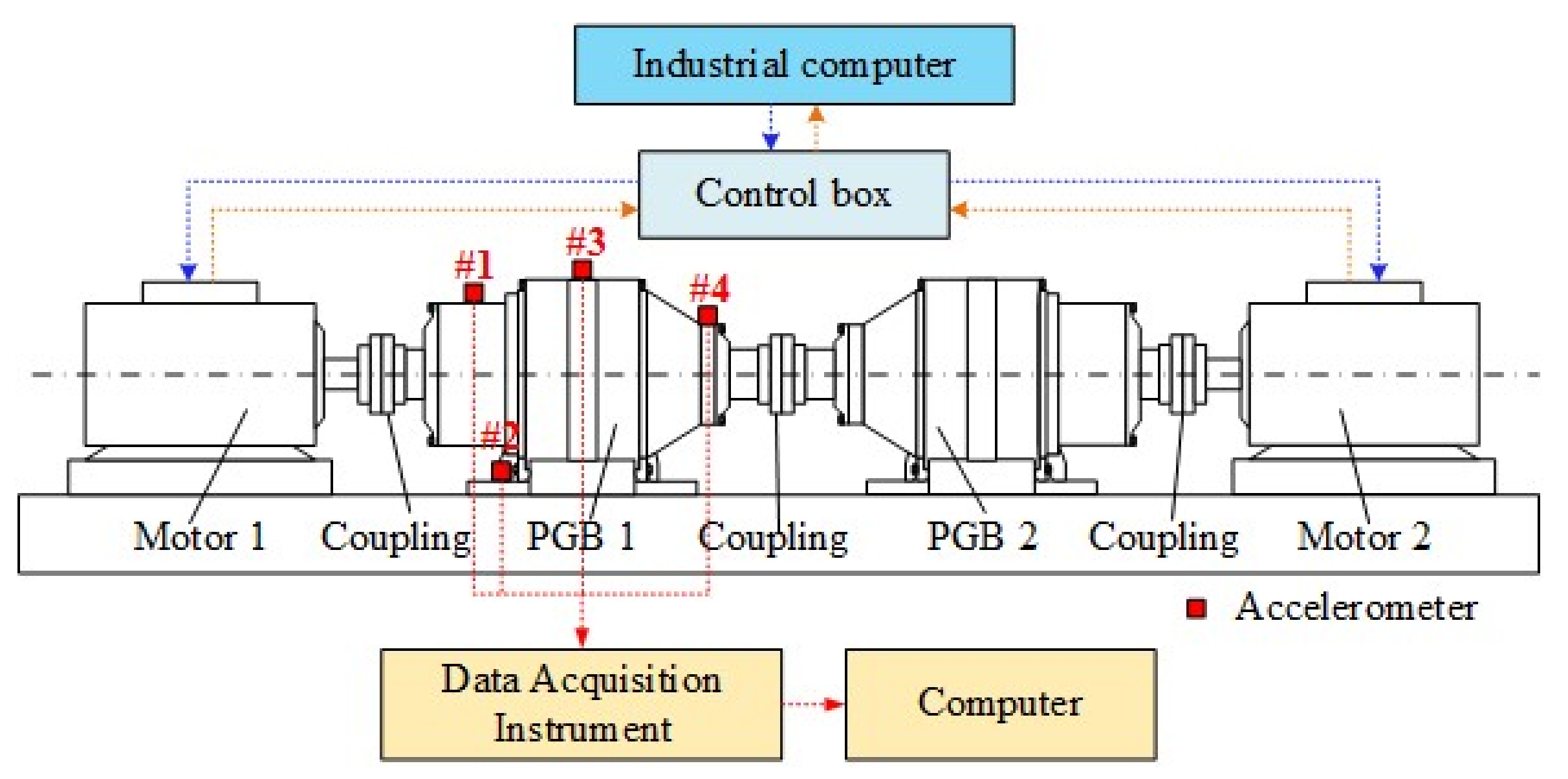
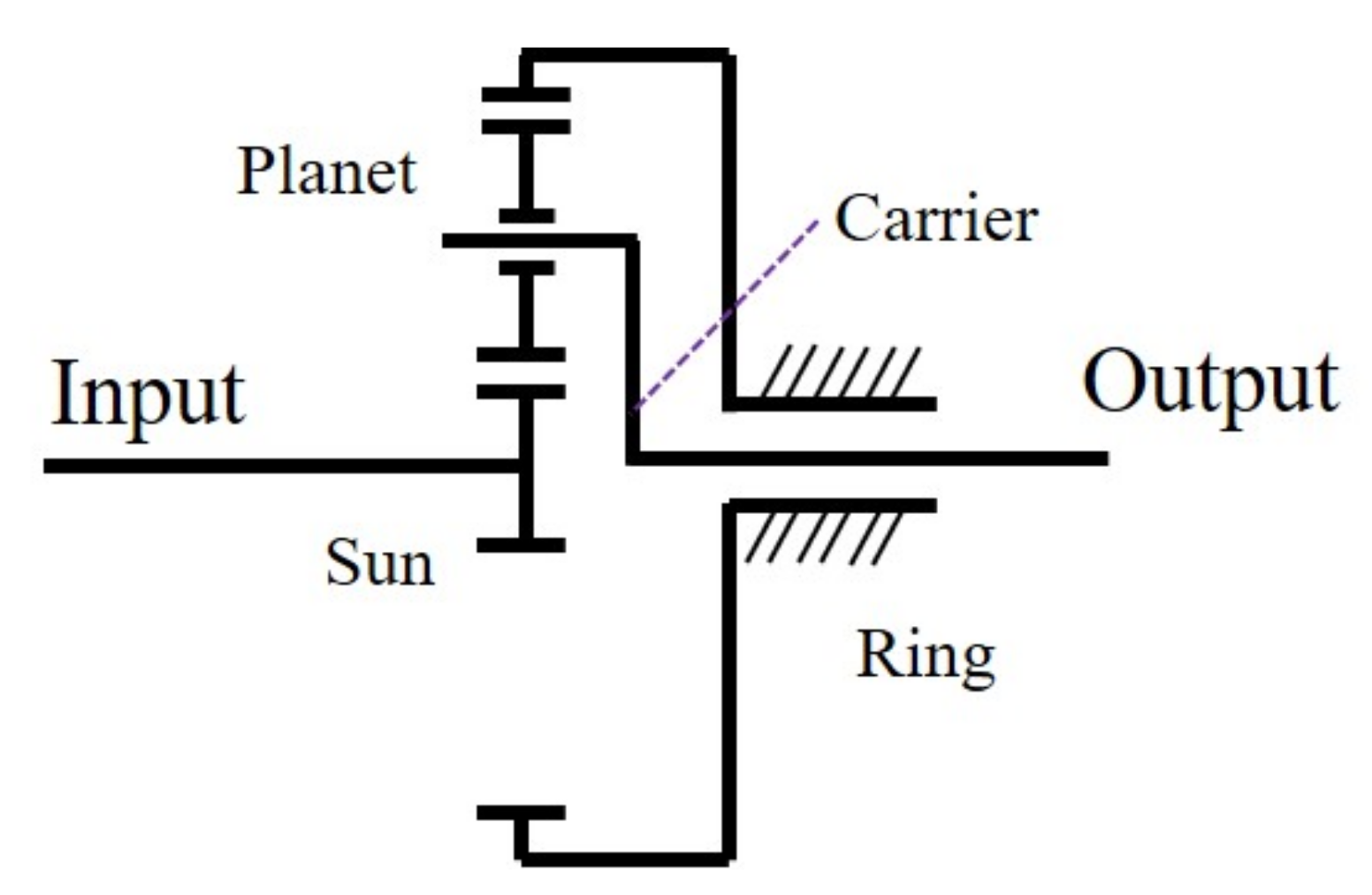
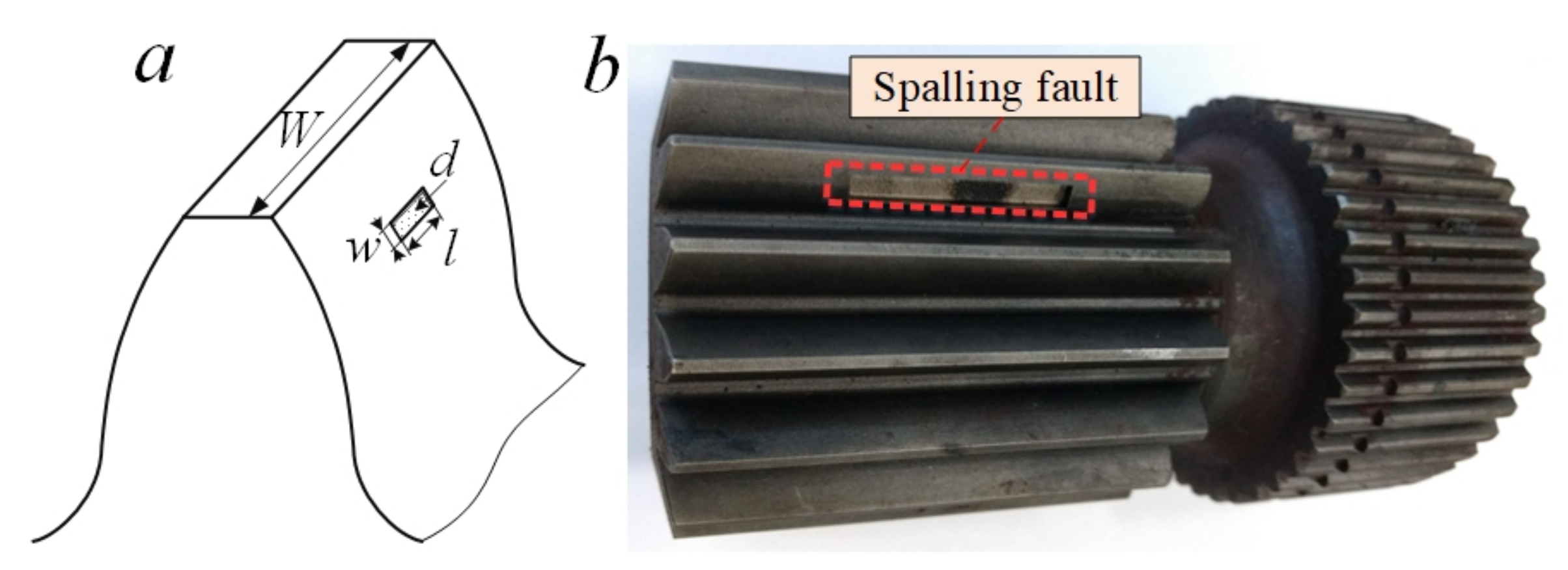
4.1. Description of the Experimental System
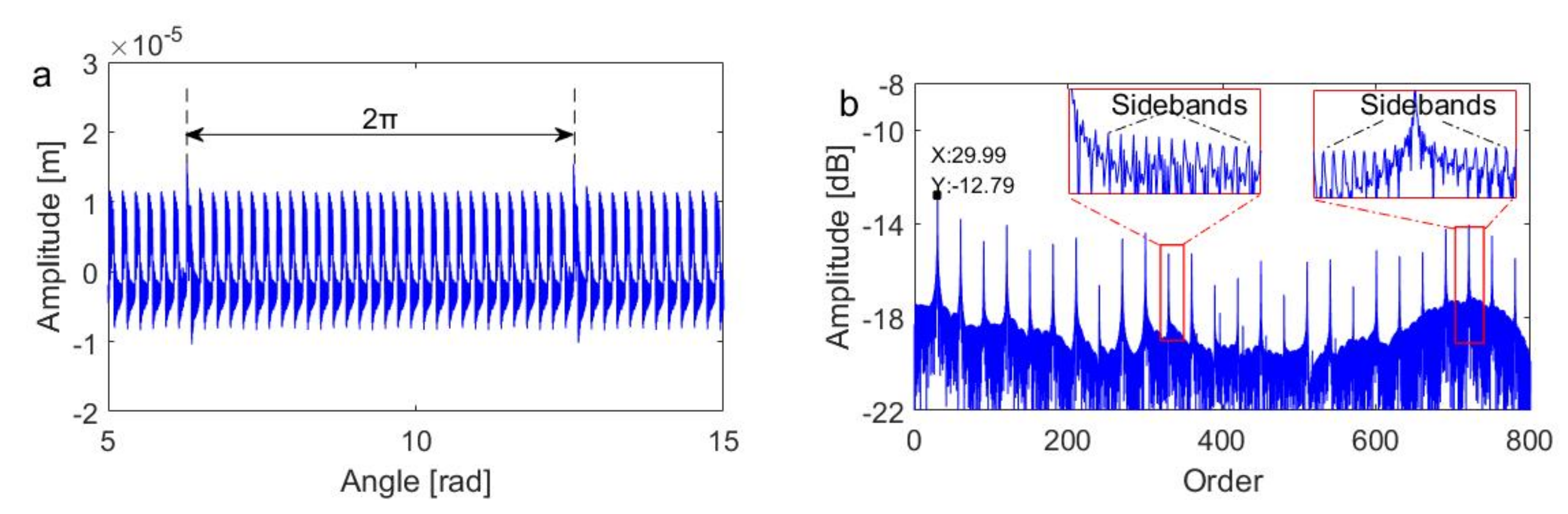
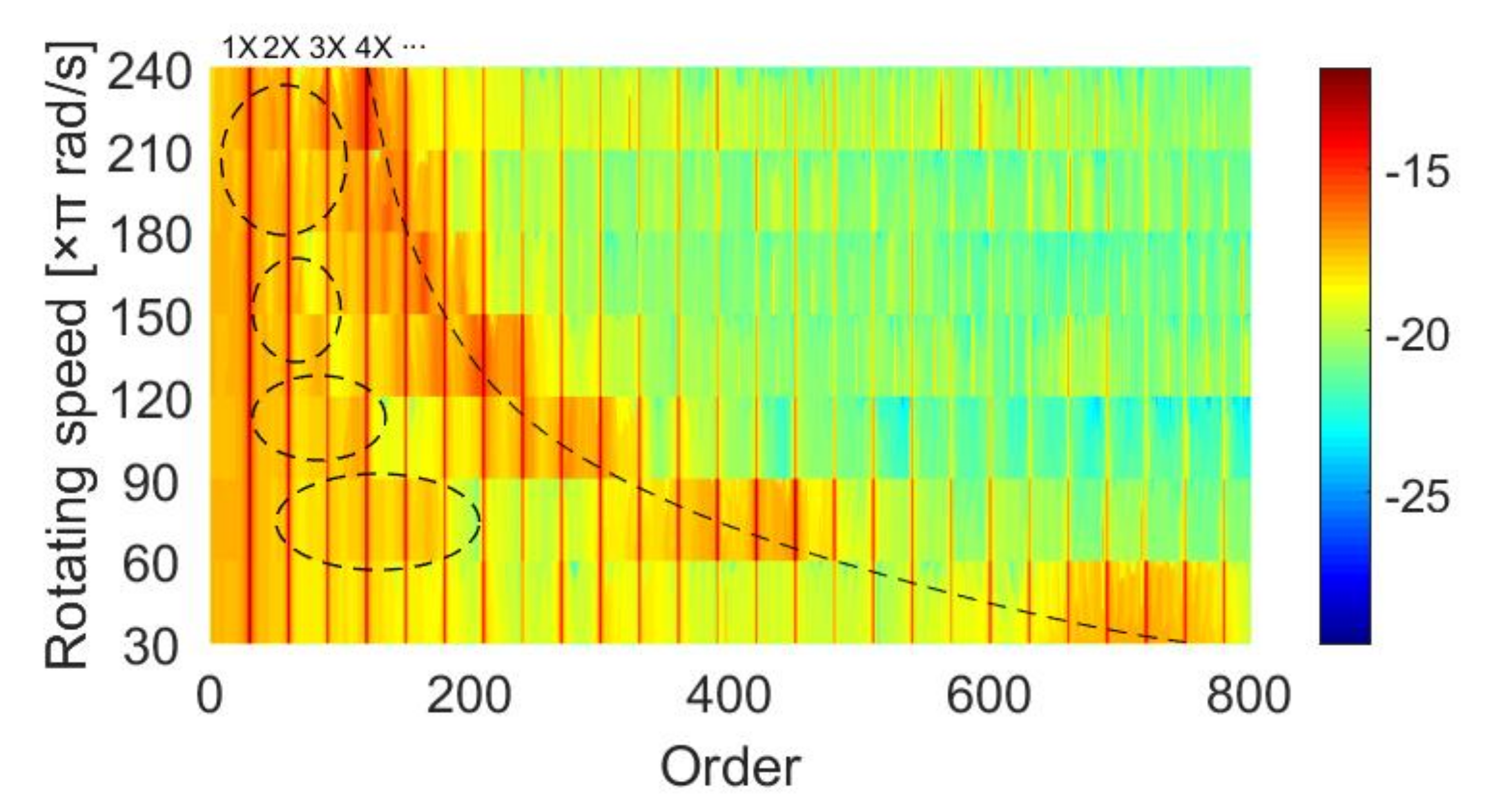
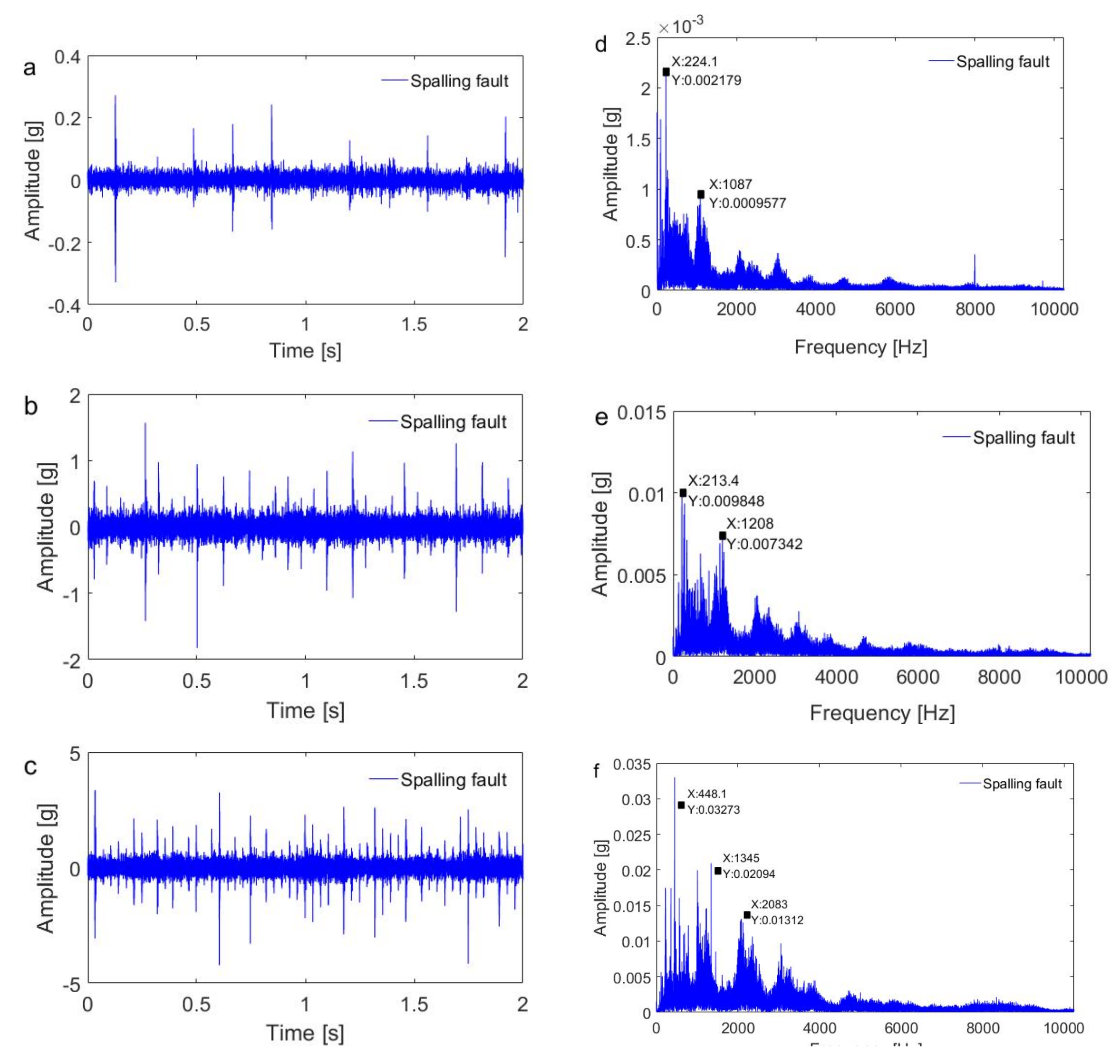
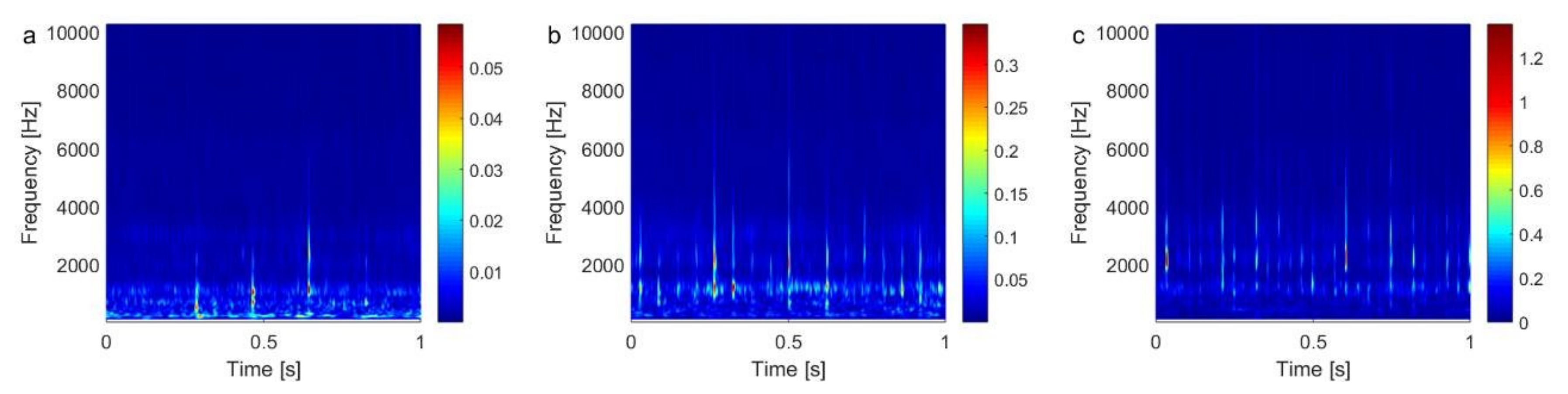
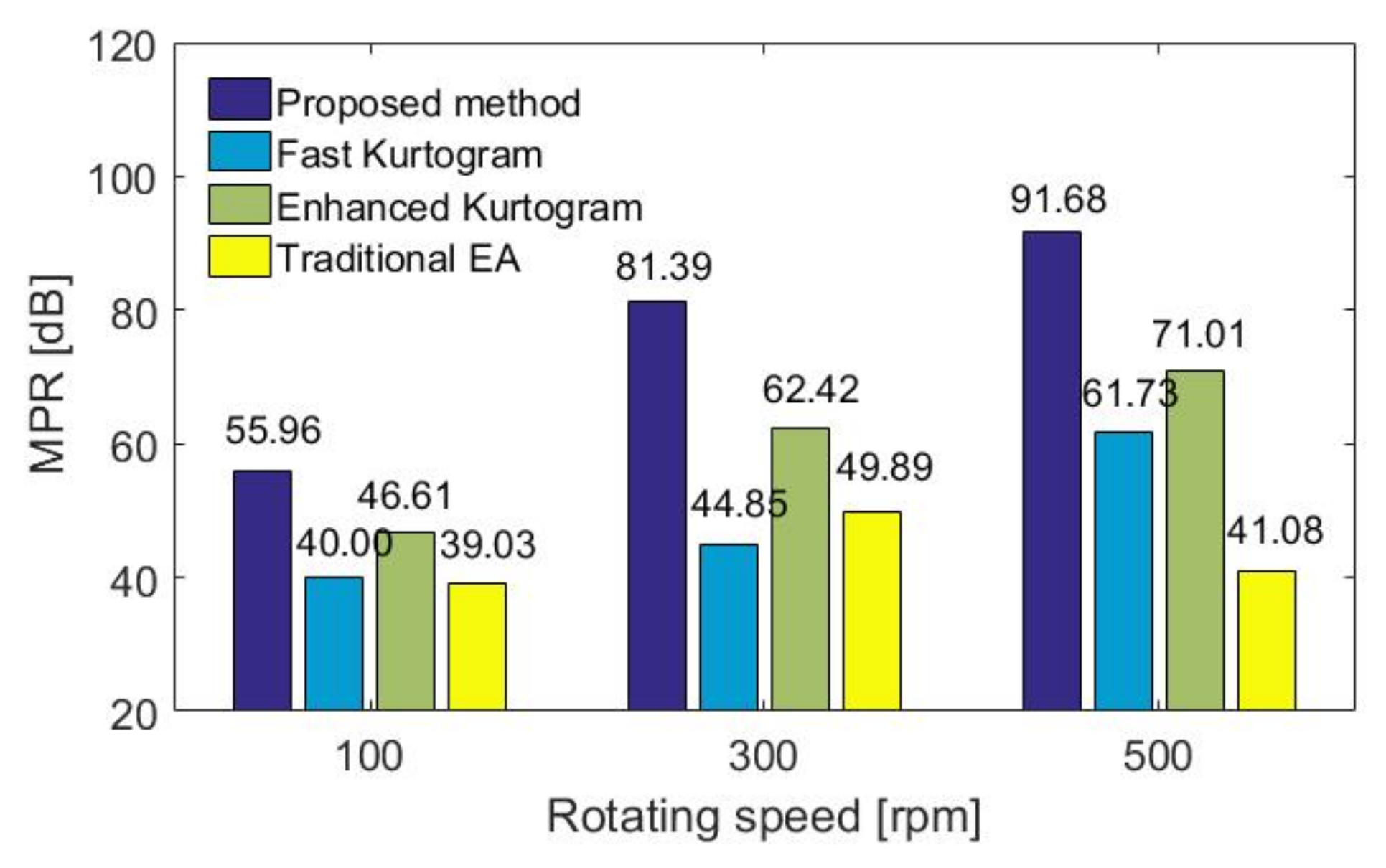
4.2. Results and Discussion
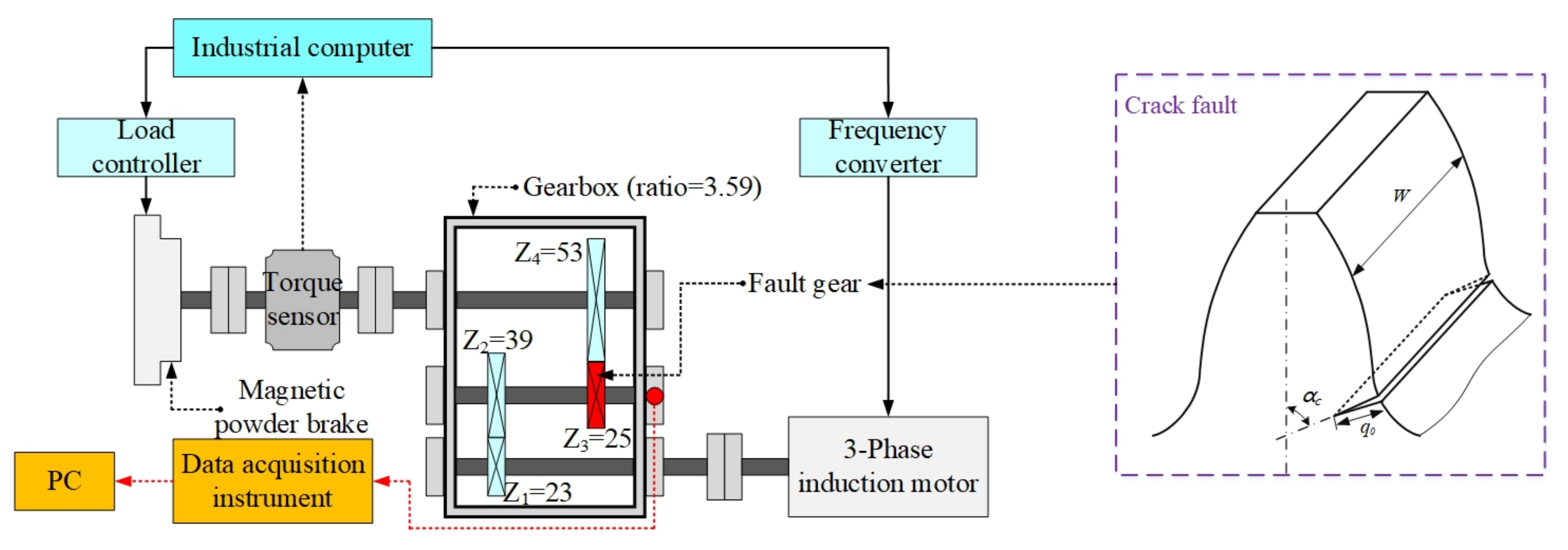
5. Validation of the Proposed Method by the Fault Diagnosis of a Fixed Shaft Gearbox with a Seeded Tooth Root Crack Fault
5.1. Description of the Experimental System
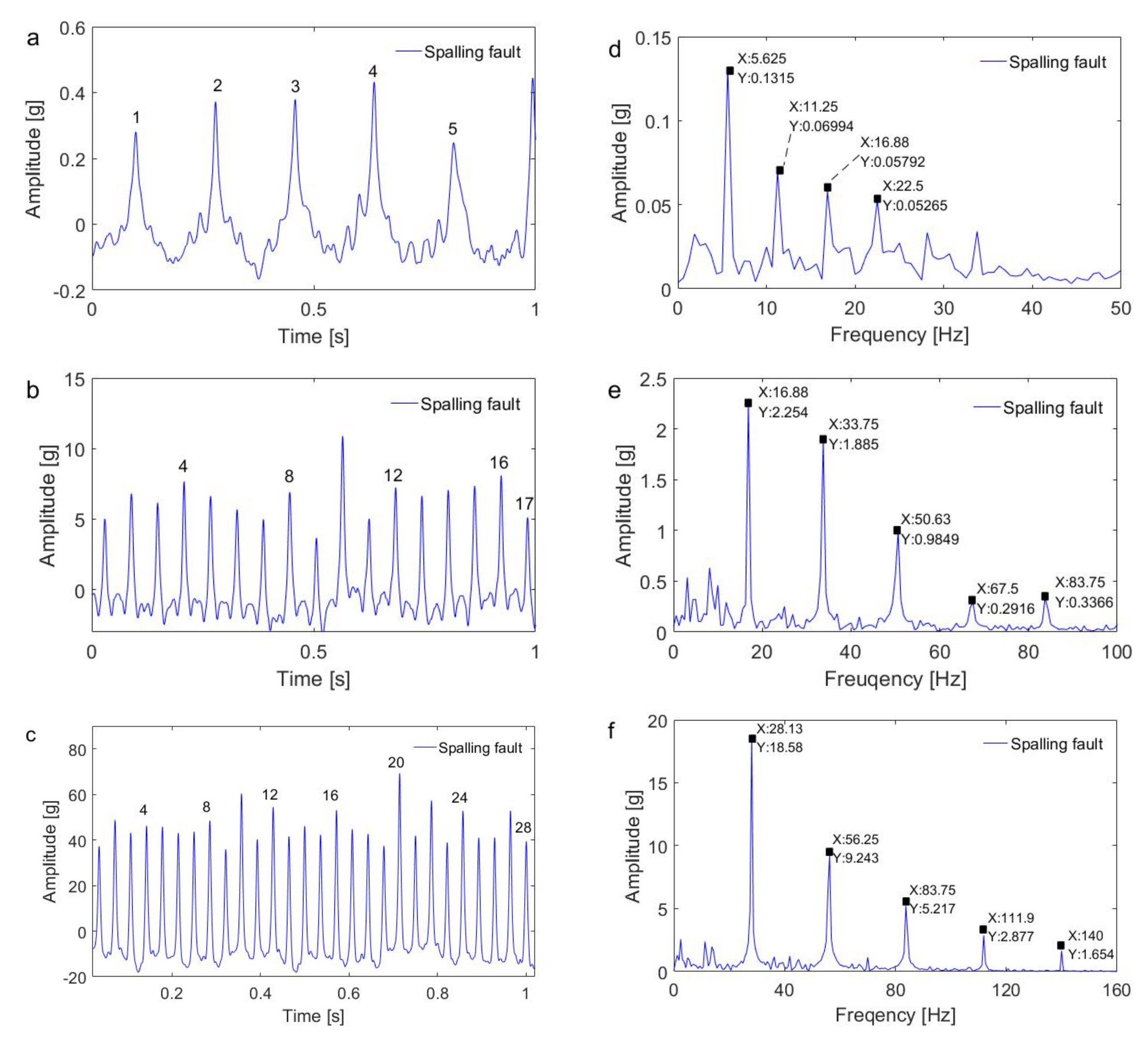
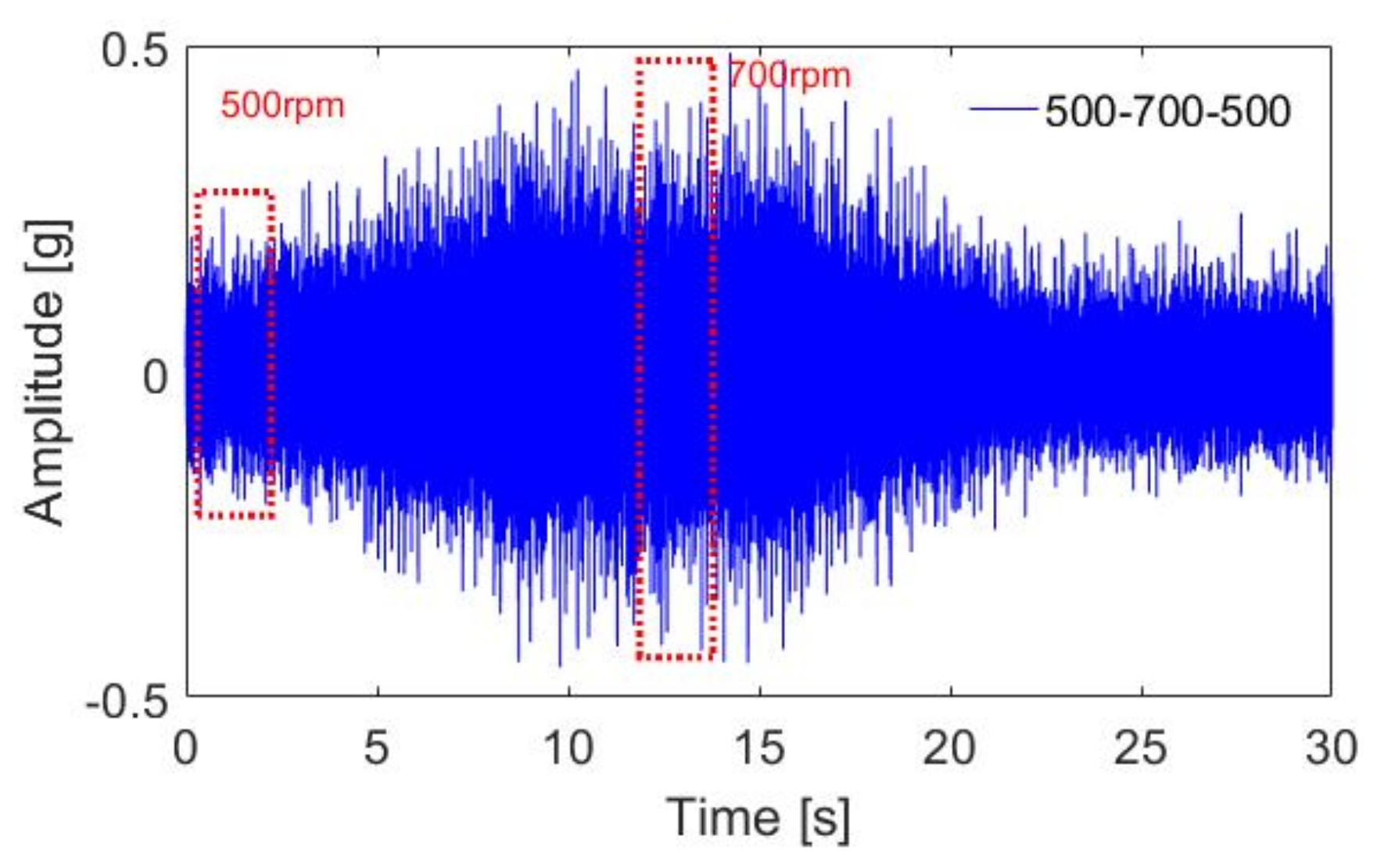
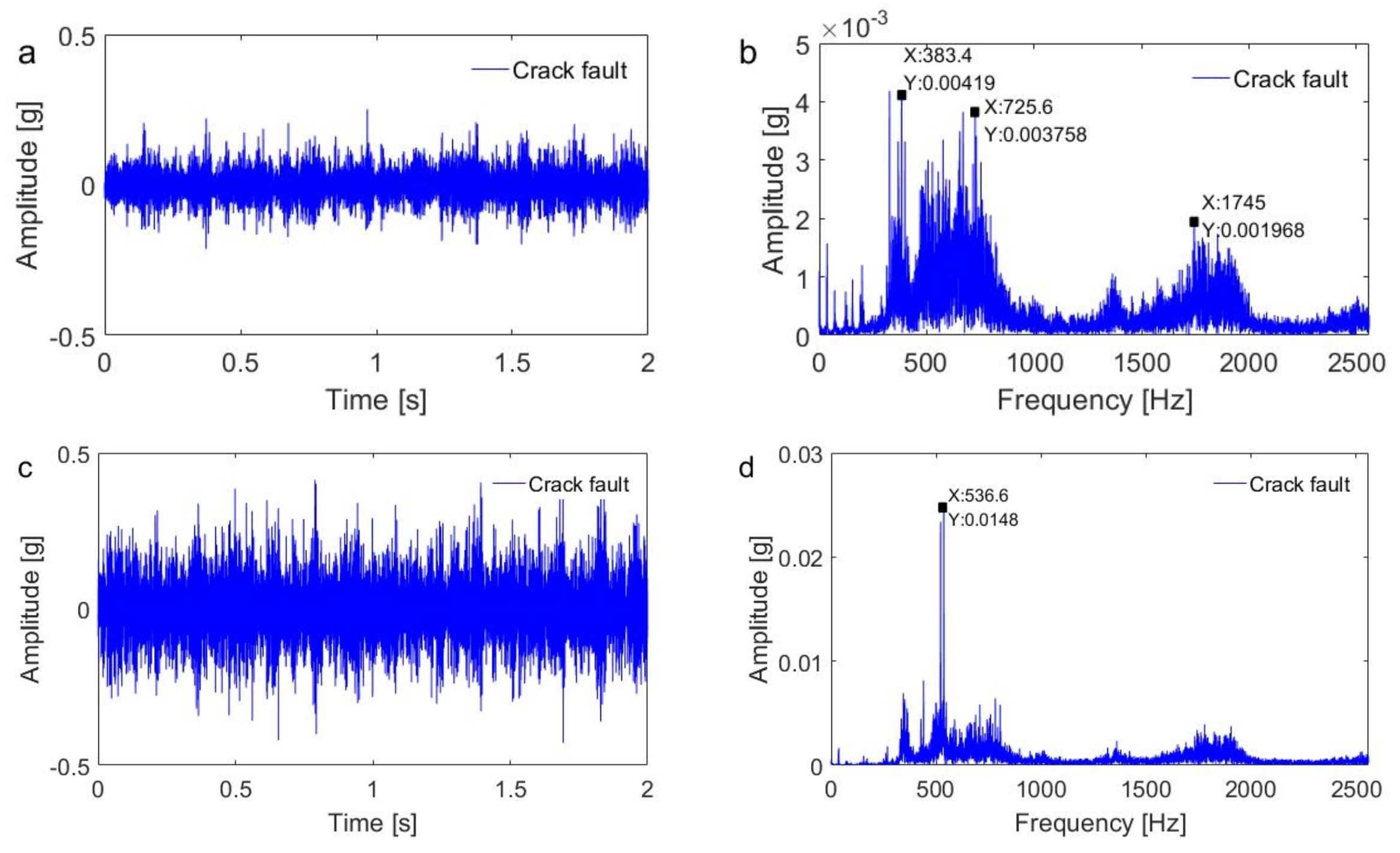
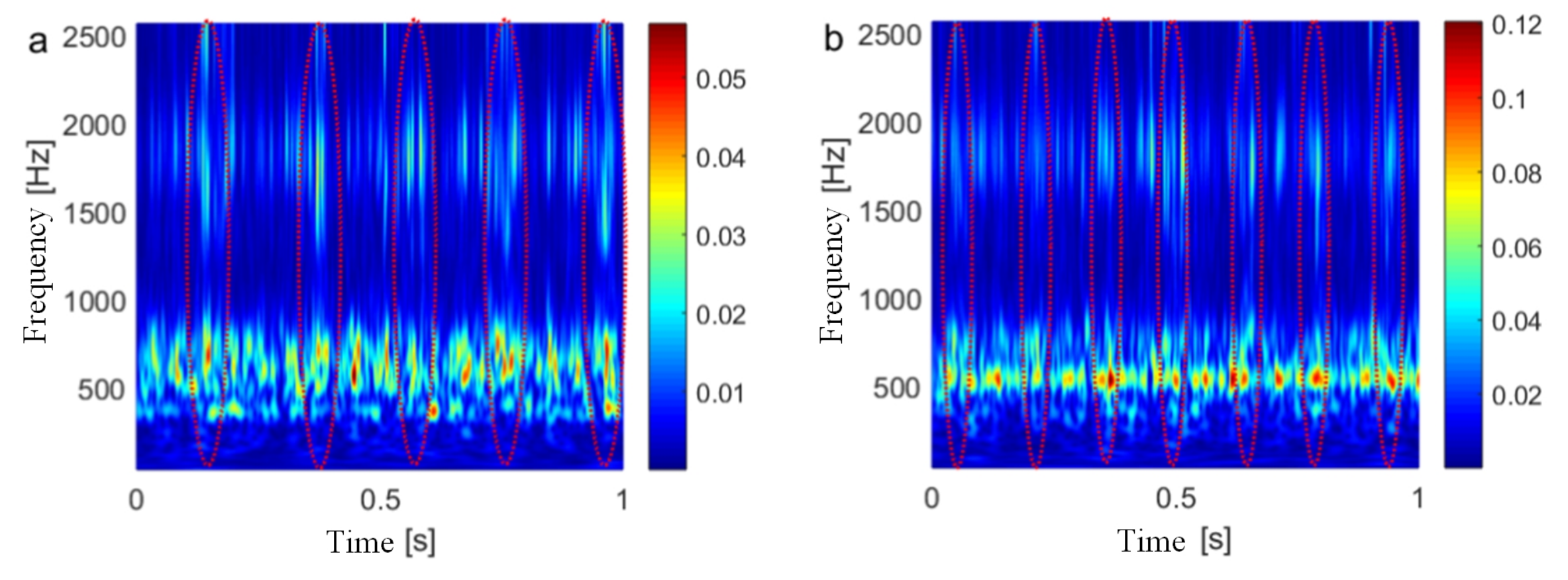
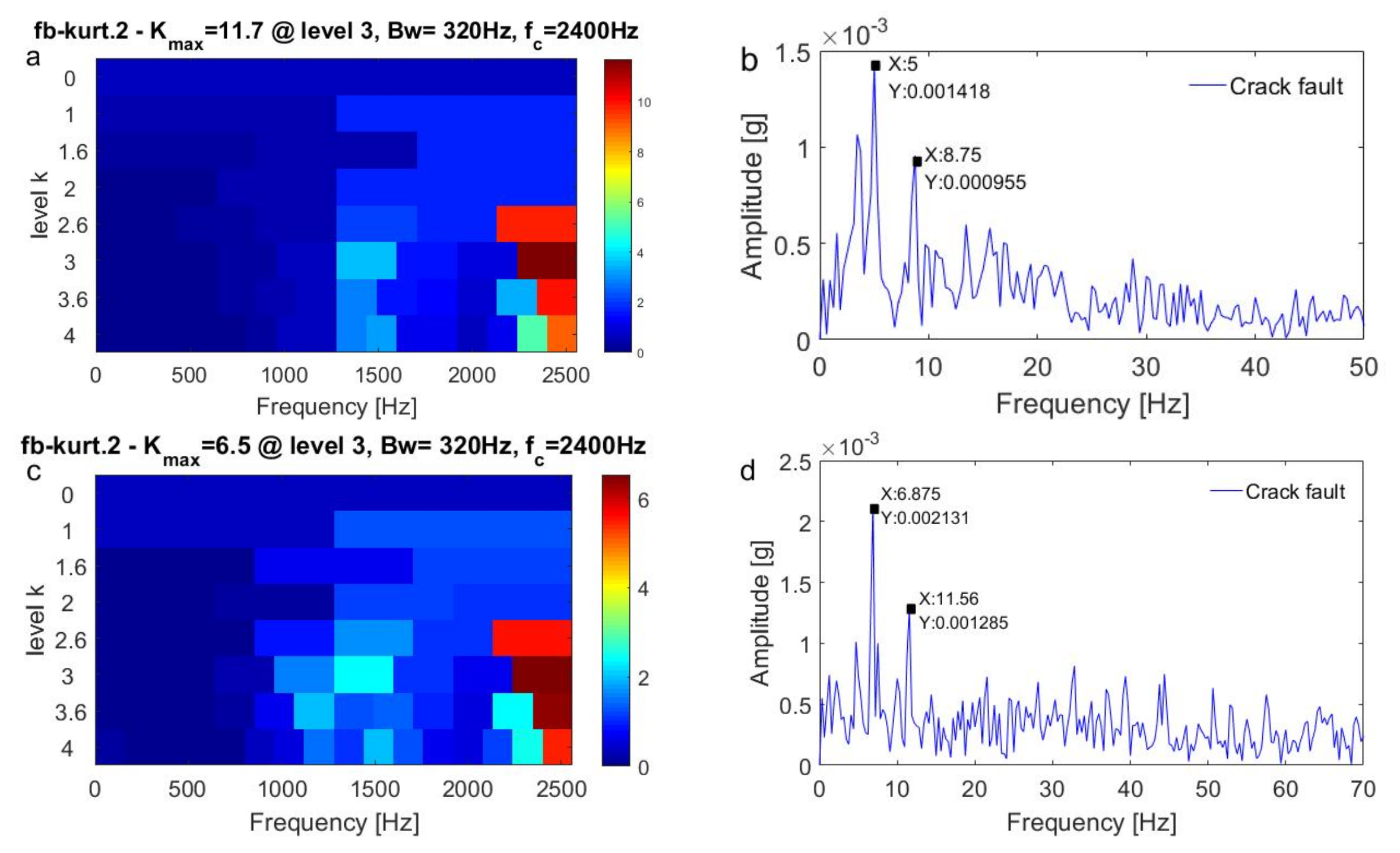
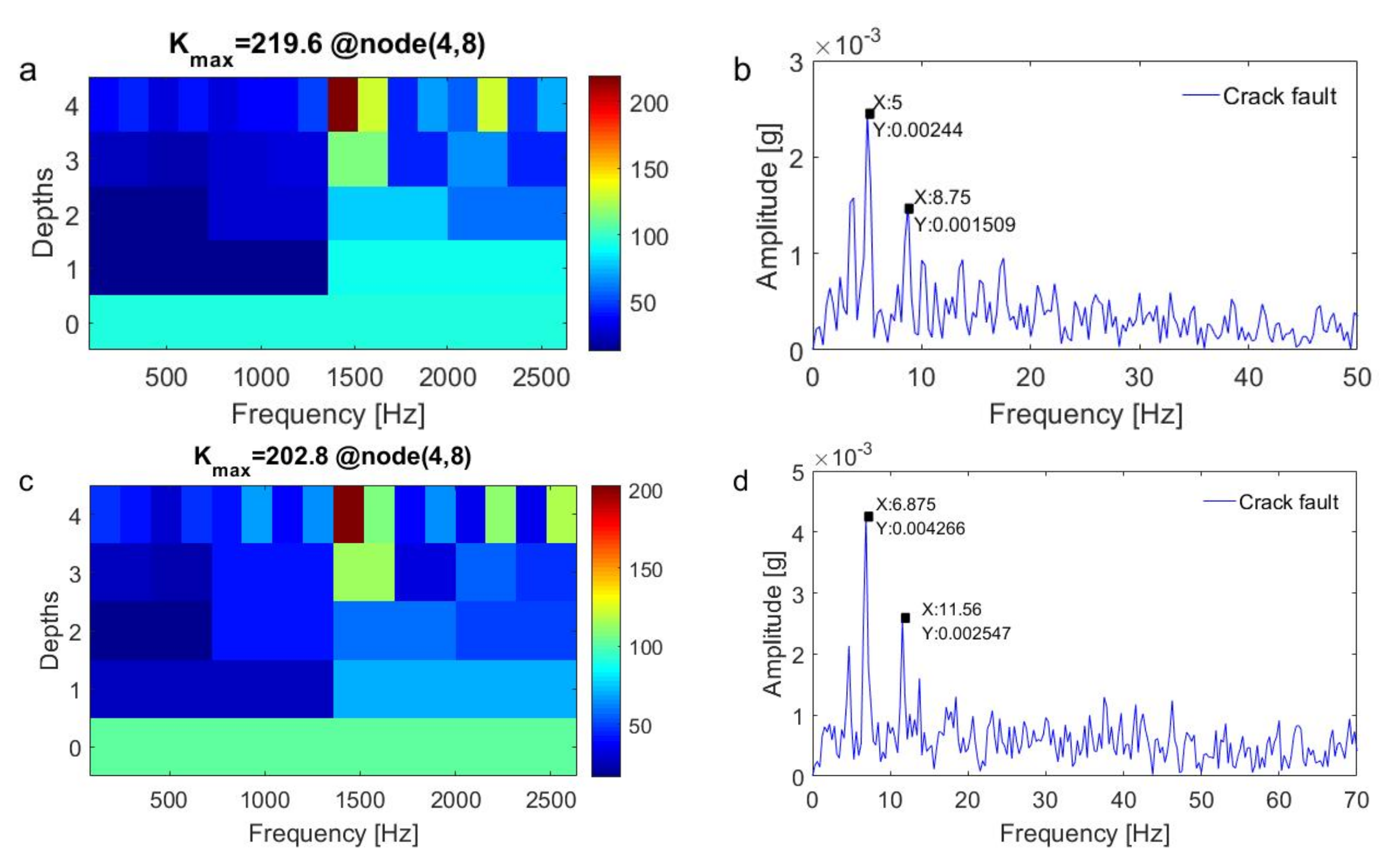
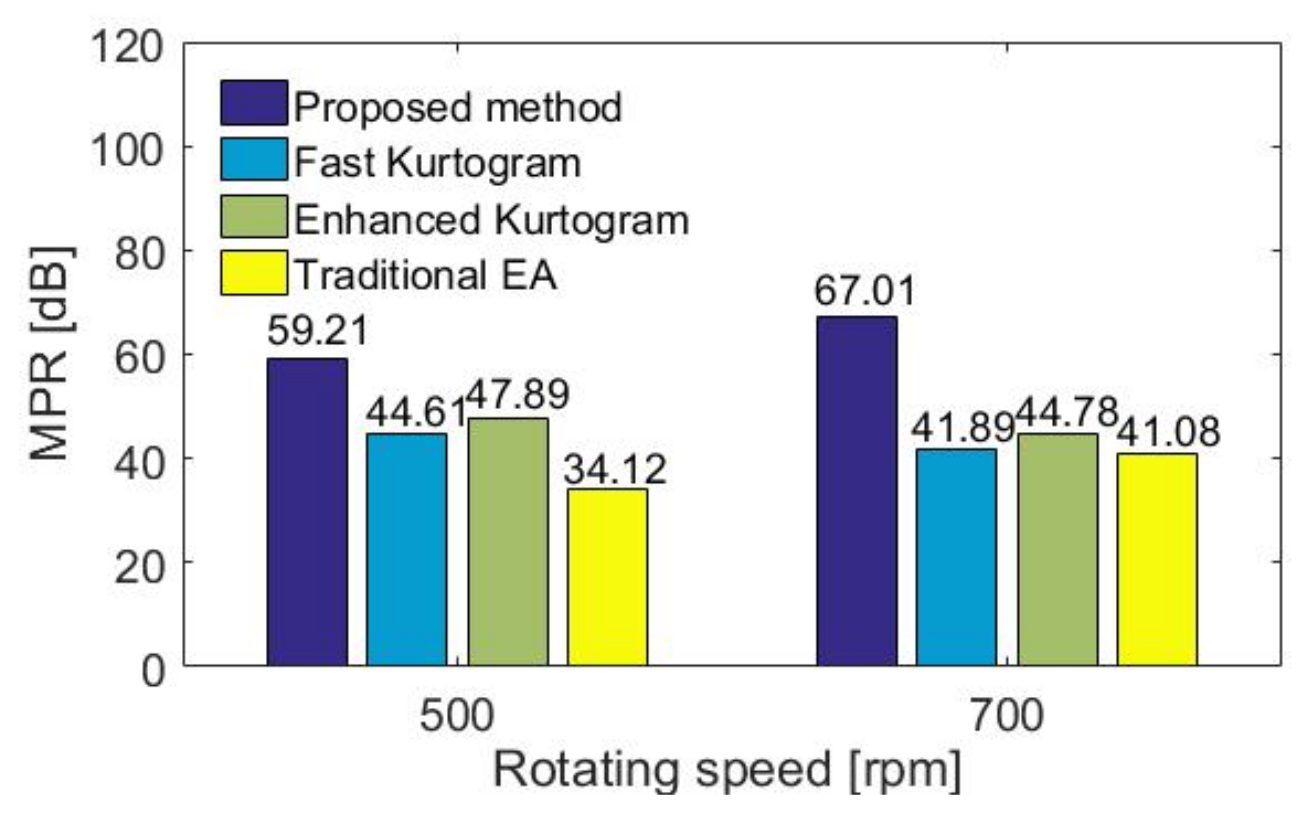
5.2. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guo, Y.; Parker, R.G. Analytical determination of mesh phase relations in general compound planetary gears. Mech. Mach. Theory 2011, 46, 1869–1887. [Google Scholar] [CrossRef]
- Wang, L.; Shao, Y. Fault feature extraction of rotating machinery using a reweighted complete ensemble empirical mode decomposition with adaptive noise and demodulation analysis. Mech. Syst. Signal Process. 2020, 138, 20. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, J.; Zhai, W.; Wang, Y.; Liu, J. Improved analytical methods for calculation of gear tooth fillet-foundation stiffness with tooth root crack. Eng. Fail. Anal. 2017, 82, 72–81. [Google Scholar] [CrossRef]
- Zhao, M.; Kang, M.; Tang, B.; Pecht, M. Multiple Wavelet Coefficients Fusion in Deep Residual Networks for Fault Diagnosis. IEEE Trans. Ind. Electron. 2019, 66, 4696–4706. [Google Scholar] [CrossRef]
- Huo, Z.; Zhang, Y.; Francq, P.; Shu, L.; Huang, J. Incipient fault diagnosis of roller bearing using optimized wavelet transform based multi-speed vibration signatures. IEEE Access 2017, 5, 19442–19456. [Google Scholar] [CrossRef] [Green Version]
- Ma, R.; Chen, Y. Research on the dynamic mechanism of the gear system with local crack and spalling failure. Eng. Fail. Anal. 2012, 26, 12–20. [Google Scholar] [CrossRef]
- Wang, L.; Shao, Y. Fault mode analysis and detection for gear tooth crack during its propagating process based on dynamic simulation method. Eng. Fail. Anal. 2017, 71, 166–178. [Google Scholar] [CrossRef]
- Chaari, F.; Baccar, W.; Abbes, M.S.; Haddar, M. Effect of spalling or tooth breakage on gearmesh stiffness and dynamic response of a one-stage spur gear transmission. Eur. J. Mech. A Solids 2008, 27, 691–705. [Google Scholar] [CrossRef]
- Kang, M.; Kim, J.; Wills, L.M.; Kim, J.M. Time-varying and multiresolution envelope analysis and discriminative feature analysis for bearing fault diagnosis. IEEE Trans. Ind. Electron. 2015, 62, 7749–7761. [Google Scholar] [CrossRef]
- Rubini, R.; Meneghetti, U. Application of the envelope and wavelet transform analyses for the diagnosis of incipient faults in ball bearings. Mech. Syst. Signal Process. 2001, 15, 287–302. [Google Scholar] [CrossRef]
- McFadden, P.D. Detecting fatigue cracks in gears by amplitude and phase demodulation of the meshing vibration. J. Vib. Acoust. 1986, 108, 165–170. [Google Scholar] [CrossRef]
- Wang, W. Early detection of gear tooth cracking using the resonance demodulation technique. Mech. Syst. Signal Process. 2001, 15, 887–903. [Google Scholar] [CrossRef]
- Bediaga, I.; Mendizabal, X.; Arnaiz, A.; Munoa, J. Ball bearing damage detection using traditional signal processing algorithms. IEEE Instrum. Meas. Mag. 2013, 16, 20–25. [Google Scholar] [CrossRef]
- Fan, X.; Zuo, M. Gearbox fault detection using Hilbert and wavelet packet transform. Mech. Syst. Signal Process. 2006, 20, 966–982. [Google Scholar] [CrossRef]
- Ni, X.; Zhao, J.; Hu, Q.; Zhang, X.; Li, H. A new improved Kurtogram and its application to planetary gearbox degradation feature analysis. J. Vibroeng. 2017, 19, 3413–3428. [Google Scholar] [CrossRef] [Green Version]
- Tra, V.; Kim, J.; Khan, S.A.; Kim, J.M. Incipient fault diagnosis in bearings under variable speed conditions using multiresolution analysis and a weighted committee machine. J. Acoust. Soc. Am. 2017, 142, EL35–EL41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Zhang, Y.; Randall, R.B. Rolling element bearing fault diagnosis based on the combination of genetic algorithms and fast kurtogram. Mech. Syst. Signal Process. 2009, 23, 1509–1517. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Z.; Miao, Q.; Zhang, X. Time—Frequency analysis based on ensemble local mean decomposition and fast kurtogram for rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2018, 103, 60–75. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zi, Y. Application of an improved kurtogram method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2011, 25, 1738–1749. [Google Scholar] [CrossRef]
- Wang, D.; Peter, W.T.; Tsui, K.L. An enhanced Kurtogram method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2013, 35, 176–199. [Google Scholar] [CrossRef]
- Ma, H.; Pang, X.; Feng, R.; Song, R.; Wen, B. Fault features analysis of cracked gear considering the effects of the extended tooth contact. Eng. Fail. Anal. 2015, 48, 105–120. [Google Scholar] [CrossRef]
- Lei, Y.; Kong, D.; Lin, J.; Zuo, M.J. Fault detection of planetary gearboxes using new diagnostic parameters. Meas. Sci. Technol. 2012, 23, 055605. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis//Proceedings of the Royal Society of London A: Mathematical, physical and engineering sciences. R. Soc. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wei, Y.; Huang, W. An improvement emd method based on the optimized rational hermite interpolation approach and its application to gear fault diagnosis. Measuremen 2015, 63, 330–345. [Google Scholar] [CrossRef]
- Yan, R.; Robert, G.; Chen, X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Singh, A.; Parey, A. Gearbox fault diagnosis under fluctuating load conditions with independent angular re-sampling technique, continuous wavelet transform and multilayer perceptron neural network. IET Sci. Meas. Technol. 2016, 11, 220–225. [Google Scholar] [CrossRef]
- Zhang, X.; He, Y.; Hao, R.; Fulei, C.H.U. Parameters optimization of continuous wavelet transform and its application in acoustic emission signal analysis of rolling bearing. Chin. J. Mech. Eng. 2007, 20, 1. [Google Scholar] [CrossRef]
- Wang, S.; Huang, W.; Zhu, Z. Transient modeling and parameter identification based on wavelet and correlation filtering for rotating machine fault diagnosis. Mech. Syst. Signal Process. 2011, 25, 1299–1320. [Google Scholar] [CrossRef]
- Fyfe, K.R.; Zuo, M.; Lin, J. Mechanical Fault Detection Based on the Wavelet De-Noising Technique. J. Vib. Acoust. 2004, 126, 9–16. [Google Scholar]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]
- Wang, H.; Ji, Y. A Revised Hilbert–Huang Transform and Its Application to Fault Diagnosis in a Rotor System. Sensors 2018, 18, 4329. [Google Scholar] [CrossRef] [Green Version]
- Ya, J.; Lu, L. Improved Hilbert–Huang transform based weak signal detection methodology and its application on incipient fault diagnosis and ECG signal analysis. Signal Process. 2014, 98, 74–87. [Google Scholar]
- Lei, Y.; Lin, J.; Zuo, M.J.; He, Z. Condition monitoring and fault diagnosis of planetary gearboxes: A review. Measurement 2014, 48, 292–305. [Google Scholar] [CrossRef]
- Widodo, A.; Kim, E.Y.; Son, J.D.; Yang, B.S.; Tan, A.C.; Gu, D.S.; Mathew, J. Fault diagnosis of low speed bearing based on relevance vector machine and support vector machine. Expert Syst. Appl. 2009, 36, 7252–7261. [Google Scholar] [CrossRef]






| Parameters | Sun Gear | Planet Gear | Ring |
|---|---|---|---|
| Number of teeth | 16 | 33 | 84 |
| Modulus/mm | 4 | 4 | 4 |
| Pressure angle/() | 20 | 20 | 20 |
| Planet number | 4 | ||
| Speed (rpm) | fsun (Hz) | fc (Hz) | fp (Hz) | fm (Hz) | fds (Hz)) |
|---|---|---|---|---|---|
| 100 | 1.667 | 0.267 | 0.412 | 22.4 | 5.6 |
| 300 | 5 | 0.8 | 1.237 | 67.2 | 16.8 |
| 500 | 8.333 | 1.333 | 2.061 | 112 | 28 |
| Speed | 1st Frequency | 2nd Frequency | High-Speed Shaft | Intermediate Shaft | Low-Speed Shaft |
|---|---|---|---|---|---|
| 500 rpm | 191.70 Hz | 122.90 Hz | 8.33 Hz | 4.91 Hz | 2.32 Hz |
| 700 rpm | 268.30 Hz | 172.00 Hz | 11.67 Hz | 6.88 Hz | 3.25 Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, W.-t.; Zeng, Q.; Shao, Y.-m.; Wang, L.-m.; Ding, X.-x. Multi-Scale Demodulation for Fault Diagnosis Based on a Weighted-EMD De-Noising Technique and Time–Frequency Envelope Analysis. Appl. Sci. 2020, 10, 7796. https://doi.org/10.3390/app10217796
Du W-t, Zeng Q, Shao Y-m, Wang L-m, Ding X-x. Multi-Scale Demodulation for Fault Diagnosis Based on a Weighted-EMD De-Noising Technique and Time–Frequency Envelope Analysis. Applied Sciences. 2020; 10(21):7796. https://doi.org/10.3390/app10217796
Chicago/Turabian StyleDu, Wei-tao, Qiang Zeng, Yi-min Shao, Li-ming Wang, and Xiao-xi Ding. 2020. "Multi-Scale Demodulation for Fault Diagnosis Based on a Weighted-EMD De-Noising Technique and Time–Frequency Envelope Analysis" Applied Sciences 10, no. 21: 7796. https://doi.org/10.3390/app10217796
APA StyleDu, W.-t., Zeng, Q., Shao, Y.-m., Wang, L.-m., & Ding, X.-x. (2020). Multi-Scale Demodulation for Fault Diagnosis Based on a Weighted-EMD De-Noising Technique and Time–Frequency Envelope Analysis. Applied Sciences, 10(21), 7796. https://doi.org/10.3390/app10217796






