Capacity Design and Cost Analysis of Converged Renewable Energy Resources by Considering Base Load Conditions in Residential and Industrial Areas
Abstract
:1. Introduction
2. Design of a System without Base Generation (Referenced Study)
2.1. Capacity Design of PV Generation Systems
2.2. Capacity Design of the ESS Systems
3. Design of the System with Base Generation (Proposed Study)
3.1. Improvements in Approach
- (1)
- Select the target area where the power generation system will be installed.
- (2)
- Collect the basic data, such as the amount of sunlight and average daily load () in the target area.
- (3)
- Calculate the annual minimum load () as the base load using the collected load data.
- (4)
- Calculate the capacity of the base power source () to supply power to the annual minimum load () and the daily base power production (). At this time, the capacity is determined larger than the annual minimum load (), and with the minimum capacity in the rated power product. Since the fuel cell, which is the base power source, can be operated with the same output all day, the daily base power production () can be obtained by multiplying the capacity of the base power source () by 24 h.
- (5)
- Calculate the middle and peak loads () by excluding as much as possible the daily base power production () from the average daily load (). Middle and peak loads are powered by photovoltaic and energy storage devices.
- (6)
- Collect details of the system components (inverter, cable, electrical energy storage, etc.).
- (7)
- Calculate the daily photovoltaic power production () by using the median and peak loads () and the previously collected details of the system components.
- (8)
- Calculate the photovoltaic generation capacity () and the energy storage capacity ().
3.2. Power Load of the Target Area (Customer)
3.3. Design of the Base Generation Capacity
3.4. Capacity Design of the PV Power Generation System and ESS
3.5. Comparison of System Design of Referenced and Current Study
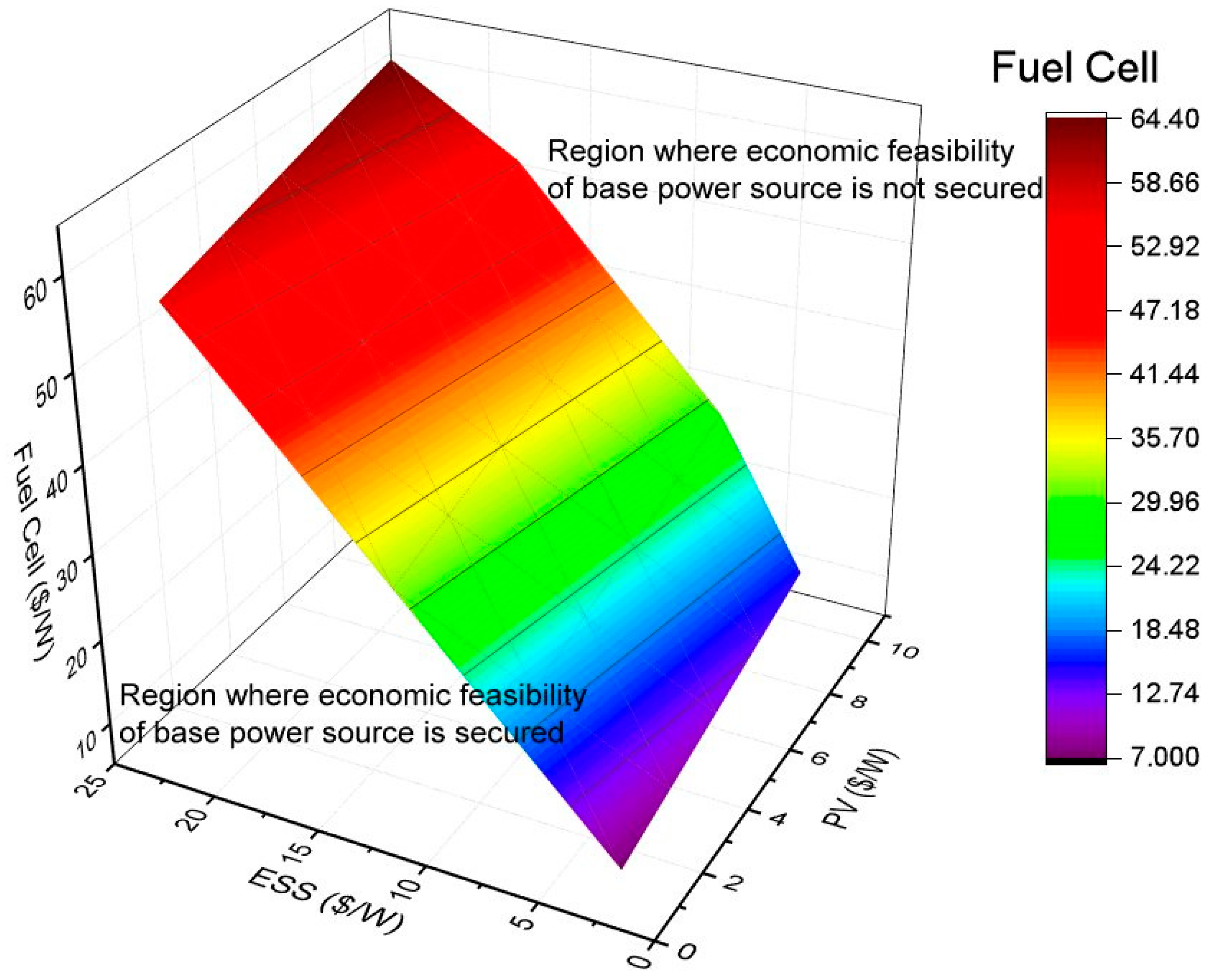
4. Economic Analysis
4.1. Cost Calculation of the System Designed with a Base Generation Power Source (Proposed Study)
4.2. Cost Comparison (Economic Analysis)
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dawoud, S.M.; Lin, X.; Okba, M.I. Hybrid renewable microgrid optimization techniques: A review. Renew. Sustain. Energy Rev. 2018, 82, 2039–2052. [Google Scholar] [CrossRef]
- Madtharad, C.; Chinabut, T. Microgrid Design for Rural Island in PEA Area. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, Scotland, 4–7 September 2018; pp. 1–5. [Google Scholar]
- Suman, G.K.; Roy, O.P. Microgrid System for A Rural Area—An Analysis of HOMER Optimised Model Using MATLAB. In Proceedings of the 2019 3rd International Conference on Recent Developments in Control, Automation & Power Engineering (RDCAPE), Noida, India, 10–11 October 2019. [Google Scholar]
- Bianchi, M.; Branchini, L.; Ferrari, C.; Melino, F. Optimal sizing of grid-independent hybrid PV–battery power systems for household sector. Appl. Energy 2014, 136, 805–816. [Google Scholar] [CrossRef]
- Arefifar, S.A.; Mohamed, Y.A.-R.I.; El-Fouly, T.H.M. Optimum Microgrid Design for Enhancing Reliability and Supply-Security. IEEE Trans. Smart Grid 2013, 4, 1567–1575. [Google Scholar] [CrossRef]
- Arangarajan, V.; Oo, A.M.T.; Shafiullah, G.M.; Seyedmahmoudian, M.; Stojcevski, A. Optimum design and analysis study of Stand-alone residential solar PV Microgrid. In Proceedings of the 2014 Australasian Universities Power Engineering Conference (AUPEC), Perth, Australia, 28 September–1 October 2014; pp. 1–7. [Google Scholar]
- Lee, C.K.; Bhang, B.G.; Kim, D.K.; Lee, S.H.; Cha, H.L.; Ahn, H.K. Estimation of Load Pattern for Optimal Planning of Stand-Alone Microgrid Networks. Energies 2018, 11, 2012. [Google Scholar] [CrossRef] [Green Version]
- Kim, G.G.; Choi, J.H.; Park, S.Y.; Bhang, B.G.; Nam, W.J.; Cha, H.L.; Park, N.; Ahn, H.K. Prediction Model for PV Performance With Correlation Analysis of Environmental Variables. IEEE J. Photovolt. 2019, 9, 832–841. [Google Scholar] [CrossRef]
- Cho, C.Y.; Lee, W.; Bhang, B.G.; Choi, J.H.; Lee, S.H.; Woo, S.C.; Ahn, H.K. Convergence Analysis of Capacities for PVs and ESS Considering Energy Self-Suciency Rates and Load Patterns of Rural Areas. Appl. Sci. 2019, 9, 5323. [Google Scholar] [CrossRef] [Green Version]
- Rezk, H.; Abdelkareem, M.A.; Ghenai, C. Performance evaluation and optimal design of stand-alone solar PV-battery system for irrigation in isolated regions: A case study in Al Minya (Egypt). Sustain. Energy Technol. Assess. 2019, 36, 100556. [Google Scholar] [CrossRef]
- Ghenai, C.; Bettayeb, M. Grid-Tied Solar PV/Fuel Cell Hybrid Power System for University Building. Energy Procedia 2019, 159, 96–103. [Google Scholar] [CrossRef]
- Sichilalu, S.; Tazvinga, H.; Xia, X. Integrated Energy Management of Grid-tied-PV-fuel Cell Hybrid System. Energy Procedia 2016, 103, 111–116. [Google Scholar] [CrossRef]
- Obara, S.; Kawai, M.; Kawae, O.; Morizane, Y. Operational planning of an independent microgrid containing tidal power generators, SOFCs, and photovoltaics. Appl. Energy 2013, 102, 1343–1357. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z.; Zhuo, R.; Wang, X. Optimal operation of independent regional power grid with multiple wind-solar-hydro-battery power. Appl. Energy 2019, 235, 1541–1550. [Google Scholar] [CrossRef]
- Chae, W.-K.; Lee, H.-J.; Won, J.-N.; Park, J.-S.; Kim, J.-E. Design and Field Tests of an Inverted Based Remote MicroGrid on a Korean Island. Energies 2015, 8, 8193–8210. [Google Scholar] [CrossRef]
- Bhang, B.G.; Lee, W.; Kim, G.; Choi, J.H.; Park, S.Y.; Ahn, H.K. Power Performance of Bifacial c-Si PV Modules with Different Shading Ratios. IEEE J. Photovolt. 2019, 9, 1413–1420. [Google Scholar] [CrossRef]
- Ndwali, P.K.; Njiri, J.G.; Wanjiru, E.M. Optimal Operation Control of Microgrid Connected PV-Diesel Generator Backup System under Time of Use Tariff. J. Control Autom. Elect. Syst. 2020, 31, 1001–1014. [Google Scholar] [CrossRef]
- Alramlawi, M.; Timothy, A.F.; Gabash, A.; Mohagheghi, E.; Li, P. Optimal Operation of PV-Diesel MicroGrid with Multiple Diesel Generators Under Grid Blackouts. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–6. [Google Scholar]
- Tang, Q.; Liu, N.; Zhang, J. Optimal Operation Method for Microgrid with Wind/PV/Diesel Generator/Battery and Desalination. J. Appl. Math. 2014, 2014, 857541. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Huang, L.; Shu, J.; Wang, H.; Ding, J. Energy Management of PV-diesel-battery Hybrid Power System for Island Stand-alone Micro-grid. Energy Procedia 2017, 105, 2201–2206. [Google Scholar] [CrossRef]
- Gharibi, M.; Askarzadeh, A. Technical and economical bi-objective design of a grid-connected photovoltaic/diesel generator/fuel cell energy system. Sustain. Cities Soc. 2019, 50, 101575. [Google Scholar] [CrossRef]
- Ghenai, C.; Bettayeb, M. Modelling and performance analysis of a stand-alone hybrid solar PV/Fuel Cell/Diesel Generator power system for university building. Energy 2019, 171, 180–189. [Google Scholar] [CrossRef]
- Das, B.K.; Zaman, F. Performance analysis of a PV/Diesel hybrid system for a remote area in Bangladesh: Effects of dispatch strategies, batteries, and generator selection. Energy 2019, 169, 263–276. [Google Scholar] [CrossRef]
- Bosisio, A.; Moncecchi, M.; Cassetti, G.; Merlo, M. Microgrid design and operation for sensible loads: Lacor hospital case study in Uganda. Sustain. Energy Technol. Assess. 2019, 36, 100535. [Google Scholar] [CrossRef]
- Krishan, O.; Suhag, S. Grid-independent PV system hybridization with fuel cell-battery/supercapacitor: Optimum sizing and comparative techno-economic analysis. Sustain. Energy Technol. Assess. 2020, 37, 100625. [Google Scholar] [CrossRef]
- Khan, M.W.; Wang, J.; Xiong, L.; Ma, M. Modelling and optimal management of distributed microgrid using multi-agent systems. Sustain. Cities Soc. 2018, 41, 154–169. [Google Scholar] [CrossRef]
- Gharibi, M.; Askarzadeh, A. Size and power exchange optimization of a grid-connected diesel generator-photovoltaic-fuel cell hybrid energy system considering reliability, cost and renewability. Int. J. Hydrogen Energy 2019, 44, 25428–25441. [Google Scholar] [CrossRef]
- Singh, S.; Chauhan, P.; Singh, N. Capacity optimization of grid connected solar/fuel cell energy system using hybrid ABC-PSO algorithm. Int. J. Hydrogen Energy 2020, 45, 10070–10088. [Google Scholar] [CrossRef]
- Saleem, M.S.; Abas, N.; Kalair, A.R.; Rauf, S.; Haider, A.; Tahir, M.S.; Sagir, M. Design and optimization of hybrid solar-hydrogen generation system using TRNSYS. Int. J. Hydrogen Energy 2020, 45, 15814–15830. [Google Scholar] [CrossRef]
- Romeri, M.V. Considering Hydrogen Fuel Cells Powertrain as Power Generation Plant. World Electr. Veh. J. 2010, 4, 933–938. [Google Scholar] [CrossRef] [Green Version]
- Staffell, I.; Scamman, D.; Abad, A.V.; Balcombe, P.; Dodds, P.E.; Ekins, P.; Shah, N.; Ward, K.R. The role of hydrogen and fuel cells in the global energy system. Energy Environ. Sci. 2019, 12, 463–491. [Google Scholar] [CrossRef] [Green Version]
- Yujin, O. Current status and prospect of the domestic renewable energy market and fuel cell power generation industry. Hana Ind. Inf. 2019, 1, 1–26. [Google Scholar]



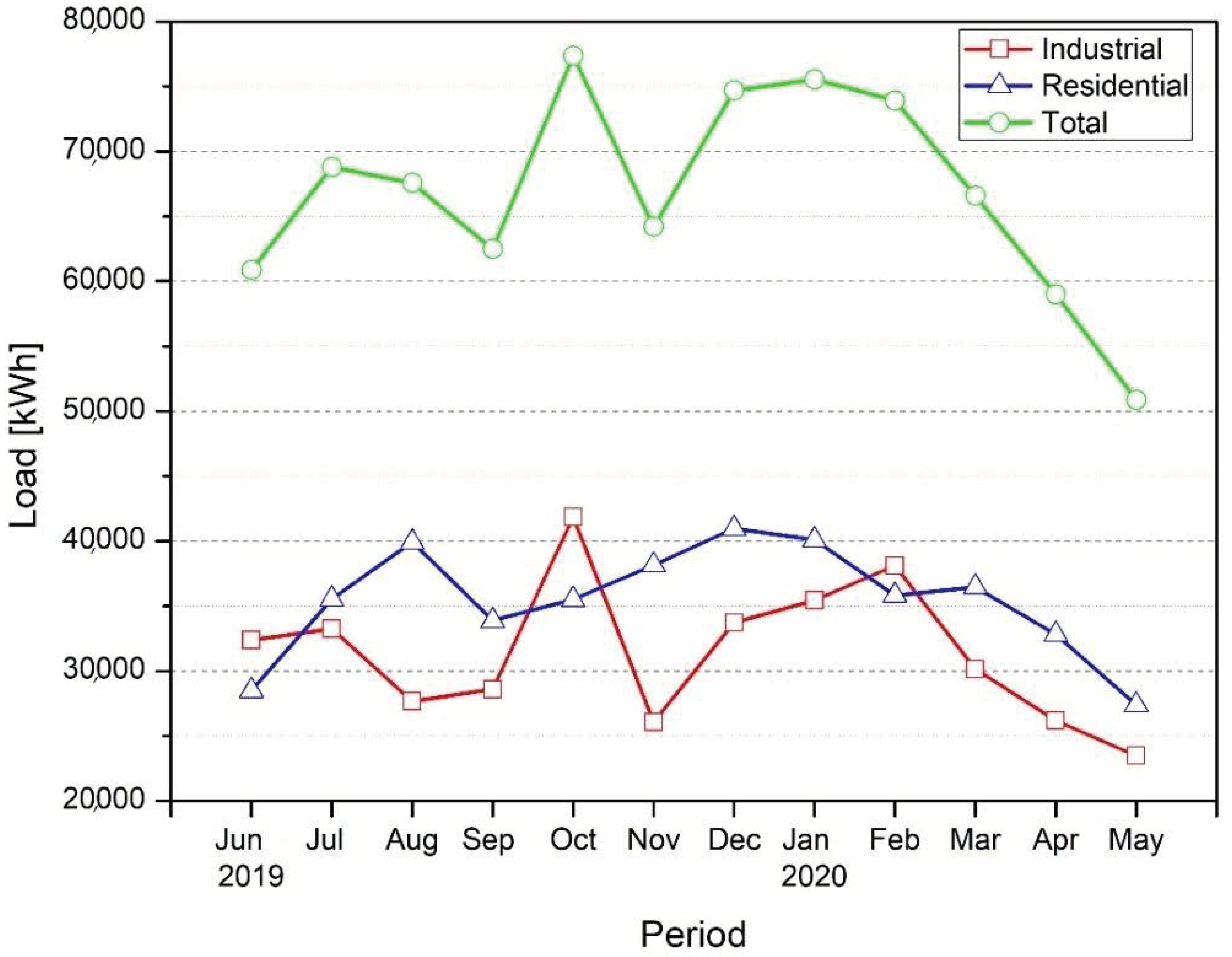


| Load | Residential Area (kWh) | Industrial Complexes (kWh) | Total (kWh) | |
|---|---|---|---|---|
| Period | ||||
| June 2019 | 28,495 | 32,370 | 60,865 | |
| July 2019 | 35,531 | 33,268 | 68,799 | |
| August 2019 | 39,920 | 27,648 | 67,568 | |
| September 2019 | 33,889 | 28,589 | 62,478 | |
| October 2019 | 35,505 | 41,842 | 77,347 | |
| November 2019 | 38,139 | 26,063 | 64,202 | |
| December 2019 | 40,964 | 33,718 | 74,682 | |
| January 2020 | 40,086 | 35,456 | 75,542 | |
| February 2020 | 35,819 | 38,096 | 73,915 | |
| March 2020 | 36,460 | 30,136 | 66,596 | |
| April 2020 | 32,823 | 26,165 | 58,988 | |
| May 2020 | 27,403 | 23,472 | 50,875 | |
| Total | 425,034 | 376,821 | 801,855 | |
| Monthly Average | 35,420 | 31,402 | 66,821 | |
| Daily Average | 1164 | 1032 | 2197 | |
| Power Generation | Referenced Research (Without Base Load Power Generation) | Current Research (With Base Load Power Generation) |
|---|---|---|
| PV () | 715.84 kW | 442.15 kW |
| ESS () | 2227.70 kWh | 1375.96 kWh |
| Fuel cell () | - | 35.00 kW |
| Component | Unit Cost |
|---|---|
| PV generation system | 1083 $/kW |
| ESS | 450 $/kWh |
| Fuel cell generation system | 4167 $/kW |
| Component | Unit Price | Installation Capacity | Cost (USD) |
|---|---|---|---|
| PV () | 1083 $/kW | 442.15 kW | 478,846.93 |
| ESS () | 450 $/kWh | 1375.96 kWh | 619,182.77 |
| Fuel cell () | 4167 $/kW | 35.00 kW | 145,845.00 |
| Total | 1,243,874.70 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.H.; Lee, W.; Hyun, J.H.; Bhang, B.G.; Choi, J.; Ahn, H.K. Capacity Design and Cost Analysis of Converged Renewable Energy Resources by Considering Base Load Conditions in Residential and Industrial Areas. Appl. Sci. 2020, 10, 7822. https://doi.org/10.3390/app10217822
Lee SH, Lee W, Hyun JH, Bhang BG, Choi J, Ahn HK. Capacity Design and Cost Analysis of Converged Renewable Energy Resources by Considering Base Load Conditions in Residential and Industrial Areas. Applied Sciences. 2020; 10(21):7822. https://doi.org/10.3390/app10217822
Chicago/Turabian StyleLee, Sang Hun, Wonbin Lee, Jin Hee Hyun, Byeong Gwan Bhang, Jinho Choi, and Hyung Keun Ahn. 2020. "Capacity Design and Cost Analysis of Converged Renewable Energy Resources by Considering Base Load Conditions in Residential and Industrial Areas" Applied Sciences 10, no. 21: 7822. https://doi.org/10.3390/app10217822
APA StyleLee, S. H., Lee, W., Hyun, J. H., Bhang, B. G., Choi, J., & Ahn, H. K. (2020). Capacity Design and Cost Analysis of Converged Renewable Energy Resources by Considering Base Load Conditions in Residential and Industrial Areas. Applied Sciences, 10(21), 7822. https://doi.org/10.3390/app10217822






