Abstract
Public key encryption with keyword search (PEKS) enables users to search over encrypted data outsourced to an untrusted server. Unfortunately, updates to the outsourced data may incur information leakage by exploiting the previously submitted queries. Prior works addressed this issue by means of forward privacy, but most of them suffer from significant performance degradation. In this paper, we present a novel forward private PEKS scheme leveraging Software Guard Extension (SGX), a trusted execution environment provided by Intel. The proposed scheme presents substantial performance improvements over prior work. Specifically, we reduce the query processing cost from to , where n is the number of encrypted data. According to our performance analysis, the overall computation time is reduced by 80% on average. Lastly, we provide a formal security definition of SGX-based forward private PEKS, as well as a rigorous security proof of the proposed scheme.
1. Introduction
Data outsourcing to cloud service providers is beneficial in terms of data management, but raises data security and privacy concerns. Encrypting data prior to outsourcing may solve the data privacy problems. However, it inevitably complicates, or sometimes hinders important data management operations such as searches over the outsourced data. Public key encryption with keyword search (PEKS) solves this dilemma, in which data senders are allowed to encrypt data using a public key such that the ciphertexts are searchable only by a data receiver whose secret key is associated with the public key [1].
Unfortunately, previous PEKS schemes are vulnerable to query leakage attacks. For example, in file injection attacks [2], an adversarial data sender generates maliciously crafted files of his choice, encrypts them with the public key of a data receiver, and then outsources it to the cloud storage. Then, the adversary observes file access patterns by monitoring which files are returned in response to queries submitted by a specific receiver, thereby leaking the receiver’s queries.
As a countermeasure, forward private PEKS schemes have been proposed, which can guarantee that the past search queries cannot be used for newly inserted files [3]. Unfortunately, the previous schemes are unsuitable for the multi-user environment where multiple data senders are existing for each receiver, which is the widespread setting in cloud-based applications (In this study, a multi-receiver environment is not considered. Thus, henceforth, a multi-user environment implies only a multi-sender environment in the paper). Thus, designing forward private PEKS that securely support multi-user setting in a scalable way is one of the challenging and important goals in the PEKS literature.
Moreover, prior works suffer from high communication overhead that degrades practicality. For example, Zhang et al. [4] achieved forward privacy by means of key revocation, which incurs costly key management tasks to distribute key update messages every time a query is processed. Zeng et al. [5] proposed a scheme to guarantee forward privacy without such key revocations. However, the scheme depends on computationally extensive cryptographic primitives, which incurs unacceptable computation costs in practice. Furthermore, the query size of their scheme depends on the time periods, leading to significant communication overheads.
To design secure and efficient schemes, one may utilize Trusted Execution Environments (TEEs) such as Intel Software Guard Extension (SGX) [6,7,8,9,10]. TEE provides memory isolation such that it loads data or code from (untrusted) main memory to the (trusted) isolated memory area, or enclave. Since TEE can protect data and processes from operating systems or hypervisors using enclaves, it can guarantee confidentiality and integrity of them even when operating systems or hypervisors are compromised. Recently, Amjad et al. [11] introduced an SGX-supported dynamic searchable symmetric encryption scheme that is forward private. However, it is also not applicable to the multi-user settings.
In this paper, we propose SPEKS, a forward private SGX-based public key encryption with keyword search scheme. To the best of our knowledge, it is the first SGX-based PEKS that achieves forward privacy in a multi-user setting. The proposed scheme uses a search counter to achieve forward privacy by unlinking the current data status with the previous queries. Specifically, both the data receiver and the cloud server share the same search counter, which is updated per each data update. Since the current data is encrypted using the latest search counter, the previous queries cannot be associated with subsequently updated data. Thus, forward privacy is guaranteed in the proposed scheme. In addition, SPEKS significantly outperforms prior works [4,5,12] and preserves forward privacy against stronger attack model by utilizing Intel SGX.
The contributions of this work are as follows:
- We propose a forward secure public key encryption with keyword search using Intel SGX, the first SGX-based PEKS scheme that achieves forward privacy in multi-user settings.
- The communication cost is significantly reduced as a single query is sufficient to search over multiple encrypted data, while prior works require numerous queries in proportional to the number of encrypted data.
- We define a security model of SGX-based forward private PEKS, and formally prove the security of our scheme.
- We implement our scheme using SGX, and evaluate the performance of our scheme and the previous schemes. According to the experiment with implementations, our scheme is significantly more efficient then the previous schemes without security degradation.
2. Background
Intel Software Guard Extension (SGX) is used for designing our construction for forward secure searchable encryption. SGX is an extension of the x86 instruction set architecture (ISA) introduced since the 6th generation Intel Skylake Processor. SGX provides Memory Isolation, Enclave Page Cache, and Software Attestation, which are major functionalities that we rely on to construct our scheme. In this section, we briefly introduce the SGX structures and basic PEKS algorithms upon which our scheme is built.
2.1. Intel Software Guard Extensions (SGX)
Memory Isolation. SGX platform can be divided into untrusted parts and trusted parts. Enclaves are trusted parts, or private regions of the physical memory whose contents are protected. The memory space for enclave is isolated from any process outside the enclave itself, including processes running at higher privilege levels. Thus, any access by other processes such as privileged operating systems, firmware, hypervisor and code in system management mode (SMM) to the enclave memory is disallowed.
The enclave memory is mapped into virtual memory of the untrusted part, and the untrusted part is executed on the ordinary process within the virtual address space. The mapping of the enclave memory is crucial, because this enables the enclave to access the host process’s entire virtual memory. However, the host process is only allowed to call enclave through certain interface. In addition, the executed code and data inside the enclave are encrypted when they reside in the untrusted part of the memory. When loaded into the enclave, on the other hand, the enclave is decrypted on the fly within the CPU. Thus, the processor protects the code from being examined by other processes, which treated as potentially hostile.
Enclave Page Cache (EPC): Enclave page cache (EPC) is memory area where the enclave code and data are placed. Using the Memory Encryption Engine (MEE), the EPC is encrypted and external reads on that memory bus can only monitor encrypted data. For EPC, a fixed amount of the main memory, limited to 128 MB, of the system is allocated to store enclave and related metadata. Since the dedicated memory is shared between enclave itself and related metadata, the enclave cache, on average, is able to use 96 MB [13]. Because of the memory limitation, enclaves sometimes need to swap pages when dealing with large data of which size exceeds the dedicated memory. During the boot phase, the SGX memory is reserved statically throughout the runtime of the system. If there are multiple enclaves, the memory is supposed to be dynamically managed by the OS and allocated to each enclave. When the page swapping occurs, the key generated at the boot-time is used for both encryption and decryption of the page. In the page swapping operations, confidentiality and integrity of the swapped-out pages can be guaranteed.
Software Attestation [14]: SGX supports software attestation feature that verifies the validity of locally or remotely created enclaves. The enclave measurement, which is the initial code loaded when the enclave is created, is used to verify the correctness of the enclave. Provided by the SGX attestation functionality, it can be assured that the measurements are authentic and associated with the benign enclave. For local attestation, EREPORT and EGETKEY instructions are used to generate the signed report and verify it at the target enclave. For remote attestation, the signature is provided by the Quoting Enclave (QE), a component of SGX. Before generating the signature, QE only accepts measurements from the hardware itself, which ensures that only legitimate enclave is measured.
2.2. Public Key Encryption with Keyword Search (PEKS)
Boneh et al. [1] first introduced the notion of public key encryption with keyword search (PEKS). Compared to symmetric searchable encryption, PEKS has better performance in data sharing. Abdalla et al. [15] gives a generic framework of PEKS and shows how to obtain public key based searchable encryption from anonymous identity-based encryption. In the PEKS scheme, a data receiver provides a gateway with a trapdoor function for keywords. Then, a data sender uses the data receiver’s public key for encrypting a keyword and sends the ciphertext to the server or the gateway. The latter applies search or test function to the search token and the ciphertext. When the keywords within the search token and the ciphertext match, the search or the test function returns 1; otherwise, 0. The scheme is proven to be secure in the standard model, but under the condition where the number of malicious clients is smaller than a specified value.
3. SPEKS Overview and Definitions
In this section, we describe a high level design of our SPEKS scheme, and show the search processes over encrypted data by users. Then, we define algorithms for SPEKS scheme and security model.
3.1. Overview
The high level design of our scheme is shown in Figure 1. In the proposed scheme, there are three system entities: data receiver (DR), data sender (DS), SGX-enabled cloud server (CS).
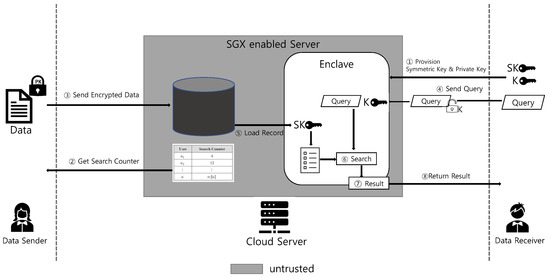
Figure 1.
High level design overview.
During the setup phase, a DR initially generates his private key , public key , and symmetric key . Using the SGX attestation protocol for enclave authentication, the DR establishes a secure channel with the enclave within the CS (shown in step ① in Figure 1). After establishing the secure connection, the DR provisions and into the enclave (step ①). The enclave stores two provisioned keys for future processes. When enclave is unloaded or rebooted, the provisioned keys can be securely stored in the local memory.
For the algorithm, a DS gets search counter of the DR, encrypts data that includes predefined keyword with the search counter, and uploads the encrypted data to the server (see step ② and ③). Then, the DR generates a search query, encrypts it with symmetric key , and transfers it to enclave within the CS using the algorithm (step ④). The enclave has provisioned keys required for decryption and the search query from the DR. For the algorithm, the data record is loaded to the enclave (step ⑤). If the data record size is greater than the EPC, the record are separated into smaller pieces and partial records are loaded multiple times to the enclave. The enclave decrypts the search query using the symmetric key and searches the matching record (step ⑥). Finally, if there is a matched result, then the enclave returns the result to the DR (step ⑦).
3.2. Algorithms and Security Definitions
SPEKS consists of four polynomial-time algorithms: .
Definition 1.
(SPEKS). A secure SPEKS is a tuple of four polynomial-time algorithms (Setup, PEKS, Trapdoor, Search) as follows:
- : It takes the security parameter as input for generating a key pair for private key and public key , and takes λ as input for generating symmetric key .
- : It takes the symmetric key , keyword w, and search counter as input. It then outputs encrypted search token .
- : It takes the public key , keyword w, user index u, and a set of data F as input. It then outputs a record .
- : It takes the private key , record , and search token as input. It then outputs F if there is a match; otherwise, ⊥.
Definition 2.
(Correctness) Let denote a -scheme consisting of the four algorithms described in Definition 1. For any correctly generated public key pair and symmetric K of the data receiver, and for any keyword w, holds with probability 1, where ciphertext and .
We define our security model based on the three steps framework introduced in [16]. For the first step, we need to formulate a leakage which means an upper bound of the information that an adversary may gather from the protocol. Second step is defining the and games for an adaptive adversary and a polynomial-time simulator . is the actual protocol and is the simulated protocol for the real game by utilizing using only the formulated leakage. Information learned in the previously executed protocols can be used by an adaptive adversary for its subsequent queries. Third step is proving that a scheme is CKA2-secure by showing that can distinguish the outputs of the games with probability close to 0. When the probability is negligibly close to 0, does not learn anything more than just the leakage stated in the first step.
Similar to the scheme introduced by Fuhry et al. [13], our scheme has an additional transaction between the cloud server and the trusted hardware, SGX. This additional transaction can be monitored by the adversary; therefore, we extended the original security model to hardware-security model. denotes the leakage on the CKA2-HW-security.
Definition 3.
(CKA2-HW-security). Let denote a scheme consisting of the four algorithms described in Definition 1. is a stateful passive adversary, and is a stateful simulator that gets the leakage functions and . Two probabilistic experiments and are described as a follow.
- : The data receiver runs and generates a key pair and symmetric key K. outputs a search counter of user, . The data sender calculates and passes to . The data receiver returns search token to after calculating . can use and the returned tokens at any time to make a query to the trusted hardware. The trusted hardware answers the query by running . If the query matches, then the search counter is incremented and returns a bit as a result of the experiment.
- : The adversary outputs search counter to the data sender. Using , the data sender creates and sends it to . The simulator creates search token and passes it to . can use and search token to make queries to , who simulates the trusted hardware. Next, with the given , returns the search result. At last, the adversary returns an output bit of the experiment.
We claim that is -secure against adaptive chosen-keyword attacks if for any probabilistic, polynomial-time algorithms , there exists a probabilistic, polynomial-time such that:
4. Construction
4.1. Cryptographic Primitive
Let and refer to IND-CPA secure public key encryption and decryption algorithm respectively, and and refer to IND-CPA secure symmetric key encryption and decryption algorithm respectively. The proposed scheme is constructed based on these symmetric and public key encryption/decryption algorithms.
4.2. Provisioning
For key sharing between the enclave and the data receiver, the data receiver provisions his private key and symmetric key to the enclave. Since the keys should not be revealed to any untrusted entity, secure connection between the data receiver and the enclave should be established using the attestation feature of SGX. During the creation of the enclave, the key pair and are created. The hardware random number generator (rdrand [17]) available in current CPUs can provide the sufficient randomness required for the key generation in practice.
Subsequently, the enclave sends the created to the quoting enclave (QE). The QE creates the signature used for verification of the measurement of the initial memory content of the enclave and the public key . With the given Intel’s public key, the data receiver verifies the signature of , , and . The data receiver is now able to encrypt and with and sends them back to the enclave. As a result, the enclave and the data receiver share the and , which they use for secure communication.
4.3. Algorithms
The proposed forward secure searchable encryption scheme with keyword search (SPEKS) consists of the following four algorithms: (Setup, PEKS, Trapdoor, Search).
Algorithm 1 gives a formal description of Setup of our SPEKS scheme. In algorithm, a data receiver (DR) generates , , and . Next, the DR provisions the and to the enclave within the cloud server, , through a secure channel. The secure channel can be established by the attestation feature provided by Intel SGX as explained in Section 4.2.
Next, Algorithm 2 provides a formal description of PEKS. In , where F denotes a set of data, a data sender (DS) first requests search counter from the cloud server (CS). Using the retrieved , the DS runs (,()) and generates searchable ciphertext . A record consists of three components , where d refers to the data, refers to the index, and refers to the searchable ciphertext. The generated record is sent to the CS.
Algorithm 3 describes the Trapdoor algorithm of our scheme. In the algorithm, the DR creates a search token with the keyword. Specifically, in the execution of , the DR uses the search counter and keyword, and generates the search token. Then, using symmetric key encryption (SKE), the DS encrypts the search token with symmetric key K. The encrypted search token is now transferred to Enclave. After transferring the search token, the DR increments his or her own search counter by 1.
Algorithm 4 describes the Search algorithm of our scheme. In Algorithm 4, Enclave checks whether search token matches . Enclave runs and retrieves keyword and search counter . Next, using the key , keyword w and search counter are retrieved from the ciphertext . The from is returned. is then incremented by one, and F with returned is returned to the DR, when matched; else, ⊥ is returned.
| Algorithm 1: |
| DR: |
| Symmetric key |
| Provision Private Key |
| and Symmetric to |
| Algorithm 2: |
| DS: |
| Request the search counter of u from the CS |
| CS: |
| Return to DS |
| DS: |
| for to do |
| ← Enc(,()) |
| ← ∪ |
| end for |
| Transfer to CS |
| CS: |
| for to do |
| ← ∪ |
| end for |
| Algorithm 3: |
| DR: |
| Transfer to |
| Algorithm 4: |
| CS: |
| Enclave: |
| for i=1 to sc’ do |
| if then |
| return |
| end if |
| end for |
| Return F to DR if match; else, ⊥ |
5. Analysis
5.1. Security Analysis
We will prove the security of our scheme by defining the leakage functions related to access pattern. Then, we will explain how our SPEKS scheme guarantees the forward privacy.
We define two leakage functions: and . function outputs a record given the search counter , which consists of encrypted data, indices, and searchable ciphertexts. Given and , function outputs the access pattern .
The access pattern contains information of search counter and records , which are stored in the untrusted memory region of the server. When the data receiver requests , the server can see which value is being returned. also leaks which record is being sent to enclave or the data receiver. In our analysis, we further utilize values access pattern [13], which, in our analysis, describes the pointers to the result values that specifically points the record with index .
Theorem 1.
(Security). The SPEKS construction is -secure.
Proof.
We consider a polynomial-time simulator for which probabilistic, polynomial-time adversary can distinguish between and with negligible probability.
- Setup: creates a new random keys and stores them.
- Simulating: gets and receives search counter . Furthermore, creates (the size of data set) encryption of keyword using . All encrypted value is given a distinct index value . outputs . Since the value of search counter and the size of the record are included in the leakage, the operations above are possible. The simulation of has the same size with the output of . In addition, the simulation result is indistinguishable from the output of due to IND-CPA-security of public key encryption scheme.
- Simulating: The simulator creates value and encrypts it as . outputs search token . Since is IND-CPA secure, the simulated is indistinguishable from the output of .
- Simulating secure hardware: At a given time t, receives search token and . uses to simulate the access pattern. begins with the first record of and follows the indices given by . The leakage determines the specific point of the record with index . □
The adversary cannot distinguish access of from simulated access due to the delivering of deterministic results. The results are consistent for each different requests made for the same keyword. Since is explicit, the number of result pointers matches and the pointers are also consistent. The pointed values are indistinguishable, because those values are encrypted IND-CCA secure.
Forward Privacy. In order to guarantee forward privacy, the past search queries should not be directly associated with the updated files. In our SPEKS scheme, we use a search counter that is supposed to be updated after each search. The search queries are generated only with private key and the search counter. Since the ciphertexts are created with the current newly updated search counters, past queries generated with past search counter values cannot match with newly updated files. Therefore, forward privacy is guaranteed in our proposed scheme.
5.2. Performance Analysis
In this section, we analyze the performance of our scheme and provide a comparative analysis with previous forward secure public key encryption with keyword search (FS-PEKS) schemes such as Zeng at al.’s [5] and Kim et al.’s [12] schemes.
Our experiment is run on a system equipped with Intel(R) Core(TM) i7-9700K CPU at 3.60 GHz, 16G DDR4 RAM. 64-bit Ubuntu 18.04.4 LTS with enabled SGX is used as an operating system. Our scheme is implemented based on Intel’s Software Guard Extension (SGX) Software Development Kit (SDK).
When considering the multi-user environment, it is important to evaluate the initial costs for key setup and key management. In order for general symmetric searchable encryption (SSE) schemes to support a multi-user environment, they need to set up the key multiple times in proportion to the number of users. For instance, if we define u as the number of data senders and as the initial cost of Diffie–Hellman key exchange protocol between a data sender and a data receiver, then the initial cost for the key setup is
However, the proposed scheme does not require key exchange protocol for each data sender, thus the key setup cost remains constant.
Furthermore, since the data receiver also needs to manage each key corresponding to each data sender, storage overhead for storing the key is also increased in proportion to the number of data senders in the previous schemes. For the key management, SSE schemes require a data receiver to store all of the keys set up for data senders. If refers to the size of a key, the overall storage overhead is
Whereas, our scheme does not require a data receiver to store multiple keys for each sender. Therefore, our scheme has constant storage overhead for key management regardless of the number of data senders, which shows high scalability of our scheme in the multi-sender environment.
Computation overhead: As shown in Figure 2, the proposed scheme has lower computation cost compared to those of Kim et al.’s and Zeng at al.’s schemes. Specifically, for algorithm, while Kim at al.’s scheme takes 3.958 ms and Zeng at al.’s takes 8.123 ms, our scheme takes just 0.0919 ms, which is significantly less overhead. Next, for generating a search token using algorithm, our scheme takes 0.02 ms, which is constant independently of the search count. However, in Kim et al.’s scheme [12], it takes 4.85 ms for a single search token, and the computational cost increases in proportion to the number of search counters. Zeng at al.’s scheme takes 12.11 ms for running , which is orders of magnitude slower than ours. In addition, for the algorithm, as shown in Table 1, it has the same complexity as our scheme in terms of the search time. However, when measuring the actual computation time in practice, the algorithm of ours takes, in average, 0.0436 ms, while the computation cost of search process in [5] depends on a set of encoded time period. This causes unnecessary computational overhead for some cases. The search algorithm in Kim et al.’s scheme takes 0.863 ms as shown in Figure 2.
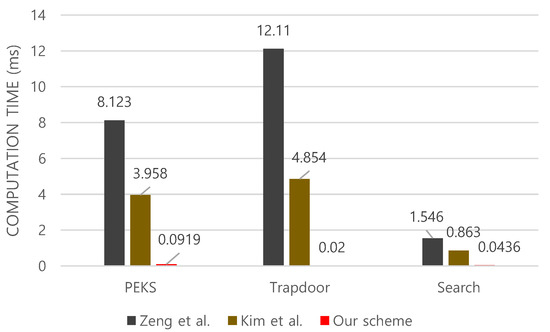
Figure 2.
Computational cost of each algorithm.

Table 1.
Efficiency comparison of public key encryption with keyword search (PEKS) schemes. ( refers to the value of search counter, refers to the number of data, refers to size of identifier, denotes number of searches made, denotes a set of encoded time period.)
This reduction in computation cost is caused by the characteristic of the trusted execution environment, especially Intel SGX in our scheme. Previous PEKS schemes [5,12] are constructed based on the pairing based cryptographic operations which leads to high computation overhead. For instance, in algorithm, our proposed scheme uses AES-GCM that is included in the SGX SDK for encryption and decryption of search query. Compared to pairing-based operations, AES-GCM is much more efficient cryptographic primitive. In addition, For algorithm, previous schemes utilize the pairing-based cryptography for searching over ciphertext. RSA or Elliptic Curve Cryptography cannot be used in such software-only based schemes, because the comparison over ciphertexts for search is not possible. However, the trusted execution environment provided by SGX enables the search process over plaintext while still guaranteeing the data privacy.
Communication overhead: As the previous revocation-based FS-PEKS scheme [4], most of the search counter-based schemes including Kim et al.’s scheme [12] generate multiple search tokens. To be specific, since public and private keys are revoked for each search phase, revocation-based FS-PEKS scheme needs to create multiple search tokens for previous ciphertext, and the size of the token depends on the number of searches made beforehand. Such an overhead becomes devastating as a number of searches are made subsequently. For instance, after 1000 searches, data receiver needs to generate 1000 search tokens. Moreover, the revocation-based approach leads to sending re-encrypted data, incurring an additional communication overhead. Likewise, Kim et al.’s scheme [12] generates a number of search tokens as the search counter increases, shown in Figure 3. Therefore, communication overhead related to the query size depends on the number of search counters. As shown in Table 1, the query size is in our scheme because it requires only a constant number of search tokens regardless of the search counter. However, in Kim et al.’s scheme [12], the number of generated search tokens increases as the search counter increases. Zeng at al,’s scheme, on the other hand, does not adopt counter-based mechanism, but still creates multiple search tokens for the search operations. As shown in Table 1, communication overhead related to query size in Zeng et al.’s scheme depends on the encoded time period. However, unlike the other previous schemes, our scheme only generates a single token regardless of the number of search counters, thus the proposed scheme is more scalable in practice.
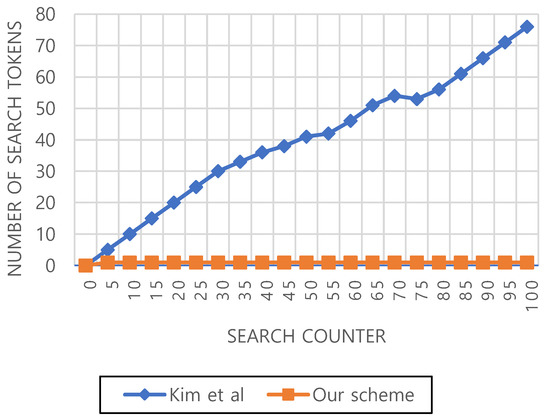
Figure 3.
Communication cost of each scheme.
Overall, the proposed scheme significantly outperforms previous FS-PEKS schemes and achieves better security by exploiting trusted execution environment, specifically Intel SGX in our scheme.
6. Related Work
In this section, we introduce the previous searchable encryption schemes and trusted execution environment (TEE).
6.1. Searchable Encryption
After the first searchable encryption (SE) was proposed by Song et al. [18], SE has been continuously studied to extend its functionality. Generally, the existing SE schemes can be classified into two types: searchable symmetric encryption (SSE) and public key encryption with keyword search (PEKS). By utilizing the symmetric key primitives [18,19,20,21], SSE schemes are generally more efficient than PEKS schemes. However, SSE schemes are not suitable for multiple data sender environments. PEKS schemes, based on the public key primitives [22,23], was first introduced by Boneh et al. [1], and it suits for multiple data sender environment due to the efficient key management. In PEKS schemes, generally, a data sender generates searchable ciphertext with a specific user’s public key. Then, the data receiver creates a search queries and retrieves the data with secret key.
6.2. TEE Based Implementations
Fisch et al. [24] first introduced functional encryption scheme using Intel SGX and formally defined the security model. Since the first adoption of Intel SGX, many studies have been made to construct encryption schemes on Intel SGX platform. Fuhry et al. [13] used Intel SGX to design HardIDX, which is an encrypted database index. The functionality of search operation is implemented inside the enclave, but does not support the update operation. In addition, Zerotrace [25] proposed generic efficient ORAM primitives using Intel SGX, and Oblix [26] was designed for oblivious search. In Oblix, update process is designed to minimize the leakage of access pattern and result size of searches. Harnessing TEE such as Intel SGX as a building block for SE scheme construction is an effective way to increase efficiency and security of the schemes in practice.
7. Conclusions
In this paper, we proposed a public key encryption with keyword search scheme guaranteeing forward privacy using Intel SGX. We formally defined a security model for the proposed TEE-based scheme. Compared with the previous schemes, our scheme shows significantly higher efficiency because the proposed scheme generates a single search token regardless of conditions; while the previous schemes require multiple search tokens. Furthermore, the proposed scheme requires significantly less computation time for creating indices, generating search tokens, and searching processes.
Our scheme considers only a multi-sender environment. Extending our scheme to the multi-receiver environment is another important and challenging issue. In addition, preserving resilience against de-synchronization attack is also an important open problem in most of the cryptographic protocols or algorithms based on shared secret information such as IV (initial vector) or counter information. Since most of the forward secure PEKS schemes are constructed based on counter values, how to make an efficient countermeasure against the de-synchronization attack over the shared counter value is also a challenging topic in the PEKS literature as an important future work.
Author Contributions
Conceptualization, H.Y. and C.H.; methodology, H.Y. and J.H.; validation, H.Y., J.H. and W.L.; formal analysis, H.Y. and C.H.; investigation, H.Y., S.M., and Y.K.; data curation, S.M. and Y.K.; writing—original draft preparation, H.Y.; writing—review and editing, H.Y., C.H., and J.H.; visualization, H.Y., S.M., and Y.K.; supervision, J.H. and W.L.; project administration, H.Y., J.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported as part of Military Crypto Research Center (UD170109ED) funded by Defense Acquisition Program Administration (DAPA) and Agency for Defense Development (ADD).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PEKS | Public Key encryption with keyword search |
| FS-PEKS | Forward Secure PEKS |
| SE | Searchable encryption |
| TEE | Trusted Execution Environment |
| SGX | Software Guard Extension |
| IND-CPA | Indistinguishable under chosen-plaintext attack |
| PKE | Public key encryption |
| SKE | Symmetric key encryption |
| CS | Cloud server |
| DS | Data sender |
| DR | Data receiver |
References
- Boneh, D.; Di Crescenzo, G.; Ostrovsky, R.; Persiano, G. Public key encryption with keyword search. In International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 2004; pp. 506–522. [Google Scholar]
- Zhang, Y.; Katz, J.; Papamanthou, C. All your queries are belong to us: The power of file-injection attacks on searchable encryption. In Proceedings of the 25th {USENIX} Security Symposium ({USENIX} Security 16), Austin, TX, USA, 10–12 August 2016; pp. 707–720. [Google Scholar]
- Bost, R. Σ oφoς: Forward secure searchable encryption. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 1143–1154. [Google Scholar]
- Zhang, X.; Xu, C.; Wang, H.; Zhang, Y.; Wang, S. FS-PEKS: Lattice-based forward secure public-key encryption with keyword search for cloud-assisted industrial Internet of Things. IEEE Trans. Depend. Secur. Comput. 2019. [Google Scholar] [CrossRef]
- Zeng, M.; Qian, H.F.; Chen, J.; Zhang, K. Forward Secure Public Key Encryption with Keyword Search for Outsourced Cloud Storage. IEEE Trans. Cloud Comput. 2019. [Google Scholar] [CrossRef]
- Anati, I.; Gueron, S.; Johnson, S.; Scarlata, V. Innovative technology for CPU based attestation and sealing. In Proceedings of the 2nd International Workshop on Hardware and Architectural Support for Security and Privacy, Tel-Aviv, Israel, 23–24 June 2013; Volume 13, p. 7. [Google Scholar]
- Costan, V.; Devadas, S. Intel SGX Explained. IACR Cryptol. EPrint Arch. 2016, 2016, 1–118. [Google Scholar]
- Hoekstra, M.; Lal, R.; Pappachan, P.; Phegade, V.; Del Cuvillo, J. Using innovative instructions to create trustworthy software solutions. HASP@ ISCA 2013, 11, 2487726–2488370. [Google Scholar]
- Intel, I. Software Guard Extensions Programming Reference, Revision 2. 2014. Available online: https://software.intel.com/sites/default/files/managed/48/88/329298-002.pdf (accessed on 15 September 2020).
- Intel, R. Software Guard Extensions (Intel R SGX). 2018. Available online: https://www.intel.com/content/www/us/en/architecture-and-technology/software-guard-extensions.html (accessed on 15 September 2020).
- Amjad, G.; Kamara, S.; Moataz, T. Forward and backward private searchable encryption with SGX. In Proceedings of the 12th European Workshop on Systems Security, Dresden, Germany, 2–5 March 2019; pp. 1–6. [Google Scholar]
- Hyeongseob Kim, C.H.; Hur, J. Forward Secure Public Key Encryption with Keyword Search for Cloud-assisted IoT. In Proceedings of the 2020 IEEE International Conference on Cloud Computing, Beijing, China, 18–24 October 2020. [Google Scholar]
- Fuhry, B.; Bahmani, R.; Brasser, F.; Hahn, F.; Kerschbaum, F.; Sadeghi, A.R. HardIDX: Practical and secure index with SGX. In IFIP Annual Conference on Data and Applications Security and Privacy; Springer: Berlin/Heidelberg, Germany, 2017; pp. 386–408. [Google Scholar]
- Johnson, S.; Scarlata, V.; Rozas, C.; Brickell, E.; Mckeen, F. Intel® software guard extensions: Epid provisioning and attestation services. White Pap. 2016, 1, 119. [Google Scholar]
- Abdalla, M.; Bellare, M.; Catalano, D.; Kiltz, E.; Kohno, T.; Lange, T.; Malone-Lee, J.; Neven, G.; Paillier, P.; Shi, H. Searchable encryption revisited: Consistency properties, relation to anonymous IBE, and extensions. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2005; pp. 205–222. [Google Scholar]
- Stefanov, E.; Papamanthou, C.; Shi, E. Practical Dynamic Searchable Encryption with Small Leakage. NDSS 2014, 71, 72–75. [Google Scholar]
- Guide, P. Intel® 64 and ia-32 Architectures Software Developer’s Manual. Volume 3B: System Programming Guide Part. 2011, Volume 2, p. 11. Available online: file:///C:/Users/MDPI/AppData/Local/Temp/253669-sdm-vol-3b.pdf (accessed on 15 September 2020).
- Song, D.X.; Wagner, D.; Perrig, A. Practical techniques for searches on encrypted data. In Proceedings of the 2000 IEEE Symposium on Security and Privacy (S&P 2000), Berkeley, CA, USA, 14–17 May 2000; IEEE: Piscataway, NJ, USA, 2000; pp. 44–55. [Google Scholar]
- Curtmola, R.; Garay, J.; Kamara, S.; Ostrovsky, R. Searchable symmetric encryption: Improved definitions and efficient constructions. J. Comput. Secur. 2011, 19, 895–934. [Google Scholar] [CrossRef]
- Islam, M.S.; Kuzu, M.; Kantarcioglu, M. Access pattern disclosure on searchable encryption: Ramification, attack and mitigation. Ndss 2012, 20, 12. [Google Scholar]
- Cash, D.; Jarecki, S.; Jutla, C.; Krawczyk, H.; Roşu, M.C.; Steiner, M. Highly-scalable searchable symmetric encryption with support for boolean queries. In Annual Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2013; pp. 353–373. [Google Scholar]
- Xu, P.; Jin, H.; Wu, Q.; Wang, W. Public-key encryption with fuzzy keyword search: A provably secure scheme under keyword guessing attack. IEEE Trans. Comput. 2012, 62, 2266–2277. [Google Scholar] [CrossRef]
- Bösch, C.; Hartel, P.; Jonker, W.; Peter, A. A survey of provably secure searchable encryption. ACM Comput. Surv. (CSUR) 2014, 47, 1–51. [Google Scholar] [CrossRef]
- Fisch, B.; Vinayagamurthy, D.; Boneh, D.; Gorbunov, S. Iron: Functional encryption using Intel SGX. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 765–782. [Google Scholar]
- Sasy, S.; Gorbunov, S.; Fletcher, C.W. ZeroTrace: Oblivious Memory Primitives from Intel SGX. IACR Cryptol. EPrint Arch. 2017, 2017, 549. [Google Scholar]
- Mishra, P.; Poddar, R.; Chen, J.; Chiesa, A.; Popa, R.A. Oblix: An efficient oblivious search index. In Proceedings of the 2018 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 21–23 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 279–296. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).