Focus-Adjustable Head Mounted Display with Off-Axis System
Abstract
:Featured Application
Abstract
1. Introduction
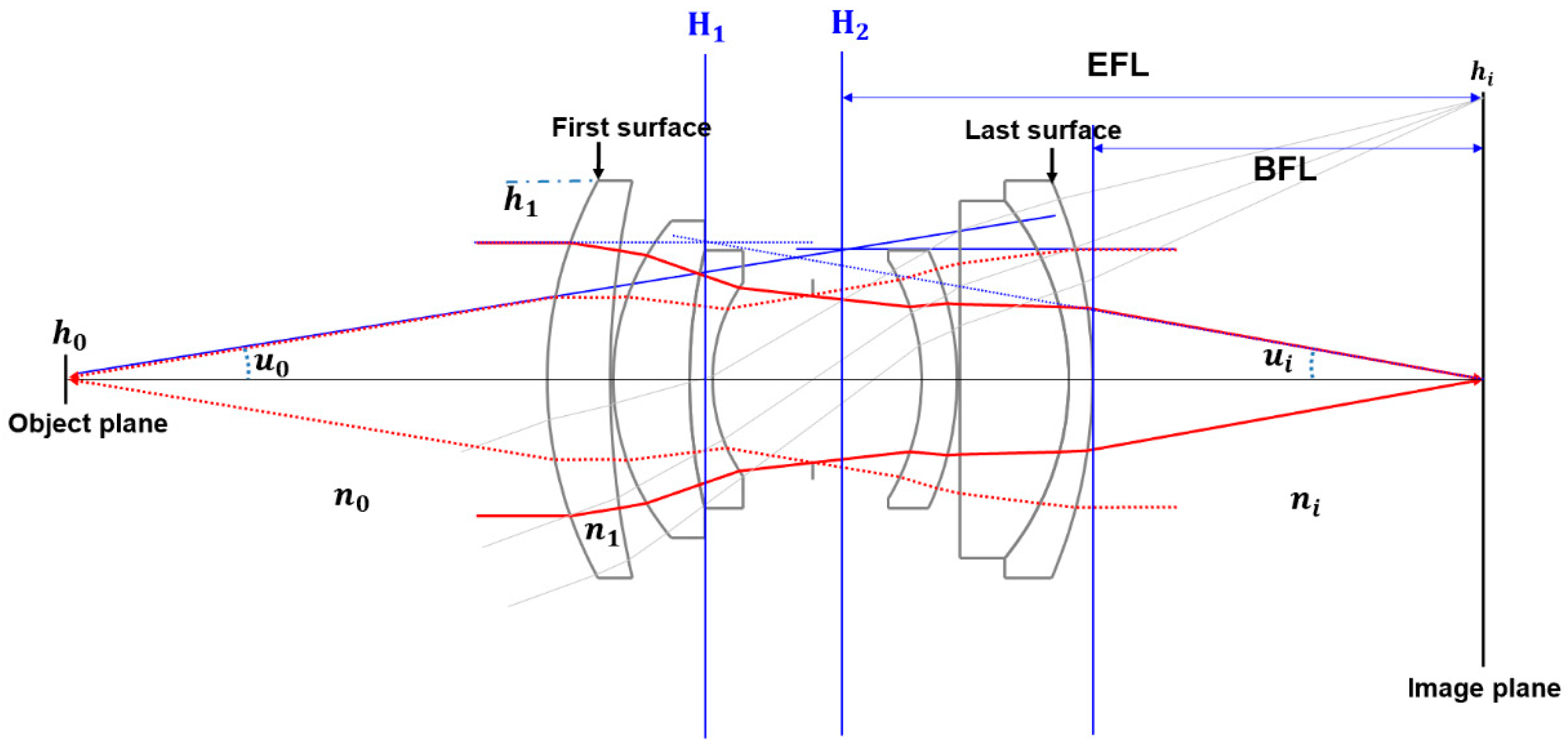
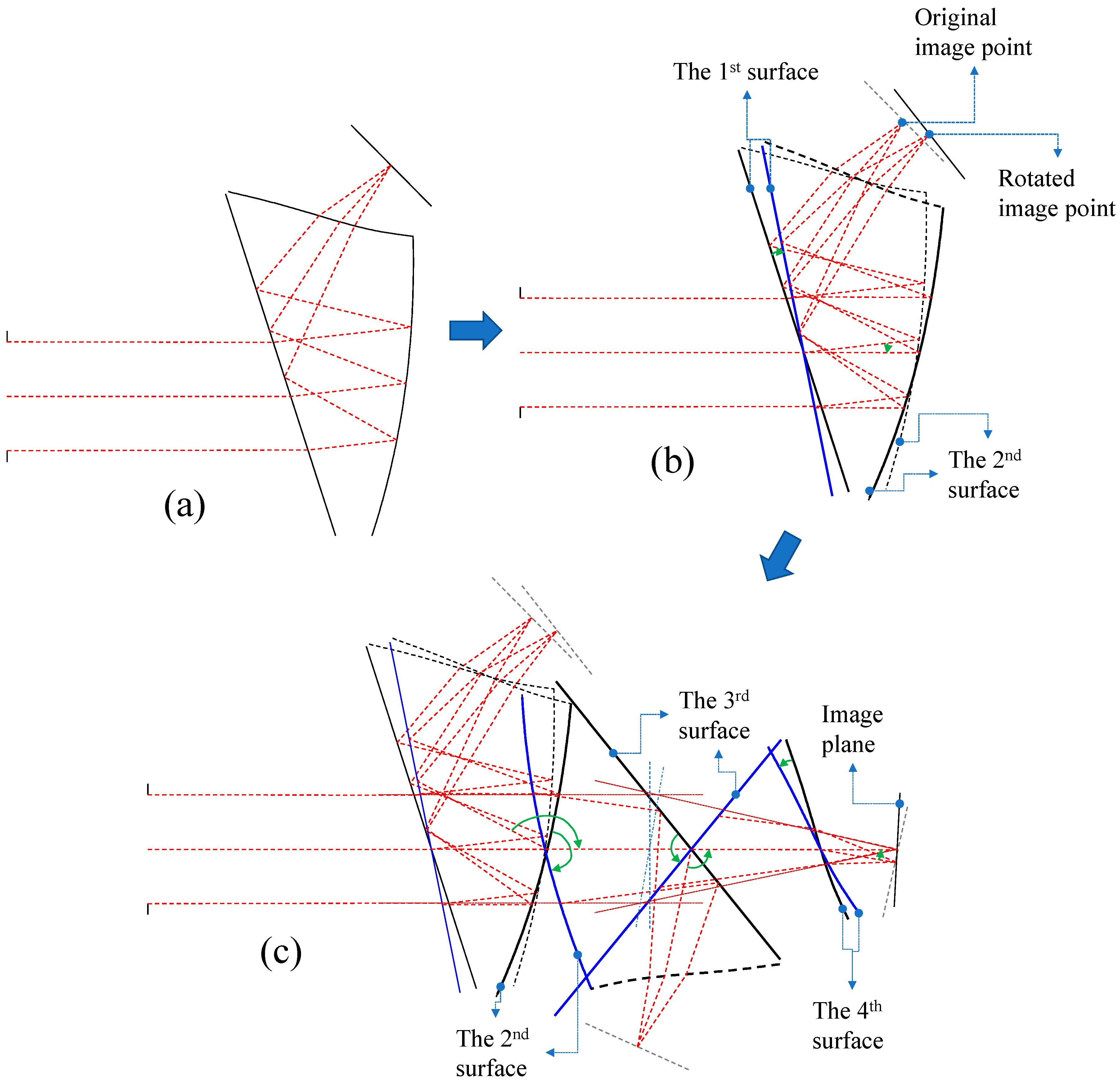
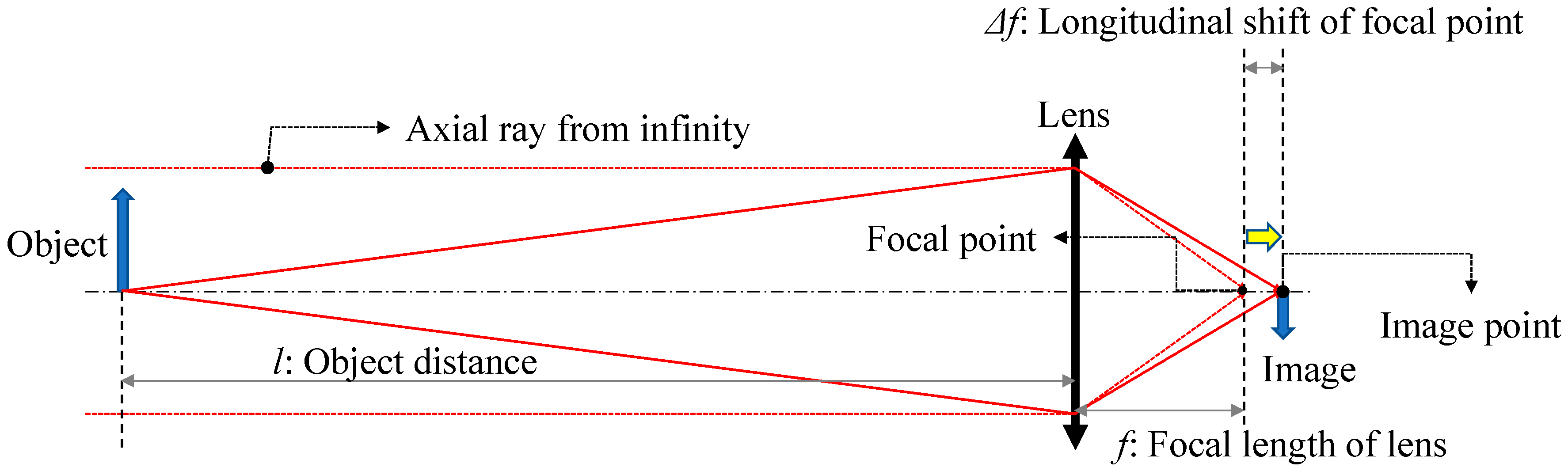
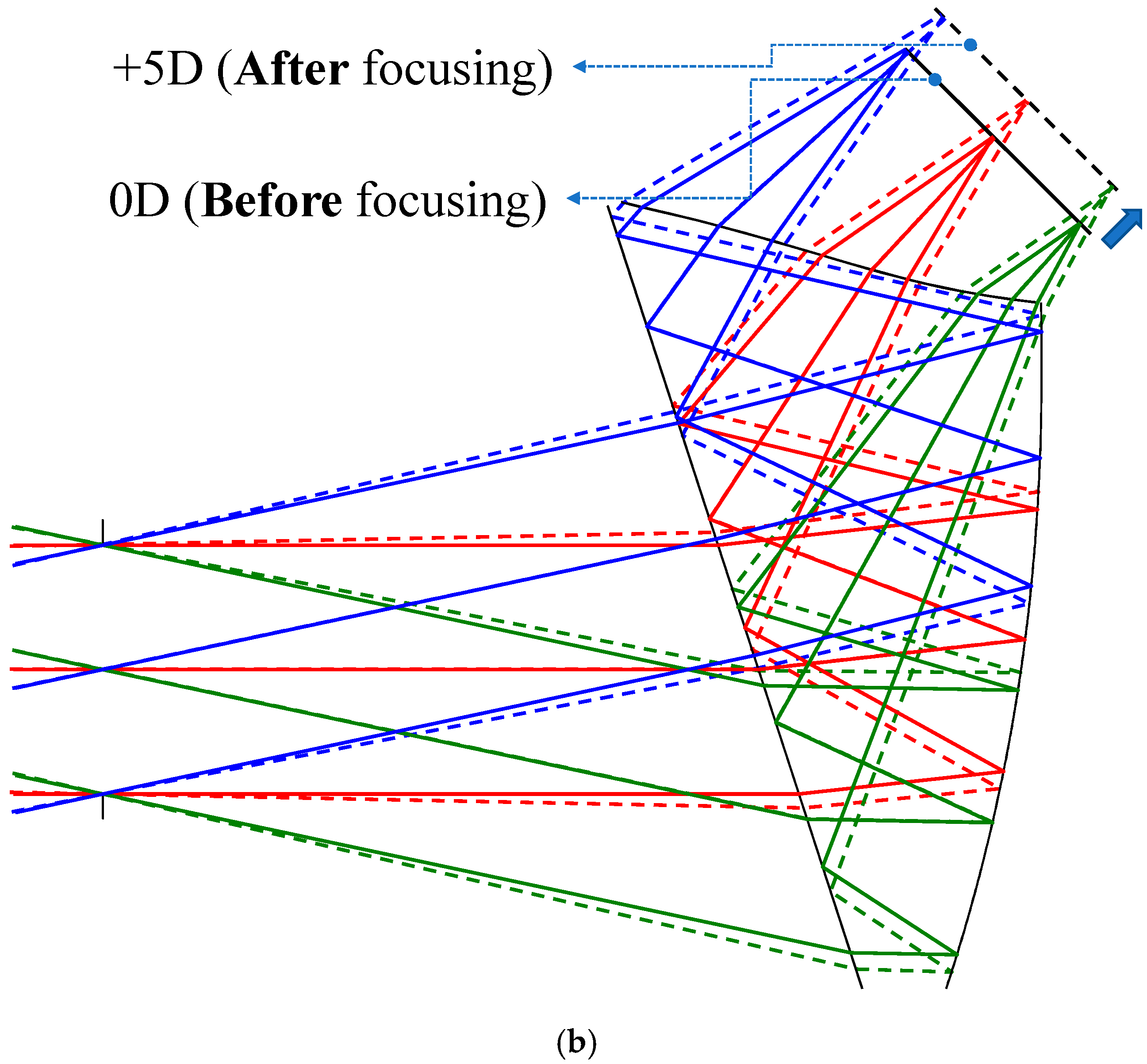
2. Materials and Methods
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bass, M.; Van Stryland, E.W.; Williams, D.R.; Wolfe, W.L. Handbook of Optics; McGraw-Hill Education: New York, NY, USA, 2001. [Google Scholar]
- Kim, K.M.; Choe, S.-H.; Ryu, J.-M.; Choi, H. Computation of analytical zoom locus using padé approximation. Mathematics 2020, 8, 581. [Google Scholar] [CrossRef] [Green Version]
- Ray, S. Applied Photographic Optics; Routledge: Oxfordshire, UK, 2002. [Google Scholar]
- Zappe, H. Fundamentals of Micro-Optics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Ullah, M.; Pratiwi, E.; Park, J.; Lee, K.; Choi, H.; Yeom, J. Wavelength discrimination (wld) tof-pet detector with doi information. Phys. Med. Biol. 2019, 65, 055003. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Li, Y.; Jing, J.; Feng, L.; Zhou, J. Design and fabrication of a compact off-axis see-through head-mounted display using a freeform surface. Opt. Express 2018, 26, 8550–8565. [Google Scholar] [CrossRef] [PubMed]
- Yuki, K. Eyepiece Optical System with Reflective Surface and Electronic Viewfinder Using It. JP2012-093478, 17 May 2012. [Google Scholar]
- Ryu, J.M. Optical System for Head Mount Display. KR 10-2015-0094891, 20 August 2015. [Google Scholar]
- Mahajan, V.N. Optical Imaging and Aberrations: Ray Geometrical Optics; SPIE Press: Washington, WA, USA, 1998. [Google Scholar]
- Araki, K. Analysis of off-axial optical systems (1). Opt. Rev. 2000, 7, 221–229. [Google Scholar] [CrossRef]
- Choi, H.; Yeom, J.-Y.; Ryu, J.-M. Development of a multiwavelength visible-range-supported opto–ultrasound instrument using a light-emitting diode and ultrasound transducer. Sensors 2018, 18, 3324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Iga, K.; Kokubun, Y. Encyclopedic Handbook of Integrated Optics; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Choi, H.; Ryu, J.-M.; Choe, S.-W. A novel therapeutic instrument using an ultrasound-light-emitting diode with an adjustable telephoto lens for suppression of tumor cell proliferation. Measurement 2019, 147, 106865. [Google Scholar] [CrossRef]
- Klingshirn, C.F. Semiconductor Optics; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Choi, H.; Jo, J.-Y.; Ryu, J.-M. A novel focal length measurement method for center-obstructed omni-directional reflective optical systems. Appl. Sci. 2019, 9, 2350. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Liang, Y.; Xu, M. Design of a see-through head-mounted display with a freeform surface. J. Opt. Soc. Korea 2015, 19, 614–618. [Google Scholar] [CrossRef] [Green Version]
- Cakmakci, O.; Rolland, J. Head-worn displays: A review. J. Disp. Technol. 2006, 2, 199–216. [Google Scholar] [CrossRef]
- Kress, B.; Starner, T. A Review of Head-Mounted Displays (HMD) Technologies and Applications for Consumer Electronics; Proc. SPIE: Baltimore, MA, USA, 2013; p. 87200A. [Google Scholar]
- Lee, S.J. HMD technology status and challenges. Broadcast Media 2007, 12, 93–99. (In Korean) [Google Scholar]
- Choi, H.; Ryu, J.; Yoon, C. Development of novel adjustable focus head mount display for concurrent image-guided treatment applications. Comput. Assisted Surg. 2017, 22, 163–169. [Google Scholar] [CrossRef]
- Lim, S.; Seo, K. AR/VR Technology Kistep Technology Trend Brief; Korea Institute of S&T Evaluation and Planing: Seoul, Korea, 2018. [Google Scholar]
- Choi, H.; Kim, S.; Kim, J.; Ryu, J.-M. Development of an omnidirectional optical system based photoacoustic instrumentation. J. Med. Imaging Health Inf. 2018, 8, 20–27. [Google Scholar] [CrossRef]
- Choi, H.; Ryu, J.M.; Kim, J.H. Tolerance analysis of focus-adjustable head-mounted displays. Curr. Opt. Photon 2017, 1, 474–490. [Google Scholar]
- Choi, H.; Ryu, J.; Yeom, J.-Y. A cost-effective light emitting diode-acoustic system for preclinical ocular applications. Curr. Opt. Photon 2018, 2, 59–68. [Google Scholar]
- J. H. Cho, J.M.R. The Basics and Application of Lens Design as Understood by the Lens Design Program; Cheonmungak Publisher: Seoul, Korea, 2013. [Google Scholar]
- Choe, S.-W.; Park, K.; Park, C.; Ryu, J.; Choi, H. Combinational light emitting diode-high frequency focused ultrasound treatment for hela cell. Comput. Assist. Surg. 2017, 22, 79–85. [Google Scholar] [CrossRef] [Green Version]
- Burdea, G.C.; Coiffet, P. Virtual Reality Technology; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Mordekhai, V. Helmet-Mounted Displays and Sights; Artech House: London, UK, 1998. [Google Scholar]
- Codev, Version 11.2 Reference Manual. Available online: https://wp.Optics.Arizona.Edu/jsasian/wp-content/uploads/sites/33/2016/02/code_v_uofaopti517newstudentorientation.pdf (accessed on 26 June 2020).
- Choi, H.; Ryu, J.; Kim, J. A novel fisheye-lens-based photoacoustic system. Sensors 2016, 16, 2185. [Google Scholar] [CrossRef] [PubMed]
- Hecht, E.; Zajac, A. Optics; Addison Wesley: Boston, MA, USA, 1974; pp. 301–305. [Google Scholar]
- Choi, H.; Ryu, J. Design of wide angle and large aperture optical system with inner focus for compact system camera applications. Appl. Sci. 2019, 10, 179. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.V.; Wu, H.-I. Biomedical Optics: Principles and Imaging; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Choi, H.; Choe, S.-W.; Ryu, J.-M. A macro lens-based optical system design for phototherapeutic instrumentation. Sensors 2019, 19, 5427. [Google Scholar] [CrossRef] [Green Version]
- Choi, H.; Ryu, J.-M.; Yeom, J.-Y. Development of a double-gauss lens based setup for optoacoustic applications. Sensors 2017, 17, 496. [Google Scholar] [CrossRef] [Green Version]
- Pedrotti, F.L.; Pedrotti, L.S. Introduction to Optics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993; Volume 2. [Google Scholar]
- Choi, H.; Jo, J.; Ryu, J.-M.; Yeom, J.-Y. Ultrawide-angle optical system design for light-emitting-diode-based ophthalmology and dermatology applications. Technol. Health Care 2019, 27, 133–142. [Google Scholar] [CrossRef] [Green Version]
- Lin, P.D. Advanced Geometrical Optics; Springer: Berlin, Germany, 2017. [Google Scholar]
- Choi, H.; Ju, Y.J.; Jo, J.H.; Ryu, J.-M. Chromatic aberration free reflective mirror-based optical system design for multispectral photoacoustic instruments. Technol. Health Care 2019, 27, 397–406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Choi, H.; Jeong, J.J.; Kim, J. Development of an estimation instrument of acoustic lens properties for medical ultrasound transducers. J. Healthcare Eng. 2017, 2017, 6580217. [Google Scholar] [CrossRef] [Green Version]
- Welford, W.T. Aberrations of Optical Systems; CRC Press: Boca Ration, FL, USA, 1986. [Google Scholar]
- Herzberger, M. Gaussian optics and gaussian brackets. J. Opt. Soc. Am. 1943, 33, 651–655. [Google Scholar] [CrossRef]
- Riaz, H.; Park, J.; Choi, H.; Kim, H.; Kim, J. Deep and densely connected networks for classification of diabetic retinopathy. Diagnostics 2020, 10, 24. [Google Scholar] [CrossRef] [Green Version]
- Ullah, M.N.; Park, C.; Pratiwi, E.; Kim, C.; Choi, H.; Yeom, J.-Y. A new positron-gamma discriminating phoswich detector based on wavelength discrimination (WLD). Nucl. Instrum. Methods Phys. Res. Sect. A 2019, 946, 162631. [Google Scholar] [CrossRef]
- Sharma, K.K. Optics: Principles and Applications; Academic Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Choi, H.; Ryu, J.-M. Photo-acoustic applications using a highly focused macro lens. J. Med. Imaging Health Inf. 2017, 7, 25–29. [Google Scholar] [CrossRef]
- Schäfer, W.; Wegener, M. Semiconductor Optics and Transport Phenomena; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]




| HMY | UMY | HCY | UCY | Rotation Angle (°) | |
|---|---|---|---|---|---|
| STO | 4.00000 | −0.00200 | 0.00000 | 0.21256 | 0.00000 |
| 2 | 4.07905 | −0.00127 | 4.30023 | 0.13571 | 6.35697 |
| 3 | −4.00114 | 0.13132 | −5.61107 | 0.04270 | 152.69759 |
| 4 | 2.46681 | −0.13133 | 5.04222 | −0.04271 | −102.10941 |
| 5 | 1.43497 | −0.21807 | 4.55093 | −0.08075 | −9.82334 |
| IMG | 0.04677 | −0.21807 | 3.89760 | −0.08075 | 0.00000 |
| EFL(Marginal ray) | 18.34265 | ||||
| EFL(Chief ray) | 18.33674 | ||||
| EFL(System matrix) | 18.82512 | ||||
| BFL(Marginal ray) | 6.58027 | ||||
| H1 to S1 | −5.74583 | ||||
| Si-1 to H2 | −12.07202 | ||||
| Object Distance | +1 D | −2 D | −4 D | ∞ (0 D) |
|---|---|---|---|---|
| ∆f(theory) | 0.372280 | 0.673348 | 1.265977 | 0 |
| ∆f (optimization) | 0.284736 | 0.579862 | 1.173932 | 0 |
| error | 0.087544 | 0.093486 | 0.092045 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, S.H.; Ryu, J.M.; Choi, H. Focus-Adjustable Head Mounted Display with Off-Axis System. Appl. Sci. 2020, 10, 7931. https://doi.org/10.3390/app10217931
Seo SH, Ryu JM, Choi H. Focus-Adjustable Head Mounted Display with Off-Axis System. Applied Sciences. 2020; 10(21):7931. https://doi.org/10.3390/app10217931
Chicago/Turabian StyleSeo, So Hyun, Jae Myung Ryu, and Hojong Choi. 2020. "Focus-Adjustable Head Mounted Display with Off-Axis System" Applied Sciences 10, no. 21: 7931. https://doi.org/10.3390/app10217931
APA StyleSeo, S. H., Ryu, J. M., & Choi, H. (2020). Focus-Adjustable Head Mounted Display with Off-Axis System. Applied Sciences, 10(21), 7931. https://doi.org/10.3390/app10217931





