Modular System-Level Modeling Method for the Susceptibility Prediction of Balise Information Transmission System
Abstract
:1. Introduction
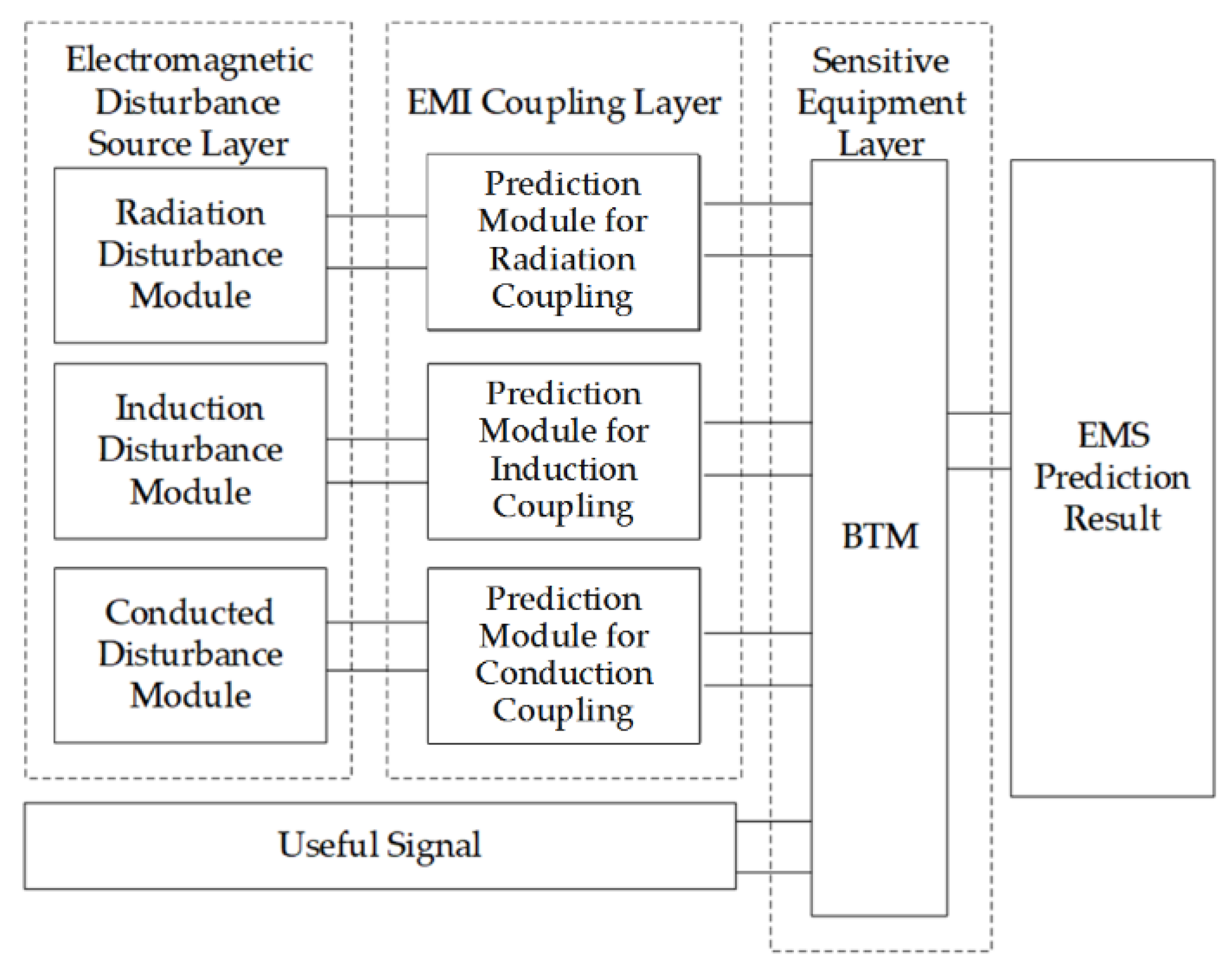
2. Modular System-Level Modeling Approach
2.1. Modular System-Level Model
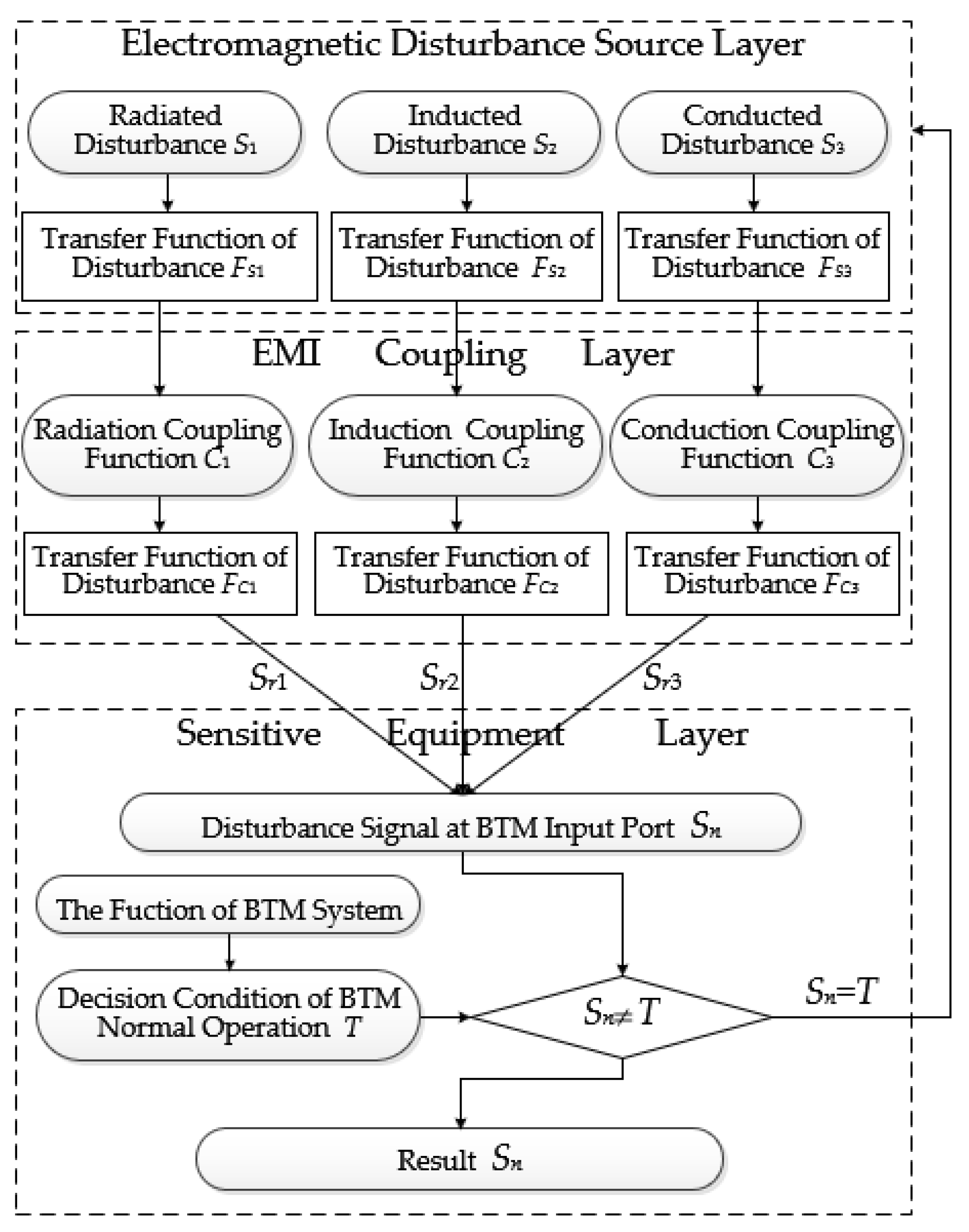
2.2. Prediction Procedure
2.3. Model for BTM Susceptibility Prediction
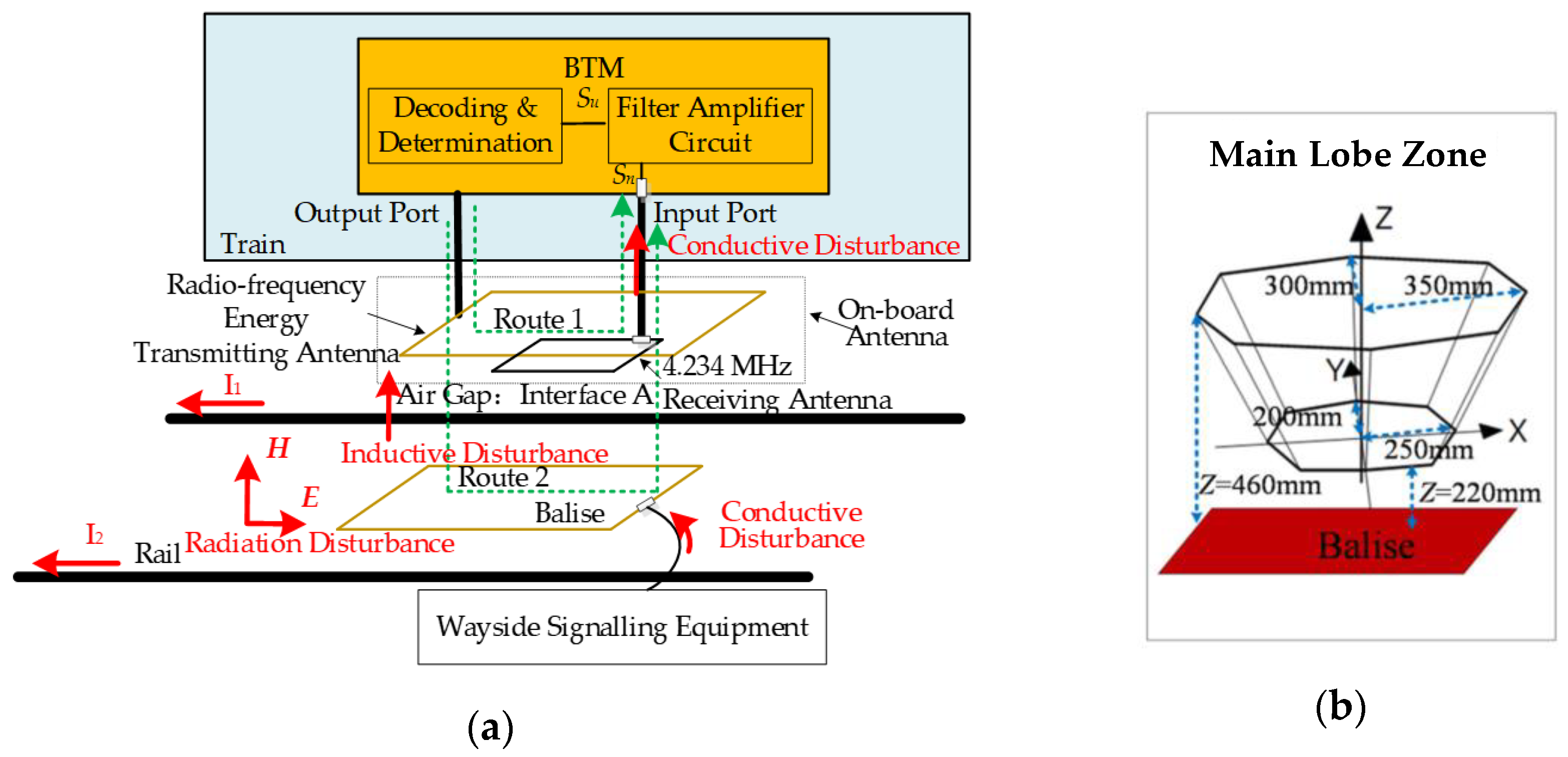
3. Modular Modeling for BTM System
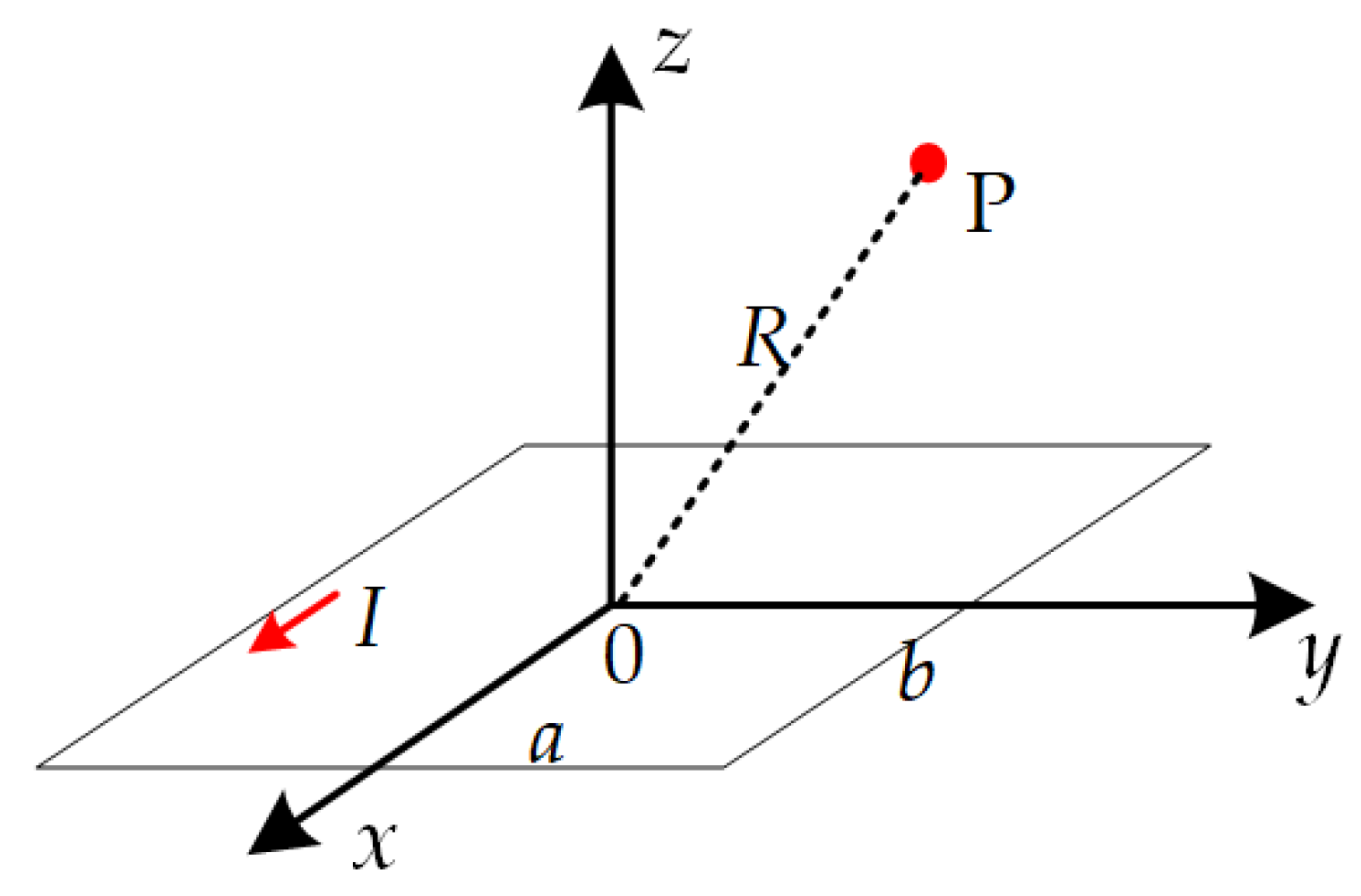
3.1. Modeling for Induction Disturbance Source Module
3.2. Modeling for Inductive Coupling Module
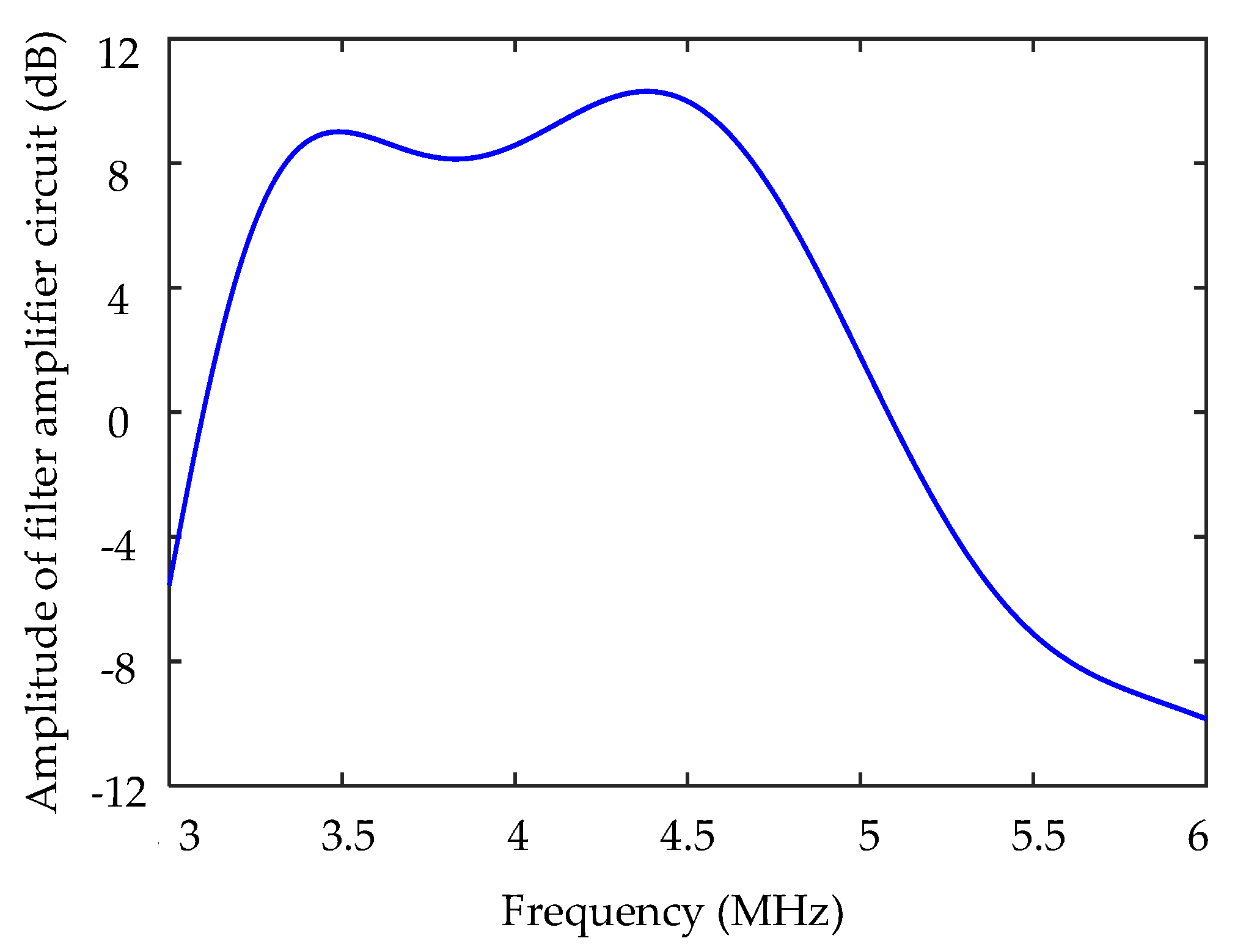
3.3. Modeling of Sensitive Equipment Module
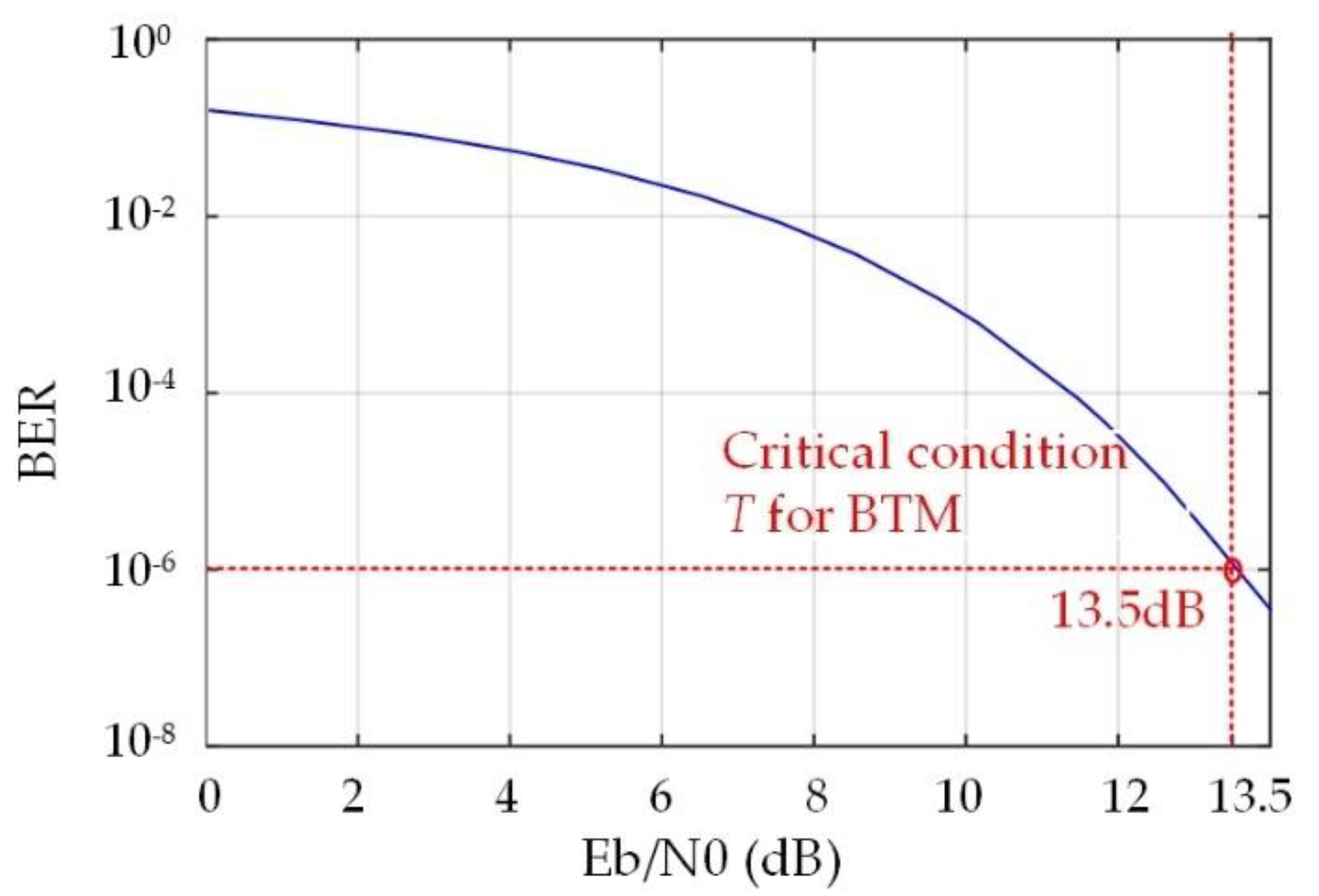
3.3.1. T for BTM System with F2
3.3.2. T for BTM System with F1 or F3
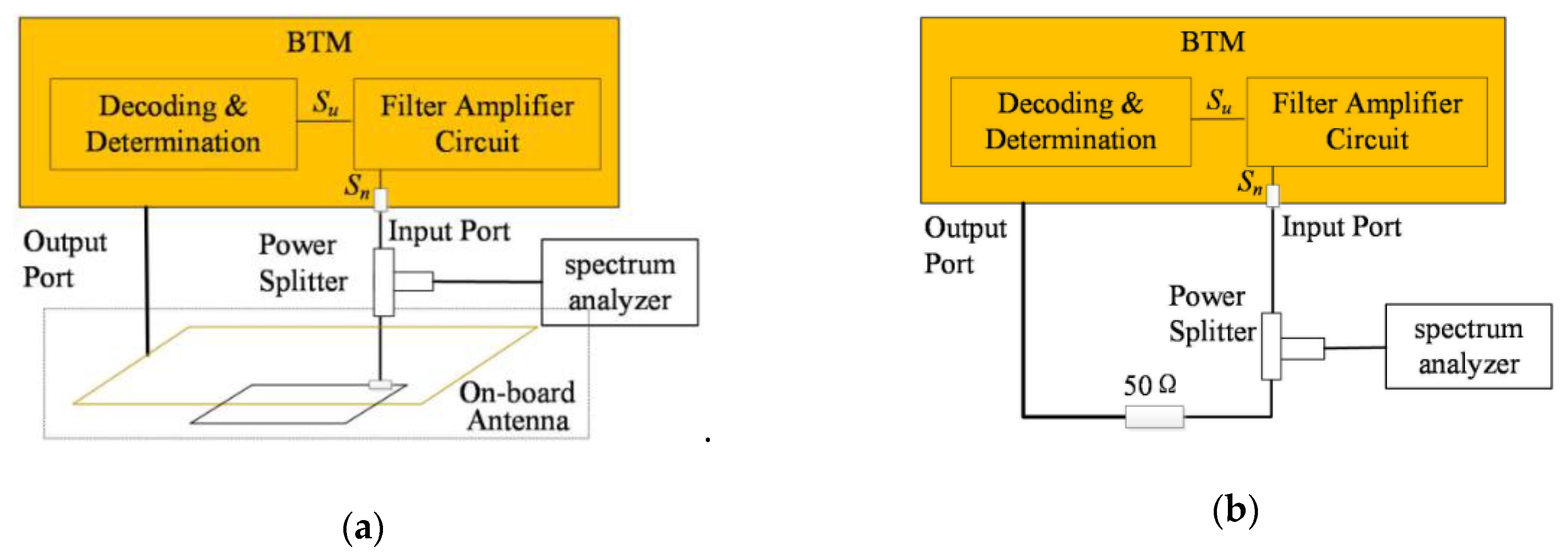
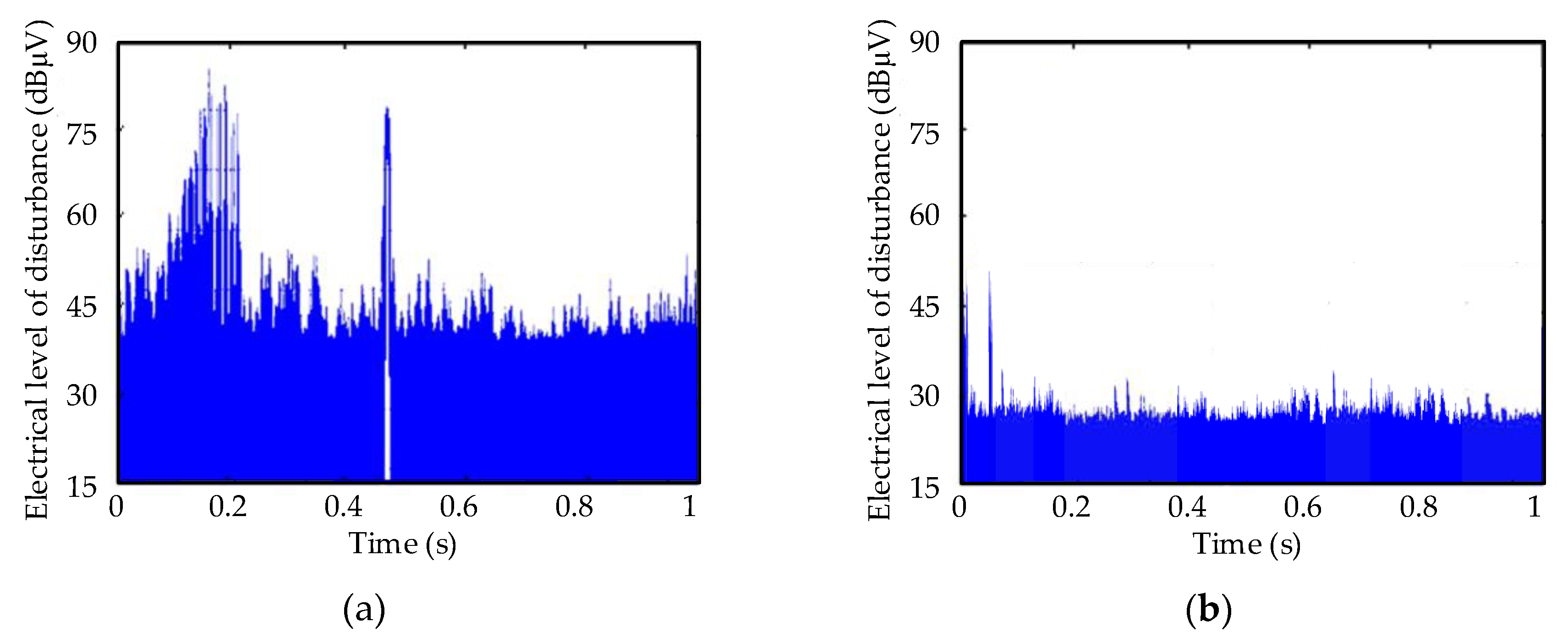
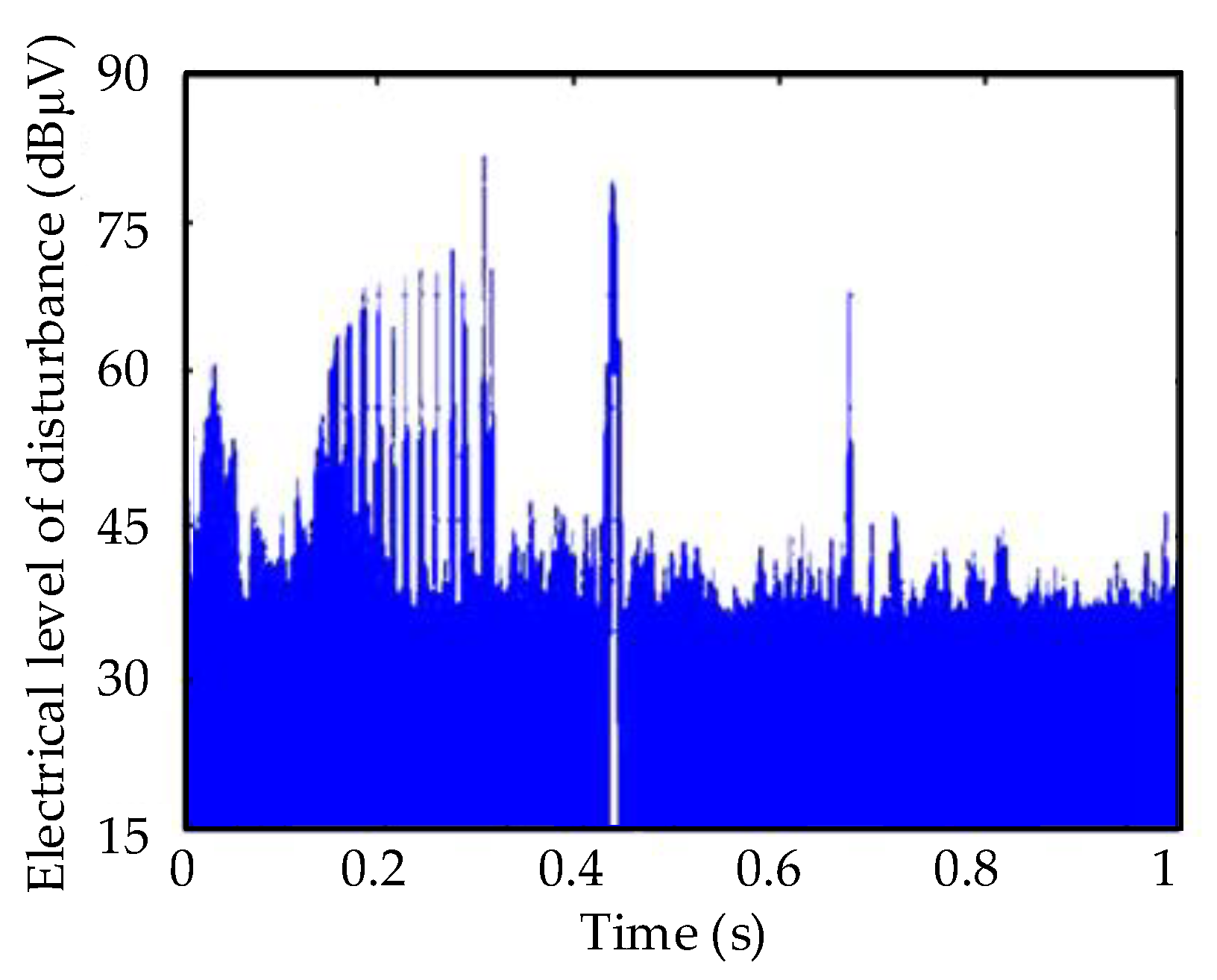
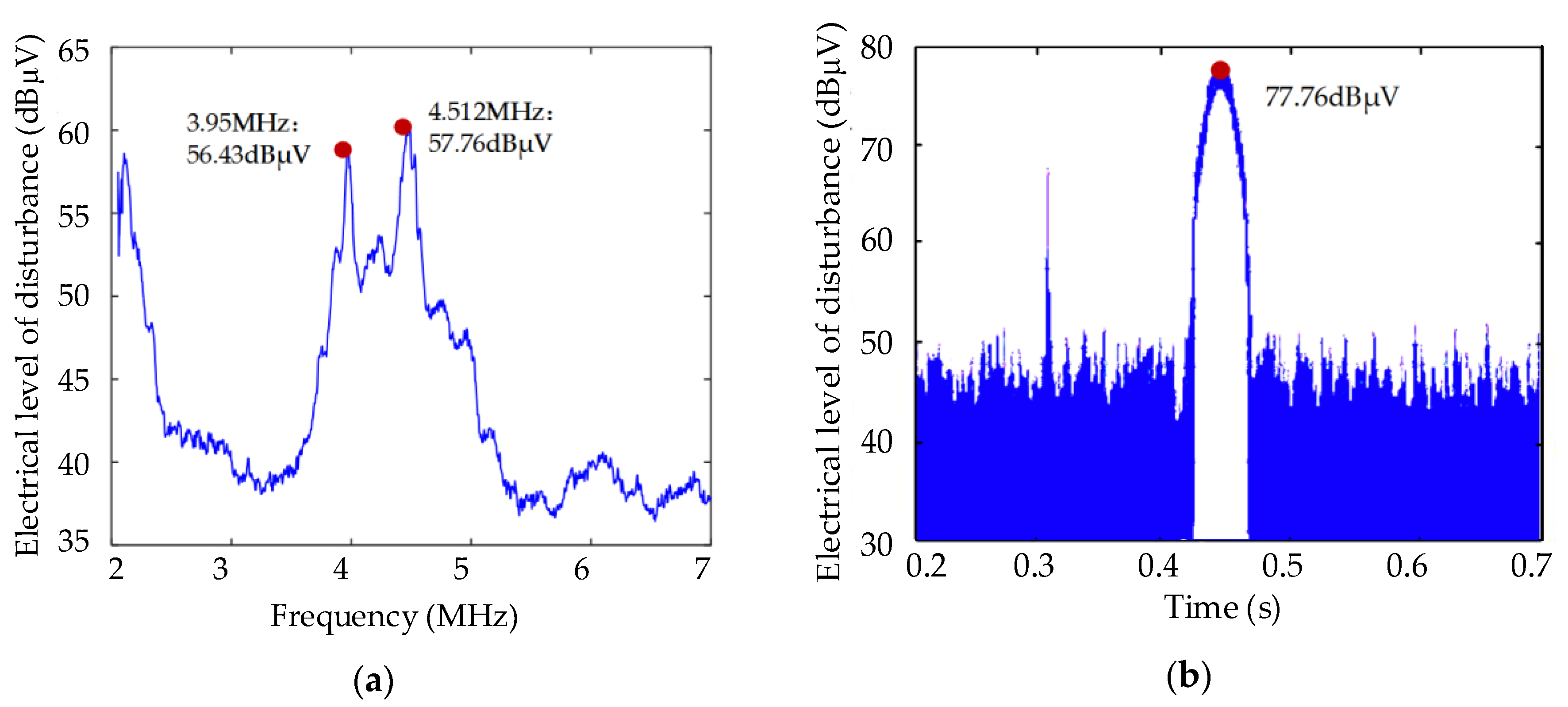
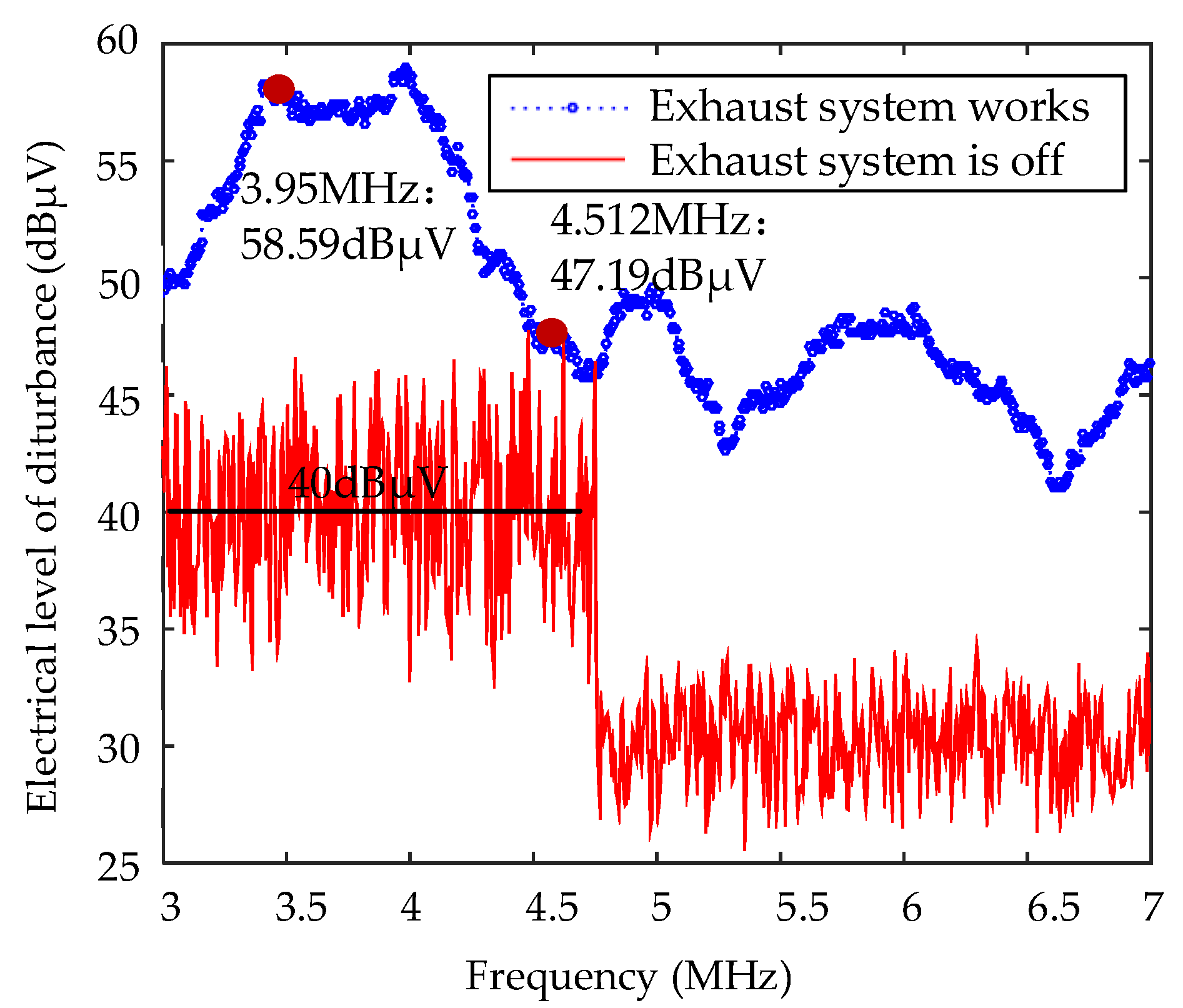
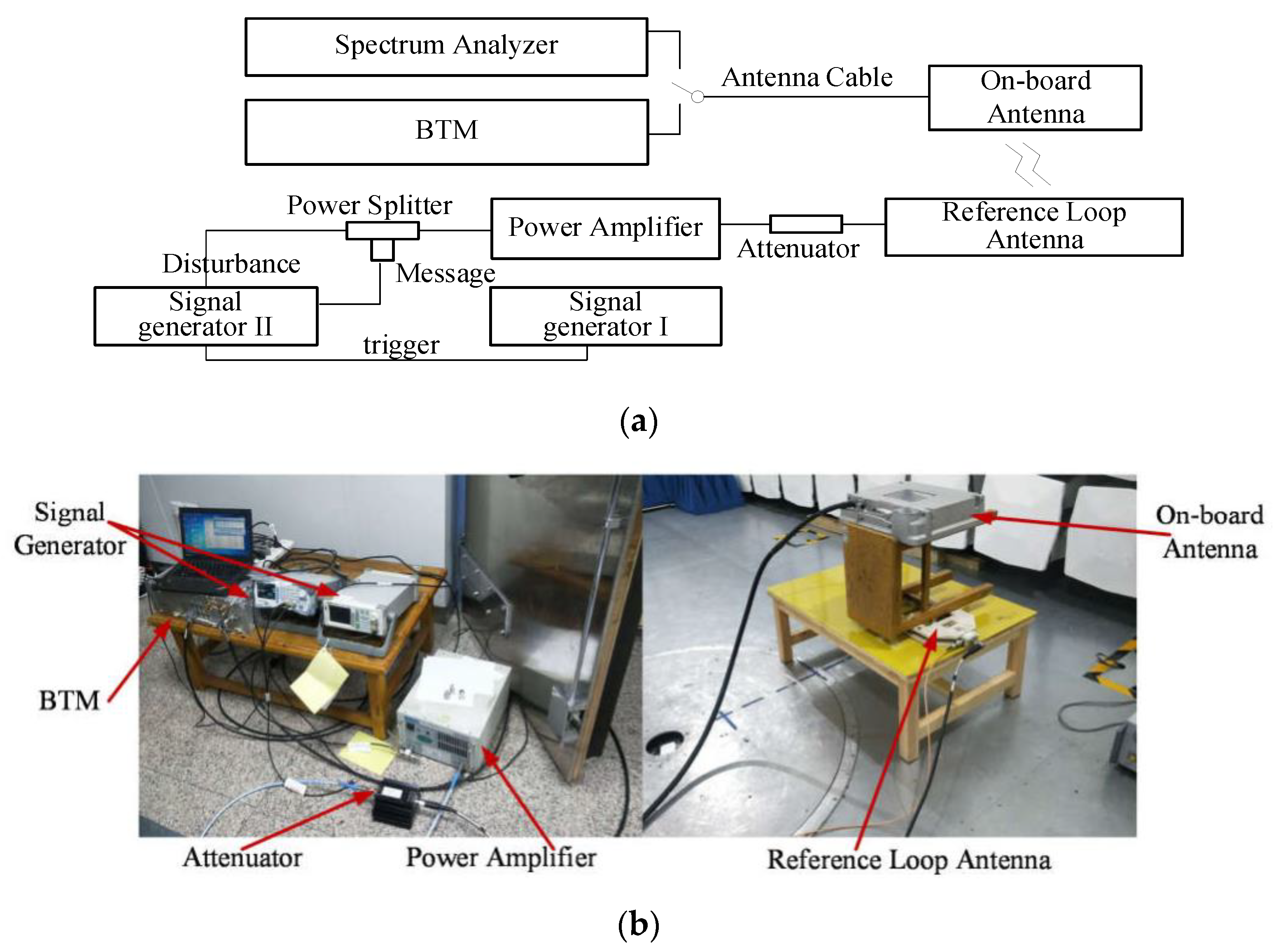
4. Analysis and Validation
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Wu, Y.; Weng, J.; Tang, Z.; Li, X.; Deng, R.H. Vulnerabilities, Attacks, and Countermeasures in Balise-Based Train Control Systems. IEEE Trans. Intell. Transp. Syst. 2016, 18, 814–823. [Google Scholar] [CrossRef]
- Sharma, R.; Lourde, M.R. Crosstalk Reduction in Balise and Infill Loops in Automatic Train Control. In Proceedings of the 2nd International Workshop on Advances in Sensors and Interface, Bari, Italy, 26–27 June 2007. [Google Scholar]
- Wang, T.; Zhao, L.-H. Modeling and optimization for balise coupling process in high speed railway. In Proceedings of the 7th IEEE International Symposium on Microwave, Antenna, Propagation, and EMC Technologies (MAPE), Xi‘an, China, 24–27 October 2017; pp. 176–179. [Google Scholar]
- Guo, Y.; Zhang, J. Analysis of electromagnetic compatibility of EMU on-board BTM equipment. J. China Railw. Soc. 2016, 38, 75–79. [Google Scholar]
- Meng, Y.; Zhao, H.; Liang, D. Research on Eletromagnetic Interference of Ballast-less Track Slab to the Transmission of Balise. In Proceedings of the IEEE Conference Electronic Control and Automatic Engineering (ECAE 2013), Hongkong, China, 1–2 December 2013; pp. 198–203. [Google Scholar]
- Mendizabal, J.; Solas, G.; Valdivia, L.J.; De Miguel, G.; Uranga, J.; Adin, I. ETCS’s Eurobalise-BTM and Euroloop-LTM Airgap Noise and Interferences Review. In Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9669, pp. 27–39. [Google Scholar]
- UNISIG. SUBSET-036: FFFIS for Eurobalise 3.0.0; UNISIG: Brussels, Belgium, 2012. [Google Scholar]
- UNISIG. SUBSET-085: Test Specification for Eurobalise FFFIS V3.0.0; UNISIG: Brussels, Belgium, 2012. [Google Scholar]
- UNISIG. SUBSET-116 Eurobalise On-Board Equipment, Susceptibility Test Specification 1.1.0; Draft; UNISIG: Brussels, Belgium, 2016. [Google Scholar]
- Adin, I.; Mendizabal, J.; Arrizabalaga, S.; Alvarado, U.; Solas, G.; Rodriguez, J. Rolling stock emission testing methodology assessment for Balise Transmission Module system interoperability. Measurement 2016, 77, 124–131. [Google Scholar] [CrossRef]
- Balghiti, Y.; Meyniel, B.; Orion, J.; Maumy, F.; Francois, E.; Besnier, P.; Drissi, M. Proposal of a specific test methodology to assess the radiated behavior of a data transmission from beacon to train. In Proceedings of the 20th International Zurich Symposium on Electromagnetic Compatibility, Zurich, Switzerland, 12–16 January 2009; pp. 433–436. [Google Scholar]
- Yuan, W.; Li, E.-P. A Systematic Coupled Approach for Electromagnetic Susceptibility Analysis of a Shielded Device with Multilayer Circuitry. IEEE Trans. Electromagn. Compat. 2005, 47, 692–700. [Google Scholar] [CrossRef]
- Fiori, F. Susceptibility of Smart Power ICs to Radio Frequency Interference. IEEE Trans. Power Electron. 2013, 29, 2787–2797. [Google Scholar] [CrossRef]
- Mehri, M.; Masoumi, N. Statistical Prediction and Quantification of Radiated Susceptibility for Electronic Systems PCB in Electromagnetic Polluted Environments. IEEE Trans. Electromagn. Compat. 2016, 59, 498–508. [Google Scholar] [CrossRef]
- Parmantier, J.-P. Numerical Coupling Models for Complex Systems and Results. IEEE Trans. Electromagn. Compat. 2004, 46, 359–367. [Google Scholar] [CrossRef]
- Peikert, T.; Garbe, H.; Potthast, S. Fuzzy-Based Risk Analysis for IT-Systems and Their Infrastructure. IEEE Trans. Electromagn. Compat. 2017, 59, 1294–1301. [Google Scholar] [CrossRef] [Green Version]
- Xiao, P.; Du, P.-A.; Ren, D.; Nie, B.-L. A Hybrid Method for Calculating the Coupling to PCB Inside a Nested Shielding Enclosure Based on Electromagnetic Topology. IEEE Trans. Electromagn. Compat. 2016, 58, 1701–1709. [Google Scholar] [CrossRef]
- Freeman, L.S.; Wu, T. Method for Derivation and Synthesis of Conducted Susceptibility Limits for System-Level EMC. IEEE Trans. Electromagn. Compat. 2015, 58, 4–10. [Google Scholar] [CrossRef]
- Yuan, X.-B.; Cai, B.; Ma, Y.; Zhang, J.; Mulenga, K.; Liu, Y.; Chen, G.; Yonghong, Y. Reliability Evaluation Methodology of Complex Systems Based on Dynamic Object-Oriented Bayesian Networks. IEEE Access 2018, 6, 11289–11300. [Google Scholar] [CrossRef]
- Genender, E.; Garbe, H.; Sabath, F. Probabilistic Risk Analysis Technique of Intentional Electromagnetic Interference at System Level. IEEE Trans. Electromagn. Compat. 2013, 56, 200–207. [Google Scholar] [CrossRef]
- Huang, Y.-S.; Weng, Y.-S.; Zhou, M. Modular Design of Urban Traffic-Light Control Systems Based on Synchronized Timed Petri Nets. IEEE Trans. Intell. Transp. Syst. 2013, 15, 530–539. [Google Scholar] [CrossRef]
- Li, M.; Wen, Y.; Zhang, J.; Zhang, D. An EMC safety assessment model to analyze complex system in high speed railways. In Proceedings of the 2017 International Conference on Electromagnetics in Advanced Applications (ICEAA), Verona, Italy, 11–15 September 2017; pp. 626–629. [Google Scholar]
- Midya, S.; Thottappillil, R. An overview of electromagnetic compatibility challenges in European Rail Traffic Management System. Transp. Res. Part C Emerg. Technol. 2008, 16, 515–534. [Google Scholar] [CrossRef]
- Hayt, W.H.; Buck, J.A. The Steady Magnetic Field. In Engineering Electromagnetics; McGraw-Hill: New York, NY, USA, 2010; pp. 180–188. [Google Scholar]
- Alexander, C.; Sadiku, M. Basic Laws in Fundamentals of Electric Circuits, 5th ed.; McGraw-Hill: New York, NY, USA, 2011; pp. 30–80. [Google Scholar]
- Ma, L.; Wen, Y.; Marvin, A.; Karadimou, E.; Armstrong, R.; Cao, H. A Novel Method for Calculating the Radiated Disturbance from Pantograph Arcing in High-Speed Railway. IEEE Trans. Veh. Technol. 2017, 66, 8734–8745. [Google Scholar] [CrossRef] [Green Version]
- Haykin, S. Passband Digital Transmission in Communication System, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2001; pp. 344–479. [Google Scholar]
- Phillips, C.L.; Parr, J.M.; Riskin, E.A. Continuous-Time linear Time-Invariant System in Signals, Systems, and Transforms, 4th ed.; Pearson Education: London, UK, 2007; pp. 89–150. [Google Scholar]
- Grivet-Talocia, S.; Gustavsen, B. Black-box Macromodeling and its EMC Applications. IEEE Electromagn. Compat. Mag. 2016, 5, 71–78. [Google Scholar] [CrossRef]








| No. | Function | Consequence |
|---|---|---|
| F1 | On-line Transmission Self-test | The interference effect could lead to temporary failures of the self-test with harmful consequences to operational reliability. |
| F2 | Balise Detection Function | The interference effect would likely lead to a “false Balise detection” with harmful consequences to the operational reliability. |
| F3 | Data Reception Function | The interference effect could lead to unrecognizable Balise telegrams with harmful consequences to operational reliability. |
| Object | Properties |
|---|---|
| Cable |
|
| Antenna |
|
| Aperture |
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Wen, Y.; Zhang, J.; Xiao, J.; Song, Y.; Geng, Q. Modular System-Level Modeling Method for the Susceptibility Prediction of Balise Information Transmission System. Appl. Sci. 2020, 10, 7944. https://doi.org/10.3390/app10217944
Zhang D, Wen Y, Zhang J, Xiao J, Song Y, Geng Q. Modular System-Level Modeling Method for the Susceptibility Prediction of Balise Information Transmission System. Applied Sciences. 2020; 10(21):7944. https://doi.org/10.3390/app10217944
Chicago/Turabian StyleZhang, Dan, Yinghong Wen, Jinbao Zhang, Jianjun Xiao, Yali Song, and Qi Geng. 2020. "Modular System-Level Modeling Method for the Susceptibility Prediction of Balise Information Transmission System" Applied Sciences 10, no. 21: 7944. https://doi.org/10.3390/app10217944
APA StyleZhang, D., Wen, Y., Zhang, J., Xiao, J., Song, Y., & Geng, Q. (2020). Modular System-Level Modeling Method for the Susceptibility Prediction of Balise Information Transmission System. Applied Sciences, 10(21), 7944. https://doi.org/10.3390/app10217944







