A Study on Data Pre-Processing and Accident Prediction Modelling for Occupational Accident Analysis in the Construction Industry
Abstract
1. Introduction
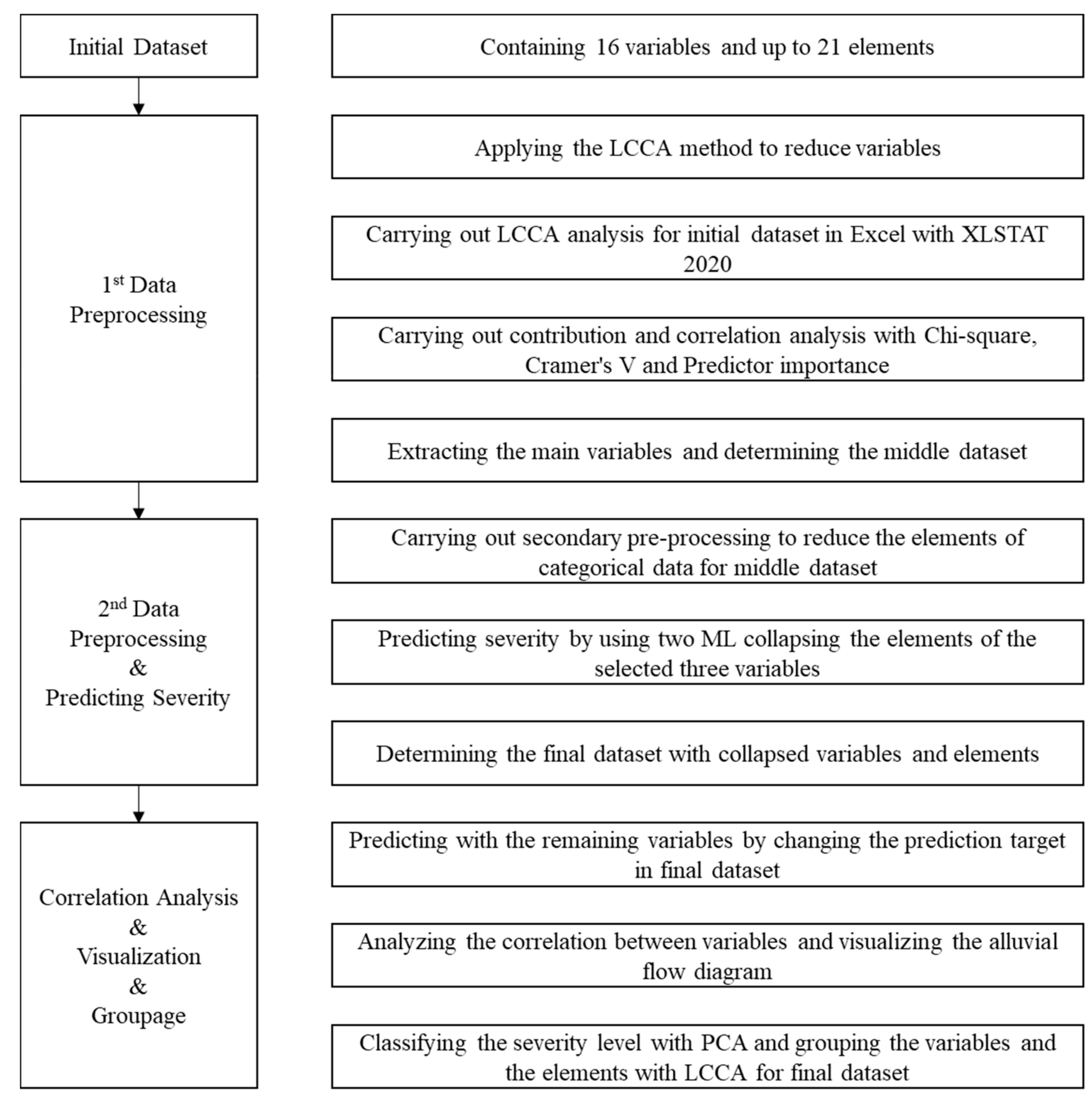
2. Materials and Methods
2.1. Initial Data and Data Description
2.2. Data Preprocessing
2.2.1. Latent Class Cluster Analysis (LCCA)
2.2.2. Chi-Square Test
2.2.3. Cramer’s V test
2.3. Machine Learning (ML)
2.3.1. Support Vector Machine (SVM)
2.3.2. Ensemble
2.4. Principal Component Analysis (PCA)
3. Results and Analysis
3.1. First Data Preprocessing for Selection of Major Variables
3.2. Second Data Preprocessing for Reduction of Elements
3.3. Prediction of Various Dependent Variables
4. Discussion
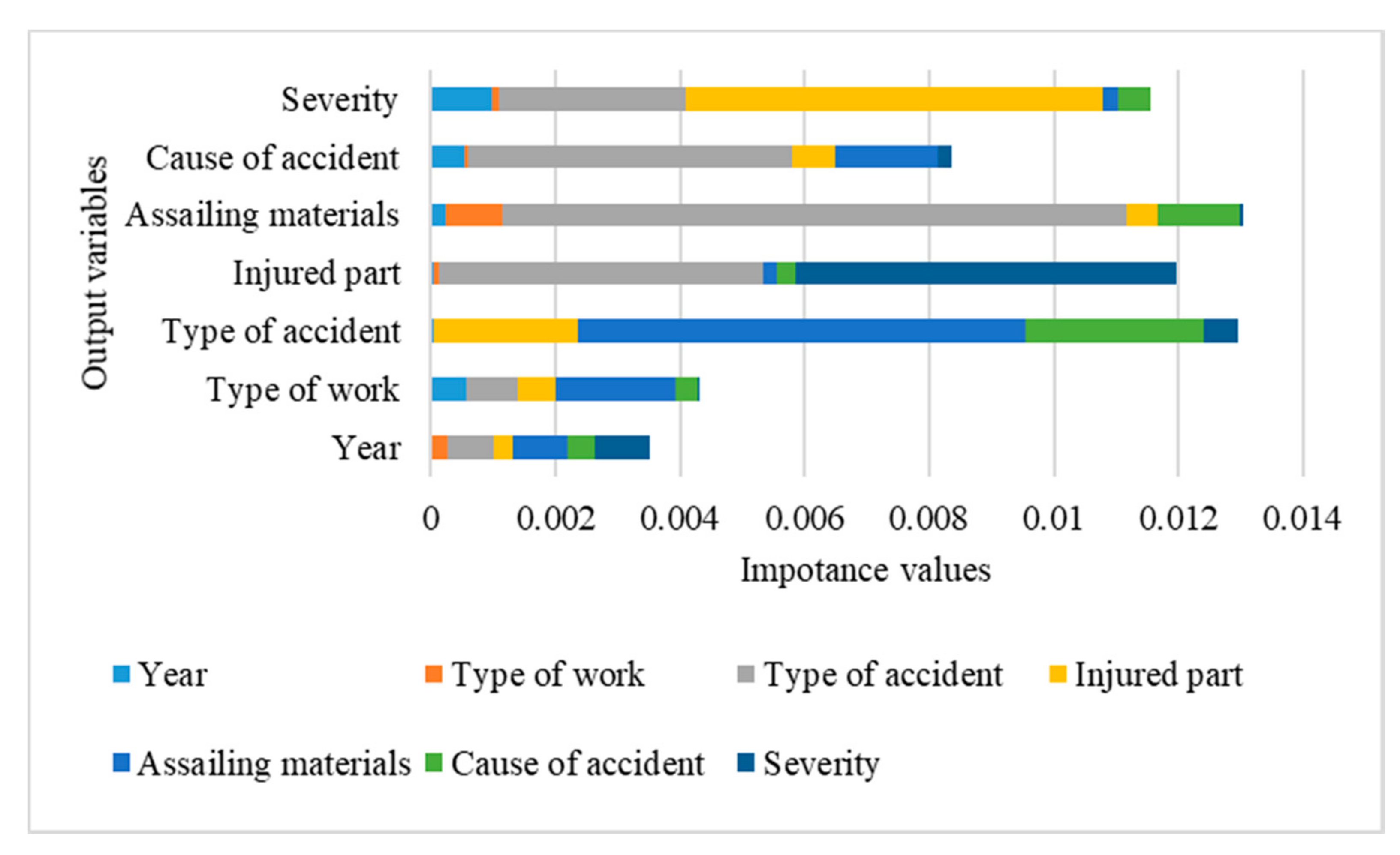
4.1. Correlation Analysis between Variables
4.2. Correlation Analysis between Elements
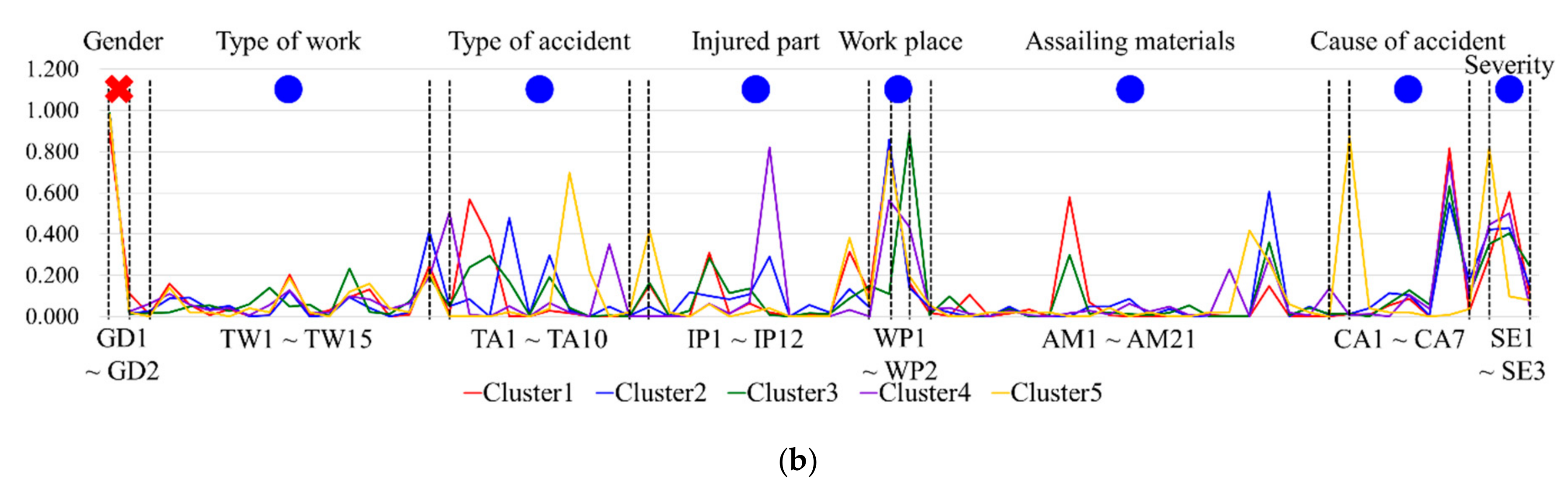
4.3. Analysis of Other Major Variables Influencing Severity
4.3.1. Grouping with LCCA
4.3.2. Visualization with PCA
5. Conclusions
- For construction accident data involving many variables and wide categories, it is possible to identify the most influential variable among many variables by using clustering, chi-square test, and other procedures.
- Because the types or categories of the major variables are numerous, it is difficult to identify meaningful relationships. Therefore, standardization and element grouping can be performed, and the accuracy can be analyzed according to the categories of the variables; through this, an optimal grouping using the fewest elements can be found.
- The correlations between factors can be analyzed by examining the correlations between and contributions of variables, using ML analysis on the optimal variable type and category.
- Through PCA and clustering, the distribution and combinations of variables that contribute to the prediction of each variable can be understood, and we anticipate that effective accident prevention measures can be established by utilizing these results.
- The severity level in the classified list of personal damage was predicted and analyzed, so this study can have some limitations. The more quantitative data such as the days of convalescence for each accident can yield more reliable results.
- There are differences in variables and elements to be filled out because construction accident data are all different in forms managed by countries and companies. Therefore, to apply the analysis method proposed in this study, the data standardization is necessary.
Author Contributions
Funding
Conflicts of Interest
References
- Ayhan, B.U.; Tokdemir, O.B. Accident Analysis for Construction Safety Using Latent Class Clustering and Artificial Neural Networks. J. Constr. Eng. Manag. 2020, 146, 04019114. [Google Scholar] [CrossRef]
- Hinze, J. Safety incentives: Do they reduce injuries? Pract. Period. Struct. Des. Constr. 2002, 7, 81–84. [Google Scholar] [CrossRef]
- Chi, C.F.; Chang, T.C.; Ting, H.I. Accident patterns and prevention measures for fatal occupational falls in the construction industry. Appl. Ergon. 2005, 36, 391–400. [Google Scholar] [CrossRef] [PubMed]
- Choudhry, R.; Fang, D.; Ahmed, S. Safety management in construction: Best practices in Hong Kong. J. Prof. Issues Eng. Educ. Pract. 2008, 134, 20–32. [Google Scholar] [CrossRef]
- Jacinto, C.; Canoa, M.; Guedes Soaresa, C. Workplace and organizational factors in accident analysis within the food industry. Saf. Sci. 2009, 47, 626–635. [Google Scholar] [CrossRef]
- Vidal, L.A.; Marle, F.; Bocquet, J. Measuring project complexity using the analytic hierarchy process. Int. J. Proj. Manag. 2011, 29, 718–727. [Google Scholar] [CrossRef]
- Matsunaga, F.T.; Brancher, J.D.; Busto, R.M. Data mining applications and techniques: A systematic review. Rev. Eletrônica Argentina-Brasil Tecnologias Informação Comunicação 2014, 1, 1–14. [Google Scholar] [CrossRef]
- Sarkar, S.; Vinay, S.; Raj, R.; Maiti, J.; Mitra, P. Application of optimized machine learning techniques for prediction of occupational accidents. Comput. Oper. Res. 2019, 106, 210–224. [Google Scholar] [CrossRef]
- Matías, J.M.; Rivas, T.; Martín, J.E.; Taboada, J. A machine learning methodology for the analysis of workplace. Int. J. Comput. Math. 2008, 85, 559–578. [Google Scholar] [CrossRef]
- Chen, H.; Luo, X. Severity prediction models for falling risk for workers at height. Procedia Eng. 2016, 164, 439–445. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques, 3rd ed.; Morgan Kaufman: Burlington, MA, USA, 2011. [Google Scholar]
- Goh, Y.M.; Chua, D. Neural network analysis of construction safety management systems: A case study in Singapore. Constr. Manag. Econ. 2013, 31, 460–470. [Google Scholar] [CrossRef]
- Patel, D.A.; Jha, K.N. Neural network model for the prediction of safe work behavior in construction projects. J. Constr. Eng. Manag. 2015, 141, 04014066. [Google Scholar] [CrossRef]
- Kim, Y.C.; Yoo, W.S.; Shin, Y. Application of artificial neural networks to prediction of construction safety accidents. J. Korean Soc. Hazard Mitig. 2017, 17, 7–14. [Google Scholar] [CrossRef]
- Yajuan, F.; Jia, C. Study on prediction model of building construction safety accidents based on GA-SVM. In Proceedings of the 2013 6th International Conference on Information Management, Innovation Management and Industrial Engineering, Xi’an, China, 23–24 November 2013; pp. 460–462. [Google Scholar]
- Zhou, Y.; Su, W.; Ding, L.; Luo, H. Predicting safety risks in deep foundation pits in subway infrastructure projects: Support vector machine approach. J. Comput. Civ. Eng. 2017, 31, 04017052. [Google Scholar] [CrossRef]
- Cho, Y.; Kim, Y.C.; Shin, Y. Prediction model of construction safety accidents using decision tree technique. J. Korea Inst. Build. Constr. 2017, 17, 294–303. [Google Scholar]
- Rivas, T.; Paz, M.; Martín, J.E.; Matías, J.M.; García, J.F.; Taboada, J. Explaining and predicting workplace accidents using data-mining techniques. Reliab. Eng. Syst. Saf. 2011, 96, 739–747. [Google Scholar] [CrossRef]
- Mistikoglu, G.; Gerek, I.H.; Erdis, E.; Mumtaz Usmen, P.E.; Cakan, H.; Kazan, E.E. Decision tree analysis of construction fall accidents involving roofers. Expert. Syst. Appl. 2015, 42, 2256–2263. [Google Scholar] [CrossRef]
- Sarkar, S.; Patel, A.; Madaan, S.; Maiti, J. Prediction of occupational accidents using decision tree approach. In Proceedings of the 2016 IEEE Annual India Conference (INDICON), Bangalore, India, 16–18 December 2016; pp. 1–6. [Google Scholar]
- An, S.H.; Park, U.Y.; Kang, K.I.; Cho, M.Y.; Cho, H.H. Application of support vector machines in assessing conceptual cost estimates. J. Comput. Civ. Eng. 2007, 21, 259–264. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Peng, H.S.; Wu, Y.W.; Chen, T.L. Estimate at completion for construction projects using evolutionary support vector machine inference model. Autom. Constr. 2010, 19, 619–629. [Google Scholar] [CrossRef]
- Sánchez, A.S.; Fernández, P.R.; Lasheras, F.S.; Juez, F.J.D.C.; Nieto, P.J.G. Prediction of work-related accidents according to working conditions using support vector machines. Appl. Math. Comput. 2011, 218, 3539–3552. [Google Scholar] [CrossRef]
- Kumar, P.R.; Ravi, V. Bankruptcy prediction in banks and firms via statistical and intelligent techniques—A review. Eur. J. Oper. Res. 2007, 180, 1–28. [Google Scholar] [CrossRef]
- Olson, D.L.; Delen, D.; Meng, Y. Comparative analysis of data mining methods for bankruptcy prediction. Decis. Support Syst. 2012, 52, 464–473. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2001. [Google Scholar]
- Freund, Y.; Schapire, R.; Abe, N. A short introduction to boosting. J. Jpn. Soc. Artif. Intell. 1999, 14, 771–780. [Google Scholar]
- Arditi, D.; Pulket, T. Predicting the outcome of construction litigation using boosted decision trees. J. Comput. Civ. Eng. 2005, 19, 387–393. [Google Scholar] [CrossRef]
- Shin, Y.; Kim, T.; Cho, H.; Kang, K.I. A formwork method selection model based on boosted decision trees in tall building construction. Automat. Constr. 2012, 23, 47–54. [Google Scholar] [CrossRef]
- Shin, Y.; Kim, D.W.; Kim, J.Y.; Kang, K.I.; Cho, M.Y.; Cho, H.H. Application of AdaBoost to the retaining wall method selection in construction. J. Comput. Civ. Eng. 2009, 23, 188–192. [Google Scholar] [CrossRef]
- Caruana, R.; Niculescu-Mizil, A. An empirical comparison of supervised learning algorithms. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 161–168. [Google Scholar]
- Bastos, J. Credit scoring with boosted decision trees. Munich Pers. RePEc Arch. 2008, 8156, 1–13. [Google Scholar]
- Oztekin, A.; Al-Ebbini, L.; Sevkli, Z.; Delen, D. A decision analytic approach to predicting quality of life for lung transplant recipients: A hybrid genetic algorithm based methodology. Eur. J. Oper. Res. 2018, 266, 639–651. [Google Scholar] [CrossRef]
- Aviad, B.; Roy, G. Classification by clustering decision tree-like classifier based on adjusted clusters. Expert Syst. Appl. 2011, 38, 8220–8228. [Google Scholar] [CrossRef]
- Leu, S.S.; Chang, C.M. Bayesian-network-based safety risk assessment for steel construction projects. Accid. Anal. Prev. 2013, 54, 122–133. [Google Scholar] [CrossRef]
- Bevilacqua, M.; Ciarapica, F.E.; Giacchetta, G. Industrial and occupational ergonomics in the petrochemical process industry: A regression tree approach. Accid. Anal. Prev. 2008, 40, 1468–1479. [Google Scholar] [CrossRef]
- Tixier, A.J.P.; Hallowell, M.R.; Balaji, R.; Bowman, D. Application of machine learning to construction injury prediction. Autom. Constr. 2016, 69, 102–114. [Google Scholar] [CrossRef]
- Salas, R.; Hallowell, M.; Balaji, R.; Bhandari, S. Safety Risk Tolerance in the Construction industry: Cross-Cultural Analysis. J. Constr. Eng. Manag. 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Alawad, H.; Kaewunruen, S.; An, A.M. Learning From Accidents: Machine Learning for Safety at Railway Stations. IEEE Access 2020, 8, 633–648. [Google Scholar] [CrossRef]
- Sameen, M.L.; Pradhan, B. Severity Prediction of Traffic Accidents with Recurrent Neural Networks. Appl. Sci. 2017, 7, 476. [Google Scholar] [CrossRef]
- Houari, R.; Bounceur, A.; Kechadi, M.; Tari, A.; Euler, R. Dimensionality reduction in data mining: A copula approach. Expert Syst. Appl. 2016, 64, 247–260. [Google Scholar] [CrossRef]
- Vermunt, J.K.; Magidson, J. Latent class cluster analysis. In Applied Latent Class Analysis; Hagenaars, J., McCutcheon, A., Eds.; Cambridge University Press: Cambridge, UK, 2002; pp. 89–106. [Google Scholar]
- Ona, J.D.; Lopez, G.; Mujalli, R.; Calvo, F.J. Analysis of traffic accidents on rural highways using latent class clustering and Bayesian Networks. Accid. Anal. Prev. 2013, 51, 1–10. [Google Scholar] [CrossRef]
- Biernacki, C.; Govaert, G. Choosing models in model-based clustering and discriminant analysis. J. Stat. Comput. Simul. 1999, 64, 49–71. [Google Scholar] [CrossRef]
- Cramér, H. Mathematical Methods of Statistics; Princeton University Press: Princeton, NJ, USA, 1946; Chapter 21; p. 282. [Google Scholar]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1993, 24, 417–441. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Kakhki, F.D.; Freeman, S.A.; Mosher, G.A. Use of Neural Networks to Identify Safety Prevention Priorities in Agro-Manufacturing Operations within Commercial Grain Elevators. Appl. Sci. 2019, 9, 4690. [Google Scholar] [CrossRef]
- Zink, A.; Rose, S. Fair regression for health care spending. Biometrics 2019, 76, 1–10. [Google Scholar] [CrossRef]
- Athey, S. Machine learning and causal inference for policy evaluation, KDD ’15. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, NSW, Australia, 10–13 August 2015; pp. 5–6. [Google Scholar]
- Choi, I.H.; Son, J.A.; Koo, J.B.; Yoon, Y.G.; Oh, T.K. Damage Assessment of Porcelain Insulators through Principal Component Analysis Associated with Frequency Response Signals. Appl. Sci. 2019, 7, 3150. [Google Scholar] [CrossRef]






| Year/Reference | Methods | Input Data | Output Data | Details |
|---|---|---|---|---|
| 2016/[37] | Random Forest, Stochastic Gradient Tree Boosting | 69 variables, such as construction materials, tools, and equipment. 9 variables, such as work procedure and carelessness | Injured area, energy source, severity | Prediction and accuracy comparison for Machine learning method using 78 construction site parameters |
| 2019/[8] | Latent Dirichlet Allocation, Support vector machine, Artificial neural network(ANN), Decision Tree | 16 variables such as accident day, month, department, outcome, impact type, injury type, and topic | Injury, near miss, property damage | Emphasized the importance of preprocessing of accident data, reduced variables with chi-square, and predicted accident types |
| 2020/[1] | Latent Class Cluster Analysis (LCCA), ANN | Categorical (project type, age (interval), occupation, experience (interval), incident case etc.), binary (incident, human factor, hazardous behavior) | Prediction for 6 accident types (recognition of risk, improper use of equipment, insufficient preventive measures, etc.) | By reducing 142 variables down to 60, the severity of construction accidents was predicted. Limitation: only binary variables were reduced |
| 2020/[38] | K-means Clustering, Principal component analysis (PCA) | Survey based score of 35 questions, considering age, employment type, career, and risk in each country | Construction risk prediction by country | PCA was performed on the survey scores, major components were extracted and grouped by k-means clustering. Limitation: the principal component values of PCA were grouped simply |
| Variable | Type | Number of Elements | Element Names |
|---|---|---|---|
| Accident classification | Categorical | 3 | Injury, death, property damage, etc. |
| Headquarter | Categorical | 3 | Housing construction, civil, plant construction |
| Process rate | Categorical | 10 | 1–10, 11–20, …, 91–100 |
| Year | Categorical | 6 | 2015, 2016, 2017, 2018, 2019, 2020 |
| Month | Categorical | 12 | 1–12 |
| Day of the week | Categorical | 7 | Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday |
| Hour | Categorical | 19 | Occupational accident occurrence time from 0 to 23:00 in hourly increments |
| Age | Categorical | 6 | 20–30, 31–40, 41–50, 51–60, 61–70, 71–80 |
| Gender | Binary | 2 | Male, Female |
| Type of work | Categorical | 15 | Carpenter, painter, scaffolder, stonemason, safety officer, welder, equipment operator, electric piping equipment worker, landscaper, window worker, structural steel/steel frame worker, concrete worker, tunnel worker, earth worker, woodworker |
| Type of accident | Categorical | 10 | Jamming, fall down, fall off, hit, collapse, struck, imbalance and uncontrolled motion, occupational diseases, mutilation/cut/puncture, fire/explosion/blast |
| Injured part | Categorical | 12 | Pelvis, ear, eye, leg, multiple head location, foot, hand, brain, mouth, nose, arm, chest/abdomen |
| Workplace | Binary | 2 | Internal work, external work |
| Assailing materials | Categorical | 21 | Formwork/shores, construction and mining machinery, stair and ladder, metal fine particles/trace elements/dust/fumes, other buildings/structures/etc., end portion and opening, fauna and flora, floor and ground/etc., scaffolding and work plate, equipment/machinery parts and appendages, hand tool nonpowered, container and pack, transporting, lifting equipment, machinery, land transportation, manpower machinery, processing equipment/machinery, natural phenomena (e.g., working environment and atmospheric conditions), material, electrical equipment/parts, debris/garbage, hand tool powered |
| Cause of accident | Categorical | 7 | Unsafe work(worker), lack of personal protective equipment(worker), facility defect/collapse(management), lack of safety measures(management), work equipment defect(worker), carelessness(worker), third-party liability(worker) |
| Severity | Categorical | 3 | slight injury, serious injury, fatal injury |
| Variables | Predictor Importance | Rank | Chi-Square p-Value | Rank | Cramer’s V | Rank | Cluster Group | Selected Variable |
|---|---|---|---|---|---|---|---|---|
| Accident classification | 0 | 12 | 7.09 × 10−6 | 6 | 0.12 | 10 | X | - |
| Headquarter | 0 | 12 | 5.74 × 10−1 | 14 | 0.04 | 14 | O | - |
| Process rate | 1.36 × 10−4 | 6 | 4.46 × 10−1 | 12 | 0.10 | 12 | X | - |
| Year | 4.46 × 10−4 | 5 | 1.20 × 10−8 | 5 | 0.17 | 5 | O | √ |
| Month | 1.06 × 10−4 | 10 | 1.84 × 10−2 | 10 | 0.14 | 8 | X | - |
| Day of the week | 0 | 12 | 9.03 × 10−1 | 15 | 0.06 | 13 | X | - |
| Hour | 1.29 × 10−4 | 7 | 3.42 × 10−2 | 11 | 0.17 | 6 | X | - |
| Age | 4.21 × 10−5 | 11 | 1.17 × 10−2 | 9 | 0.11 | 11 | X | - |
| Gender | 1.11 × 10−4 | 9 | 1.73 × 10−4 | 7 | 0.13 | 9 | X | - |
| Type of work | 6.65 × 10−4 | 4 | 8.55 × 10−3 | 8 | 0.16 | 7 | O | √ |
| Type of accident | 2.07 × 10−3 | 2 | 1.59 × 10−20 | 2 | 0.27 | 2 | O | √ |
| Injured part | 7.94 × 10−3 | 1 | 2.36 × 10−78 | 1 | 0.48 | 1 | O | √ |
| Work place | 0 | 12 | 5.30 × 10−1 | 13 | 0.04 | 15 | O | - |
| Assailing materials | 1.15 × 10−3 | 3 | 1.26 × 10−9 | 4 | 0.25 | 3 | O | √ |
| Cause of accident | 1.14 × 10−4 | 8 | 9.76 × 10−11 | 3 | 0.19 | 4 | O | √ |
| No. | Case | ML Method | Accuracy | Accuracy (Nested CV Applied) |
|---|---|---|---|---|
| 1 | A-B(15)-C-D(12)-E(21)-F | Ensemble | 72.17% | 70.19% |
| SVM | 94.60% | 58.32% | ||
| 2 | A-B(15)-C-D(12)-E(6)-F | Ensemble | 71.34% | 69.26% |
| SVM | 93.98% | 55.87% | ||
| 3 | A-B(15)-C-D(5)-E(21)-F | Ensemble | 68.02% | 69.57% |
| SVM | 93.67% | 55.66% | ||
| 4 | A-B(15)-C-D(5)-E(6)-F | Ensemble | 68.33% | 69.26% |
| SVM | 92.63% | 54.36% | ||
| 5 | A-B(5)-C-D(12)-E(21)-F | Ensemble | 69.57% | 66.87% |
| SVM | 91.28% | 57.54% | ||
| 6 | A-B(5)-C-D(12)-E(6)-F | Ensemble | 68.54% | 66.87% |
| SVM | 89.30% | 56.41% | ||
| 7 | A-B(5)-C-D(5)-E(21)-F | Ensemble | 67.29% | 66.87% |
| SVM | 89.62% | 55.02% | ||
| 8 | A-B(5)-C-D(5)-E(6)-F | Ensemble | 67.08% | 67.29% |
| SVM | 87.54% | 55.45% |
| Output Variable | Method | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|---|
| Year | Ensemble | 34.50% | 41.93% | 26.63% | 32.57% |
| SVM | 26.69% | 16.89% | 21.08% | 18.75% | |
| Type of work | Ensemble | 66.04% | 30.28% | 21.79% | 25.34% |
| SVM | 64.46% | 23.06% | 16.54% | 19.26% | |
| Type of accident | Ensemble | 50.34% | 32.05% | 37.12% | 34.40% |
| SVM | 37.24% | 28.72% | 19.44% | 23.19% | |
| Injured part | Ensemble | 48.86% | 29.31% | 27.10% | 28.16% |
| SVM | 45.03% | 36.26% | 22.71% | 27.93% | |
| Assailing materials | Ensemble | 53.27% | 28.63% | 33.86% | 31.03% |
| SVM | 48.34% | 27.25% | 15.15% | 19.47% | |
| Cause of accident | Ensemble | 69.89% | 31.47% | 24.95% | 27.84% |
| SVM | 66.24% | 33.51% | 21.08% | 25.88% | |
| Severity | Ensemble | 67.29% | 68.60% | 65.14% | 66.82% |
| SVM | 55.45% | 52.59% | 54.40% | 53.48% |
| Cluster ID | Attributes | Probabilities of Current Cluster | Being Observed (Total) | Being Observed | Percentage | |
|---|---|---|---|---|---|---|
| Variable | Element | (in the Cluster) | ||||
| Cluster 1 | Assailing material | Permanent fixture | 0.594 | 244 | 220 | 90.16% |
| Type of accident | Fall down | 0.566 | 250 | 217 | 86.80% | |
| Type of accident | Fall off | 0.358 | 174 | 132 | 75.86% | |
| Injured part | Outside of the lower body | 0.439 | 271 | 160 | 59.04% | |
| Severity | Serious injury | 0.343 | 462 | 240 | 51.95% | |
| Cluster 2 | Type of accident | Hit | 0.457 | 157 | 122 | 77.71% |
| Type of accident | Struck | 0.313 | 128 | 92 | 71.88% | |
| Cause of accident | Third-party liability | 0.657 | 85 | 61 | 71.76% | |
| Assailing material | Heavy non-fixture | 0.565 | 337 | 148 | 43.92% | |
| Injured part | Outside of the upper body | 0.403 | 395 | 105 | 26.58% | |
| Cluster 3 | Type of accident | Mutilation, Cut, Puncture | 0.376 | 71 | 64 | 90.14% |
| Assailing material | Light non-fixture (equipment) | 0.531 | 109 | 91 | 83.49% | |
| Type of accident | Jamming | 0.357 | 108 | 66 | 61.11% | |
| Injured part | Outside of the upper body | 0.871 | 395 | 143 | 36.20% | |
| Type of work | Civil | 0.241 | 138 | 43 | 31.16% | |
| Cluster 4 | Severity | Fatal injury | 0.961 | 127 | 114 | 89.76% |
| Injured part | Inside the upper body | 0.400 | 76 | 47 | 61.84% | |
| Injured part | Face | 0.395 | 110 | 46 | 41.82% | |
| Year | 2019 | 0.383 | 254 | 88 | 34.65% | |
| Type of accident | Fall off | 0.356 | 174 | 42 | 24.14% | |
| Cluster 5 | Cause of accident | Unsafe work | 0.825 | 54 | 45 | 83.33% |
| Type of accident | Occupational diseases | 0.169 | 11 | 9 | 81.82% | |
| Type of accident | Imbalance and uncontrolled motion | 0.778 | 58 | 42 | 72.41% | |
| Injured part | Inside the lower body | 0.470 | 111 | 25 | 22.52% | |
| Assailing material | Heavy non-fixture | 0.678 | 337 | 37 | 10.98% | |
| Cluster ID. | Conceptual Definition | Number of Data Entries (Percentage (%)) |
|---|---|---|
| Cluster 1 | Serious injury to the outside of the lower body from a permanent fixture (floor, etc.) by fall down and fall off accidents | 369(38) |
| Cluster 2 | Injury to the outside of the upper body from being hit or struck by a heavy non-fixture (construction material) | 259(27) |
| Cluster 3 | Injury due to mutilation, cut, or puncture on the outside of the upper body whilst using light non-fixture (equipment) | 165(17) |
| Cluster 4 | Fatal injury on the inside of the upper body and face from fall off | 118(12) |
| Cluster 5 | Injury to the inside of the lower body (pelvis) from unbalanced and uncontrolled movements during heavy non-fixture work | 53(6) |
| Total | 963(100) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.Y.; Yoon, Y.G.; Oh, T.K.; Park, S.; Ryu, S.I. A Study on Data Pre-Processing and Accident Prediction Modelling for Occupational Accident Analysis in the Construction Industry. Appl. Sci. 2020, 10, 7949. https://doi.org/10.3390/app10217949
Lee JY, Yoon YG, Oh TK, Park S, Ryu SI. A Study on Data Pre-Processing and Accident Prediction Modelling for Occupational Accident Analysis in the Construction Industry. Applied Sciences. 2020; 10(21):7949. https://doi.org/10.3390/app10217949
Chicago/Turabian StyleLee, Jae Yun, Young Geun Yoon, Tae Keun Oh, Seunghee Park, and Sang Il Ryu. 2020. "A Study on Data Pre-Processing and Accident Prediction Modelling for Occupational Accident Analysis in the Construction Industry" Applied Sciences 10, no. 21: 7949. https://doi.org/10.3390/app10217949
APA StyleLee, J. Y., Yoon, Y. G., Oh, T. K., Park, S., & Ryu, S. I. (2020). A Study on Data Pre-Processing and Accident Prediction Modelling for Occupational Accident Analysis in the Construction Industry. Applied Sciences, 10(21), 7949. https://doi.org/10.3390/app10217949







