Credibility Based Imbalance Boosting Method for Software Defect Proneness Prediction
Abstract
:1. Introduction
2. Related Work
2.1. Software Defect Prediction
2.2. Class-Imbalance Learning
2.2.1. Data-Level Methods
2.2.2. Algorithm-Level Methods
3. Methodology
3.1. Problem Formulation
3.2. Proposed Credibility-Based Imbalance Boosting Method
| Algorithm 1 |
|
3.2.1. Calculate the Credibility Factors of Synthetic Samples
3.2.2. Update the Weights of Synthetic Samples in Boosting Iterations
4. Experimental Design
4.1. Benchmark Datasets
4.2. Baseline Methods
- MAHAKIL. It is a novel synthetic oversampling approach that is based on the chromosomal theory of inheritance for software defect prediction, which is proposed by Bennin et al. [44] in 2017. MAHAKIL utilizes features of two parent instances in order to generate a new synthetic instance which ensures that the artificial sample falls within the decision boundary of any classification algorithm.
- AdaBoost. It is one of the most well-known and commonly used ensemble learning algorithms, which is proposed by Freund and Schapire [46] in 1995. AdaBoost iteratively generates a series of base classifiers. In each iteration, the classifier is trained on training dataset with specific distribution weights of instances and it is assigned a model weight according to the training error. The distribution weight of training instances is then updated. Specifically, the training instances that are misclassified get a higher weight, otherwise get a smaller weight, which ensures the decision boundary will be adjusted to the misclassified instances. AdaBoost was identified as one of the top ten most influential data mining algorithms [79].
- AdaC2. AdaC2, proposed by Sun et al. [45], combines the advantages of cost-sensitive learning and AdaBoost. Sun et al. [45] argued that AdaBoost treats samples of different types (classes) equally, which is inconsistent with the common situation that the minority class samples usually are more important that the majority class ones. AdaC2 introduces the cost items into the weight update formula of AdaBoost by outside the exponent.
- SMOTE. It is proposed by Chawla et al. [40], which is the most famous and widely used oversampling approach for addressing class-imbalance problem. SMOTE tries to alleviate the imbalance of the original imbalanced dataset by generating synthetic minority class samples in the region of original minority class samples.
4.3. Performance Measures
4.4. Statistical Test
 to show that our CIB significantly outperforms the baseline with larger effect size, light gray cell
to show that our CIB significantly outperforms the baseline with larger effect size, light gray cell  to show significant improvement with medium effect size, and silvery gray
to show significant improvement with medium effect size, and silvery gray  to show significant improvement with small effect size.
to show significant improvement with small effect size.4.5. Experimental Settings
4.5.1. Validation Method
4.5.2. Parameter Settings
4.5.3. Base Classifier
5. Experimental Results
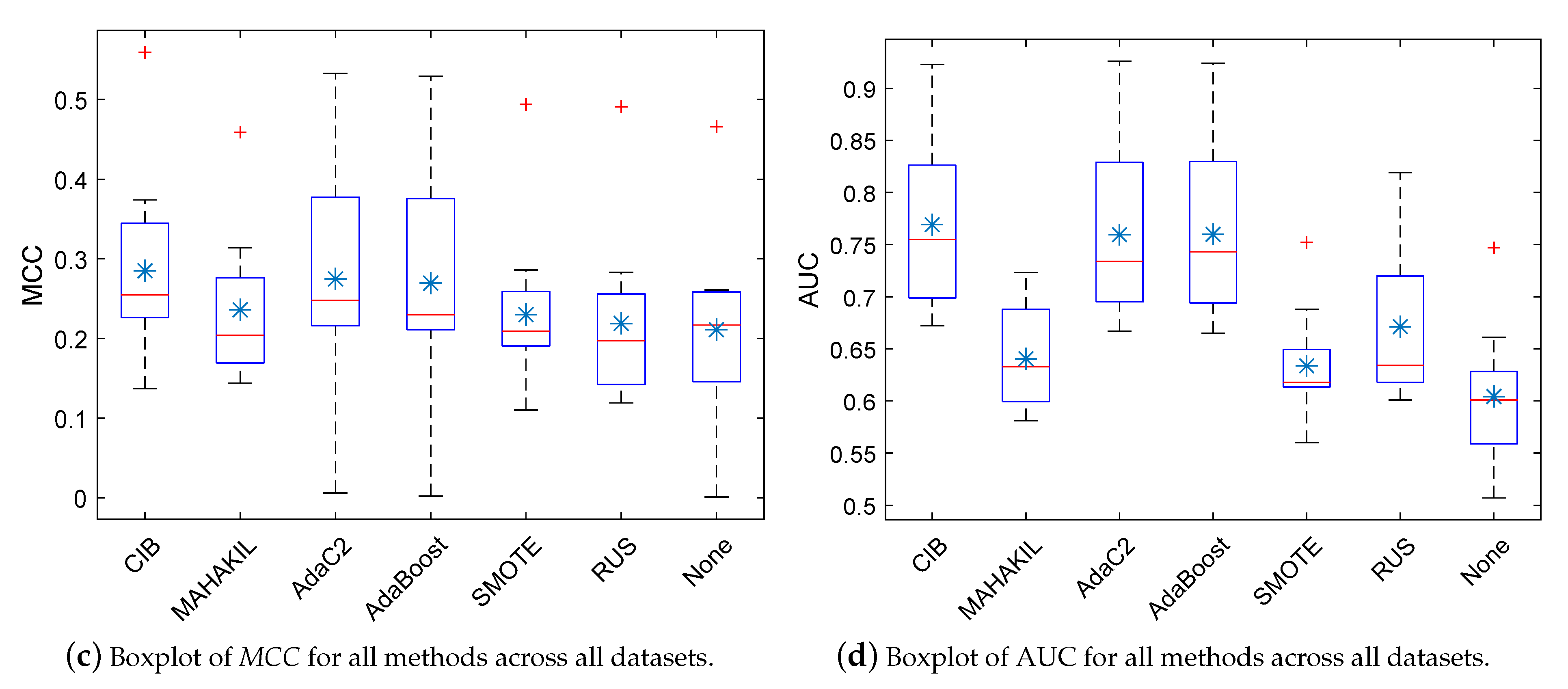
5.1. RQ1: How Effective Is CIB? How Much Improvement Can It Obtain Compared with the Baselines?
 , the light gray
, the light gray  , and the silvery gray
, and the silvery gray  indicate that the proposed CIB significantly outperforms the corresponding baseline with large, moderate, and small effect size, respectively. If the baseline significantly outperforms our CIB or the effect size is negligible, then the corresponding table-cell of this baseline is marked with a white background. Checkmark ✓ represents that the corresponding method has no significant difference when compared with the best method.
indicate that the proposed CIB significantly outperforms the corresponding baseline with large, moderate, and small effect size, respectively. If the baseline significantly outperforms our CIB or the effect size is negligible, then the corresponding table-cell of this baseline is marked with a white background. Checkmark ✓ represents that the corresponding method has no significant difference when compared with the best method.5.2. RQ2: How Is the Generalization Ability of CIB?
5.3. RQ3: How Much Time Does It Take for CIB to Run?
6. Discussion
6.1. Why CIB Works?
6.2. Class-Imbalance Learning Is Necessary When Building Software Defect Prediction Models
6.3. Is CIB Comparable to Rule-Based Classifiers?
6.4. Is CIB Applicable for Cross-Project Defect Prediction?
6.5. Threats to Validity
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SDP | Software defect prediction |
| CIB | Credibility based imbalance boosting method |
| SOTA | State-of-the-art |
References
- Song, Q.; Jia, Z.; Shepperd, M.; Ying, S.; Liu, J. A General Software Defect-Proneness Prediction Framework. IEEE Trans. Softw. Eng. 2011, 37, 356–370. [Google Scholar] [CrossRef] [Green Version]
- Ostrand, T.J.; Weyuker, E.J.; Bell, R.M. Predicting the Location and Number of Faults in Large Software Systems. IEEE Trans. Softw. Eng. 2005, 31, 340–355. [Google Scholar] [CrossRef]
- Menzies, T.; Greenwald, J.; Frank, A. Data Mining Static Code Attributes to Learn Defect Predictors. IEEE Trans. Softw. Eng. 2007, 33, 2–13. [Google Scholar] [CrossRef]
- Gao, K.; Khoshgoftaar, T.M. A Comprehensive Empirical Study of Count Models for Software Fault Prediction. IEEE Trans. Reliab. 2007, 56, 223–236. [Google Scholar] [CrossRef]
- Shepperd, M.; Song, Q.; Sun, Z.; Mair, C. Data Quality: Some Comments on the NASA Software Defect Datasets. IEEE Trans. Softw. Eng. 2013, 39, 1208–1215. [Google Scholar] [CrossRef] [Green Version]
- Kamei, Y.; Shihab, E.; Adams, B.; Hassan, A.E.; Mockus, A.; Sinha, A.; Ubayashi, N. A Large-Scale Empirical Study of Just-in-Time Quality Assurance. IEEE Trans. Softw. Eng. 2013, 39, 757–773. [Google Scholar] [CrossRef]
- Catal, C. Software fault prediction: A literature review and current trends. Expert Syst. Appl. 2011, 38, 4626–4636. [Google Scholar] [CrossRef]
- Malhotra, R. An extensive analysis of search-based techniques for predicting defective classes. Comput. Electr. Eng. 2018, 71, 611–626. [Google Scholar] [CrossRef]
- McCabe, T.J. A Complexity Measure. IEEE Trans. Softw. Eng. 1976, SE-2, 308–320. [Google Scholar] [CrossRef]
- Halstead, M.H. Elements of Software Science; Elsevier Computer Science Library: Operational Programming Systems Series; North-Holland: New York, NY, USA, 1977. [Google Scholar]
- Kemerer, C.; Chidamber, S. A Metrics Suite for Object Oriented Design. IEEE Trans. Softw. Eng. 1994, 20, 476–493. [Google Scholar] [CrossRef] [Green Version]
- Madeyski, L.; Jureczko, M. Which process metrics can significantly improve defect prediction models? An empirical study. Softw. Qual. J. 2014, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Lo, D.; Xia, X.; Zhang, Y.; Sun, J. Deep Learning for Just-in-Time Defect Prediction. In Proceedings of the 2015 IEEE International Conference on Software Quality, Reliability and Security, Vancouver, BC, Canada, 3–5 August 2015; pp. 17–26. [Google Scholar] [CrossRef] [Green Version]
- Khoshgoftaar, T.M.; Allen, E.B.; Jones, W.D.; Hudepohl, J.I. Classification tree models of software quality over multiple releases. In Proceedings of the 10th International Symposium on Software Reliability Engineering (Cat. No.PR00443), Boca Raton, FL, USA, 1–4 November 1999; pp. 116–125. [Google Scholar] [CrossRef]
- Jin, C.; Jin, S.W. Prediction Approach of Software Fault-proneness Based on Hybrid Artificial Neural Network and Quantum Particle Swarm Optimization. Appl. Soft Comput. 2015, 35, 717–725. [Google Scholar] [CrossRef]
- Turhan, B.; Menzies, T.; Bener, A.B.; Di Stefano, J. On the relative value of cross-company and within-company data for defect prediction. Empir. Softw. Eng. 2009, 14, 540–578. [Google Scholar] [CrossRef] [Green Version]
- Miholca, D.L.; Czibula, G.; Czibula, I.G. A novel approach for software defect prediction through hybridizing gradual relational association rules with artificial neural networks. Inf. Sci. 2018, 441, 152–170. [Google Scholar] [CrossRef]
- Laradji, I.H.; Alshayeb, M.; Ghouti, L. Software defect prediction using ensemble learning on selected features. Inf. Softw. Technol. 2015, 58, 388–402. [Google Scholar] [CrossRef]
- Ryu, D.; Jang, J.I.; Baik, J. A Hybrid Instance Selection Using Nearest-Neighbor for Cross-Project Defect Prediction. J. Comput. Sci. Technol. 2015, 30, 969–980. [Google Scholar] [CrossRef]
- Ma, Y.; Luo, G.; Zeng, X.; Chen, A. Transfer learning for cross-company software defect prediction. Inf. Softw. Technol. 2012, 54, 248–256. [Google Scholar] [CrossRef]
- Xia, X.; Lo, D.; Pan, S.J.; Nagappan, N.; Wang, X. HYDRA: Massively Compositional Model for Cross-Project Defect Prediction. IEEE Trans. Softw. Eng. 2016, 42, 977–998. [Google Scholar] [CrossRef]
- Nam, J.; Pan, S.J.; Kim, S. Transfer defect learning. In Proceedings of the 2013 35th International Conference on Software Engineering (ICSE), San Francisco, CA, USA, 18–26 May 2013; pp. 382–391. [Google Scholar] [CrossRef]
- Wang, S.; Liu, T.; Tan, L. Automatically Learning Semantic Features for Defect Prediction. In Proceedings of the 38th International Conference on Software Engineering; ICSE ’16; ACM: New York, NY, USA, 2016; pp. 297–308. [Google Scholar] [CrossRef]
- Chen, L.; Fang, B.; Shang, Z.; Tang, Y. Negative samples reduction in cross-company software defects prediction. Inf. Softw. Technol. 2015, 62, 67–77. [Google Scholar] [CrossRef]
- Jing, X.; Wu, F.; Dong, X.; Qi, F.; Xu, B. Heterogeneous Cross-company Defect Prediction by Unified Metric Representation and CCA-based Transfer Learning. In Proceedings of the 2015 10th Joint Meeting on Foundations of Software Engineering; ESEC/FSE 2015; ACM: New York, NY, USA, 2015; pp. 496–507. [Google Scholar] [CrossRef]
- Li, Z.; Jing, X.Y.; Wu, F.; Zhu, X.; Xu, B.; Ying, S. Cost-sensitive transfer kernel canonical correlation analysis for heterogeneous defect prediction. Autom. Softw. Eng. 2018, 25, 201–245. [Google Scholar] [CrossRef]
- Nam, J.; Fu, W.; Kim, S.; Menzies, T.; Tan, L. Heterogeneous Defect Prediction. IEEE Trans. Softw. Eng. 2018, 44, 874–896. [Google Scholar] [CrossRef] [Green Version]
- Ryu, D.; Choi, O.; Baik, J. Value-cognitive Boosting with a Support Vector Machine for Cross-project Defect Prediction. Empir. Softw. Eng. 2016, 21, 43–71. [Google Scholar] [CrossRef]
- Hosseini, S.; Turhan, B.; Mäntylä, M. A benchmark study on the effectiveness of search-based data selection and feature selection for cross project defect prediction. Inf. Softw. Technol. 2018, 95, 296–312. [Google Scholar] [CrossRef] [Green Version]
- Boehm, B.; Basili, V.R. Software Defect Reduction Top 10 List. Computer 2001, 34, 135–137. [Google Scholar] [CrossRef]
- Hall, T.; Beecham, S.; Bowes, D.; Gray, D.; Counsell, S. A Systematic Literature Review on Fault Prediction Performance in Software Engineering. IEEE Trans. Softw. Eng. 2012, 38, 1276–1304. [Google Scholar] [CrossRef]
- Arisholm, E.; Briand, L.C.; Johannessen, E.B. A systematic and comprehensive investigation of methods to build and evaluate fault prediction models. J. Syst. Softw. 2010, 83, 2–17. [Google Scholar] [CrossRef]
- Pak, C.; Wang, T.T.; Su, X.H. An Empirical Study on Software Defect Prediction Using Over-Sampling by SMOTE. Int. J. Softw. Eng. Knowl. Eng. 2018, 28, 811–830. [Google Scholar] [CrossRef]
- Malhotra, R.; Khanna, M. An empirical study for software change prediction using imbalanced data. Empir. Softw. Eng. 2017, 22, 2806–2851. [Google Scholar] [CrossRef]
- He, Z.; Peters, F.; Menzies, T.; Yang, Y. Learning from open-source projects: An empirical study on defect prediction. In Proceedings of the 2013 ACM/IEEE International Symposium on Empirical Software Engineering and Measurement, Baltimore, MD, USA, 10–11 October 2013; pp. 45–54. [Google Scholar]
- Menzies, T.; Turhan, B.; Bener, A.; Gay, G.; Cukic, B.; Jiang, Y. Implications of Ceiling Effects in Defect Predictors. In Proceedings of the 4th International Workshop on Predictor Models in Software Engineering; PROMISE ’08; ACM: New York, NY, USA, 2008; pp. 47–54. [Google Scholar] [CrossRef] [Green Version]
- Khoshgoftaar, T.M.; Geleyn, E.; Nguyen, L.; Bullard, L. Cost-Sensitive Boosting in Software Quality Modeling. In Proceedings of the 7th IEEE International Symposium on High Assurance Systems Engineering; HASE ’02; IEEE Computer Society: Washington, DC, USA, 2002; pp. 51–60. [Google Scholar]
- Zheng, J. Cost-sensitive boosting neural networks for software defect prediction. Expert Syst. Appl. 2010, 37, 4537–4543. [Google Scholar] [CrossRef]
- Siers, M.J.; Islam, M.Z. Software defect prediction using a cost sensitive decision forest and voting, and a potential solution to the class imbalance problem. Inf. Syst. 2015, 51, 62–71. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Int. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Han, H.; Wang, W.Y.; Mao, B.H. Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning; Advances in Intelligent Computing ICIC 2005; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3644, pp. 878–887. ISBN 978-3-540-28226-6. [Google Scholar]
- Barua, S.; Islam, M.M.; Yao, X.; Murase, K. MWMOTE-Majority weighted minority oversampling technique for imbalanced data set learning. IEEE Trans. Knowl. Data Eng. 2014, 26, 405–425. [Google Scholar] [CrossRef]
- Menzies, T.; Krishna, R.; Pryor, D. The Promise Repository of Empirical Software Engineering Data. 2015. Available online: http://openscience.us/repo (accessed on 10 October 2020).
- Ebo Bennin, K.; Keung, J.; Phannachitta, P.; Monden, A.; Mensah, S. MAHAKIL: Diversity Based Oversampling Approach to Alleviate the Class Imbalance Issue in Software Defect Prediction. IEEE Trans. Softw. Eng. 2017, 44, 534–550. [Google Scholar] [CrossRef]
- Sun, Y.; Kamel, M.S.; Wong, A.K.C.; Wang, Y. Cost-sensitive Boosting for Classification of Imbalanced Data. Pattern Recognit. 2007, 40, 3358–3378. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A desicion-theoretic generalization of on-line learning and an application to boosting. In Computational Learning Theory; Vitányi, P., Ed.; Springer: Berlin, Germany, 1995; pp. 23–37. [Google Scholar]
- Wang, J.; Shen, B.; Chen, Y. Compressed C4. 5 models for software defect prediction. In Proceedings of the 2012 12th International Conference on Quality Software, Xi’an, China, 27–29 August 2012; pp. 13–16. [Google Scholar]
- Vashisht, V.; Lal, M.; Sureshchandar, G. Defect prediction framework using neural networks for software enhancement projects. J. Adv. Math. Comput. Sci. 2016, 16, 1–12. [Google Scholar] [CrossRef]
- Elish, K.O.; Elish, M.O. Predicting defect-prone software modules using support vector machines. J. Syst. Softw. 2008, 81, 649–660. [Google Scholar] [CrossRef]
- Okutan, A.; Yıldız, O.T. Software defect prediction using Bayesian networks. Empir. Softw. Eng. 2014, 19, 154–181. [Google Scholar] [CrossRef] [Green Version]
- Dejaeger, K.; Verbraken, T.; Baesens, B. Toward Comprehensible Software Fault Prediction Models Using Bayesian Network Classifiers. IEEE Trans. Softw. Eng. 2013, 39, 237–257. [Google Scholar] [CrossRef]
- Czibula, G.; Marian, Z.; Czibula, I.G. Software defect prediction using relational association rule mining. Inf. Sci. 2014, 264, 260–278. [Google Scholar] [CrossRef]
- Pan, C.; Lu, M.; Xu, B.; Gao, H. An Improved CNN Model for Within-Project Software Defect Prediction. Appl. Sci. Basel 2019, 9, 2138. [Google Scholar] [CrossRef] [Green Version]
- Shi, K.; Lu, Y.; Chang, J.; Wei, Z. PathPair2Vec: An AST path pair-based code representation method for defect prediction. J. Comput. Lang. 2020, 59, 100979. [Google Scholar] [CrossRef]
- Sun, Z.; Song, Q.; Zhu, X. Using Coding-Based Ensemble Learning to Improve Software Defect Prediction. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2012, 42, 1806–1817. [Google Scholar] [CrossRef]
- Khoshgoftaar, T.M.; Allen, E.B. Ordering Fault-Prone Software Modules. Softw. Qual. J. 2003, 11, 19–37. [Google Scholar] [CrossRef]
- Khoshgoftaar, T.; Gao, K.; Szabo, R.M. An Application of Zero-Inflated Poisson Regression for Software Fault Prediction. In Proceedings of the 12th International Symposium on Software Reliability Engineering; ISSRE ’01; IEEE Computer Society: Washington, DC, USA, 2001; pp. 66–73. [Google Scholar]
- Fagundes, R.A.A.; Souza, R.M.C.R.; Cysneiros, F.J.A. Zero-inflated prediction model in software-fault data. IET Softw. 2016, 10, 1–9. [Google Scholar] [CrossRef]
- Quah, T.S.; Thwin, M.M.T. Prediction of software development faults in PL/SQL files using neural network models. Inf. Softw. Technol. 2004, 46, 519–523. [Google Scholar] [CrossRef]
- Rathore, S.S.; Kumar, S. Linear and non-linear heterogeneous ensemble methods to predict the number of faults in software systems. Knowl.-Based Syst. 2017, 119, 232–256. [Google Scholar] [CrossRef]
- Mahmood, Z.; Bowes, D.; Lane, P.C.R.; Hall, T. What is the Impact of Imbalance on Software Defect Prediction Performance? In Proceedings of the 11th International Conference on Predictive Models and Data Analytics in Software Engineering; PROMISE ’15; ACM: New York, NY, USA, 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Tantithamthavorn, C.; McIntosh, S.; Hassan, A.E.; Matsumoto, K. The Impact of Automated Parameter Optimization on Defect Prediction Models. IEEE Trans. Softw. Eng. 2019, 45, 683–711. [Google Scholar] [CrossRef] [Green Version]
- Krishna, R.; Menzies, T. Bellwethers: A Baseline Method For Transfer Learning. IEEE Trans. Softw. Eng. 2018. [Google Scholar] [CrossRef] [Green Version]
- Kamei, Y.; Monden, A.; Matsumoto, S.; Kakimoto, T.; Matsumoto, K. The Effects of Over and Under Sampling on Fault-prone Module Detection. In Proceedings of the First International Symposium on Empirical Software Engineering and Measurement (ESEM 2007), Madrid, Spain, 20–21 September 2007; pp. 196–204. [Google Scholar] [CrossRef]
- Seiffert, C.; Khoshgoftaar, T.M.; Van Hulse, J.; Folleco, A. An Empirical Study of the Classification Performance of Learners on Imbalanced and Noisy Software Quality Data. Inf. Sci. 2014, 259, 571–595. [Google Scholar] [CrossRef]
- Yang, X.; Lo, D.; Xia, X.; Sun, J. TLEL: A two-layer ensemble learning approach for just-in-time defect prediction. Inf. Softw. Technol. 2017, 87, 206–220. [Google Scholar] [CrossRef]
- Wang, S.; Yao, X. Using Class Imbalance Learning for Software Defect Prediction. IEEE Trans. Reliab. 2013, 62, 434–443. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, G.H.; Bouzerdoum, A.; Phung, S.L. Learning Pattern Classification Tasks with Imbalanced Data Sets. Pattern Recognit. 2009, 193–208. [Google Scholar] [CrossRef] [Green Version]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar] [CrossRef] [Green Version]
- Ling, C.X.; Yang, Q.; Wang, J.; Zhang, S. Decision trees with minimal costs. In Proceedings of the Machine Learning, Proceedings of the Twenty-First International Conference (ICML 2004), Banff, AB, Canada, 4–8 July 2004. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Liu, X.Y. Training Cost-Sensitive Neural Networks with Methods Addressing the Class Imbalance Problem. IEEE Trans. Knowl. Data Eng. 2006, 18, 63–77. [Google Scholar] [CrossRef]
- Khoshgoftaar, T.M.; Golawala, M.; Hulse, J.V. An Empirical Study of Learning from Imbalanced Data Using Random Forest. In Proceedings of the 19th IEEE International Conference on Tools with Artificial Intelligence(ICTAI 2007), Patras, Greece, 29–31 October 2007; Volume 2, pp. 310–317. [Google Scholar] [CrossRef]
- Fan, W.; Stolfo, S.J.; Zhang, J.; Chan, P.K. AdaCost: Misclassification Cost-Sensitive Boosting. In Proceedings of the Sixteenth International Conference on Machine Learning, ICML ’99, Bled, Slovenia, 27–30 June 1999; pp. 97–105. [Google Scholar]
- Chen, S.; He, H.; Garcia, E.A. RAMOBoost: Ranked minority oversampling in boosting. IEEE Trans. Neural Networks 2010, 21, 1624–1642. [Google Scholar] [CrossRef]
- Chawla, N.V.; Lazarevic, A.; Hall, L.O.; Bowyer, K.W. SMOTEBoost: Improving Prediction of the Minority Class in Boosting. In Knowledge Discovery in Databases; PKDD 2003; Springer: Berlin, Germany, 2003; pp. 107–119. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Wohlin, C.; Runeson, P.; Höst, M.; Ohlsson, M.C.; Regnell, B.; Wesslén, A. Experimentation in Software Engineering; Springer: Berlin, Germany, 2012. [Google Scholar]
- Gray, D.; Bowes, D.; Davey, N.; Sun, Y.; Christianson, B. The misuse of the NASA metrics data program data sets for automated software defect prediction. In Proceedings of the 15th Annual Conference on Evaluation Assessment in Software Engineering (EASE 2011), Durham, UK, 11–12 April 2011; pp. 96–103. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Kumar, V.; Quinlan, J.R.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2007, 14, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Menzies, T.; Dekhtyar, A.; Distefano, J.; Greenwald, J. Problems with Precision: A Response to “comments on ‘data mining static code attributes to learn defect predictors’”. IEEE Trans. Softw. Eng. 2007, 33, 637–640. [Google Scholar] [CrossRef] [Green Version]
- Peters, F.; Menzies, T.; Gong, L.; Zhang, H. Balancing Privacy and Utility in Cross-Company Defect Prediction. IEEE Trans. Softw. Eng. 2013, 39, 1054–1068. [Google Scholar] [CrossRef] [Green Version]
- Tantithamthavorn, C.; Hassan, A.E.; Matsumoto, K. The Impact of Class Rebalancing Techniques on the Performance and Interpretation of Defect Prediction Models. IEEE Trans. Softw. Eng. 2018. [Google Scholar] [CrossRef] [Green Version]
- Bowes, D.; Hall, T.; Harman, M.; Jia, Y.; Sarro, F.; Wu, F. Mutation-aware Fault Prediction. In Proceedings of the 25th International Symposium on Software Testing and Analysis; ISSTA 2016; ACM: New York, NY, USA, 2016; pp. 330–341. [Google Scholar] [CrossRef] [Green Version]
- Maratea, A.; Petrosino, A.; Manzo, M. Adjusted F-measure and kernel scaling for imbalanced data learning. Inf. Sci. 2014, 257, 331–341. [Google Scholar] [CrossRef]
- Bradley, A.P. The Use of the Area Under the ROC Curve in the Evaluation of Machine Learning Algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef] [Green Version]
- Matthews, B.W. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochim. Et Biophys. Acta 1975, 405, 442. [Google Scholar] [CrossRef]
- Zhang, F.; Mockus, A.; Keivanloo, I.; Zou, Y. Towards building a universal defect prediction model with rank transformed predictors. Empir. Softw. Eng. 2016, 21, 2107–2145. [Google Scholar] [CrossRef]
- Shepperd, M.; Bowes, D.; Hall, T. Researcher Bias: The Use of Machine Learning in Software Defect Prediction. IEEE Trans. Softw. Eng. 2014, 40, 603–616. [Google Scholar] [CrossRef] [Green Version]
- He, P.; Li, B.; Liu, X.; Chen, J.; Ma, Y. An Empirical Study on Software Defect Prediction with a Simplified Metric Set. Inf. Softw. Technol. 2015, 59, 170–190. [Google Scholar] [CrossRef] [Green Version]
- Cliff, N. Ordinal Methods for Behavioral Data Analysis; Psychology Press: New York, NY, USA, 1996. [Google Scholar]
- Romano, J.; Kromrey, J.D.; Coraggio, J.; Skowronek, J. Appropriate statistics for ordinal level data: Should we really be using t-test and Cohen’sd for evaluating group differences on the NSSE and other surveys. In Proceedings of the Annual Meeting of the Florida Association of Institutional Research, Tallahassee, FL, USA, 2–6 July 2006; pp. 1–33. [Google Scholar]
- Macbeth, G.; Razumiejczyk, E.; Ledesma, R. Cliff’s delta calculator: A non-parametric effect size program for two groups of observations. Univ. Psychol. 2011, 10, 545–555. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; pp. 241–247. [Google Scholar]
- Yu, X.; Liu, J.; Yang, Z.; Jia, X.; Ling, Q.; Ye, S. Learning from Imbalanced Data for Predicting the Number of Software Defects. In Proceedings of the 2017 IEEE 28th International Symposium on Software Reliability Engineering (ISSRE), Toulouse, France, 23–26 October 2017; pp. 78–89. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, D.; Zhao, Y.; Cui, Z.; Ni, C. Software defect number prediction: Unsupervised vs supervised methods. Inf. Softw. Technol. 2019, 106, 161–181. [Google Scholar] [CrossRef]
- Frank, E.; Hall, M.A.; Witten, I.H. Data Mining: Practical Machine Learning Tools and Techniques, 4th ed.; Morgan Kaufmann: Burlington, MA, USA, 2016. [Google Scholar]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993. [Google Scholar]
- Challagulla, V.U.B.; Bastani, F.B.; Yen, I.-L.; Paul, R.A. Empirical assessment of machine learning based software defect prediction techniques. In Proceedings of the 10th IEEE International Workshop on Object-Oriented Real-Time Dependable Systems, Sedona, AZ, USA, 2–4 February 2005; pp. 263–270. [Google Scholar] [CrossRef]
- Shahrjooi Haghighi, A.; Abbasi Dezfuli, M.; Fakhrahmad, S. Applying Mining Schemes to Software Fault Prediction: A Proposed Approach Aimed at Test Cost Reduction. In Proceedings of the World Congress on Engineering (WCE 2012), London, UK, 4–6 July 2012; pp. 1–5. [Google Scholar]
- Cohen, W.W. Fast Effective Rule Induction. In Proceedings of the Twelfth International Conference on Machine Learning; Morgan Kaufmann: San Francisco, CA, USA, 1995; pp. 115–123. [Google Scholar]
- Tantithamthavorn, C.; McIntosh, S.; Hassan, A.E.; Matsumoto, K. An Empirical Comparison of Model Validation Techniques for Defect Prediction Models. IEEE Trans. Softw. Eng. 2017, 43, 1–18. [Google Scholar] [CrossRef]





| Dataset | # of Metrics | # of Instances | # of Defective Instances | Defect Ratio |
|---|---|---|---|---|
| CM1 | 37 | 327 | 42 | 0.1284 |
| KC1 | 21 | 1183 | 314 | 0.2654 |
| KC3 | 39 | 194 | 36 | 0.1856 |
| MC1 | 38 | 1988 | 46 | 0.0231 |
| MC2 | 39 | 125 | 44 | 0.352 |
| MW1 | 37 | 253 | 27 | 0.1067 |
| PC1 | 37 | 705 | 61 | 0.0865 |
| PC2 | 36 | 745 | 16 | 0.0215 |
| PC3 | 37 | 1077 | 134 | 0.1244 |
| PC4 | 37 | 1287 | 177 | 0.1375 |
| JM1 | 21 | 7782 | 1672 | 0.2149 |
| Predicted | |||
|---|---|---|---|
| Positive | Negative | ||
| Actual | Positive | TP | FN |
| Negative | FP | TN | |
| No. | Class | Score | No. | Class | Score |
|---|---|---|---|---|---|
| 1 | P | 0.9 | 11 | P | 0.43 |
| 2 | P | 0.8 | 12 | N | 0.39 |
| 3 | N | 0.7 | 13 | P | 0.38 |
| 4 | P | 0.6 | 14 | N | 0.27 |
| 5 | N | 0.59 | 15 | N | 0.26 |
| 6 | P | 0.55 | 16 | N | 0.25 |
| 7 | N | 0.33 | 17 | P | 0.24 |
| 8 | N | 0.47 | 18 | N | 0.23 |
| 9 | P | 0.76 | 19 | N | 0.12 |
| 10 | N | 0.49 | 20 | N | 0.15 |
| Data | Our CIB | MAHAKIL [44] | AdaC2 [45] | AdaBoost [46] | SMOTE [40] | RUS [35] | None |
|---|---|---|---|---|---|---|---|
| CM1 | 28.3 ± 5.1✓ | 28.6 ± 5.1 | 18.9 ± 6.1 | 19.4 ± 5.5 | 30.8 ± 4.7 | 29.8 ± 3.7✓ | 20.4 ± 7.6 |
| KC1 | 44.3 ± 2.1 | 41.4 ± 1.9 | 42.6 ± 1.5 | 41.7 ± 1.8 | 40.6 ± 2.7 | 43.3 ± 2.2 ✓ | 35.6 ± 2.7 |
| KC3 | 40.4 ± 4.7 | 40.0 ± 5.7 ✓ | 32.6 ± 7.0 | 32.5 ± 5.9 | 40.2 ± 4.1 ✓ | 39.6 ± 5.6 ✓ | 34.4 ± 7.2 |
| MC1 | 23.8 ± 4.9 | 16.6 ± 4.8 | 41.3 ± 6.2 ✓ | 41.4 ± 6.9 | 13.1 ± 3.8 | 9.6 ± 1.1 | 11.9 ± 6.3 |
| MC2 | 58.2 ± 4.4 | 54.2 ± 4.6 | 55.8 ± 5.2 | 54.3 ± 5.8 | 50.4 ± 6.2 | 51.2 ± 6.0 | 46.6 ± 5.7 |
| MW1 | 31.0 ± 4.6 | 26.3 ± 6.0 | 30.0 ± 6.5 ✓ | 26.2 ± 7.1 | 28.4 ± 5.6 | 23.7 ± 3.6 | 29.4 ± 8.0 ✓ |
| PC1 | 41.5 ± 4.4 | 34.2 ± 3.4 | 40.7 ± 4.0 ✓ | 40.4 ± 5.4 ✓ | 35.0 ± 4.5 | 30.1 ± 2.2 | 30.7 ± 6.7 |
| PC2 | 14.8 ± 5.6 ✓ | 15.7 ± 7.8 | 1.4 ± 3.0 | 0.8 ± 2.4 | 13.3 ± 6.5 ✓ | 9.5 ± 1.4 | 0.6 ± 1.9 |
| PC3 | 37.7 ± 2.9 | 34.1 ± 2.8 | 28.9 ± 3.4 | 28.0 ± 3.0 | 33.7 ± 3.1 | 36.7 ± 2.2 ✓ | 27.0 ± 4.7 |
| PC4 | 62.1 ± 1.9 | 53.6 ± 2.2 | 58.6 ± 2.6 | 58.2 ± 2.4 | 56.6 ± 2.0 | 54.5 ± 1.5 | 53.0 ± 2.7 |
| JM1 | 37.4 ± 0.9 | 34.7 ± 1.2 | 33.9 ± 1.0 | 33.8 ± 0.7 | 33.9 ± 1.2 | 41.1 ± 0.5 | 27.6 ± 1.8 |
| Average | 38.1 | 34.5 | 35 | 34.2 | 34.2 | 33.6 | 28.8 |
| Improvement of Average | 10.6% | 9% | 11.4% | 11.6% | 13.7% | 32.3% | |
| Win/Tie/Lose | 8/3/0 | 8/2/1 | 9/1/1 | 8/3/0 | 6/4/1 | 10/1/0 | |
 ,
,  , and
, and  indicate that our CIB method significantly outperforms the corresponding baseline with large, moderate, and small effect size, respectively.
indicate that our CIB method significantly outperforms the corresponding baseline with large, moderate, and small effect size, respectively.| Data | Our CIB | MAHAKIL [44] | AdaC2 [45] | AdaBoost [46] | SMOTE [40] | RUS [35] | None |
|---|---|---|---|---|---|---|---|
| CM1 | 17.5 ± 1.5 | 18.5 ± 1.3 ✓ | 12.0 ± 3.2 | 12.4 ± 2.9 | 19.0 ± 1.0 | 18.0 ± 1.9 | 12.9 ± 3.6 |
| KC1 | 31.4 ± 0.4 | 31.6 ± 0.4 | 30.7 ± 0.3 | 30.5 ± 0.4 | 30.9 ± 0.9 | 32.8 ± 0.8 | 28.0 ± 1.0 |
| KC3 | 23.4 ± 1.7 | 23.4 ± 1.9 ✓ | 20.3 ± 3.0 | 20.9 ± 2.6 | 23.4 ± 1.6 ✓ | 23.4 ± 1.7 ✓ | 21.1 ± 2.9 |
| MC1 | 6.5 ± 0.9 | 5.2 ± 1.2 | 7.7 ± 0.7 | 7.7 ± 0.7 ✓ | 5.1 ± 1.2 | 4.4 ± 0.6 | 3.3 ± 1.5 |
| MC2 | 35.6 ± 2.2 | 35.6 ± 3.0 ✓ | 35.5 ± 2.3 | 36.1 ± 1.5 ✓ | 36.8 ± 1.4 ✓ | 36.9 ± 3.4 | 35.6 ± 1.8 ✓ |
| MW1 | 15.5 ± 1.9 ✓ | 15.1 ± 2.1 ✓ | 14.0 ± 2.5 | 12.9 ± 2.9 | 15.3 ± 2.3 ✓ | 15.7 ± 2.1 | 13.7 ± 3.5 |
| PC1 | 16.0 ± 0.7 | 15.4 ± 0.8 | 15.7 ± 0.6 | 15.5 ± 1.0 | 15.7 ± 0.6 | 12.3 ± 1.8 | 14.3 ± 1.6 |
| PC2 | 3.3 ± 1.1 ✓ | 3.9 ± 1.8 | 0.3 ± 0.6 | 0.2 ± 0.5 | 3.4 ± 1.6 ✓ | 3.0 ± 1.1 | 0.2 ± 0.5 |
| PC3 | 19.7 ± 0.5 | 19.1 ± 0.8 | 17.2 ± 0.9 | 17.0 ± 0.8 | 19.6 ± 0.4 ✓ | 17.0 ± 1.4 | 16.5 ± 2.1 |
| PC4 | 20.2 ± 0.6 | 21.0 ± 0.5 | 21.6 ± 0.3 ✓ | 21.7 ± 0.2 | 20.5 ± 0.4 | 15.0 ± 1.5 | 21.3 ± 0.4 |
| JM1 | 26.7 ± 0.2 | 26.1 ± 0.4 | 25.2 ± 0.2 | 25.3 ± 0.2 | 25.6 ± 0.4 | 29.0 ± 0.1 | 22.2 ± 0.9 |
| Average | 19.6 | 19.5 | 18.2 | 18.2 | 19.6 | 18.9 | 17.2 |
| Improvement of Average | 0.4% | 7.8% | 7.8% | 0.2% | 4% | 14.1% | |
| Win/Tie/Lose | 4/4/3 | 8/1/2 | 8/1/2 | 4/4/3 | 4/4/3 | 9/1/1 | |
 ,
,  , and
, and  indicate our CIB method significantly outperforms the corresponding baseline with large, moderate, and small effect size, respectively.
indicate our CIB method significantly outperforms the corresponding baseline with large, moderate, and small effect size, respectively.| Data | Our CIB | MAHAKIL [44] | AdaC2 [45] | AdaBoost [46] | SMOTE [40] | RUS [35] | None |
|---|---|---|---|---|---|---|---|
| CM1 | 18.4 ± 5.6 ✓ | 16.9 ± 5.9 | 12.6 ± 6.7 | 13.7 ± 6.4 | 19.4 ± 5.7 | 17.3 ± 5.6 ✓ | 12.7 ± 7.7 |
| KC1 | 25.5 ± 2.7 ✓ | 20.4 ± 2.6 | 25.6 ± 2.0 | 24.7 ± 2.4 ✓ | 20.9 ± 2.7 | 17.7 ± 2.7 | 21.7 ± 2.5 |
| KC3 | 28.7 ± 6.1 | 27.0 ± 6.9 ✓ | 23.1 ± 8.4 | 23.0 ± 6.8 | 26.7 ± 5.2 ✓ | 23.2 ± 8.1 | 25.4 ± 8.5 ✓ |
| MC1 | 22.9 ± 4.8 | 15.8 ± 5.1 | 43.5 ± 5.9 ✓ | 44.0 ± 7.0 | 11.0 ± 4.0 | 12.8 ± 2.4 | 13.4 ± 7.7 |
| MC2 | 37.4 ± 6.9 | 31.4 ± 7.6 | 36.1 ± 8.3 ✓ | 34.5 ± 7.8 | 23.3 ± 8.4 | 21.1 ± 9.3 | 22.0 ± 8.3 |
| MW1 | 23.3 ± 5.3 | 17.0 ± 6.8 | 24.8 ± 7.2 ✓ | 21.4 ± 7.7 | 19.0 ± 6.4 | 11.9 ± 5.7 | 26.0 ± 8.7 |
| PC1 | 36.3 ± 4.8 | 27.8 ± 3.9 | 38.3 ± 4.4 ✓ | 38.6 ± 5.6 | 28.6 ± 5.2 | 26.4 ± 3.6 | 26.1 ± 6.8 |
| PC2 | 13.7 ± 6.0 ✓ | 14.4 ± 8.2 | 0.6 ± 3.3 | 0.2 ± 2.8 | 11.8 ± 7.1 ✓ | 13.2 ± 3.3 ✓ | 0.1 ± 2.0 |
| PC3 | 28.9 ± 3.3 | 24.3 ± 3.2 | 23.2 ± 3.7 | 22.4 ± 3.6 | 23.6 ± 3.6 | 28.3 ± 3.4 ✓ | 20.1 ± 4.2 |
| PC4 | 55.9 ± 2.2 | 45.9 ± 2.6 | 53.3 ± 2.9 | 52.9 ± 2.7 | 49.4 ± 2.3 | 49.1 ± 2.1 | 46.6 ± 2.9 |
| JM1 | 22.5 ± 1.0 | 18.7 ± 1.2 | 21.1 ± 1.1 | 21.0 ± 0.9 | 19.3 ± 1.2 | 19.7 ± 0.8 | 18.0 ± 1.1 |
| Average | 28.5 | 23.6 | 27.5 | 26.9 | 23 | 21.9 | 21.1 |
| Improvement of Average | 20.8% | 3.7% | 5.8% | 23.9% | 30.2% | 35.1% | |
| Win/Tie/Lose | 8/3/0 | 6/3/2 | 7/2/2 | 8/3/0 | 8/3/0 | 9/1/1 | |
 ,
,  , and
, and  indicate our CIB method significantly outperforms the corresponding baseline with large, moderate, and small effect size, respectively.
indicate our CIB method significantly outperforms the corresponding baseline with large, moderate, and small effect size, respectively.| Data | Our CIB | MAHAKIL [44] | AdaC2 [45] | AdaBoost [46] | SMOTE [40] | RUS [35] | None |
|---|---|---|---|---|---|---|---|
| CM1 | 72.7 ± 2.2 | 59.6 ± 4.4 | 73.4 ± 3.0 ✓ | 74.3 ± 3.4 | 61.3 ± 5.2 | 62.9 ± 4.1 | 55.0 ± 5.3 |
| KC1 | 67.8 ± 1.2 ✓ | 59.2 ± 2.2 | 68.1 ± 0.9 | 67.5 ± 1.5 ✓ | 60.2 ± 1.5 | 60.1 ± 1.6 | 58.6 ± 1.9 |
| KC3 | 72.2 ± 3.8 | 61.1 ± 5.8 | 69.5 ± 3.6 | 69.3 ± 3.4 | 61.7 ± 5.0 | 63.4 ± 6.1 | 58.9 ± 5.4 |
| MC1 | 83.3 ± 2.4 | 69.6 ± 4.6 | 85.7 ± 4.0 | 85.6 ± 3.3 ✓ | 65.8 ± 4.9 | 70.4 ± 4.3 | 60.1 ± 5.2 |
| MC2 | 75.5 ± 2.8 | 66.4 ± 4.6 | 73.9 ± 3.8 | 74.8 ± 4.0 ✓ | 61.5 ± 3.9 | 61.8 ± 5.9 | 61.4 ± 5.7 |
| MW1 | 69.1 ± 3.1 ✓ | 58.1 ± 6.6 | 69.5 ± 3.9 ✓ | 69.7 ± 2.6 | 62.4 ± 4.1 | 60.4 ± 5.0 | 54.5 ± 6.8 |
| PC1 | 85.9 ± 1.7 | 70.2 ± 4.2 | 84.0 ± 1.9 | 84.3 ± 2.1 | 68.8 ± 4.0 | 73.5 ± 3.5 | 66.1 ± 5.5 |
| PC2 | 79.4 ± 5.6 | 63.7 ± 10.1 | 72.4 ± 5.1 | 72.4 ± 4.9 | 56.0 ± 10.1 | 72.5 ± 4.7 | 50.7 ± 2.2 |
| PC3 | 80.6 ± 1.2 | 63.3 ± 2.9 | 79.6 ± 1.3 | 79.0 ± 1.3 | 61.8 ± 3.0 | 69.7 ± 3.1 | 63.3 ± 3.7 |
| PC4 | 92.3 ± 0.5 ✓ | 72.3 ± 2.3 | 92.6 ± 0.5 | 92.4 ± 0.6 ✓ | 75.2 ± 2.3 | 81.9 ± 1.8 | 74.7 ± 3.9 |
| JM1 | 67.2 ± 0.5 | 61.0 ± 0.8 | 66.7 ± 0.6 | 66.5 ± 0.5 | 62.3 ± 0.8 | 61.8 ± 0.7 | 61.4 ± 1.1 |
| Average | 76.9 | 64 | 75.9 | 76 | 63.4 | 67.1 | 60.4 |
| Improvement of Average | 20.1% | 1.3% | 1.2% | 21.4% | 14.6% | 27.3% | |
| Win/Tie/Lose | 11/0/0 | 6/4/1 | 5/4/2 | 11/0/0 | 11/0/0 | 11/0/0 | |
 ,
,  , and
, and  indicate our CIB method significantly outperforms the corresponding baseline with large, moderate, and small effect size, respectively.
indicate our CIB method significantly outperforms the corresponding baseline with large, moderate, and small effect size, respectively.| Data | Our CIB | MAHAKIL [44] | AdaC2 [45] | AdaBoost [46] | SMOTE [40] | RUS [35] | None |
|---|---|---|---|---|---|---|---|
| CM1 | [26.5, 30.1] | [26.8, 30.4] | [16.7, 21.1] | [17.4, 21.4] | [29.1, 32.5] | [28.5, 31.1] | [17.7, 23.1] |
| KC1 | [43.5, 45.1] | [41.0, 42.6] | [42.1, 43.1] | [41.1, 42.3] | [39.6, 41.6] | [42.5, 44.1] | [34.6, 36.6] |
| KC3 | [38.7, 42.1] | [38.0, 42.0] | [30.1, 35.1] | [30.4, 34.6] | [38.7, 41.7] | [37.6, 41.6] | [31.8, 37.0] |
| MC1 | [22.0, 25.6] | [14.9, 18.3] | [39.1, 43.5] | [38.9, 43.9] | [11.7, 14.5] | [9.2, 10.0] | [9.6, 14.2] |
| MC2 | [56.6, 59.8] | [52.6, 55.8] | [53.9, 57.7] | [52.2, 56.4] | [48.2, 52.6] | [49.1, 53.3] | [44.6, 48.6] |
| MW1 | [29.4, 32.6] | [24.3, 28.5] | [27.7, 32.3] | [23.7, 28.7] | [26.4, 30.4] | [22.4, 25.0] | [26.5, 32.3] |
| PC1 | [39.9, 43.1] | [31.8, 35.0] | [39.3, 42.1] | [38.5, 42.3] | [33.4, 36.6] | [29.3, 30.9] | [28.3, 33.1] |
| PC2 | [12.8, 16.8] | [12.9, 18.5] | [0.3, 2.5] | [−0.1, 1.7] | [11.0, 15.6] | [9.0, 10.0] | [−0.1, 1.3] |
| PC3 | [36.7, 38.7] | [31.4, 34.2] | [27.7, 30.1] | [26.9, 29.1] | [32.6, 34.8] | [35.9, 37.5] | [25.3, 28.7] |
| PC4 | [61.4, 62.8] | [52.7, 54.9] | [57.7, 59.5] | [57.3, 59.1] | [55.9, 57.3] | [54.0, 55.0] | [52.0, 54.0] |
| JM1 | [37.0, 37.8] | [33.7, 34.9] | [33.5, 34.3] | [33.7, 34.3] | [33.3, 34.5] | [40.7, 41.1] | [26.3, 27.9] |
| Data | Our CIB | MAHAKIL [44] | AdaC2 [45] | AdaBoost [46] | SMOTE [40] | RUS [35] | None |
|---|---|---|---|---|---|---|---|
| CM1 | [17.0, 18.0] | [18.0, 19.0] | [10.9, 13.1] | [11.4, 13.4] | [18.6, 19.4] | [17.3, 18.7] | [11.6, 14.2] |
| KC1 | [31.3, 31.5] | [31.5, 31.7] | [30.6, 30.8] | [30.4, 30.6] | [30.6, 31.2] | [32.5, 33.1] | [27.6, 28.4] |
| KC3 | [22.8, 24.0] | [22.7, 24.1] | [19.2, 21.4] | [20.0, 21.8] | [22.8, 24.0] | [22.8, 24.0] | [20.1, 22.1] |
| MC1 | [6.2, 6.8] | [4.8, 5.6] | [7.4, 8.0] | [7.4, 8.0] | [4.7, 5.5] | [4.2, 4.6] | [2.8, 3.8] |
| MC2 | [34.8, 36.4] | [34.5, 36.7] | [34.7, 36.3] | [35.6, 36.6] | [36.3, 37.3] | [35.7, 38.1] | [35.0, 36.2] |
| MW1 | [14.8, 16.2] | [14.3, 15.9] | [13.1, 14.9] | [11.9, 13.9] | [14.5, 16.1] | [14.9, 16.5] | [12.4, 15.0] |
| PC1 | [15.7, 16.3] | [15.1, 15.7] | [15.5, 15.9] | [15.1, 15.9] | [15.5, 15.9] | [11.7, 12.9] | [13.7, 14.9] |
| PC2 | [2.9, 3.7] | [3.3, 4.5] | [0.1, 0.5] | [0.0, 0.4] | [2.8, 4.0] | [2.6, 3.4] | [0.0, 0.4] |
| PC3 | [19.5, 19.9] | [18.8, 19.4] | [16.9, 17.5] | [16.7, 17.3] | [19.5, 19.7] | [16.5, 17.5] | [15.7, 17.3] |
| PC4 | [20.0, 20.4] | [20.8, 21.2] | [21.5, 21.7] | [21.6, 21.8] | [20.4, 20.6] | [14.5, 15.5] | [21.2, 21.4] |
| JM1 | [26.6, 26.8] | [25.9, 26.3] | [25.1, 25.3] | [25.2, 25.4] | [25.4, 25.8] | [29.0, 29.0] | [21.8, 22.6] |
| Data | Our CIB | MAHAKIL [44] | AdaC2 [45] | AdaBoost [46] | SMOTE [40] | RUS [35] | None |
|---|---|---|---|---|---|---|---|
| CM1 | [16.4, 20.4] | [14.8, 19.0] | [10.2, 15.0] | [11.4, 16.0] | [17.4, 21.4] | [15.3, 19.3] | [9.9, 15.5] |
| KC1 | [24.5, 26.5] | [19.6, 21.6] | [24.9, 26.3] | [23.8, 25.6] | [19.9, 21.9] | [16.7, 18.7] | [20.8, 22.6] |
| KC3 | [26.5, 30.9] | [24.5, 29.5] | [20.1, 26.1] | [20.6, 25.4] | [24.8, 28.6] | [20.3, 26.1] | [22.4, 28.4] |
| MC1 | [21.2, 24.6] | [14.0, 17.6] | [41.4, 45.6] | [41.5, 46.5] | [9.6, 12.4] | [11.9, 13.7] | [10.6, 16.2] |
| MC2 | [34.9, 39.9] | [28.7, 34.1] | [33.1, 39.1] | [31.7, 37.3] | [20.3, 26.3] | [17.8, 24.4] | [19.0, 25.0] |
| MW1 | [21.4, 25.2] | [14.7, 19.5] | [22.2, 27.4] | [18.6, 24.2] | [16.7, 21.3] | [9.9, 13.9] | [22.9, 29.1] |
| PC1 | [34.6, 38.0] | [25.2, 28.8] | [36.7, 39.9] | [36.6, 40.6] | [26.7, 30.5] | [25.1, 27.7] | [23.7, 28.5] |
| PC2 | [11.6, 15.8] | [11.5, 17.3] | [−0.6, 1.8] | [−0.8, 1.2] | [9.3, 14.3] | [12.0, 14.4] | [−0.6, 0.8] |
| PC3 | [27.7, 30.1] | [21.5, 24.5] | [21.9, 24.5] | [21.1, 23.7] | [22.3, 24.9] | [27.1, 29.5] | [18.6, 21.6] |
| PC4 | [55.1, 56.7] | [44.8, 47.4] | [52.3, 54.3] | [51.9, 53.9] | [48.6, 50.2] | [48.3, 49.9] | [45.6, 47.6] |
| JM1 | [22.1, 22.9] | [17.9, 19.1] | [20.6, 21.6] | [20.8, 21.6] | [18.9, 20.1] | [19.2, 20.0] | [17.2, 18.4] |
| Data | Our CIB | MAHAKIL [44] | AdaC2 [45] | AdaBoost [46] | SMOTE [40] | RUS [35] | None |
|---|---|---|---|---|---|---|---|
| CM1 | [71.9, 73.5] | [58.0, 61.2] | [72.3, 74.5] | [73.1, 75.5] | [59.4, 63.2] | [61.4, 64.4] | [53.1, 56.9] |
| KC1 | [67.4, 68.2] | [58.5, 59.7] | [67.8, 68.4] | [67.0, 68.0] | [59.7, 60.7] | [59.5, 60.7] | [57.9, 59.3] |
| KC3 | [70.8, 73.6] | [59.1, 63.3] | [68.2, 70.8] | [68.1, 70.5] | [59.9, 63.5] | [61.2, 65.6] | [57.0, 60.8] |
| MC1 | [82.4, 84.2] | [68.0, 71.2] | [84.3, 87.1] | [84.4, 86.8] | [64.0, 67.6] | [68.9, 71.9] | [58.2, 62.0] |
| MC2 | [74.5, 76.5] | [64.8, 68.0] | [72.5, 75.3] | [73.4, 76.2] | [60.1, 62.9] | [59.7, 63.9] | [59.4, 63.4] |
| MW1 | [68.0, 70.2] | [55.7, 60.5] | [68.1, 70.9] | [68.8, 70.6] | [60.9, 63.9] | [58.6, 62.2] | [52.1, 56.9] |
| PC1 | [85.3, 86.5] | [68.0, 71.6] | [83.3, 84.7] | [83.5, 85.1] | [67.4, 70.2] | [72.2, 74.8] | [64.1, 68.1] |
| PC2 | [77.4, 81.4] | [60.1, 67.3] | [70.6, 74.2] | [70.6, 74.2] | [52.4, 59.6] | [70.8, 74.2] | [49.9, 51.5] |
| PC3 | [80.2, 81.0] | [60.4, 63.4] | [79.1, 80.1] | [78.5, 79.5] | [60.7, 62.9] | [68.6, 70.8] | [62.0, 64.6] |
| PC4 | [92.1, 92.5] | [71.9, 73.9] | [92.4, 92.8] | [92.2, 92.6] | [74.4, 76.0] | [81.3, 82.5] | [73.3, 76.1] |
| JM1 | [67.1, 67.5] | [60.7, 61.5] | [66.4, 66.8] | [66.2, 66.8] | [61.9, 62.7] | [61.5, 62.1] | [60.8, 62.0] |
| Dataset | # of Metrics | # of Instances | # of Defective Instances | Defect Ratio |
|---|---|---|---|---|
| ant-1.7 | 20 | 745 | 166 | 0.2228 |
| camel-1.6 | 20 | 965 | 188 | 0.1948 |
| ivy-2.0 | 20 | 352 | 40 | 0.1136 |
| jedit-4.1 | 20 | 312 | 79 | 0.2532 |
| log4j-1.0 | 20 | 135 | 34 | 0.2519 |
| prop-6 | 20 | 660 | 66 | 0.1 |
| tomcat | 20 | 858 | 77 | 0.0897 |
| xalan-2.6 | 20 | 885 | 411 | 0.4644 |
| xerces-1.3 | 20 | 453 | 69 | 0.1523 |
| Data | Our CIB | MAHAKIL [44] | AdaC2 [45] | AdaBoost [46] | SMOTE [40] | RUS [35] | None |
|---|---|---|---|---|---|---|---|
| CM1 | 11.05 | 2.2 | 0.53 | 0.23 | 0.38 | 0.03 | 0.02 |
| KC1 | 30.03 | 1.98 | 0.83 | 0.73 | 0.39 | 0.03 | 0.03 |
| KC3 | 3.52 | 0.56 | 0.25 | 0.17 | 0.2 | 0.02 | 0.01 |
| MC1 | 279.27 | 6.08 | 1.38 | 0.97 | 0.41 | 0.02 | 0.03 |
| MC2 | 2.11 | 0.36 | 0.22 | 0.06 | 0.22 | 0 | 0.01 |
| MW1 | 5.92 | 0.7 | 0.22 | 0.14 | 0.2 | 0 | 0.01 |
| PC1 | 31.56 | 2.16 | 0.52 | 0.38 | 0.23 | 0.02 | 0.01 |
| PC2 | 41.45 | 2.25 | 0.33 | 0.2 | 0.23 | 0 | 0.01 |
| PC3 | 64.95 | 2.83 | 0.88 | 0.83 | 0.28 | 0.02 | 0.03 |
| PC4 | 87 | 3.14 | 0.86 | 0.83 | 0.42 | 0.03 | 0.07 |
| JM1 | 1898.88 | 10.11 | 14.59 | 10.94 | 1.84 | 0.28 | 0.31 |
| Average | 223.25 | 2.94 | 1.87 | 1.41 | 0.44 | 0.04 | 0.05 |
| Data | Our CIB | MAHAKIL [44] | AdaC2 [45] | AdaBoost [46] | SMOTE [40] | RUS [35] | None |
|---|---|---|---|---|---|---|---|
| CM1 | 0.203 | 0.219 | 0.203 | 0.266 | 0.156 | 0.313 | 0.225 |
| KC1 | 0.188 | 0.172 | 0.141 | 0.125 | 0.406 | 0.109 | 0.127 |
| KC3 | 0.141 | 0.094 | 0.125 | 0.125 | 0.188 | 0.172 | 0.134 |
| MC1 | 0.172 | 0.078 | 0.172 | 0.109 | 0.172 | 0.141 | 0.122 |
| MC2 | 0.141 | 0.078 | 0.172 | 0.109 | 0.125 | 0.141 | 0.112 |
| MW1 | 0.141 | 0.109 | 0.141 | 0.172 | 0.172 | 0.156 | 0.162 |
| PC1 | 0.156 | 0.078 | 0.156 | 0.172 | 0.141 | 0.125 | 0.119 |
| PC2 | 0.188 | 0.094 | 0.156 | 0.125 | 0.125 | 0.203 | 0.158 |
| PC3 | 0.141 | 0.094 | 0.125 | 0.125 | 0.125 | 0.125 | 0.139 |
| PC4 | 0.141 | 0.078 | 0.141 | 0.156 | 0.141 | 0.156 | 0.127 |
| JM1 | 0.234 | 0.094 | 0.141 | 0.172 | 0.234 | 0.125 | 0.115 |
| Average | 0.168 | 0.108 | 0.152 | 0.151 | 0.18 | 0.161 | 0.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, H.; Wang, S.; Li, G. Credibility Based Imbalance Boosting Method for Software Defect Proneness Prediction. Appl. Sci. 2020, 10, 8059. https://doi.org/10.3390/app10228059
Tong H, Wang S, Li G. Credibility Based Imbalance Boosting Method for Software Defect Proneness Prediction. Applied Sciences. 2020; 10(22):8059. https://doi.org/10.3390/app10228059
Chicago/Turabian StyleTong, Haonan, Shihai Wang, and Guangling Li. 2020. "Credibility Based Imbalance Boosting Method for Software Defect Proneness Prediction" Applied Sciences 10, no. 22: 8059. https://doi.org/10.3390/app10228059
APA StyleTong, H., Wang, S., & Li, G. (2020). Credibility Based Imbalance Boosting Method for Software Defect Proneness Prediction. Applied Sciences, 10(22), 8059. https://doi.org/10.3390/app10228059





