Online Reinforcement Learning-Based Control of an Active Suspension System Using the Actor Critic Approach
Abstract
1. Introduction
2. Methods
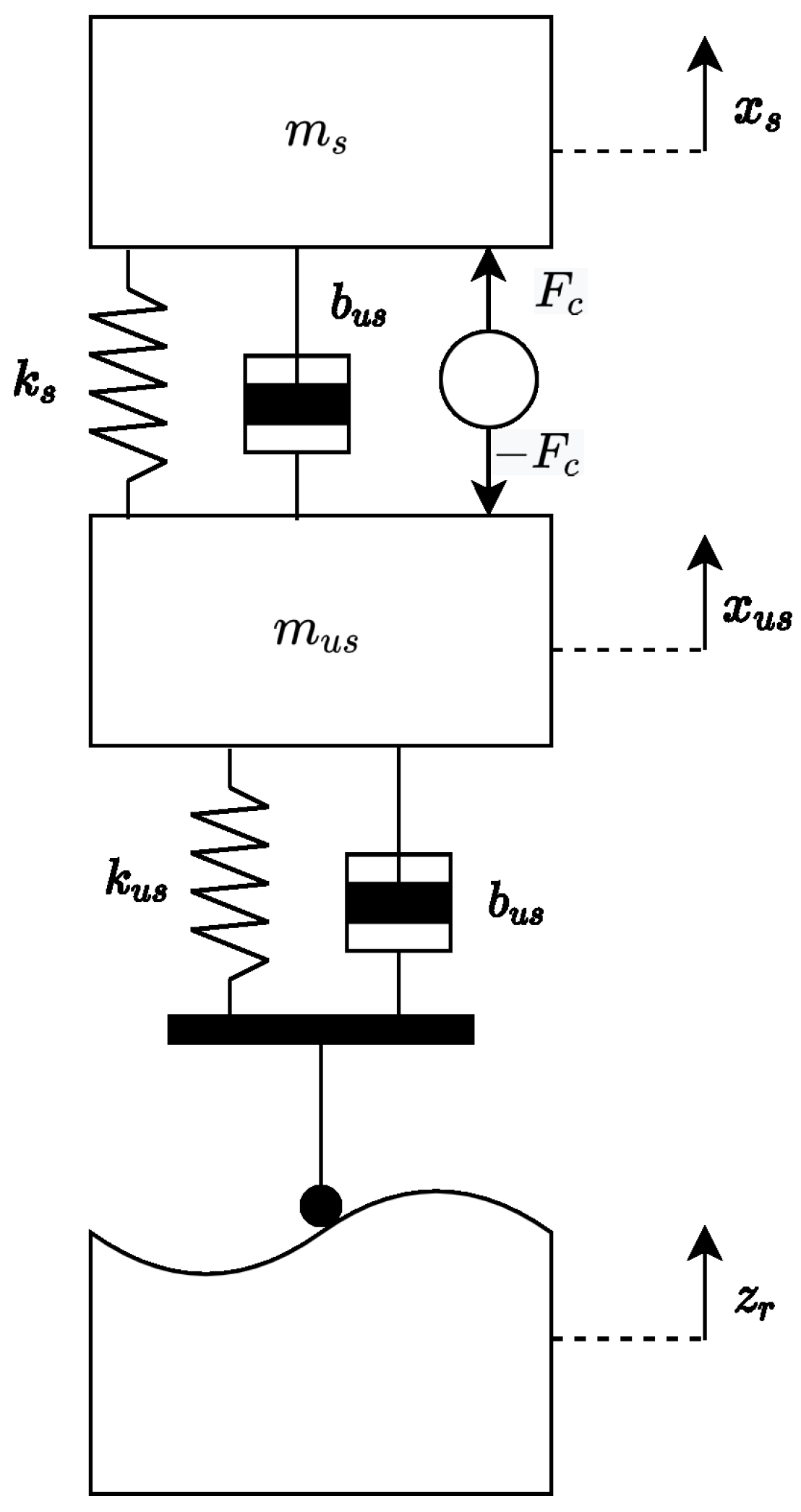
2.1. Modeling of the Active Suspension System
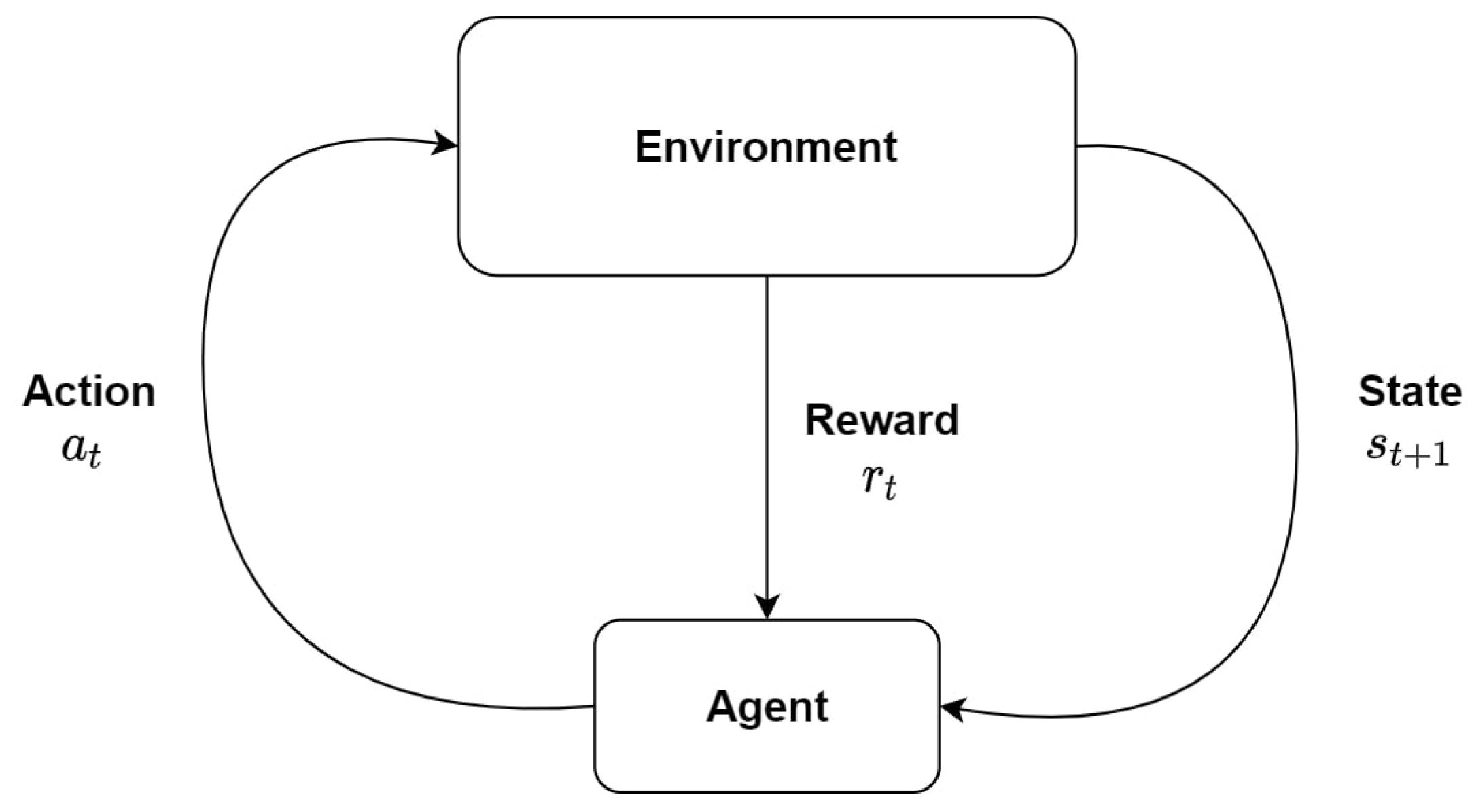
2.2. Reinforcement Learning
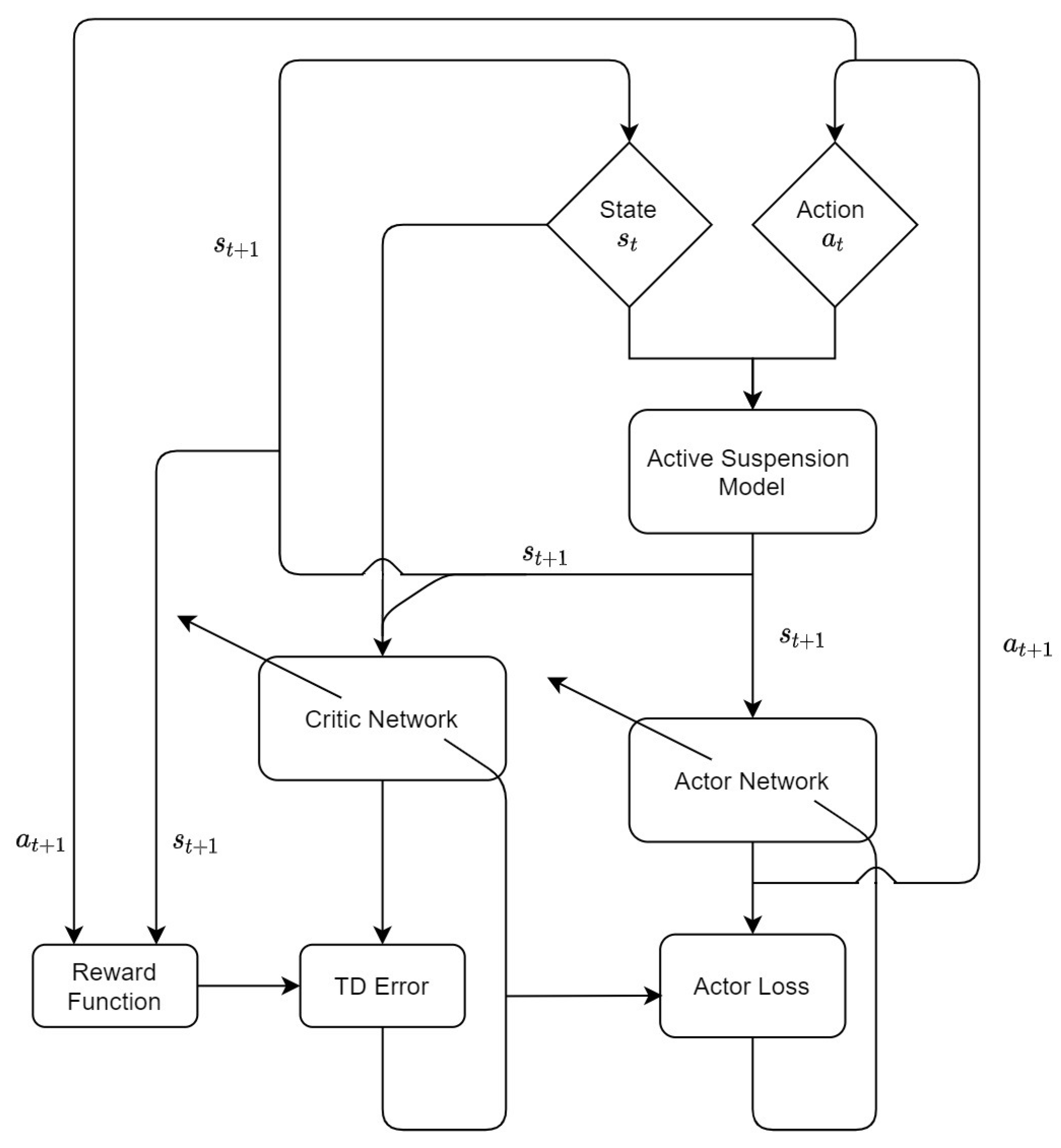
2.2.1. TD Advantage Actor Critic Algorithm
| Algorithm 1: TD Advantage Actor Critic. |
| Initialize the Critic Network and the Actor Network |
| for episode = 1:M |
| Start from the initial state |
| for i = 1:N |
| Sample action |
| Execute action in the environment and obtain the reward r and step to the next state |
| Calculate the temporal difference error |
| Update the Critic parameters by minimizing |
| Update the Actor parameters by minimizing the Loss = |
| Set |
| end |
| end |
2.2.2. Reward Function
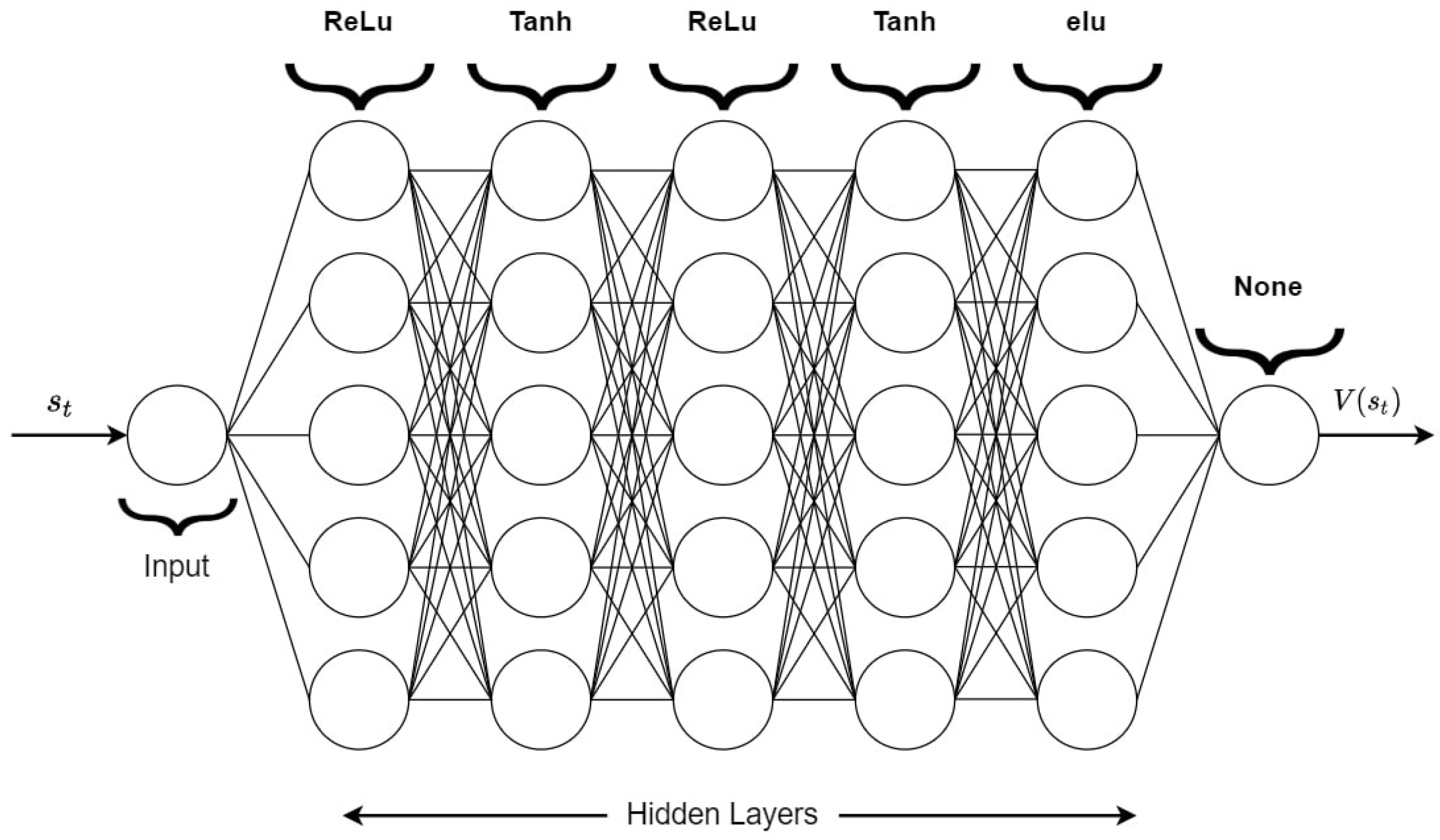
2.2.3. Learning and Optimization
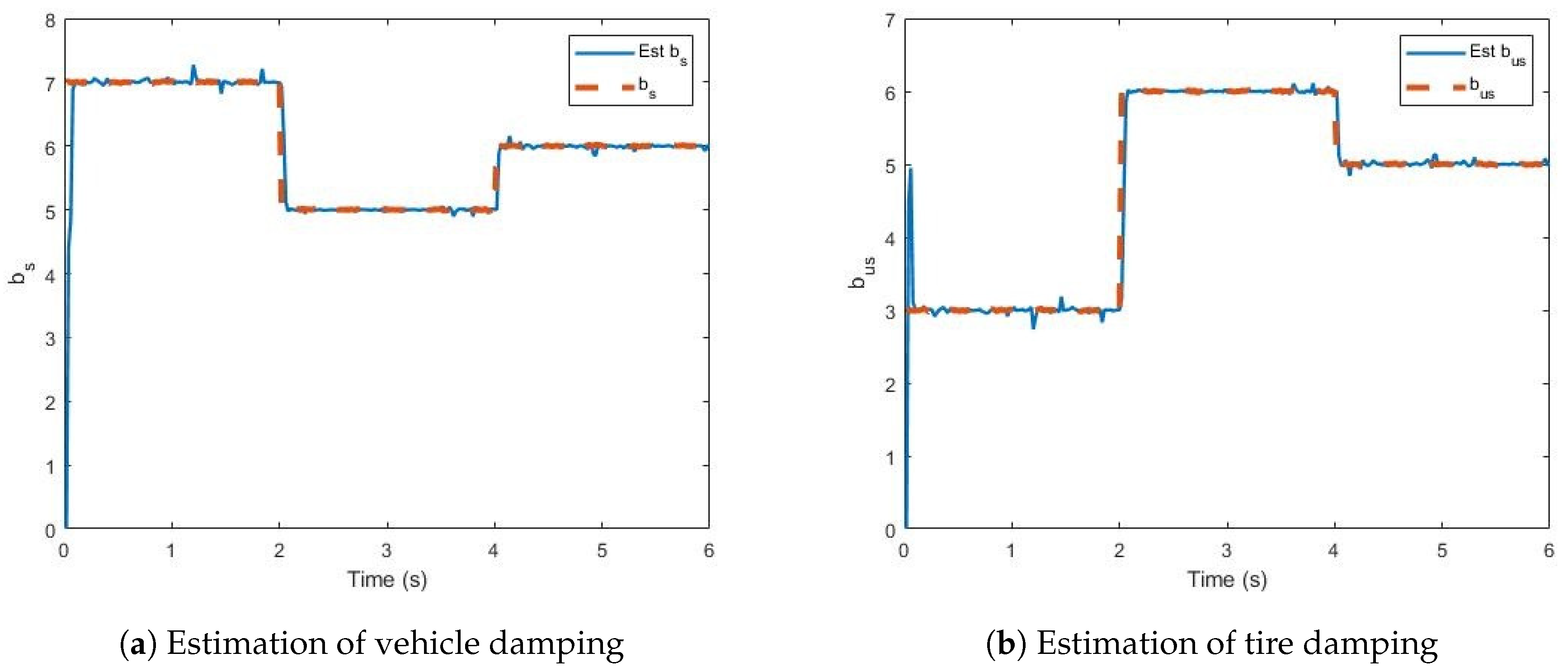
2.3. Online Estimation
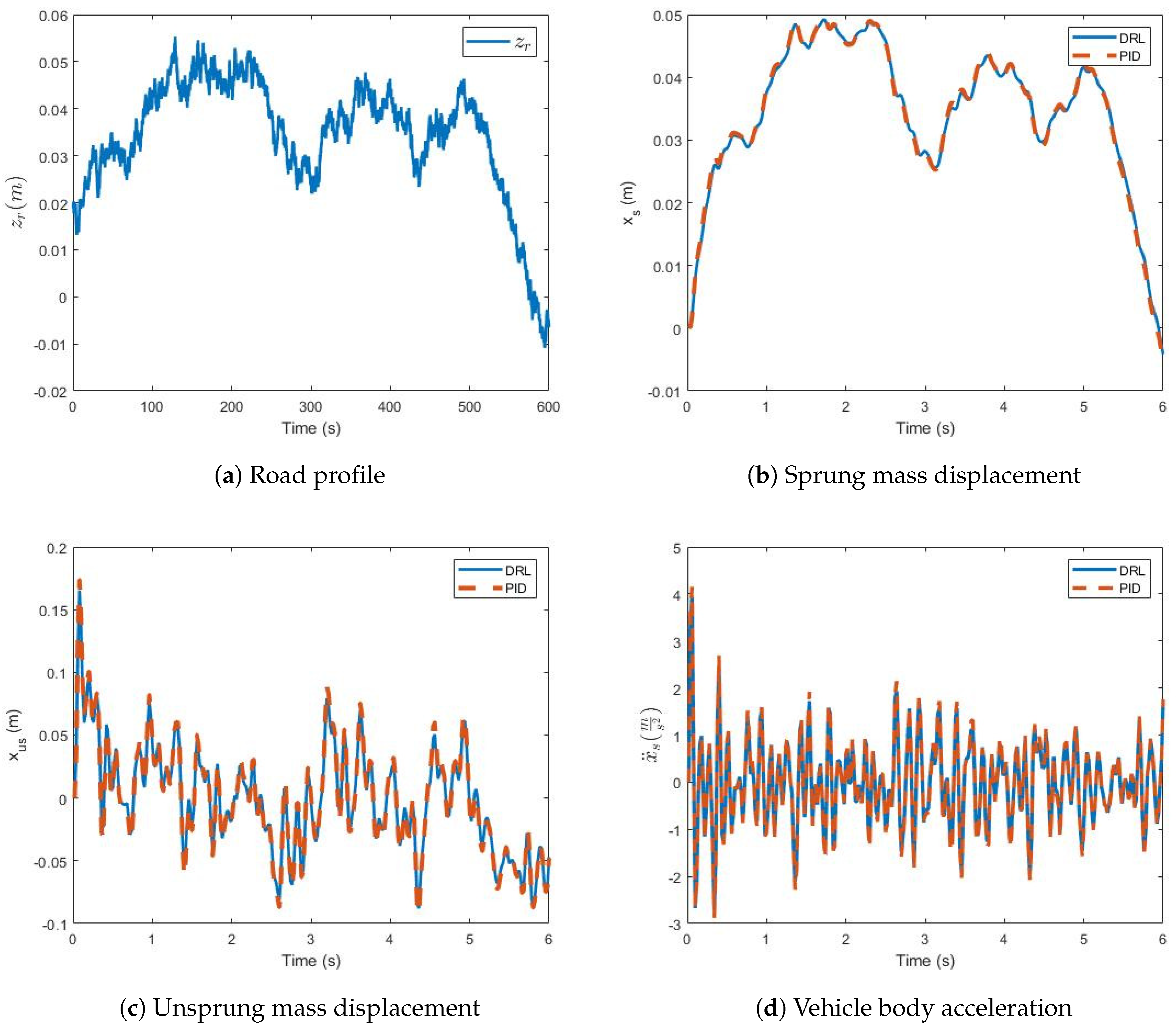
3. Results and Discussion
3.1. Scenario 1
3.2. Scenario 2
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ramsbottom, M.; Crolla, D.; Plummer, A.R. Robust adaptive control of an active vehicle suspension system. J. Automob. Eng. 1999, 213, 1–17. [Google Scholar] [CrossRef]
- Kim, C.; Ro, P. A sliding mode controller for vehicle active suspension systems with non-linearities. J. Automob. Eng. 1998, 212, 79–92. [Google Scholar] [CrossRef]
- Ekoru, J.E.; Dahunsi, O.A.; Pedro, J.O. Pid control of a nonlinear half-car active suspension system via force feedback. In Proceedings of the IEEE Africon’11, Livingstone, Zambia, 13–15 September 2011; pp. 1–6. [Google Scholar]
- Talib, M.H.A.; Darns, I.Z.M. Self-tuning pid controller for active suspension system with hydraulic actuator. In Proceedings of the 2013 IEEE Symposium on Computers & Informatics (ISCI), Langkawi, Malaysia, 7–9 April 2013; pp. 86–91. [Google Scholar]
- Salem, M.; Aly, A.A. Fuzzy control of a quarter-car suspension system. World Acad. Sci. Eng. Technol. 2009, 53, 258–263. [Google Scholar]
- Mittal, R. Robust pi and lqr controller design for active suspension system with parametric uncertainty. In Proceedings of the 2015 International Conference on Signal Processing, Computing and Control (ISPCC), Waknaghat, India, 24–26 September 2015; pp. 108–113. [Google Scholar]
- Ghazaly, N.M.; Ahmed, A.E.N.S.; Ali, A.S.; El-Jaber, G. H∞ control of active suspension system for a quarter car model. Int. J. Veh. Struct. Syst. 2016, 8, 35–40. [Google Scholar] [CrossRef]
- Huang, S.; Lin, W. A neural network based sliding mode controller for active vehicle suspension. J. Automob. Eng. 2007, 221, 1381–1397. [Google Scholar] [CrossRef]
- Heidari, M.; Homaei, H. Design a pid controller for suspension system by back propagation neural network. J. Eng. 2013, 2013, 421543. [Google Scholar] [CrossRef]
- Zhao, F.; Dong, M.; Qin, Y.; Gu, L.; Guan, J. Adaptive neural networks control for camera stabilization with active suspension system. Adv. Mech. Eng. 2015, 7. [Google Scholar] [CrossRef]
- Qin, Y.; Xiang, C.; Wang, Z.; Dong, M. Road excitation classification for semi-active suspension system based on system response. J. Vib. Control 2018, 24, 2732–2748. [Google Scholar] [CrossRef]
- Konoiko, A.; Kadhem, A.; Saiful, I.; Ghorbanian, N.; Zweiri, Y.; Sahinkaya, M.N. Deep learning framework for controlling an active suspension system. J. Vib. Control 2019, 25, 2316–2329. [Google Scholar] [CrossRef]
- Gordon, T.; Marsh, C.; Wu, Q. Stochastic optimal control of active vehicle suspensions using learning automata. J. Syst. Control Eng. 1993, 207, 143–152. [Google Scholar] [CrossRef]
- Marsh, C.; Gordon, T.; Wu, Q. Application of learning automata to controller design in slow-active automobile suspensions. Veh. Syst. Dyn. 1995, 24, 597–616. [Google Scholar] [CrossRef]
- Frost, G.; Gordon, T.; Howell, M.; Wu, Q. Moderated reinforcement learning of active and semi-active vehicle suspension control laws. J. Syst. Control Eng. 1996, 210, 249–257. [Google Scholar] [CrossRef]
- Bucak, İ.Ö.; Öz, H.R. Vibration control of a nonlinear quarter-car active suspension system by reinforcement learning. Int. J. Syst. Sci. 2012, 43, 1177–1190. [Google Scholar] [CrossRef]
- Chen, H.C.; Lin, Y.C.; Chang, Y.H. An actor-critic reinforcement learning control approach for discrete-time linear system with uncertainty. In Proceedings of the 2018 International Automatic Control Conference (CACS), Taoyuan, Taiwan, 4–7 November 2018; pp. 1–5. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Åström, K.J.; Wittenmark, B. Adaptive Control; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Apkarian, J.; Abdossalami, A. Active Suspension Experiment for Matlabr/Simulinkr Users—Laboratory Guide; Quanser Inc.: Markham, ON, Canada, 2013. [Google Scholar]



| Parameter | Value |
|---|---|
| Sprung mass | 2.45 kg |
| Damping of the car body damper | 7.5 s/m |
| Stiffness of the car body | 900 N/m |
| Unsprung mass | 1 kg |
| Damping of tire | 5 s/m |
| Stiffness of the tire | 2500 N/m |
| Type | Function | Derivative |
|---|---|---|
| Linear | 1 | |
| Tanh | ||
| Sigmoid | ||
| ReLu | 1 0 | |
| elu | 1 | |
| Sofmax | = |
| Number | Actor | Critic | Accumulated Rewards | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Hidden Layers Number of Neurons: 5 | Output Layers | Hidden Layers Number of Neurons: 18 | Output Layer | −16,034 | ||||||||
| elu | sigmoid | Relu | Tanh | Linear | ReLu | elu | Linear | ||||||
| 2 | Hidden Layers Number of Neurons: 5 | Output Layers | Hidden Layers Number of Neurons: 5 | Output Layer | −10,328 | ||||||||
| elu | Linear | ReLu | elu | Tanh | elu | Tanh | elu | Linear | |||||
| 3 | Hidden Layers Number of Neurons: 5 | Output Layers | Hidden Layers Number of Neurons: 5 | Output Layer | −106,950 | ||||||||
| ReLu | Tanh | ReLu | Linear | ReLu | ReLu | Tanh | Linear | ||||||
| 4 | Hidden Layers Number of Neurons: 10 | Output Layers | Hidden Layers Number of Neurons: 18 | Output Layer | −10,867 | ||||||||
| elu | sigmoid | Relu | Tanh | Linear | ReLu | elu | Tanh | elu | Tanh | elu | Linear | ||
| 5 | Hidden Layers Number of Neurons: 10 | Output Layers | Hidden Layers Number of Neurons: 18 | Output Layer | −10,956 | ||||||||
| ReLu | sigmoid | ReLu | Tanh | Linear | ReLu | elu | Tanh | elu | Tanh | elu | Linear | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fares, A.; Bani Younes, A. Online Reinforcement Learning-Based Control of an Active Suspension System Using the Actor Critic Approach. Appl. Sci. 2020, 10, 8060. https://doi.org/10.3390/app10228060
Fares A, Bani Younes A. Online Reinforcement Learning-Based Control of an Active Suspension System Using the Actor Critic Approach. Applied Sciences. 2020; 10(22):8060. https://doi.org/10.3390/app10228060
Chicago/Turabian StyleFares, Ahmad, and Ahmad Bani Younes. 2020. "Online Reinforcement Learning-Based Control of an Active Suspension System Using the Actor Critic Approach" Applied Sciences 10, no. 22: 8060. https://doi.org/10.3390/app10228060
APA StyleFares, A., & Bani Younes, A. (2020). Online Reinforcement Learning-Based Control of an Active Suspension System Using the Actor Critic Approach. Applied Sciences, 10(22), 8060. https://doi.org/10.3390/app10228060






