Numerical Analysis of the Bottom Thickness of Closed Rectangular Tanks Used as Pontoons
Abstract
:1. Introduction
2. Materials and Methods
2.1. Calculation Method
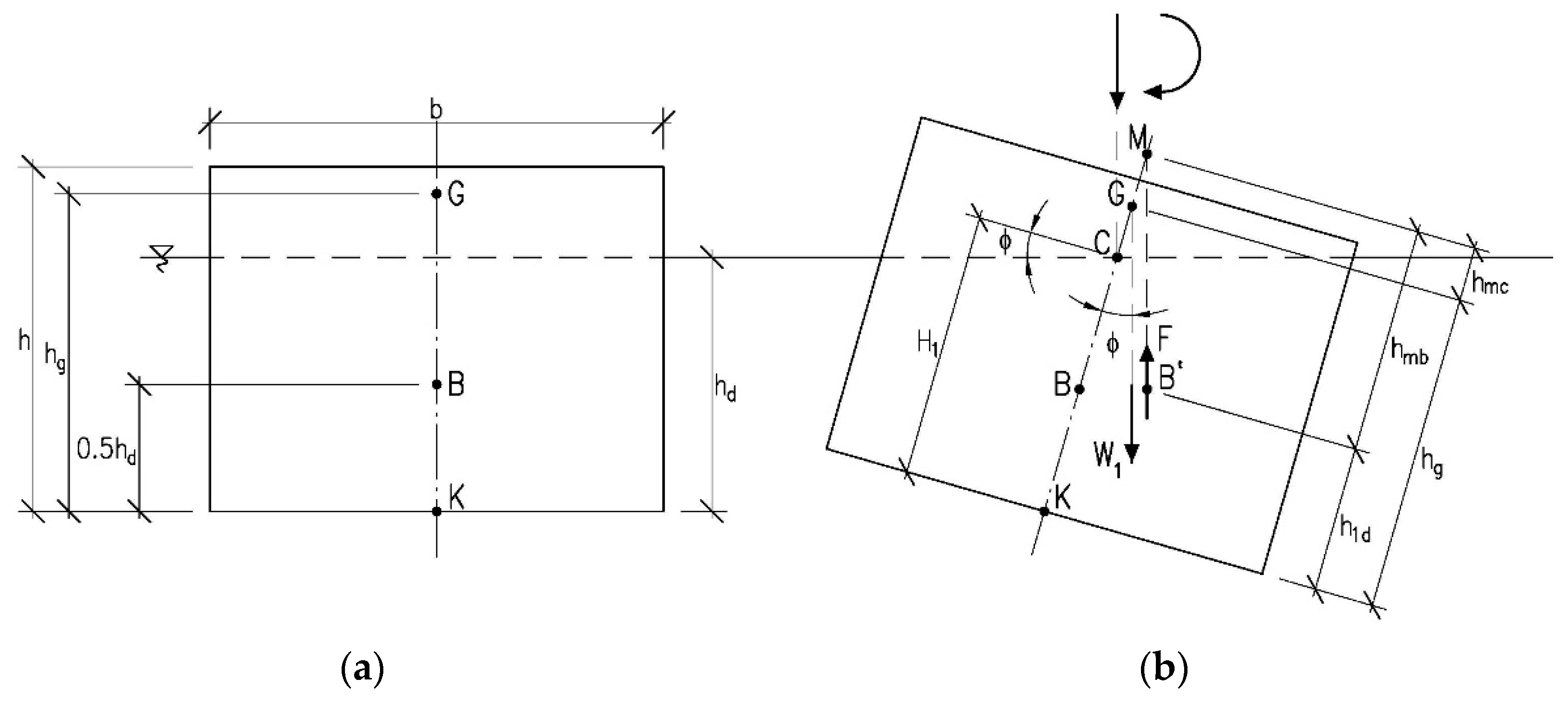
2.2. Verification of Pontoon Buoyancy and Stability
3. Results
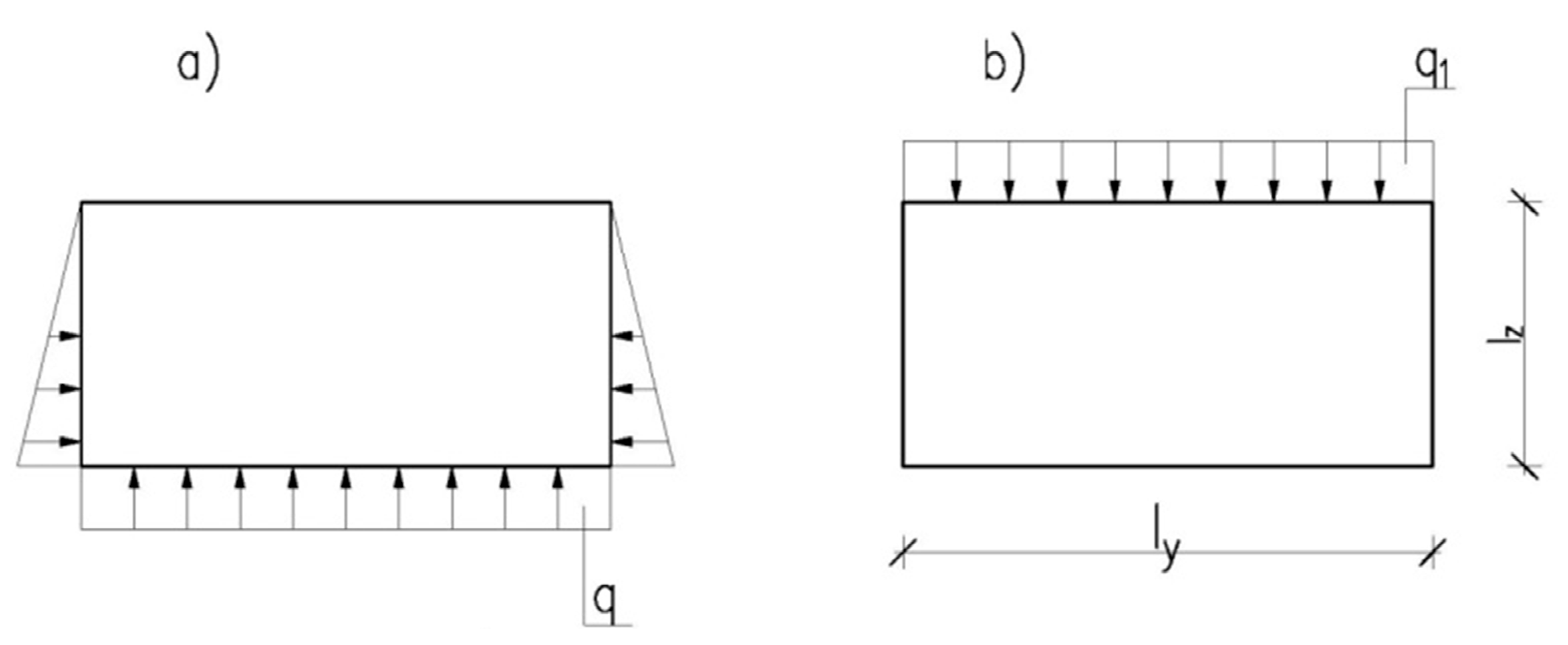
3.1. Static Analysis of the Tanks
3.2. Calculation Results of Buoyancy and Stability
4. Discussion
5. Conclusions
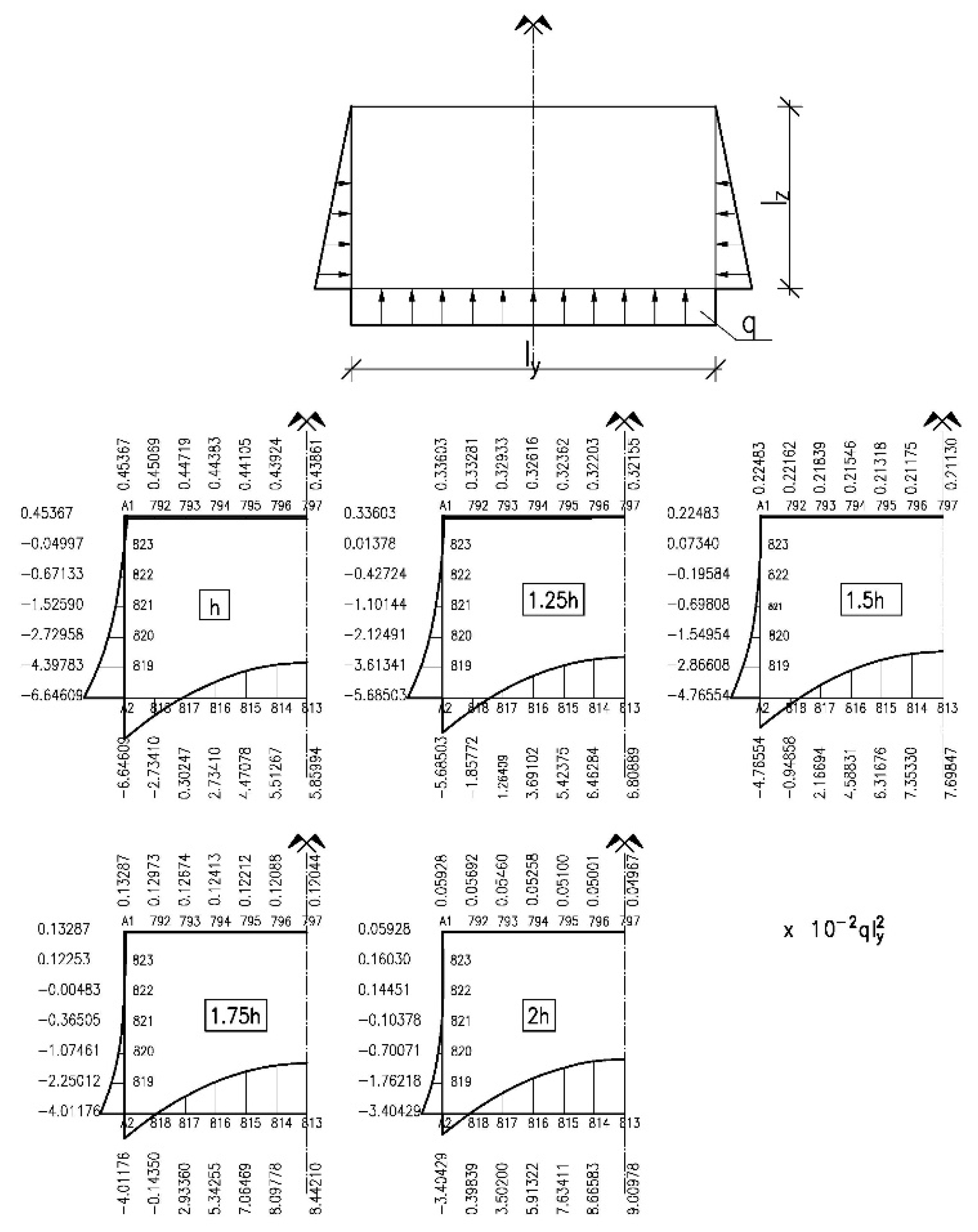
- Thickening of the bottom plate in relation to the constant and identical wall and upper plate thickness, at all points of the calculated tanks, led to a reduction in deflections as the bottom thickness increased.
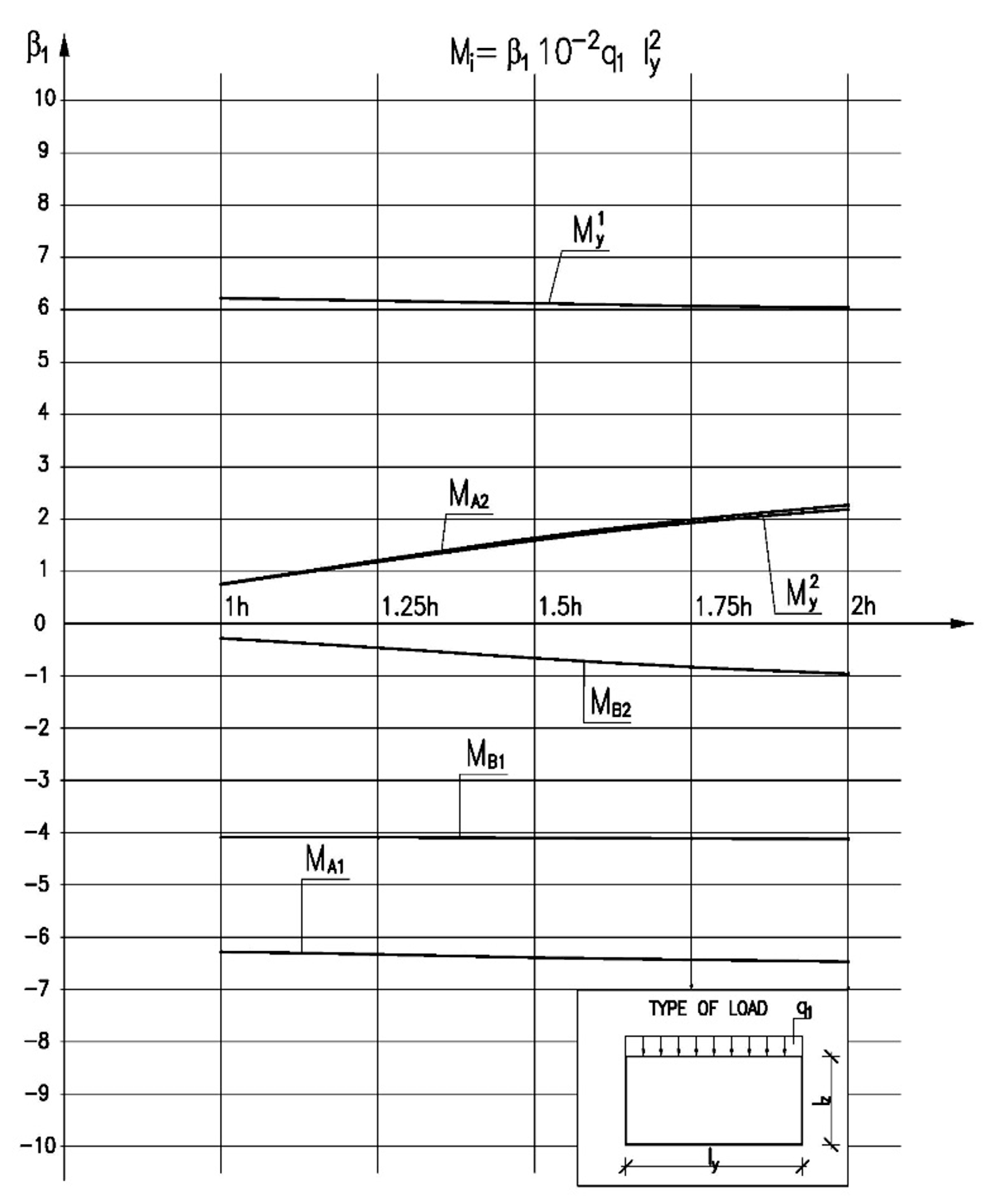
- Hydrostatic load on tank walls and uniform load on the bottom combined with an increase in the bottom thickness led to an increase in bending moments acting in the middle of the bottom plate span towards a shorter span (My2, Figure 3), while reducing bending moments at other points of the tank.
- Uniform load on the upper plate in tanks with a thicker bottom led to an increase in bending moments, but only in the bottom, both in fastening moments (MA2 and MB2, Figure 3) and in the moment acting in the centre of the plate towards a shorter span (My2, Figure 3). Bending moments at other points of the tank practically did not change.
- An increase in the thickness of the bottom plate leads to a change in the size of the pontoon’s tilt angle, which enables it to change easily, to smaller than required by applicable regulations (in this case φ ≤ 6°).
Funding
Acknowledgments
Conflicts of Interest
References
- Halicka, A.; Franczak, D. Design of Reinforced Concrete Tanks. Volume 2. Tanks for Liquids; Wydawnictwo Naukowe PWN: Warsaw, Poland, 2014. [Google Scholar]
- Buczkowski, W.; Szymczak-Graczyk, A.; Walczak, Z. Experimental validation of numerical static calculations for a monolithic rectangular tank with walls of trapezoidal cross-section. Bull. Pol. Acad. Sci. Tech. Sci. 2017, 65, 799–804. [Google Scholar] [CrossRef] [Green Version]
- Szymczak-Graczyk, A. Rectangular plates of a trapezoidal cross-section subjected to thermal load. IOP Conf. Ser. Mater. Sci. Eng. 2019, 603, 032095. [Google Scholar] [CrossRef]
- D’Amato, M.; Laterza, M.; Casamassima, V.M. Seismic Performance Evaluation of Multi-Span Existing Masonry Arch Bridge. Open Civ. Eng. J. 2017, 11 (Suppl. 5), 1191–1207. [Google Scholar] [CrossRef]
- Pelà, L.; Aprile, A.; Benedetti, A. Seismic Assessment of masonry arch bridges. Eng. Struct. 2009, 31, 1777–1788. [Google Scholar] [CrossRef]
- Mazurkiewicz, B. Yacht Ports and Marinas. Design; Fundacja Promocji Przemysłu Okrętowego i Gospodarki Morskiej: Gdańsk, Poland, 2010. [Google Scholar]
- Szymczak-Graczyk, A. Floating platforms made of monolithic closed rectangular tanks. Bull. Pol. Acad. Sci. Tech. Sci. 2018, 66, 209–219. [Google Scholar] [CrossRef]
- PN–EN 14504:2010: Inland Waterway Vessels. Floating Harbors. Requirements, Tests; Polish Standardization Committee: Warsaw, Poland, 2010.
- Wang, C.M. Great, Ideas Float on the Top. In Large Floating Structures: Technological Advances; Wang, C.M., Wang, B.T., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–36. [Google Scholar]
- Holcombe, S. Applications and Huge Potential Demand for Amphibious Structures. In Proceedings of the First International Conference on Amphibious Architecture, Design & Engineering, Waterloo, ON, Canada, 25–28 June 2017; Volume 138. [Google Scholar]
- Nakajima, T.; Umeyama, M. A New Concept for the Safety of Low-lying Land Areas from Natural Disasters. J. Ocean Eng. Mar. Energy 2015, 1, 19–29. [Google Scholar] [CrossRef] [Green Version]
- Ostrowska-Wawryniuk, K.; Piątek, Ł. Lightweight Prefabricated Floating Buildings for Shallow Inland Waters. Design and Construction of The Floating Hotel Apartment in Poland. J. Water Land Dev. 2020, 44, 118–125. [Google Scholar] [CrossRef]
- Gołaś, J. Introduction to the Theory of Plates; Opole University of Technology Publishing House: Opole, Poland, 1972. [Google Scholar]
- Donnell, L.H. Beams, Plates and Shells; McGraw-Hill: New York, NY, USA, 1976. [Google Scholar]
- Naghdi, P.M. The Theory of Shells and Plates; Handbuch der Physick: Berlin, Germany, 1972. [Google Scholar]
- Panc, V. Theries of Elastic Plates; Academia: Prague, Czech Republic, 1975. [Google Scholar]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Coatings; Arkady: Warszawa, Poland, 1962. [Google Scholar]
- Szlilard, R. Theory and Analysis of Plates. Classical and Numerical Methods; Prentice Hall, Englewood Cliffs: Bergen, NJ, USA; Prentice-Hall: Upper Saddle River, NJ, USA, 1974. [Google Scholar]
- Ugural, A.C. Stresses in Plates and Shells; McGraw-Hill: New York, NY, USA, 1981. [Google Scholar]
- Wilde, P. Variational approach of finite differences in the theory of plate. In Proceedings of the Materials of XII Scientific Conference of the Committee of Science PZiTB and the Committee of Civil Engineering of Polish Academy of Sciences, Krynica, Poland, 12–17 September 1966. [Google Scholar]
- Tribiłło, R. Application of the generalized finite difference method for plate calculations. Arch. Inżynierii Lądowej 1975, 2, 579–586. [Google Scholar]
- Son, M.; Sang Jung, H.; Hee Yoon, H.; Sung, D.; Suck Kim, J. Numerical Study on Scale Effect of Repetitive Plate-Loading Test. Appl. Sci. 2019, 9, 4442. [Google Scholar] [CrossRef] [Green Version]
- Kączkowski, Z. Plates. Static Calculations; Arkady: Warszawa, Poland, 2000. [Google Scholar]
- Rapp, B.E. Chapter 30—Finite Difference Method. In Microfluidics: Modelling, Mechanics and Mathematics, Micro and Nano Technologies; Rapp, B.E., Ed.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 623–631. [Google Scholar] [CrossRef]
- Blazek, J. Chapter 3—Principles of Solution of the Governing Equations. In Computational Fluid Dynamics: Principles and Applications; Blazek, J., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 29–72. [Google Scholar] [CrossRef]
- Sadd, M.H. Chapter 5—Formulation and Solution Strategies. In Elasticity, Theory, Applications, and Numerics; Sadd, M.H., Ed.; Academic Press, Elsevier: Cambridge, MA, USA, 2005; pp. 83–102. [Google Scholar] [CrossRef]
- Szymczak-Graczyk, A. Numerical analysis of the impact of thermal spray insulation solutions on floor loading. Appl. Sci. 2020, 10, 1016. [Google Scholar] [CrossRef] [Green Version]
- Numayr, K.S.; Haddad, R.H.; Haddad, M.A. Free vibration of composite plates using the finite difference method. Thin-Walled Struct. 2004, 42, 399–414. [Google Scholar] [CrossRef]
- Z44, Recommendations for the Design of Offshore Hydrotechnical Structures, Z1–Z46; No. 21; Gdańsk University of Technology, Department of Maritime Construction. Studies and Materials: Gdańsk, Poland, 1997.
- AS 3962-2001: The Australian Standard: Guidelines for Design of Marinas; Standards Australia International Ltd.: Sydney, Australian, 2001.
- PN-EN 1992-1-1:2008 Eurocode 2. Design of Concrete Structures. Part 1-1. General Rules and Rules for Buildings; Polish Standardization Committee: Warsaw, Poland, 2008.
- Buczkowski, W.; Szymczak-Graczyk, A. The influence of the thickness of the bottom of the work and static stability of the pontoon made as a monolithic closed, reinforced concrete tank. In Modelling of structures and Engineering Structures; SGGW: Warsaw, Poland, 2014. [Google Scholar]
- Buczkowski, W.; Szymczak-Graczyk, A.; Walczak, Z. The analysis of static works of closed monolithic rectangular tanks. In Proceedings of the IV International Scientific Conference, Durability of Construction Work—Science and Research, Poznań, Poland, 19–21 November 2014. [Google Scholar]
- Szymczak-Graczyk, A. Floating Platforms Made from Monolithic, Closed Rectangular Tanks. Ph.D. Thesis, SGGW, Warsaw, Poland, 2014. [Google Scholar]
- Jiang, D.; Tan, K.H.; Wang, C.M.; Ong, K.C.G.; Bra, H.; Jin, J.; Kim, M.O. Analysis and design of floating prestressed concrete structures in shallow waters. Mar. Struct. 2018, 59, 301–320. [Google Scholar] [CrossRef]
- Spychalski, K.; Szymczak-Graczyk, A. Multi-criteria analysis of the selection of structural types of floating platforms. Mater. Bud. 2020, 2, 2–4. [Google Scholar] [CrossRef]
- Seifa, M.S.; Inoue, Y. Dynamic analysis of floating bridges. Mar. Struct. 1998, 11, 29–46. [Google Scholar] [CrossRef]
- Laks, I.; Walczak, Z. Modelling of the impact of the retention reservoir on the flood protection of the city—A case study for the city of Kalisz (Central Poland). IOP Conf. Ser. Mater. Sci. Eng. 2019, 603, 022066. [Google Scholar] [CrossRef] [Green Version]
- Laks, I.; Walczak, Z.; Szymczak-Graczyk, A.; Ksit, B.; Mądrawski, J. Hydraulic and legal conditions for buildings in floodplains—A case study for the city of Kalisz (Poland). IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 102050. [Google Scholar] [CrossRef]



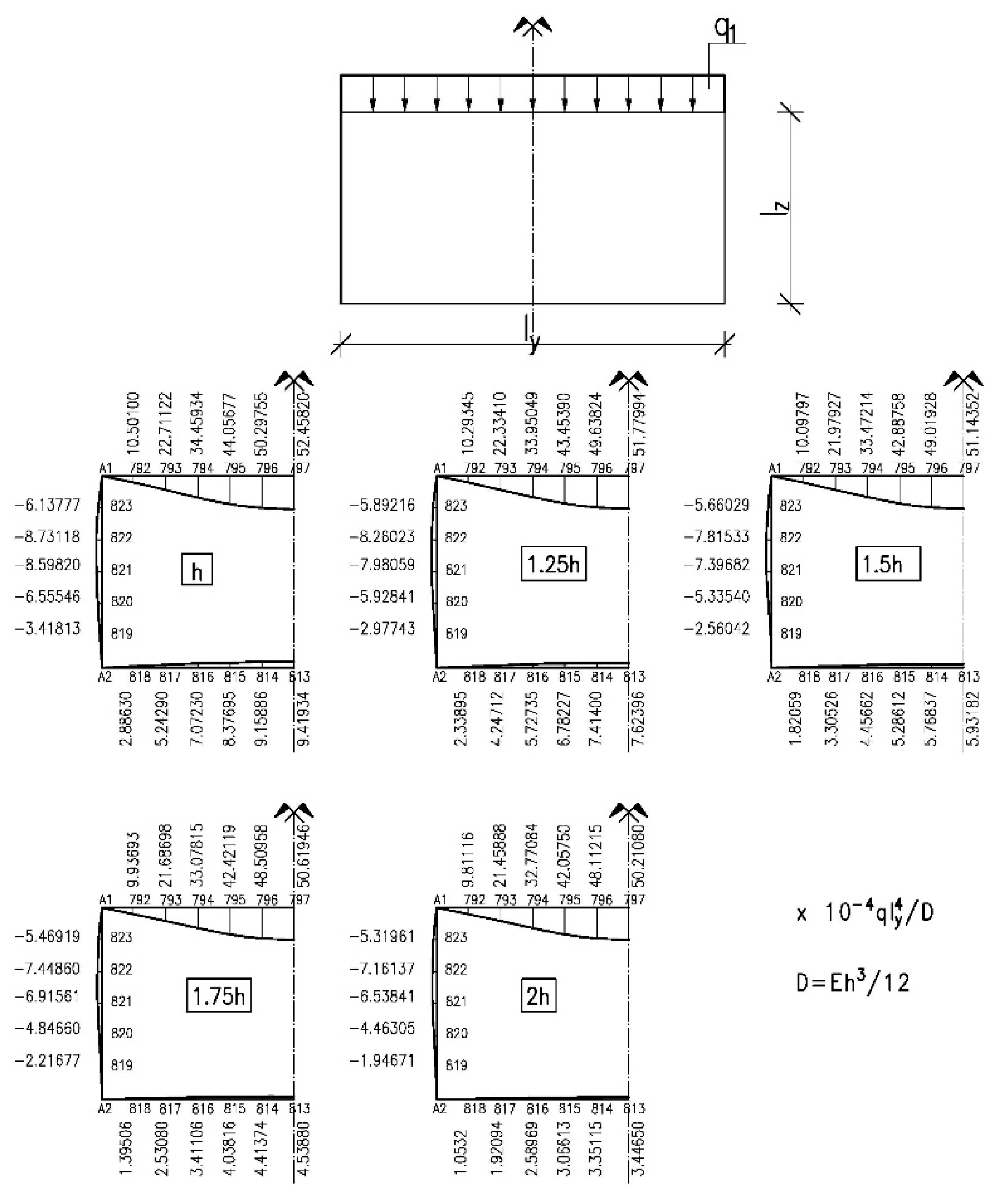


| Compared Value | Bottom Thickness in Relation to the Thickness of Tank Walls and the Upper Plate h | ||||
|---|---|---|---|---|---|
| 1 h | 1.25 h | 1.5 h | 1.75 h | 2 h | |
| w1 | 5.52276 | 4.05760 | 2.67487 | 1.53470 | 0.64370 |
| w2 | 47.92313 | 30.63693 | 21.04255 | 15.00900 | 10.94071 |
| Mx1 | 0.013431 | 0.01201 | 0.01015 | 0.00835 | 0.00642 |
| My1 | 0.43861 | 0.32156 | 0.21129 | 0.12044 | 0.04967 |
| Mx2 | 0.01189 | 0.02881 | 0.04903 | 0.07703 | 0.01040 |
| My2 | 5.85994 | 6.80889 | 7.69847 | 8.44210 | 9.00978 |
| Mx3 | −0.00469 | −0.00501 | −0.00475 | −0.00488 | −0.00333 |
| Mz3 | −1.52590 | −1.09941 | −0.69717 | −0.36497 | −0.10378 |
| My4 | −0.22551 | −0.16301 | −0.10056 | −0.05156 | −0.01411 |
| Mz4 | −0.04943 | 0.05892 | 0.18169 | 0.28149 | 0.36022 |
| MA1 | 0.45367 | 0.33603 | 0.22483 | 0.13288 | 0.05928 |
| MA2 | −6.64609 | −5.68503 | −4.76554 | −4.01176 | −3.40429 |
| MB1 | −0.03675 | −0.05803 | −0.09301 | −0.12098 | −0.14385 |
| MB2 | −4.47676 | −3.90449 | −3.32288 | −2.86228 | −2.50630 |
| Compared Value | Bottom Thickness in Relation to the Thickness of Tank Walls and the Upper Plate h | ||||
|---|---|---|---|---|---|
| 1 h | 1.25 h | 1.5 h | 1.75 h | 2 h | |
| w1 | 52.45820 | 51.77994 | 51.14352 | 50.61946 | 50.21080 |
| w2 | 9.41934 | 7.62396 | 5.93182 | 4.53880 | 3.44650 |
| Mx1 | 0.01328 | 0.01206 | 0.01068 | 0.00943 | 0.00825 |
| My1 | 6.22265 | 6.16866 | 6.11809 | 6.07649 | 6.04413 |
| Mx2 | 0.01493 | 0.02697 | 0.03994 | 0.05515 | 0.00761 |
| My2 | 0.75018 | 1.18460 | 1.59133 | 1.93058 | 2.18944 |
| Mx3 | −0.00531 | −0.00506 | −0.00451 | −0.00418 | −0.00325 |
| Mz3 | −2.75005 | −2.34321 | −2.36535 | −2.21184 | −2.09146 |
| My4 | −0.43140 | −0.40992 | −0.38776 | −0.36965 | −0.35549 |
| Mz4 | −0.90169 | −0.86478 | −0.82122 | −0.78400 | −0.75396 |
| MA1 | −6.28306 | −6.33845 | −6.39055 | −6.43357 | −6.46783 |
| MA2 | 0.76584 | 1.21608 | 1.64339 | 1.99491 | 2.27454 |
| MB1 | −4.09582 | −4.09701 | −4.10487 | −4.11243 | −4.11926 |
| MB2 | 0.27686 | 0.46413 | 0.66433 | 0.83138 | 0.96283 |
| Bottom Thickness of the Analysed Tanks (m) | Pontoon Buoyancy | Pontoon Stability with Half of the Upper Plate Loaded 1.0 kN/m2 | |||||
|---|---|---|---|---|---|---|---|
| At Self-Weight Load | At Uniform Load 3.0 kN/m2 | ||||||
| Immersion Depth hd (m) | Freeboardh f (m) | Immersion Depth hd (m) | Freeboardh f (m) | Metacentric Heighth mc (m) | Tilt Angle φ (°) | Freeboardh f (m) | |
| 0.08 | 0.66 | 0.59 | 0.96 | 0.29 | 0.35 | 7.16 | 0.38 |
| 0.10 | 0.71 | 0.54 | 1.01 | 0.24 | 0.37 | 6.38 | 0.35 |
| 0.12 | 0.75 | 0.50 | 1.05 | 0.20 | 0.38 | 5.86 | 0.32 |
| 0.14 | 0.80 | 0.45 | 1.10 | 0.15 | 0.41 | 5.15 | 0.29 |
| 0.16 | 0.84 | 0.41 | 1.14 | 0.11 | 0.42 | 4.77 | 0.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szymczak-Graczyk, A. Numerical Analysis of the Bottom Thickness of Closed Rectangular Tanks Used as Pontoons. Appl. Sci. 2020, 10, 8082. https://doi.org/10.3390/app10228082
Szymczak-Graczyk A. Numerical Analysis of the Bottom Thickness of Closed Rectangular Tanks Used as Pontoons. Applied Sciences. 2020; 10(22):8082. https://doi.org/10.3390/app10228082
Chicago/Turabian StyleSzymczak-Graczyk, Anna. 2020. "Numerical Analysis of the Bottom Thickness of Closed Rectangular Tanks Used as Pontoons" Applied Sciences 10, no. 22: 8082. https://doi.org/10.3390/app10228082





