Effect of the Anti-Yaw Damper on Carbody Vertical Vibration and Ride Comfort of Railway Vehicle
Abstract
:1. Introduction
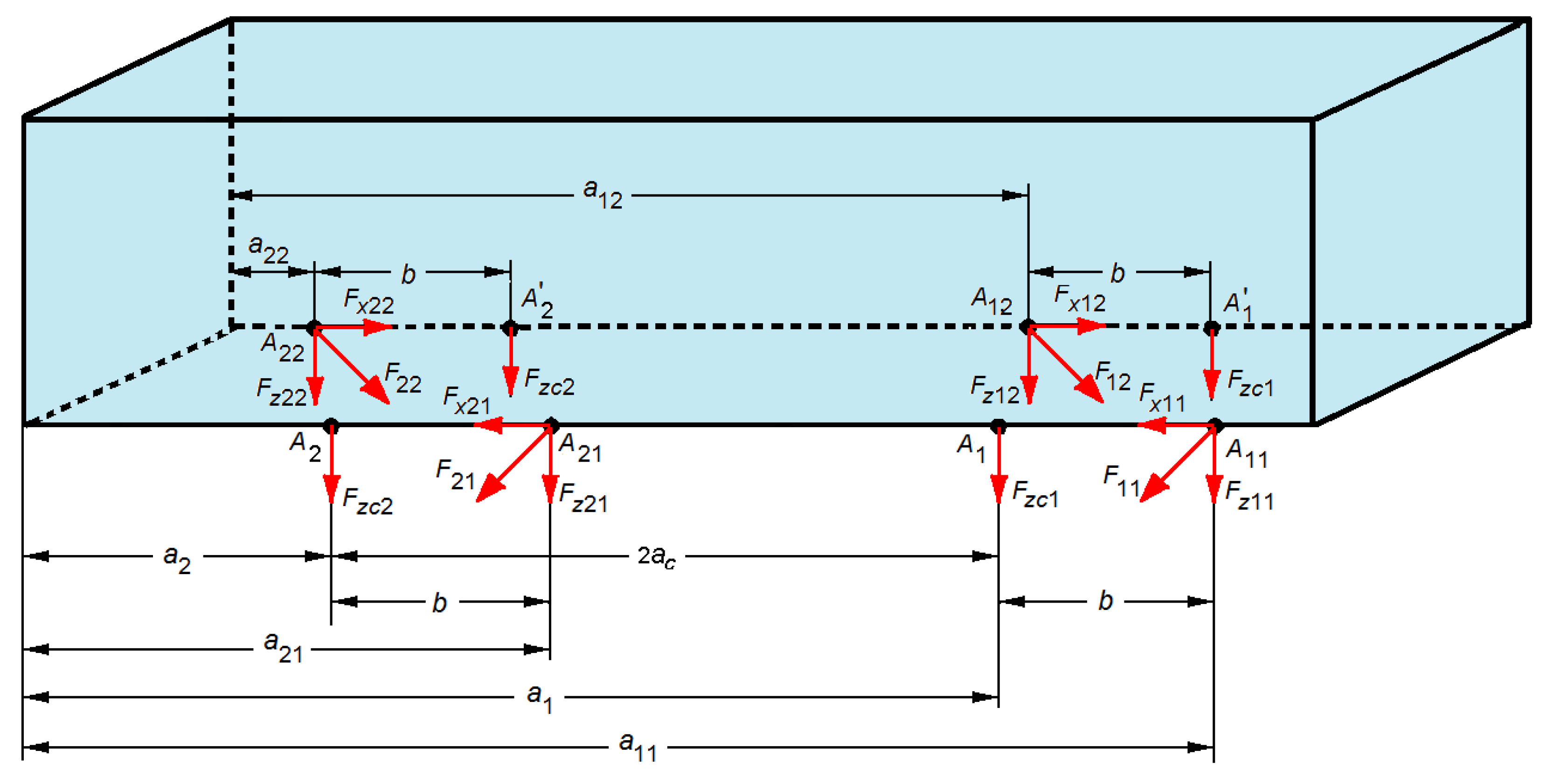
2. Mechanical Model of Railway Vehicle
3. Equations of Motion
4. The Vehicle Dynamic Response to the Track Vertical Irregularities
5. Evaluation of Ride Comfort during Vertical Vibrations
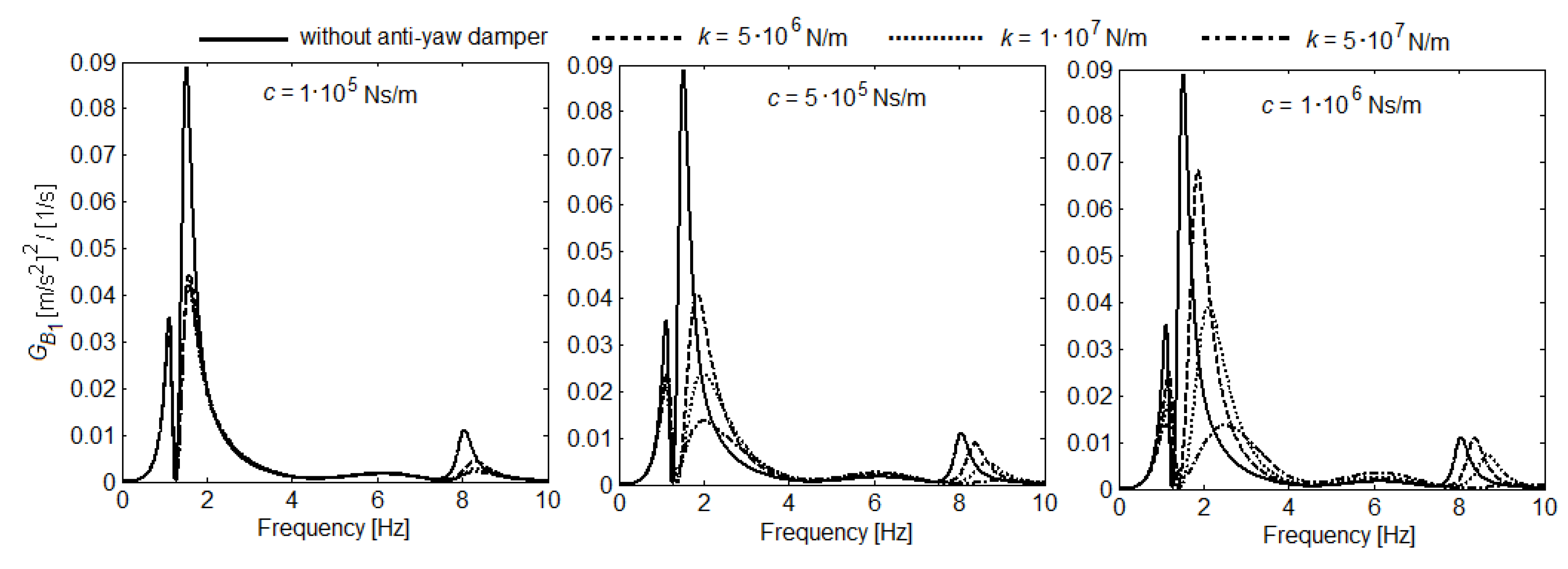
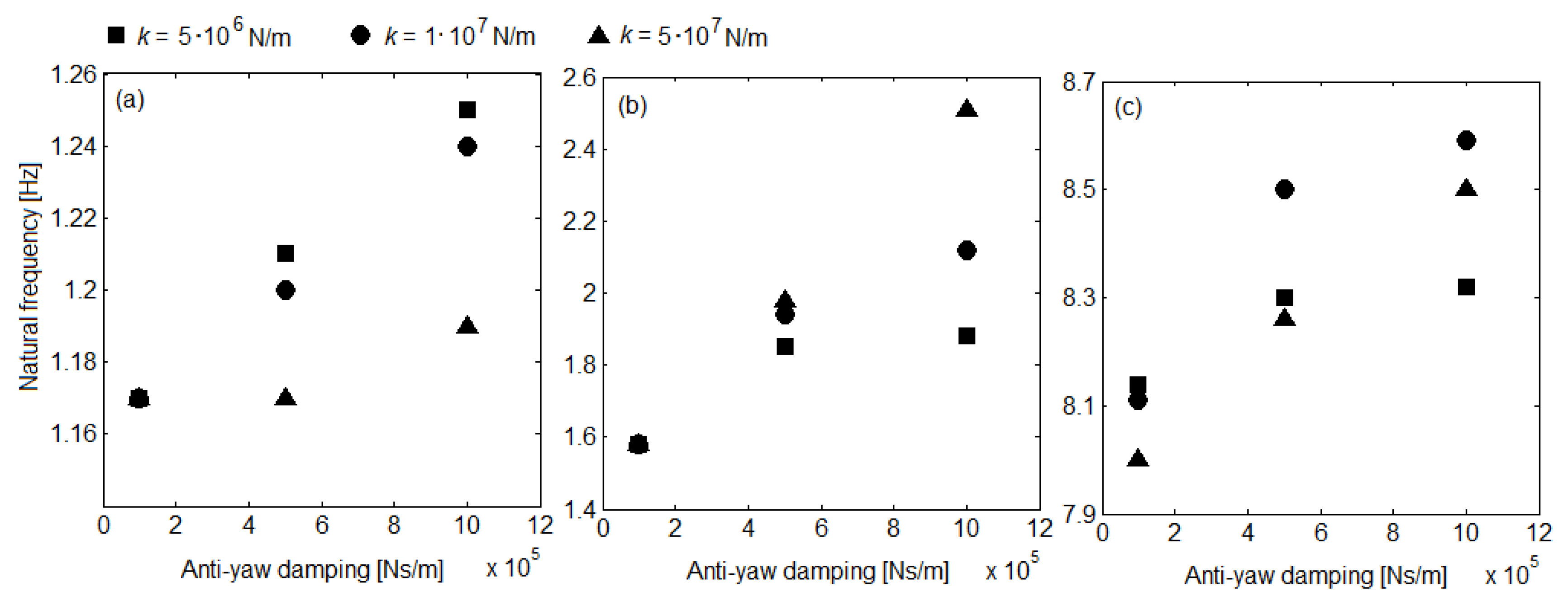
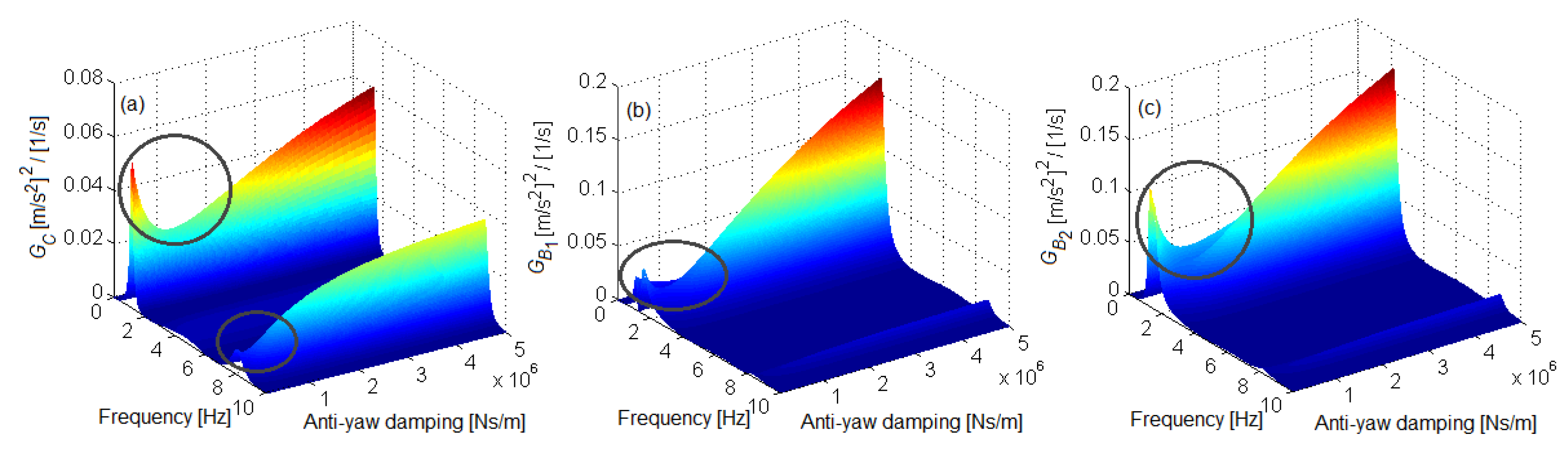
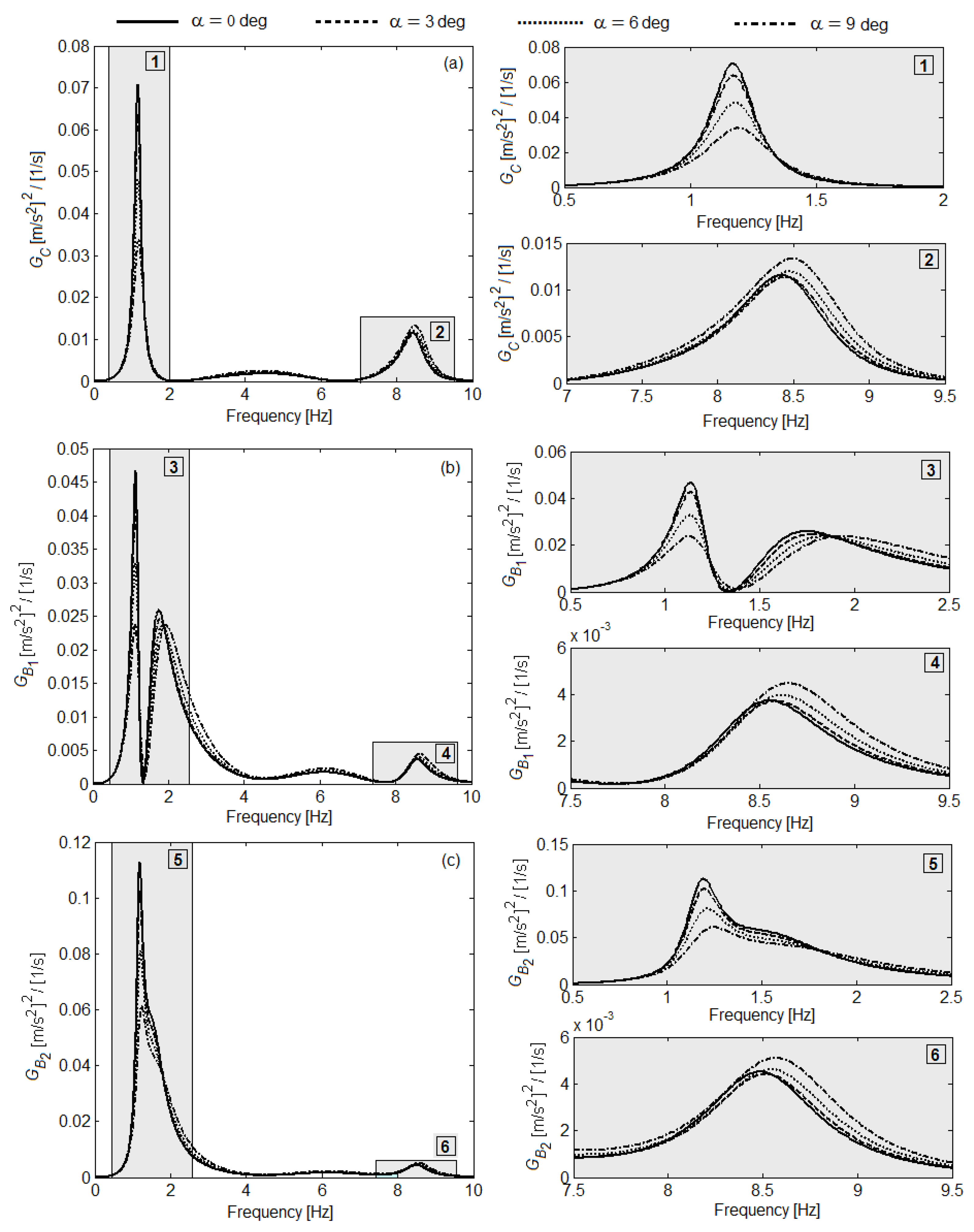
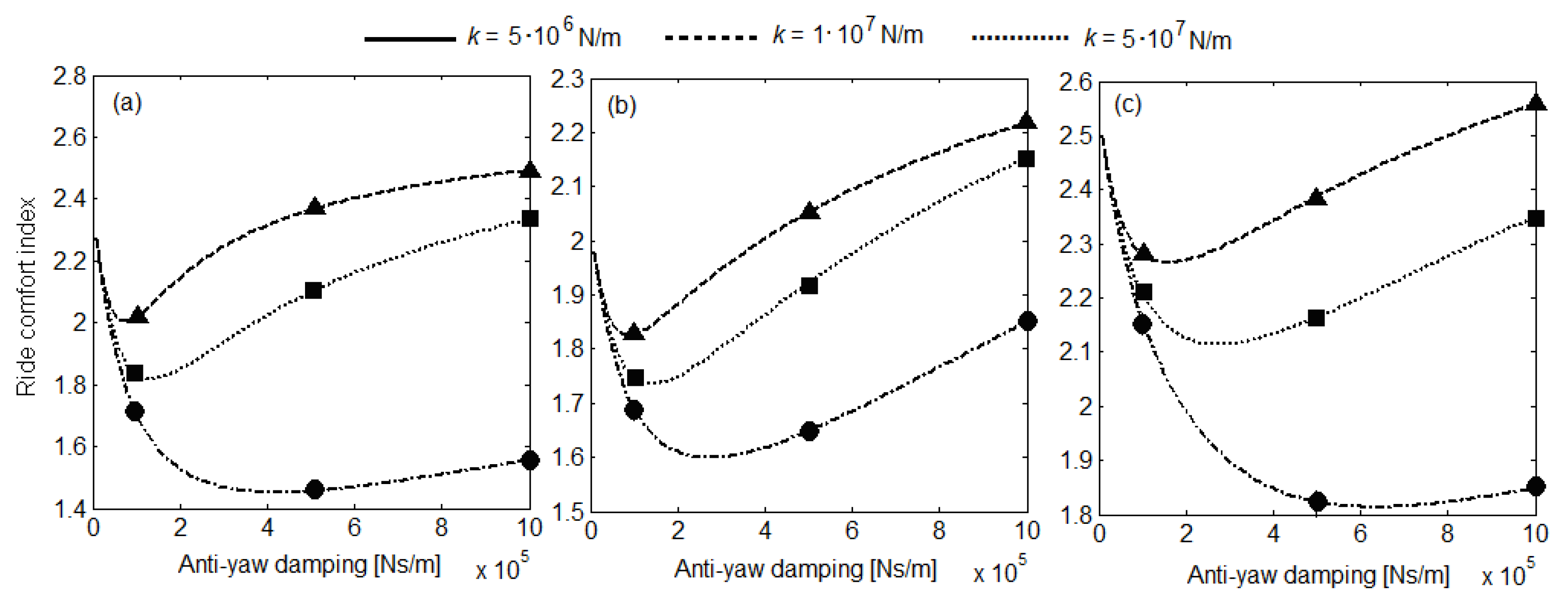
6. Results of Numerical Simulationsand Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kim, Y.-G.; Kwon, H.-B.; Kim, S.-W.; Kim, C.-K.; Kim, T.-W. Correlation of ride comfort evaluation methods for railway vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2003, 217, 73–88. [Google Scholar] [CrossRef]
- Kim, Y.G.; Choi, S.; Kim, S.-W.; Kim, Y.-M.; Park, T.W. An Experimental Study on the Ride Comfort of the Korean High-Speed Train. Exp. Tech. 2009, 33, 30–37. [Google Scholar] [CrossRef]
- Kardas-Cinal, E. Ride comfort for various passenger positions in a railway vehicle—Simulation study. Arch. Transp. 2010, 22, 189–199. [Google Scholar] [CrossRef]
- Mansfield, N.J. Human Response to Vibration; 2005. Available online: https://docs.wind-watch.org/Mansfield-human-response-vibration.pdf (accessed on 17 November 2020).
- Griffin, M. Handbook of Human Vibration; Elsevier BV: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Nakagawa, C.; Suzuki, H. Effects of Train Vibrations on Passenger PC Use. Q. Rep. RTRI 2005, 46, 200–205. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, H. Effects of the range and frequency of vibrations on the momentary riding comfort evaluation of a railway vehicle. Jpn. Psychol. Res. 1998, 40, 156–165. [Google Scholar] [CrossRef]
- Munawir, T.I.T.; Abu Samah, A.A.; Rosle, M.A.A.; Azlis-Sani, J.; Hasnan, K.; Sabri, S.; Ismail, S.; Yunos, M.N.A.M.; Bin, T.Y. A Comparison Study on the Assessment of Ride Comfort for LRT Passengers. IOP Conf. Ser. Mater. Sci. Eng. 2017, 226, 012039. [Google Scholar] [CrossRef] [Green Version]
- Cheli, F.; Corradi, R. On rail vehicle vibrations induced by track unevenness: Analysis of the excitation mechanism. J. Sound Vib. 2011, 330, 3744–3765. [Google Scholar] [CrossRef]
- Young, T.; Li, C. Vertical Vibration Analysis of Vehicle/Imperfect Track Systems. Veh. Syst. Dyn. 2003, 40, 329–349. [Google Scholar] [CrossRef]
- Dumitriu, M. Analysis of the Dynamic Response in the Railway Vehicles to the Track Vertical Irregularities. Part I: The Theoretical Model and the Vehicle Response Functions. J. Eng. Sci. Technol. Rev. 2015, 8, 24–31. [Google Scholar] [CrossRef]
- Mazilu, T. Analysis of infinite structure response due to moving wheel in the presence of irregularities via Green’s functions method. Proc. Rom. Acad. Ser. A Math. Phys. Tech. Sci. Inf. Sci. 2009, 10, 139–150. [Google Scholar]
- Mazilu, T. Green’s functions for analysis of dynamic response of wheel/rail to vertical excitation. J. Sound Vib. 2007, 306, 31–58. [Google Scholar] [CrossRef]
- Pombo, J.; Ambrósio, J. An alternative method to include track irregularities in railway vehicle dynamic analyses. Nonlinear Dyn. 2011, 68, 161–176. [Google Scholar] [CrossRef]
- Orvanäs, A. Methods for Reducing Vertical Carbody Vibrations of a Rail Vehicle. Report in Railway Technology Stockholm; KTH Engineering Sciences Department of Aeronautical and Vehicle Engineering, Division of Rail Vehicles: Stockholm, Sweden, 2010. [Google Scholar]
- Takigami, T.; Tomioka, T. Investigation to Suppress Bending Vibration of Railway Vehicle Carbodies using Piezoelectric Elements. Q. Rep. RTRI 2005, 46, 225–230. [Google Scholar] [CrossRef] [Green Version]
- Kamada, T.; Kiuchi, R.; Nagai, M. Suppression of railway vehicle vibration by shunt damping using stack type piezoelectric transducers. Veh. Syst. Dyn. 2008, 46, 561–570. [Google Scholar] [CrossRef]
- Kamada, T.; Hiraizumi, K.; Nagai, M. Active vibration suppression of lightweight railway vehicle body by combined use of piezoelectric actuators and linear actuators. Veh. Syst. Dyn. 2010, 48, 73–87. [Google Scholar] [CrossRef]
- Tomioka, T.; Takigami, T. Reduction of bending vibration in railway vehicle carbodies using carbody–bogie dynamic interaction. Veh. Syst. Dyn. 2010, 48, 467–486. [Google Scholar] [CrossRef]
- Sugahara, Y.; Watanabe, N.; Takigami, T.; Koganei, R. Vertical vibration suppression system for railway vehicles based on primary suspension damping control—system development and vehicle running test results. Q. Rep. RTRI 2011, 52, 13–19. [Google Scholar] [CrossRef]
- Tomioka, T. Reduction of car body elastic vibration using high-damping elastic supports for under-floor equipment. Railw. Technol. Avalanche 2012, 41, 245–270. [Google Scholar]
- Aida, K.-I.; Tomioka, T.; Takigami, T.; Akiyama, Y.; Sato, H. Reduction of Carbody Flexural Vibration by the High-damping Elastic Support of Under-floor Equipment. Q. Rep. RTRI 2015, 56, 262–267. [Google Scholar] [CrossRef] [Green Version]
- Dumitriu, M. A new passive approach to reducing the carbody vertical bending vibration of railway vehicles. Veh. Syst. Dyn. 2017, 55, 1787–1806. [Google Scholar] [CrossRef]
- Dumitriu, M.; Cruceanu, C. Approaches for reducing structural vibration of the carbody railway vehicles. In Proceedings of the 21st Innovative Manufacturing Engineering & Energy International Conference (IManE&E 2017), Iaşi, Romania, 24–27 May 2017; Volume 112, p. 07006. Available online: https://www.matec-conferences.org/articles/matecconf/abs/2017/26/matecconf_imane2017_07006/matecconf_imane2017_07006.html (accessed on 17 November 2020).
- Gong, D.; Zhou, J.; Sun, W.; Sun, Y.; Xia, Z. Method of multi-mode vibration control for the carbody of high-speed electric multiple unit trains. J. Sound Vib. 2017, 409, 94–111. [Google Scholar] [CrossRef]
- Gong, D.; Zhou, J.; Sun, W. Passive control of railway vehicle car body flexural vibration by means of under frame dampers. J. Mech. Sci. Technol. 2017, 31, 555–564. [Google Scholar] [CrossRef]
- Schandl, G.; Lugner, P.; Benatzky, C.; Kozek, M.; Stribersky, A. Comfort enhancement by an active vibration reduction system for a flexible railway car body. Veh. Syst. Dyn. 2007, 45, 835–847. [Google Scholar] [CrossRef]
- Dumitriu, M. Ride comfort enhancement in railway vehicle by the reduction of the carbody structural flexural vibration. IOP Conf. Ser. Mater. Sci. Eng. 2017, 227, 012042. Available online: https://iopscience.iop.org/article/10.1088/1757-899X/227/1/012042 (accessed on 17 November 2020). [CrossRef] [Green Version]
- Dumitriu, M. Study on Improving the Ride Comfort in Railway Vehicles Using Anti-Bending Dampers. Appl. Mech. Mater. 2018, 880, 207–212. [Google Scholar] [CrossRef]
- Dumitriu, M.; Stănică, D.I. An approach to improving the ride comfort of the railway vehicles. UPB Sci. Bull. Ser. D Mech. Eng. 2020, 82, 81–98. [Google Scholar]
- Tomioka, T.; Takigami, T.; Suzuki, Y. Numerical analysis of three-dimensional flexural vibration of railway vehicle car body. Veh. Syst. Dyn. 2006, 44, 272–285. [Google Scholar] [CrossRef]
- Huang, C.; Zeng, J.; Luo, G.; Shi, H. Numerical and experimental studies on the car body flexible vibration reduction due to the effect of car body-mounted equipment. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 232, 103–120. [Google Scholar] [CrossRef] [Green Version]
- Diana, G.; Cheli, F.; Collina, A.; Corradi, R.; Melzi, S. The Development of a Numerical Model for Railway Vehicles Comfort Assessment Through Comparison With Experimental Measurements. Veh. Syst. Dyn. 2002, 38, 165–183. [Google Scholar] [CrossRef]
- Dumitriu, M. On the Critical Points of Vertical Vibration in a Railway Vehicle. Arch. Mech. Eng. 2014, 61, 609–625. [Google Scholar] [CrossRef]
- Dumitriu, M.; Crăciun, C. Modelling of structural flexibility of the carbody railway vehicles. In Proceedings of the MATEC Web of Conferences—21st Innovative Manufacturing Engineering & Energy International Conference, Iasi, Romania, 24–27 May 2017; Volume 112, p. 07007. [Google Scholar]
- Yang, G.; Wang, C.; Xiang, F.; Xiao, S. Effect of train carbody’s parameters on vertical bending stiffness performance. Chin. J. Mech. Eng. 2016, 29, 1120–1127. [Google Scholar] [CrossRef]
- Shi, H.; Wu, P. Flexible vibration analysis for car body of high-speed EMU. J. Mech. Sci. Technol. 2016, 30, 55–66. [Google Scholar] [CrossRef]
- Dumitriu, M.; I Stănică, D. Vertical bending vibration analysis of the car body of railway vehicle. IOP Conf. Ser. Mater. Sci. Eng. 2019, 564, 012104. [Google Scholar] [CrossRef]
- Dumitriu, M.; Cruceanu, C. Influences of Carbody Vertical Flexibility on Ride Comfort of Railway Vehicles. Arch. Mech. Eng. 2017, 64, 219–238. [Google Scholar] [CrossRef]
- Dumitriu, M.; Stănică, D.I. Influence of the Primary Suspension Damping on the Ride Comfort in the Railway Vehicles. Mater. Sci. Forum 2019, 957, 53–62. [Google Scholar] [CrossRef]
- Huang, L.; Zeng, J.; Zhou, X.; Song, Y. Mechanical model of yaw damper and its application in the simulation of vehicle system dynamics. IOP Conf. Ser. Mater. Sci. Eng. 2018, 397, 012051. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Chi, M.; Cai, W.; Wang, X. Study on Piecewise Linear Model of Anti-yaw Damper and Test Analysis. In Proceedings of the 2015 International Industrial Informatics and Computer Engineering Conference, Xi’an, China, 10–11 January 2015; pp. 1179–1189. [Google Scholar]
- Mazilu, T. An analysis of bogie hunting instability. UPB Sci. Bull. Ser. D Mech. Eng. 2009, 71, 63–78. [Google Scholar]
- Aida, K.-I.; Akiyama, Y.; Nakajima, D.; Tanaka, T.; Takigami, T.; Tomioka, T.; Miyamoto, T.; Nishiyama, Y.; Imaoka, N. Influence of yaw dampers on vertical vibration of railway vehicle carbody and verification of effect by the new mounting structure of yaw damper. In Proceedings of the Transportation and Logistics Conference; Japan Society of Mechanical Engineers: Tokyo, Japan, 2017; p. 3102. [Google Scholar]
- Nakajima, D.; Aida, K.-I.; Akiyama, Y.; Takigami, T.; Tomioka, T.; Nishiyama, Y.; Tanaka, T.; Miyamoto, T.; Imaoka, N. Development of a new mounting structure of yaw damper to reduce railway carbody vibration. Trans. JSME 2017, 83, 17-00078. (In Japanese) [Google Scholar] [CrossRef] [Green Version]
- I Stanica, D.; Dumitriu, M. Critical points numerical analysis of ride comfort of the flexible railway carbody. IOP Conf. Ser. Mater. Sci. Eng. 2019, 682, 012004. [Google Scholar] [CrossRef]
- C 116. Interaction between Vehicles and Track, RP 1, Power Spectral Density of Track Irregularities, Part 1: Definitions, Conventions and Available Data; UIC: Utrecht, The Netherlands, 1971. [Google Scholar]
- UIC 513R. Guidelines for Evaluating Passenger Comfort In Relation to Vibration in Railway Vehicles; International Union of Railways: Paris, France, 1994. [Google Scholar]
- EN 12299. Railway Applications. Ride Comfort for Passengers. Measurement and Evaluation; British Standard: London, UK, 1999. [Google Scholar]
- Zhou, J.; Wenjing, S. Analysis on geometric filtering phenomenon and flexible car body resonant vibration of railway vehicles. J. Tongji Univ. Nat. Sci. 2009, 37, 1653–1657. [Google Scholar]
- Zhou, J.; Goodall, R.; Ren, L.; Zhang, H. Influences of car body vertical flexibility on ride quality of passenger railway vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 223, 461–471. [Google Scholar] [CrossRef] [Green Version]
- Gong, D.; Gu, Y.J.; Zhou, J.S. Study on Geometry Filtering Phenomenon and Flexible Car Body Resonant Vibration of Articulated Trains. Adv. Mater. Res. 2013, 787, 542–547. [Google Scholar] [CrossRef]
- Gong, D.; Zhou, J.; Sun, W.-J. On the resonant vibration of a flexible railway car body and its suppression with a dynamic vibration absorber. J. Vib. Control. 2012, 19, 649–657. [Google Scholar] [CrossRef]
- Dumitriu, M. Analysis of the dynamic response in the railway vehicles to the track vertical irregularities. Part II: The numerical analysis. J. Eng. Sci. Technol. Rev. 2015, 8, 32–39. [Google Scholar] [CrossRef]
- Wu, J.; Qiu, Y. Analysis of ride comfort of high-speed train based on a train-seat-human model in the vertical direction. Veh. Syst. Dyn. 2020, 1–27. [Google Scholar] [CrossRef]









| Ride Comfort Index NMV | Significance |
|---|---|
| NMV < 1 | Very comfortable |
| 1 ≤ NMV < 2 | Comfortable |
| 2 ≤ NMV< 4 | Medium |
| 4 ≤ NMV < 5 | Uncomfortable |
| NMV ≥ 5 | Very uncomfortable |
| mc = 34,000 kg | 2kzc = 1.2 MN/m |
| mb = 3200 kg | 2czc = 34.28 kNs/m |
| Jc = 1,963,840 kg·m2 | 4kzb = 4.4 MN/m |
| Jb = 2048 kg·m2 | 4czb = 52.21 kNs/m |
| EI = 3.158·109 Nm2 | Lc = 26.4 m |
| mmc = 35,224 kg | 2ac = 19 m; 2ab = 2.56 m |
| kmc = 88.998 MN/m | h = 1.6 m |
| cmc = 53.117 kNm/s | b = 1 m |
| k [N/m] | At Carbody Center | Against the Front Bogie | Against the Rear Bogie | |||
|---|---|---|---|---|---|---|
| c [Ns/m] | c [Ns/m] | c [Ns/m] | ||||
| 5·106 | 0.7·105 | 2.00 | 0.9·105 | 1.83 | 1.6·105 | 2.26 |
| 1·107 | 1.3·105 | 1.82 | 1.4·105 | 1.74 | 2.7·105 | 2.11 |
| 5·107 | 4.2·105 | 1.45 | 2.7·105 | 1.60 | 6.3·105 | 1.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dumitriu, M.; Stănică, D.I. Effect of the Anti-Yaw Damper on Carbody Vertical Vibration and Ride Comfort of Railway Vehicle. Appl. Sci. 2020, 10, 8167. https://doi.org/10.3390/app10228167
Dumitriu M, Stănică DI. Effect of the Anti-Yaw Damper on Carbody Vertical Vibration and Ride Comfort of Railway Vehicle. Applied Sciences. 2020; 10(22):8167. https://doi.org/10.3390/app10228167
Chicago/Turabian StyleDumitriu, Mădălina, and Dragoș Ionuț Stănică. 2020. "Effect of the Anti-Yaw Damper on Carbody Vertical Vibration and Ride Comfort of Railway Vehicle" Applied Sciences 10, no. 22: 8167. https://doi.org/10.3390/app10228167
APA StyleDumitriu, M., & Stănică, D. I. (2020). Effect of the Anti-Yaw Damper on Carbody Vertical Vibration and Ride Comfort of Railway Vehicle. Applied Sciences, 10(22), 8167. https://doi.org/10.3390/app10228167





