Enhancing Structural Performance of Short Fiber Reinforced Objects through Customized Tool-Path
Abstract
:1. Introduction
- (1)
- A novel design methodology for FDM parts assisted by finite element analysis;
- (2)
- A customized tool-path algorithm for FDM that maximizes the effect of fiber reinforcement under the given loading and boundary conditions.
2. Background
2.1. Anisotropy of FDM Parts
2.2. Carbon Fiber Reinforced Polymer (CFRP)
2.3. Tool Path for FDM
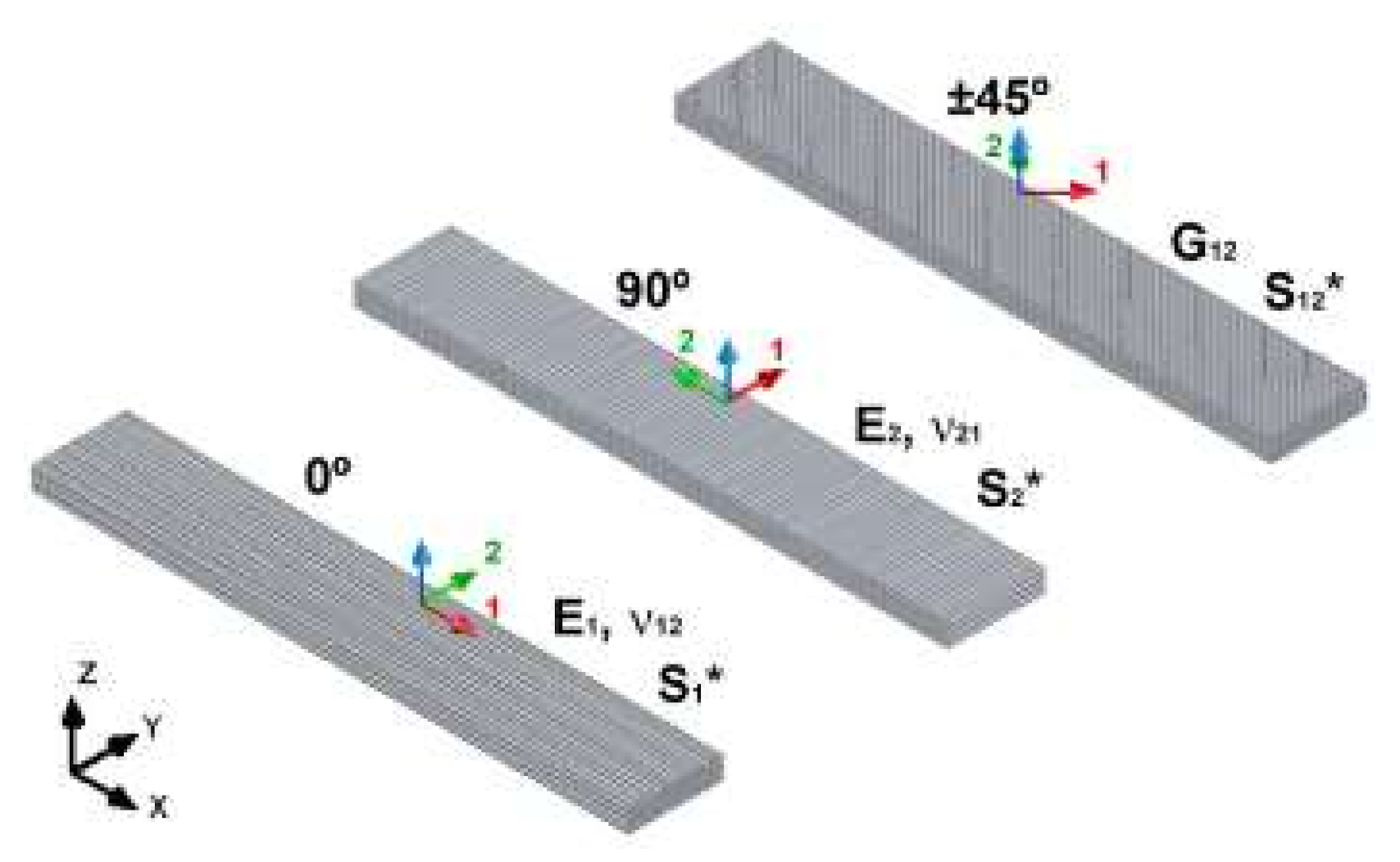
3. Material Characterization
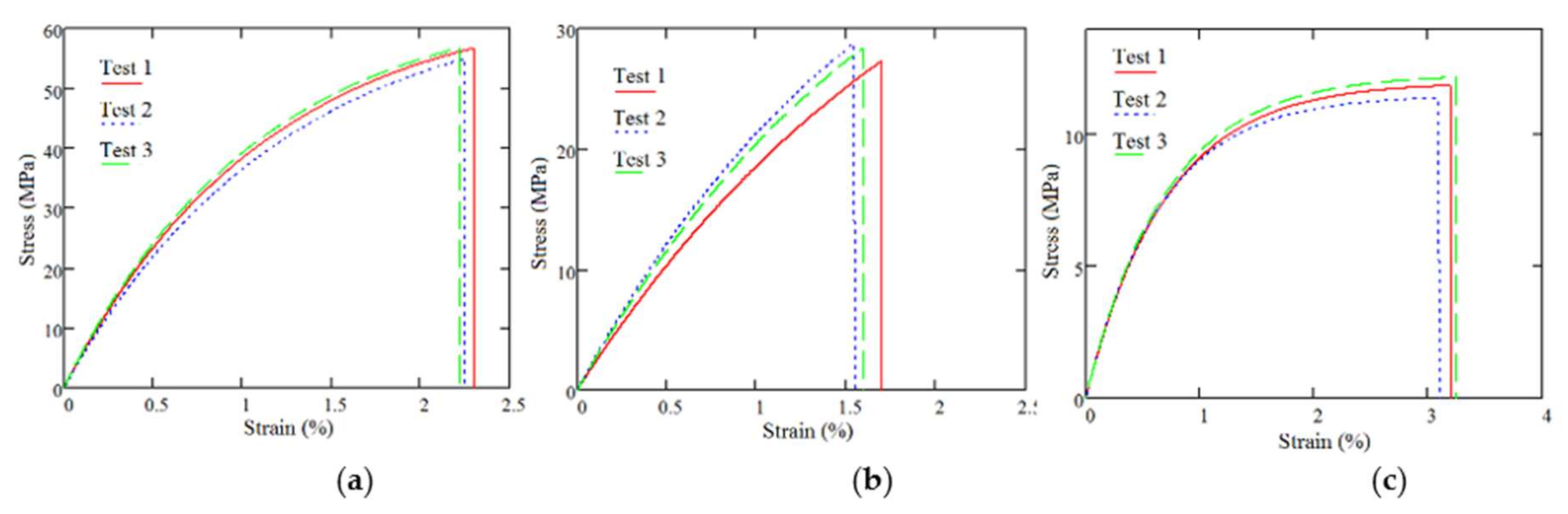
3.1. Mechanical Property Measurement
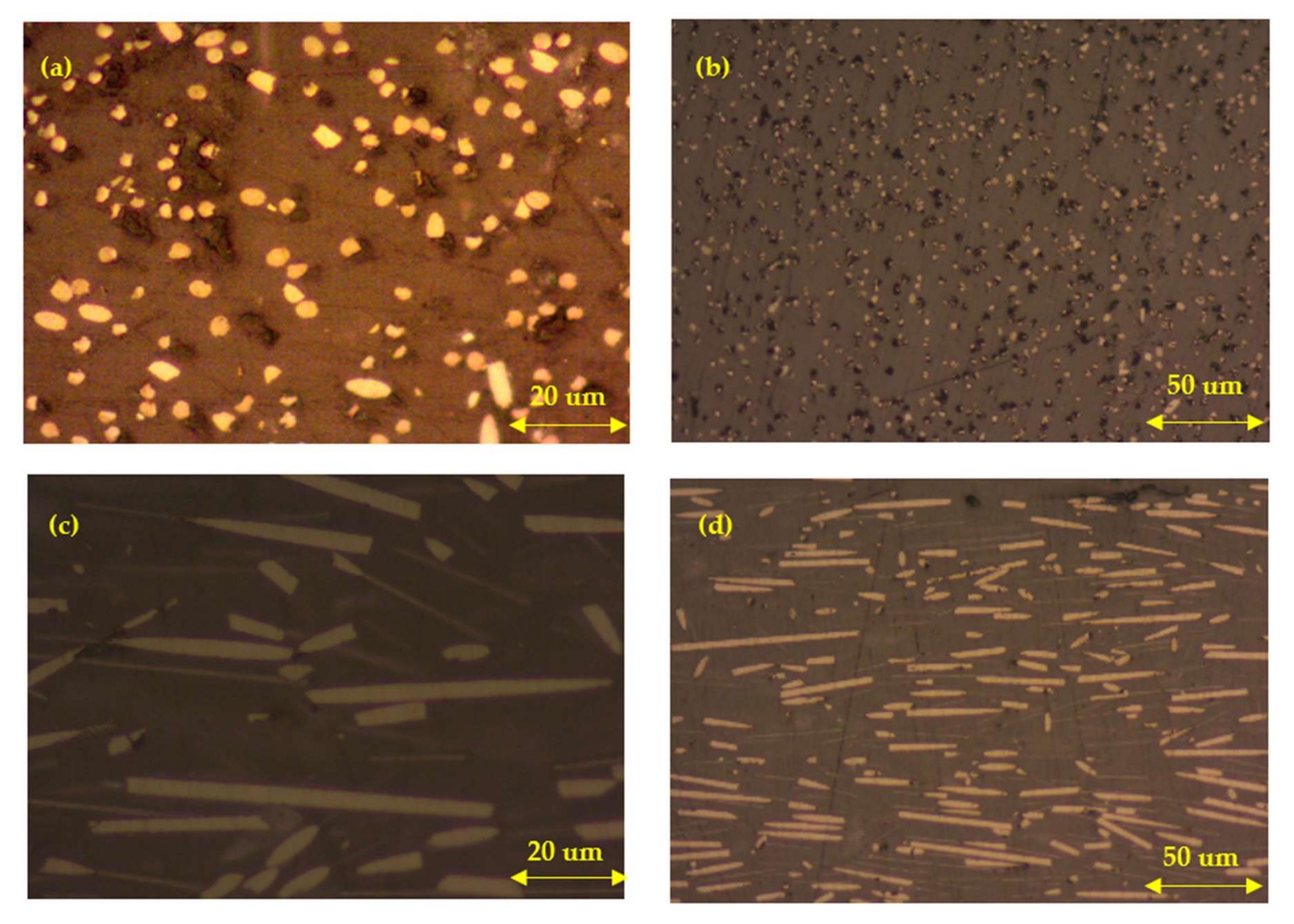
3.2. Fiber Orientation
4. Customized Tool-Path Development
4.1. FE Analysis
4.2. Location Angle and Radius Filter
4.3. Angle Difference Filter
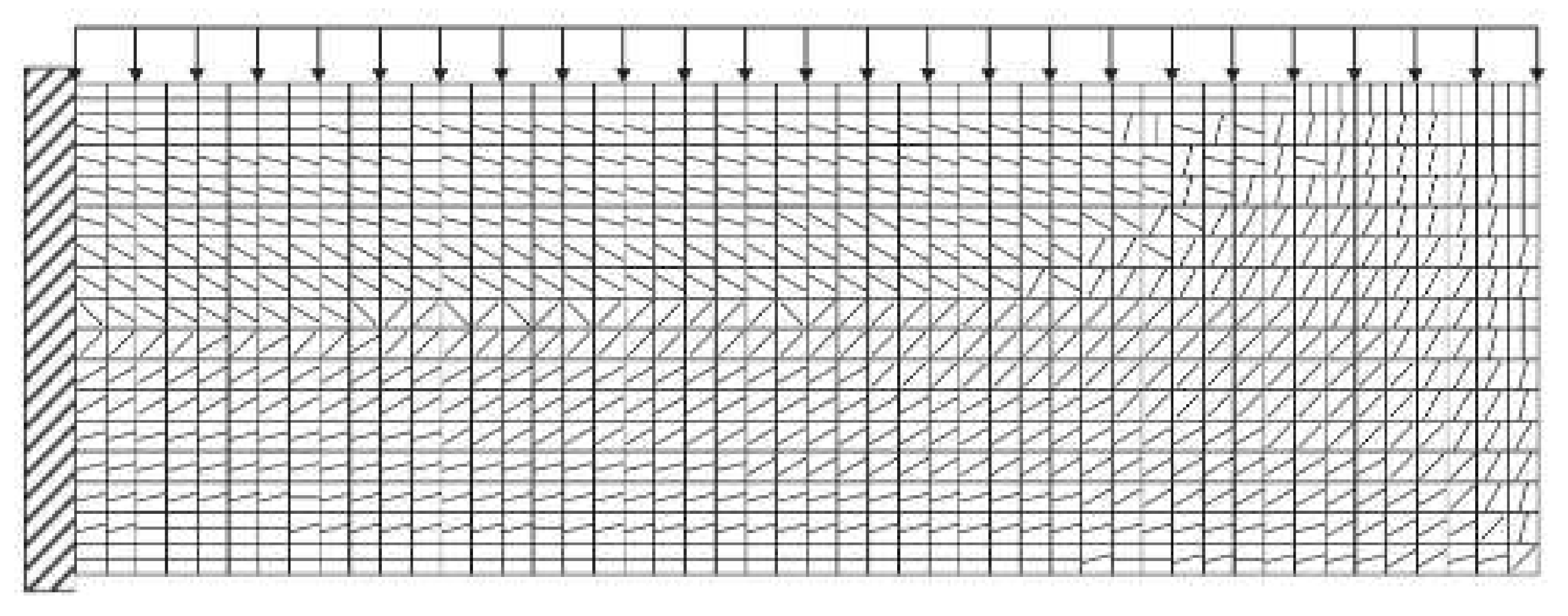
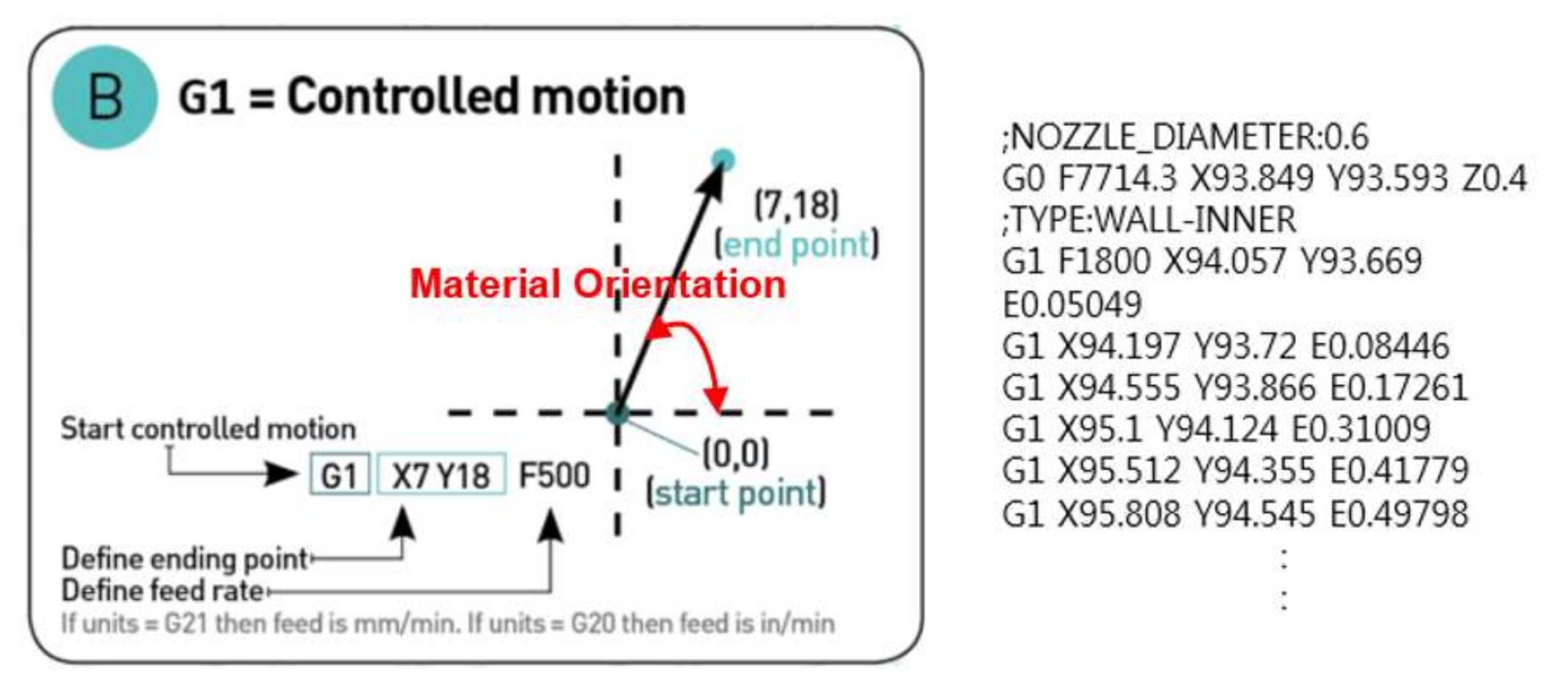
4.4. Creation of Printing Path and Sections
4.5. FE Modeling of Printed Object
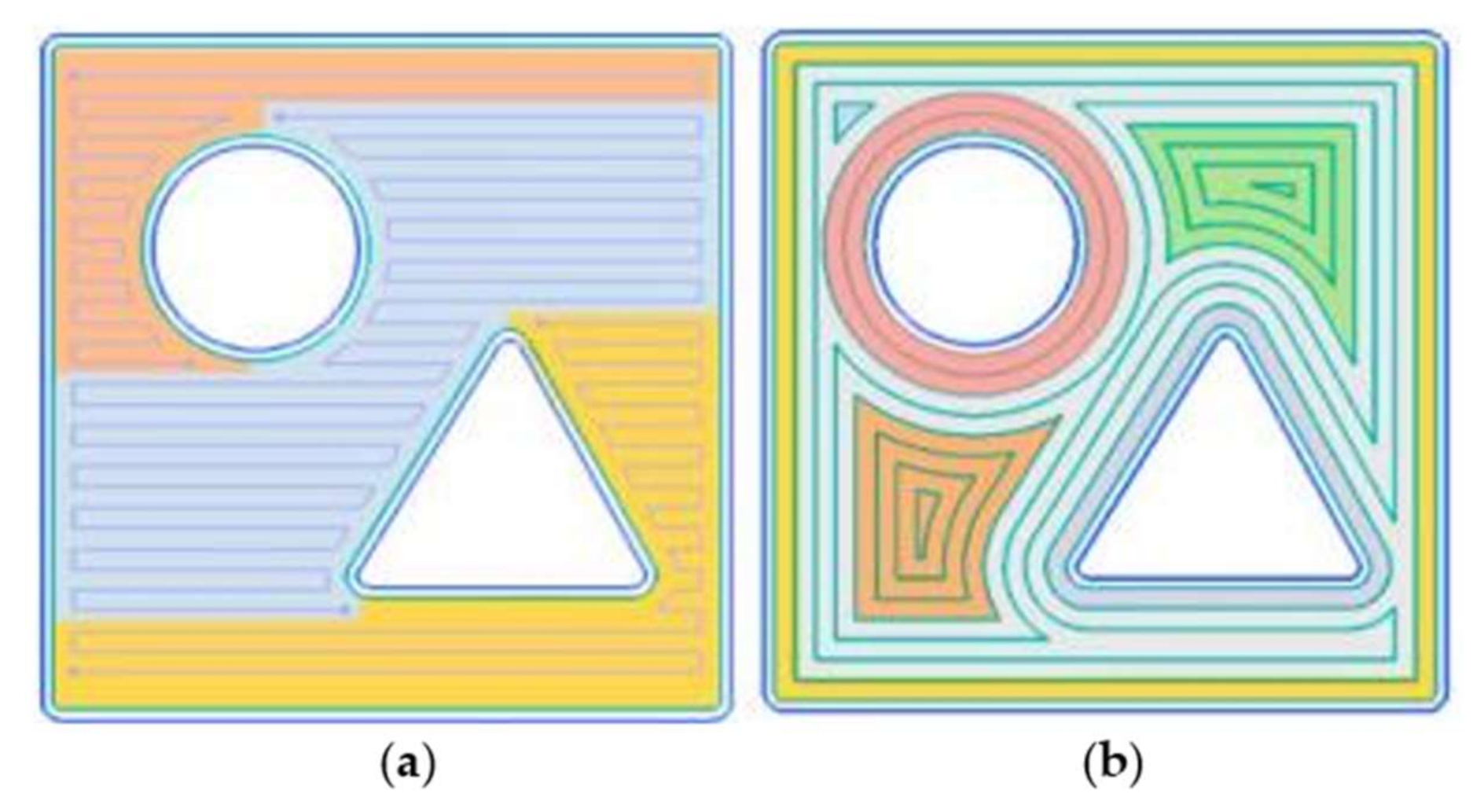
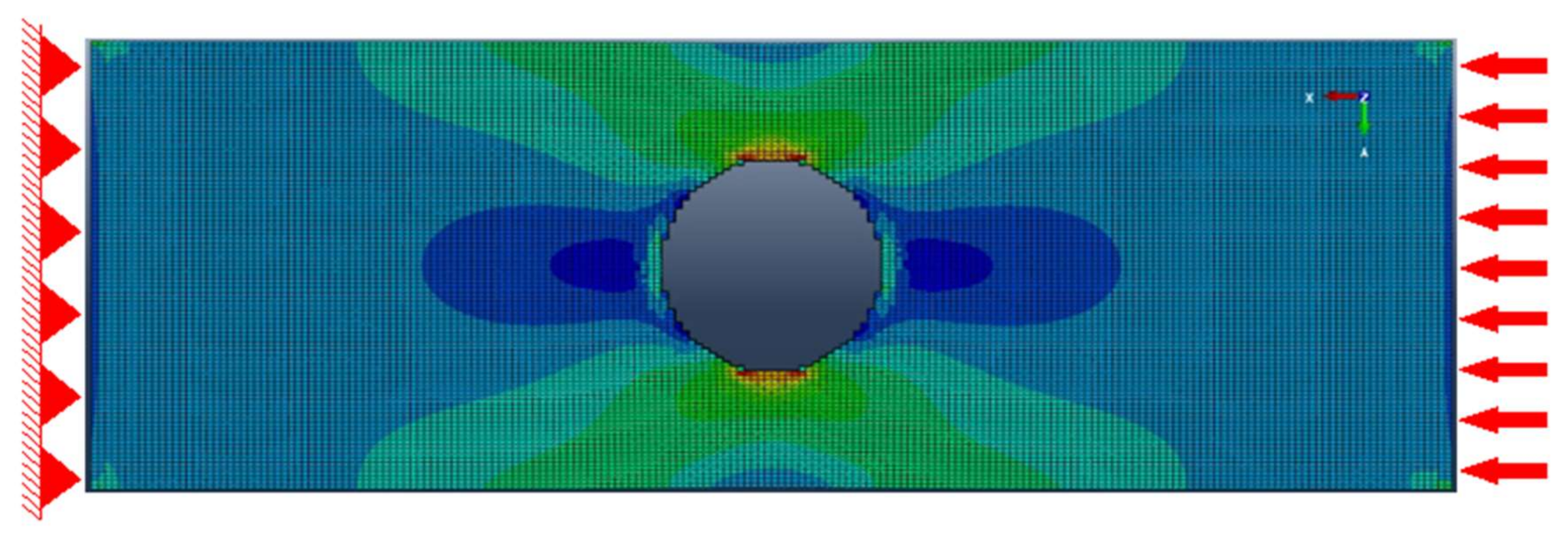
5. Case Study-Hole Plate
5.1. Problem Statement—Hole Plate
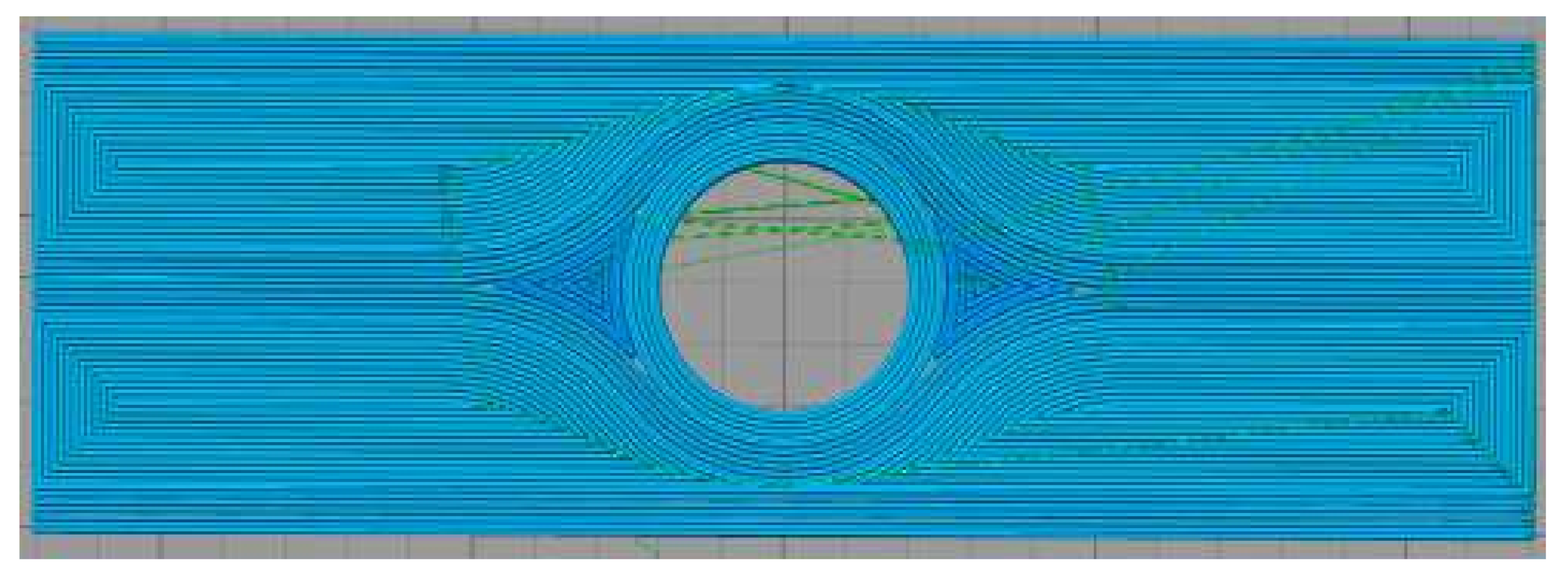
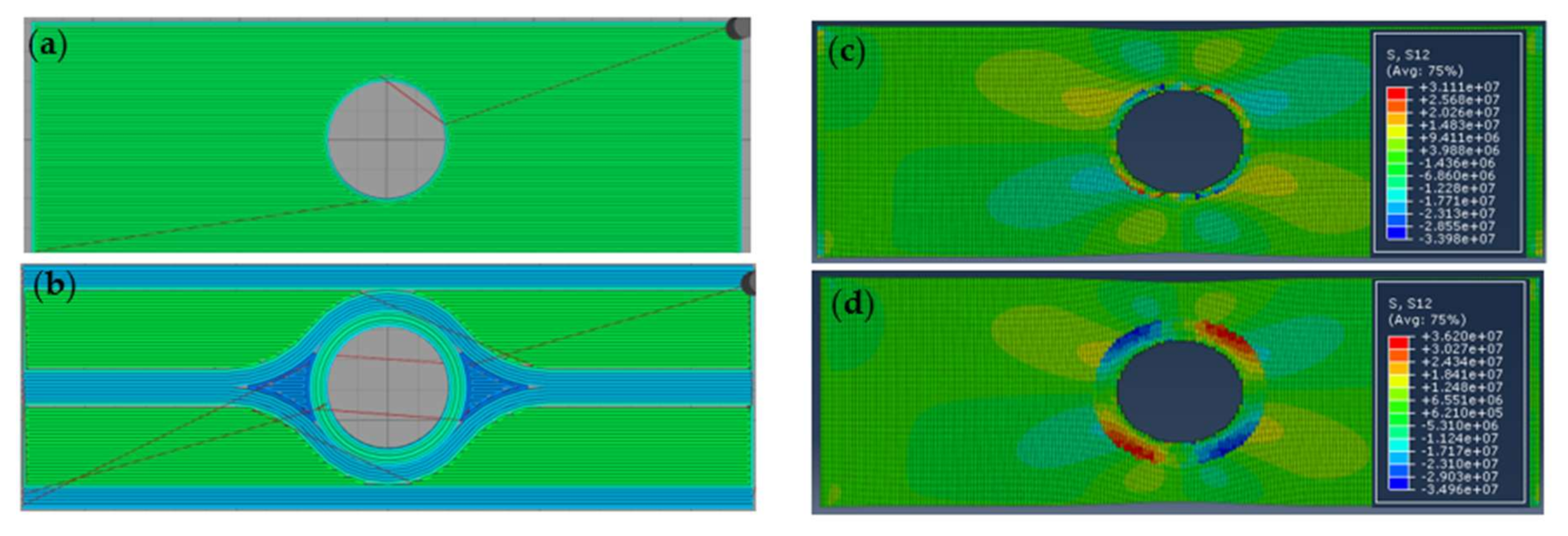
5.2. Tool Path Development—Hole Plate
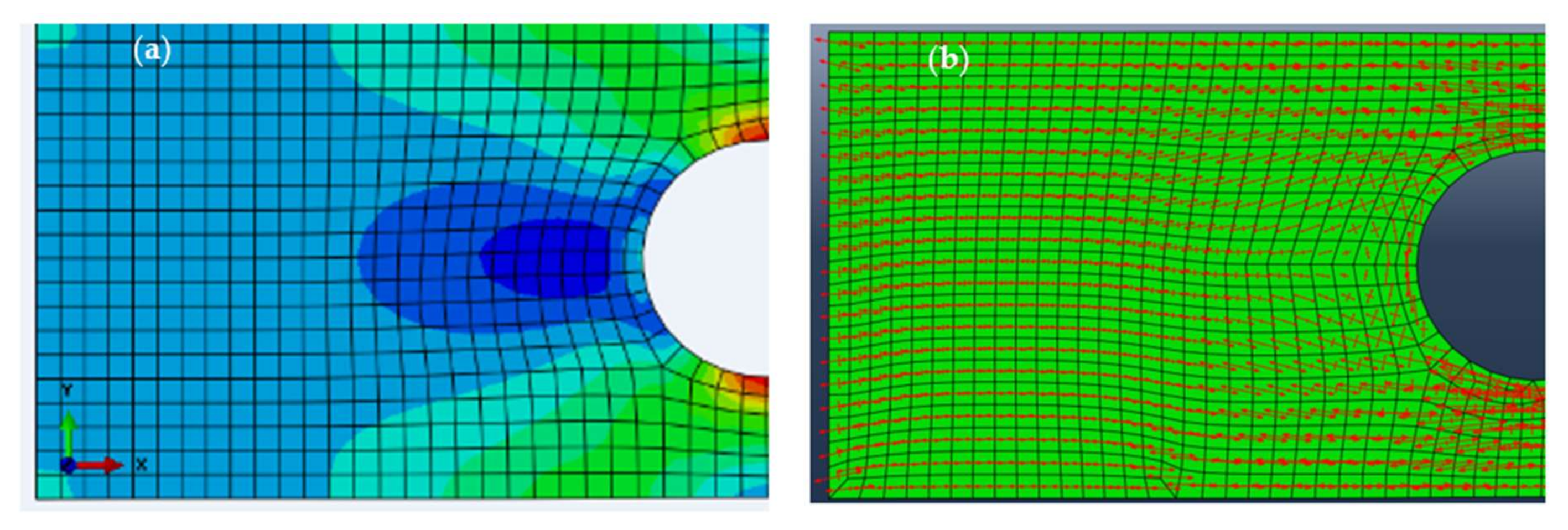
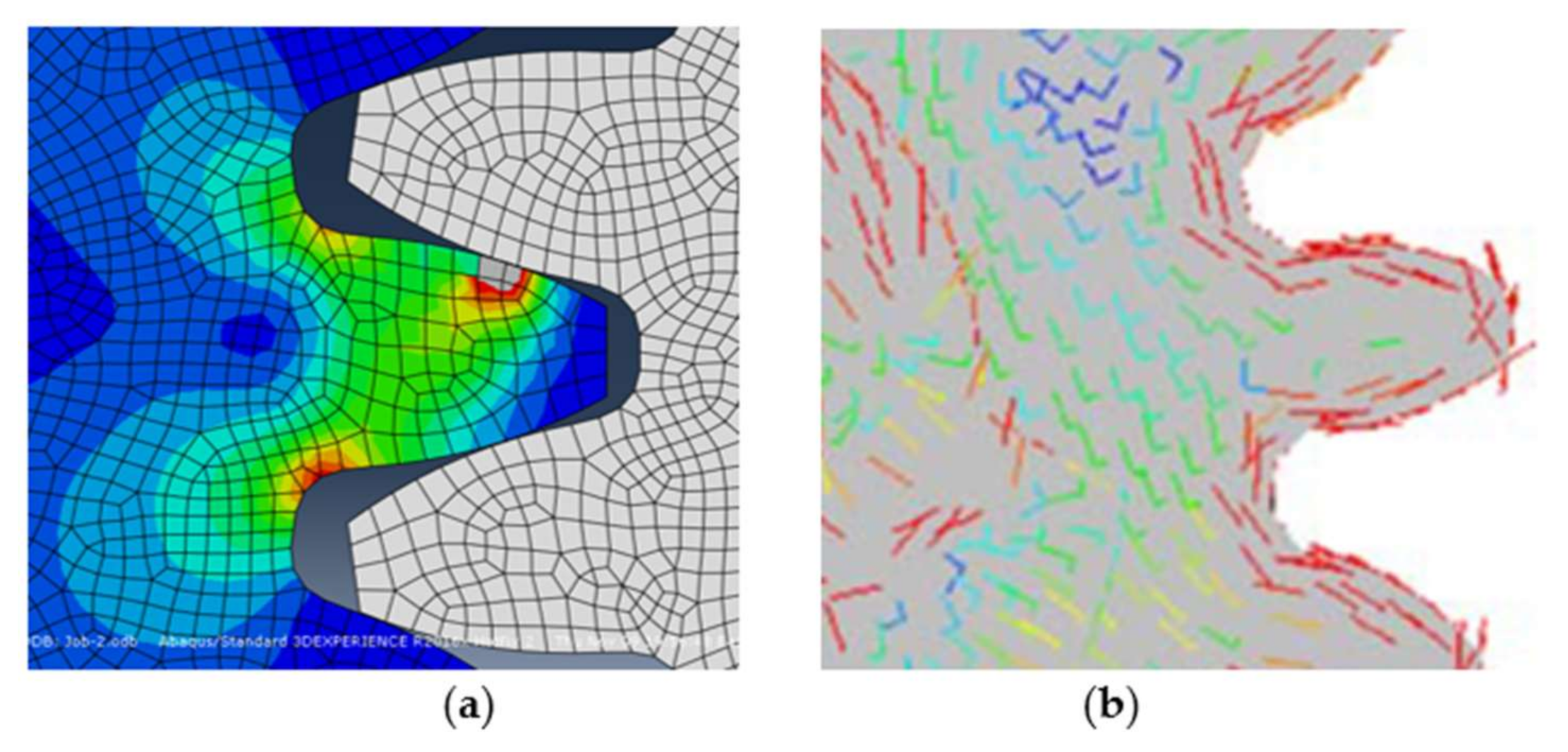
5.3. FE Modeling—Hole Plate
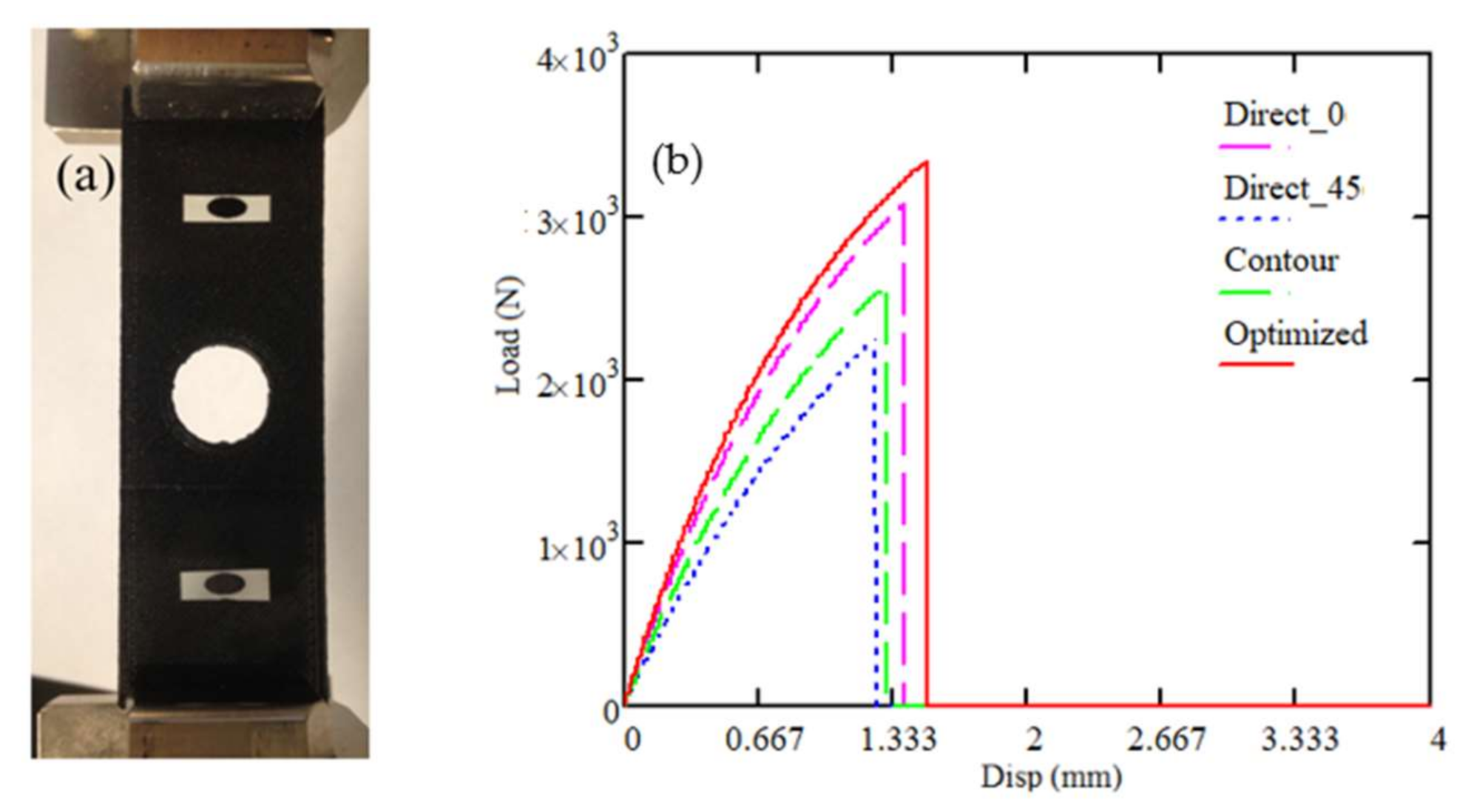
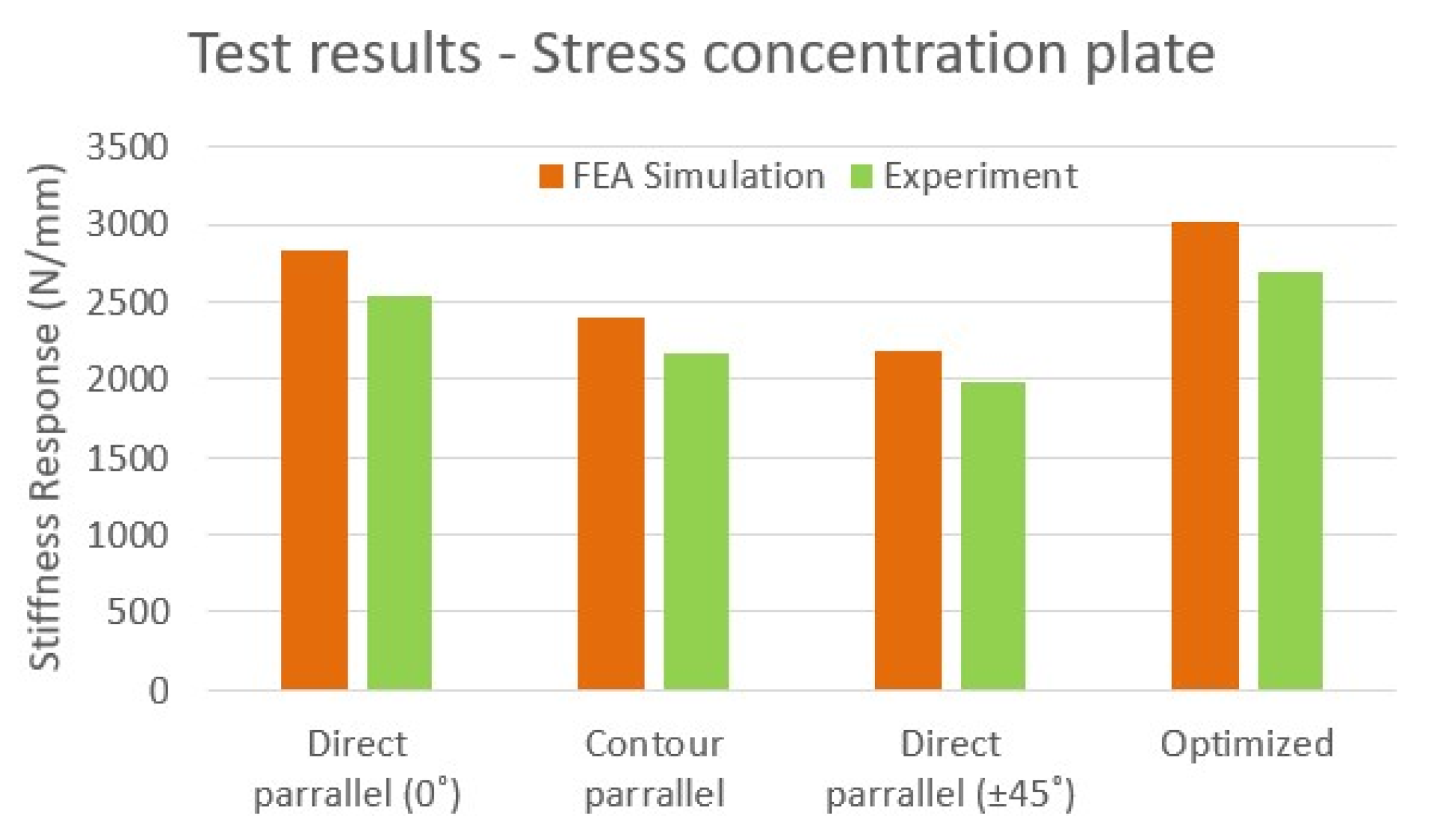
5.4. Tensile Test—Hole Plate
6. Case Study—Spur Gear
6.1. Problem Statement—Spur Gear
6.2. Determination of Fiber Orientations—Spur Gear
6.3. Tool Path Development—Spur Gear
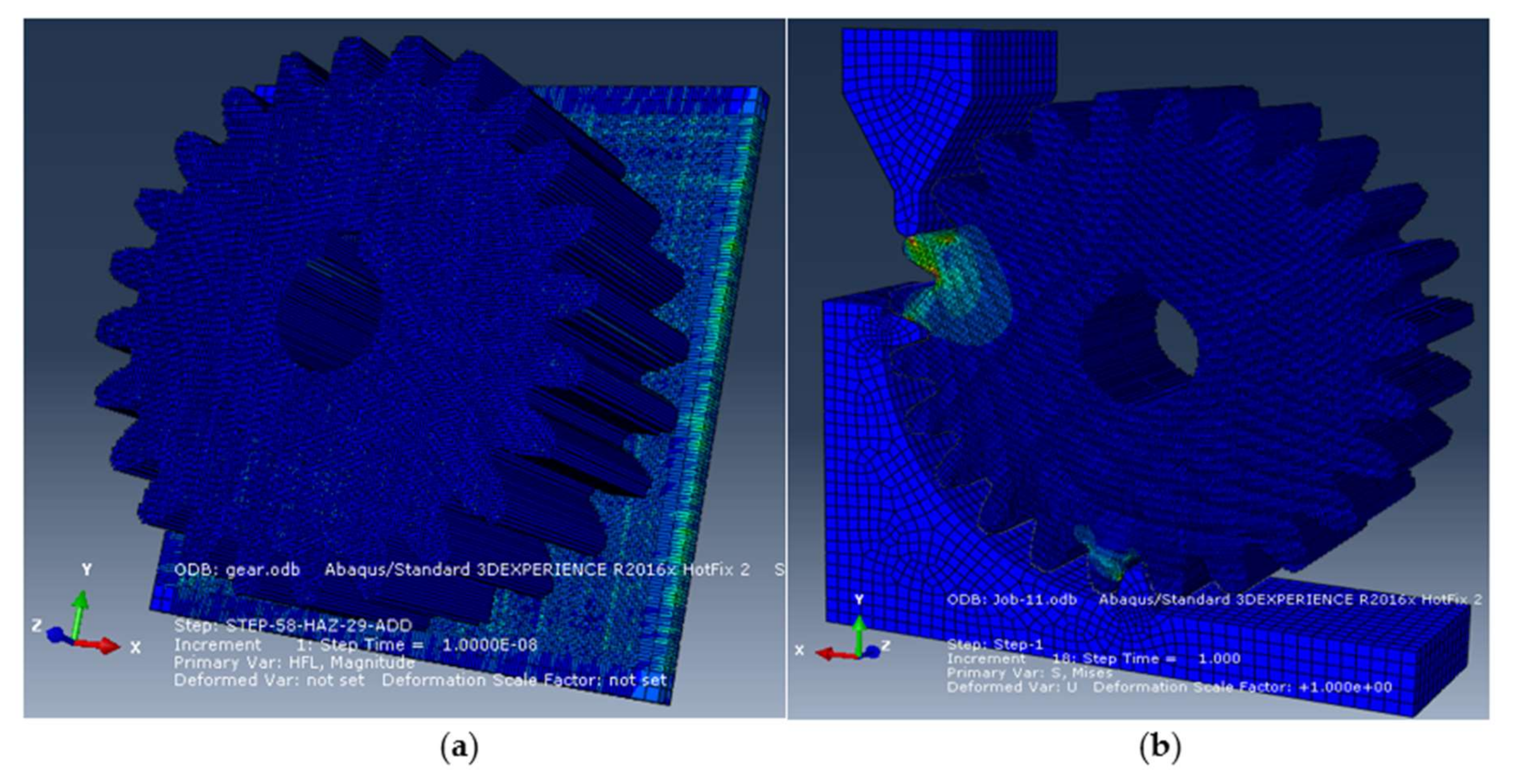
6.4. FE Modeling—Spur Gear
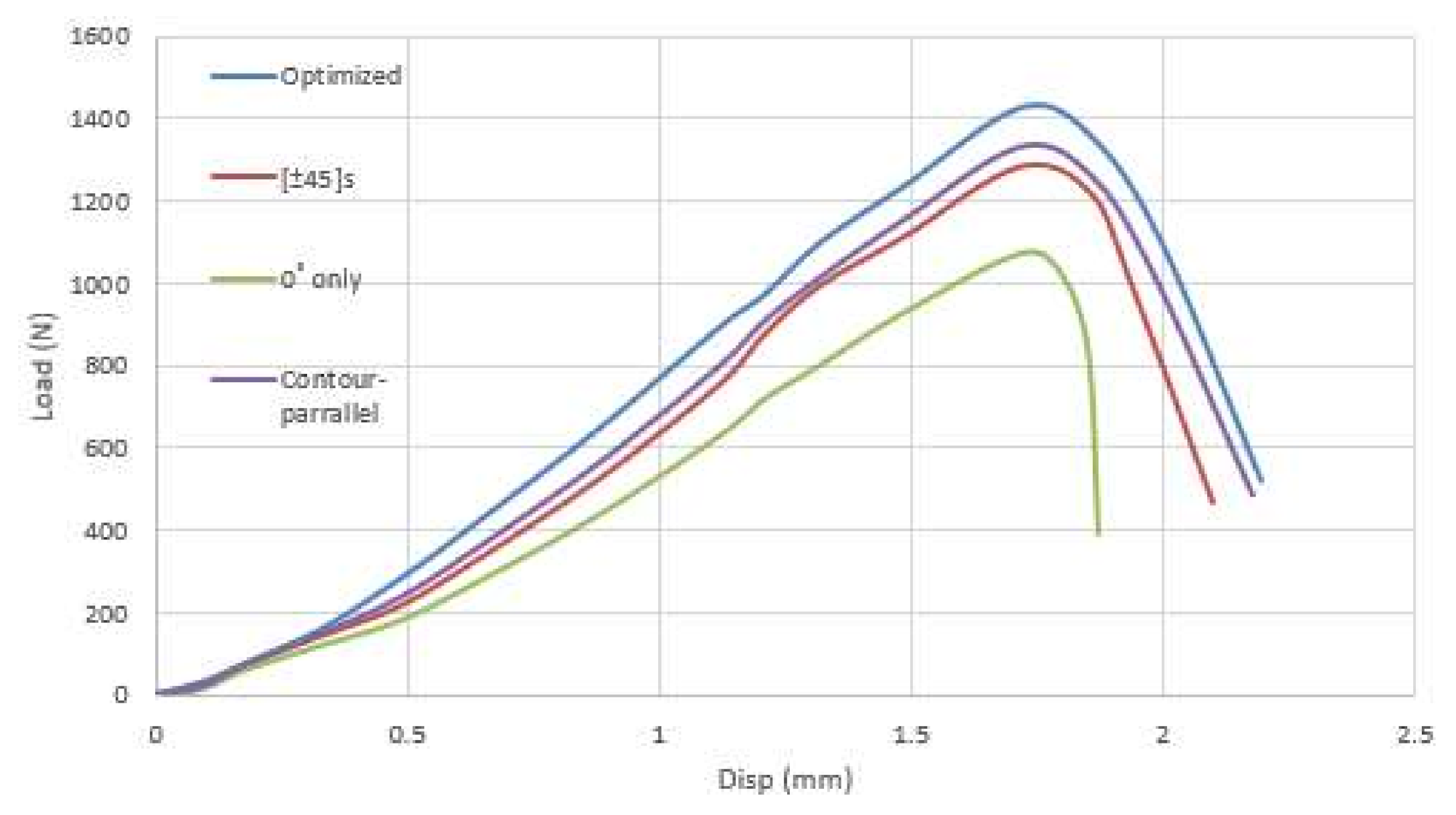
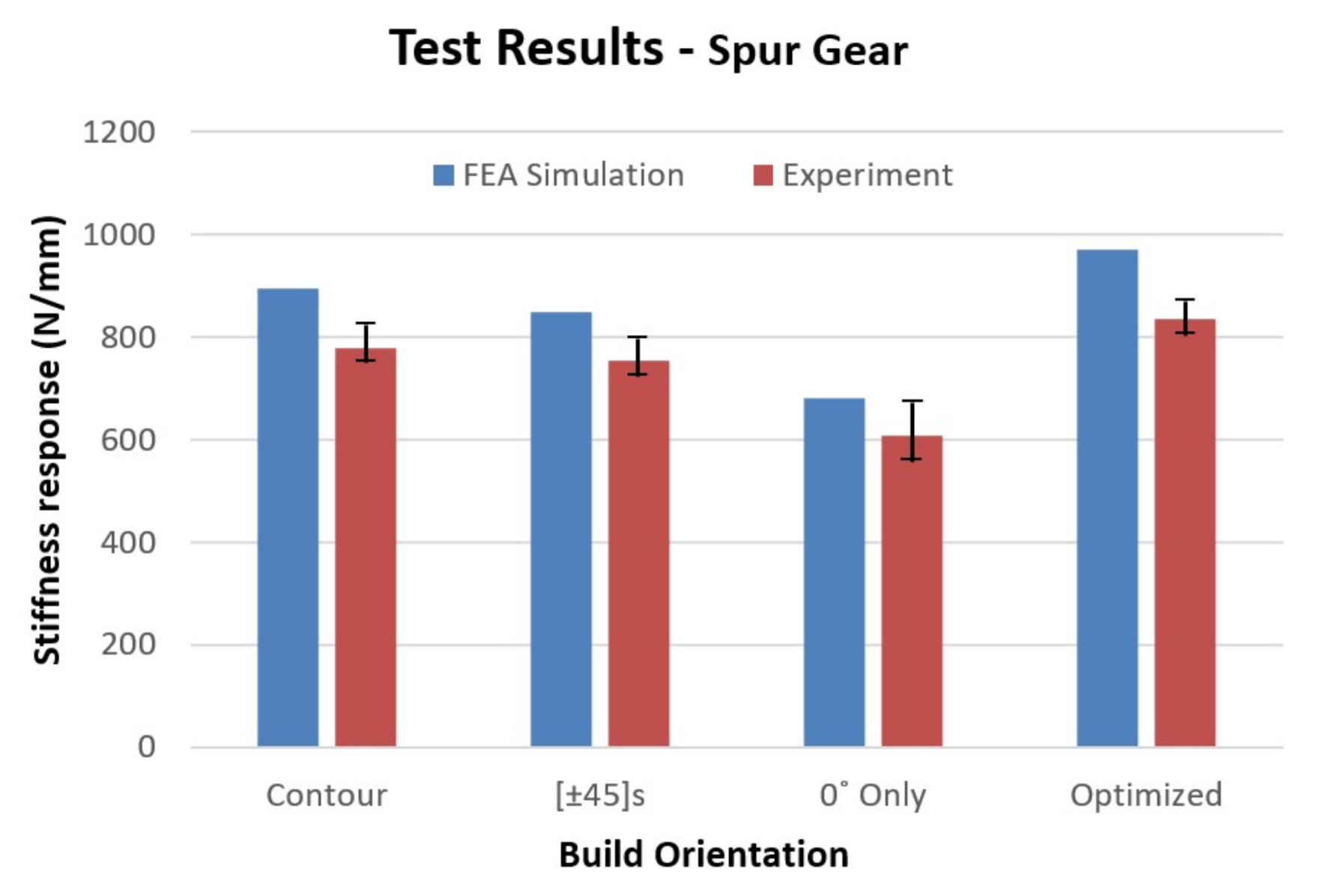
6.5. Stiffness Test—Spur Gear
7. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Campbell, T.; Williams, C.; Ivanova, O.; Garrett, B. Could 3D Printing Change the World? Atlantic Council: Washington, DC, USA, 2011; p. 16. [Google Scholar]
- Vaezi, M.; Seitz, H.; Yang, S. A review on 3D micro-additive manufacturing technologies. Int. J. Adv. Manuf. Technol. 2013, 67, 1721–1754. [Google Scholar] [CrossRef]
- Scott, J.; Gupta, N.; Weber, C.; Newsome, S. Additive manufacturing: Status and opportunities. Sci. Technol. Policy Inst. 2012, 1–19. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.W.; Stucker, B. Additive manufacturing technologies: Rapid prototyping to direct digital manufacturing. Assem. Autom. 2010. [Google Scholar] [CrossRef]
- Seepersad, C.C. Challenges and opportunities in design for additive manufacturing, 3D print. Addit. Manuf. 2014, 1, 10–13. [Google Scholar]
- Lipson, H.M.K. Fabricated the New World of 3D Printing, 1st ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2013; pp. 1–5. [Google Scholar]
- Rodríguez, J.F.; Thomas, J.P.; Renaud, J.E. Mechanical behavior of acrylonitrile butadiene styrene (ABS) fused deposition materials. Experimental investigation. Rapid Prototyp. J. 2001, 7, 48–158. [Google Scholar] [CrossRef]
- Pandey, M.P.; Venkata, R.N.; Dhande, S.G. Slicing procedures in layered manufacturing: A review. Rapid Prototyp. J. 2003, 9, 274–288. [Google Scholar] [CrossRef] [Green Version]
- Galantucci, L.M.; Lavecchia, F.; Percoco, G. Experimental study aiming to enhance the surface finish of fused deposition modeled parts. CIRP Ann. Manuf. Technol. 2009, 58, 189–192. [Google Scholar] [CrossRef]
- Galantucci, L.M.; Lavecchia, F.; Percoco, G. Quantitative analysis of a chemical treatment to reduce roughness of parts fabricated using fused deposition modeling. CIRP Ann. Manuf. Technol. 2010, 59, 247–250. [Google Scholar] [CrossRef]
- Garg, A.; Bhattacharya, A.; Batish, A. Chemical vapor treatment of ABS parts built by FDM: Analysis of surface finish and mechanical strength. Int. J. Adv. Manuf. Technol. 2017, 89, 2175–2191. [Google Scholar] [CrossRef]
- Tiwary, V.; Arunkumar, P.; Deshpande, A.S.; Khorate, V. Studying the effect of chemical treatment and fused deposition modelling process parameters on surface roughness to make acrylonitrile butadiene styrene patterns for investment casting process. Int. J. Rapid Manuf. 2015, 5, 276–288. [Google Scholar] [CrossRef]
- Singhal, S.K.; Pandey, A.P.; Pandey, P.M.; Nagpal, A.K. Optimum part deposition orientation in stereolithography. Comput. Aided. Des. Appl. 2005, 2, 319–328. [Google Scholar] [CrossRef]
- Panda, S.K. Optimization of fused deposition modelling (FDM) process parameters using bacterial foraging technique. Intell. Inf. Manag. 2009, 1, 89–97. [Google Scholar] [CrossRef] [Green Version]
- Blok, L.G.; Longana, M.L.; Yu, H.; Woods, B.K.S. An investigation into 3D printing of fi bre reinforced thermoplastic composites. Addit. Manuf. 2018, 22, 176–186. [Google Scholar]
- Ulu, E.; Korkmaz, E.; Yay, K.; Ozdoganlar, B.O.; Burak Kara, B.L. Enhancing the structural performance of additively manufactured objects through build orientation optimization. J. Mech. Des. 2015, 137, 111410. [Google Scholar] [CrossRef]
- Zaldivar, R.J.; Witkin, D.B.; McLouth, T.; Patel, D.N.; Schmitt, K.; Nokes, J.P. Influence of processing and orientation print effects on the mechanical and thermal behavior of 3D-printed ULTEM® 9085 material. Addit. Manuf. 2017, 13, 71–80. [Google Scholar] [CrossRef]
- Buj-Corral, I.; Domínguez-Fernández, A.; Durán-Llucià, R. Influence of print orientation on surface roughness in fused deposition modeling (FDM) processes. Materials 2019, 12, 3834. [Google Scholar] [CrossRef] [Green Version]
- El-Gizawy, A.S.; Corl, S.; Graybill, B. Process-induced properties of FDM products. In Proceedings of the ICMET International Conference on Mechanical Engineerings and Technology Congress & Exposition, Paris, France, 27–29 July 2011; p. 7. [Google Scholar]
- Hill, N.; Haghi, M. Deposition direction-dependent failure criteria for fused deposition modeling polycarbonate. Rapid Prototyp. J. 2014, 20, 221–227. [Google Scholar] [CrossRef]
- Torrado Perez, A.R.; Roberson, D.A.; Wicker, R.B. Fracture surface analysis of 3D-printed tensile specimens of novel ABS-based materials. J. Fail. Anal. Prev. 2014, 14, 343–353. [Google Scholar] [CrossRef]
- Hwang, S.; Reyes, E.I.; Moon, S.K.; Rumpf, R.C.; Kim, N.S. Thermo-mechanical characterization of metal/polymer composite filaments and printing parameter study for fused deposition modeling in the 3D printing process. J. Electron. Mater. 2015, 44, 771–777. [Google Scholar] [CrossRef]
- Zhong, W.; Li, F.; Zhang, Z.; Song, L.; Li, Z. Short fiber reinforced composites for fused deposition modeling. Mater. Sci. Eng. A 2001, 301, 125–130. [Google Scholar] [CrossRef]
- Shofner, M.L.; Lozano, K.; Rodríguez-Macías, F.J.; Barrera, E.V. Nanofiber-reinforced polymers prepared by fused deposition modeling. J. Appl. Polym. Sci. 2003, 89, 3081–3090. [Google Scholar] [CrossRef]
- Matsuzaki, R.; Ueda, M.; Namiki, M.; Jeong, T.-K.; Asahara, H.; Horiguchi, K.; Nakamura, T.; Todoroki, A.; Hirano, Y. Three-dimensional printing of continuous-fiber composites by in-nozzle impregnation. Sci. Rep. 2016, 6, 23058. [Google Scholar] [CrossRef]
- Compton, B.G.; Lewis, J.A. 3D-printing of lightweight cellular composites. Adv. Mater. 2014, 26, 5930–5935. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Xu, X.; Stringer, J. Optimization of process planning for reducing material waste in extrusion based additive manufacturing. Robot. Comput. Integr. Manuf. 2019, 59, 317–325. [Google Scholar] [CrossRef]
- Jiang, J.; Xu, X.; Stringer, J. Optimisation of multi-part production in additive manufacturing for reducing support waste. Virtual Phys. Prototyp. 2019, 14, 219–228. [Google Scholar] [CrossRef]
- El-Midany, T.T.; Elkeran, A.; Tawfik, H. Toolpath pattern comparison contour-parallel with direction-parallel. In Proceedings of the Geometric Modeling and Imaging-New Trends (GMAI’06), London, UK, 5–7 July 2006; pp. 77–82. [Google Scholar]
- Jin, G.Q.; Li, W.D.; Gao, L. An adaptive process planning approach of rapid prototyping and manufacturing. Robot. Comput. Integr. Manuf. 2013, 29, 23–38. [Google Scholar] [CrossRef]
- Jin, Y.; He, Y.; Fu, G.; Zhang, A.; Du, J. A non-retraction path planning approach for extrusion-based additive manufacturing. Robot. Comput. Integr. Manuf. 2017, 48, 132–144. [Google Scholar] [CrossRef]
- Liao, G.; Li, Z.; Cheng, Y.; Xu, D.; Zhu, D.; Jiang, S.; Guo, J.; Chen, X.; Xu, G.; Zhu, Y. Properties of oriented carbon fiber/polyamide 12 composite parts fabricated by fused deposition modeling. Mater. Des. 2018, 139, 283–292. [Google Scholar] [CrossRef]
- Goh, G.D.; Dikshit, V.; Nagalingam, A.P.; Goh, G.L.; Agarwala, S.; Sing, S.L.; Wei, J.; Yeong, W.Y. Characterization of mechanical properties and fracture mode of additively manufactured carbon fiber and glass fiber reinforced thermoplastics. Mater. Des. 2018, 137, 79–89. [Google Scholar] [CrossRef]
- Ferreira, R.T.L.; Amatte, I.C.; Dutra, T.A.; Bürger, D. Experimental characterization and micrography of 3D printed PLA and PLA reinforced with short carbon fibers. Compos. Part B 2017, 124, 88–100. [Google Scholar] [CrossRef]
- Bay, R.S.; Tucker, C.L. Stereological measurement and error estimates for three-dimensional fiber orientation. Polym. Eng. Sci. 1992, 32, 240–253. [Google Scholar] [CrossRef]
- Stegmann, J.; Lund, E. Discrete material optimization of general composite shell structures. Int. J. Numerical Methods Eng. 2005, 62, 2009–2027. [Google Scholar] [CrossRef]
- Kim, J. Optimization of Design and Manufacturing Process of Fusion Filament Fabrication (fff) 3D Printing. Ph.D. Thesis, West Virginia University, Morgantown, WV, USA, 2018. [Google Scholar]















| Property | Direction | CFRP-Nylon | ASTM |
|---|---|---|---|
| Young’s Modulus | 0° | 4.14 GPa | D638 |
| 90° | 2.15 Gpa | ||
| Shear Modulus | ±45° | 1.12 Gpa | D3518 |
| Tensile Strength | 0° | 56.6 Mpa | D638 |
| 90° | 28.3 Mpa | ||
| Shear Strength | ±45° | 11.9 Mpa | D3518 |
| Elongation | 0° | 2.30% | D638 |
| 90° | 1.59% | ||
| Poisson’s ratio | ν12 | 0.391 | D638 |
| ν21 | 0.203 |
| Orientation | a11 | a12 | a13 | a22 | a23 | a33 |
|---|---|---|---|---|---|---|
| % | 0.825 | 0.123 | 0.082 | 0.03 | 0.004 | 0.0056 |
| Stiffness Response (N/mm) | Failure Strength (N) | Max. Displacement (mm) | |
|---|---|---|---|
| Direct-parallel (0°) | 2544.0 | 3087 | 1.39 |
| Contour-parallel | 2161.7 | 2592 | 1.30 |
| Direct-parallel (±45°) | 1983.4 | 2262 | 1.25 |
| Optimized | 2687.0 | 3349 | 1.50 |
| Stiffness Response (N/mm) | Failure Strength (N) | Max Disp (mm) | |
|---|---|---|---|
| Contour | 778.6 | 1330 | 2.18 |
| Optimized | 834.6 | 1430 | 2.19 |
| [±45°]s | 754.6 | 1287 | 2.10 |
| 0° only | 607.0 | 1073 | 1.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Kang, B.S. Enhancing Structural Performance of Short Fiber Reinforced Objects through Customized Tool-Path. Appl. Sci. 2020, 10, 8168. https://doi.org/10.3390/app10228168
Kim J, Kang BS. Enhancing Structural Performance of Short Fiber Reinforced Objects through Customized Tool-Path. Applied Sciences. 2020; 10(22):8168. https://doi.org/10.3390/app10228168
Chicago/Turabian StyleKim, Jaeyoon, and Bruce S. Kang. 2020. "Enhancing Structural Performance of Short Fiber Reinforced Objects through Customized Tool-Path" Applied Sciences 10, no. 22: 8168. https://doi.org/10.3390/app10228168
APA StyleKim, J., & Kang, B. S. (2020). Enhancing Structural Performance of Short Fiber Reinforced Objects through Customized Tool-Path. Applied Sciences, 10(22), 8168. https://doi.org/10.3390/app10228168





