Selection Strategy of Vibration Feature Target under Centrifugal Pumps Cavitation
Abstract
:1. Introduction
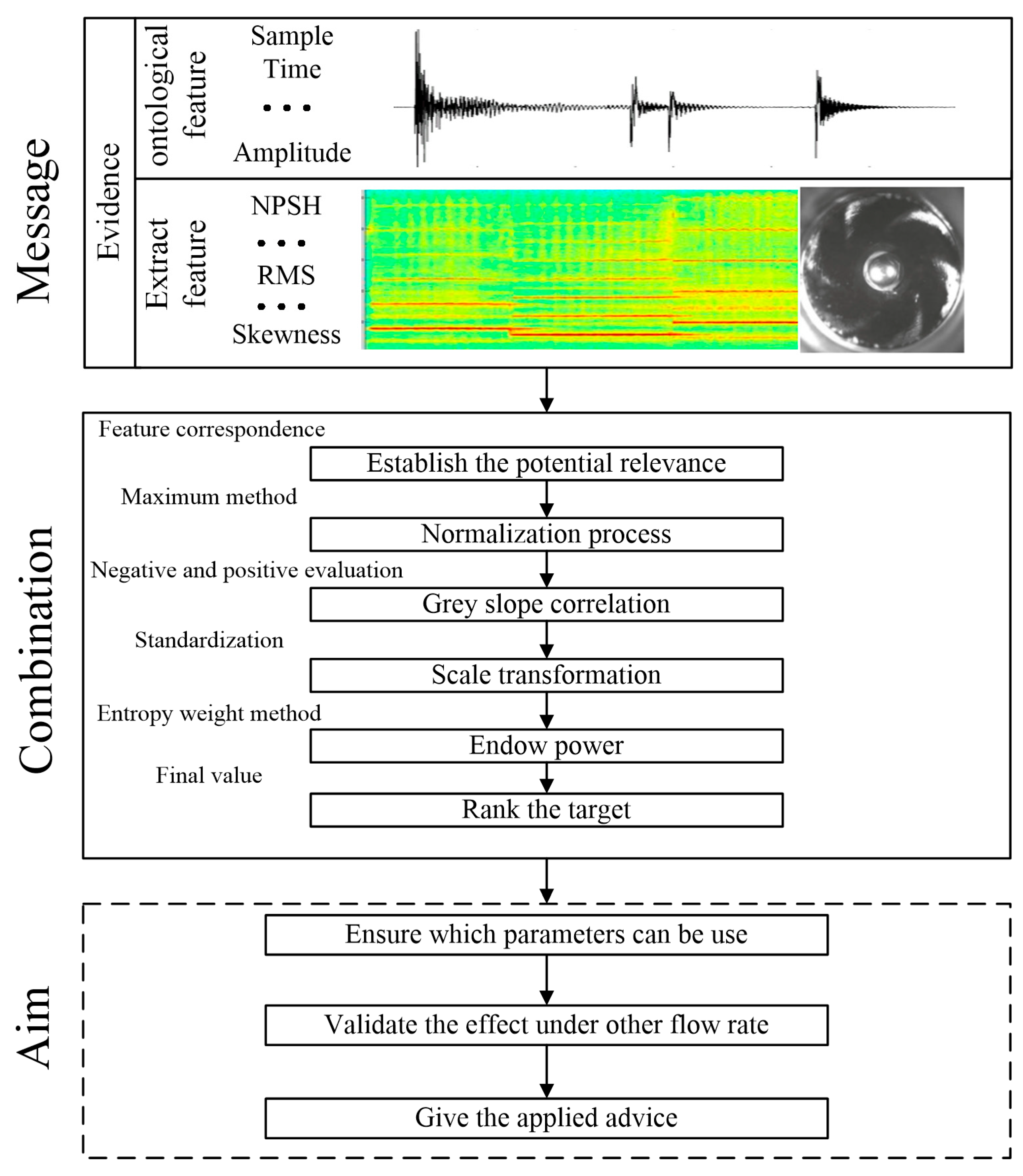
2. Grey Relation Entropy Analysis Method
2.1. Grey Slope Correlation Method
2.2. Weight Entropy Method
2.3. Calculation Process
3. Signal Capture and Pretreatment
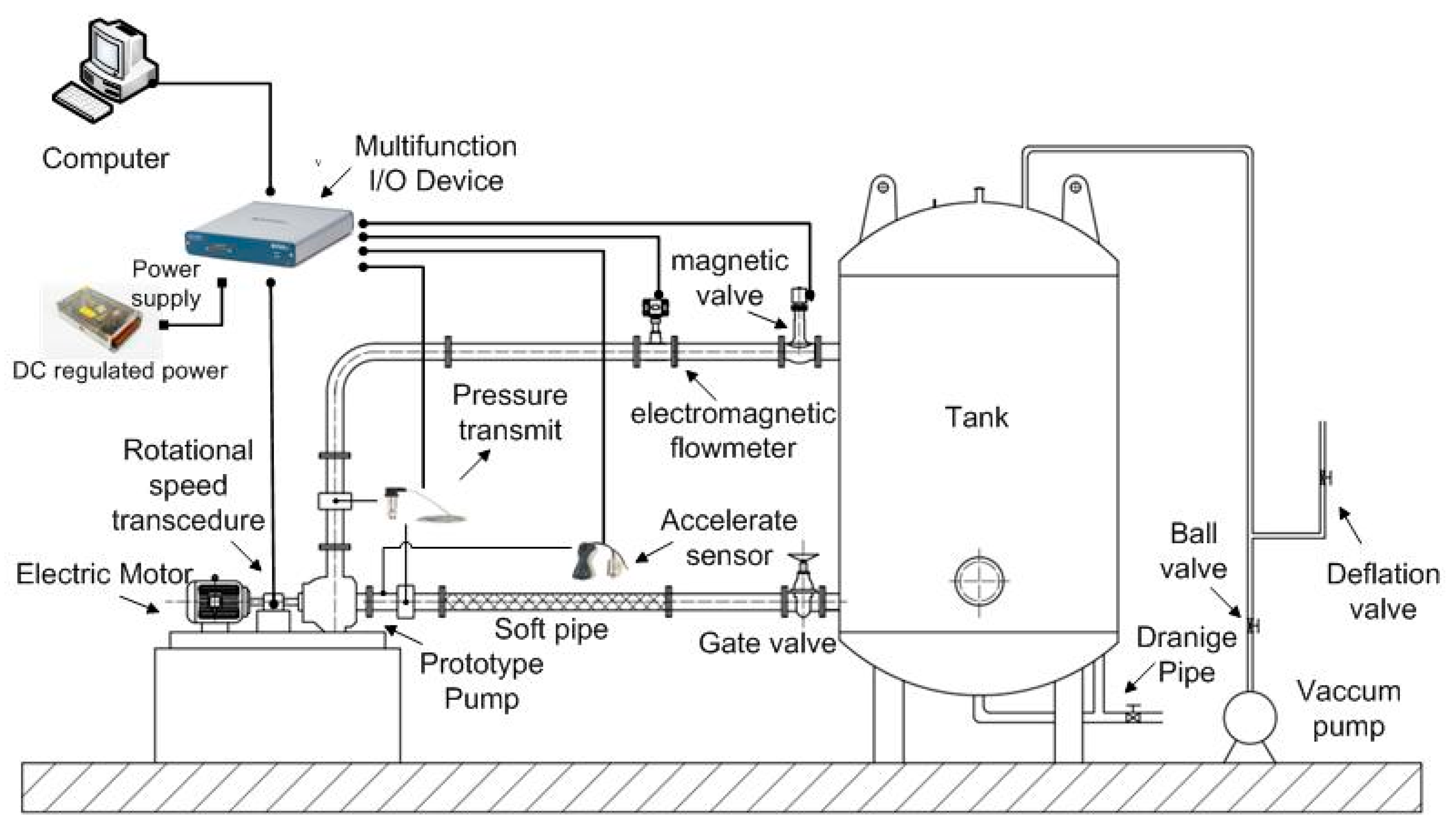
3.1. Test Rig
3.2. Experiment Instrument
3.3. Experiment Method
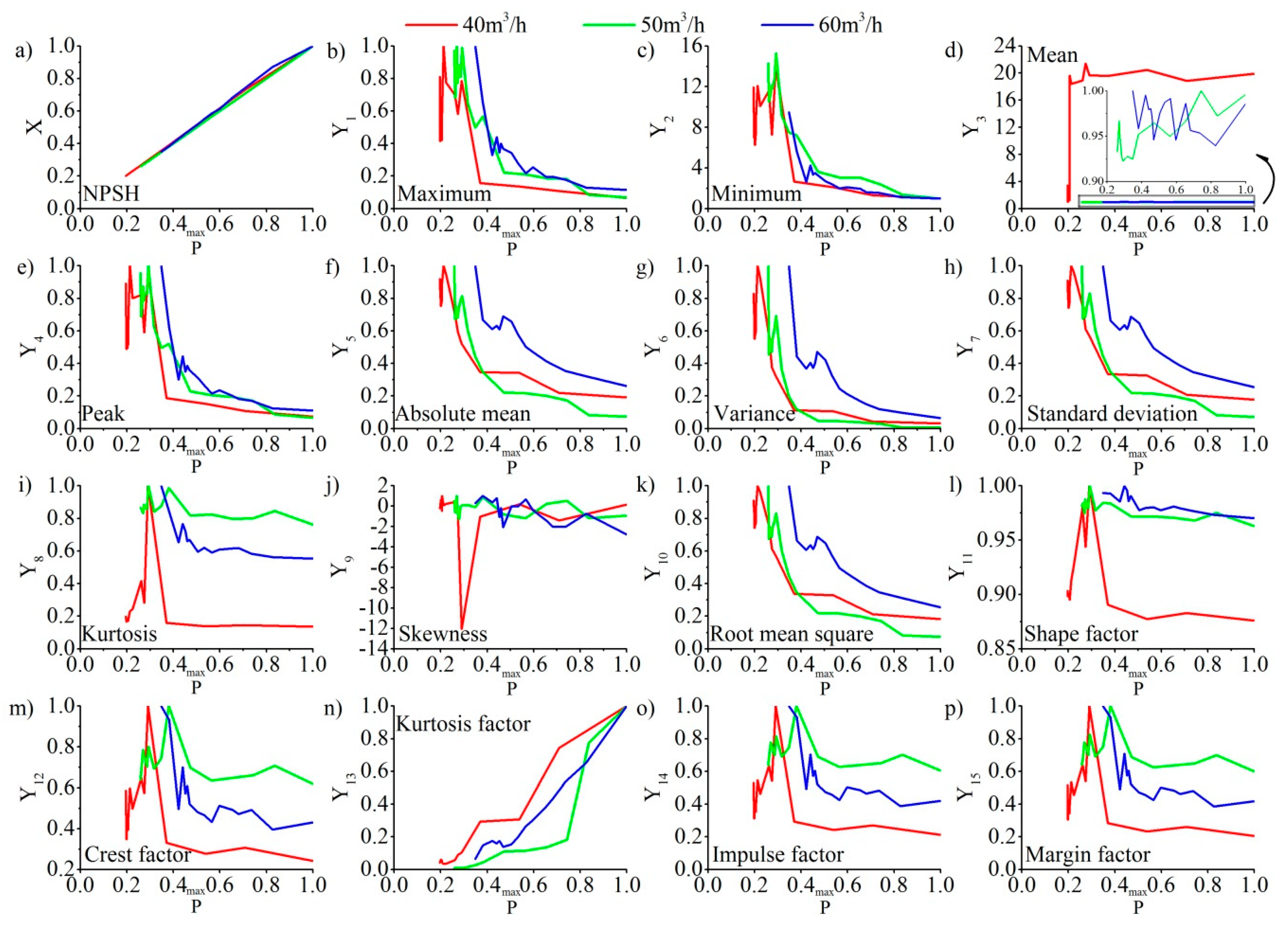
3.4. Data Pretreatment
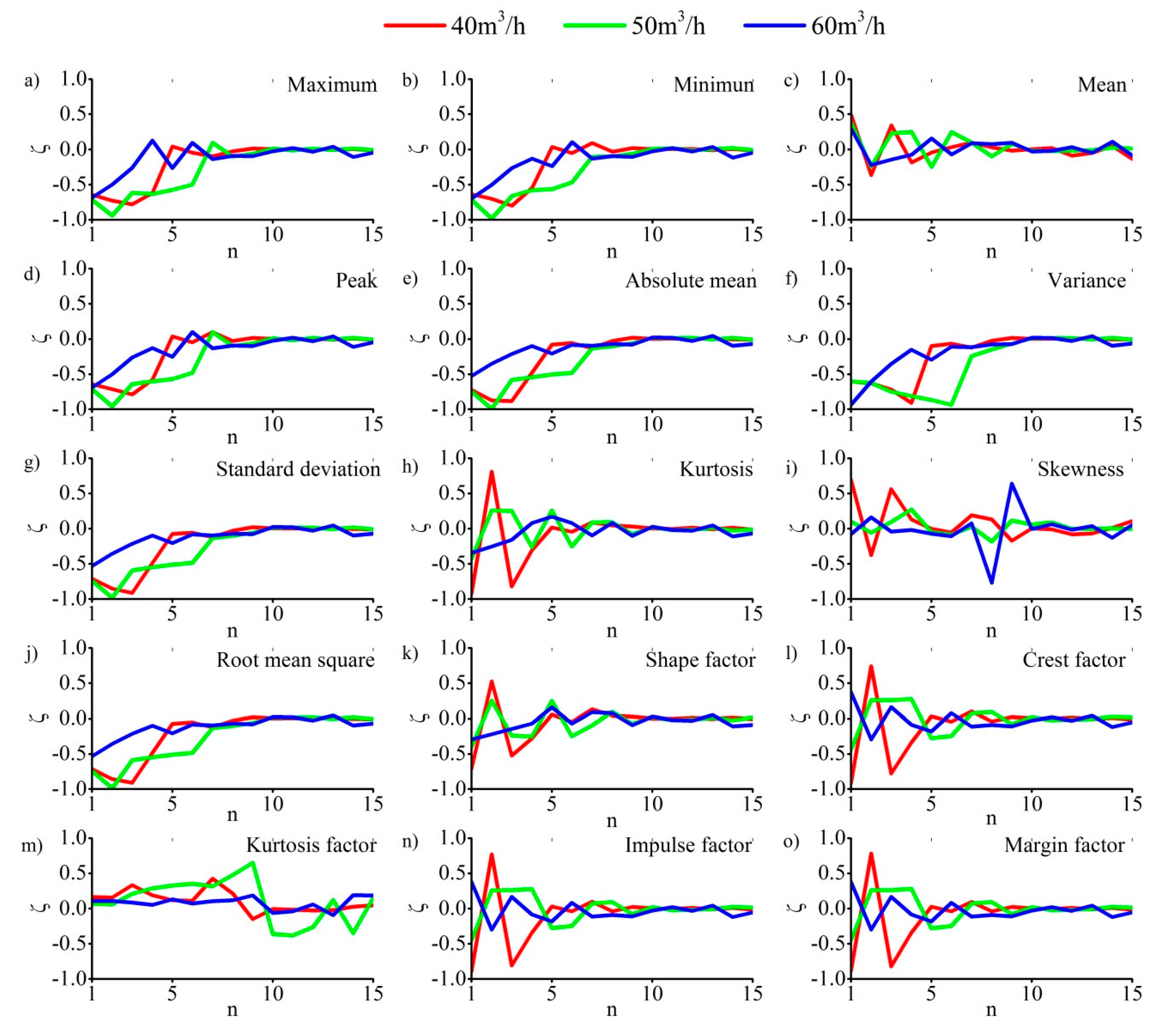
4. Analysis and Methodology
- 40 m3/h: variance > absolute mean > root mean square > standard deviation > skewness > mean > kurtosis factor > maximum > margin factor> peak > impulse factor> minimum > crest factor > kurtosis > shape factor.
- 50 m3/h: kurtosis factor > variance > root mean square > standard deviation > absolute mean > maximum > peak > skewness > minimum > margin factor > impulse factor > crest factor > kurtosis > mean >shape factor.
- 60 m3/h: kurtosis factor > kurtosis > shape factor > skewness > mean > variance > margin factor > impulse factor > crest factor > minimum > maximum > peak > standard deviation > root mean square > absolute mean.
- Average: kurtosis factor > variance > absolute mean > root mean square > standard deviation > skewness > maximum > peak > mean > kurtosis > minimum > shape factor > margin factor > impulse factor > crest factor.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hu, Q.; Ohata, E.F.; Silva, F.H.S.; Ramalho, G.L.B.; Han, T.; RebouçasFilho, P.P. A new online approach for classification of pumps vibration patterns based on intelligent IoT system. Measurement 2020, 151, 107138. [Google Scholar] [CrossRef]
- He, D.; Wang, X.; Li, S.; Lin, J.; Zhao, M. Identification of multiple faults in rotating machinery based on minimum entropy deconvolution combined with spectral kurtosis. Mech. Syst. Signal Process. 2016, 81, 235–249. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, X.; Li, J.; Du, X. Experimental study on the vibrational performance and its physical origins of a prototype reversible pump turbine in the pumped hydro energy storage power station. Renew. Energy 2019, 130, 667–676. [Google Scholar] [CrossRef]
- Muhirwa, A.; Cai, W.-H.; Su, W.-T.; Liu, Q.; Binama, M.; Li, B.; Wu, J. A review on remedial attempts to counteract the power generation compromise from draft tubes of hydropower plants. Renew. Energy 2020, 150, 743–764. [Google Scholar] [CrossRef]
- Zhu, D.; Tao, R.; Xiao, R.; Pan, L. Solving the runner blade crack problem for a Francis hydro-turbine operating under condition-complexity. Renew. Energy 2020, 149, 298–320. [Google Scholar] [CrossRef]
- Černetič, J.; Čudina, M. Estimating uncertainty of measurements for cavitation detection in a centrifugal pump. Measurement 2011, 44, 1293–1299. [Google Scholar] [CrossRef]
- Li, Y.; Feng, G.; Li, X.; Si, Q.; Zhu, Z. An experimental study on the cavitation vibration characteristics of a centrifugal pump at normal flow rate. J. Mech. Sci. Technol. 2018, 32, 4711–4720. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R.; Towsyfyan, H. An Experimental Study on Vibration Signatures for Detecting Incipient Cavitation in Centrifugal Pumps Based on Envelope Spectrum Analysis. J. Appl. Fluid Mech. 2019, 12, 2057–2067. [Google Scholar] [CrossRef]
- Li, S.; Chu, N.; Yan, P.; Wu, D.; Antoni, J. Cyclostationary approach to detect flow-induced effects on vibration signals from centrifugal pumps. Mech. Syst. Signal Process. 2019, 114, 275–289. [Google Scholar] [CrossRef]
- Lu, J.; Liu, X.; Zeng, Y.; Zhu, B.; Hu, B.; Yuan, S.; Hua, H. Detection of the Flow State for a Centrifugal Pump Based on Vibration. Energies 2019, 12, 3066. [Google Scholar] [CrossRef] [Green Version]
- Heo, Y.; Kim, K.-J. Characterization of a water pump for drum-type washing machine by vibration power approach. Mech. Syst. Signal Process. 2015, 54–55, 367–376. [Google Scholar] [CrossRef]
- Rapur, J.S.; Tiwari, R. Automation of multi-fault diagnosing of centrifugal pumps using multi-class support vector machine with vibration and motor current signals in frequency domain. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 278. [Google Scholar] [CrossRef]
- Milovančević, M.; Nikolić, V.; Petkovic, D.; Vracar, L.; Veg, E.; Tomic, N.; Jović, S. Vibration analyzing in horizontal pumping aggregate by soft computing. Measurement 2018, 125, 454–462. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, R. Time-frequency analysis and support vector machine in automatic detection of defect from vibration signal of centrifugal pump. Measurement 2017, 108, 119–133. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, Z.; Ma, J.; Li, L. Fault Diagnosis of a Hydraulic Pump Based on the CEEMD-STFT Time-Frequency Entropy Method and Multiclass SVM Classifier. Shock Vib. 2016, 2016, 1–8. [Google Scholar] [CrossRef]
- Stan, M.; Pana, I.; Minescu, M.; Ichim, A.; Teodoriu, C. Centrifugal Pump Monitoring and Determination of Pump Characteristic Curves Using Experimental and Analytical Solutions. Processes 2018, 6, 18. [Google Scholar] [CrossRef] [Green Version]
- KäHler, G.; Bonelli, F.; Gonnella, G.; Lamura, A. Cavitation inception of a van der Waals fluid at a sack-wall obstacle. Phys. Fluids 2015, 27, 123307. [Google Scholar] [CrossRef] [Green Version]
- Dong, L.; Zhao, Y.; Dai, C. Detection of Inception Cavitation in Centrifugal Pump by Fluid-Borne Noise Diagnostic. Shock Vib. 2019, 2019, 1–15. [Google Scholar] [CrossRef]
- Zhang, N.; Yang, M.; Gao, B.; Li, Z. Vibration Characteristics Induced by Cavitation in a Centrifugal Pump with Slope Volute. Shock Vib. 2015, 2015, 1–10. [Google Scholar] [CrossRef]
- Lu, J.; Yuan, S.; Siva, P.; Yuan, J.; Ren, X.; Zhou, B. The characteristics investigation under the unsteady cavitation condition in a centrifugal pump. J. Mech. Sci. Technol. 2017, 31, 1213–1222. [Google Scholar] [CrossRef]
- Rapur, J.S.; Tiwari, R. Experimental fault diagnosis for known and unseen operating conditions of centrifugal pumps using MSVM and WPT based analyses. Measurement 2019, 147, 106809. [Google Scholar] [CrossRef]
- Azizi, R.; Attaran, B.; Hajnayeb, A.; Ghanbarzadeh, A.; Changizian, M. Improving accuracy of cavitation severity detection in centrifugal pumps using a hybrid feature selection technique. Measurement 2017, 108, 9–17. [Google Scholar] [CrossRef]
- Rapur, J.S.; Tiwari, R. On-line Time Domain Vibration and Current Signals Based Multi-fault Diagnosis of Centrifugal Pumps Using Support Vector Machines. J. Nondestruct. Eval. 2018, 38, 6. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R.; Mishra, R. Experimental Investigation of the Effect of Air Injection on Performance and Detection of Cavitation in the Centrifugal Pump Based on Vibration Technique. Arab. J. Sci. Eng. 2020, 45, 5657–5671. [Google Scholar] [CrossRef]
- Li, S.; Zhang, J.; Li, P.; Wang, Y.; Wang, Q. Influencing Factors of Driving Decision-Making Under the Moral Dilemma. IEEE Access 2019, 7, 104132–104142. [Google Scholar] [CrossRef]
- Qin, C.; Li, B.; Shi, B.; Qin, T.; Xiao, J.; Xin, Y. Location of substation in similar candidates using comprehensive evaluation method base on DHGF. Measurement 2019, 146, 152–158. [Google Scholar] [CrossRef]
- Uzun, G. Analysis of grey relational method of the effects on machinability performance on austempered vermicular graphite cast irons. Measurement 2019, 142, 122–130. [Google Scholar] [CrossRef]
- Chang, H.; Shi, W.; Li, W.; Wang, C.; Ramesh, K.A. Experimental Optimization of Jet Self-Priming Centrifugal Pump Based on Orthogonal Design and Grey-Correlational Method. J. Therm. Sci. 2020, 29, 241–250. [Google Scholar] [CrossRef]
- Wang, X.L.; An, C.; Fu, Q.; Zhu, R.S.; Lu, Y.G.; Cai, Z.; Jiang, X.F. Grey relational analysis and optimization of guide vane for reactor coolant pump in the coasting transient process. Ann. Nucl. Energy 2019, 133, 431–440. [Google Scholar] [CrossRef]
- Yao, W.P.; Yao, W.L.; Yao, D.Z.; Guo, D.Q.; Wang, J. Shannon entropy and quantitative time irreversibility for different and even contradictory aspects of complex systems. Appl. Phys. Lett. 2020, 116, 014101. [Google Scholar] [CrossRef]
- Sun, H.; Luo, Y.; Yuan, S.; Yin, J. Hilbert spectrum analysis of unsteady characteristics in centrifugal pump operation under cavitation status. Ann. Nucl. Energy 2018, 114, 607–615. [Google Scholar] [CrossRef]
- Sun, H.; Yuan, S.; Luo, Y. Characterization of cavitation and seal damage during pump operation by vibration and motor current signal spectra. Proc. Inst. Mech. Eng. Part A J. Power Energy 2018, 233, 132–147. [Google Scholar] [CrossRef]
- Sun, H.; Yuan, S.; Luo, Y. Cyclic Spectral Analysis of Vibration Signals for Centrifugal Pump Fault Characterization. IEEE Sens. J. 2018, 18, 2925–2933. [Google Scholar] [CrossRef]


| Name | Symbol | Value |
|---|---|---|
| Designed flow rate | Qd | 50 m3/h |
| Designed head | Hd | 37 m |
| Rated rotational speed | n | 3000 r/min |
| Impeller inlet diameter | D1 | 74 mm |
| Impeller outlet diameter | D2 | 174 mm |
| Impeller outlet width | b2 | 12 mm |
| Blades | Z | 6 |
| Volute diameter | D3 | 184 mm |
| Rated Power | p | 5 kW |
| Target | 40 | 50 | 60 | Average |
|---|---|---|---|---|
| Maximum | 0.5084 | 0.8431 | 0.5090 | 0.6398 |
| Minimum | 0.4455 | 0.5725 | 0.5108 | 0.5130 |
| Mean | 0.7145 | 0.3881 | 0.8119 | 0.6131 |
| Peak | 0.4465 | 0.8429 | 0.5086 | 0.6187 |
| Absolute mean | 0.9254 | 0.9343 | 0.4888 | 0.8102 |
| Variance | 0.9472 | 0.9541 | 0.5519 | 0.8424 |
| Standard deviation | 0.9237 | 0.9344 | 0.4899 | 0.8099 |
| Kurtosis | 0.4068 | 0.4199 | 0.8836 | 0.5416 |
| Skewness | 0.7447 | 0.5816 | 0.8498 | 0.7093 |
| Root mean square | 0.9238 | 0.9345 | 0.4899 | 0.8100 |
| Shape factor | 0.3774 | 0.2944 | 0.8706 | 0.4790 |
| Crest factor | 0.4453 | 0.4200 | 0.5117 | 0.4534 |
| Kurtosis factor | 0.6869 | 0.9923 | 0.9162 | 0.8690 |
| Impulse factor | 0.4463 | 0.4201 | 0.5126 | 0.4541 |
| Margin factor | 0.44 | 0.4201 | 0.5130 | 0.4543 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, R.; Yuan, J. Selection Strategy of Vibration Feature Target under Centrifugal Pumps Cavitation. Appl. Sci. 2020, 10, 8190. https://doi.org/10.3390/app10228190
Cao R, Yuan J. Selection Strategy of Vibration Feature Target under Centrifugal Pumps Cavitation. Applied Sciences. 2020; 10(22):8190. https://doi.org/10.3390/app10228190
Chicago/Turabian StyleCao, Ruijia, and Jianping Yuan. 2020. "Selection Strategy of Vibration Feature Target under Centrifugal Pumps Cavitation" Applied Sciences 10, no. 22: 8190. https://doi.org/10.3390/app10228190
APA StyleCao, R., & Yuan, J. (2020). Selection Strategy of Vibration Feature Target under Centrifugal Pumps Cavitation. Applied Sciences, 10(22), 8190. https://doi.org/10.3390/app10228190






