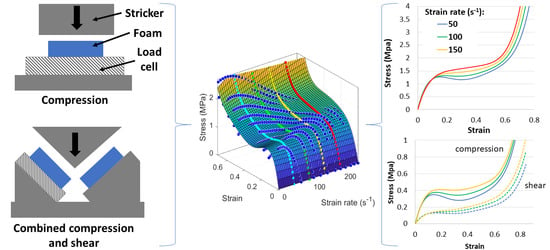
Strain Rate Dependent Behavior of Vinyl Nitrile Helmet Foam in Compression and Combined Compression and Shear
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Foam Samples
2.2. Quasi-Static Compression
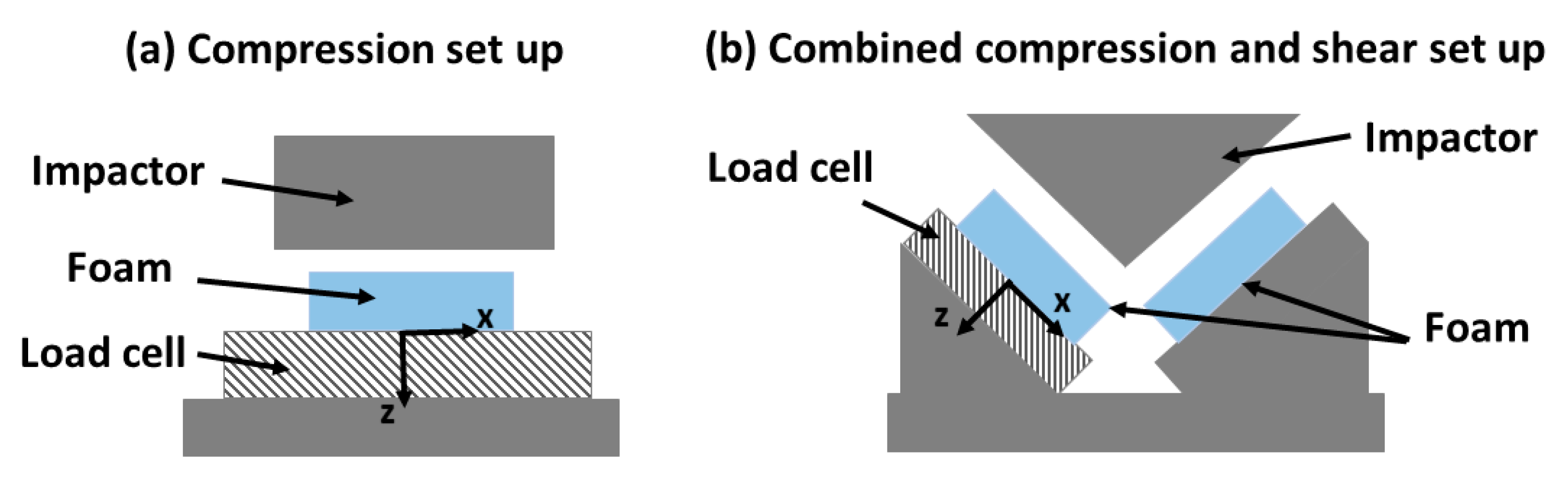
2.3. Impact Tests in Compression and Combined Compression and Shear
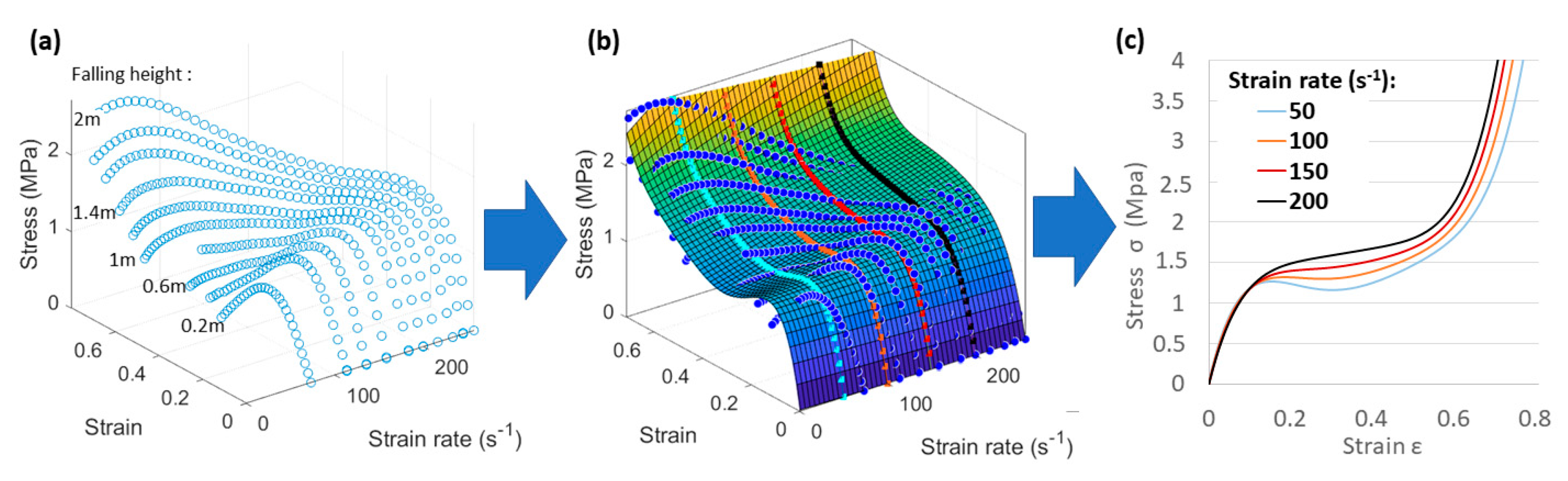
2.4. Data Analysis
3. Results
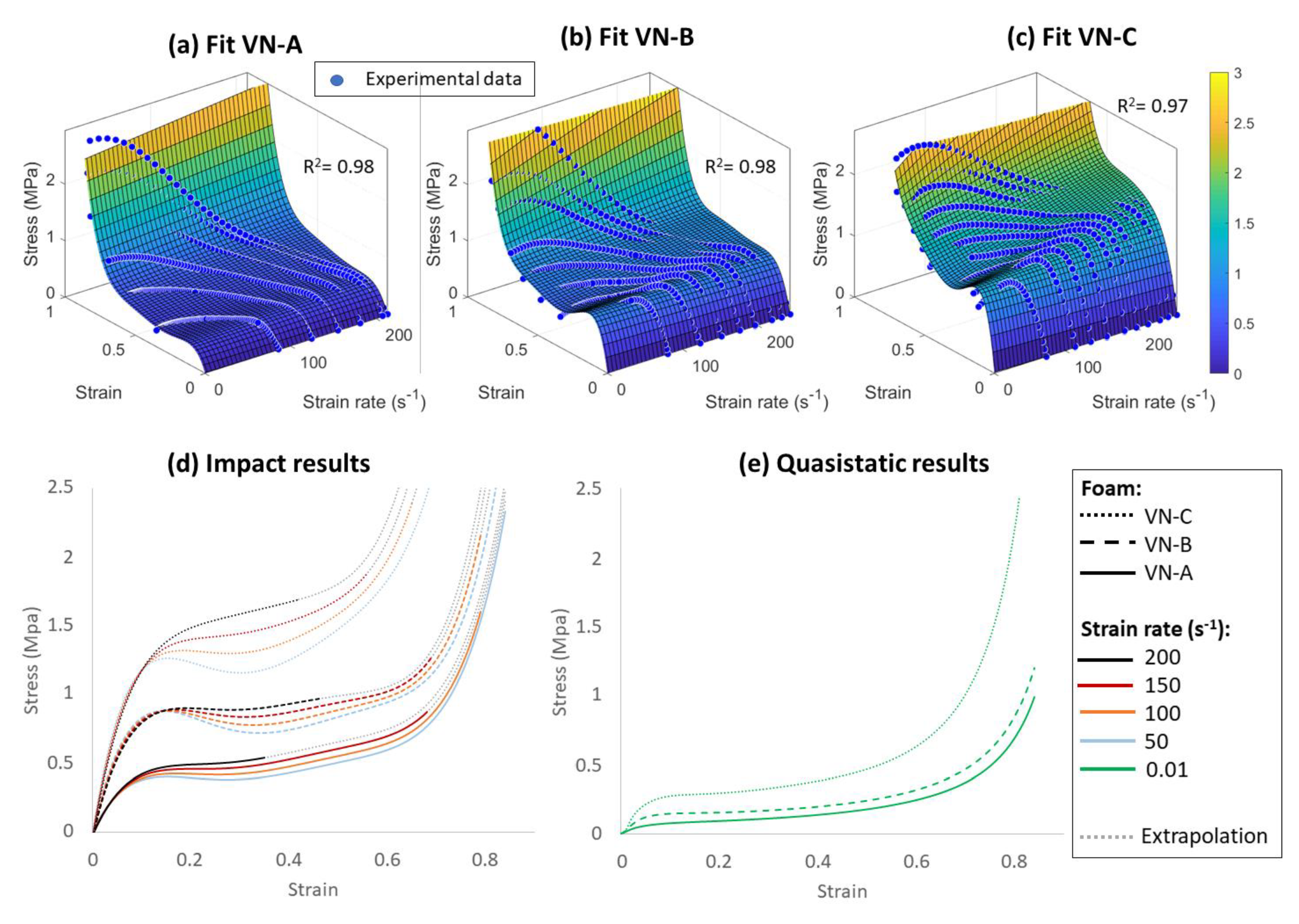
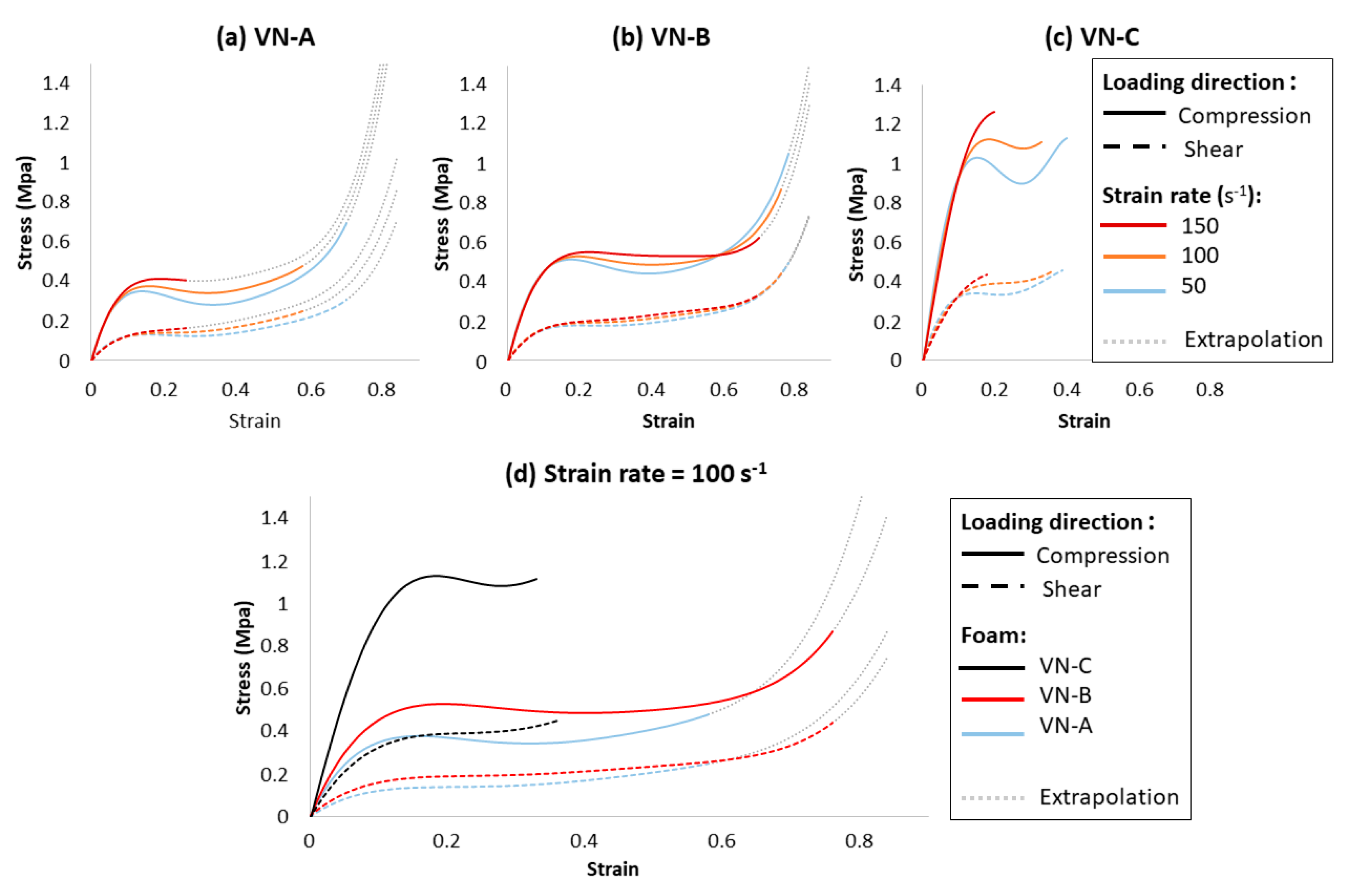
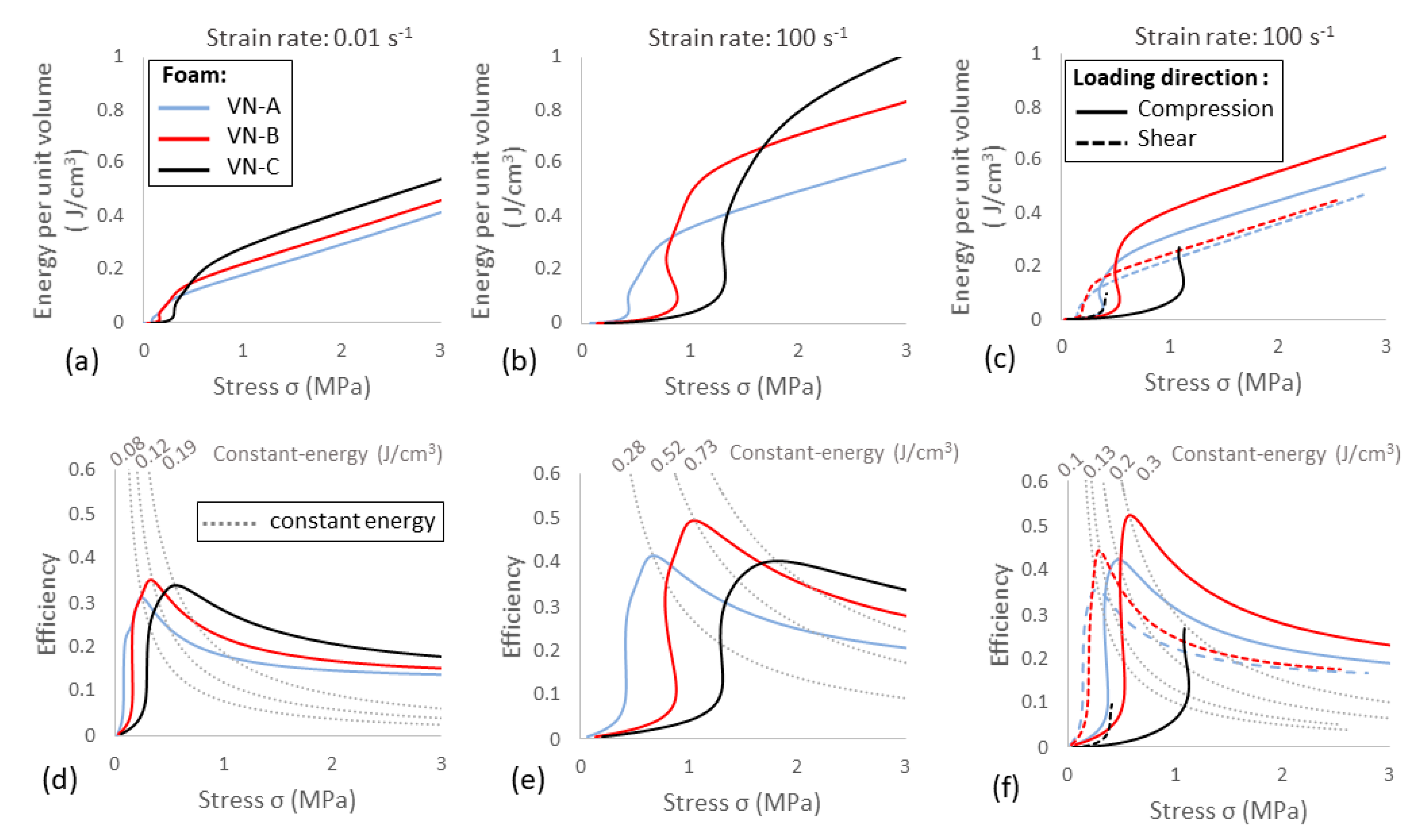
3.1. Effect of Density
3.2. Effect of the Strain Rate
3.3. Effect of the Loading Direction
4. Discussion
4.1. Effect of the Strain Rate
4.2. Effect of Density
4.3. Vinyl Nitrile Foam vs. Expanded Polypropylene Foam
4.4. Use of the Results and Future Work
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Gimbel, G.M.; Hoshizaki, T.B. Compressive properties of helmet materials subjected to dynamic impact loading of various energies. Eur. J. Sport Sci. 2008, 8, 341–349. [Google Scholar] [CrossRef]
- Meehan, A. Influence of VN Foam Liner Density on Impact Attenuation of an Ice Hockey Helmet; University of Ottawa: Ottawa, ON, Canada, 2017. [Google Scholar]
- Rousseau, P.; Hoshizaki, T.B.; Gilchrist, M.D. For ASTM F-08: Protective Capacity of Ice Hockey Player Helmets against Puck Impacts. In Mechanism of Concussion in Sports; Ashare, A., Ziejewski, M., Eds.; ASTM International: West Conshohocken, PA, USA, 2014; pp. 196–207. ISBN 978-0-8031-7582-2. [Google Scholar]
- Viano, D.C.; Withnall, C.; Halstead, D. Impact Performance of Modern Football Helmets. Ann. Biomed. Eng. 2012, 40, 160–174. [Google Scholar] [CrossRef] [PubMed]
- Avalle, M.; Belingardi, G.; Montanini, R. Characterization of polymeric structural foams under compressive impact loading by means of energy-absorption diagram. Int. J. Impact Eng. 2001, 25, 455–472. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1999; ISBN 1-316-02542-X. [Google Scholar]
- Koohbor, B.; Kidane, A.; Lu, W.-Y.; Sutton, M.A. Investigation of the dynamic stress–strain response of compressible polymeric foam using a non-parametric analysis. Int. J. Impact Eng. 2016, 91, 170–182. [Google Scholar] [CrossRef] [Green Version]
- Krundaeva, A.; De Bruyne, G.; Gagliardi, F.; Van Paepegem, W. Dynamic compressive strength and crushing properties of expanded polystyrene foam for different strain rates and different temperatures. Polym. Test. 2016, 55, 61–68. [Google Scholar] [CrossRef] [Green Version]
- Bailly, N.; Llari, M.; Donnadieu, T.; Masson, C.; Arnoux, P.-J. Numerical Reconstruction of Traumatic Brain Injury in Skiing and Snowboarding. Med. Sci. Sports Exerc. 2018. [Google Scholar] [CrossRef]
- Aare, M.; Halldin, P. A New Laboratory Rig for Evaluating Helmets Subject to Oblique Impacts. Traffic Inj. Prev. 2003, 4, 240–248. [Google Scholar] [CrossRef]
- Mills, N.J.; Gilchrist, A. Oblique impact testing of bicycle helmets. Int. J. Impact Eng. 2008, 35, 1075–1086. [Google Scholar] [CrossRef]
- Rowson, S.; Duma, S.M. Development of the STAR evaluation system for football helmets: Integrating player head impact exposure and risk of concussion. Ann. Biomed. Eng. 2011, 39, 2130–2140. [Google Scholar] [CrossRef]
- Papka, S.; Kyriakides, S. Biaxial crushing of honeycombs—Part 1: Experiments. Int. J. Solids Struct. 1999, 36, 4367–4396. [Google Scholar] [CrossRef]
- Deshpande, V.; Fleck, N. Multi-axial yield behaviour of polymer foams. Acta Mater. 2001, 49, 1859–1866. [Google Scholar] [CrossRef]
- Chung, J.; Waas, A.M. Compressive response of circular cell polycarbonate honeycombs under inplane biaxial static and dynamic loading. Part I: Experiments. Int. J. Impact Eng. 2002, 27, 729–754. [Google Scholar] [CrossRef]
- Hong, S.-T.; Pan, J.; Tyan, T.; Prasad, P. Quasi-static crush behavior of aluminum honeycomb specimens under compression dominant combined loads. Int. J. Plast. 2006, 22, 73–109. [Google Scholar] [CrossRef]
- Taher, S.T.; Thomsen, O.T.; Dulieu-Barton, J.M.; Zhang, S. Determination of mechanical properties of PVC foam using a modified Arcan fixture. Compos. Part Appl. Sci. Manuf. 2012, 43, 1698–1708. [Google Scholar] [CrossRef]
- Mosleh, Y.; Bosche, K.V.; Depreitere, B.; Sloten, J.V.; Verpoest, I.; Ivens, J. Effect of polymer foam anisotropy on energy absorption during combined shear-compression loading. J. Cell. Plast. 2018, 54, 597–613. [Google Scholar] [CrossRef]
- Hou, B.; Ono, A.; Abdennadher, S.; Pattofatto, S.; Li, Y.L.; Zhao, H. Impact behavior of honeycombs under combined shear-compression. Part I: Experiments. Int. J. Solids Struct. 2011, 48, 687–697. [Google Scholar] [CrossRef]
- Mills, N.J.; Gilchrist, A. Shear and compressive impact of polypropylene bead foam. Cell. Polym. 1999, 18, 157–174. [Google Scholar]
- Hong, S.-T.; Pan, J.; Tyan, T.; Prasad, P. Dynamic crush behaviors of aluminum honeycomb specimens under compression dominant inclined loads. Int. J. Plast. 2008, 24, 89–117. [Google Scholar] [CrossRef]
- Ling, C.; Ivens, J.; Cardiff, P.; Gilchrist, M.D. Deformation response of EPS foam under combined compression-shear loading. Part II: High strain rate dynamic tests. Int. J. Mech. Sci. 2018, 145, 9–23. [Google Scholar] [CrossRef]
- Weißenborn, O.; Ebert, C.; Gude, M. Modelling of the strain rate dependent deformation behaviour of rigid polyurethane foams. Polym. Test. 2016, 54, 145–149. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Q.M. Dynamic compressive behaviour of cellular materials: A review of phenomenon, mechanism and modelling. Int. J. Impact Eng. 2018, 112, 74–115. [Google Scholar] [CrossRef] [Green Version]
- Duncan, O.; Allen, T.; Foster, L.; Gatt, R.; Grima, J.N.; Alderson, A. Controlling Density and Modulus in Auxetic Foam Fabrications—Implications for Impact and Indentation Testing. In Proceedings of the 12th Conference of the International Sports Engineering Association, Brisbane, Australia, 26–29 March 2018; Volume 2, p. 250. [Google Scholar] [CrossRef] [Green Version]
- Tang, N.; Lei, D.; Huang, D.; Xiao, R. Mechanical performance of polystyrene foam (EPS): Experimental and numerical analysis. Polym. Test. 2019, 73, 359–365. [Google Scholar] [CrossRef]
- Allen, T.; Hewage, T.; Newton-Mann, C.; Wang, W.; Duncan, O.; Alderson, A. Fabrication of Auxetic Foam Sheets for Sports Applications. Phys. Status Solidi B 2017, 254, 1700596. [Google Scholar] [CrossRef] [Green Version]
- Rowson, B.; Rowson, S.; Duma, S.M. Hockey STAR: A Methodology for Assessing the Biomechanical Performance of Hockey Helmets. Ann. Biomed. Eng. 2015, 43, 2429–2443. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Least-Squares Fitting—MATLAB & Simulink. Available online: https://www.mathworks.com/help/curvefit/least-squares-fitting.html (accessed on 25 March 2020).
- Miltz, J.; Gruenbaum, G. Evaluation of cushioning properties of plastic foams from compressive measurements. Polym. Eng. Sci. 1981, 21, 1010–1014. [Google Scholar] [CrossRef]
- Miltz, J.; Ramon, O. Energy absorption characteristics of polymeric foams used as cushioning materials. Polym. Eng. Sci. 1990, 30, 129–133. [Google Scholar] [CrossRef]
- Bouix, R.; Viot, P.; Lataillade, J.-L. Polypropylene foam behaviour under dynamic loadings: Strain rate, density and microstructure effects. Int. J. Impact Eng. 2009, 36, 329–342. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.M.; Magkiriadis, I.; Harrigan, J.J. Compressive Strain at the Onset of Densification of Cellular Solids. J. Cell. Plast. 2006, 42, 371–392. [Google Scholar] [CrossRef]
- Mills, N. Polymer Foams Handbook: Engineering and Biomechanics Applications and Design Guide; Butterworth-Heinemann: Oxford, UK, 2007; ISBN 978-0-08-047544-8. [Google Scholar]
- Sun, Y.; Li, Q.M.; Lowe, T.; McDonald, S.A.; Withers, P.J. Investigation of strain-rate effect on the compressive behaviour of closed-cell aluminium foam by 3D image-based modelling. Mater. Des. 2016, 89, 215–224. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Q.M.; McDonald, S.A.; Withers, P.J. Determination of the constitutive relation and critical condition for the shock compression of cellular solids. Mech. Mater. 2016, 99, 26–36. [Google Scholar] [CrossRef] [Green Version]
- Burbank, S.D.; Smith, L.V. Dynamic characterization of rigid foam used in finite element sports ball simulations. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2012. [Google Scholar] [CrossRef]
- Shepherd, T.; Winwood, K.; Venkatraman, P.; Alderson, A.; Allen, T. Validation of a Finite Element Modeling Process for Auxetic Structures under Impact. Phys. Status Solidi B 2020, 257, 1900197. [Google Scholar] [CrossRef]
- Rusch, K.C. Load–compression behavior of flexible foams. J. Appl. Polym. Sci. 1969, 13, 2297–2311. [Google Scholar] [CrossRef]
- Avalle, M.; Belingardi, G.; Ibba, A. Mechanical models of cellular solids: Parameters identification from experimental tests. Int. J. Impact Eng. 2007, 34, 3–27. [Google Scholar] [CrossRef]
- Altair. Altair Engineering RADIOSS Theory Manual, 14.0 Version, Large Displacement Finite Element Analysis PART 2; Altair Engineering, Inc.: Troy, MI, USA, 2015. [Google Scholar]
- Hallquist, J.O. LS-DYNA Keyword User’s Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2007; Volume 970, pp. 299–800. [Google Scholar]
- Croop, B.; Lobo, H.; DatapointLabs. Selecting material models for the simulation of foams in LS-DYNA. In Proceedings of the 7th European LS-Dyna Conference, Salzburg, Austria, 14–15 May 2009; pp. 1–6. [Google Scholar]
| E* (Mpa) | εpl | σpl (Mpa) | εeff. | σeff .(Mpa) | Weff. (J/cm3) | 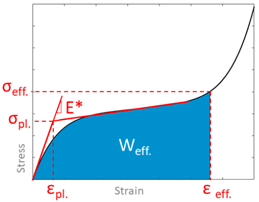 | ||||
| Quasi-static Compression (0.01 s−1) | ||||||||||
| VN-A | 1.60 | 0.03 | 0.05 | 0.63 | 0.25 | 0.08 | ||||
| VN-B | 2.89 | 0.04 | 0.12 | 0.62 | 0.33 | 0.12 | ||||
| VN-C | 4.81 | 0.05 | 0.23 | 0.57 | 0.56 | 0.19 | ||||
| Impact Compression (100 s−1) | ||||||||||
| VN-A | 7.71 | 0.049 | 0.38 | 0.62 | 0.68 | 0.28 | ||||
| VN-B | 16.30 | 0.052 | 0.85 | 0.64 | 1.05 | 0.52 | ||||
| VN-C | 22.24 | 0.054 | 1.21 | 0.57 | 1.82 | 0.73 | ||||
| Impact Compression and Shear (100 s−1) | σs/σc at εpl. | Ws/Wc at εpl. | σs/σc at eff. | Ws/Wc at eff. | ||||||
| VN-A_comp. | 6.75 | 0.053 | 0.36 | 0.58 | 0.48 | 0.20 | 0.32 | 0.38 | 0.52 | 0.44 |
| VN-A_shear | 2.31 | 0.050 | 0.12 | 0.61 | 0.27 | 0.10 | ||||
| VN-B_comp. | 8.02 | 0.066 | 0.53 | 0.64 | 0.58 | 0.30 | 0.31 | 0.37 | 0.49 | 0.41 |
| VN-B_shear | 2.83 | 0.058 | 0.16 | 0.65 | 0.29 | 0.13 | ||||
| VN-C_comp. | 12.64 | 0.085 | 1.08 | NA | NA | NA | 0.32 | 0.36 | NA | NA |
| VN-C_shear | 5.61 | 0.062 | 0.35 | NA | NA | NA | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bailly, N.; Petit, Y.; Desrosier, J.-M.; Laperriere, O.; Langlois, S.; Wagnac, E. Strain Rate Dependent Behavior of Vinyl Nitrile Helmet Foam in Compression and Combined Compression and Shear. Appl. Sci. 2020, 10, 8286. https://doi.org/10.3390/app10228286
Bailly N, Petit Y, Desrosier J-M, Laperriere O, Langlois S, Wagnac E. Strain Rate Dependent Behavior of Vinyl Nitrile Helmet Foam in Compression and Combined Compression and Shear. Applied Sciences. 2020; 10(22):8286. https://doi.org/10.3390/app10228286
Chicago/Turabian StyleBailly, Nicolas, Yvan Petit, Jean-Michel Desrosier, Olivier Laperriere, Simon Langlois, and Eric Wagnac. 2020. "Strain Rate Dependent Behavior of Vinyl Nitrile Helmet Foam in Compression and Combined Compression and Shear" Applied Sciences 10, no. 22: 8286. https://doi.org/10.3390/app10228286
APA StyleBailly, N., Petit, Y., Desrosier, J. -M., Laperriere, O., Langlois, S., & Wagnac, E. (2020). Strain Rate Dependent Behavior of Vinyl Nitrile Helmet Foam in Compression and Combined Compression and Shear. Applied Sciences, 10(22), 8286. https://doi.org/10.3390/app10228286