Precision Analysis and Design of Rotating Coil Magnetic Measurements System
Abstract
:Featured Application
Abstract
1. Introduction
2. Mathematical Modeling
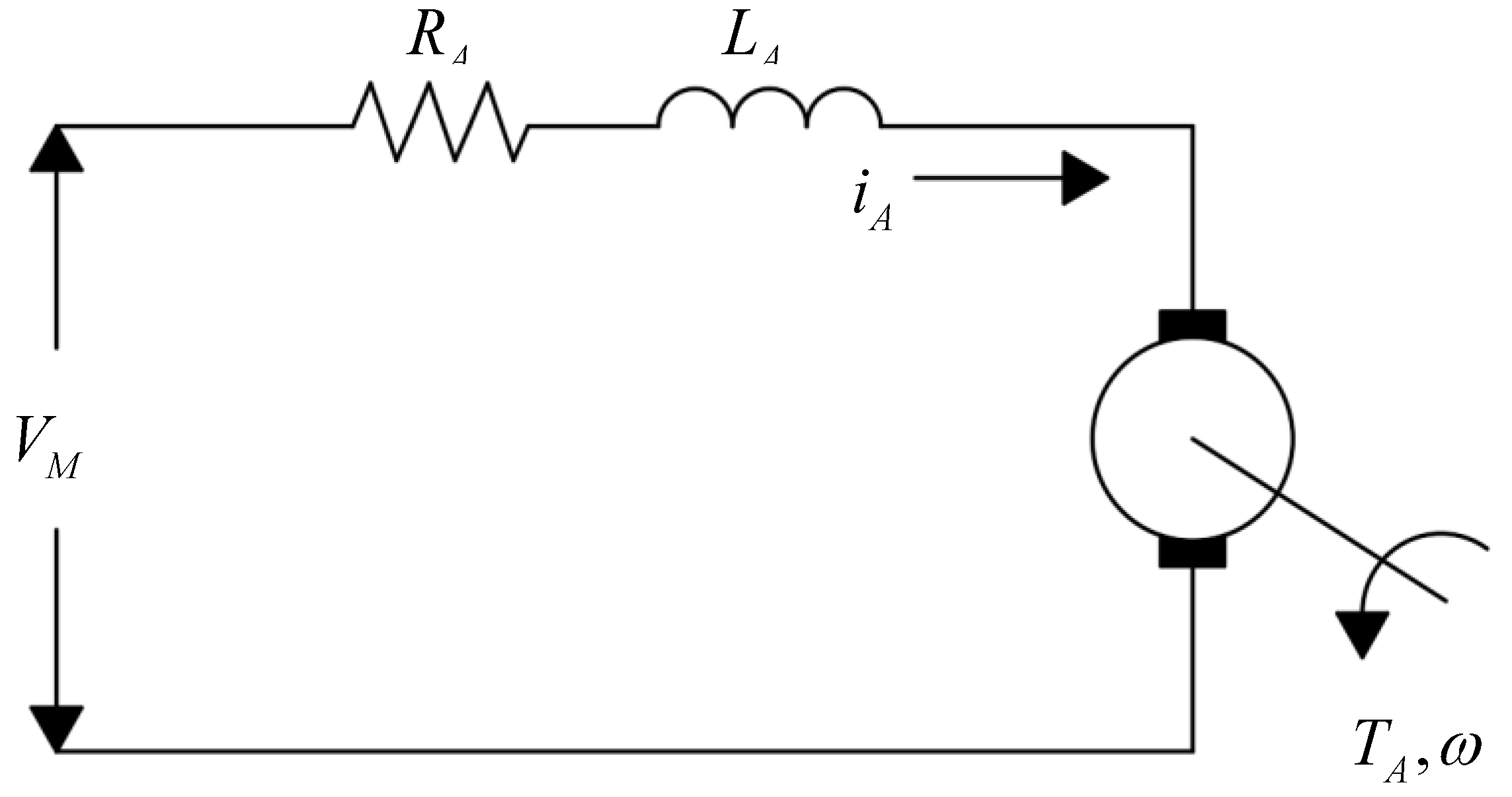
2.1. Mathematical Model of the DC Motor
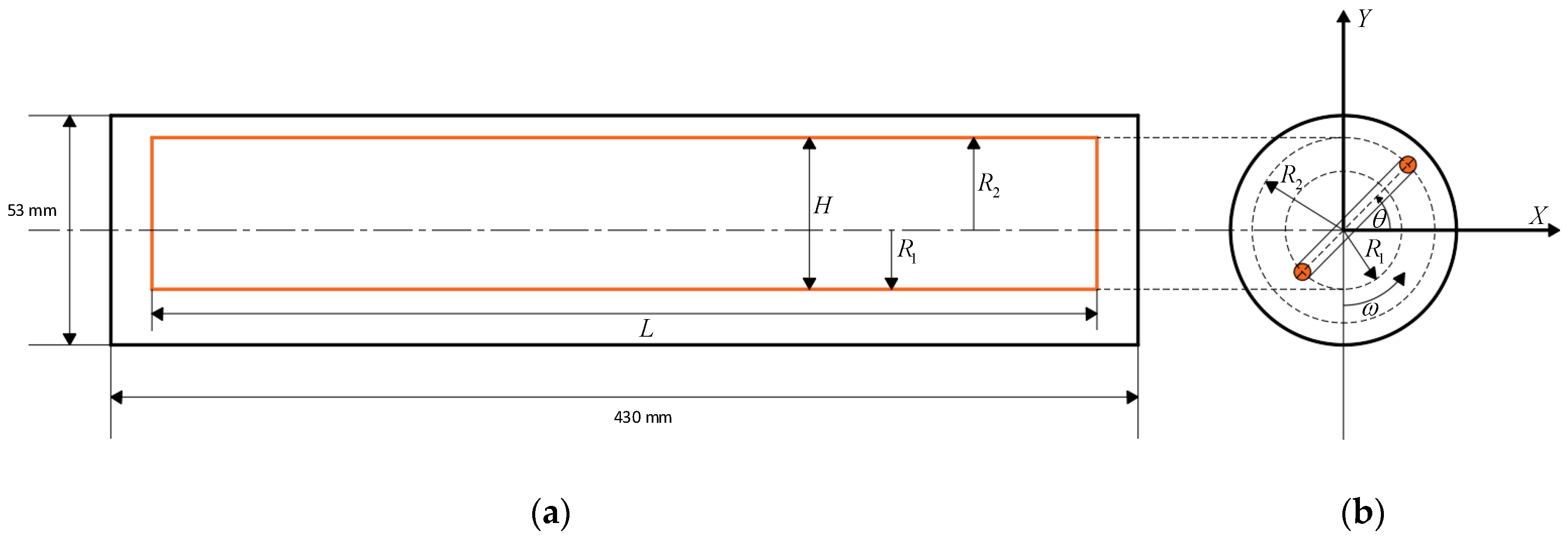
2.2. Mathematical Model of a Rotating Coil Rod
3. Experimental Setup
3.1. A Magnetic Measurement Equipment Setup
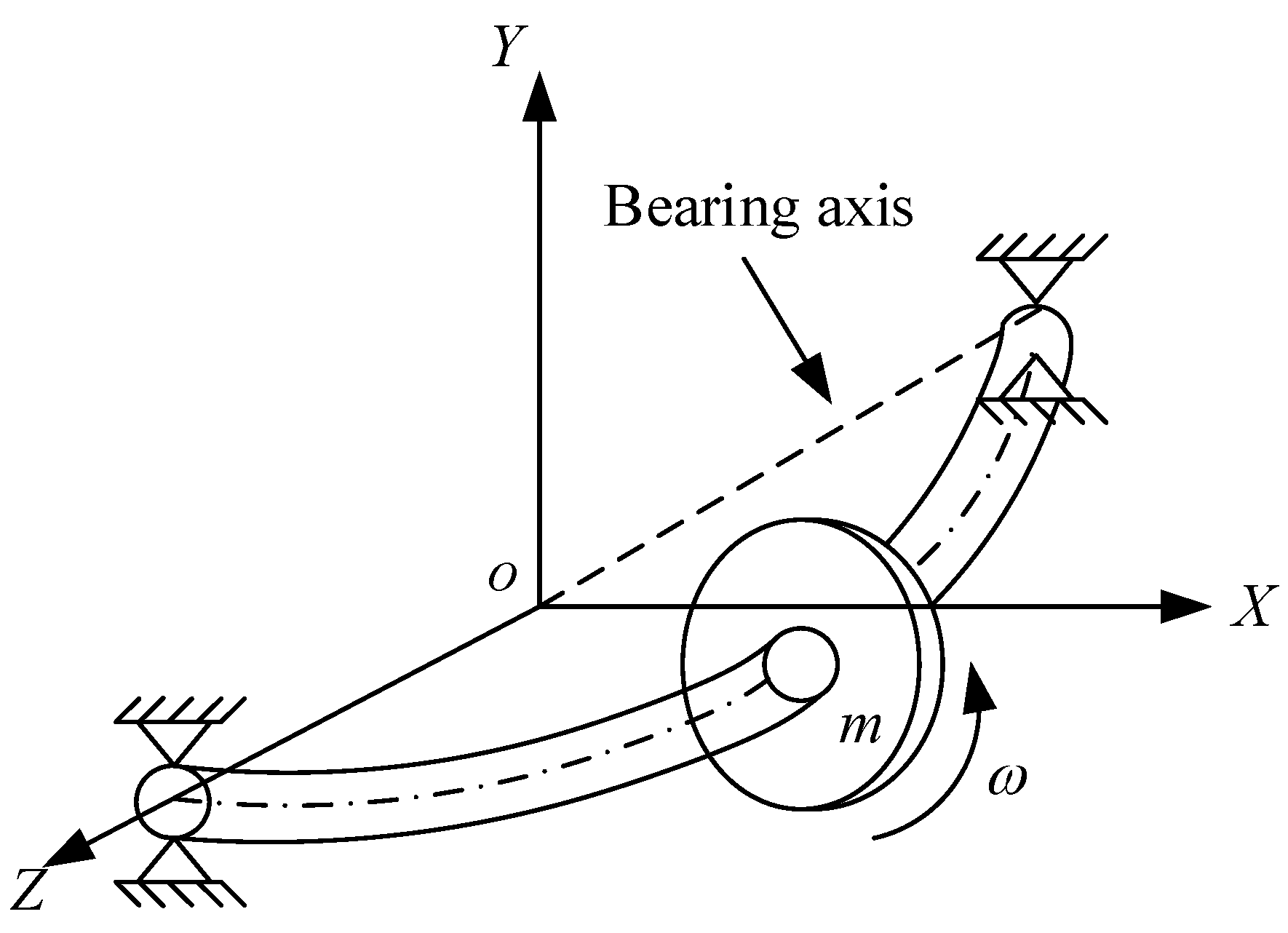
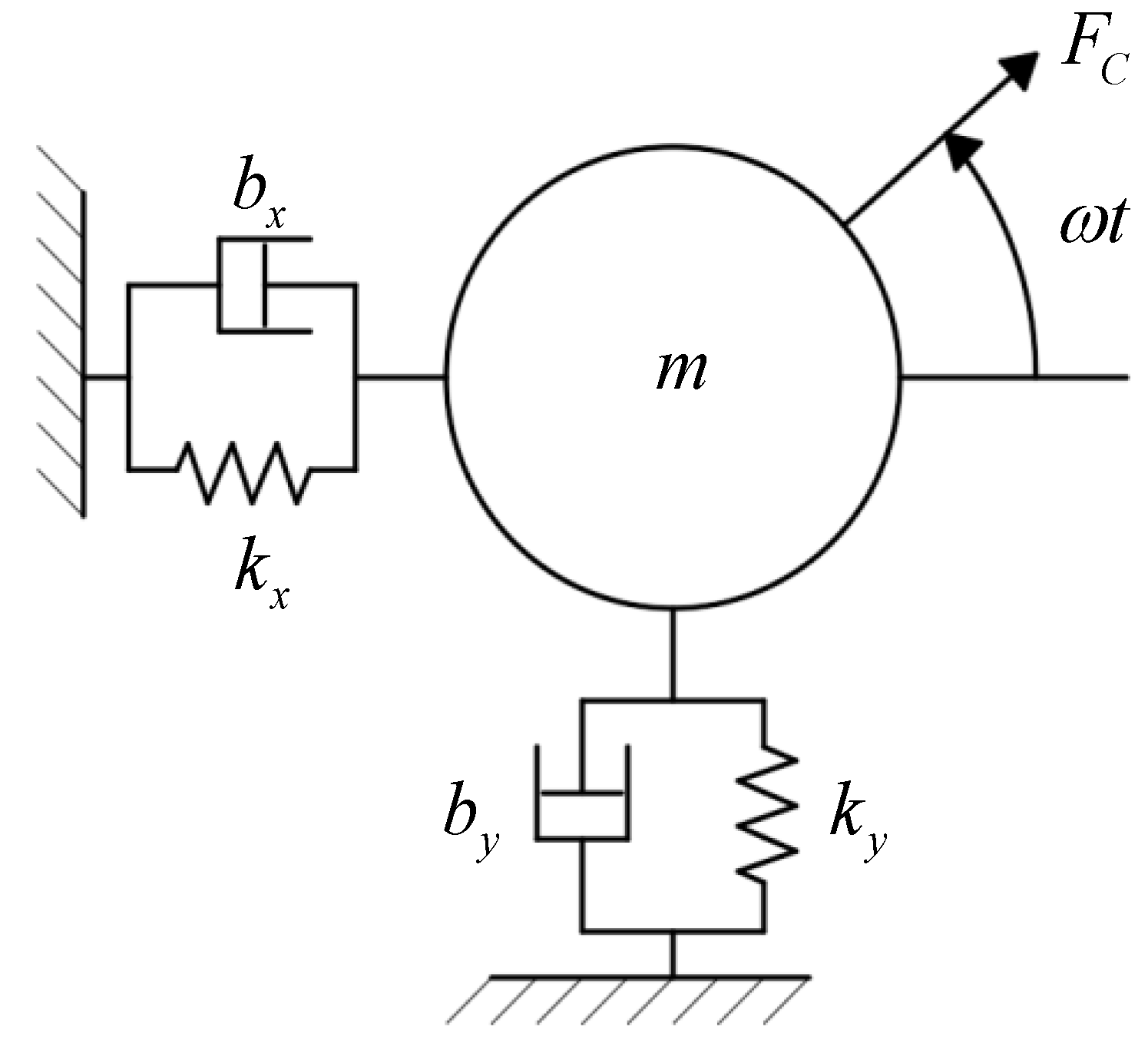
3.2. A Whirling Measurement Equipment of the Rotating Coil
4. Results and Discussion
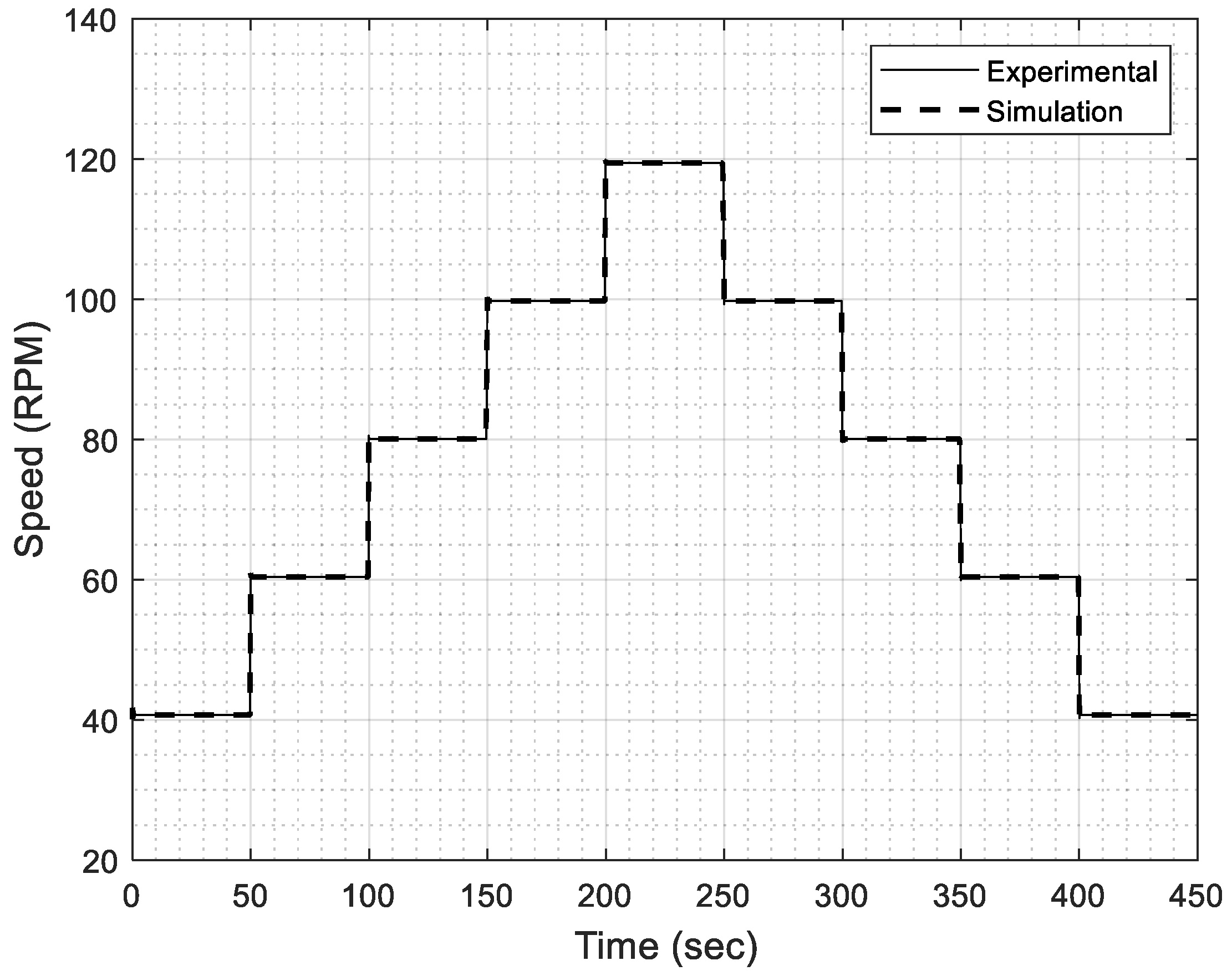
4.1. Estimation of the DC Motor’s Mathematical Model
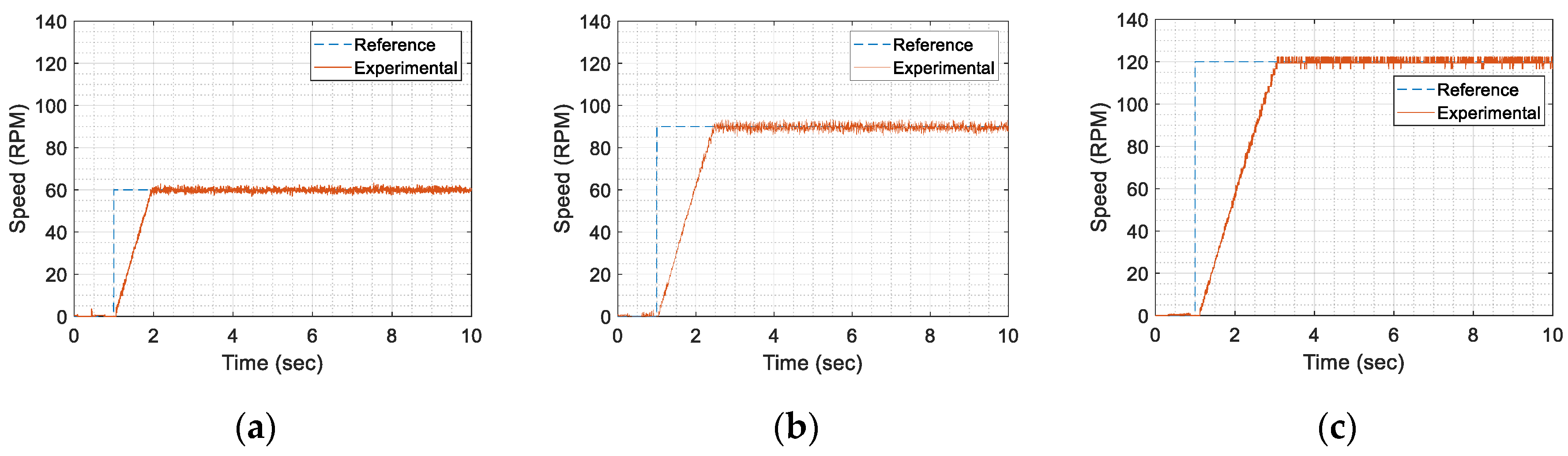
4.2. Test Results of the Speed Control System with a PI Controller
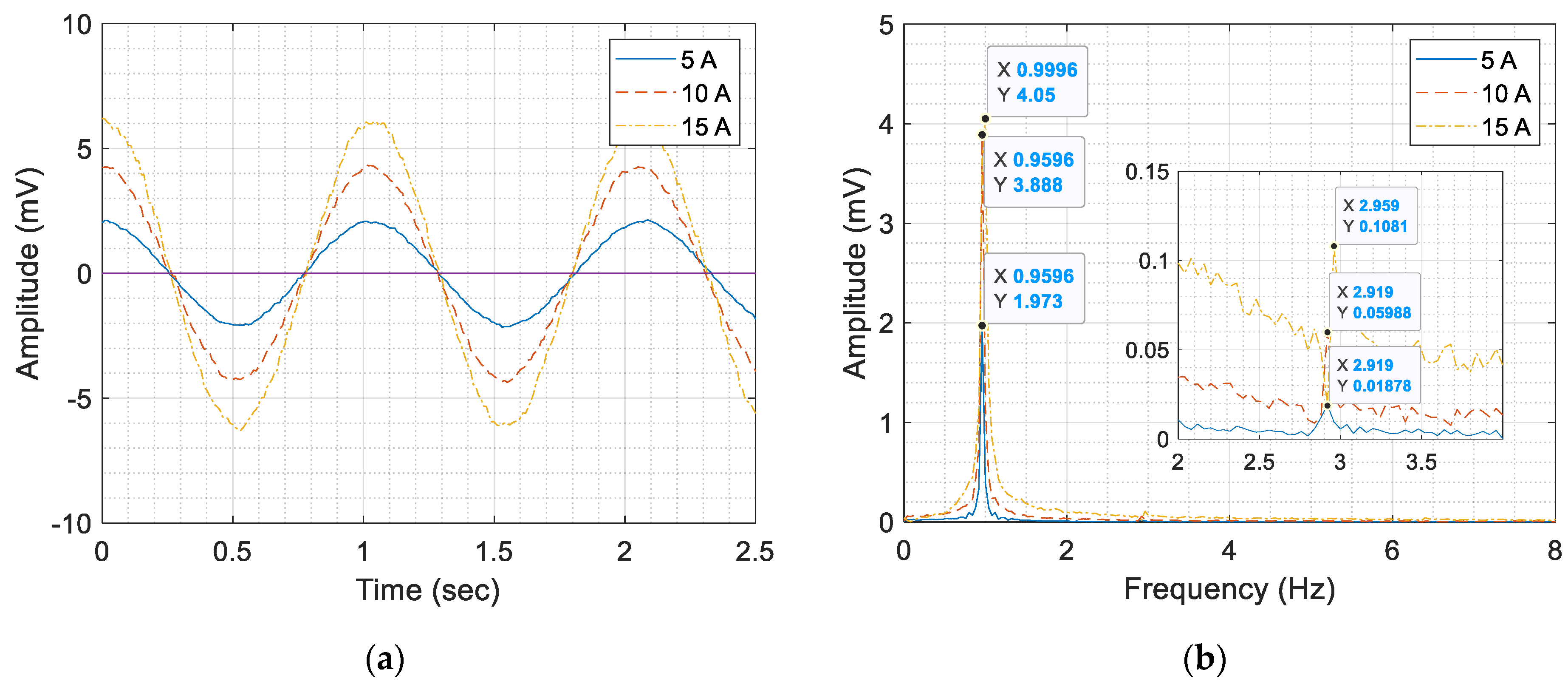
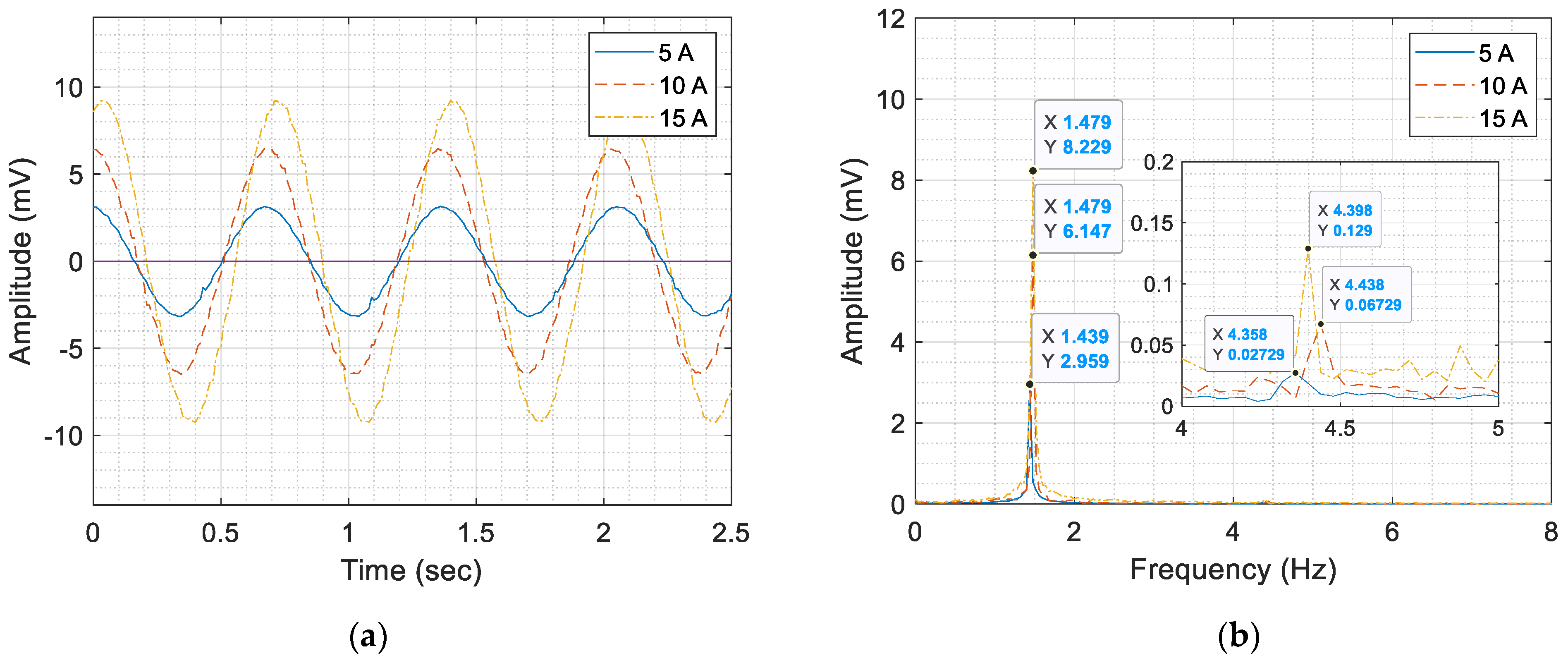
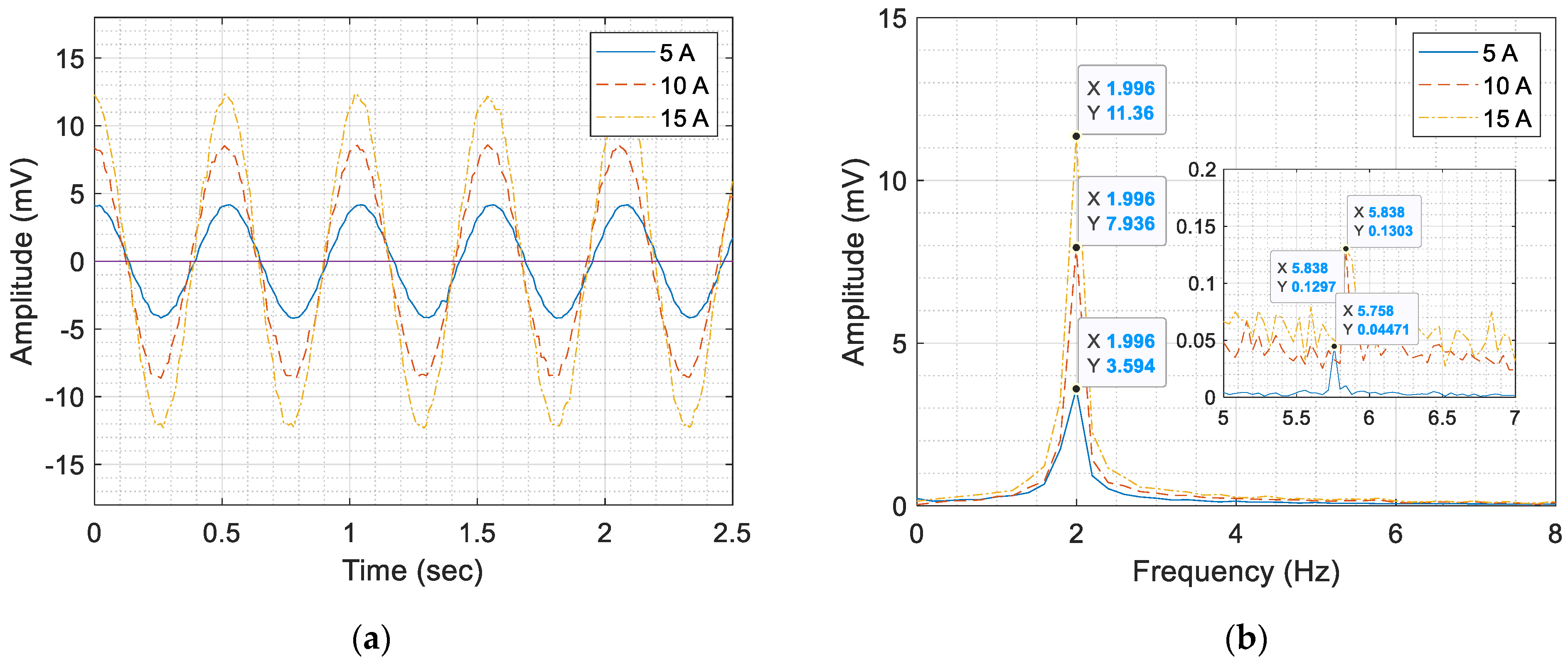
4.3. The Results of Dipole Magnet Field Measurement (Skew Dipole Magnets)
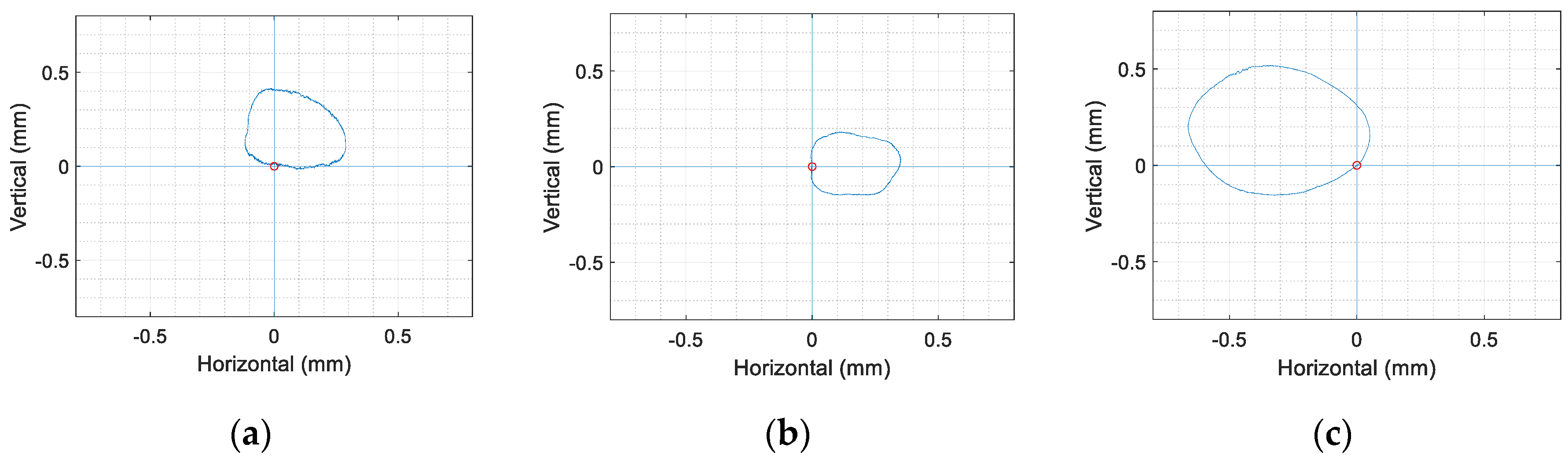
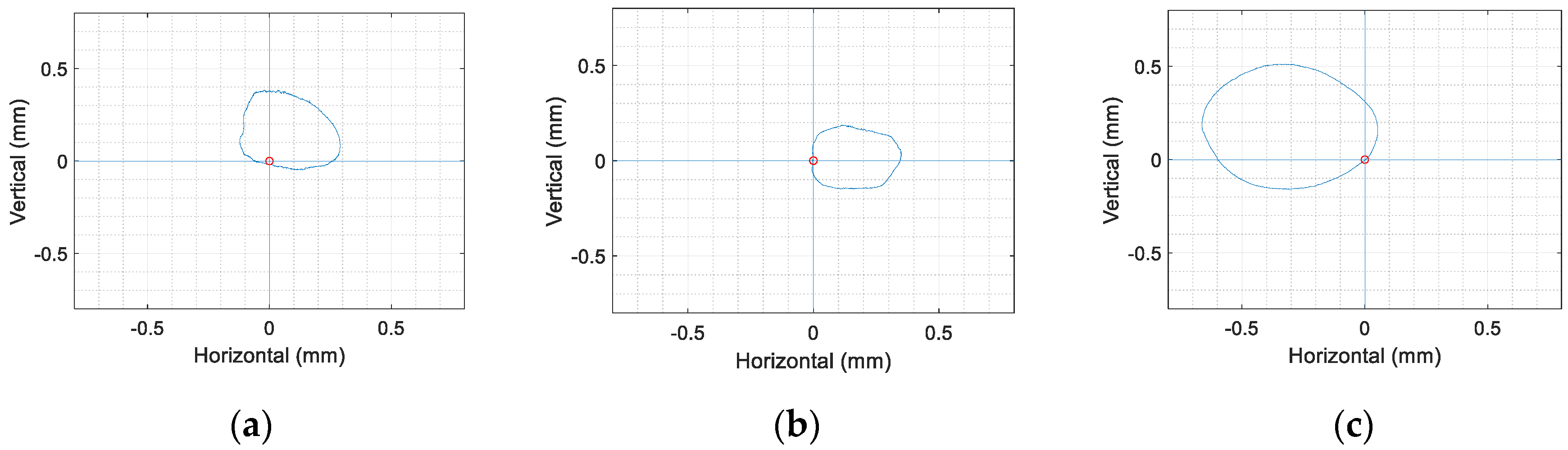
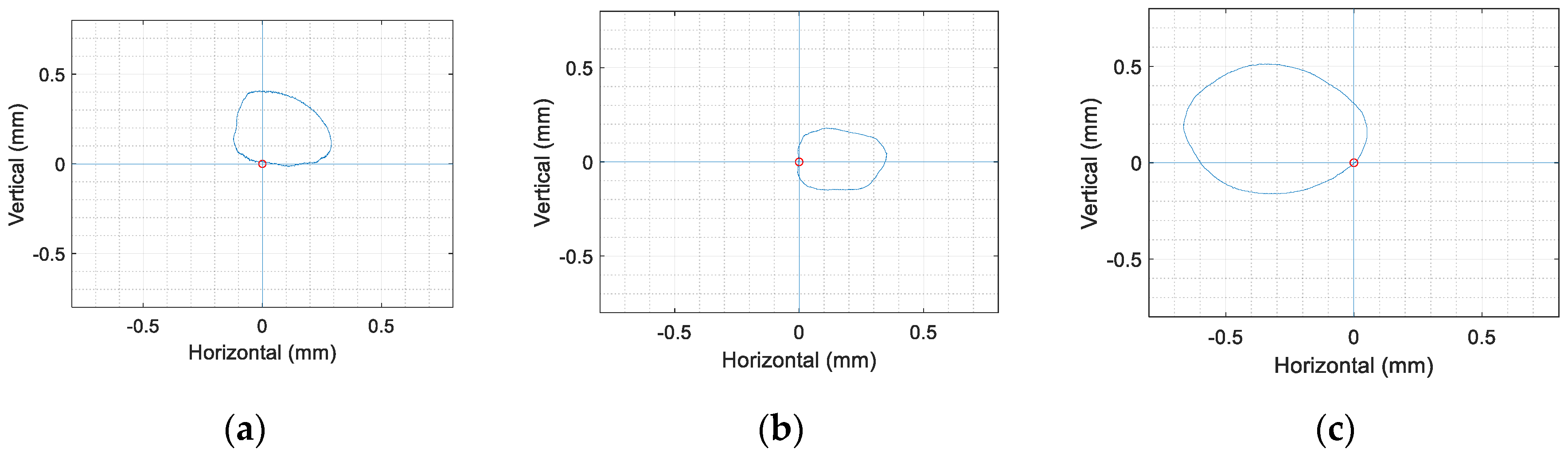
4.4. Measuring the Orbit, the Whirling of the Rotating Coil
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kang, W.; Deng, C.D.; Li, Q.; Li, L.; Chen, W.; Yin, B.G.; Zhou, J.X.; Sun, X.J.; Chen, F.S.; Shi, C.T. Research and Development of the AC Magnets for CSNS/RCS. IEEE Trans. Appl. Supercond. 2012, 22, 4001204. [Google Scholar] [CrossRef]
- Sunwong, P.; Boonwanna, S.; Chaichuay, P.; Klysubun, P.; Kwankasem, A.; Preecha, C. Design and fabrication of a combined function magnet prototype for Siam photon source. In Proceedings of the 9th international particle accelerator conference (IPAC2018), Vancouver, BC, Canada, 29 April–4 May 2018. [Google Scholar] [CrossRef]
- Petrone, C.; Nugteren, J.V.; Bajas, H.; Bottura, L.; Kirby, G.; Rossi, L.; Russenschuck, S. Measurement and Analysis of the Dynamic Effects in an HTS Dipole Magnet. IEEE Trans. Appl. Supercond. 2018, 28, 1–4. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.J.; Ni, G.L.; Chen, W.; Sun, X.J. Rotating coil magnetic measurement system and measurement results of quadrupole prototype for BEPCII storage ring. In Proceedings of the 2005 Particle Accelerator Conference (PAC), Knoxville, TN, USA, 16–20 May 2005; ISBN 0-7803-8859-3. [Google Scholar]
- Peng, Q.; Yin, B.; Zhou, J.; Wu, Y.; Brueck, H.; Stolper, M.; Shi, W. Harmonic coil design, Fabrication and commissioning for European XFEL linear accelerator superconducting magnets field measurement. IEEE Trans. Appl. Supercond. 2010, 20, 2015–2018. [Google Scholar] [CrossRef]
- Rogacki, P.; Fiscarelli, L.; Russenschuck, S.; Hameyer, K. Development of a rotating-coil scanner for superconducting accelerator magnets. J. Sens. Sens. Syst. 2020, 9, 99–107. [Google Scholar] [CrossRef]
- Arpaia, P.; Bottura, L.; Cimmino, P.; Giloteaux, D.; Masi, A.; Perez, J.G.; Spiezia, G.; Walckiers, L. A fast-digital integrator for magnetic field measurements at Cern. In Proceedings of the 2006 IEEE Instrumentation and Measurement Technology Conference, Sorrento, Italy, 24–27 April 2006; ISBN 0-7803-9359-7. [Google Scholar]
- Li, L.; Kang, W.; Wang, Z.; Li, S.; Zhang, S.; Yin, B.; Zhou, J.; Shi, C. Magnetic Field Measurement of the Quadrupole and sextupole magnets for HLS-II storage ring. IEEE Trans. Appl. Supercond. 2014, 24, 1–4. [Google Scholar] [CrossRef]
- DiMarco, J.; Chlachidze, G.; Makulski, G.; Makulski, A.; Orris, D.; Tartaglia, M.; Tompkins, J.C.; Velev, G.V.; Wang, X. Application of PCB and FDM technologies to magnetic measurement probe system development. IEEE Trans. Appl. Supercond. 2012, 23, 9000505. [Google Scholar] [CrossRef]
- Gunter, E. Understanding amplitude and phase in rotating machinery. In Proceedings of the Vibration Institute 33 Annual Meeting, Harrisburg, PA, USA, 23–27 June 2009. [Google Scholar]
- Xul, J.; Zheng, X.; Zhang, J.; Liu, X. Vibration characteristics of unbalance response for motorized spindle system. Procedia Eng. 2017, 174, 331–340. [Google Scholar] [CrossRef]
- Yamamoto, G.K.; Costa, C.; Sousa, J.S.S. A smart experimental setup for vibration measurement and imbalance fault detection in rotating machinery. Case Stud. Mech. Syst. Signal Process. 2016, 4, 8–18. [Google Scholar] [CrossRef] [Green Version]
- Verma, A.K.; Sarangi, S.; Kolekar, M.K. Experimental investigation of misalignment effects on rotor shaft vibration and on stator current signature. J. Fail. Anal. Preven. 2014, 14, 125–138. [Google Scholar] [CrossRef]
- Hariharan, V.; Srinivasan, P.S.S. Vibration analysis of misaligned shaft-ball bearing system. Indian J. Sci. Technol. 2009, 2, 45–50. [Google Scholar] [CrossRef]
- Kumar, P.; Prabhat, P.K.; Kumar, M.; Choudhary, S.D. Speed control of dc motor using PID smart controller. Int. J. Eng. Res. 2014, 5, 1044–1053. [Google Scholar]
- Ni, S.A.; Mathew, L.; Chatterji, S. Comparative analysis of speed control of dc motor using AI technique. Int. J. Eng. Res. Appl. 2013, 3, 1137–1146. [Google Scholar]
- Othman, K.A.; Kamal, M.M.; Mamat, N.; Yati, N. System identification of discrete model for DC motor positioning. In Proceedings of the 8th WSEAS International Conference on Circuits, systems, electronics, control & signal processing (CSECS), Puerto De La Cruz, Canary Islands, Spain, 14–16 December 2009; pp. 212–216, ISBN 978-960-474-139-7. [Google Scholar]
- Tang, W.J.; Liu, Z.T.; Wnag, Q. DC motor speed control based on system identification and PID auto tuning. In Proceedings of the 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; ISBN 978-988-15639-3-4. [Google Scholar]
- Arpaia, P.; Buzio, M.; Golluccio, G.; Walckiers, L. In situ calibration of rotating sensor coils for magnet testing. Rev. Sci. Instrum. 2012, 83, 013306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arpaia, P.; Buzio, M.; Köster, O.; Russenschuck, S.; Severino, G. Rotating-coil calibration in a reference quadrupole, considering roll-angle misalignment and higher-order harmonics. Measurement 2016, 87, 74–82. [Google Scholar] [CrossRef] [Green Version]
- Arpaia, P.; Bottura, L.; Fiscarelli, L.; Walckiers, L. Performance of a fast-digital integrator in on-file magnetic measurements for particle accelerators. Rev. Sci. Instrum. 2012, 83, 024702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arpaia, P.; Buzio, M.; Golluccio, G.; Walckiers, L. A polyvalent harmonic coil testing method for small-aperture magnets. Rev. Sci. Instrum. 2012, 83, 085116. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.X.; Zhou, H.; Guo, X.P.; Yan, Y. Rotor Fault Diagnosis and Simulation Based on LabVIEW. Res. J. Appl. Sci. 2013, 19, 3670–3674. [Google Scholar] [CrossRef]
- Costa, C.D.; Gama, R.S.D.; Nascimento, C.E.; Brandao, I.M.; Medeiros, E.C.D.; Mathias, M.H. Orbit analysis for imbalance fault detection in rotating machinery. J. Electr. Electron. Eng. 2018, 13, 43–45. [Google Scholar]
- Monte, M.; Verbelen, F.; Vervisch, B. The use of orbitals and full spectra to identify misalignment. In Structural Health Monitoring; Springer: Cham, Switzerland, 2014; Volume 5, pp. 215–222. ISBN 978-3-319-04570-2. [Google Scholar]
- Professional Plastics. Available online: https://professionalplastics.com/G-10FR4ROD (accessed on 12 November 2020).






| Parameter | Value |
|---|---|
| RA | 3.2715 |
| LA | 2.0487 H |
| JA | 14.7729 kg⋅m2 |
| KT | 9.6361 × 10−3 N⋅m/A |
| KB | 7.0103 × 10−2 kg⋅m2 |
| b | 5.8634 N⋅m/rad/s |
| Controller | Kp | Ki |
|---|---|---|
| Gain | 0.00697 | 0.03100 |
| Motor Speed Control | |||
|---|---|---|---|
| Speed (RPM) | 60 | 90 | 120 |
| Minimum value | 56.97 | 85.73 | 116.67 |
| Maximum value | 63.19 | 93.46 | 122.22 |
| % Error | 5.53 | 4.40 | 2.79 |
| Speed (RPM) | The Current Supplied to the Magnetic Coil | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Current 5 A | Current 10 A | Current 15 A | ||||||||||
| 1X | 2X | 3X | 4X | 1X | 2X | 3X | 4X | 1X | 2X | 3X | 4X | |
| 60 | 1.973 | - | 0.0187 | - | 2.959 | - | 0.0273 | - | 3.594 | - | 0.0447 | - |
| 90 | 3.888 | - | 0.0589 | - | 6.147 | - | 0.0672 | - | 7.936 | - | 0.1297 | - |
| 120 | 4.050 | - | 0.1081 | - | 8.229 | - | 0.1290 | - | 11.360 | - | 0.1303 | - |
| Speed (RPM) | Driver End (DE) | Center | Non-Driver End (NDE) | |||
|---|---|---|---|---|---|---|
| Vertical (mm) | Horizontal (mm) | Vertical (mm) | Horizontal (mm) | Vertical (mm) | Horizontal (mm) | |
| 60 | 0.45102 | 0.41182 | 0.33640 | 0.36045 | 0.67548 | 0.71642 |
| 90 | 0.43618 | 0.41610 | 0.34074 | 0.35740 | 0.68422 | 0.71754 |
| 120 | 0.43747 | 0.41229 | 0.34025 | 0.36174 | 0.68325 | 0.71866 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Odngam, S.; Preecha, C.; Sanwong, P.; Thongtan, W.; Srisertpol, J. Precision Analysis and Design of Rotating Coil Magnetic Measurements System. Appl. Sci. 2020, 10, 8454. https://doi.org/10.3390/app10238454
Odngam S, Preecha C, Sanwong P, Thongtan W, Srisertpol J. Precision Analysis and Design of Rotating Coil Magnetic Measurements System. Applied Sciences. 2020; 10(23):8454. https://doi.org/10.3390/app10238454
Chicago/Turabian StyleOdngam, Soontorn, Chaiyut Preecha, Prapaiwan Sanwong, Woramet Thongtan, and Jiraphon Srisertpol. 2020. "Precision Analysis and Design of Rotating Coil Magnetic Measurements System" Applied Sciences 10, no. 23: 8454. https://doi.org/10.3390/app10238454
APA StyleOdngam, S., Preecha, C., Sanwong, P., Thongtan, W., & Srisertpol, J. (2020). Precision Analysis and Design of Rotating Coil Magnetic Measurements System. Applied Sciences, 10(23), 8454. https://doi.org/10.3390/app10238454






