Early Warning Signals for Bearing Failure Using Detrended Fluctuation Analysis
Abstract
1. Introduction
2. Experimental Platform and Vibration Data Sets
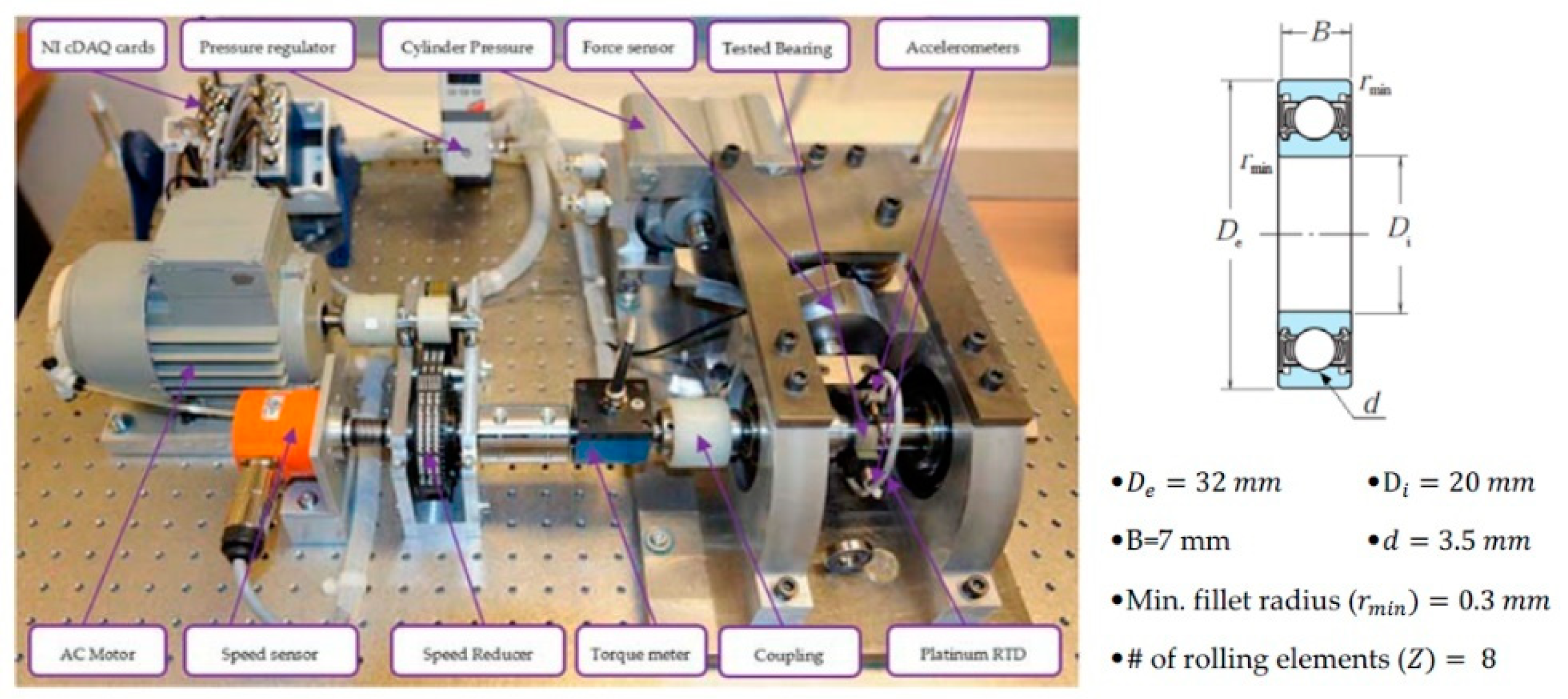
2.1. Experimental Configuration
- The rotating module: it is composed of an asynchronous motor, a primary shaft, a speed reducer (gearbox), and a secondary shaft with a speed sensor. The asynchronous motor has a rated power of 250 W and an output speed of 2830 rpm. The gearbox consists of two pulleys connected by a timing belt. The main function of the gearbox is maintaining the speed of the secondary shaft at less than 2000 rpm while delivering a rated torque.
- The loading module: this has a pneumatic jack that generates a force acting on a lever arm. Then, the lever arm amplifies this force and transmits it as a radial force to the ball bearing under test. Adjusting the lever arm can help create different loading conditions on the bearing.
- The measurement module: different types of sensors are used to measure the radial force applied on the bearing, the rotation speed of the secondary shaft holding the bearing, and the torque delivered to the bearing. In addition, two high-frequency accelerometers (DYTRAN 3035B) are mounted perpendicularly to measure the horizontal and the vertical accelerations during the degradation test. In the measurement system, the temperature of the tested bearing is measured via one temperature sensor (PT100).
2.2. Vibration Data Sets
3. Materials and Methods
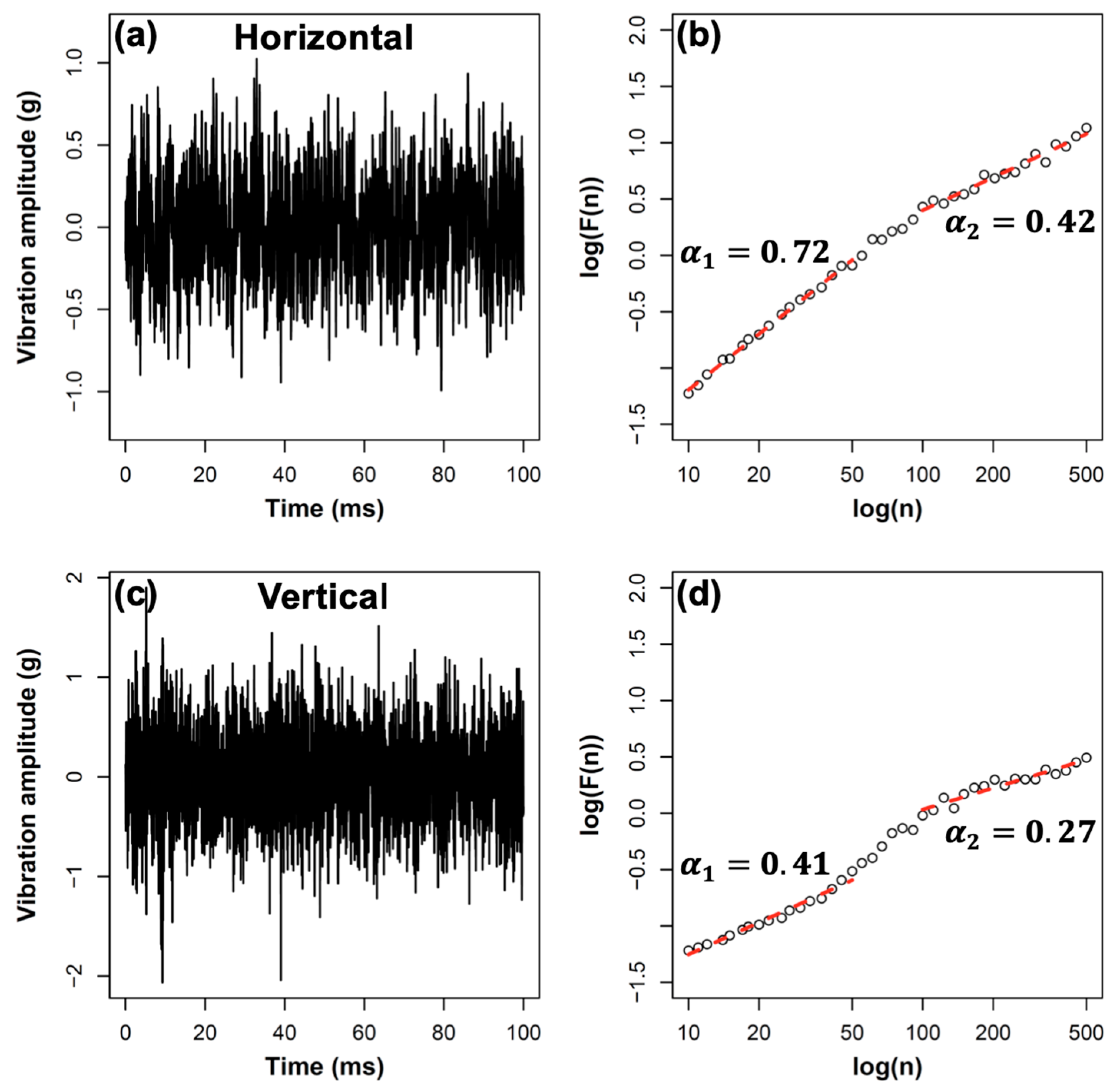
3.1. DFA Method
- Subtract the mean of the time series and compute the integrated time series, , as shown in Equation (1).
- Divide the integrated series into equally spaced boxes, . Inside each box, detrend the series segment by subtracting it from its best linear fit, . Repeat this step for different box sizes ().
- Compute the fluctuation function (), as shown in Equation (2), by finding the RMS value of the detrended time series:
- Plot the fluctuation function (F(n)) versus the box size (n) on log–log scale. The scaling exponent () represents the slope of the best linear fit.
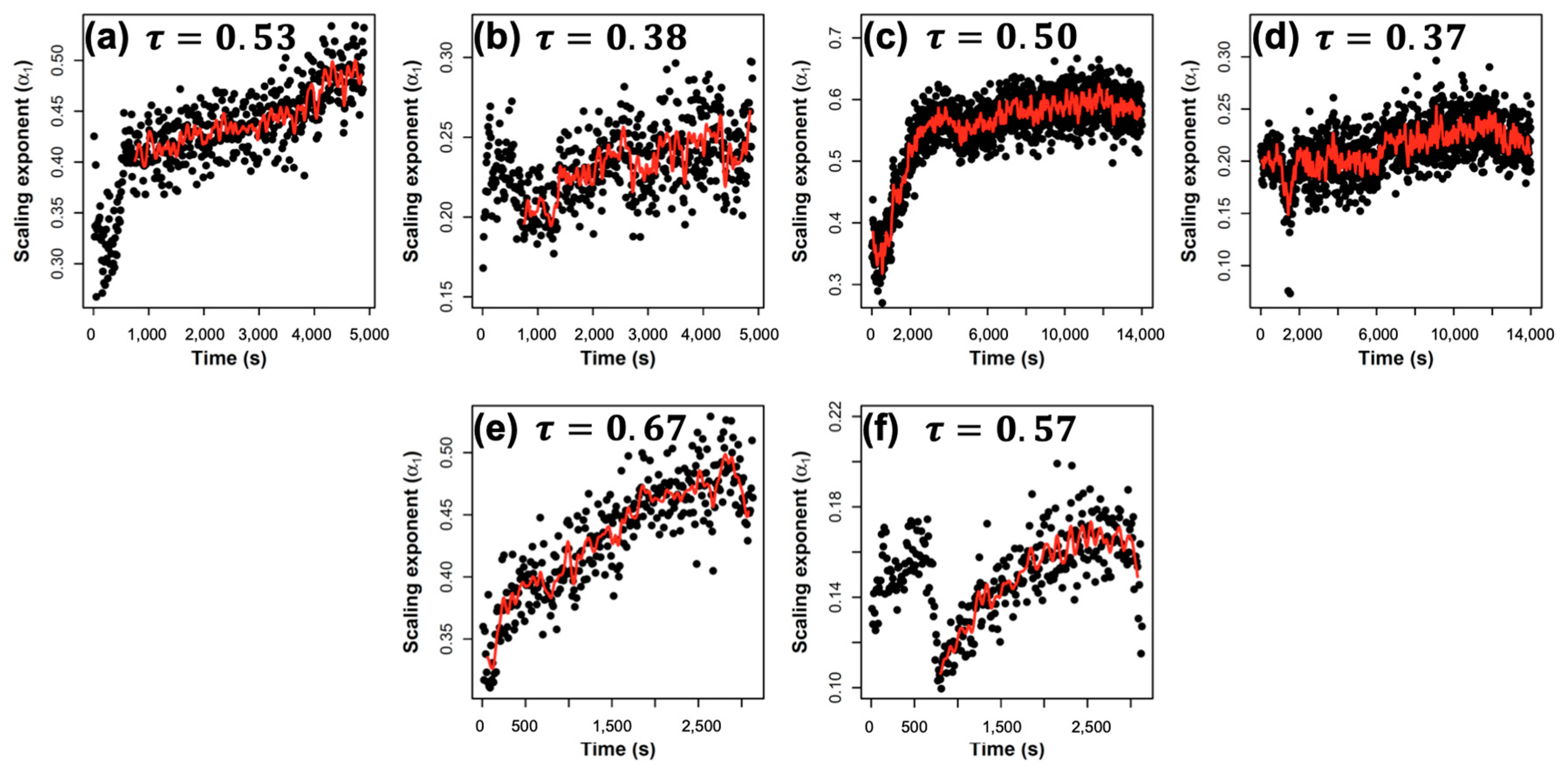
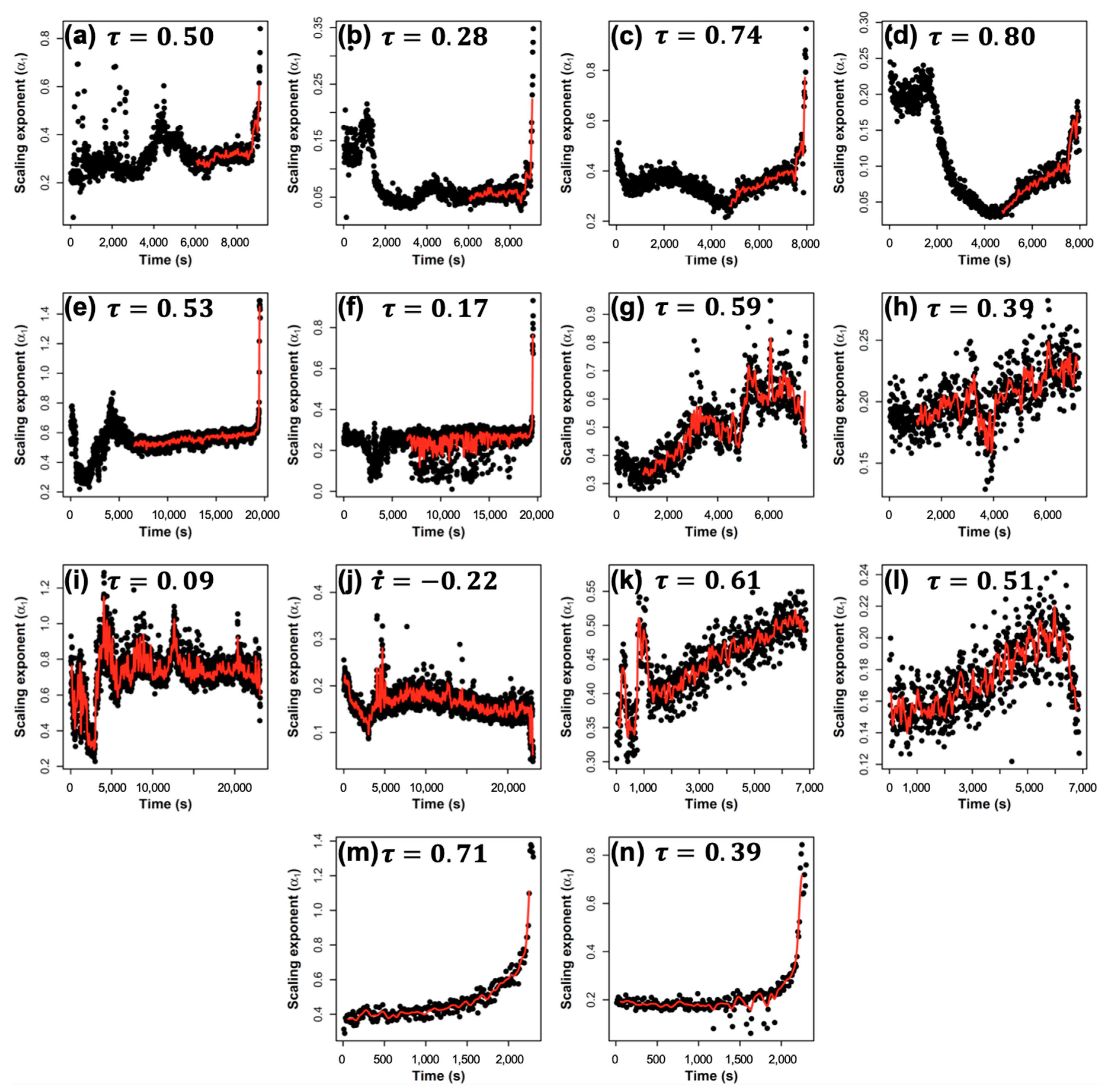
3.2. Kendall’s Tau Coefficient
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| DFA | Detrended fluctuation analysis |
| EWS | Early warning signal |
| REB | Rolling element bearing |
| PbM | Physics-based model |
| DDM | Data-driven model |
| RMS | Root mean square |
| RUL | Remaining useful life |
| SK | Spectral kurtosis |
| PF | Particle filter |
| VMD | Variational model decomposition |
| Diameter of the outer race | |
| Diameter of the inner race | |
| Number of rolling elements | |
| Diameter of rolling elements | |
| Minimum fillet radius | |
| B | Bearing width |
| Box size | |
| Integrated time series | |
| Best linear fit of time series inside a box of size n | |
| Fluctuation function | |
| Scaling exponent | |
| Short-range scaling exponent | |
| Long-range scaling exponent | |
| Kendall’s tau coefficient |
References
- Atamuradov, V.; Medjaher, K.; Camci, F.; Zerhouni, N.; Dersin, P.; Lamoureux, B. Machine health indicator construction framework for failure diagnostics and prognostics. J. Signal Process. Syst. 2020, 92, 591–609. [Google Scholar] [CrossRef]
- Rezamand, M.; Kordestani, M.; Carriveau, R.; Ting, D.S.-K.; Orchard, M.E.; Saif, M. Critical wind turbine components prognostics: A comprehensive review. IEEE Trans. Instrum. Meas. 2020, 69, 9306–9328. [Google Scholar] [CrossRef]
- Li, X.; Ding, Q.; Sun, J.-Q. Remaining useful life estimation in prognostics using deep convolution neural networks. Reliab. Eng. Syst. Saf. 2018, 172, 1–11. [Google Scholar] [CrossRef]
- Diez-Olivan, A.; del Ser, J.; Galar, D.; Sierra, B. Data fusion and machine learning for industrial prognosis: Trends and perspectives towards Industry 4.0. Inf. Fusion 2019, 50, 92–111. [Google Scholar] [CrossRef]
- Wang, J.; Wen, G.; Yang, S.; Liu, Y. Remaining useful life estimation in prognostics using deep bidirectional LSTM neural network. In Proceedings of the 2018 Prognostics and System Health Management Conference (PHM-Chongqing), Chongqing, China, 26–28 October 2018; pp. 1037–1042. [Google Scholar]
- Yadav, O.P.; Pahuja, G.L. Bearing health assessment using time domain analysis of vibration signal. Int. J. Image Graph. Signal Process. (IJIGSP) 2020, 12, 27–40. [Google Scholar]
- Wang, D.; Tsui, K.; Miao, Q. Prognostics and health management: A review of vibration based bearing and gear health indicators. IEEE Access 2018, 6, 665–676. [Google Scholar] [CrossRef]
- Bao, W.; Tu, X.; Hu, Y.; Li, F. Envelope spectrum L-Kurtosis and its application for fault detection of rolling element bearings. IEEE Trans. Instrum. Meas. 2020, 69, 1993–2002. [Google Scholar] [CrossRef]
- Bastami, A.R.; Bashari, A. Rolling element bearing diagnosis using spectral kurtosis based on optimized impulse response wavelet. J. Vib. Control 2019, 26, 175–185. [Google Scholar] [CrossRef]
- Medjaher, K.; Zerhouni, N.; Baklouti, J. Data-driven prognostics based on health indicator construction: Application to PRONOSTIA’s data. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 1451–1456. [Google Scholar]
- Li, N.; Lei, Y.; Lin, J.; Ding, S.X. An improved exponential model for predicting remaining useful life of rolling element bearings. IEEE Trans. Ind. Electron. 2015, 62, 7762–7773. [Google Scholar] [CrossRef]
- Wang, P.; Yan, R.; Gao, R.X. Multi-mode particle filter for bearing remaining life prediction. In Proceedings of the International Manufacturing Science and Engineering Conference, College Station, TX, USA, 18–22 June 2018. [Google Scholar]
- Ahmad, W.; Khan, S.; Kim, J.-M. A hybrid prognostics technique for rolling element bearings using adaptive predictive models. IEEE Trans. Ind. Electron. 2018, 65, 1577–1584. [Google Scholar] [CrossRef]
- Singleton, R.K.; Strangas, E.G.; Aviyente, S. Extended Kalman filtering for remaining-useful-life estimation of bearings. IEEE Trans. Ind. Electron. 2015, 62, 1781–1790. [Google Scholar] [CrossRef]
- Soualhi, A.; Medjaher, K.; Zerhouni, N. Bearing health monitoring based on Hilbert-Huang transform, support vector machine and regression. IEEE Trans. Instrum. Meas. 2015, 64, 52–62. [Google Scholar] [CrossRef]
- Hu, S.; Xiao, H.; Yi, C. A novel detrended fluctuation analysis method for gear fault diagnosis based on variational mode decomposition. Shock Vib. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, H.; Lv, Y.; Wang, T.; Xu, Z. Detrended fluctuation analysis and hough transform based self-adaptation double-scale feature extraction of gear vibration signals. Shock Vib. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Lin, J.; Chen, Q. A novel method for feature extraction using crossover characteristics of nonlinear data and its application to fault diagnosis of rotary machinery. Mech. Syst. Signal Process. 2014, 48, 174–187. [Google Scholar] [CrossRef]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Chebel-Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An experimental platform for bearings accelerated degradation tests. In Proceedings of the 2012 IEEE international conference on Prognostics and Health Management, Denver, CO, USA, 18–21 June 2012; pp. 1–8. [Google Scholar]
- Johns-Rahnejat, P.M.; Dolatabadi, N.; Rahnejat, H. Analytical elastostatic contact mechanics of highly-loaded contacts of varying conformity. Lubricants 2020, 8, 89. [Google Scholar] [CrossRef]
- Okamoto, Y.; Kitahara, K.; Ushijima, K.; Aoyama, S.; Xu, H.; Jones, G.J. A study for wear and fatigue on engine bearings by using EHL analysis. JSAE Rev. 2000, 21, 189–196. [Google Scholar] [CrossRef]
- Gabelli, A.; Morales-Espejel, G.E.; Ioannides, E. Particle damage in Hertzian contacts and life ratings of rolling bearings. Tribol. Trans. 2008, 51, 428–445. [Google Scholar] [CrossRef]
- Adamczak, S.; Zmarzły, P. Research of the influence of the 2D and 3D surface roughness parameters of bearing raceways on the vibration level. J. Phys. Conf. Ser. 2019, 1183, 1–10. [Google Scholar] [CrossRef]
- Adamczak, S.; Zmarzły, P. Influence of raceway waviness on the level of vibration in rolling-element bearings. Bull. Polish Acad. Sci. Tech. Sci. 2017, 65, 541–551. [Google Scholar] [CrossRef]
- Xia, H.; Tang, G.; Lan, Y. Long-range temporal correlations in kinetic roughening. J. Stat. Phys. 2020, 178, 800–813. [Google Scholar] [CrossRef]
- Martin-Montoya, L.A.; Aranda-Camachob, N.M.; Quimbay, C.J. Long-range correlations and trends in Colombian seismic time series. Phys. A Stat. Mech. Appl. 2015, 421, 124–133. [Google Scholar] [CrossRef]
- Shalalfeh, L.; Bogdan, P.; Jonckheere, E. Evidence of long-range dependence in power grid. In Proceedings of the IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Mariani, M.C.; Asante, P.; Bhuiyan, M.A.M.; Beccar-Varela, M.P.; Sebastian, J.; Tweneboah, O.K. Long-range correlations and characterization of financial and volcanic time series. Mathematics 2020, 8, 441. [Google Scholar] [CrossRef]
- Nakata, A.; Kaneko, M.; Evans, N.; Shigematsu, T.; Kiyono, K. Long-range cross-correlation between heart rate and physical activity in daily life. In Proceedings of the 11th Conference of the European Study Group on Cardiovascular Oscillations (ESGCO), Pisa, Italy, 15 July 2020; pp. 1–2. [Google Scholar]
- Peng, C.-K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef]
- Gao, R.; Yan, R. Non-stationary signal processing for bearing health monitoring. Int. J. Manuf. Res. 2006, 1, 18–40. [Google Scholar] [CrossRef]
- Hu, K.; Ivanov, P.; Chen, Z.; Carpena, P.; Stanley, H. Effect of Trends on Detrended Fluctuation Analysis. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2001, 64, 011114. [Google Scholar] [CrossRef]
- Nes, E.; Scheffer, M. Slow Recovery from Perturbations as a Generic Indicator of a Nearby Catastrophic Shift. Am. Nat. 2007, 169, 738–747. [Google Scholar]
- Held, H.; Kleinen, T. Detection of climate system bifurcations by degenerate fingerprinting. Geophys. Res. Lett. 2004, 31, L23207. [Google Scholar] [CrossRef]
- Shalalfeh, L.; Bogdan, P.; Jonckheere, E. Kendall’s tau of frequency Hurst exponent as blackout proximity Margin. In Proceedings of the 2016 IEEE International Conference on Smart Grid Communications (SmartGridComm), Sydney, Australia, 6–9 November 2016; pp. 466–471. [Google Scholar]






| Characteristics | Value |
|---|---|
| Bearing type | NSK 6804DD |
| Basic dynamic load rating (N) | 4000 |
| Basic static load rating (N) | 2470 |
| Limiting speed (rpm) | 13,000 |
| Sealant | rubber sealed (DD) |
| Inner/outer ring material | steel |
| Lubricant | grease |
| Operating Conditions | |||
|---|---|---|---|
| Condition 1 | Condition 2 | Condition 3 | |
| Synchronous motor rated power (W) | 250 | 250 | 250 |
| Running speed of synchronous motor (rpm) | 2830 | 2830 | 2830 |
| Applied torque (primary shaft) (N.m.) | 0.843 | 0.843 | 0.843 |
| Running speed of secondary shaft (rpm) | 1800 | 1650 | 1500 |
| Transferred torque (secondary shaft) (N.m.) | 1.326 | 1.447 | 1.591 |
| Bearing running speed (rpm) | 1800 | 1650 | 1500 |
| Radial load (N) | 4000 | 4200 | 5000 |
| Data sets | Bearing 1_1 | Bearing 2_1 | Bearing 3_1 |
| Bearing 1_2 | Bearing 2_2 | Bearing 3_2 | |
| Bearing 1_3 | Bearing 2_3 | Bearing 3_3 | |
| Bearing 1_4 | Bearing 2_4 | ||
| Bearing 1_5 | Bearing 2_5 | ||
| Bearing 1_6 | Bearing 2_6 | ||
| Bearing 1_7 | Bearing 2_7 | ||
| Axis | Scaling Exponent | 0–5000 s | 5000–10,000 s | 10,000–15,000 s | 15,000–20,000 s | 20,000–25,000 s | 25,000–28,000 s |
|---|---|---|---|---|---|---|---|
| H | 0.43 ± 0.10 | 0.74 ± 0.08 | 0.90 ± 0.07 | 1.02 ± 0.04 | 1.01 ± 0.05 | 0.98 ± 0.09 | |
| 0.63 ± 0.11 | 0.45 ± 0.08 | 0.40 ± 0.11 | 0.32 ± 0.09 | 0.32 ± 0.09 | 0.27 ± 0.10 | ||
| V | 0.18 ± 0.03 | 0.29 ± 0.04 | 0.40 ± 0.15 | 0.45 ± 0.04 | 0.59 ± 0.07 | 0.47 ± 0.11 | |
| 0.45 ± 0.09 | 0.45 ± 0.06 | 0.36 ± 0.08 | 0.25 ± 0.05 | 0.24 ± 0.06 | 0.23 ± 0.08 |
| Data Set | Axis | Range 1 | Range 2 | ||
|---|---|---|---|---|---|
| 1_1 | Horizontal | 10–50 | 100–500 | ||
| Vertical | 10–50 | 100–500 | |||
| 1_2 | Horizontal | 10–25 | 100–500 | ||
| Vertical | 10–50 | 100–500 | |||
| 1_3 | Horizontal | 10–25 | 100–500 | ||
| Vertical | 10–50 | 100–500 | |||
| 1_4 | Horizontal | 10–25 | 100–500 | ||
| Vertical | 10–50 | 100–500 | |||
| 1_5 | Horizontal | 10–25 | 100–500 | ||
| Vertical | 10–50 | 100–500 | |||
| 1_6 | Horizontal | 10–25 | 100–500 | ||
| Vertical | 10–50 | 100–500 | |||
| 1_7 | Horizontal | 10–25 | 100–500 | ||
| Vertical | 10–50 | 100–500 | |||
| 2_1 | Horizontal | 10–50 | 100–500 | ||
| Vertical | 10–50 | 100–500 | |||
| 2_2 | Horizontal | 10–50 | 100–500 | ||
| Vertical | 10–50 | 100–500 | |||
| 2_3 | Horizontal | 10–50 | 100–500 | ||
| Vertical | 10–50 | 100–500 | |||
| 2_4 | Horizontal | 10–50 | 100–500 | ||
| Vertical | 10–50 | 200–500 | |||
| 2_5 | Horizontal | 10–50 | 100–500 | ||
| Vertical | 10–50 | −0.22 | 200–500 | ||
| 2_6 | Horizontal | 10–50 | 100–500 | ||
| Vertical | 10–50 | 200–500 | |||
| 2_7 | Horizontal | 10–50 | 100–500 | ||
| Vertical | 10–50 | 100–500 | |||
| 3_1 | Horizontal | 10–50 | 100–500 | ||
| Vertical | 10–50 | 100–500 | |||
| 3_2 | Horizontal | 10–50 | 100–500 | ||
| Vertical | 10–50 | 100–500 | |||
| 3_3 | Horizontal | 10–50 | 100–500 | ||
| Vertical | 10–50 | 100–500 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shalalfeh, L.; AlShalalfeh, A. Early Warning Signals for Bearing Failure Using Detrended Fluctuation Analysis. Appl. Sci. 2020, 10, 8489. https://doi.org/10.3390/app10238489
Shalalfeh L, AlShalalfeh A. Early Warning Signals for Bearing Failure Using Detrended Fluctuation Analysis. Applied Sciences. 2020; 10(23):8489. https://doi.org/10.3390/app10238489
Chicago/Turabian StyleShalalfeh, Laith, and Ashraf AlShalalfeh. 2020. "Early Warning Signals for Bearing Failure Using Detrended Fluctuation Analysis" Applied Sciences 10, no. 23: 8489. https://doi.org/10.3390/app10238489
APA StyleShalalfeh, L., & AlShalalfeh, A. (2020). Early Warning Signals for Bearing Failure Using Detrended Fluctuation Analysis. Applied Sciences, 10(23), 8489. https://doi.org/10.3390/app10238489





