Crack Detection and Crack Length Measurement with the DC Potential Drop Method–Possibilities, Challenges and New Developments
Abstract
:1. Introduction
2. Crack Length Measurement with the DC-Potential Drop Method
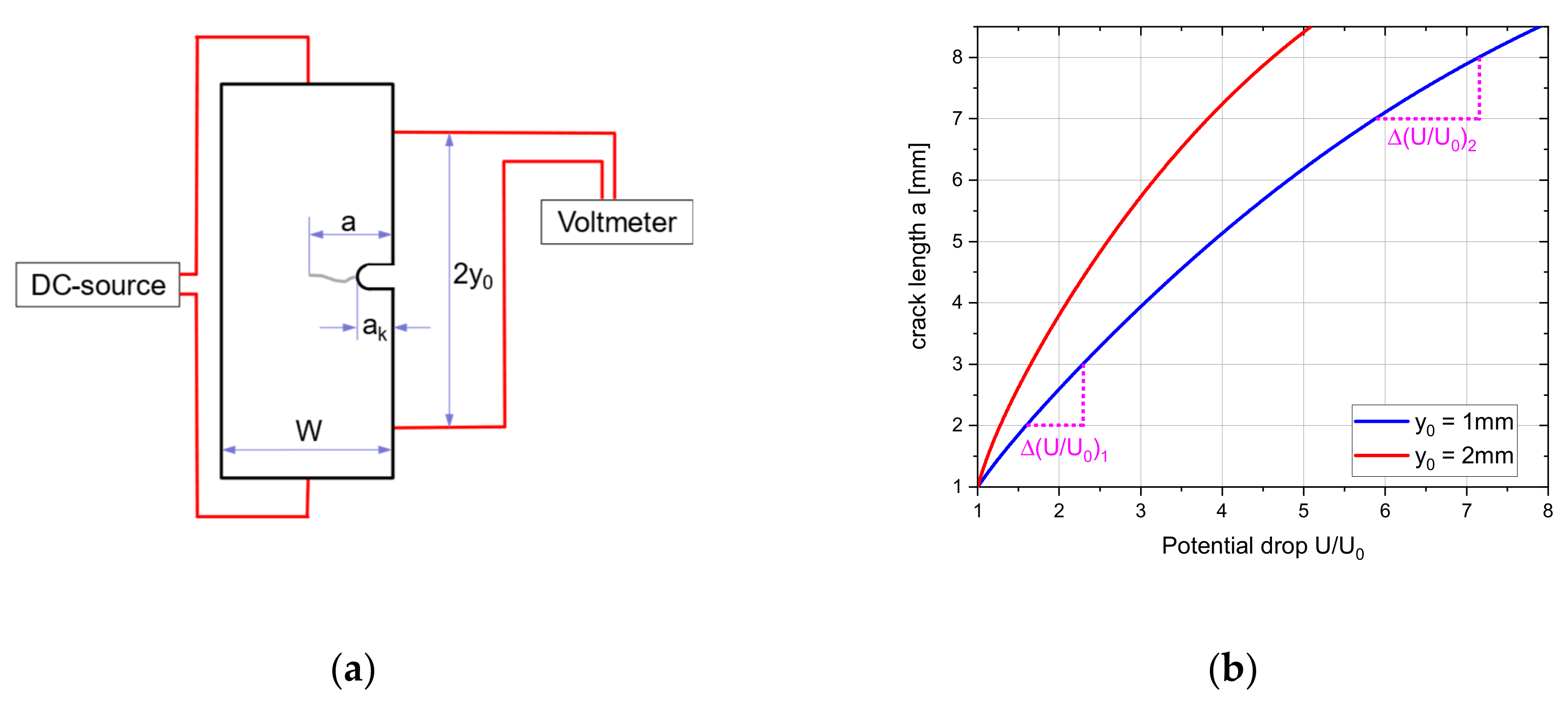
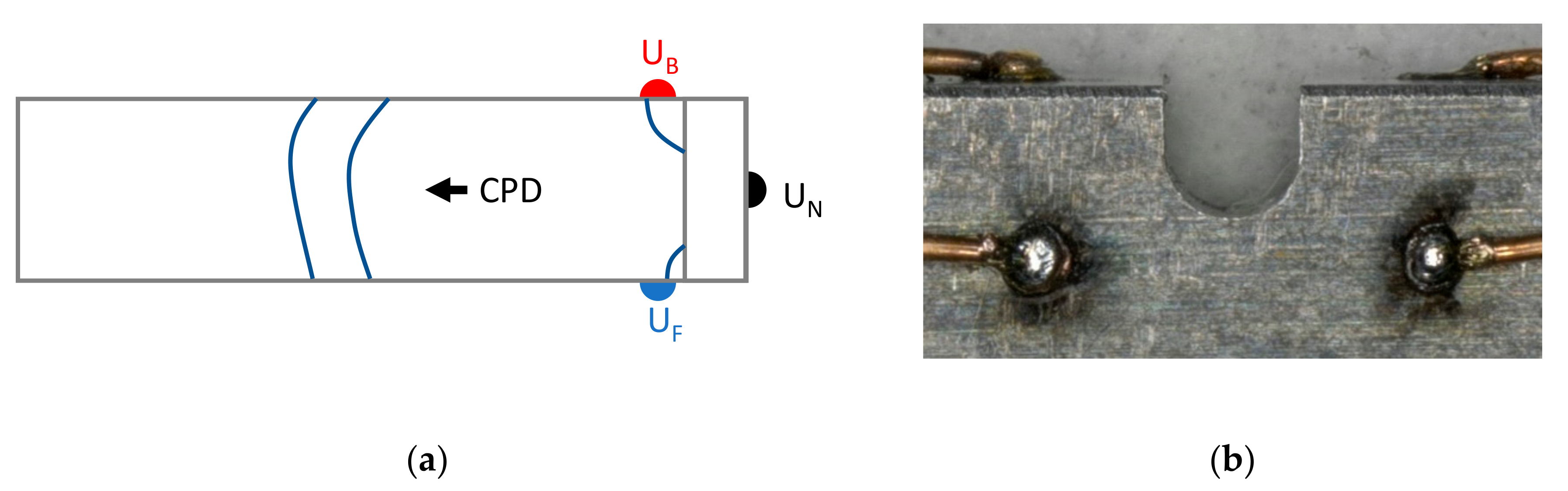
2.1. Experimental Setup
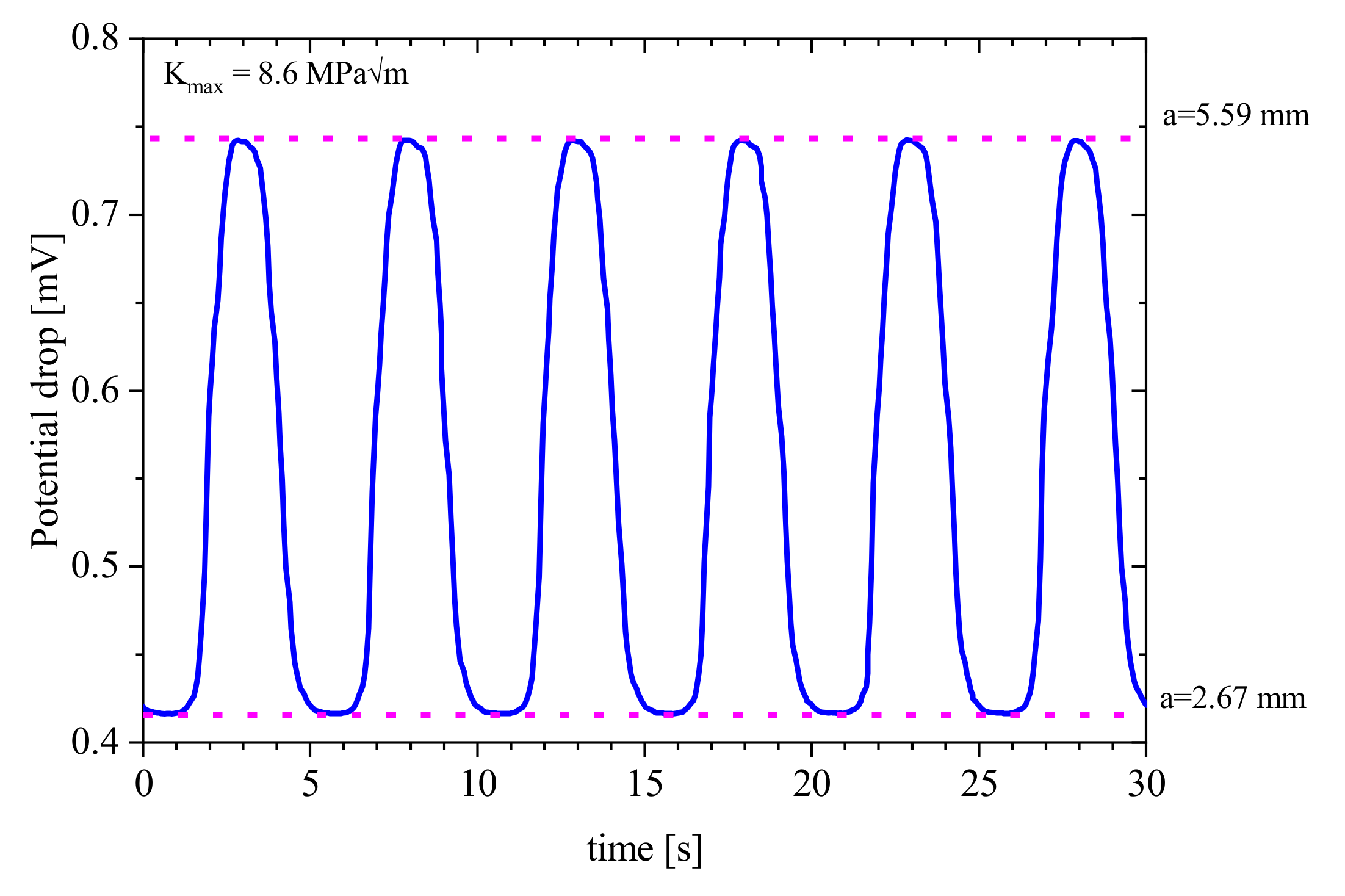
2.2. Calibration of the Crack Length Measurement
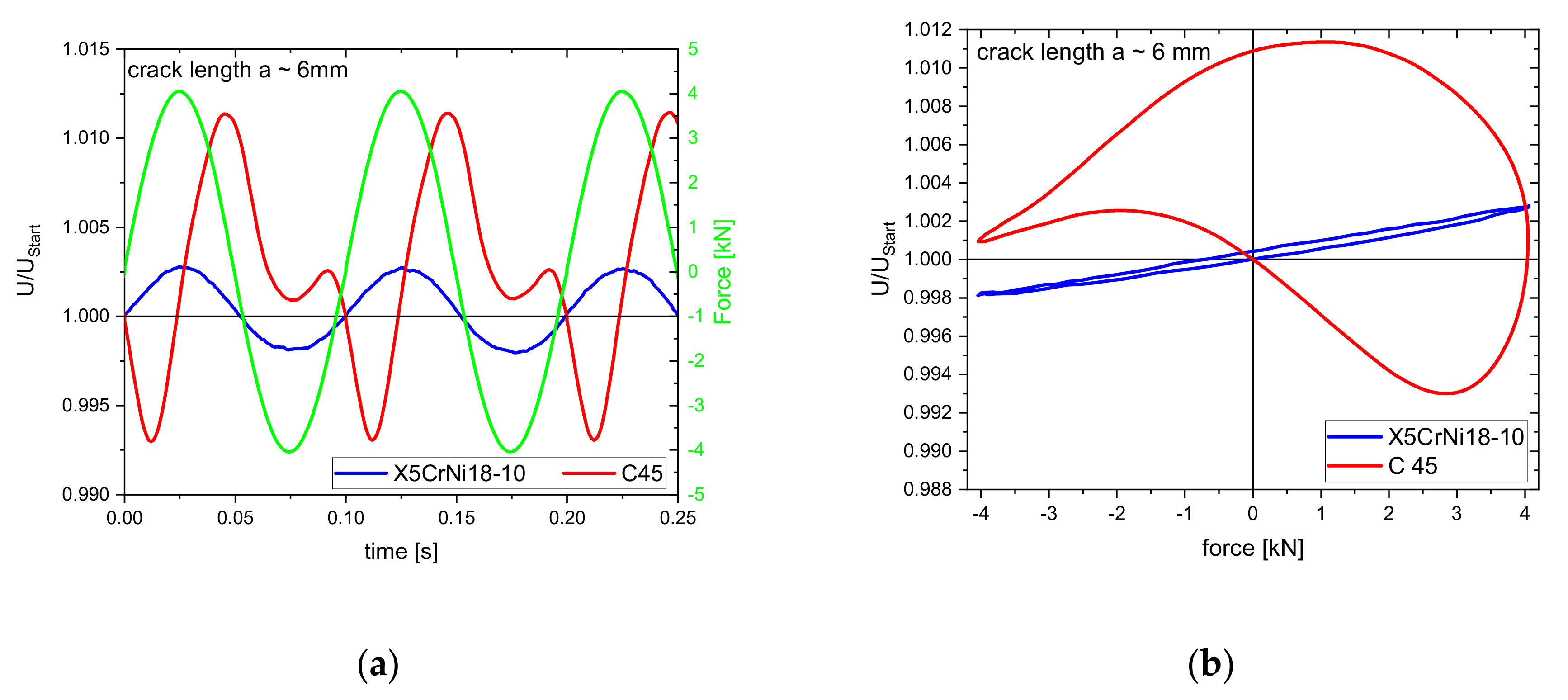
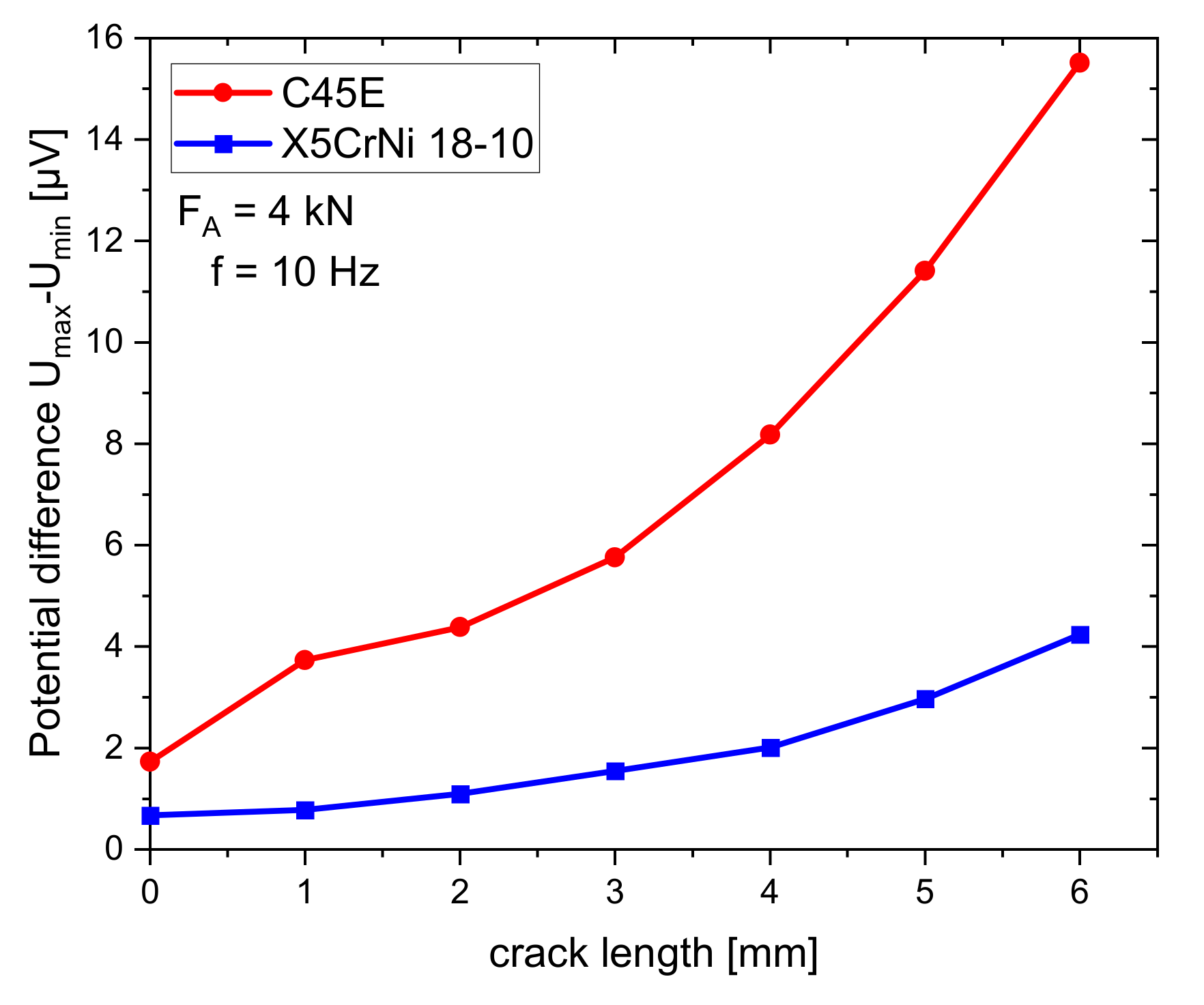
2.3. Influence of Temperature and Atmosphere
2.4. Investigation of Ferromagnetic Alloys–The Villari Effect
3. Crack Detection and Crack Localization with Multiple PD Measurements
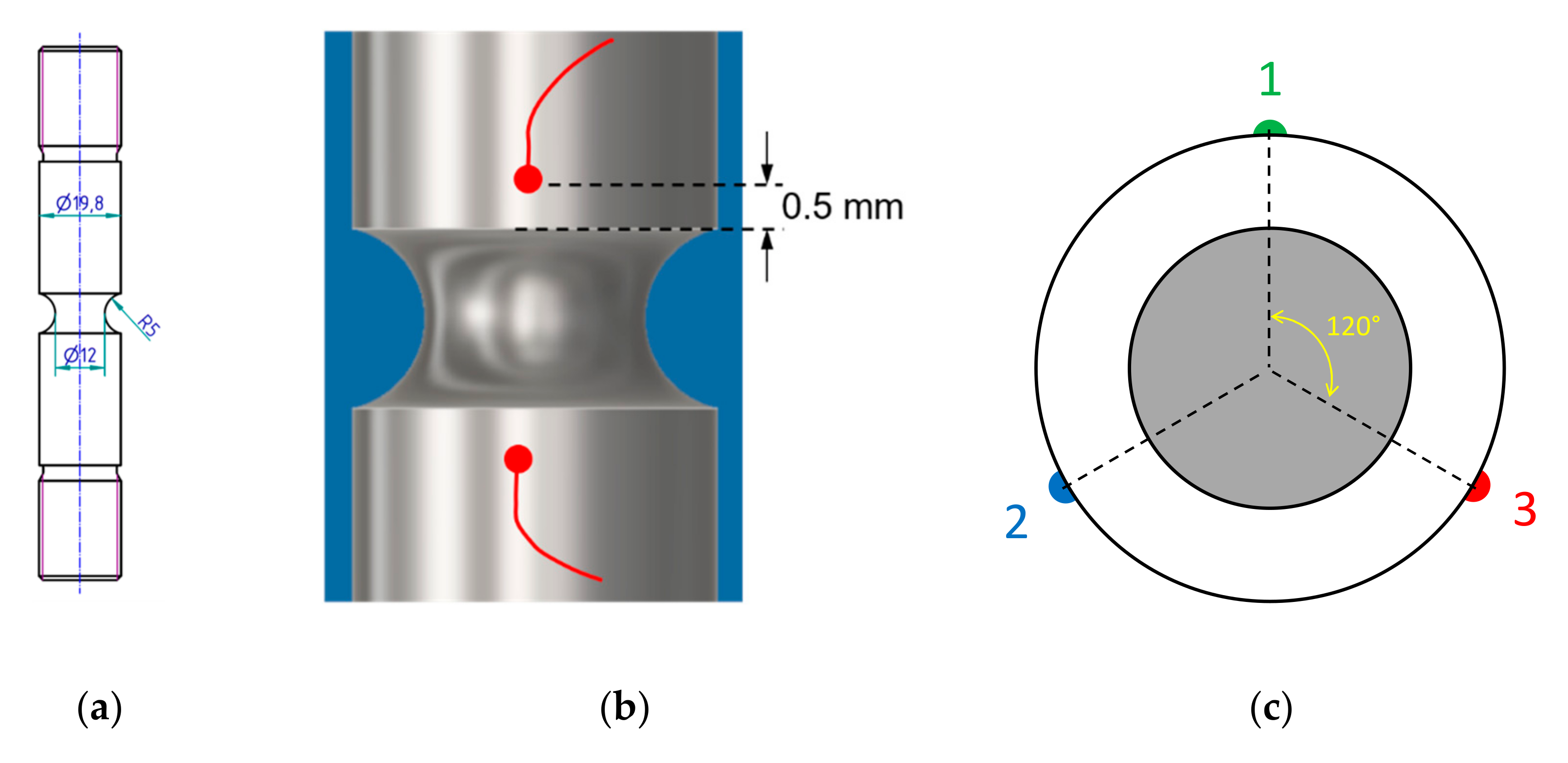
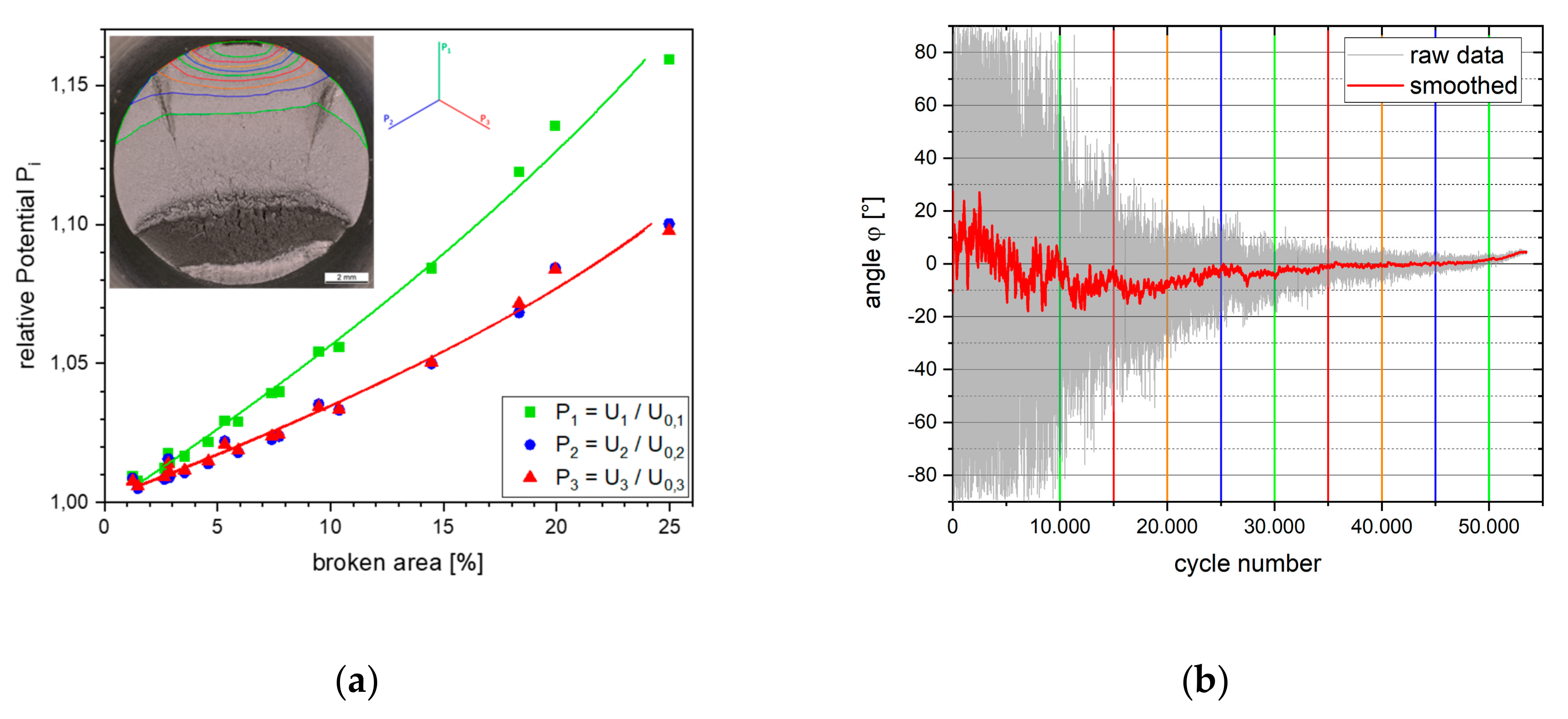
3.1. Crack Detection in Round Bars
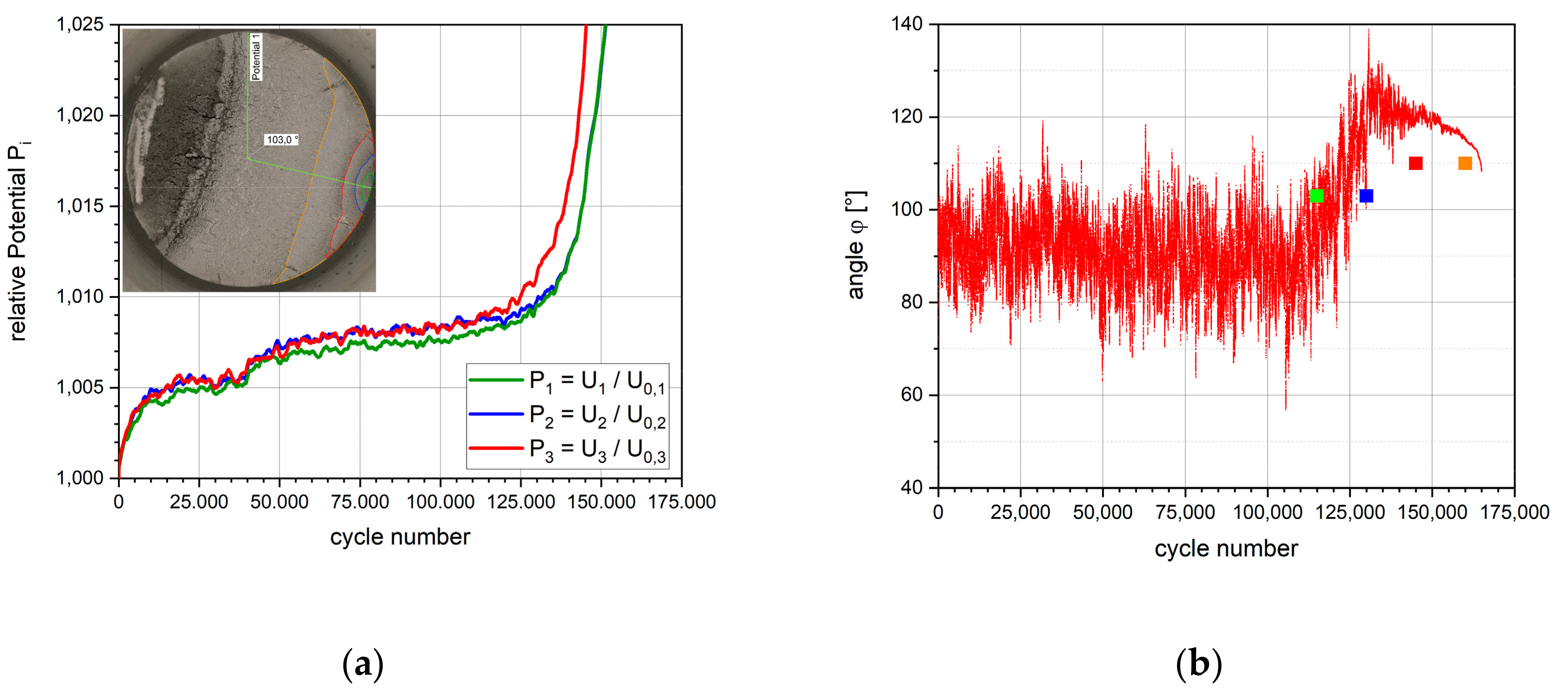
3.2. Crack Detection in Single Edge Notched Specimens
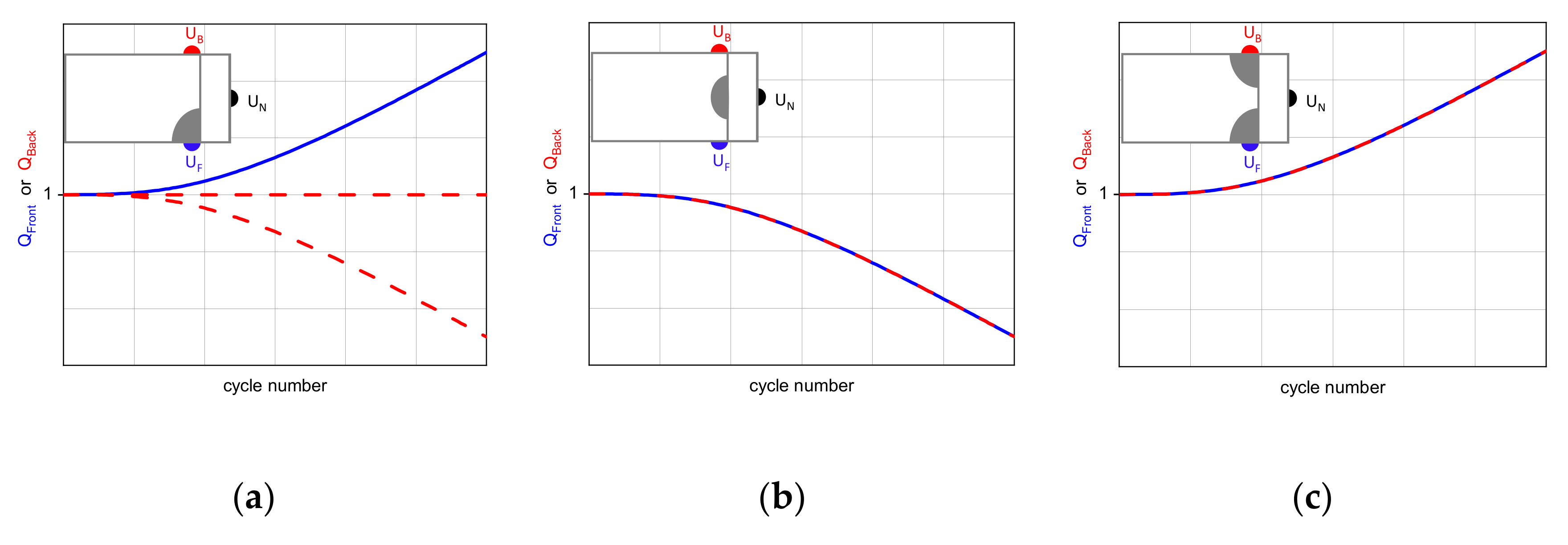
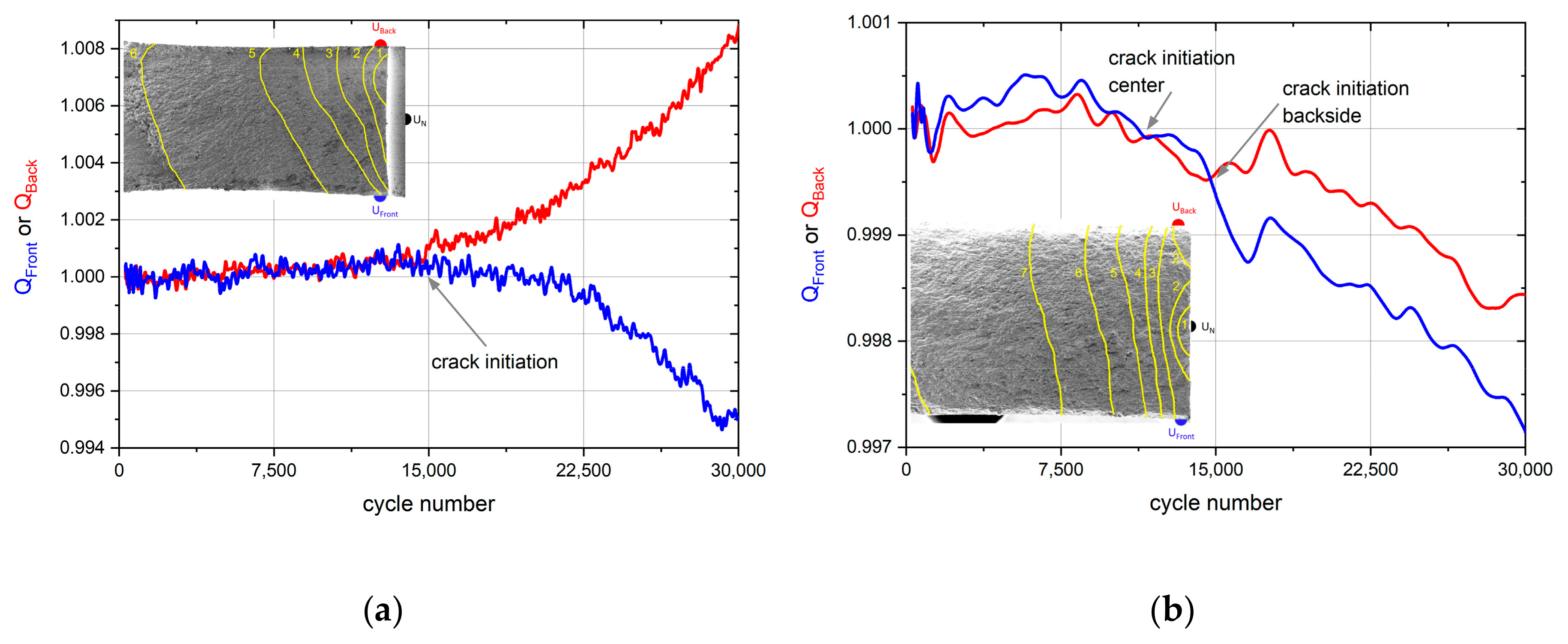
- Figure 11a: When a crack is initiated near the frontside (backside) QFront (QBack) increases while QBack (QFront) decreases or remains constant.
- Figure 11b: When a crack is initiated in the center of the notch root a decrease of both potential quotients takes place.
- Figure 11c: When cracks are initiated on the front and backside at the same time, both quotients are rising.
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Daneshpour, S.; Dyck, J.; Ventzke, V.; Huber, N. Crack retardation mechanism due to overload in base material and laser welds of Al alloys. Int. J. Fatigue 2012, 42, 95–103. [Google Scholar] [CrossRef] [Green Version]
- Mueller, I.; Rementeria, R.; Caballero, F.G.; Kuntz, M.; Sourmail, T.; Kerscher, E. A Constitutive Relationship between Fatigue Limit and Microstructure in Nanostructured Bainitic Steels. Materials 2016, 9, 831. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Middleton, C.A.; Gaio, A.; Greene, R.J.; Patterson, E.A. Towards Automated Tracking of Initiation and Propagation of Cracks in Aluminium Alloy Coupons Using Thermoelastic Stress Analysis. J. Nondestr. Eval. 2019, 38. [Google Scholar] [CrossRef] [Green Version]
- Sakagami, T.; Mizokami, Y.; Shiozawa, D.; Izumi, Y.; Moriyama, A. TSA based evaluation of fatigue crack propagation in steel bridge members. Procedia Struct. Integr. 2017, 5, 1370–1376. [Google Scholar] [CrossRef]
- Durif, E.; Réthoré, J.; Combescure, A.; Fregonese, M.; Chaudet, P. Controlling Stress Intensity Factors During a Fatigue Crack Propagation Using Digital Image Correlation and a Load Shedding Procedure. Exp. Mech. 2012, 52, 1021–1031. [Google Scholar] [CrossRef]
- E08 Committee. Test Method for Measurement of Fatigue Crack Growth Rates, 13a; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]
- Fleck, N.A. Fatigue Crack Measurement-Compliance methods for measurement of crack length. In Fatigue Crack Measurement: Techniques and Applications; Marsh, K.J., Ed.; Engineering Materials Advisory Services Ltd.: Warrington, UK, 1991. [Google Scholar]
- Johnson, H.H. Calibrating the Electric Potential Method for Studying Slow Crack Growth. Mater. Res. Stand. 1965, 5, 442–445. [Google Scholar]
- Ritchie, R.O.; Garrett, G.G.; Knott, J.F. Crack-Growth Monitoring: Optimisation of the Electrical Potential Method Using an Analogue Method. Int. J. Fract.Mech. 1971, 7, 462–467. [Google Scholar] [CrossRef]
- Aronson, G.H.; Ritchie, R.O. Optimization of the Electrical Potential Technique for Crack Growth Monitoring in Compact Test Pieces Using Finite Element Analysis. J. Test. Eval. 1979, 7, 208–215. [Google Scholar]
- Chretien, G.; Sarrazin-Baudoux, C.; Leost, L.; Hervier, Z. Near-threshold fatigue propagation of physically short and long cracks in Titanium alloy. Procedia Struct. Integr. 2016, 2, 950–957. [Google Scholar] [CrossRef]
- Bär, J.; Tiedemann, D. Experimental investigation of short crack growth at notches in 7475-T761. Procedia Struct. Integr. 2017, 5, 793–800. [Google Scholar] [CrossRef]
- Funk, M.; Bär, J. DCPD based detection of the transition from short to long crack propagation in fatigue experiments on the aluminum alloy 7475 T761. Procedia Struct. Integr. 2019, 17, 183–189. [Google Scholar] [CrossRef]
- Lambourg, A.; Henaff, G.; Nadot, Y.; Gourdin, S.; Pujol d’Andrebo, Q.; Pierret, S. Optimization of the DCPD technique for monitoring the crack propagation from notch root in localized plasticity. Int. J. Fatigue 2020, 130, 105228. [Google Scholar] [CrossRef]
- Černý, I. The use of DCPD method for measurement of growth of cracks in large components at normal and elevated temperatures. Eng. Fract. Mech. 2004, 71, 837–848. [Google Scholar] [CrossRef]
- Bär, J.; Volpp, T. Vollautomatische Experimente zur Ermüdungsrissausbreitung. Materialprüfung 2001, 43, 242–247. [Google Scholar]
- Tesch, A.; Pippan, R.; Döker, H. New testing procedure to determine da/dN–ΔK curves at different, constant R-values using one single specimen. Int. J. Fatigue 2007, 29, 1220–1228. [Google Scholar] [CrossRef]
- Moreno, B.; Zapatero, J.; Dominguez, J. An experimental analysis of fatigue crack growth under random loading. Int. J. Fatigue 2003, 25, 597–608. [Google Scholar] [CrossRef]
- Raja, M.K.; Mahadevan, S.; Rao, B.P.C.; Behera, S.P.; Jayakumar, T.; Raj, B. Influence of crack length on crack depth measurement by an alternating current potential drop technique. Meas. Sci. Technol. 2010, 21, 105702. [Google Scholar] [CrossRef]
- Bauschke, H.-M.; Schwalbe, K.-H. Measurement of the depth of surface cracks using the Direct Current Potential Drop Method. Mater. Werkst. 1985, 16, 156–165. [Google Scholar] [CrossRef]
- Meriaux, J.; Fouvry, S.; Kubiak, K.J.; Deyber, S. Characterization of crack nucleation in TA6V under fretting–fatigue loading using the potential drop technique. Int. J. Fatigue 2010, 32, 1658–1668. [Google Scholar] [CrossRef] [Green Version]
- Doremus, L.; Nadot, Y.; Henaff, G.; Mary, C.; Pierret, S. Calibration of the potential drop method for monitoring small crack growth from surface anomalies–Crack front marking technique and finite element simulations. Int. J. Fatigue 2015, 70, 178–185. [Google Scholar] [CrossRef]
- Hartweg, M.; Bär, J. Analysis of the crack location in notched steel bars with a multiple DC potential drop measurement. Procedia Struct. Integr. 2019, 17, 254–261. [Google Scholar] [CrossRef]
- Campagnolo, A.; Bär, J.; Meneghetti, G. Analysis of crack geometry and location in notched bars by means of a three-probe potential drop technique. Int. J. Fatigue 2019, 124, 167–187. [Google Scholar] [CrossRef]
- Gilbey, D.M.; Pearson, S. Measurement of the Length of a Central or Edge Crak in a Sheet of Metal by an Electrical Resistance Method, Royal Aircraft Establishment Technical Report No. 66402. 1966. Available online: http://resolver.tudelft.nl/uuid:bf6a128c-8834-49e1-9fec-f0d8ae935f41 (accessed on 27 November 2020).
- Campagnolo, A.; Meneghetti, G.; Berto, F.; Tanaka, K. Calibration of the potential drop method by means of electric FE analyses and experimental validation for a range of crack shapes. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 2272–2287. [Google Scholar] [CrossRef]
- Halliday, M.D.; Beevers, C.J. The d.c. Electrical Potential Method for Crack Length Measurement. In The Measurement of Crack Length and Shape during Fracture and Fatigue; Beevers, C.J., Ed.; Engineering Materials Advisory Services: Warley, West Midlands, UK, 1980; pp. 85–112. ISBN 0950682004. [Google Scholar]
- Hicks, M.A.; Pickard, A.C. A comparison of theoretical and experimental methods of calibrating the electrical potential drop technique for crack length determination. Int. J. Fract. 1982, 20, 91–101. [Google Scholar] [CrossRef]
- Austen, I.M. Measurement of Crack Length and Data Analysis in Corrosion Fatigue. In The Measurement of Crack Length and Shape during Fracture and Fatigue; Beevers, C.J., Ed.; Engineering Materials Advisory Services: Warley, West Midlands, UK, 1980; pp. 164–189. ISBN 0950682004. [Google Scholar]
- Druce, S.G.; Booth, G.S. The Effect of Errors in the Geometrie and Electrical Measurements on Crack Length Monitoring by the Potential Drop Technique. In The Measurement of Crack Length and Shape during Fracture and Fatigue; Beevers, C.J., Ed.; Engineering Materials Advisory Services: Warley, West Midlands, UK, 1980; pp. 136–163. ISBN 0950682004. [Google Scholar]
- Riemelmoser, F.O.; Pippan, R.; Weinhandl, H.; Kolednik, O. The Influence of Irregularities in the Crack Shape on the Crack Extension Measurement by Means of the Direct-Current-Potential-Drop Method. J. Test. Eval. 1999, 27, 42–46. [Google Scholar]
- Ljustell, P. Fatigue crack growth experiments on specimens subjected to monotonic large scale yielding. Eng. Fract. Mech. 2013, 110, 138–165. [Google Scholar] [CrossRef]
- Ljustell, P.; Alfredsson, B. Variable amplitude fatigue crack growth at monotonic large scale yielding experiments on stainless steel 316L. Eng. Fract. Mech. 2013, 109, 310–325. [Google Scholar] [CrossRef]
- Sposito, G. Advances in Potential Drop Techniques for Non-Destructive Testing. Ph.D. Thesis, Imperial College London, London, UK, January 2009. Available online: https://spiral.imperial.ac.uk/handle/10044/1/4373 (accessed on 27 November 2020).
- Hartman, G.A.; Johnson, D.A. D-C electric-potential method applied to thermal/mechanical fatigue crack growth. Exp. Mech. 1987, 27, 106–112. [Google Scholar] [CrossRef]
- Volpp, T. Einfluß der Atmosphäre auf das Rißausbreitungsverhalten partikelverstärkter Aluminiumlegierungen für den Einsatz in Luft- und Raumfahrt. Ph.D. Thesis, Universität der Bundeswehr München, Neubiberg, Germany, 1999. [Google Scholar]
- Davis, F.H.; Plumbridge, W.J. Magnetostriction Effects in Crack Length Measurements. Fatigue Fract. Eng. Mater. Struct. 1988, 11, 241–250. [Google Scholar] [CrossRef]
- Kaleta, J.; Zebracki, J. Application of the Villari Effect in a Fatigue Examination of Nickel. Fatigue Fract. Eng. Mater. Struct. 1996, 19, 1435–1443. [Google Scholar] [CrossRef]
- Bi, Y.; Jiles, D.C. Dependence of Magnetic Properties on Crack Size in Steels–Magnetics. IEEE Trans. Magn. 1998, 34, 2021–2023. [Google Scholar] [CrossRef]
- Verpoest, I.; Aernoudt, E.; Deruyttere, A.; Neyrinck, M. An Improved, A.C. Potential Drop Method for Detecting Surface Microcracks during Fatigue Tests of Unnotched Specimens. Fatigue Fract. Eng. Mater. Struct. 1981, 3, 203–217. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bär, J. Crack Detection and Crack Length Measurement with the DC Potential Drop Method–Possibilities, Challenges and New Developments. Appl. Sci. 2020, 10, 8559. https://doi.org/10.3390/app10238559
Bär J. Crack Detection and Crack Length Measurement with the DC Potential Drop Method–Possibilities, Challenges and New Developments. Applied Sciences. 2020; 10(23):8559. https://doi.org/10.3390/app10238559
Chicago/Turabian StyleBär, Jürgen. 2020. "Crack Detection and Crack Length Measurement with the DC Potential Drop Method–Possibilities, Challenges and New Developments" Applied Sciences 10, no. 23: 8559. https://doi.org/10.3390/app10238559
APA StyleBär, J. (2020). Crack Detection and Crack Length Measurement with the DC Potential Drop Method–Possibilities, Challenges and New Developments. Applied Sciences, 10(23), 8559. https://doi.org/10.3390/app10238559




